Kurtosis corrected sound pressure level as a noise metric for risk assessment of occupational noises

Abstract

Current noise guidelines use an energy-based noise metric to predict the risk of hearing loss, and thus ignore the effect of temporal characteristics of the noise. The practice is widely considered to underestimate the risk of a complex noise environment, where impulsive noises are embedded in a steady-state noise. A basic form for noise metrics is designed by combining the equivalent sound pressure level (SPL) and a temporal correction term defined as a function of kurtosis of the noise. Several noise metrics are developed by varying this basic form and evaluated utilizing existing chinchilla noise exposure data. It is shown that the kurtosis correction term significantly improves the correlation of the noise metric with the measured hearing losses in chinchillas. The average SPL of the frequency components of the noise that define the hearing loss with a kurtosis correction term is identified as the best noise metric among tested. One of the investigated metrics, the kurtosis-corrected A-weighted SPL, is applied to a human exposure study data as a preview of applying the metrics to human guidelines. The possibility of applying the noise metrics to human guidelines is discussed.

INTRODUCTION

Most noise guidelines currently in use such as International Standard Organization (ISO-1999, 1990) recommend safe levels of noise exposure based on the equal energy hypothesis (EEH). The EEH assumes that hearing loss is a function of only the total exposure energy, independent of the temporal characteristics of the noise (Robinson, 1968; Prince et al., 1997). The EEH based approach has been used to establish and implement noise guidelines because of its simplicity. However, the approach is generally considered appropriate for steady-state noise but not for complex noise, a steady-state noise embedded with impulsive noises (Ahroon et al., 1993). Some researchers have argued for the application of EEH in complex noise environments (Atherley and Martin, 1971; Guberan et al., 1971; Atherley, 1973), which however has largely been rebutted both by laboratory studies (Dunn et al., 1991; Hamernik and Qiu, 2001; Lei et al., 1994; Hamernik et al., 1974) and by epidemiological studies (Sulkowski and Lipowczan, 1982; Thiery and Meyer-Bisch, 1988).

The current guideline of National Institute for Occupational Safety and Health (NIOSH, 1998) suggests a 140-dB sound pressure level (SPL) limit should be used for impulsive noise, and the 85-dBA permissible exposure limit (PEL) with a 3-dB exchange rule should be used for complex noises. It also notes that “(if) the effects are synergistic, the 85-dBA PEL and 3-dB exchange rule would still be protective to a smaller extent than for the steady-state noise.” This suggests the need for more research to determine: (1) if synergistic effects exist in the complex noise problem and (2) a quantification of the synergistic effects has to be included in future noise guidelines. The first issue, existence of synergetic effects was quite clearly confirmed by many animal noise exposure studies (Dunn et al., 1991; Lei et al., 1994). The second issue, the need for quantification of synergetic effects has motivated this study.

Recent studies on animal exposure (Hamernik and Qiu, 2001; Hamernik et al., 2003b) have shown that kurtosis effectively discriminates the risk of hearing loss in chinchilla for noise exposures with the same level and different temporal characteristics. Thus, SPL combined with a kurtosis correction term may serve as a good noise metric for assessment of the risk of noise of widely different temporal characteristics. Zhao et al. (2010) combined an energy-based metric with a temporal correction term to evaluate human noise exposure study data. In this work, the kurtosis correction was made through the exposure time. The correction term was determined to match dose-response relationship (DRR) of the two groups, respectively, exposed to a complex noise environment and a Gaussian noise environment. Because the study used only one set of data, generality of the correction form has yet to be established. In this work, the best form of the kurtosis corrected SPL is identified based on chinchilla noise exposure test data, taking advantage of abundant DRR obtained from direct, controlled experiments. The result is applied to the human exposure data obtained by Zhao et al. (2010) as a preview of possible application of the result for human.

EXPERIMENTAL DATA

The current study uses noise exposure data for 273 chinchillas of 23 groups provided by collaborators at SUNY Plattsburgh. Each of the 23 animal groups consisting of 9–16 chinchillas was exposed to a specially designed, different noise environment. Eighteen groups were exposed to 100-dBA noises (1 Gaussian, 17 complex), two groups to 95-dBA noises (1 Gaussian and 1 complex), and three groups to 90-dBA noises (1 Gaussian and 2 complex). Animals were exposed to a given noise for 24-h per day, for five consecutive days. The hearing threshold level (HTL) was measured from the auditory evoked potential (AEP) at 0.5, 1, 2, 4, 8, and 16 kHz for each animal before the exposure, daily during the test and 30 days after the completion of the exposure. From the AEP data, permanent threshold shift (PTS) and temporary threshold shift (TTS) are calculated. Outer hair cell (OHC) losses and inner hair cell (IHC) losses in 0.5, 1, 2, 4, 8, and 16 kHz bands were also measured. The noise data digitally recorded for 5-min with the 48 kHz sampling was given as a part of the data to the authors. More detailed descriptions of the noises and experimental protocols are available in various publications (Hamernik et al., 1989; Hamernik et al., 2003a; Hamernik et al., 2007). The PTS data is used as the primary measure in the current research because it is used as the basis for the noise induced hearing loss (NIHL) in all noise guidelines.

Availability of the digitally recorded noise time histories makes the exposure data highly valuable, as it enables re-processing of the data from different angles. The analytic wavelet transform (AWT) developed by Zhu and Kim (2006) and Zhu et al. (2009) was applied in this work to obtain time histories of the full-octave frequency components at 0.5, 1, 2, 4, 8, and 16 kHz. From these time histories, equivalent SPL (L_eq) of the frequency components was calculated as listed in Table TABLE I.. Fast Fourier transform (FFT) can also be applied instead of AWT to obtain the frequency components. Kurtosis of the noise was calculated from the original pressure time histories.

Table 1.

The overall and frequency-by-frequency equivalent SPLs (L_eq) and kurtosis of the 23 noises used to expose chinchillas. Frequency-by-frequency L_eq is calculated for a full-octave component at 0.5, 1, 2, 4, 8, and 16 kHz center frequencies. The kurtosis value is calculated from the pressure time history of the noise. $PT{S}_{5124}=\frac{1}{4}(PT{S}_5+PT{S}_1+PT{S}_2+PT{S}_4),$ where PTS₅, PTS₁, PTS₂, PTS₄ are the average of the PTS of the chinchillas in the group measured at 0.5, 1, 2, 4, 8, and 16 kHz.

	Leq (dB)
Group Index	Overall	0.5 kHz	1 kHz	2 kHz	4 kHz	8 kHz	16 kHz	β (kurtosis)	PTS5124 (dB)
G-44	101.1	80.7	92.9	93.00	95.4	93.3	93.9	32.7	29.39
G-49	101.5	84.5	93.8	93.6	95.4	93.17	92.7	33.2	39.56
G-50	101.6	85.5	85.4	96.9	90.99	95.15	94.6	20.8	10.41
G-51	100.3	80.0	95.7	94.3	94.49	90.29	85.4	101.8	22.13
G-52	102.5	86.7	97.5	94.8	94.56	93.98	93.7	52.9	28.17
G-53	101.1	82.8	95.2	94.0	96.06	92.7	89.4	97.9	27.39
G-54	102.0	85.2	96.1	94.1	94.0	93.08	94.6	35.9	23.97
G-55	103.3	94.7	93.1	89.5	91.2	95.9	94.1	25.6	30.93
G-59	103.4	99.2	93.4	93.7	88.6	92.8	93.4	30.9	13.64
G-60	102.4	86.1	96.1	94.1	95.0	94.2	94.7	35.6	29.17
G-61	102.7	91.4	89.5	87.8	92.1	96.5	97.09	3.0	9.5
G-63	100.9	83.5	98.4	94.2	92.0	85.6	79.2	117.1	34.20
G-64	102.4	86.9	93.2	91.3	93.3	95.5	97.0	8.4	20.00
G-65	102.1	94.2	93.2	89.3	90.0	94.3	88.2	118.8	24.05
G-66	102.8	90.6	90.9	89.9	92.8	98.3	95.5	14.8	17.23
G-68	103.1	94.2	93.6	89.6	90.2	95.4	95.5	58.4	22.05
G-69	99.9	69.3	74.3	99.3	91.1	82.2	75.2	77.4	9.1
G-70	101.5	85.2	92.3	92.6	95.6	93.2	93.6	27.1	25.21
G-47	92.4	80.7	79.3	78.2	82.05	86.4	86.6	3.0	1.3
G-48	92.6	75.9	87.2	85.08	84.4	83.4	84.3	33.3	6.16
G-56	93.4	82.3	81.4	80.4	83.1	89.2	84.9	36.04	4.5
G-57	97.3	86.8	85.6	83.3	85.5	90.8	91.5	3.0	8.0
G-58	96.4	79.5	91.2	88.6	88.4	87.3	87.9	41.5	13.23

Kurtosis is defined as the fourth standardized moment about the mean of the data:

$$\frac{E{(x-m)}^4}{s^4},$$ (1)

where s is the standard deviation of x, E(·) represents the expected value of quantity, m is the mean of x. Kurtosis describes the peakedness of a distribution, which is independent of the overall level and was suggested as a metric of impulsiveness by Erdreich (1985). Kurtosis of Gaussian noises is approximately 3 as represented in noises G-61, G-47, and G-57 in Table TABLE I..

DEVELOPMENT OF THE NEW NOISE METRIC

The performance of the noise metric is evaluated by its correlation with the NIHL defined in a way most compatible with the definition used in human guidelines. Unacceptable occupational hearing loss is defined in NIOSH guideline (NIOSH, 1998) by material hearing impairment, which is having a 25-dB or higher HTL averaged for 1, 2, 3, and 4 kHz. As the PTS of chinchillas was measured at 0.5, 1, 2, 4, 8, and 16 KHz, missing the 3 kHz component, the average of PTS at 0.5, 1, 2, and 4 kHz or at 1, 2, and 4 kHz could be used as an approximate definition of NIHL in the correlation study. In this study, the former PTS₅₁₂₄ is chosen, which is defined as follows:

$$PT{S}_{5124}=\frac{1}{4}(PT{S}_5+PT{S}_1+PT{S}_2+PT{S}_4).$$ (2)

where PTS₅, PTS₁, PTS₂, and PTS₄ are the average of PTS measured at 0.5, 1, 2, and 4 kHz from chinchillas in each group. PTS₅₁₂₄ of each of the 23 groups of chinchillas is shown in the last column of Table TABLE I.

Design of the noise metric

While kurtosis is a very good differentiator of the risk of noises of the same energy but different temporal characteristics, it cannot be used as a noise metric by itself because it is an energy-independent parameter. For example, Gaussian noises of 50- and 100-dBA, which clearly have different noise risks, have the same kurtosis value. Therefore, it is logical to incorporate kurtosis with the SPL to create the new noise metric. After testing several alternatives, the basic form of the new metric was determined as follows:

$${L^{\prime }}_{eq}=L_{eq}+\lambda {\log \hspace{0.17em}}_{10}\frac{\beta }{{\beta }_G},$$ (3)

where _L^′eq is the kurtosis corrected L_eq, λ is a positive constant to be determined from the dose-response correlation study, β is the kurtosis of the noise, and β_G is the kurtosis of the Gaussian noise. Notice that no correction is made for a Gaussian noise. A complex noise has a kurtosis higher than that of β_G; therefore, it has a positive correction term that represents the higher risk of the noise.

Six noise metrics shown in Table TABLE II. are compared for their correlations with NIHL, which include two traditional metrics without a kurtosis correction term: equivalent and A-weighted equivalent SPLs, L_eq, and L_Aeq. The third metric without a correction term, L_eq,5124, is defined as

$$L_{eq,5124}=\frac{1}{4}(L_{eq,5}+L_{eq,1}+L_{eq,2}+L_{eq,4}),$$ (4)

where L_eq,5, L_eq,1, L_eq,2, L_eq,4 are equivalent SPLs of the 0.5, 1, 2, and 4 kHz full-octave components, respectively. L_eq,5124 is chosen by matching its form with the form of the NIHL defined in Eq. 4 expecting a good performance based on the cochlea position theory (Zwislocki and Nguyen, 1999; Price, 1979). _L^′eq, _L^′Aeq and _L^′eq,5124 in Table TABLE II. are kurtosis corrected versions of the first three metrics according to the scheme in Eq. 3. It is noted that L_eq,5124, _L^′eq, _L^′Aeq and _L^′eq,5124 are new noise metrics studied for the first time in this paper.

Table 2.

Results of regression analysis of the noise metrics as functions of PTS₅₁₂₄. λ is the coefficient of the kurtosis correction term and r² is the r-square value (square of the correlation coefficient) between the metric and NIHL defined as PTS₅₁₂₄.

Metric number	Metric	λ	r2 value
1	Leq	N∕A	0.41
2	LAeq	N∕A	0.46
3	Leq,5124	N∕A	0.61
4	${L^{\prime }}_{eq}=L_{eq}+\lambda {\log \hspace{0.17em}}_{10}\frac{\beta }{{\beta }_G}$	4.80	0.54
5	${L^{\prime }}_{Aeq}=L_{Aeq}+\lambda {\log \hspace{0.17em}}_{10}\frac{\beta }{{\beta }_G}$	4.04	0.54
6	${L^{\prime }}_{eq,5124}=L_{eq,5124}+\lambda {\log \hspace{0.17em}}_{10}\frac{\beta }{{\beta }_G}$	3.07	0.67

Correlation study

The correlation analysis of the noise metric and the NIHL (PTS₅₁₂₄) is conducted by applying a linear regression analysis to 23 pairs of the metric and PTS₅₁₂₄ data. For the first three metrics with no correction term in Table TABLE II., L_eq, L_Aeq, L_eq5124 , the analysis becomes a single-variable regression analysis. For example, the linear regression equation of L_eq is

$$PT{S}_{5124}=b_0+b_1{L}_{eq}+\in$$ (5)

where ε is the error to be minimized. From Eq. 5, the best fitting regression line, i.e., the values of b₀ and b₁, are determined, and r² value and the square of the correlation coefficient are calculated. r² = 1 indicates a perfect correlation and r² = 0 indicates no correlation between the metric and NIHL.

Multiple predictor regression models are constructed for the last three metrics in Table TABLE II., which has a kurtosis correction term. For example, the regression equation for ${L^{\prime }}_{eq}=L_{eq}+\lambda {\log \hspace{0.17em}}_{10}\frac{\beta }{{\beta }_G}$ becomes

$$PT{S}_{5124}=b_0+b_{Leq}{L}_{eq}+b_{k1}lo{g}_{10}\frac{\beta }{\beta G}+\in$$ (6)

The regression analysis obtains the best values for b_o, b_Leq, and b_k1 that minimizes ε. $\lambda =\frac{b_{k1}}{b_{Leq}}$ and corresponding r² values are obtained for each metric. The correlation study result is summarized in Table TABLE II..

Between the two traditional metrics, L_Aeq has a slightly better r² value than L_eq, which supports the practice of using L_Aeq over L_eq in noise guidelines. Among the metrics without the correction tern, L_eq,5124 shows by far the best correlation, which is expected from the cochlea position theory. Kurtosis correction improves correlation of all three metrics L_eq, L_Aeq, and L_eq,5124. Overall, _L^′eq,5124 shows the best correlation with the NIHL. The best two metrics are _L^′eq,5124 and L_eq,5124. The kurtosis correction term does not improve L_Aeq and L_eq,5124 as much as it does for L_eq.

Table TABLE III. shows r² values of the kurtosis correction term with L_eq, L_Aeq, and L_eq,5124. It is seen that the correction term is least correlated with L_eq. This explains why adding the correction term to L_eq makes the biggest difference of the performance of the metric.

Table 3.

r² values of the correlation between the kurtosis correction term and the basis noise metric. L_eq has the smallest r² value; thus are least correlated with the correction term. This explains that adding the correction term to L_eq has the biggest effect as it is shown in Table TABLE II..

	Leq	LAeq	Leq,5124
$\lambda {\text{log}}_{10}\frac{\beta }{{\beta }_G}$	0.05	0.11	0.26

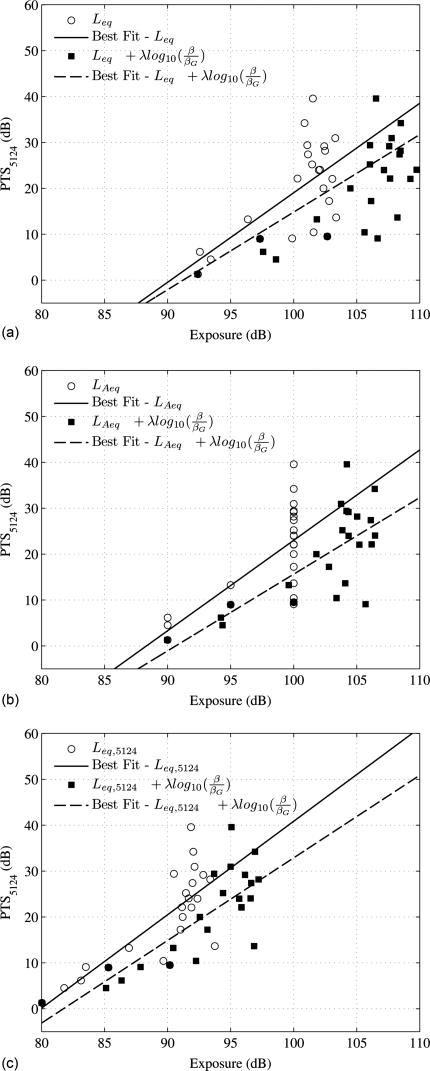
Figure 1 shows the scatter plots of the PTS₅₁₂₄ values against the metric values with the regressed line. Each point represents the PTS₅₁₂₄-metric pair of the 23 animal groups. Scatter plots are compared for L_eq and _L^′Aeq in Fig. 1A, for L_Aeq and _L^′Aeq in Fig. 1B, and for L_eq and _L^′Aeq in Fig. 1C. It is seen that the correction term improves the correlation for all three metrics.

Figure 1.

Scatter plots of the PTS₅₁₂₄ values against the metric values with the regressed lines. Each point represents the pair of the average PTS₅₁₂₄ of the chinchillas in the group exposed to one specific type of noise and the metric calculated for the noise. (A) against L_eq and _L^′eq, (B) against L_Aeq and _L^′Aeq, and (C) against L_eq,5124 and _L^′eq,5124. It is seen that adding the kurtosis correction term improves the correlation between the metric and PTS₅₁₂₄.

Although it is the third best metric, _L^′Aeq has an advantage. Because it is based on L_Aeq, the noise metric used in most current noise guidelines, and it can be used with a current noise guideline without any changes by simply adopting _L^′Aeq in the place of L_Aeq. For example, 85-dBA PEL and 3-dB exchange rule in the current NIOSH guideline can be used if they are defined in terms of _L^′Aeq.

APPLICATION TO HUMAN DATA

The corrected A-weighted SPL developed in this study, _L^′Aeq, was tested against the human data gathered by Hamernik and his collaborators in China (Zhao et al., 2010). L_eq,5124 and _L^′eq,5124 could not be tested because the digital noise exposure time histories of the noises were not available to the authors. Among 195 subjects who participated in the survey, 32 subjects were exposed to complex noises of the average kurtosis of 44 for 123 ± 7.1 yr and 163 subjects were exposed to a Gaussian noise (β = 3) for 12.7 ± 8.4 yr. The adjusted high frequency noise induced hearing loss (AHFNIHL) was used as the NIHL. AHFNIHL is defined as the percentage of population having a higher HTL by 30 dB or more than the 50th percentile of the age and gender matched population found in the ISO standard in Annex B in either ear at 3, 4, or 6 kHz (ISO-1999, 1990). The cumulative noise exposure (CNE) index was used as the noise metric (dose), which is defined:

$$CNE=L_{Aeq,8hr}+10lo{g}_{10}T,$$ (7)

where T is the exposure duration measured in years.

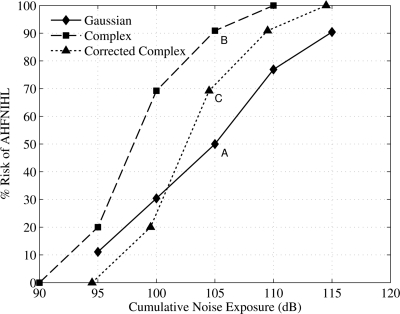
Similar to the procedure adopted in the original study (Zhao et al., 2010), the subjects are separated into 5-dB CNE bins to study the metric–NIHL relationship. In Fig. 2, the solid line with filled diamond symbols shows the relationship of the group exposed to the Gaussian noise, and the dashed-line with filled square symbols shows the relationship of the group exposed to complex noises. The difference between the NIHL values of the two curves associated with the same CNE value can be considered as the additional risk of the complex noise, which is ignored in current noise guidelines. Figure 2 shows that the complex noise induces significantly higher NIHL than the Gaussian noise of the same CNE value.

Figure 2.

Effect of kurtosis correction on the measured human NIHL data. AHFNIHL is percentage of the subjects having a higher HTL by 30 dB or more than the control group. Solid line with filled diamond symbol represents the CNE-NIHL relationship of the group exposed to Gaussian noises, dashed line filled square symbol represents the CNE-NIHL relationship of the group exposed to complex noise, and dotted line with filled triangle symbol represents (kurtosis corrected CNE) CNE′-NIHL relationship of the group exposed to complex noises. CNE′-NIHL curve of the complex noise becomes much closer to the CNE-NIHL curve of the Gaussian noise, which the kurtosis correction reduces underestimation of the risk of complex noises.

Zhao et al. (2010) developed the kurtosis corrected metric CNE′ as follows:

$$CN{E}^{\prime }=L_{Aeq,8hr}+\frac{ln(\beta )+1.9}{log(2)}lo{g}_{10}T$$ (8)

The correction in Eq. 8 was determined so that CNE′-NIHL relationship of the group exposed to complex noises (β = 44) is best matched with CNE-NIHL relationship of the group exposed to the Gaussian noise (β = 44) and CNE′ reduces to CNE for a Gaussian noise (β = 3). The correction form in Eq. 8 was determined based on only one set of data; therefore generality of the correction is not known.

The correction scheme we developed [see Eq. 3] is independent of the exposure time length; therefore, CNE′, the kurtosis-corrected CNE, according to our scheme is defined as follows:

$$\begin{array}{c}CN{E}^{\prime }={L^{\prime }}_{Aeq,8hr}+10lo{g}_{10}T=L_{Aeq,8hr}+\lambda lo{g}_{10}\frac{\beta }{\beta G}+10lo{g}_{10}T\\ =CNE+\lambda lo{g}_{10}\frac{\beta }{{\beta }_G}\end{array}$$ (9)

where λ = 4.02 as it was identified for _L^′Aeq previously. As the complex noises in this study have the average kurtosis value β = 44 and CNE′ = CNE + 4.69. The relationship between the AHFNIHL and CNE′ of the complex noises group is shown as the dotted line with filled triangle symbols in Fig. 2. Improvement due to kurtosis correction term is readily apparent. The metric–NIHL relationships of the Gaussian and complex noises have become much closer to each other, which imply that the corrected metric CNE′ will reduce underestimation of the risk of exposure to complex noises. For example, without the kurtosis correction, the AHFNIHL associated with a noise of CNE = 105 is 50% if the noise is Gaussian (point A in Fig. 2) or 90% if the noise is a complex noise of β = 44 (point B). With the kurtosis correction, the AHFNIHL associated with a noise of CNE′ = 105 is 50% if the noise is Gaussian (point A) and 70% if the noise is a complex noise of β = 44 (point C). Similar improvement is observed at other levels. This suggests that the use of a kurtosis corrected metric will enable to assess the risk of complex noises more accurately. It is noted that the above demonstration should be interpreted qualitatively because the model developed based on chinchilla data was applied to human data without any adjustments for effects of different definitions in NIHL (PTS₅₁₂₄ vs PTS₁₂₃₄; short-term cute shorter exposure vs long-term exposure). More studies will be necessary to realize the potential benefit of adopting a kurtosis corrected noise metric.

DISCUSSIONS

Basic hypotheses used in development of new noise metrics

The approach adopted in this work is developing new noise metrics by using chinchilla noise exposure data and then applying them to assess the risk of human noise exposure. It takes advantage of abundant, directly measured noise exposure study data. The approach obviously involves various errors because it uses the chinchilla data for human application. Besides the expected differences in the DRR of the human and chinchilla, definitions of the dose and response (NIHL) are different. For example, NIOSH guideline defines dose as 8-h exposure during extended durations of exposure, while chinchillas were exposed to 5 days continuous exposures; response in NIOSH guideline is defined as having 25-dB or higher HTL averaged for 1, 2, 3, and 4 kHz, while it is defined as the PTS averaged for 0.5, 1, 2, and 4 kHz in chinchillas. Therefore, the approach in this work implicitly adopts the following hypotheses:

• (1)Human and chinchillas have similar DRR in a relative sense. That is, if a given noise causes higher NIHL than the other noise in chinchillas, the same will occur in human.
• (2)Long- and short-term exposures have similar DRR in a relative sense. That is, if one noise causes higher NIHL than the other noise in a short-term exposure, the same will occur in a long-term exposure also.

The above hypotheses are plausible when the similarity of the auditory systems of human and chinchillas is considered; however, empirical validation is still needed. The first hypothesis may be validated by using animal tests, for example by showing that the noise metric developed from chinchilla data applies to other species such as guinea pigs. The second hypothesis will have to be validated by applying the new noise metric to a sufficient number of human exposure study data. Future human studies for this purpose will have to record the time history of the noise to permit kurtosis correction. Such validation will still be indirect and limited because of the nature of the human data. Workers’ exposures will be inevitably cross sectional and not longitudinal in their careers (e.g., 30 yr). Furthermore, non-occupational noise exposure, individual health effects, ototoxic chemicals, and drugs are uncontrolled factors that will confound such analyses. For example, it is highly unlikely that the noise to which workers are exposed will remain the same over a long duration; there are many uncontrollable factors such as exposure to recreational noises or effects of other illnesses.

Reference kurtosis β_G

The basic form of the new noise metric, ${L^{\prime }}_{eq}=L_{eq}+\lambda {\log \hspace{0.17em}}_{10}\frac{\beta }{{\beta }_G}$, was designed so that Gaussian noises are the reference noise exposure. Current noise guidelines may be considered as the result of empirical data accumulated for a long period of time for most common occupational noise environments, which may have higher kurtosis than β_G. In this case, using β_G as the reference kurtosis in the correction may result in over-evaluation of the risk of complex noises. A better reference kurtosis may be identified by surveying “typical” occupational noise environments.

Modification of _L^′eq,5124 to utilize it in human guidelines

_L^′eq,5124 was adopted because PTS and NIHL of chinchillas were measured at 0.5, 1, 2, and 4 kHz, not at 1, 2, 3, and 4 kHz that most human guidelines adopt to define NIHL. Therefore, _L^′eq,1234 has to be used for human application instead of _L^′eq,5124, while using the same λ value identified for _L^′eq,5124 from the chinchilla data. The effects of this simplification will have to be further investigated.

Potential application of the new noise metrics to human guidelines

Among the three best noise metrics, _L^′Aeq is the easiest to apply in human guidelines as it was mentioned, because adopting it in a noise guideline does not require any other changes. Some manipulation is necessary to use _L^′eq,1234 because it does not represent the overall SPL. Because using _L^′eq,1234 can be viewed as a type of weighting, one option is using _L^″eq,1234, a scaled _L^′eq,1234 defined as follows:

$${L^{″}}_{eq,1234}={L^{\prime }}_{eq,1234}+(L_{eqA,G}-L_{eq,1234,G})={L^{″}}_{eq1234}+9.2$$ (10)

where L_eqA,G − L_eq,_1234,G is the difference of the A-weighted SPL and L_eq,1234 of the Gaussian-white noise, which is 9.2-dB, independent of the level of the noise. If the noise is Gaussian-white noise, _L^′eq,1234=L_eq,1234,G; therefore, _L^″eq,5124 reduces to L_Aeq. _L^″eq,1234 defined in Eq. 10 can be used in place of L_Aeq in the noise guideline.

CONCLUSIONS

It has been widely regarded that current noise guidelines underestimate risk of complex noises because they employ A-weighted equivalent SPL (L_Aeq) as the noise metric which ignores the effect of temporal characteristics of the noise (NIOSH, 1998). To address this problem, a new form of noise metric with a temporal correction term was designed as ${L^{\prime }}_{eq}=L_{eq}+\lambda {\log \hspace{0.17em}}_{10}\frac{\beta }{\beta G},$, where β and β_G are kurtosis values of the given and Gaussian noises. This basic form was designed so that no correction is made for Gaussian noises, and higher corrections are made for more kurtosis complex noises. Six noise metrics including four new metrics developed by varying the basic form were evaluated utilizing chinchilla noise exposure test data for their correlations with the NIHL in chinchillas. NIHL was defined as the average of the PTS at 0.5, 1, 2, and 4 kHz to make it similar to the definition used in human guidelines. Evaluation showed that the kurtosis correction term generally improves correlations of the metric with NIHL. The metric _L^′eq,5124 (kurtosis corrected L_eq,5124) showed the highest correlation with NIHL, where L_eq,5124 is the average of L_eq of 0.5, 1, 2, and 4 kHz components of the noise, followed by L_eq,5124 and _L^′Aeq (kurtosis corrected L_Aeq). The r² values (square of the correlation coefficient) of the correlations of these three best metrics were 0.67, 0.61, and 0.54, respectively, compared to 0.46 of the current noise metric L_Aeq. _L^′Aeq was applied to a set of human noise exposure data obtained from two groups, respectively, exposed to a Gaussian noise environment and a complex noise environment, which showed a good potential of the approach proposed in this work.