A multiplexed immunoassay system based upon reciprocating centrifugal microfluidics

Abstract

A novel, centrifugal disk-based micro-total analysis system (μTAS) for low cost and high throughput semi-automated immunoassay processing was developed. A key innovation in the disposable immunoassay disk design is in a fluidic structure that enables very efficient micro-mixing based on a reciprocating mechanism in which centrifugal acceleration acting upon a liquid element first generates and stores pneumatic energy that is then released by a reduction of the centrifugal acceleration, resulting in a reversal of direction of flow of the liquid. Through an alternating sequence of high and low centrifugal acceleration, the system reciprocates the flow of liquid within the disk to maximize incubation/hybridization efficiency between antibodies and antigen macromolecules during the incubation/hybridization stage of the assay. The described reciprocating mechanism results in a reduction in processing time and reagent consumption by one order of magnitude.

INTRODUCTION

Immunoassays are a common standard for diagnostics of many conditions and diseases and are one of the main research tools used across the life sciences. Since their implementation in 1950s by Yalow and Berson¹ in the form of radiolabelled insulin assays, immunoassays have emerged as one of the largest and fastest growing segments of in vitro diagnostics and clinical chemistry. Today immunoassays are most commonly used for the detection of the presence of antibodies and antigens for a variety of infectious diseases, as well as for measuring the levels of macromolecules such as hormones, growth factors, and tumor markers in bodily fluids for toxicological screening and many other applications. Clinical diagnostic immunoassay kits are a rapidly growing business with annual sales in the tens of billions of dollars. They are simple and inexpensive to implement, and have high specificity and selectivity. The working principle of immunoassays is based on the highly specific affinity of antibodies for antigens, making for thermodynamically stable complexes. Detection of such complexes can be carried out in a variety of ways, such as with radioisotopes in radio immunoassays (RIA), colorimetric as in enzyme-linked immunosorbent assays (ELISAs), and fluorometric like in fluoroimmunoassays.² Furthermore, immunoassays can be performed in a bulk solution, in which case they are referred to as homogenous immunoassays and on a solid surface where they are called heterogeneous immunoassays. The colorimetric detection of the formation of antigen-antibody complexes is the most common and least expensive form of an immunoassay and is the foundation for the ELISA presented in this article. The ELISA technique is commonly used to elucidate the concentrations of specific proteins in a sample and has been successfully adapted to a microarray format.^{3, 4, 5} Besides their utility in diagnostics, immunoassays are an important tool in drug discovery. Often, thousands of antigens must be screened in search for the most effective vaccine or drug, or for discovering new biomarkers. This requirement makes the protein microarray a suitable tool for such applications because it enables the simultaneous analysis of a large number of proteins in a single experiment using a relatively small sample volume.⁶

Immunoassays can be performed in a high throughput and parallelized fashion by using either the ELISA plate technique, where typically a 96-well plate runs a single analyte simultaneously, or by the enzyme-linked immunospot method, commonly referred to as ELISPOT technique⁷ where multiple analytes can be detected from a single array on a glass slide. In an indirect colorimetric heterogeneous ELISPOT performed for evaluating the stimulated host response to a new vaccine, a set of antigens from an infectious organism are spotted onto a solid support (solid phase), such as glass, polystyrene, polymethylmethacrylate, or a nitrocellulose membrane to make a protein microarray.⁸ This microarray is then exposed to the diluted serum of a patient that has developed immunity to the specific infectious agent, resulting in the specific attachment of patient antibodies (found in the serum) to the immobilized antigens. The antibodies are then detected by secondary antibodies, conjugated to an enzyme such as alkaline phosphatase, and developed using an appropriate substrate² to detect the presence of antibody/antigen complexes.^{9, 10, 11} The signal intensities quantified from precipitated chromogenic products on the membrane reveal the antigens that elicit the best immune responses.

The process of manually exposing the antigen microarrays to sera, washing, incubation with the secondary antibody, incubation with substrate, and analysis of the results is labor intensive and requires a well-equipped laboratory setting. Furthermore, the extended exposure to infected samples increases the operators’ risk of infection. Today, as a standard practice, large scale automated immunoassay and ELISA plate washer/reader liquid handling robots are used in order to reduce the exposure risk and accelerate the process flow. These large-scale operations are, nevertheless, inadequate for the point of need use, and costs are prohibitive for small laboratories.

For the reasons presented above, numerous efforts have been undertaken to automate fully functional ELISAs that are integrated on micro-structured platforms known as micro-total analysis systems (μTAS).^{12, 13, 14} The aim of such studies is not only to automate the assays but also to decrease the consumption of sample, to minimize the footprint of the instrumentation involved and to reduce costs. This could make ELISAs on μTAS platforms suitable for on-site analysis and make them affordable for a much wider community.^{15, 16, 17} There is also a considerable emphasis put on speeding up the immunoassay process, which tends to be quite slow. The latter is due to the fact that bimolecular antigen/antibody interactions rely solely on molecular diffusion. The diffusion coefficient for large protein molecules such as antibodies is in the order of 10⁻¹⁰m²/s.¹⁸ This means that each antibody can only travel about 2.5 mm during an overnight incubation without agitation. As such, only a small number of antibodies in solution reach the solid-liquid interface to interact with their complimentary antigens on the surface. Generally, the rate of formation of antigen-antibody complexes, which is proportional to the concentration of the antibodies and antigens, dictates the required incubation time for generating a detectable result. This is why it is desirable to introduce other transport mechanisms such as migration and convection into the system to cause turbulence in the antibody solution and/or to generate flow and increase the rate of formation of antigen-antibody complexes^{19, 20} by employing different innovative methods.

A promising methodology that has been examined in recent decades as a candidate for μTAS is the fabrication of microfluidic systems on rotating platforms, or compact discs (CD).^{21, 22} Such platforms exploit the forces induced by rotating the platform around a fixed center to drive a fluid within the system and control its flow. Precise fluidic propulsion, regulation, and redirection is realized by carefully designing the size of features and their proximity to each other on the platform, and also by controlling the rotational speed and acceleration rates, hence, balancing centrifugal, Coriolis, and surface forces. Beads of different sizes are often used to serve both as solid phases functionalized with capture antigens and to increase the interaction rate by intermittently mixing the reagents on the disk.^{16, 17, 18, 19, 20, 21, 22, 23} The rate of interaction will also increase by flowing the antibody solution over the array of immobilized antigens and hence increasing the rate of mass transport.^{24, 25, 26} Rotating platforms are especially suitable for flow-through capture systems because the flow can be readily generated by the centrifugal acceleration.

Although these CD-based microfluidic systems exhibit superior performance characteristics for analyzing small numbers of target molecules, they are not well suited for processing large arrays of antigens. The shortcoming comes from the fact that as the footprint of the array increases so does the volume of the reagents and buffers required for running the assay, resulting in a high rate of sample (antibody) consumption. In addition, in a single-pass flow-through scheme, only a small number of antibodies are sequestered by the antigens immobilized on the solid phase. As a consequence of this, the expensive and sometimes scarce sample will leave the system unconsumed properly. This is why it desirable to flow the sample over the array in a cyclical, or reciprocating, manner to take advantage of favorable kinetics offered by flow-through capture systems on an automated CD-based platform.

In this report we present a semi-automated centrifugal microfluidic platform for faster protein microarray processing (Fig. 1). The system is based on a novel technique introduced recently by us for reciprocating fluid samples on a CD to enhance mixing in a miniaturized bioassay chamber.²⁷ It works by using the centrifugal acceleration field acting upon a liquid within a rotating disk to generate and store pneumatic energy for later use in reversing the direction of flow of the liquid as centrifugal acceleration is reduced (by reducing angular frequency). Through a sequence of steps increasing and decreasing centrifugal acceleration (Fig. 2), the system allows one to reciprocate the flow of liquid within a fluidic system. The reciprocating fluid causes mixing and maximizes encounters and specific interactions between molecules in the liquid and solid phase. This results in a reduction in the time necessary to perform a bioassay. In addition, because of the miniaturized nature of the system, reagent consumption is minimized.

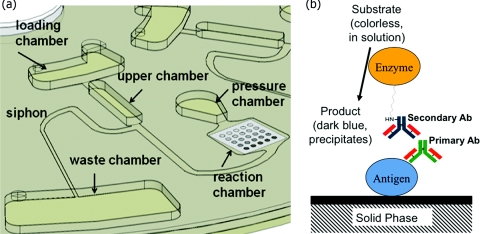
Figure 1.

(a) Schematic illustration of the fluidic system. (b) Schematic illustration of antibody capture at each array element.

Figure 2.

(a) Time-lapse images of the system in operation. (i) Liquid is added to the loading reservoir, (ii) compression of air in pressure chamber as a result of high rpm, (iii) relaxation of air and pumping of liquid towards the center, (iv) increase of rpm to maximum, (v) priming of the siphon as the liquid level rises above the crest of the siphon, and (vi) the empty system. (b) Flow reciprocation work cycle profile: angular frequency vs. time.

To evaluate the performance of the reciprocating fluidic system, we developed a set of numerical simulations and compared the antigen-antibody interaction results between three different modes: flow-reciprocation, single flow-through, and passive diffusion. Results of the simulations demonstrated that the reciprocating flow mode yields superior capture rates over those of the passive diffusion mode and are more comparable to the capture rates in single flow-through mode. To experimentally validate the simulation results, we incubated arrays of human sera (containing antibodies) with a solution containing goat anti-human Immunoglobulin G (IgG) proteins conjugated to alkaline phosphatase and compared the signal intensities for the same assay performed both manually (passive diffusion) and using the reciprocating fluidic system. We then calibrated the reciprocating system by optimizing parameters such as concentration of proteins on the solid phase and in the liquid phase, incubation time, and number of reciprocation cycles for each step, as well as the number of washes required to reduce non-specific adsorption in between each of the steps.

For proof of concept, we set up an immunoscreening experiment by making arrays of Burkholderia antigens and probing them with infected and naive sera. Burkholderia is a bacterial pathogen that attacks the human respiratory system and causes Melioidosis. Symptoms may include pain in the chest, bones, or joints, cough, skin infections, lung nodules, and pneumonia.²⁸

The main considerations driving the miniaturization and automation of immunoassays are the high cost of reagents such as antibodies and antigens, the high cost of qualified labor, and the long assay times involved. In this work we have demonstrated, based on proof-of-concept results, that by using the described reciprocating fluidic system we were able to perform an immunoassay with a ∼75% reduction in reagent consumption and a ∼85% reduction in assay time.

MATERIALS AND METHODS

Design of the reciprocating flow-based immunoassay CD

The CD-based fluidic structure shown in Fig. 1 consists of several fluidic elements that are milled 1.3 mm deep into the CD plastic including a loading chamber, an upper chamber, a pressure chamber for storing pneumatic pressure, and a waste chamber. The design also includes a shallow reaction chamber that is 100 μm deep and where antibodies dissolved in the flowing liquid bond with antigens immobilized on an array, as well as several microchannels with depths ranging from 350 μm to 1 mm for transferring liquid between the named chambers. After injecting 25 μl of liquid in the loading reservoir, the disk starts to rotate with a high acceleration rate and follows the angular frequency profile presented in Fig. 2b. The pressure differential, ΔP_c, induced at a high angular speed of 7000 rpm²¹ drives the liquid downstream, over the antigen array, and into the pressure chamber resulting in compression of the air trapped in the pressure chamber.²⁷ The high rotational acceleration rate (10 000 rpm/s) prevents the liquid from priming the siphon valve at this point. Next, the angular speed is gradually reduced to decrease the centrifugal force and release the stored pneumatic energy. This causes the flow to reverse direction and move towards the upper chamber, passing over the antigen array again. The minimum angular frequency at which the flow reaches the crest of the siphon for priming the siphon depends on the properties of both the liquid and the contact angle of the polymer surface and is established empirically. This sequence of increasing and decreasing angular speed is repeated for several cycles to increase the capture rate by transporting the antibodies to the array on the surface of the reaction chamber.

To transfer the sample to the waste chamber at the end of the incubation period, angular frequency of rotation is decreased from 10 000 rpm/s to 480 rpm to release the pneumatic pressure abruptly and force the liquid to reach the crest of the siphon and prime it. The capillary valve draws the liquid almost completely into the waste chamber and the system is ready for introduction of the next fluid. Figure 2a shows the time-lapse images of the system during operation.

Modeling of the antigen-antibody interaction

Having adequate knowledge of the kinetics of the antigen-antibody interaction at the solid-liquid interface is useful for optimizing assay parameters. The binding of an antibody to an antigen is a fast and specific bimolecular interaction that in a simplified form may be described by the following equilibrium:²⁹

$$Ag+Ab\underset{k_r}{\overset{k_f}{\iff }}Ag:Ab,$$ (1)

where Ag represents antigens, Ab the antibodies, Ag: Ab the antigen-antibody complex, and k_f and k_r the association and dissociation rate constants, respectively. According to this model, antigens immobilized on the solid phase, Ag, sequester the antibodies, Ab, from the bulk of the fluid, that are in the vicinity forming the complex Ab: Ag on the solid phase. Here we consider only specific interactions between antibodies from the bulk liquid and the solid phase-bound antigens and neglect any non-specific interactions leading to adsorption of the antibodies directly to the solid phase. Areas of the solid phase not spotted with antigens were blocked with protein array blocking buffer (Whatman, USA) to prevent as much as possible such non-specific interactions. The interaction rate is controlled by a number of parameters including the temperature, length of the molecule, the immobilization method, and concentration of antigens and antibodies. Heterogeneous antigen-antibody interactions³⁰ involve both the liquid and the solid phase; in a first step one must consider the transport of antibodies in the bulk of the solution to the solid phase and next, the formation of an antibody-antigen complex on the solid phase. Assuming a uniform velocity and concentration distribution along the width of the reaction channel, simulation of the solid phase antigen-antibody interaction with both convection and diffusion as transport mechanisms can be simplified to a two-dimensional, time-dependent system of equations.

In the bulk of the solution, the equation of mass transport of antibodies is written as

$$\frac{\partial c}{\partial t}+u\frac{\partial c}{\partial x}=D\left({\nabla }^{2}c\right),$$ (2)

where u is the velocity component in the direction along the flow, D is the analyte diffusivity, and ∇ is the gradient operator. For the second step in the heterogeneous interaction, assuming that the rate of change in concentration of bound antibodies on the surface (solid phase), c_surf, is only a function of the rate of antibody capture occurring on the surface, the conservation of mass equation for the reactive surface can be simplified to

$$\frac{d{c}_{\mathit{surf}}}{dt}=R_H,$$ (3)

where R_H is the rate of capture on the reactive surface and can be presented as²⁹

$$R_H=k_{f}c(c_{s,\max }-c_{\mathit{surf}})+k_r{c}_{\mathit{surf}}.$$ (4)

Here c_{s, max} is the concentration of antigens spotted on the surface. To investigate the proposed reciprocating flow-through system, the time dependent, two-dimensional system of equations introduced above was solved by using COMSOL (COMSOL Inc., Burlington, CA) version 3.4 running on a personal computer with the MS Windows XP operating system, a 2.66 GHz processor, and 4 GB of RAM. For modeling purposes five identical reaction sites, 100 μm in diameter were defined on the lower surface of a two-dimensional channel with a height and length of 0.1 and 6.0 mm, respectively, as shown in Fig. 3. A fully developed parabolic velocity profile of u=6U_m(y∕H)(1−y∕H) with no slip boundary conditions and a maximum velocity of U_m in the center of the channel was assumed for the flow in the channel. The initial concentration of the antibodies in the flow was assumed to be c(t = 0) = C_in. It was also assumed that the interaction between antibodies and antigens started at time zero, and as such, the initial concentration of the antigen/antibody complex was c_surf(t = 0) = 0. Boundary conditions included concentration of C_in at the channel entrance, convective flux at the channel exit (for the open channel) and zero mass flux on all the other boundaries except for the reaction sites with spotted antigens. In order to study the effect of various parameters on the rate of antibody capture, it was expedient to cast the governing equations, their boundaries, and initial conditions in a non-dimensional form as follows:

$$\begin{array}{ccc}& & u^{*}=\frac{u}{U_m},x^{*}=\frac{x}{H},y^{*}=\frac{y}{H},c^{*}=\frac{c}{C_{in}},t^{*}=\frac{t{U}_m}{H},\hfill \\ & & c_{\mathit{surf}}^{*}=\frac{c_{\mathit{surf}}}{c_{s,\max }},k_f^{*}=\frac{k_{f}H}{U_m}{C}_{in},k_r^{*}=\frac{k_{r}H}{U_m}.\hfill \end{array}$$

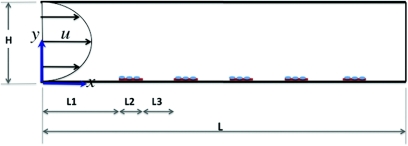
Figure 3.

Schematic showing of the capture chamber (not to scale). The channel height and length are H = 100 μm and L = 6 mm, respectively. Five capture sites of L2 = 100 μm are located on the lower wall of the chamber and are L3 = 800 μm apart. The first capture site is located L1 = 1mm from the channel entrance. A fully developed flow with a parabolic profile is assumed to enter the chamber.

Conservation of mass in the bulk is then normalized as

$$\frac{\partial c^{*}}{\partial t^{*}}+u\frac{\partial u^{*}}{\partial x^{*}}=\frac{1}{Pe}\left(\frac{{\partial }^2{c}^{*}}{\partial x^2}+\frac{{\partial }^2{c}^{*}}{\partial y^2}\right),$$ (5)

where Pe is the Peclet number, a non-dimensional term defined as the ratio of the mass transport by convection to the mass transport by diffusion.³¹

The equation for conservation of mass on the reactive surface is normalized as

$$\frac{d{c}_s^{*}}{d{t}^{*}}=R_H^{*}=\frac{R_{H}H}{c_{s,\max }{U}_m}.$$ (6)

From Eq. 4 the rate of capture term can be expressed in a normalized format as

$$R_H=k_f^{*}{c}^{*}\left(1-c_s^{*}\right)-k_r^{*}{c}_s^{*}.$$ (7)

Boundary and initial conditions in the normalized form can be expressed as

$$\begin{array}{ccc}& & u^{*}\left(y^{*}\right)=6y^{*}(1-y^{*}),c^{*}(t^{*}=0)=1,\hfill \\ & & c^{*}(x^{*}=0)=1,c_s^{*}(t^{*}=0)=0,\hfill \end{array}$$

convective flux: n.( − (1/Pe)∇*c*(x* = L/H)) = n.c*u*, zero flux: n.(−(1∕Pe)∇^*c^*(y^*=±1)+c^*(y^*=±1)u^*)=0, where there is no capture of antibodies, and inward flux: $\partial c^{*}∕\partial t^{*}=k_f^{*}{c}^{*}(1-c_s^{*})-k_r^{*}{c}_s^{*}$ on capture surfaces. In order to simulate the solid-phase antigen-antibody complex formation the conservation of mass equation 5 is coupled with the surface-capture-rate equations 6, 7 through the variable c, concentration of the antibodies in the bulk of the solution. The software then converts the governing equations to a set of time dependent nonlinear algebraic equations. A non-uniform triangular mesh partitions the entire geometric domain into small elements that are connected at nodes. The set of equations are then solved at each node for each dependent variable using the finite element method.

The association and dissociation rate constants for protein antibodies bonding to antigens immobilized at solid surfaces were set to 1.2 × 10⁶ 1/Ms and 2.9 × 10⁻⁴1/s, respectively.³⁰ Some of the other parameters used in the simulation including the initial concentration of the spotted antigen array, concentration of the solution at the inlet, volume of the consumed sample, and the reaction time are listed in Table 1. With an assumed flow rate of 40 μl/min for both flow-through and reciprocating hybridization yields a Reynolds number (Re) of ∼ 0.1 that categorizes the flow as fully laminar.

Table 1.

Initial and boundary conditions used in computational modeling of the interaction channel.

	Passive	Flow-through	Reciprocating
c(t = 0) (M)	3.6 × 10−7	3.6 × 10−7	3.6 × 10−7
Cs, max  (mol/m2)	Five spots of 1.0, 0.3, 0.1, 0.03, or 0.01 mg∕ml
Cin (M)	NA	1 × 10−9	1 × 10−9
Analyte volume (μl)	10	300	10

Immunoassay experimental setup

The experimental setup as described previously³² included a mechanical spin-stand assembly consisting of a NEMA 23 servomotor (PMB21B-00114-00) and an amplifier/controller (PC3406Ai-001-E), both made by Pacific Scientific. MS Visual Basic 2008 was used to develop the graphical user interface to control the motor. Image acquisition was performed using a digital video recording system including a high-speed camera (Basler A301bc, 640×480 pixels, 80 fps max, 10×zoom lens), a strobe light (PerkinElmer MVS-4200), and a retro-reflective fiber optic sensor (Banner D10 Expert Fiber-Optic Sensor), and a personal computer running Windows Vista Operating System. To capture images, a reflective rectangular tape was placed on the edge of the CD to actuate the fiber optic sensor. As the CD rotated, the reflective tape passed underneath the sensor, triggering the camera and strobe light to capture one image frame per rotation. A Hewlett Packcard ScanJet 9200 scanner was employed to digitize the images of developed arrays on the disks at the end of each experiment.

Fabrication of the microfluidics CD

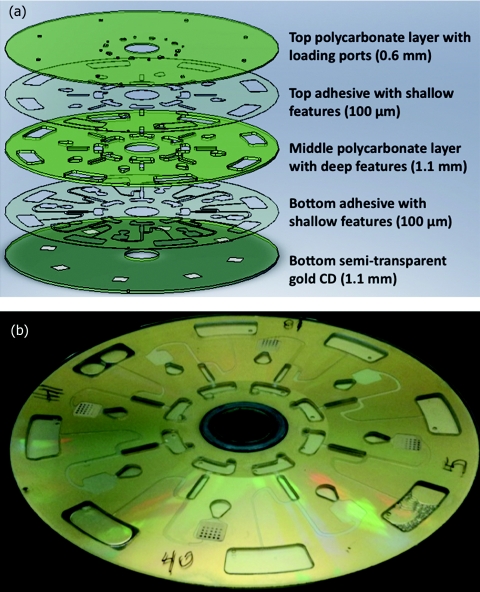
The fluidic system was designed using SolidWorks 2007 (SolidWorks Corporation, Concord, MA) and fabricated by layered assembly of polycarbonate plastic parts and pressure sensitive adhesives as depicted in Fig. 4. Deep features were machined in 1.1 mm polycarbonate sheets (McMaster-Carr, Santa Fe Springs, CA) using a QuickCircuit 5000 CNC router machine (T-Tech Corporation, New Morgan, PA). Microchannels and the reaction chamber were patterned in a 100-μm-thick pressure sensitive double adhesive (DFM 200 made by FLEXcon, Spencer, MA) using a Graphtec CE-2000 vinyl cutter (Graphtec America Inc., USA). All loading and ventilation holes were drilled in a blank DVD (0.6 mm thick) using the QuickCircuit CNC. The bottom layer consisted of a translucent CD (1.2 mm thick) coated with 100 nm of gold on which were cast eight 6 × 6 mm nitrocellulose membranes (Grace Bio-Labs, Bend, OR). All the layers were then aligned and bonded together to create a fluidic system with a diameter of 120 mm and a total thickness of 3.5 mm.

Figure 4.

(a) Schematic drawing of the microfluidic CD fabricated from 3 thick polycarbonate plates bonded together with 2 pressure sensitive double-sided adhesive layers. (b) Photograph of an assembled CD with developed IgG arrays.

Microarray printing

Immunoglobulin G proteins (Jackson ImmunoResearch Laboratories, West Grove, PA) with 5 different concentrations ranging from 0.1 to 0.001 mg/ml and 3 Burkholderia antigens with concentrations ranging from 0.5 to 1.0 mg/ml, prepared as described previously,²⁸ were spotted onto nitrocellulose membranes on semi-translucent gold-coated disks using an OmniGrid 50 array printer (Genomic Solutions, Holliston, MA). In the case of Burkholderia, each antigen of the same concentration was printed 3 times at different area of the pads.

The use of human immunoglobulins to optimize assay conditions

All reagents and buffers were aliquoted for use in both manual and centrifugal experiments carried out side-by-side using nitrocellulose membranes cast on CDs to minimize experimental variations. For manual experiments membranes were dehydrated with Protein Array Blocking Buffer for 30 min and then incubated with Alkaline Phosphatase-conjugated goat anti-human secondary antibody diluted to 1/100 in protein blocking buffer for 1 h at room temperature. After 3 washes with TTBS buffer containing Tris (hydroxymethyl)-aminomethane (Tris), pH 7.6, containing 0.05% (vol/vol) Tween 20 and 0.5 M NaCl, the slides were developed with 1-step Nitro-Blue Tetrazolium Chloride/5-Bromo-4-Chloro-39-Indolyphosphate p-Toluidine Salt (NBT/BCIP) substrate (Thermo Fisher Scientific, Walthan, MA). Immediately after the spots were developed, the reaction was terminated by two washes with deionized (DI) water and the disks were dried with a brief centrifugation at 3000 rpm. Centrifugal-based assays were performed by sequential application of the reagents and buffers to the microfluidic system in the same order. At each step, 25 μl of liquid was injected into the loading chamber; the disk was mounted onto the spin-stand and rotated at angular speeds varying with time according to the profile presented in Fig. 2b. Incubation times for each step varied according to Table 2. The disks were dried by piercing the pressure chambers, to allow ventilation, followed by centrifugation. Images of the developed arrays on both disks were then digitized using a Hewlett Packard ScanJet 9200 scanner and the spot intensities were quantified using Perkin Elmer QuantArray software. The results were imported into a Microsoft Excel Spreadsheet and analyzed.

Table 2.

Comparing different steps followed in manual and reciprocating methods for developing IgG microarrays.

	Manual	Reciprocating
Blocking buffer	30 min on a rocker	1 min
Goat anti-human IgG conjugated with AP	60 min on a rocker	Varying (2.5, 5, 7, or 20 min)
TTBS	Three quick washes and 3 washes of 5 min	2.5 min
TBS	Three quick washes and 3 washes of 5 min	1.5 min
NBT∕BCIP substrate	4 min	3.5 min
DI water	5 min	1.5 min

Screening assays using Burkholderia antigens

The probing procedure was performed as listed in Table 1 with an additional incubation step with sera of infected and naive individuals (collected in Singapore) followed by additional washing steps with TTBS before applying secondary antibody. The sera were diluted to 1/200 in Protein Array Blocking Buffer containing a final concentration of 30% E. coli lysate (McLabs, San Francisco, CA) and incubated at room temperature for 1 h on a rocking platform with frequency of 0.5 Hz.

RESULTS AND DISCUSSION

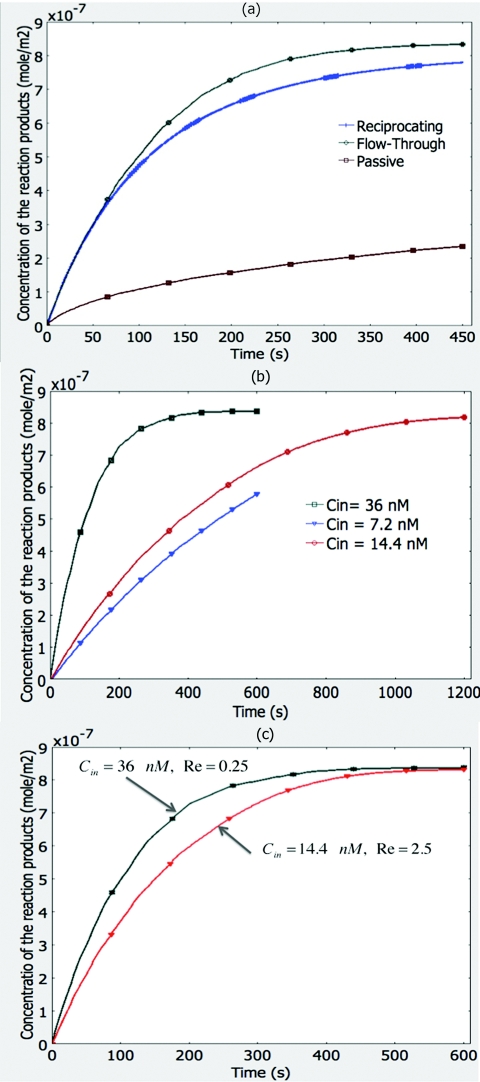
Increasing the incidence of encounters in bimolecular interactions is of paramount interest in microarray technology. In small structures and flows with low Re in the range of smaller than 1–10, molecular diffusion is considered the primary method of transportation for molecules in the bulk of the flow to the molecules bound at the solid phase. Molecular diffusion, which is the movement of particles by Brownian motion from more concentrated to less concentrated spaces as described by Darcy's law is a slow and inefficient process.³⁰ Research studies have demonstrated that bimolecular interactions in micro-domains could be increased by inducing the flow streamlines to cross each other, a phenomenon known as chaotic advection, and hence, promoting local mixing.^{33, 34} That is why we designed our fluidic system to utilize centrifugal and capillary forces as well as pneumatic pressure to promote mixing and increase the frequency of bimolecular encounters. Through a series of numerical simulations we studied the performance of the system, and in particular, the effectiveness of flow reciprocation upon the incidence of encounters between solid-phase-bound antigens and antibodies. We used the parameters of goat anti-human IgG antibodies dissolved in the liquid phase and human IgG proteins spotted on the solid phase and the kinetics of complex formation between them to solve the set of equations introduced in the Materials and Methods section. The simulation results presented in Fig. 5a compare the rate of complex formation between antigens and antibodies for different incubation modes: passive, single flow-through, and reciprocating flow. These graphs demonstrate similar results for both single flow-through and reciprocating flow regimes. Reciprocation of the flow promotes almost the same fast rate of complex formation while it consumes only a fraction of the sample volume. The single flow-through mode achieves equilibrium state after 7 min; while the reciprocating flow mode reaches about 93% completion. This decrease is predictable since the rate of complex formation decreases with time as the flow reciprocates and the concentration of the antibodies in the bulk solution decreases. In comparison, the passive diffusion mode is much slower (about 23% completion after 7 min) due to the small diffusivity of the antibodies in the bulk of the solution. Influence of the antibody concentration on the rate of complex formation is demonstrated in the simulation results presented in Fig. 5b. The figure shows the concentration of the complex as a function of time in a flow-through mode for three initial antibody concentrations of 7.2, 14.1, and 36.0 nM. The rate of complex formation between antigens and antibodies reaches its equilibrium state in a longer period of time for smaller initial antibody concentrations because they will have to travel longer distances to reach the surface where antigens are spotted. One way to compensate for the small antibody concentration and boost complex formation kinetics is to transport the antibodies in the solution faster over the capture surface by increasing the velocity of the flow. The simulation results presented in Fig. 5c demonstrate this by comparing two flow-through modes with initial antibody concentrations of 36 nM and 14 nM and the Re of 0.25 and 2.5, respectively. Both modes reach the equilibrium state in about 8 min.

Figure 5.

Simulation results. (a) Comparing three modes of incubation: Single flow through, reciprocating flow, and passive diffusion between human IgG antigens and a goat anti-human IgG antibodies. (b) Effect of the antibody concentration on the rate of complex formation. Antigen-antibody complex formation decreases and reaches an equilibrium state in a longer time as the initial concentration of the analyte decreases. (c) Influence of the flow Reynolds number on the rate of complex formation. Antigen-antibody complex formation increases and reaches an equilibrium state earlier as the flow velocity increases. This difference is more visible for antibodies with smaller initial concentration.

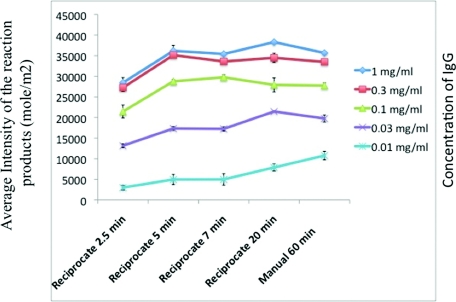
We then set out to reconcile the theoretical results with experimental data. Our first goal was to calibrate the reciprocating flow system to get results comparable with conventional microarray processing methods in a shorter period of time and with a fraction of the initial consumption of antibodies. We pursued this by probing arrays of human serum (IgG) spots of serially diluted concentrations with alkaline phosphatase-conjugated goat anti-human IgG secondary antibody under varying incubation times, flow rates, and number of washes between incubations for preventing non-specific adsorption. Figure 6 presents the average spot intensities of developed IgG microarrays for different incubation times. Table 2 shows the optimal times for performing other incubation and washing steps. A reciprocating cycle of 30 s equivalent to a Re of ∼0.25 was used for experiments carried out under flow reciprocation. The initial antibody concentration was kept constant at 36 nM. The curves demonstrate that after about 5 min of incubation with flow reciprocation, the complex formation reaches its equilibrium state and generates the same spot intensity when compared with the results from a 1 h incubation using the conventional method that was performed with constant mixing on a rocker.

Figure 6.

Experimental results; comparing the intensities of IgG microarrays developed using the reciprocating flow system with different incubation times and intensities of IgG microarrays developed using the manual method with incubation time of 1 h.

In order to evaluate our reciprocating flow system for performing immunoassay using human sera, we probed microarrays of Burkholderia antigens with infected and naive serum samples and tested the system using the calibration data obtained from our prior experiments with human sera. Figure 7a compares the normalized signal intensities of arrays developed using both the manual and reciprocating flow methods. In order to account for the background noise varying over different arrays, average intensity of the IgG control spots on each array was used to normalize the intensities of spots on the same array. Data presented under infected and naive categories are the average of data collected over all arrays probed with infected and naive sera, respectively. Data presented in this figure shows higher signal intensity for arrays developed using the manual method. However, this difference is due to a higher background noise, because the same trend is repeated in both results categorized as infected and naive. We demonstrated this relative effect in Fig. 7b where the ratio of average signal intensities of arrays probed with infected sera over that of the arrays probed with naive sera is plotted and compared between the manual and reciprocating methods. Table 3 shows t-test between infected and naive sera by two methods. All three antigens, BPSL3319, BPSS1492, and BPSL2697 show significant differences between infected and naive sera by both methods. These t-test values demonstrate that the centrifugal method can be used for detection of Burkholderia infection, or by using the adequate binders, for any particular antibody or antigen.

Figure 7.

Experimental results of Burkholderia immunoassay. (a) Comparison of normalized signal intensities of infected and naive sera using reciprocating flow and passive diffusion methods. Data were normalized by dividing the intensity of each spot over the average intensity of positive control IgG spots. (b) Overall ratio of the signal intensity of arrays developed using infected sera to signal intensity of arrays developed using naive sera for both manual and reciprocating methods.

Table 3.

Comparing the t-test between infected and naïve sera. All three antigens show significant differences between infected and naïve sera in both manual and flow-reciprocating methods.

Manual (p value)	Reciprocating (p value)
BPSL3319	5.40 × 10−3	2.68 × 10−2
BPSS1492	4.10 × 10−6	2.64 × 10−7
BPSL2697	3.72 × 10−6	1.75 × 10−5

CONCLUSIONS

We have presented a novel solution for the inherent problems of microarray processing on a CD using centrifugal microfluidics. By reciprocating flow between the center and perimeter of a disk with relatively small usable area (100² mm²), we were able to maximize the exposure of the antigen array to the serum solution. In doing so, we employed flow-through microfluidics and active mixing phenomena to develop a faster and semi-automated methodology for processing microarrays. Continuing work is aimed at the complete automation of the assay within the microfluidics CD and will be reported elsewhere.