Abstract
Purpose: With the introduction of flattening filter free (FFF) linear accelerators to radiation oncology, new analytical source models for a FFF beam applicable to current treatment planning systems is needed. In this work, a multisource model for the FFF beam and the optimization of involved model parameters were designed.
Methods: The model is based on a previous three source model proposed by Yang [“A three-source model for the calculation of head scatter factors,” Med. Phys. 29, 2024–2033 (2002)]. An off axis ratio (OAR) of photon fluence was introduced to the primary source term to generate cone shaped profiles. The parameters of the source model were determined from measured head scatter factors using a line search optimization technique. The OAR of the photon fluence was determined from a measured dose profile of a 40×40 cm2 field size with the same optimization technique, but a new method to acquire gradient terms for OARs was developed to enhance the speed of the optimization process. The improved model was validated with measured dose profiles from 3×3 to 40×40 cm2 field sizes at 6 and 10 MV from a TrueBeam™ STx linear accelerator. Furthermore, planar dose distributions for clinically used radiation fields were also calculated and compared to measurements using a 2D array detector using the gamma index method.
Results: All dose values for the calculated profiles agreed with the measured dose profiles within 0.5% at 6 and 10 MV beams, except for some low dose regions for larger field sizes. A slight overestimation was seen in the lower penumbra region near the field edge for the large field sizes by 1%–4%. The planar dose calculations showed comparable passing rates (>98%) when the criterion of the gamma index method was selected to be 3%∕3 mm.
Conclusions: The developed source model showed good agreements between measured and calculated dose distributions. The model is easily applicable to any other linear accelerator using FFF beams as the required data include only the measured PDD, dose profiles, and output factors for various field sizes, which are easily acquired during conventional beam commissioning process.
Keywords: flattening filter free beam, beam source model, head scatter, optimization, TrueBeam
INTRODUCTION
Conventional linear accelerators used flattening filters to achieve uniform dose at specific depths across the treatment field. In recent years, with the introduction of dynamic multileaf collimator (MLC) and optimizing techniques for intensity modulated radiation therapy (IMRT), it has been possible to generate arbitrary dose distributions across the treatment field. Then, there is no longer a need to use a flattening filter to make uniform dose distributions. The flattening filter has several disadvantages, such as increased radiation dose outside of the field due to scattered radiation from the flattening filter, electron contamination, and inefficiency of delivered photon fluence.2 Because of this, the Tomotherapy machine has removed the flattening filter to increase dose rate and consequently reduce beam-on time during treatment.3 Newly developed linear accelerators, such as the TrueBeam™ (Varian Medical System, Palo Alto, CA), are equipped with flattening filter free (FFF) modes4 and can achieve increased dose rate by a factor of 2–4, while reducing the head scatter, out of field exposure to the patient, and leakage dose through the MLC and collimators.
Several studies have been reported regarding the dosimetric properties of a FFF linear accelerator.2, 5, 6, 7, 8, 9, 10 Vassiliev et al.2 investigated increased dose rate, depth dose distributions, lateral dose profiles, total scatter factors, and transmission factors through the MLC of a FFF beam by modifying a commercial linear accelerator. Dose rates increased by a factor of 2.3 (for 6 MV) to 5.5 (for 18 MV) and it also could achieve lower out of field dose, less variation of total scatter factor, and less variation of the shape of lateral dose profile with depths. Cashmore9 also reported similar results of dosimetric properties for a 6 MV FFF beam using an Elekta Precise linear accelerator. Vassiliev et al., Fu et al., Titt et al., Pönisch et al., Sikora et al., and Sawkey et al. also reported great benefits of the FFF linear accelerators using Monte Carlo (MC)-based simulations.5, 6, 7, 8, 10, 11 In addition, some of them suggested novel methods of beam source modeling that could be used to improve the speed of MC-based dose calculation.8, 10 However, these methods are computationally intensive and it is difficult to apply them in clinical treatment planning.
Treatment planning systems (TPSs) have used various analytical models to improve computational efficiency. Noteworthy is that analytical source models using two focal source planes have been suggested to represent head scatter factors at arbitrary positions and to model dose distributions in the penumbra region with various field shapes.12, 13, 14, 15 More recently, Yang et al.1, 16 proposed a three source model, which used three source planes to count for primary fluence, scattered fluences from the primary collimator, and the flattening filter. The model explained the changes of head scatter factors with various field sizes and most of the calculated head scatter factors agreed with the measured values within 0.4%.
Previously proposed beam source models were designed for conventional linear accelerators equipped with flattening filters. In practice, there has been no technique applicable to model the FFF beam. In general, the dose profile of the FFF beam is peaked at the middle and detailed shapes are different for each linear accelerator and energy. The source model parameters should then be determined based on measured dosimetric data to represent machine specific characteristics using optimization technique.17 The purposes of this study are to establish an analytical beam source model for FFF beams and develop a fast optimization technique to determine optimum model parameters. The previous three source model was modified to accommodate the specifics of FFF beams. Furthermore, a collapsed cone convolution dose calculation algorithm was used to model the dose distribution of the FFF beams, which could be easily applied to the design of a TPS. Measurements using TrueBeam™ were performed to validate the proposed model.
MATERIALS AND METHODS
Background theory
The three source model proposed by Yang et al.1, 16 aimed to calculate delivered photon fluence at an arbitrary point. This model assumed that photon fluence from a linear accelerator can be divided into three components: A primary photon source from the target with a point source distribution, a scattered source with a planar disk shape which is from primary collimators in the gantry head, and a scattered source with exponential terms which is from the flattening filter in the gantry head. We denote these three sources to “primary source,” “first scattered source,” and “second scattered source,” respectively. Each source distribution function can be expressed in the following equations:
| (1) |
where Srcprimary is a primary source strength per unit area, Srcsp is a first scattered source strength per unit area from the primary collimator, and Srcsf is a second scattered source strength per unit area from the flattening filter. R01 and R02 are the inner radius and outer radius of the planar disk-shaped source. Photon fluence at any arbitrary position can be calculated by integrating the above strength functions with a backprojected area on each source plane. The general form of integration can be expressed as
| (2) |
where Asrc1, Asrc2, and Asrc3 are the projected area on primary source plane, first scattered source plane, and second scattered source plane through block or MLC aperture. FISW̱src1, FISW̱src2, and FISW̱src3 are the inverse square law factors to consider the effect of beam divergence. The distances from isocenter to each source plane are usually 100, 96, and 87.5 cm, which are from the results of Monte Carlo simulations in a previous published paper.1 A schematic diagram to represent the geometrical relationships of various parameters is illustrated in Fig. 1.
Figure 1.
Schematic diagram to calculate delivered fluence at a point of calculation using three source beam model.
Modification for FFF beam
A FFF beam generates a cone shaped dose profile due to the absence of the flattening filter. The main goal of FFF beam source modeling is to reproduce the measured dose profiles as close as possible for various clinical field sizes. Such dose profiles are from the nonuniform fluence distribution interacting with a media. To account for this, an off axis ratio (OAR) of the photon fluence to the previous three source model was introduced. Also, it was assumed that second scattered source (Srcsf) had nonzero strength to account for any potential, albeit small, contributions of scattered photons from the target, monitoring chamber, and other structures in the gantry head. The modified source model can be expressed as
| (3) |
where R(rb) is an OAR value of the photon fluence at a distance rb. OAR is normalized by the center value. rb is the projected off axis distance to a reference plane (e.g., SAD 100 cm). Fopen(xb,yb,zb) is an “opened ratio factor” through the edge of block or MLC. Because the voxel size for a dose (or fluence) calculation ranges from 2.5 to 10 mm and is limited by calculation time, it is important to consider the partially opened (or blocked) ratio of the delivered fluence at each voxel through the edge of block or MLC. Fopen is an important parameter in determining the exact dose shape in the penumbra region. We divided each one voxel to 8×8×8 subvoxels and examined whether each subvoxel is blocked or not through the block or MLC leaves. Then, Fopen was defined to the number of passed subvoxels divided by the number of total subvoxels. R(rb) is determined from measured dose profile data acquired during the beam commissioning process. The detailed method to determine optimized R(rb) will be described in Sec. 2E.
Optimization of the parameters in the multisource model
Optimum Cp, Csp, A0, k, R01, and R02 in the source distribution functions can be determined by comparing measured head scatter factors with calculated factors for various field sizes. For circular field sizes, head scatter factor (Sc) can be simply expressed by modifying Eqs. 1, 2 (Ref. 1)
| (4) |
where Rsp and Rsf are the projected radius of the field from isocenter to each plane of Srcsp and Srcsf through the beam aperture. The calculated Sc values can be fit to the measured Sc values by adjusting optimum coefficients such as Cp, Csp, A0, k, R01, and R02. A line search method18 based on steepest decent gradient method was used to determine optimum parameters. In this method, the objective function and gradient values of each parameter are defined as
| (5) |
| (6) |
where Xi is an optimizing value such as Cp, Csp, A0, k, R01, and R02. ri is the radius of equivalent circular fields from the measured square fields. As the objective function F is decreased, the calculated Sc becomes closer to the measured Sc. To reduce F, each Xi was updated with a proper step length given
| (7) |
where λi is a step length characterizing the decreasing rate of the parameter Xi. Its valuable is determined empirically. If the decreasing ratio of Xi is too large, λi is reduced by a factor of 0.5. Equation 7 was repeated until the decreasing rate of F per optimization iteration reached a tolerance value. The initial step length and tolerance level were set to 0.05 and 0.0001.
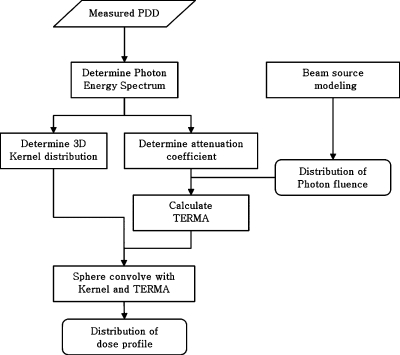
Dose calculation
A general collapsed cone convolution algorithm was implemented to convolve total energy released per unit mass (TERMA) with the kernel distribution for the dose calculation. The flow chart for the dose calculation procedure is illustrated in Fig. 2. A detailed explanation of dose calculation algorithm is not the focus of this study. A simple description of the process of the implemented dose calculation algorithm is as follows: The energy spectrum for photon beam was determined using measured percent depth dose (PDD) data. It was assumed that the spectrum distribution with photon energy followed the log-normal distribution given in Eq. 8. It has been shown that this model simulates the spectrum of MV photon for medical linear accelerator well.19
| (8) |
where I(E) is the relative photon intensity for energy E. The shape of the photon spectrum can be described with two parameters: Mean value μ and standard deviation σ. A line search optimization method was also used to determine the optimum μ and σ. An objective function was defined for the sums of differences between the calculated PDD and measured PDD. An optimization process was similar to that in Sec. 2C. The determined photon spectrum was used to compose a 3D kernel distribution from published monoenergy kernel data20 and used to determine the mean attenuation coefficient for the TERMA calculation. The TERMA value deposited at a point in a media was calculated with precalculated fluence from our source model using the equation below
| (9) |
where is a point (xb,yb,zb), is a delivered fluence at a point in a media, E is a photon energy, μ∕ρ is a linear attenuation coefficient, fsoften is a beam softening factor, and is a density scaled pathway from the source to the point . denoted to all related attenuation factors from the source to the point.
Figure 2.
Flow chart of dose calculation process. The dose calculation algorithm is general collapsed cone convolution algorithm.
To convolve the calculated TERMA with the kernel distribution, 96 collapsed cone lines were spread to all directions from each voxel with the TERMA. The optimum number of cone lines was determined from simple tests by increasing the number of azimuthally angle and zenithal angle. As we increased the number of cone lines to 128, especially the number of zenithal angle, the calculated dose agreed with measured dose slightly better (<1%), but the time of convolution was increased by ∼30; 96 cone lines were an optimum number between the accuracy of calculation and the efficiency of calculation time. Voxel lists that traversed by each cone line were extracted using a ray-tracing method. Then, kernel values at each traversed voxel were assigned by considering penetrated effective length as in the following equation:
| (10) |
where is the dose at a point , is the partial dose from a point to the point , M is the number of cone lines (=96), and is the kernel value from the point to the point , which represents the dose fractions deposited in all directions by electrons and scattered photons originating at primary photon interactions. An accumulative kernel was also used rather than a differential kernel to increase the dose accuracy at the voxel where the source with TERMA and the destination receiving dose are the same.21
Determination of OAR of photon fluence by using optimization
To produce a dose profile closely resembling the measured FFF beam profile, the OAR function of the photon fluence in Eq. 3 should be determined from the measured data for the linac. Direct measurement of the photon fluence is difficult as it usually requires a build-up cap when using an air chamber detector for MV photon energies and the volume of the chamber cavity and build-up cap can blur the fluence profiles. Several alternative methods, such as the deconvolution algorithm or deblurring algorithm to eliminate the detector volume effect,22, 23, 24, 25 have been proposed, but these methods entail extra measurements and complex data processing. Film dosimetry is another option, but it suffers from a tedious process and limited reliability. For these reasons, measured dose values in water from the beam commissioning process are usually used in TPS.
To determine optimum OAR values of photon fluence from the measured dose profiles, we treated them as optimizing parameters. The spatial range of OAR values was set from 0 to 25 cm with 0.5 cm resolution, leading to 50 OAR values to be determined. The line search method described in Sec. 2C was used to fit the calculated dose profile to the measured dose, which yielded the optimum OAR values. To speed up the calculation, we derived an exact partial differential equation of the gradient function by analyzing all processes of the dose calculation with Eqs. 9, 10.
The objective function is defined in the following equation:
| (11) |
where and are the calculated and measured doses at , respectively. N is the total number of calculation points for the profile. The gradient term at OAR value Rj can be expressed as
| (12) |
where Rj is a jth off axis value at radial distance rj that is a projected distance at the reference plane (e.g., SAD=100 cm). The partial differential form of can be expressed with Eqs. 3, 9, 10 as
| (13) |
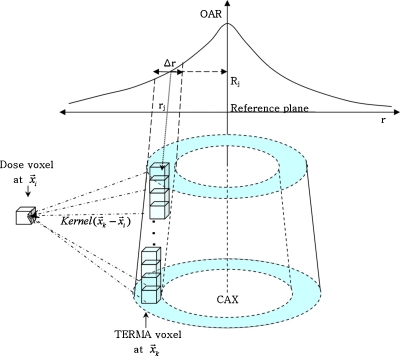
The partial differential with Rj means that only TERMA voxels which are affected by the change of OAR value Rj need to be considered in the differentiation process. Those voxels exist in a truncated cone shell of which the projected inner radius and outer radius to the reference plane correspond to rj−0.5⋅Δr and rj+0.5⋅Δr. Figure 3 describes the distribution of TERMA voxels affected by the change of Rj.
Figure 3.
The distribution of TERMA voxels which are affected by the change of OAR value Rj: Related voxels exist in the truncated cone shell region.
By using Eqs. 2, 9, 12, 13, the exact differential form of the gradient function can be simply expressed as
| (14) |
where L means the number of TERMA voxels in a truncated cone shell at the radial distance rj. Gradient function G(Rj) is independent of the OAR values Rj. Before starting the optimization iteration process, G(Rj) can be easily calculated and stored into memory buffers. Then, the optimization process is sped up since there is no longer a need to calculate G(Ri) again per iteration.
The measured dose profiles from 3×3 to 40×40 cm2 from a TrueBeam™ were collected and the OAR of the photon fluence using the profile of 40×40 cm2 was derived. Then, we calculated dose profiles at various field sizes using the derived OAR and compared them to the measured dose profiles.
Evaluations
Twelve clinical 6 MV FFF fields were used to evaluate the accuracy of the proposed source model. Six MLC field files with approximately 8–10 cm of equivalent field size and another six files with approximately 15–20 cm of equivalent field size were selected from conventional radiation treatment plans of either a brain sarcoma or a pelvis treatment. 2D planar dose distributions for a FFF beam were recalculated with our dose calculation algorithm and compared to measured data at a depth of 5 cm and 100 cm of source to detector distance. A 2D array detector (PTW Seven29, Germany) with water equivalent slab phantoms were used for measurements and the 6 MV FFF beam was delivered by the TrueBeam™ linac. All measured and calculated data were normalized to a center dose value and compared to each other through the gamma index method.26 The criteria of acceptance was set to 3% of dose difference and 3 mm of distance to agreement.
RESULTS
Optimized parameters of multisource model for FFF beam
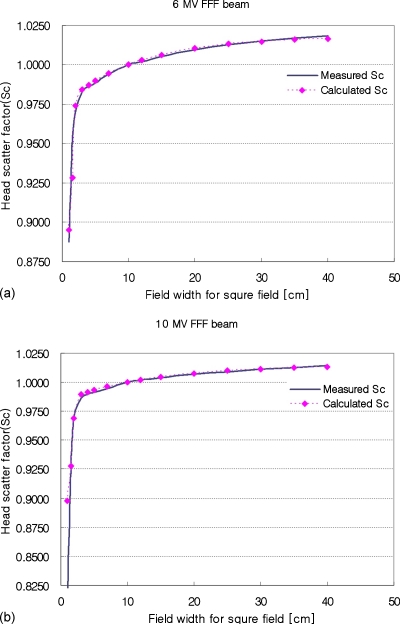
The optimized parameters for the multisource model are listed in Table 1 and the calculated results of head scatter factors (Sc) using the optimized parameters are shown in Fig. 4. The calculated Sc values for a 6 MV FFF beam agreed with the measurements to within 0.2%, except for some small fields. For a field size of 1.5×1.5 cm2, the difference between the measured Sc and calculated Sc was higher by 0.0266 (0.9548 vs 0.9282, respectively). However, the difference was reduced to 0.012 at 1×1 cm2 field size. The difference seemed to be the result of inaccuracies in small field dosimetry, since the measurement for all fields smaller than 3×3 cm2 were performed with an edge detector.
Table 1.
Optimized parameters of the multisource model for a flattening filter free beam on the Varian TrueBeam™ linear accelerator.
| Beam | Cp | Csp (cm2) | A0 (cm−1) | k (cm−1) | R01 [cm] | R02 [cm] |
|---|---|---|---|---|---|---|
| 6 MV FFF | 0.905 45 | 0.026 21 | 0.001 16 | 0.159 54 | 0.20 | 1.17 |
| 10 MV FFF | 0.908 61 | 0.023 76 | 0.000 73 | 0.140 25 | 0.20 | 1.24 |
Figure 4.
Comparison between measured and calculated head scatter factor (Sc) for both 6 and 10 MV FFF beams on the Varian TrueBeam™ linear accelerator.
For the 10 MV FFF beam, calculated Sc values were in good agreement for fields larger than 3×3 cm2, but the differences for small fields were increased up to 9% for a field size of 1×1 cm2. The measured Sc values sharply dropped to very low values (0.8158 for 1×1 cm2), while the calculated value was still fairly high (0.8979 for 1×1 cm2). The decreasing tendency of measured Sc for those small fields seemed to be unnatural and as the source model tried to fit the result during the optimization process. This issue is discussed in Sec. 4.
Optimized off axis ratio and calculated dose profiles
Figure 5 shows the results of an optimized OAR of photon fluence for 6 and 10 MV FFF beams. Because the maximum field width used for optimization was 40 cm, the values larger than 20 cm from the beam center are extrapolated values. The shape of the OAR for photon fluence was different from that of an OAR for dose. The OAR of fluence was much larger than that of radiation dose because most of the fluence was smeared and blurred during the convolution process which modeled the transportation of secondary electrons produced by photon interactions. The 10 MV OAR was smaller than the 6 MV OAR since accelerated electrons with higher energy produce more forward scattered photons when they interacted with the tungsten target.
Figure 5.
Determined off axis ratio of photon fluence for FFF beam. Off axis distance is the projected distance at SAD=100 cm. The optimized values are plotted from 0 to 20 cm and interpolated values were plotted thereafter.
Figures 67 show the measured and calculated dose profiles using an optimized OAR of fluence for 6 and 10 MV FFF beams. All dose values for the calculated profiles agreed with the measured dose profiles within 0.5%, except for some low dose regions for larger field sizes. For the large field sizes, calculated values near the field edge showed slight overestimation by 1%–4%, but it is efficient enough for routine clinical uses.
Figure 6.
Comparison between measured and calculated dose profile at 10 cm depth for a 6 MV FFF beam on Varian TrueBeam™. Field sizes are from 3×3 to 40×40 cm2.
Figure 7.
Comparison between measured and calculated dose profile at 10 cm depth for a 10 MV FFF beam on Varian TrueBeam™. Field sizes are from 3×3 to 40×40 cm2.
Comparison of planar dose distributions for the clinically used fields
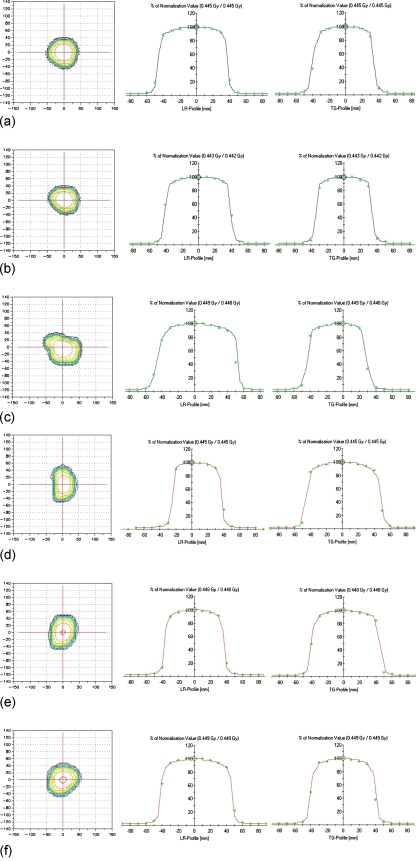
Figures 89 show the comparison between calculated and measured dose distributions from a 2D array detector. All fields except one large field [Fig. 9b] agreed well with measured data for all regions. Passing rates using a gamma index evaluation for the five fields ranged from 96% to 100% when the criteria of dose difference and distance to agreement were set to 3% and 3 mm, respectively. One large field case [Fig. 9b] showed slight underestimation of calculated dose at the field edge where the boundary of the Y jaws and the side of the MLC leaf were identical. The passing rate of that field was 94.22%. When the criteria of dose difference and distance to agreement were changed to 2% and 2 mm, the passing rate of the eleven fields decreased to 90%–95%.
Figure 8.
Evaluations of 2D planar dose distributions for a FFF beam for clinically used small radiation fields. Cases (a)–(c) are conventional brain sarcoma fields of which equivalent field sizes are about 8×8 to 10×10 cm2. LR means the direction from left to right and TG means the direction from table to gantry. The square point at the 2D dose map means “not passed” point for the gamma index evaluation.
Figure 9.
Evaluations of 2D planar dose distributions for a FFF beam for clinically used large radiation fields. Cases (a)–(c) are conventional pelvis treatment fields of which equivalent field sizes are about 15×15 to 20×20 cm2. LR means the direction from left to right and TG means the direction from table to gantry. The square point at the 2D dose map means “not passed” point for the gamma index evaluation.
DISCUSSION
The contributions of the three beam sources to the total photon fluence for a FFF beam were very different from that of a with flattening filter (WFF) beam. Calculated contribution was 84.6% for the primary source, 11.3% for the first scattered source, and 4.1% for the second scattered source for a 40×40 cm2 field size and a 6 MV FFF photon beam. A 10 MV FFF beam also showed similar results, with contributions of the primary, first, and second scattered sources to be 86.6%, 10.4%, and 3.0%, respectively. Compared to the results of a 6 MV WFF beam (82.9%, 6.1%, and 11.0%), the contribution of the primary source was similar, but the first scattered source was increased by 5.3% and the second scattered source was reduced by 6.9%. The results confirmed our assumption that the contribution of the second scattered source is small but nonvanishing for a FFF beam. This source models the scatters arising from structures such as the tungsten target, monitoring chamber, and mirror in the gantry head.
The calculated Sc for 10 MV FFF beam showed an overestimated value (0.898) for a field size of 1×1 cm2 compared to the measured value (0.817). Our source model may have the possibility to generate slight dose disagreements for field sizes of 1.5×1.5 cm2 or less and there are two possible reasons for this. First, there is an inherent limitation of our source model itself in that the inner and outer radius of the annulus for the first scattered source greatly affects the calculated results for such small field sizes when the source plane is integrated with the projected area. In addition, if the field size is smaller than 1×1 cm2, the first scattered source term cannot affect the total fluence and the primary source is still a constant contribution. Only the second scattered source can contribute to the change of total fluence with field size. This causes a limitation of modeling for all small field cases. The second reason is the inherent measurement error for small field dosimetry. The edge detector has an efficiently small sensitive volume which lends itself well to small filed dosimetry. However, accurate alignment of the chamber is a technical problem since any small detector positioning error may produce a large output difference for small fields. Previous studies regarding the three source model have not shown the Sc values at 3×3 cm2 field size or less,1, 27 possibly for this reason.
Dosimetric error for small fields may not be critical in conventional radiation treatment because most of the clinical fields are larger than 3×3 cm2. However, this error may be critical for radiosurgery fields or highly modulated IMRT dynamic fields,28 especially with sliding window techniques where output for small fields is relatively important.
The agreements between the measured and calculated dose profiles were in good agreement and within 0.5%. A slight overestimation was seen in the lower penumbra region near the field boundary for a 40×40 cm2 field size, which was 3% for 6 MV and 4% for 10 MV FFF beams. This can be explained by the limitation of the maximum field size that is used during the optimization process. The optimization process used to determine OAR values was based on a measured dose profile for a field size of 40×40 cm2 and the OAR values were determined from the beam center to 20 cm of off axis distance. OARs larger than 20 cm could not be determined accurately because the dose in that region for a 40×40 cm2 profile was very small due to small, out of field dose and thus it could not contribute well to the objective function. We used interpolated OAR values in that region and that has the possibility to produce a small error in calculated dose. Extra tuning of the OAR in that region may alleviate this problem.
A slight underestimation for irregular fields appeared at the region where the edge of jaw and the side of MLC leaf were identical [Fig. 9b]. The side of leaf contains the tongue or groove face and this face produced less attenuated fluence. This effect is also related to the well-known “tongue and groove effect” of the MLC. Our current model has ignored this effect. Accurate modeling of the dosimetric properties for the novel HDMLC on the Varian linac is another evolving issue and it should be important for IMRT and stereotactic radiosurgery.28 When we enlarged the size of the collimators by 0.5 cm, this dosimetric error disappeared.
The optimization process used to determine the OAR required a predetermined distribution of photon spectrum for the FFF beam since the dose calculation required the energy-weighted mean attenuation coefficient for the TERMA calculation and energy-weighted mean 3D kernel distribution. Furthermore, the optimization of photon spectrum also required OAR values because the PDD is affected by the fluence distribution of neighboring voxels, which is also affected by the OAR. Thus, the two processes of optimization affect each other. To solve this circular process of optimization, the OAR optimization with a well-known WFF beam spectrum was started first and then the distribution of the spectrum with the predetermined OAR was reoptimized. The two processes were repeated until the results were satisfied. Five or six repetitions were sufficient to get optimum results.
We tested our optimization performance on a PC with Intel Core 2 Quad CPU (Q6600, 2.4 GHz) and 3 GB RAM. The time efficiency of the proposed method is compared to a more conventional approach of directly computing Eq. 6. It took ∼20 s to compute the value of the objective function. When the conventional method is employed to calculate a gradient function, the time was found to be two times longer (i.e., 40 s). The total computing time for 15 iterations, as typically required to get the optimal solution, is thus 40 s×15×50=30 000 s, where 50 is the number of OAR values involved in the computation. When the proposed method was used, it took only 330 s because the gradient function was derived directly from Eq. 14. Our method was 90 times faster than that of the conventional approach. On the circular process of optimization, it took about 600 s additionally to optimize each photon spectrum. For five repeated circular optimization processes for the photon spectrum and OAR, total time was 77.5 m.
We used a log-nominal statistic distribution function with only two parameters to describe the virtual photon spectrum. In our experience, this probability function showed good agreement with clinical WFF photon beams from 4 to 15 MV. For the FFF beams, a derived spectrum for a 6 MV was similar to that of a 4 MV WFF photon beam since the major contributions to the objective function were the differences in dose beyond the depth of maximum dose for the PDDs. Table 2 shows the fluence weighted mean energy of the optimized spectrum for field sizes of 3×3 and 40×40 cm2 and this tendency is similar to the previous result by Vassiliev et al.7 However, our spectrum model showed a slight overdose in the build-up region by 5%–20%.
Table 2.
The fluence weighted mean photon energy at optimized spectra at the field sizes of 3×3 and 40×40 cm2. The values in parenthesis are other published results by Vassiliev et al. (Ref. 7).
| Beam | Optimized mean energy and standard deviation (σ) for 3×3 cm2 (MeV) | Optimized mean energy and standard deviation (σ) for 40×40 cm2 (MeV) |
|---|---|---|
| 6 MV FFF | Mean E=1.38, σ=0.94 | Mean E=1.29 (1.28), σ=0.64 |
| 6 MV WFF | Mean E=1.67, σ=1.29 | Mean E=1.56 (1.75), σ=0.83 |
| 10 MV FFF | Mean E=2.22, σ=1.86 | Mean E=2.07, σ=1.73 |
| 10 MV WFF | Mean E=2.74, σ=2.34 | Mean E=2.48, σ=2.10 |
Using only two parameters in Eq. 7 is not sufficient to simulate the real spectrum of the FFF beam on the TrueBeam™ linac. There are two methods to overcome this problem: Using the actual photon spectrum of a FFF beam from Monte Carlo simulations or using an arbitrary spectrum distribution for optimization. However, if we consider an actual beam commissioning process for clinical use, the Monte Carlo method is not a good solution because of its long time-consuming process and its difficulty in describing the true geometry of a FFF linac. Using an arbitrary spectrum distribution function also requires long computational time during optimization due to complicated gradient terms required from the objective function for partial derivation of energy and the local minima problem, which is frequently encountered during optimization. Recently, GPU based computation with parallel processing or cloud computing have been suggested as a good solution to overcome the limitation of computing time.29, 30, 31, 32
CONCLUSION
We developed a multisource model for accurate modeling of FFF beams and designed an optimization process to determine the modeling parameters. The results seemed to be acceptable over all clinical fields. The required data for optimization are only the measured PDD, dose profiles, and output factors for various field sizes, which are easily acquired during conventional beam commissioning. Our algorithm can then be applied to any other linear accelerator using a FFF beam. Further modification may be required to account for MLC scatter correction for small field sizes and implemented into the treatment planning system, since that greatly affects the total dose distributions for IMRT or intensity modulated radiosurgery using small beam apertures. The dosimetric properties of the Varian HDMLC is not yet well-known, but may be similar to that of other linear accelerator used for radiosurgery.
ACKNOWLEDGMENTS
This work was supported by the National Research Foundation of Korea (NRFK) grant funded by the Korean government (MEST) (Grant No. K20901000001-09E0100-00110), the Korea Science and Engineering Foundation (KOSEF) grant funded by the Korea Ministry of Education, Science, and Technology (MEST) (Grant No. K20901000001-09E0100-00110), Varian Medical Systems, NCI (Grant No. 1R01 CA98523), and NSF (Grant No. 0854492). The authors wish to thank Soon-Nyung Huh of University of Florida Proton Therapy Institute for his help in advices and comments for this study.
References
- Yang Y., Xing L., Boyer A. L., Song Y., and Hu Y., “A three-source model for the calculation of head scatter factors,” Med. Phys. 29, 2024–2033 (2002). 10.1118/1.1500767 [DOI] [PubMed] [Google Scholar]
- Vassiliev O. N., Titt U., Pönisch F., Kry S. F., Mohan R., and Gillin M. T., “Dosimetric properties of photon beams from a flattening filter free clinical accelerator,” Phys. Med. Biol. 51, 1907–1917 (2006). 10.1088/0031-9155/51/7/019 [DOI] [PubMed] [Google Scholar]
- Jeraj R., Mackie T. R., Balog J., Olivera G., Pearson D., Kapatoes J., Ruchala K., and Reckwerdt P., “Radiation characteristics of helical tomotherapy,” Med. Phys. 31, 396–404 (2004). 10.1118/1.1639148 [DOI] [PubMed] [Google Scholar]
- Kim T. -H., Zhu L., Suh T. -S., and Xing L., “IMRT inverse planning optimization with non-uniform beams by using total-variation regularization (TVR),” Med. Phys. 37, 57–66 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Titt U., Vassiliev O. N., Pönisch F., Dong L., Liu H., and Mohan R., “A flattening filter free photon treatment concept evaluation with Monte Carlo,” Med. Phys. 33, 1595–1602 (2006). 10.1118/1.2198327 [DOI] [PubMed] [Google Scholar]
- Pönisch F., Titt U., Vassiliev O. N., Kry S. F., and Mohan R., “Properties of unflattened photon beams shaped by a multileaf collimator,” Med. Phys. 33, 1738–1746 (2006). 10.1118/1.2201149 [DOI] [PubMed] [Google Scholar]
- Vassiliev O. N., Titt U., Kry S. F., Pönisch F., Gillin M. T., and Mohan R., “Monte Carlo study of photon fields from a flattening filter-free clinical accelerator,” Med. Phys. 33, 820–827 (2006). 10.1118/1.2174720 [DOI] [PubMed] [Google Scholar]
- Sikora M., Dohm O., and Alber M., “A virtual photon source model of an Elekta linear accelerator with integrated mini MLC for Monte Carlo based IMRT dose calculation,” Phys. Med. Biol. 52, 4449–4463 (2007). 10.1088/0031-9155/52/15/006 [DOI] [PubMed] [Google Scholar]
- Cashmore J., “The characterization of unflattened photon beams from a 6 MV linear accelerator,” Phys. Med. Biol. 53, 1933–1946 (2008). 10.1088/0031-9155/53/7/009 [DOI] [PubMed] [Google Scholar]
- Sawkey D. and Faddegon B. A., “Simulation of large x-ray fields using independently measured source and geometry details,” Med. Phys. 36, 5622–5632 (2009). 10.1118/1.3259729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu W., Dai J., Hu Y., Han D., and Song Y., “Delivery time comparison for intensity-modulated radiation therapy with/without flattening filter: A planning study,” Phys. Med. Biol. 49, 1535–1547 (2004). 10.1088/0031-9155/49/8/011 [DOI] [PubMed] [Google Scholar]
- Sharpe M. B., Jaffray D. A., Battista J. J., and Munro P., “Extrafocal radiation: A unified approach to the prediction of beam penumbra and output factors for megavoltage x-ray beam,” Med. Phys. 22, 2065–2073 (1995). 10.1118/1.597648 [DOI] [PubMed] [Google Scholar]
- Yu M. K. and Sloboca R., “Analytical representation of head scatter factors for shaped photon beams using a two-component x-ray source model,” Med. Phys. 23, 973–984 (1996). 10.1118/1.597827 [DOI] [PubMed] [Google Scholar]
- Jursinic P. A., “Clinical implementation of a two-component x-ray source model for calculation of head-scatter factors,” Med. Phys. 24, 2001–2007 (1997). 10.1118/1.598113 [DOI] [PubMed] [Google Scholar]
- Zhu T. C. and Bjärngard B. E., “Head scatter off-axis for megavoltage x rays,” Med. Phys. 30, 533–543 (2003). 10.1118/1.1556609 [DOI] [PubMed] [Google Scholar]
- Yang Y. and Xing L., “Incorporating leaf transmission and header scatter corrections into MLC leaf sequences for IMRT,” Int. J. Radiat. Oncol., Biol., Phys. 55, 1121–1134 (2003). 10.1016/S0360-3016(02)04417-6 [DOI] [PubMed] [Google Scholar]
- Tillikainen L., Siljamäki S., Helminen H., Alakuijala J., and Pyyry J., “Determination of parameters for a multiple-source model of megavoltage photon beams using optimization methods,” Phys. Med. Biol. 52, 1441–1467 (2007). 10.1088/0031-9155/52/5/015 [DOI] [PubMed] [Google Scholar]
- Nocedal J. and Wright S. J., Numerical Optimization (Springer-Verlag, New York, 1999). 10.1007/b98874 [DOI] [Google Scholar]
- Bloch P. and McDonough J., “Extraction of the photon spectra from measured beam parameters,” Med. Phys. 25, 752–757 (1998). 10.1118/1.598257 [DOI] [PubMed] [Google Scholar]
- Mackie T. R., Bielajew A. F., Rogers D. W. O., and Battista J. J., “Generation of photon energy deposition kernels using the EGS Monte Carlo code,” Phys. Med. Biol. 33, 1–20 (1988). 10.1088/0031-9155/33/1/001 [DOI] [PubMed] [Google Scholar]
- Lu W., Olivera G. H., Chen M. -L., Reckwerdt P. J., and Mackie T. R., “Accurate convolution/superposition for multi-resolution dose calculation using cumulative tabulated kernels,” Phys. Med. Biol. 50, 655–680 (2005). 10.1088/0031-9155/50/4/007 [DOI] [PubMed] [Google Scholar]
- Higgins P. D., Siskind L., Sibata C. H., and Sohn J. W., “Deconvolution of detector size effect for small field measurement,” Med. Phys. 22, 1663–1666 (1995). 10.1118/1.597427 [DOI] [PubMed] [Google Scholar]
- Herrup D., Chu J., Cheung H., and Pankuch M., “Determination of penumbral widths from ion chamber measurements,” Med. Phys. 32, 3636–3640 (2005). 10.1118/1.2128086 [DOI] [PubMed] [Google Scholar]
- Sahoo N., Kazi A. M., and Hoffman M., “Semi-empirical procedures for correcting detector size effect on clinical MV x-ray beam profiles,” Med. Phys. 35, 5124–5133 (2008). 10.1118/1.2989089 [DOI] [PubMed] [Google Scholar]
- Fox C., Simon T., Simon B., Dempsey J. F., Kahler D., Palta J. R., Liu C., and Yan G., “Assessment of the setup dependence of detector response functions for mega-voltage linear accelerators,” Med. Phys. 37, 477–484 (2010). 10.1118/1.3284529 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Low D. A., Harms W. B., Mutic S., and Purdy J. A., “A technique for the quantitative evaluation of dose distributions,” Med. Phys. 25, 656–661 (1998). 10.1118/1.598248 [DOI] [PubMed] [Google Scholar]
- Yan G., Liu C., Lu B., Palta J. R., and Li J. G., “Comparison of analytic source models for head scatter factor calculation and planar dose calculation for IMRT,” Phys. Med. Biol. 53, 2051–2067 (2008). 10.1088/0031-9155/53/8/004 [DOI] [PubMed] [Google Scholar]
- Solberg T., Kavanagh B., and Medin P., in Image Guided and Adaptive Radiation Therapy, edited by Timmerman R. and Xing L. (Lippincott Williams and Wilkins, Baltimore, 2009), pp. 85–98. [Google Scholar]
- Badal A. and Badano A., “Accelerating Monte Carlo simulations of photon transport in a voxelized geometry using a massively parallel graphics processing unit,” Med. Phys. 36, 4878–4880 (2009). 10.1118/1.3231824 [DOI] [PubMed] [Google Scholar]
- Hissoiny S., Ozell B., and Després P., “Fast convolution-superposition dose calculation on graphics hardware,” Med. Phys. 36, 1998–2005 (2009). 10.1118/1.3120286 [DOI] [PubMed] [Google Scholar]
- Hissoiny S., Ozell B., and Després P., “A convolution-superposition dose calculation engine for GPUs,” Med. Phys. 37, 1029–1037 (2010). 10.1118/1.3301618 [DOI] [PubMed] [Google Scholar]
- Pratx G. and Xing L., “GPU computing in medical physics: A review,” Med. Phys. 37 (2010). 10.1118/1.3469122 [DOI] [PubMed]