Randomization-Based Inference within Principal Strata

Abstract

In randomized studies, treatment comparisons conditional on intermediate post-randomization outcomes using standard analytic methods do not have a causal interpretation. An alternate approach entails treatment comparisons within principal strata defined by the potential outcomes for the intermediate outcome that would be observed under each treatment assignment. In this paper, we develop methods for randomization-based inference within principal strata. The proposed methods are compared with existing large-sample methods as well as traditional intent-to-treat approaches. This research is motivated by HIV prevention studies where few infections are expected and inference is desired within the always-infected principal stratum, i.e., all individuals who would become infected regardless of randomization assignment.

1 INTRODUCTION

1.1 Principal Stratification

Sometimes in randomized studies, treatment comparisons conditional on intermediate post-randomization outcomes are of interest. For example, in vaccine studies, a common question of interest is whether infections in vaccinated individuals are more or less severe than infections in unvaccinated individuals (Hudgens and Halloran 2006). Unfortunately, the estimands underlying standard methods typically employed for these comparisons do not have a causal interpretation (Rosenbaum 1984). To address this deficiency, Frangakis and Rubin (2002) proposed a general framework for comparing treatments adjusting for the intermediate post-randomization outcomes. In particular, they defined causal effect estimands within strata determined by a cross-classification of individuals defined by the joint potential intermediate post-randomization outcomes under each of the treatments being compared. Since these “principal strata” are not affected by treatment assignment, they can be conditioned on just as any pre-treatment covariate. Accordingly, causal effect estimands within principal strata do not suffer from the complications of standard post-randomization adjusted estimands.

The simple framework of principal stratification has a wide range of applications. For example, in HIV prevention studies an objective is understanding the effects of a preventive treatment (e.g., vaccine administered prior to infection) on post-infection events, such as severe disease or death. Assessing a treatment’s effect on post-infection outcomes is challenging since such outcomes may only be defined for infected individuals and standard comparisons between infected treated individuals and infected controls are subject to selection bias (Halloran and Struchiner 1995; Hernán, Hernández-Díaz and Robins 2004). Moreover, because the set of individuals who would become infected if assigned treatment is likely not identical to the set of those who would become infected if not assigned treatment, comparisons that condition on infection do not have a causal interpretation. Recently, methods have been developed to assess causal treatment effects on post-infection outcomes in the principal strata of individuals who would be infected regardless of treatment assignment (Hudgens, Hoering and Self 2003; Gilbert, Bosch and Hudgens 2003; Mehrotra, Li and Gilbert 2006; Shepherd, Gilbert, Jemiai and Rotnitzky 2006; Shepherd, Gilbert and Lumley 2007). Similarly, in studies to prevent mother-to-child HIV transmission the outcome of interest is long term HIV infection status among infants not infected at or shortly after birth (Chasela et al. 2010). When infants are randomly assigned treatment at birth, the principal stratum of interest is individuals who would not be infected shortly after birth regardless of treatment assignment. Other settings where principal stratification has been applied include treatment noncompliance (Angrist, Imbens and Rubin 1996; Baker, Frangakis and Lindeman 2007), truncation by death (Robins 1995; Zhang and Rubin 2003) and evaluation of surrogate endpoints (Gilbert and Hudgens 2008; Joffe and Greene 2009).

Methods for inference within principal strata often appeal to large sample frequentist or Bayesian theory. Assumptions typically used to aid in the identification of principal strata membership and draw inference within strata include the stable unit treatment value assumption, independent treatment assignment and monotonicity. However, additional assumptions are needed in order to completely identify principal strata membership in the both treatment groups. For example, assumptions in the form of selection bias models have been suggested to attain identifiability (e.g., see Gilbert et al. 2003; Shephard et al. 2006). These models are helpful if one can elicit prior information regarding the selection bias model parameter (Scharfstein, Halloran, Chu and Daniels 2006; Shepherd, Gilbert and Mehrotra 2007). Alternatively, large sample bounds of the distribution of the outcome of interest in the control group and therefore of treatment effect can be obtained assuming maximum possible levels of positive and negative selection bias (Zhang and Rubin 2003; Hudgens et al. 2003; Imai 2008). These upper and lower bound estimates of treatment effect provide the full range of estimates consistent with the observed data. To draw inference about these estimates, large sample frequentist methods such as profile likelihood CIs (Hudgens and Halloran 2006) or bootstrap tests (Gilbert et al. 2003; Mehrotra et al. 2006) have been employed.

1.2 Randomization-Based Inference

Randomized studies are the clinical trial gold standard for evaluating treatment effects because randomization (i) produces in expectation comparable groups with respect to measured and unmeasured covariates and (ii) provides a basis for statistical inference. Regarding (ii) randomization inference is based on distributions created from the randomization process rather than assuming random sampling of individuals from an infinite population (Koch, Gillings and Stokes 1980; Rubin 1991; Rosenbaum 2002a). Unfortunately, the benefits of conducting a randomized study are lost when conditioning on an intermediate post-randomization outcome, as the treatment and control groups are no longer comparable. Ideally one would like to conduct randomization-based inference within principal strata determined by the set of intermediate potential outcomes. However, while randomization inferential methods have been proposed in the instrumental variable setting (Rosenbaum 1996; Rosenbaum 2002a; Imbens and Rosenbaum 2005; Hansen and Bowers 2009), to date a general approach to randomization inference within principal strata has not been developed.

Another benefit of randomization-based inference is that the methods are exact, allowing for inference in small to intermediate sample size settings where methods based on asymptotic approximations may be inappropriate (Imbens and Rosenbaum 2005). In the HIV vaccine setting, small trials are often employed to screen possible vaccines for larger Phase III efficacy studies (Rida, Fast, Hoff and Fleming 1997). For instance, Mehrotra et al. (2006) describe a proof-of-concept (POC) efficacy trial where the study is ceased after just 50 HIV infections are observed in the vaccine and placebo arms combined. In these small sample settings, Bayesian inference about treatment effects within principal strata may not be ideal if investigators are hesitant to make assumptions regarding prior distributions. On the other hand, large sample frequentist methods may lead to incorrect inferences in such settings. For example, simulation studies have demonstrated inflated type I error of bootstrap tests and under-coverage of bootstrap and Wald based confidence intervals (CIs) when the principal stratum of interest is small (Hudgens et al. 2003; Gilbert et al. 2003; Shepherd et al. 2007; Jemiai, Rotnitzky, Shepherd, and Gilbert 2007). It will be seen that the proposed method lifts these limitations.

1.3 Outline

This paper considers randomization-based methods for inference within principal strata. The main development is an exact test for a causal treatment effect within principal strata. In section 2, the principal stratum exact test (PSET) is developed. Section 3 presents simulation results comparing the PSET to a large sample frequentist approach for testing a treatment effect within principal strata. In Section 4 the PSET is applied to two studies on mother-to-child transmission of HIV. Section 5 provides some empirical comparisons between the PSET and intent-to-treat (ITT) based tests. Section 6 describes an extension of the PSET to allow for adjustments for covariates. In Section 7 exact CIs for treatment effect are derived by inverting the PSET. Section 8 concludes with a discussion and the Appendix includes several proofs.

2 PRINCIPAL STRATUM EXACT TEST

2.1 Assumptions and Notation

Suppose there are n individuals assigned to treatment or control. Assume:

A.1 Stable Unit Treatment Value Assumption (SUTVA) (Rubin 1980)

Treatment assignment of one individual does not affect another individual’s outcomes (no interference) and there are not multiple versions of treatment.

Under SUTVA, let s_i(z) denote the potential intermediate post-randomization out-come and y_i(z) denote the outcome of interest of the i^th individual given treatment assignment z, where z = 0 for control and z = 1 for treatment. Assume the intermediate post-randomization outcome is binary. For ease of presentation, assume the intermediate outcome represents infection status. As such, s_i(z) = 1 if the i^th individual is infected when assigned treatment z and s_i(z) = 0 if uninfected. The principal strata are formed by classifying individuals according to their pair of infection potential outcomes (s_i(1), s_i(0)). The always-infected (AI) principal stratum is defined as the individuals with s_i(0) = s_i(1) = 1, i.e., individuals who would be infected regardless of treatment assignment. Similarly the harmed stratum is defined as those individuals with s_i(0) = 0, s_i(1) = 1; the protected stratum by s_i(0) = 1, s_i(1) = 0; and the immune (never-infected) stratum by s_i(0) = s_i(1) = 0.

The goal of this paper is to develop a principal stratum exact test of treatment effect on a post-infection outcome, y, among individuals within a principal stratum. Assume the stratum of interest is the AI stratum such that the desired comparison is between {y_i(1): s_i(0) = s_i(1) = 1} and {y_i(0): s_i(0) = s_i(1) = 1}. While motivated by infectious disease settings where the AI stratum is of interest, the PSET is applicable to alternative strata such as the immune stratum as well as other settings. For example, if the intermediate variable represents compliance status, the principal strata of interest might be those that are always compliant regardless of assigned treatment (Angrist et al. 1996). Likewise, if the intermediate variable is survival status, the principal strata of interest might comprise those that always survive regardless of treatment assignment (Zhang and Rubin 2003). These other applications are discussed further in Section 8.2.

To develop a PSET of treatment effect on the post-infection outcome, consider testing the sharp null hypothesis

$$H_0:y_i(1)=y_i(0)\text{for}\text{all}i\in \mathcal{A}\mathcal{J},$$ (1)

where 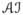≡ {i: s_i(1) = s_i(0) = 1} is the set of individuals in the AI stratum. Using terminology of VanderWeele (2008), the null (1) corresponds to no principal stratum direct effect. An exact test requires the resulting p-value, p, be exact in the sense that Pr[p ≤ α] ≤ α for each α ∈ [0, 1] under the null (Casella and Berger 2002).

While each individual has four potential outcomes (s_i(1), s_i(0), y_i(1), y_i(0)), only two of these outcomes are observed dependent on treatment assignment, either (s_i(1), y_i(1)) or (s_i(0), y_i(0)). Let Z_i denote the treatment assignment for individual i and let Z = (Z₁, …, Z_n). To make inference about treatment effect, the treatment assignment mechanism must be specified or modeled. This paper uses randomization inference whereby the randomization distribution induced by the experimental design forms the basis for statistical inference (Rubin 1991). In particular, the potential outcomes are considered fixed features of the finite population of individuals while Z_i is considered a random variable. Let $S_i^{\mathit{obs}}\equiv Z_i{s}_i(1)+(1-Z_i)s_i(0)$ denote the observed intermediate post-randomization outcome and define $Y_i^{\mathit{obs}}$ analogously. Both $S_i^{\mathit{obs}}$ and $Y_i^{\mathit{obs}}$ are random variables since they depend on Z_i. To develop a test of (1), assume independent treatment assignment:

A.2 Independent treatment assignment

Pr[Z = z] = Pr[Z = z′] for any z, z′ such that ${\sum }_{i=1}^n{z}_i={\sum }_{i=1}^n{z}_i^{\prime }$ where z = (z₁, …, z_n), ${\mathit{z}}^{\prime }=(z_1^{\prime },\dots ,z_n^{\prime })$ are treatment assignment vectors.

If principal stratum membership was known, for the AI stratum in particular, the development of an exact test of (1) would be straight forward. As assumptions A.1 and A.2 are generally not sufficient to identify principal stratum membership, an additional assumption often made is that treatment does not cause infections:

A.3 Monotonicity: s_i(1) ≤ s_i(0) for all i ∈ {1, …, n}

Assumption A.3 identifies AI stratum membership for individuals assigned to treatment. Specifically, A.3 implies infected treated individuals (i.e., $S_i^{\mathit{obs}}=Z_i=1$) would have become infected if assigned control (i.e., s_i(0) = 1) and are therefore members of the AI stratum i.e., $\{i:S_i^{\mathit{obs}}=1,Z_i=1\}\subseteq \mathcal{A}\mathcal{J}$. Unfortunately, A.1–A.3 do not identify AI stratum membership for individuals in the control group because infected control individuals are a mixture of members of the AI and protected strata.

In Section 2.3 the PSET of (1) is developed under A.1-A.3. In infectious disease settings A.1 may be violated due to interference between individuals, although this is unlikely in certain settings such as mother-to-child transmission studies. A.2 generally holds in randomized studies. While A.3 cannot be verified from the observable data, it has testable implications. For example, A.3 implies a non-negative average causal treatment effect on infection, i.e., $n^{-1}{\sum }_{i=1}^n\{s_i(0)-s_i(1)\}\ge 0$. Should the data provide evidence to the contrary, A.3 can be rejected. Even if the proportion infected is not higher in the treated arm, the veracity of A.3 may be questionable in some settings. For example, results from a recent HIV vaccine trial (Buchbinder et al. 2008) suggest certain vaccine recipients were more likely to be infected than placebo recipients. Similar concerns arise in vaccine development for other viruses (Greenwood 1997, Tirado and Yoon 2003). A vaccine that causes many infections is likely of no utility, making inference about post-infection endpoints moot. However, if a vaccine causes a few infections but prevents many more, then effects on post-infection endpoints are of interest but invoking A.3 may be dubious. Violations of A.3 are discussed further in Sections 3 and 4.

2.2 Example with Binary Outcome

Suppose for now that y_i(z) is a binary variable where y_i(z)=1 if the event of interest occurs (e.g., death or severe disease), 0 otherwise. To test (1), first imagine we know exactly which individuals are in 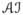. Then the following 2 × 2 table can be constructed

$$\begin{array}{cccc}& \text{Event}& \text{No}\text{Event}& \\ \text{Treatment}& {\sum }_{i\in \mathcal{A}\mathcal{J}}{Z}_i{Y}_i^{\mathit{obs}}& {\sum }_{i\in \mathcal{A}\mathcal{J}}{Z}_i(1-Y_i^{\mathit{obs}})& {\sum }_{i\in \mathcal{A}\mathcal{J}}{Z}_i\\ \text{Control}& {\sum }_{i\in \mathcal{A}\mathcal{J}}(1-Z_i)Y_i^{\mathit{obs}}& {\sum }_{i\in \mathcal{A}\mathcal{J}}(1-Z_i)(1-Y_i^{\mathit{obs}})& {\sum }_{i\in \mathcal{A}\mathcal{J}}(1-Z_i)\\ & {\sum }_{i\in \mathcal{A}\mathcal{J}}{Y}_i^{\mathit{obs}}& {\sum }_{i\in \mathcal{A}\mathcal{J}}(1-Y_i^{\mathit{obs}})& m\end{array}$$ (2)

where m ≡ 1 is the number of individuals in 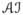. Under the sharp null, $Y_i^{\mathit{obs}}=y_i(0)$ implying (2) can equivalently be written as

$$\begin{array}{cccc}& \text{Event}& \text{No}\text{Event}& \\ \text{Treatment}& {\sum }_{i\in \mathcal{A}\mathcal{J}}{Z}_i{y}_i(0)& {\sum }_{i\in \mathcal{A}\mathcal{J}}{Z}_i(1-y_i(0))& {\sum }_{i\in \mathcal{A}\mathcal{J}}{Z}_i\\ \text{Control}& {\sum }_{i\in \mathcal{A}\mathcal{J}}(1-Z_i)y_i(0)& {\sum }_{i\in \mathcal{A}\mathcal{J}}(1-Z_i)(1-y_i(0))& {\sum }_{i\in \mathcal{A}\mathcal{J}}(1-Z_i)\\ & {\sum }_{i\in \mathcal{A}\mathcal{J}}{y}_i(0)& {\sum }_{i\in \mathcal{A}\mathcal{J}}(1-y_i(0))& m\end{array}$$ (3)

For randomization-based inference, the potential outcomes are fixed features of the finite population. The column totals of (3) depend only on the potential outcomes and thus can be considered fixed. Therefore, conditional on the row totals, (1) can be tested by applying Fisher’s exact test to (2) where the p-value is obtained by calculating the probability of each possible table using the hypergeometric distribution.

Because principal strata membership is not completely known, we cannot construct (2). Instead the following table of infected individuals is observable

$$\begin{array}{cccc}& \text{Event}& \text{No}\text{Event}& \\ \text{Treatment}& \sum Z_i{S}_i^{\mathit{obs}}{Y}_i^{\mathit{obs}}& \sum Z_i{S}_i^{\mathit{obs}}(1-Y_i^{\mathit{obs}})& \sum Z_i{S}_i^{\mathit{obs}}\\ \text{Control}& \sum (1-Z_i)S_i^{\mathit{obs}}{Y}_i^{\mathit{obs}}& \sum (1-Z_i)S_i^{\mathit{obs}}(1-Y_i^{\mathit{obs}})& \sum (1-Z_i)S_i^{\mathit{obs}}\\ & \sum S_i^{\mathit{obs}}{Y}_i^{\mathit{obs}}& \sum S_i^{\mathit{obs}}(1-Y_i^{\mathit{obs}})& \sum S_i^{\mathit{obs}}\end{array}$$ (4)

where here and in the sequel Σ denotes the summation over i = 1, …, n.

To develop an exact test of (1), information from (4) can be used to make inference about the unobservable table (3). Under A.3, $Z_i{S}_i^{\mathit{obs}}=1$ implies i ∈ 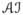. Thus assuming A.3, under (1) the observable table (4) can be written as

$$\begin{array}{cccc}& \text{Event}& \text{No}\text{Event}& \\ \text{Treatment}& {\sum }_{i\in \mathcal{A}\mathcal{J}}{Z}_i{y}_i(0)& {\sum }_{i\in \mathcal{A}\mathcal{J}}{Z}_i(1-y_i(0))& {\sum }_{i\in \mathcal{A}\mathcal{J}}{Z}_i\\ \text{Control}& \sum (1-Z_i)S_i^{\mathit{obs}}{y}_i(0)& \sum (1-Z_i)S_i^{\mathit{obs}}(1-y_i(0))& \sum (1-Z_i)S_i^{\mathit{obs}}\\ & \sum S_i^{\mathit{obs}}{y}_i(0)& \sum S_i^{\mathit{obs}}{y}_i(0)& \sum S_i^{\mathit{obs}}\end{array}$$ (5)

Table (5) differs from (3) only in that the principal stratum membership of control recipients who become infected is unknown. This problem is analogous to conducting a test in the presence of nuisance parameters. The following section will detail how an exact p-value for testing (1) can be obtained by conducting exact tests over a range of plausible values of the nuisance parameters and defining the exact p-value as a function of the largest p-value from this set of exact tests.

2.3 PSET Development

Now assume that y_i(1) and y_i(0) are any type of event and not necessarily binary. Let ${\mathit{Y}}_1^{ai}\equiv \{Y_i^{\mathit{obs}}:Z_i=1,i\in \mathcal{A}\mathcal{J}\}$ and ${\mathit{Y}}_0^{ai}\equiv \{Y_i^{\mathit{obs}}:Z_i=0,i\in \mathcal{A}\mathcal{J}\}$ and define $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})$ as the p-value for an exact randomization-based test of (1) assuming AI membership were known. For example, if no ties exist in ( ${\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai}$) then the usual exact Wilcoxon rank sum test could be employed to compute $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})$.

As illustrated in Section 2.2, the set of AI stratum membership indicators for the infected control individuals can be viewed as unknown nuisance parameters. Analogous to Barnard’s test, an exact test can be constructed by conducting a test for each possible AI subset of the infected control individuals and reporting the largest p-value (Barnard 1947). Unfortunately, this approach is overly conservative because it almost always fails to reject (1). Specifically, the set of possible AI subsets from infected control individuals includes subsets comprising only one individual. Provided there is at least one infected control individual with a post-infection outcome y_i(0) that is not significantly different from {y_i(1): s_i(1) = 1, Z_i = 1}, (1) will not be rejected. Furthermore, this approach ignores information available about the AI stratum. While the observed data do not identify which infected control individuals are in the AI stratum, the data do provide some information about the number of control individuals in the AI stratum. Thus an alternative approach is to view the number of control individuals in the AI stratum as the nuisance parameter and to obtain bounds for possible values of this nuisance parameter based on the observed data.

Let M₀ ≡ (1 − Z_i) and M₁ ≡ Z_i be the number of individuals in 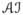assigned control and treatment such that M₀ + M₁ = m. Since the number of individuals in 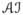does not depend on Z, m is fixed, whereas M₀ and M₁ are random variables. Under A.3, $M_1\equiv \sum I[Z_i=S_i^{\mathit{obs}}=1]$ is observable. In contrast, M₀ is not observable.

Suppose contrary to fact that M₀ is observed. Then an exact p-value could be obtained by performing an exact test for all possible selections of M₀ individuals from {i: Z_i = 0, $S_i^{\mathit{obs}}=1$} and taking the maximum of the resulting p-values. Define this p-value as

$$p^{ai}(M_0)\equiv max\{p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0):{\mathit{Y}}_0\in \mathrm{\Omega }(M_0)\}$$ (6)

where Ω(M₀) of size equals the set of subsets of { $Y_i^{\mathit{obs}}:Z_i=0,S_i^{\mathit{obs}}=1$} of size M₀.

Although M₀ is not observed, it is bounded above by $\sum I[Z_i=S_i^{\mathit{obs}}=1]$. Moreover, the observed M₁ provides information about m and thus M₀. Specifically, conditional on the total number assigned treatment ΣZ_i, under assumption A.2 an exact 100(1 − γ)% CI for m, say C_γ ≡ [L_m, U_m], can be computed based on $\sum Z_i{S}_i^{\mathit{obs}}={\sum }_{i\in \mathcal{A}\mathcal{J}}{Z}_i$ using standard results about simple random sampling (e.g., Thompson 2002). Then, following Berger and Boos (1994), define

$$p_{\gamma }^{ai}\equiv max\{p^{ai}(\stackrel{\sim }{m}-M_1):\stackrel{\sim }{m}\in C_{\gamma }\}+\gamma .$$ (7)

The following proposition indicates that $p_{\gamma }^{ai}$ is an exact p-value for testing (1).

Proposition 1

For any γ ∈ [0, 1], $Pr[p_{\gamma }^{ai}\le \alpha ]\le \alpha$ for all α ∈ [0, 1] under H₀ (1).

The choice of γ should be made prior to looking at the data in a formal hypothesis testing scenario as the proposition holds only assuming γ is fixed. Section 3 presents simulation studies which provide empirical evidence suggesting γ = α/2 may be recommended in certain settings. For tests where p^ai(m̃ − M₁) tend to decrease as m̃ increases, letting $U_m=\sum S_i^{\mathit{obs}}$ and computing a one-sided (1 − γ)% CI for m to obtain L_m should result in a test with higher power compared to using a two-sided CI.

2.4 Computations

Calculating p^ai(M₀) can be computationally intensive as it requires performing $\left(\begin{array}{c}\sum (1-Z_i)S_i^{\mathit{obs}}\\ M_0\end{array}\right)$ exact tests corresponding to Ω(M₀). In many settings, the computation requirements can be reduced by implicitly determining $max\{p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0):{\mathit{Y}}_0\in \mathrm{\Omega }(M_0)\}$ without having to calculate $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0)$ for each Y₀ ∈ Ω(M₀). The proposition below shows how p^ai(M₀) can be implicitly determined for a particular class of test statistics.

First consider the situation where AI membership is known such that the exact p-value $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})$ can be calculated. Let j₁, j₂, …, j_m denote the labels of individuals in AI such that 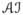= {j₁, …, j_m} and ${\mathit{Y}}_1^{ai}\cup {\mathit{Y}}_0^{ai}=\{Y_{j1}^{\mathit{obs}},Y_{j2}^{\mathit{obs}},\dots ,Y_{jm}^{\mathit{obs}}\}$. Let y^ai denote the vector ( $Y_{j1}^{\mathit{obs}},Y_{j2}^{\mathit{obs}},\dots ,Y_{jm}^{\mathit{obs}}$), which is fixed under the null (1), and correspondingly let Z^ai = (Z_j1, Z_j2, …, Z_jm). Following Rosenbaum (2002a), let t(Z^ai, y^ai) denote the test statistic corresponding to $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})$. Assuming large values of t(Z^ai, y^ai) are considered evidence against the null (1), the exact one-sided p-value is calculated as

$$p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})=\frac{\mid \{{\mathit{z}}^{ai}\in {\mathrm{\Omega }}_m^{ai}:t({\mathit{z}}^{ai},{\mathit{y}}^{ai})\ge t({\mathit{Z}}^{ai},{\mathit{y}}^{ai})\}\mid }{\left(\begin{array}{c}m\\ M_1\end{array}\right)}$$ (8)

where |A| denotes the number of elements in the set A and ${\mathrm{\Omega }}_m^{ai}$ denotes the set of possible treatment assignment vectors of length m with M₁ ones and M₀ zeros.

Define the test statistic t(z^ai, y^ai) to be effect increasing (Rosenbaum 2002a) if t(z^ai, y^ai1) ≥ t (z^ai, y^ai2) for two possible response vectors y^ai1 and y^ai2 whenever $(y_j^{ai1}-y_j^{ai2})(2z_j^{ai}-1)\ge 0$ for j = 1, …, m where in general u_j denotes the j^th element of vector u. Informally, t is effect increasing if the value of the statistic increases when responses for the treated group are increased and the responses for the control group are decreased. Next define t(z^ai, y^ai) to be invariant if $t({\mathit{z}}^{ai},{\mathit{y}}^{ai})=t({\mathit{z}}_{jk}^{ai},{\mathit{y}}_{jk}^{ai})$ for all j, k, where in general u_jk denotes the vector formed by interchanging the j^th and k^th elements of u. In words, t(z^ai, y^ai) is invariant if permuting the labels of individuals does not change the value of the statistic. Many common statistics such as Fisher’s exact test statistic and the Wilcoxon rank sum statistic are invariant and effect increasing (Rosenbaum 2002a). According to the proposition below, for invariant and effect increasing statistics $max\{p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0):{\mathit{Y}}_0\in \mathrm{\Omega }(M_0)\}$ can be determined by calculating a single p-value.

Proposition 2

If t(z^ai, y^ai) is invariant and effect increasing, then $p^{ai}(M_0)=p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai}[1:M_0])$ where ${\mathit{Y}}_0^{ai}[1:M_0]$ is the set of M₀ largest values of { $Y_i^{\mathit{obs}}:Z_i=0,S_i^{\mathit{obs}}=1$}.

2.5 Positive Effect

The choice of test statistic used for conducting the PSET of (1) will be dictated by the type of post-infection outcome (e.g., whether y is binary, ordinal, continuous, etc) and alternative hypothesis of interest. One possible alternative hypothesis is that treatment has a positive effect (Rosenbaum 2002; see also Lehmann 1998) in the AI stratum, i.e.,

$$H_A:y_i(1)\ge y_i(0)\text{for}\text{all}i\in \mathcal{A}\mathcal{J}$$ (9)

where the inequality in (9) is strict for at least one i ∈ 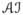. In words, treatment has a positive effect if it increases y for at least one individual and does not decrease y for any individual in AI. The additivity model y_i(1) − y_i(0) = δ for all i ∈ 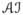and constant δ > 0 is a special case of (9). If the test statistic t is effect increasing, the following proposition shows the PSET is an unbiased test of (1) against (9), i.e., the PSET is at least as likely to reject H₀ at the α significance level when H_A holds as compared to when H₀ holds.

Proposition 3

If t(z^ai, y^ai) is effect increasing, then $Pr[p_{\gamma }^{ai}<\alpha \mid H_A]\ge Pr[p_{\gamma }^{ai}<\alpha \mid H_0]$.

2.6 Plug-in P-value Alternative

An alternative testing approach that has been proposed for addressing the presence of nuisance parameters entails conditioning on estimates of the unknown parameters; the resulting p-value is sometimes referred to as the “plug-in p-value” (Bayarri and Berger 2000). For example, a plug-in p-value approach has been advocated as an alternative to Fisher’s exact test (Storer and Kim 1990). Plug-in p-values are computationally straight forward and asymptotically exact under certain assumptions about the form of the test statistic (Robins, van der Vaart, and Ventura 2000). Considering m to be a nuisance parameter when testing (1), a plug-in type p-value can be defined by conditioning on an unbiased estimate M̂ = nM₁/ΣZ_i (Thompson 2002) of m:

$$p_{\mathit{plug}}^{ai}\equiv p^{ai}(\widehat{M}-M_1)\equiv max\{p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0):{\mathit{Y}}_0\in \mathrm{\Omega }(\widehat{M}-M_1)\}$$

Unfortunately such an approach does not take into account uncertainty about m and therefore $p_{\mathit{plug}}^{ai}$ is not guaranteed to be exact. For example, consider the following population of 8 individuals with potential infection and post-infection outcomes s_i(z) and y_i(z) where y_i(z) = * indicates the post-infection outcome is not defined if s_i(z) = 0. Suppose by design Pr[ΣZ_i = 4] = 1.

i	si(0)	si(1)	yi(0)	yi(1)	i	si(0)	si(1)	yi(0)	yi(1)
1	1	1	8	8	5	1	1	4	4
2	1	1	7	7	6	1	0	3	*
3	1	1	6	6	7	1	0	2	*
4	1	1	5	5	8	1	0	1	*

Suppose a one-sided Wilcoxon rank sum test is used to test (1), where $t({\mathit{Z}}^{ai},{\mathit{Y}}^{ai})={\sum }_{i\in \mathcal{A}\mathcal{J}}{R}_i^{ai}{Z}_i^{ai}$ with $R_i^{ai}$ denoting the rank of $Y_i^{\mathit{obs}}$ among { $Y_i^{\mathit{obs}}:i\in \mathcal{A}\mathcal{J}$} and the p-value is computed by (8). Then for α = 0.05, $Pr[p_{\mathit{plug}}^{ai}\le \alpha ]=0.07>\alpha$ because $p_{\mathit{plug}}^{ai}\le \alpha$ for 5 of the $\left(\begin{array}{c}8\\ 4\end{array}\right)=70$ possible treatment assignment permutations.

3 SIMULATION STUDY

A primary objective of preventive HIV vaccine trials is to assess whether vaccination has an effect on viral load in individuals who become infected. Gilbert et al. (2003) and Hudgens et al. (2003) developed bootstrap tests of the null hypothesis that vaccination has no effect on viral load in the AI principal stratum. To evaluate the operating characteristics (type I error and power) of these proposed tests, they conducted simulation studies of HIV vaccine trials with 2000 HIV negative individuals randomized 1:1 to either vaccine or placebo under various assumptions regarding the rates of infection in the vaccine and placebo arms. In settings where the expected number of observed infections was moderate or large, the proposed tests preserved the nominal type I error probability. However, in settings where the expected number of observed infections was small (45 infections in the placebo arm, 31.5 in the vaccine arm), the bootstrap tests demonstrated inflated type I error. Therefore we conducted a simulation study under identical assumptions to assess how the PSET performs in comparison.

Let z = 0 for placebo individuals and z = 1 for vaccinated individuals. For assignment z, s_i(z) = 1 if an individual is infected and y_i(z) is the log-transformed viral load when s_i(z) = 1. Thus, the null (1) corresponds to the vaccine having no effect on viral load in the AI principal stratum. It is of interest to test the null against the one-sided alternative that viral load is higher when vaccinated, given concerns that an HIV vaccine may actually increase viral load in breakthrough infections (Hudgens et al. 2003).

The following steps were performed for each trial simulation. First, s_i(0) was set equal to 1 for i = 1, …, 90 and s_i(0) = 0 for i = 91, …, 2000. For i = 1, …, 90, y_i(0) was randomly generated from a normal distribution with mean 4.5 and standard deviation 0.6. Next, selection bias was simulated by setting s_i(1) = 1 for the 63 individuals with the largest values of y_i(0) and s_i(1) = 0 otherwise. Thus vaccination caused a 30% reduction in the number of infections, with only individuals who would have low viral load if not vaccinated being protected from infection by vaccine. Vaccine effect on viral load was simulated by letting y_i(1) = y_i(0) + δ for i ∈ 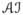. Finally, 1000 individuals were randomly assigned placebo, the remaining 1000 assigned vaccine and the observed outcomes were selected from (s_i(1), s_i(0), y_i(1), y_i(0)) accordingly.

For each simulated dataset, the PSET, nonparametric mean bootstrap test of Hudgens et al. (2003) and plug-in p-value from Section 2.6 were calculated. For the PSET, we used a one-sided 100(1 − γ)% CI of m to obtain L_m and a Wilcoxon rank sum test to compute the conditional p-value p^ai(M₀) in (6). Simulations using a two-sided 100(1 − γ)% CI to obtain L_m and U_m resulted in reduced power compared to the one-sided approach (results not shown). Table 1 gives the empirical type I error and power of the PSET for various values of γ and significance level α, based on 10,000 simulations per combination of γ and α. As expected, in all scenarios the empirical type I error of the PSET was less than α. In contrast, for α = 0.05 the empirical type I errors of the bootstrap test and plug-in p-value were 0.11 and 0.19 respectively, i.e., over twice the nominal level. For α = 0.05 the power of the PSET was highest for γ = 0.030. For α = 0.10, γ = 0.05 yielded the greatest power. Thus, choosing γ = α/2 may be recommended in this setting.

Table 1.

Empirical type 1 error and power for α significance level, 100(1 − γ)% CI for m, and δ increase in log₁₀ viral load in the AI stratum, where δ = 0 under the null hypothesis (1)

α	γ	δ = 0	δ = 1/3	δ = 2/3
0.05	0.005	0.001	0.09	0.65
0.05	0.010	0.002	0.12	0.72
0.05	0.020	0.003	0.16	0.77
0.05	0.025	0.004	0.16	0.77
0.05	0.030	0.005	0.17	0.78
0.05	0.040	0.003	0.15	0.77
0.05	0.045	0.002	0.13	0.73
0.10	0.010	0.004	0.18	0.79
0.10	0.050	0.009	0.29	0.89
0.10	0.090	0.009	0.25	0.86
0.10	0.095	0.005	0.21	0.84

Additional simulation studies were conducted to compare the power of the PSET to the bootstrap test when the AI stratum sample size was increased. Specifically, the simulations studies described above were repeated twice, but with 90 and 135 expected observed infections in the placebo arm and vaccination causing a 30% reduction in the number of infections in both scenarios. For 90 expected placebo arm infections, the empirical type I error and power for δ = 1/3 and 2/3 were 0.004, 0.426, and 0.990 and 0.057, 0.742, and 0.999 for the PSET and bootstrap tests respectively. For 135 expected placebo arm infections, the empirical type I error and power for δ = 1/3 and 2/3 were 0.005, 0.664, and 0.999 and 0.039, 0.908, and 1.00 for the PSET and bootstrap tests respectively. Thus for larger AI stratum the bootstrap test controlled the type I error and had greater power than the PSET for small δ.

As discussed in Section 2.1, the veracity of A.3 may be of concern in some settings. To assess the robustness of the PSET when A.3 is violated, additional simulations were conducted where some individuals infected under vaccine belong to the harmed stratum. Data were simulated as described in the original scenario (where 90 individuals were infected if not vaccinated), except that 6 (10%) of the 63 individuals infected if vaccinated were from the harmed stratum. In particular, for each trial, s_i(0) and y_i(0) were generated as described above. Selection bias was simulated by setting s_i(1) = 1 for a random selection of 57 of the 63 individuals with the largest values of y_i(0). Vaccine effect on viral load in the AI stratum was simulated by letting y_i(1) = y_i(0) + δ for these individuals. Harmed individuals were then simulated by setting s_i(1) = 1 for i = 91, …, 96 and generating y_i(1) from the same normal distribution used to generate y_i(0). All subsequent steps of the simulation were the same as before. The PSET empirical type I error and power for δ = 1/3 and 2/3 were 0.003, 0.108, and 0.649. That is, the PSET type I error was less than the nominal α despite A.3 not holding, and the PSET power was slightly diminished relative to simulations where A.3 holds. Similar results were obtained when 20% and 30% of individuals infected when vaccinated were members of the harmed stratum.

4 APPLICATIONS

4.1 Zambia Exclusive Breastfeeding (ZEB) Study

The ZEB study was a randomized study to evaluate whether abrupt weaning at 4 months as compared to continued breastfeeding increases survival of children of HIV infected mothers (Kuhn et al. 2008). The trial was conducted in 958 HIV-infected women and their infants in Lusaka, Zambia with 481 children randomized to the intervention and 477 randomized to standard practice of continued breastfeeding. Randomization occurred at one month post-partum to allow for sufficient preparation time for weaning at 4 months. Kuhn et al. present an analysis of the effect of weaning on survival through 24 months based on a log-rank test comparing survival between randomization groups for the subset of infants who became HIV-infected prior to 4 months but survived more than 4 months. A total of 62 individuals in the intervention arm were HIV-infected and alive at 4 months, 39 (63%) who died prior to 24 months. Likewise, 70 in the standard practice arm were HIV-infected and alive at 4 months, 32 (46%) who died prior to 24 months. The log-rank p-value was 0.007, leading Kuhn et al. to conclude that there is evidence of a harmful effect of weaning on survival among HIV positive infants alive at 4 months.

Because the reported analysis conditions on infection and survival status at 4 months, the results do not necessarily have a causal interpretation and could be due to selection bias. Specifically, any differences between the study arms during months 1–4 could affect infection and survival status at 4 months. For instance, at month 2 women in the intervention group were counseled on techniques for weaning and given a three month supply of infant formula and fortified weaning cereal. This may have caused women in the intervention group to wean earlier than had they been randomized to the control group, in turn perhaps impacting HIV acquisition. In fact, more women in the intervention arm weaned by 4 months (37 versus 18) and, possibly because of this, fewer infants in the intervention arm became HIV positive at or before 4 months (71 versus 81).

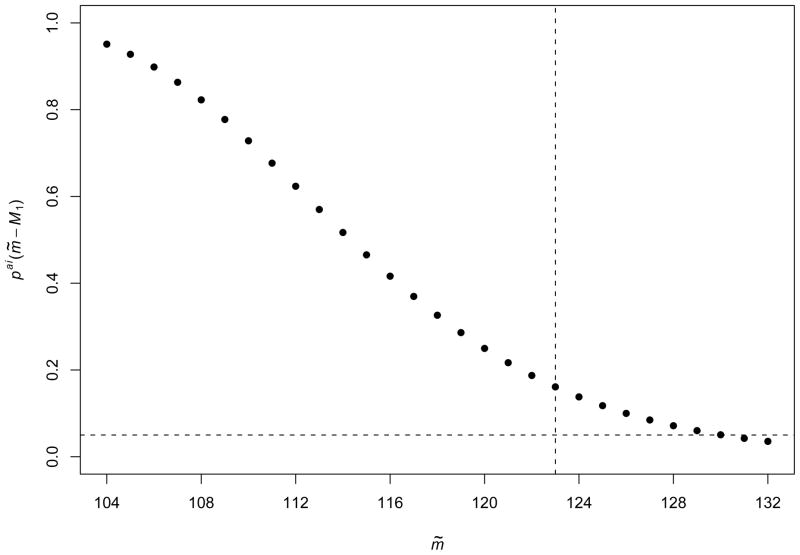
The principal stratum of interest is the AI stratum, defined as all individuals who would be HIV-infected and alive at 4 months regardless of randomization assignment. The PSET was used to test the null hypothesis of no effect of the intervention on death in the AI stratum. To compute (6), a one-sided Fisher’s exact test was used where each individual was classified as having died or not. An exact log-rank test might be preferable for calculating the conditional p-values, however the individual death and censoring times were not reported by Kuhn et al. For γ = 0.025, the PSET resulted in $p_{\gamma }^{ai}=0.98$ suggesting no evidence of a harmful effect of weaning on survival for the AI stratum. The one-sided CI for m, i.e., the total number of infants in the AI stratum, is 104 to 132. Figure 1 plots the p-values from Fisher’s exact test conditional on m = m̃ for each m̃ ∈ C_γ = [104, 132]. While a Fisher’s exact test using all available data and ignoring the potential for selection bias is less than α = 0.05 (p-value= 0.0355), 27 of the 29 conditional p-values are greater than 0.05. Additionally, even testing the hypothesis using the plug-in p-value (i.e. m = M̂) results in $p_{\mathit{plug}}^{ai}=0.1611>\alpha$. In order reject to (1) based on the PSET for α = 0.05 and γ = 0.025, 58 of 62 individuals would have had to die in the intervention arm compared to the 32 of 70 in the standard practice arm ( $p_{\gamma }^{ai}=0.0375$).

Figure 1.

Plot of the 29 conditional p-values, p^ai(m̃ − M₁), for mother-to-child HIV transmission weaning study. Horizontal reference line indicates significance level α = 0.05. Vertical reference line indicates $p_{\mathit{plug}}^{ai}$ where m̃ = M̂ = nM₁/ΣZ_i = 123

4.2 Breastfeeding, Antiretroviral and Nutrition (BAN) Study

The BAN study was a randomized trial of infants of HIV infected mothers to evaluate whether daily administration of nevirapine (NVP) to the infant through 28 weeks decreased risk of HIV transmission via breastfeeding to infants when compared to a control arm receiving no antiretroviral therapy (Chasela et al. 2010). A total of 668 mothers and their infants were randomized to control while 852 were randomized to infants receiving NVP. Fewer mother-infant pairs were randomized to control because the data and safety monitoring board (DSMB) stopped enrollment in this arm early. The effect of NVP on infection status through 28 weeks was assessed using a log-rank test that compared infection between treatment groups for all infants who were not infected at two weeks. Of the 632 infants not infected at two weeks in the control arm, 32 (5.1%) were infected by 28 weeks. Likewise, of the 815 infants not infected at two weeks in the NVP arm, 12 (1.5%) were infected by 28 weeks. The log-rank p-value was < 0.001, suggesting NVP prevents breastmilk transmission of HIV. However, these results do not have an immediate causal interpretation and could be subject to selection bias because the analysis conditions on a post-randomization outcome: HIV infection status at two weeks. To guard against this Chasela et al. also reported results from an ITT analysis of all infants randomized, including those infected before two weeks. However, a primary objective of BAN was to investigate the effect of NVP to prevent breastmilk transmission. Thus the investigators were primarily interested only in infections occurring after two weeks, as infants who were HIV positive by two weeks may have been infected in utero or during birth. Because daily NVP from birth could potentially effect infection status at two weeks, the groups of infants not infected at two weeks in each study arm may not be comparable.

The principal stratum of interest is the never-infected (NI) stratum, defined as individuals who would be HIV uninfected at two weeks regardless of randomization assignment. The PSET can be used to test the null of no treatment effect on infection by 28 weeks in the NI stratum. In contrast to the AI stratum, membership in the NI stratum is known for control individuals not infected at two weeks since by A.3 infants not infected at two weeks when assigned control would also not be infected at two weeks when assigned NVP. On the other hand, membership in the NI stratum is unknown for infants assigned NVP not infected at two weeks. Thus the PSET can be conducted in the NI stratum with the roles of the treated and control individuals reversed relative to conducting the PSET in the AI stratum. For given γ, denote the PSET p-value for the test of no principal stratum direct effect in the NI stratum by $p_{\gamma }^{ni}$, which is computed analogous to (7). Because enrollment was stopped early in one arm, we compute $p_{\gamma }^{ni}$ using only data available prior to the DSMB decision. These data include all the control arm infants described above but only 670 of the infants in the NVP arm, 639 of who were not infected at two weeks. Of these 639 infants, 10 (1.6%) were infected by 28 weeks. Because the BAN study was a multi-arm trial, the analysis plan stipulated that tests between the NVP and control arms be conducted at the α = 0.025 significance level. Letting γ = 0.0125 and using a one-sided Fisher’s exact test, the PSET resulted in $p_{\gamma }^{ai}=0.0131$ indicating a benefit of NVP among infants who were immune to infection at two weeks. Using an exact log-rank test with Monte Carlo sampling (Mehta and Patel 2007) yielded a similar result with $p_{\gamma }^{ai}=0.0127$.

4.3 Sensitivity Analysis

As discussed in Sections 2 and 3, A.3 is a key assumption of the PSET. In the BAN study, comparison of infection rates at two weeks provides no evidence that monotonicity is violated, with the proportion infected at two weeks slightly lower in the NVP arm. Additionally, multiple other studies (Mofenson 2009) have shown daily administration of NVP protects infants from breastmilk transmission of HIV and to date there is no evidence suggesting NVP may cause HIV transmission. Nonetheless, when A.3 may be of concern, a sensitivity analysis can be conducted.

To illustrate one possible sensitivity analysis, suppose there was concern about A.3 in the BAN study. Without A.3 the 632 control arm infants uninfected at two weeks are not all necessarily members of the NI stratum. Rather, some of these infants may belong to the harmed stratum, i.e., they may have been infected by two weeks if randomized to NVP. Suppose h of the 632 are from the harmed stratum. If these h infants could be identified, the PSET could be conducted based on the remaining 632 − h control arm infants uninfected at two weeks. Because the h infants cannot be identified without additional assumptions, the sensitivity analysis entails considering different scenarios. Specifically, divide the h infants into h₁ from the 600 control arm infants not infected by 28 weeks and h₂ = h − h₁ from the 32 control arm infants infected by 28 weeks. Then conduct the PSET for different combinations of (h₁, h₂). For the BAN study the PSET p-value (based on a one-sided Fisher’s exact test) is more sensitive to changes in h₂ than h₁. For example, for γ =0.0125, h₁ = 8 and h₂ = 0 yields $p_{\gamma }^{ni}=0.013$, while h₁ = 0 and h₂ = 8 yields $p_{\gamma }^{ni}<0.027$. Holding h₁ = 0 fixed, $p_{\gamma }^{ni}<0.025$ for h₂ = 0, 1, 2, …, 7 and $p_{\gamma }^{ni}>0.025$ for h₂ > 7. In words, NVP was beneficial in the NI stratum at the 0.025 significance level provided no more than 7 of the 32 control arm infants infected by week 28 were from the harmed stratum.

5 COMPARISONS WITH ITT APPROACHES

Principal stratification provides a method for dealing with possible selection bias induced by conditioning on an intermediate post-randomization outcome. Alternatively, an ITT based approach can be employed. The ITT principle generally refers to analyzing all individuals according to randomization assignment. ITT has become the gold standard in clinical trials as it ensures the validity of testing the null hypothesis of no treatment effect (assuming perfect compliance) and helps minimize bias such that observed differences in outcomes between the groups can be attributed to the treatment under study. The ITT approach does however have some potential drawbacks. For instance, in the infectious disease setting, unlike principal stratification the ITT approach does not clearly differentiate treatment effects on infection and post-infection outcomes. Also, it is conceptually challenging to define post-infection outcomes for non-infected individuals. Similarly, quality of life outcomes may be considered undefined in individuals not alive (Rubin 2006).

To obviate the latter problem, Chang, Guess and Heyse (1994) proposed an ITT-based burden of illness (BOI) test for assessing treatment effect on disease severity by assigning burden of illness scores to each incident infection, with individuals who escape infection receiving a score of zero. Denote the observed disease severity scores by $W_i^{\mathit{obs}}$ where $W_i^{\mathit{obs}}=Y_i^{\mathit{obs}}$ if $S_i^{\mathit{obs}}=1$ and $W_i^{\mathit{obs}}=0$ if $S_i^{\mathit{obs}}=0$. Then define ${\mathit{W}}_1^{\mathit{ITT}}\equiv \{W_i^{\mathit{obs}}:Z_i=1\},{\mathit{W}}_0^{\mathit{ITT}}\equiv \{W_i^{\mathit{obs}}:Z_i=0\}$ and $p({\mathit{W}}_1^{\mathit{ITT}},{\mathit{W}}_0^{\mathit{ITT}})$ as the p-value for an exact randomization-based test comparing ${\mathit{W}}_1^{\mathit{ITT}}$ and ${\mathit{W}}_0^{\mathit{ITT}}$. As opposed to (1), the null hypothesis of the randomization BOI test is H₀: w_i(1) = w_i(0) for all i ∈ {1, …, n}. Assuming $Y_i^{\mathit{obs}}>0$ whenever $S_i^{\mathit{obs}}=1$, it follows that the null hypothesis of the BOI test is equivalent to testing the composite hypothesis:

$$H_0:s_i(1)=s_i(0)\text{and}{y}_i(1)=y_i(0)\text{for}\text{all}i\in \{1,\dots ,n\},$$ (10)

Because the BOI test may have poor power when infections are rare, Follmann, Fay, and Proschan (2009) proposed the chop-lump test as an alternative ITT test of (10). For this method, a test statistic is calculated based on a subset of the data obtained by removing (or “chopping”) $min\{\sum (1-Z_i)(1-S_i^{\mathit{obs}}),\sum Z_i(1-S_i^{\mathit{obs}})\}$ observations where $W_i^{\mathit{obs}}=0$ from each randomization group such that the remaining data from at least one of the groups has no observations where $W_i^{\mathit{obs}}=0$. The test statistic (e.g., difference in means between groups) is computed based on this subset. Randomization-based p-values are obtained in the usual fashion, i.e., by considering all possible randomization assignments of the n individuals and computing the test statistic for each possibility.

For the simulation scenario of Section 3, the power was < 0.05 for the BOI for all δ and 0.181, 0.370 and 0.483 for the chop-lump for δ = 1/3, 2/3 and 1 respectively. For these tests, let $W_i^{\mathit{obs}}=0$ for uninfected individuals ( $S_i^{\mathit{obs}}=0$) and $W_i^{\mathit{obs}}=Y_i^{\mathit{obs}}$ for infected individuals ( $S_i^{\mathit{obs}}=1$). Then for both tests the Wilcoxon rank sum test statistic was used to compare $W_i^{\mathit{obs}}$ and one-sided p-values were computed corresponding to the vaccine causing higher viral load. The lack of power for the ITT tests in this setting is partially due to the opposite direction of vaccine effects on infection and viral load, i.e., for δ > 0 the vaccine is protecting some individuals but causing a higher viral load in the AI stratum.

To compare the BOI, chop-lump and PSET when the vaccine only effects the post-infection outcome, additional simulations were conducted similar to that described in Section 3 except we let s_i(1) = s_i(0) for all i such that the expected number of observed infections was 45 for each arm. For α = 0.05, the empirical type I error and power for δ = 1/3, 2/3 and 1 were 0.049, 0.061, 0.062 and 0.063 for the BOI test; 0.048, 0.365, 0.747 and 0.898 for the chop-lump; and 0.002, 0.100, 0.644 and 0.978 for the PSET (with γ = 0.025). That is, the PSET is markedly more powerful test than the BOI approach for all δ and comparable in power to the chop-lump for larger values of δ. Mehrotra et al. (2006) presented similar findings when comparing large-sample frequentist based principal stratification tests with a BOI test.

The PSET is unambiguously better for testing principal stratum direct effects than the BOI, chop-lump and other ITT-based tests in settings where treatment z has an effect on infection s but not on the post-infection outcome y. For then the ITT-based tests may reject (10) even though the null hypothesis of interest (1) is true (i.e. treatment has no effect on the post-infection outcome y). For example, consider the scenario described in Section 3 where vaccine causes a 30% reduction in the number of infections, there are 45 expected infections in the placebo arm, and δ = 0 (i.e., (1) is true). Suppose the alternative hypothesis of interest is that the vaccine reduces viral load. In this scenario, one-sided BOI and chop-lump tests reject (10) at the α = 0.05 level of significance for over 50% of the simulated data sets. In other words, the BOI and chop-lump tests do not have the correct size for testing (1) when there is a treatment effect on s.

6 ADJUSTING FOR COVARIATES

Covariate adjustment is often used in analysis of randomized experiments to account for chance imbalances that may exist between study arms, thereby allowing for more precise inference. Following Rosenbaum (2002b), in this section we consider extending the PSET to incorporate baseline (i.e., pre-randomization) covariates. This approach entails first regressing the outcomes of interest on covariates and then conducting an exact test on the residuals. Ideally, the residuals obtained from the regression model are less variable than the original outcomes of interest, resulting in increased power of the PSET. The appeal of this approach is no distributional assumptions about the response nor the selected regression model are required. As before, randomization inference is employed such that the potential outcomes as well as the covariates are assumed to be fixed features of the finite population and not affected by treatment assignment.

6.1 PSET Development Adjusting for Covariates

Let x_i represent the baseline covariate value for individual i. Denote the function that creates residuals from y_i(z) and x_i by g such that g(y_i(z), x_i) = e_i(z) where e_i(z) is the residual for the i^th individual when assigned treatment z. Under the null hypothesis (1), y_i(1) = y_i(0) and therefore e_i(1) = e_i(0) for all i ∈ 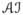. Therefore, a test of (1) can be constructed using the residuals.

The covariate-adjusted PSET is constructed in a similar fashion to the PSET from Section 2.3 except $Y_i^{\mathit{obs}}$ is replaced with the observed residuals, $E_i^{\mathit{obs}}=Z_i{e}_i(1)+(1-Z_i)e_i(0)$. The exact randomization-based test used to obtain $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})$ need not be the same test used on the residuals as the choice of tests depends on the characteristics of y_i(z), x_i and g(,). For example, consider the logistic regression setting where y_i(z) is binary, x_i has no ties and g(y, x) = y − exp(β̂₀ + β̂₁x)/{1+exp(β̂₀ + β̂₁x)} where β̂₀ and β̂₁ are obtained by maximum likelihood estimation. Resulting values for e_i(z) will typically have no ties. Accordingly, Fisher’s exact test could be used to obtain $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})$ while a Wilcoxon rank sum test could be used on the residuals.

6.2 Simulations

To assess the power of the covariate adjusted PSET, the simulation scenario described in Section 3 was updated to include baseline CD4 count, a measure of immune function. Baseline CD4 count x_i was assumed to be normally distributed with mean 850 and standard deviation 300. For all individuals who would be infected if assigned control, CD4 count x_i and post-infection log viral load when receiving control y_i(0) were simulated under various levels of correlation (ρ = 0.0, 0.1, …, 0.9). Residuals were obtained using $g(Y_i^{\mathit{obs}},x_i)=Y_i^{\mathit{obs}}-({\widehat{\beta }}_0+{\widehat{\beta }}_1{x}_i)$ where β̂₀ and β̂₁ are solutions to the normal equations for the linear regression model of $Y_i^{\mathit{obs}}$ on x_i for all i with $S_i^{\mathit{obs}}=1$. A one-sided 100(1 − γ)% CI was computed to obtain L_m and a one-sided Wilcoxon rank sum test of the residuals was used to obtain the conditional p-values p^ai(M₀) in (6).

Results of the simulations for α = 0.05 and γ = 0.025 are displayed in Table 2. Comparing to Table 1, adjusting for x_i increased the power of the PSET when ρ > .5, markedly so for the larger value of δ. For weak levels of correlation, an increase in power was not observed; for ρ=0 there was a slight loss of power when adjusting for the covariate. While the covariate-adjusted PSET is not guaranteed to increase power compared to the unadjusted PSET, it is still guaranteed to be exact.

Table 2.

Empirical type 1 error and power for α = 0.05, γ = 0.025, and δ increase in log₁₀ viral load in the AI stratum, where δ = 0 under the null hypothesis (1), when adjusting for baseline CD4 count at various levels of ρ between viral load and CD4 count

ρ	δ = 0	δ = 1/3	δ = 2/3
0.0	0.004	0.16	0.76
0.1	0.004	0.16	0.76
0.2	0.004	0.16	0.77
0.3	0.003	0.16	0.78
0.4	0.003	0.16	0.80
0.5	0.002	0.17	0.82
0.6	0.002	0.18	0.85
0.7	0.001	0.21	0.90
0.8	0.001	0.27	0.96
0.9	< 0.001	0.50	> 0.99

7 CONFIDENCE INTERVALS

The PSET can be used to form an exact CI for a principal stratum direct effect. Suppose treatment effect in the AI stratum is additive such y_i(1) − y_i(0) = δ₀ for all i ∈ 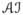. Then a CI for the principal stratum direct effect δ₀ can be obtained by inverting a generalized version of the PSET developed in Section 2.3. The CI is constructed by conducting the generalized PSET for all possible values of δ₀ and forming the set of values where the test is not rejected (Lehmann 1959, Rosenbaum 2002).

The first step is to adapt the PSET to allow for testing a more general null hypothesis. For some constant δ not necessarily equal to zero, consider testing:

$$H_0:y_i(1)-y_i(0)=\delta \text{for}\text{all}i\in \mathcal{A}\mathcal{J},$$ (11)

Note under (11) that $(Y_i^{\mathit{obs}}-\delta )Z_i+Y_i^{\mathit{obs}}(1-Z_i)=(y_i(1)-\delta )Z_i+y_i(0)(1-Z_i)=y_i(0)$ is constant. Thus the PSET of (11) can be constructed as in Section 2.3 except $Y_i^{\mathit{obs}}$ is replaced with $Y_i^{\mathit{obs}}-\delta$ for individuals where Z_i = 1 (Rosenbaum 2002a). A one-sided 100(1 − α)% CI for the true δ₀ is formed by the set of all δ where a one-sided test of (11) is not rejected.

More specifically, let $p_{\delta }({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})=p({\mathit{Y}}_1^{ai}-\delta ,{\mathit{Y}}_0^{ai})$ denote the one-sided p-value from an exact randomization-based test of (11) using $Y_i^{\mathit{obs}}-\delta$ for individuals where Z_i = 1, and let $p_{\delta }^{ai}(M_0)=max\{p_{\delta }({\mathit{Y}}_1^{ai},{\mathit{Y}}_0):{\mathit{Y}}_0\in \mathrm{\Omega }(M_0)\}$ and $p_{\gamma ,\delta }^{ai}=max\{p_{\delta }^{ai}(\stackrel{\sim }{m}-M_1):\stackrel{\sim }{m}\in C_{\gamma }\}+\gamma$. Let δ_min and δ_max denote the lower and upper limits of the range of possible values for δ₀. Following Mehta and Patel (2007), define the lower bound of the 100(1 − α)% one-sided CI of δ₀ by ${\mathrm{\Delta }}_{\gamma }^{\alpha }=sup\{\delta :p_{\gamma ,\stackrel{\sim }{\delta }}^{ai}\le \alpha \text{for}\text{all}\stackrel{\sim }{\delta }<\delta \}$ . If there does not exist δ such that $p_{\gamma ,\stackrel{\sim }{\delta }}^{ai}\le \alpha$ for all δ̃ < δ then ${\mathrm{\Delta }}_{\gamma }^{\alpha }$ is set to δ_min. The upper bound of the CI is set to δ_max. According to the following proposition, the interval [ ${\mathrm{\Delta }}_{\gamma }^{\alpha }$, δ_max] is an exact one-sided 100(1 − α)% CI of the principal stratum direct effect δ₀ because the probability of covering the true value of δ₀ is at least (1 − α).

Proposition 4

For γ ∈ [0, 1] and α ∈ [0, 1], $Pr[{\delta }_0\in [{\mathrm{\Delta }}_{\gamma }^{\alpha },{\delta }_{\mathit{max}}]]\ge 1-\alpha$.

8 DISCUSSION

8.1 Summary

In randomized studies, comparisons between randomized groups that condition on intermediate post-randomization outcomes generally do not have a causal interpretation. An alternate approach entails comparisons within principal strata defined by the intermediate potential outcomes that would be observed under each randomization assignment. In this paper, we develop exact, randomization-based methods for inference about the treatment effect within a principal stratum. The three key assumptions for the PSET are SUTVA (A.1), random treatment assignment (A.2), and monotonicity (A.3); no assumptions are required about random sampling or that particular parametric distributions hold. Simulation studies indicate the PSET can be as or more powerful than ITT approaches when treatment has no impact on the intermediate post-randomization outcome. The power of the PSET can be increased by adjusting for baseline covariates and exact CIs for the principal stratum direct effect can be obtained by inverting the PSET.

8.2 Other applications

This work is motivated by infectious disease prevention studies where the treatment is some preventive measure (such as a vaccine), the intermediate variables s is infection, and the outcome of interest y is a post-infection endpoint (such as death). Two other settings where principal stratification methods are typically employed include truncation by death (Zhang and Rubin 2003) and non-compliance (Angrist et al. 1996). For the truncation by death problem, the PSET can readily be employed. In this setting, the intermediate variable s is death (0 for alive, 1 for death), the outcome of interest y is some measurement such as quality of life that is only well defined when individuals are alive, and the principal stratum of interest is the set of individuals who would be alive under either treatment assignment. The stratum of interest {i: s_i(0) = s_i(1) = 0} is directly analogous to the never infected principal stratum discussed in Section 4.2. Here the monotonicity assumption A.3 indicates no individuals would die due to treatment.

In the non-compliance setting, the intermediate variable s is compliance to randomization assignment z and the goal is to make inference about the outcome of interest y for those individuals who would comply under either randomization assignment. Following Angrist et al. (1996), let s_i(z) = 1 if individual i actually receives treatment and s_i(z) = 0 if individual i receives control when assigned z. If individual i always complies with their randomization assignment then s_i(z) = z. Thus the principal stratum of interest, the compliers, is {i: s_i(0) = 0, s_i(1) = 1}. Typically a form of monotonicity is assumed such that there are no individuals who always defy their randomization assignment, i.e., {i: s_i(0) = 1, s_i(1) = 0} is empty. Additionally, often it is assumed that randomization assignment has no effect on individuals who ignore treatment assignment, i.e., y_i(0) = y_i(1) if s_i(0) = s_i(1). Under this exclusion restriction and assuming monotonicity, the principal stratum direct effect null

$$H_0:y_i(0)=y_i(1)\text{for}\text{all}i\in \{j:s_j(0)=0,s_j(1)=1\}$$ (12)

will be true if and only if the ITT null

$$H_0:y_i(0)=y_i(1)\text{for}i\in \{1,\dots ,n\},$$ (13)

is true, so that the usual randomization tests of (13) can be used to test (12), as suggested by Rosenbaum (1996).

If one is not willing to make the exclusion restriction assumption above (e.g., see Jo 2002), then (12) and (13) are not equivalent and thus the usual randomization (ITT) tests will generally not have the correct size for testing (12), since effects of randomization on y in non-compliers can lead to rejection of (13) even though (12) is true. In certain settings treatment may not be available to individuals randomized to control (e.g., see Ten Have et al. 2003, Little et al. 2009), so that s_i(0) = 0 always. In this setting and assuming monotonicity, the PSET applies; individuals with $Z_i=S_i^{\mathit{obs}}=1$ must be compliers (just as infected treated individuals must be in the AI stratum) and individuals with $Z_i=S_i^{\mathit{obs}}=0$ are a mixture of compliers and never takers (just as infected controls are a mixture of individuals from the protected and AI strata).

8.3 Future Directions

We close by mentioning five possible avenues of future research. (i) The development of the PSET as an exact test of (1) arose from viewing individuals’ principal stratum memberships as partially unknown nuisance parameters and then employing the approach developed by Berger and Boos (1994). Other approaches to testing in the presence of nuisance parameters might be adapted to the principal stratification setting, giving rise to exact tests of (1) different from the PSET in this paper. (ii) Extensions to observational settings where assumption A.2 does not necessarily hold could be considered. For examples of permutation inference in observational studies see Rosenbaum (1984 Rosenbaum (2002). (iii) A method for obtaining an exact CI of the principal stratum direct effect by inverting the PSET was presented in Section 7. This method assumes the treatment effect is additive (i.e., constant) within the principal stratum of interest. Future research could entail relaxing this assumption. Similar to Rosenbaum (2001), one approach might entail extending the PSET to the more general null hypothesis H₀: y_i(1) − y_i(0) = δ_0i for i ∈ 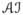where the individual treatment effects δ_0i may differ between individuals; this extended PSET could then, perhaps, be inverted to obtain a CI for the average principal stratum direct effect (VanderWeele 2008). (iv) As discussed in Sections 2, 3 and 4, the monotonicity assumption may be dubious in certain settings. Additional investigation is needed into weakening assumption A.3. (v) Covariate adjustment was considered in Section 6 as a method for possibly increasing the power of the PSET. Alternatively, baseline covariates could be used to predict principal stratum membership (e.g., see Roy et al. 2008) and perhaps this information could somehow be incorporated within the randomization-based inference framework.

APPENDIX: PROOF OF PROPOSITIONS

Proof of Proposition 1

Proof

Suppose H₀ (1) is true. Fix γ ∈ [0, 1] and α ∈ [0, 1]. If γ > α, then $p_{\gamma }^{ai}=max\{p^{ai}(\stackrel{\sim }{m}-M_1):\stackrel{\sim }{m}\in C_{\gamma }\}+\gamma >\alpha$. Therefore $Pr[p_{\gamma }^{ai}\le \alpha ]=0\le \alpha$. If γ ≤ α, then

$$\begin{array}{l}Pr[p_{\gamma }^{ai}\le \alpha ]=Pr[p_{\gamma }^{ai}\le \alpha ,m\in C_{\gamma }]+Pr[p_{\gamma }^{ai}\le \alpha ,m\in {\overline{C}}_{\gamma }]\\ \le Pr[max\{p^{ai}(\stackrel{\sim }{m}-M_1):\stackrel{\sim }{m}\in C_{\gamma }\}+\gamma \le \alpha ,m\in C_{\gamma }]+Pr[m\in {\overline{C}}_{\gamma }]\\ \le Pr[p^{ai}(m-M_1)+\gamma \le \alpha ,m\in C_{\gamma }]+\gamma \\ \le Pr[p^{ai}(m-M_1)\le \alpha -\gamma ]+\gamma \\ \le \alpha -\gamma +\gamma =\alpha \end{array}$$

where the 2^nd inequality holds because max{p^ai(m̃ − M₁): m̃ ∈ C_γ} ≥ p^ai(m − M₁) when m ∈ C_γ and the 4^th inequality holds due to the following Lemma.

Lemma

p^ai(m − M₁) is an exact p-value, i.e., Pr[p^ai(m − M₁) ≤ α] ≤ α for each α ∈ [0, 1] under the null (1).

Proof of Lemma

Suppose H₀ (1) is true.

$$\begin{array}{l}Pr[p^{ai}(m-M_1)\le \alpha ]=Pr[max\{p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0):{\mathit{Y}}_0\in \mathrm{\Omega }(M_0)\}\le \alpha ]\\ \le Pr[p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})\le \alpha ]\le \alpha \end{array}$$

where the 1^st inequality holds because $max\{p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0):{\mathit{Y}}_0\in \mathrm{\Omega }(M_0)\}\ge p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})$ and the 2^nd inequality holds because $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai})$ is an exact p-value under (1).

Proof of Proposition 2

Proof

Assume t is an invariant and effect increasing statistic. The proposition is proved if we can show $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai}[1:M_0])\ge p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0)$ for all Y₀ ∈ Ω(M₀). Let Y₀ be an element of Ω (M₀) and define the labels k₁,…, k_m such that ${\mathit{Y}}_1^{ai}\cup {\mathit{Y}}_0=\{Y_{k_1}^{\mathit{obs}},\dots ,Y_{k_m}^{\mathit{obs}}\}$. Let $Y^{ai1}=(Y_{k_1}^{\mathit{obs}},Y_{k_2}^{\mathit{obs}},\dots ,Y_{k_m}^{\mathit{obs}})$ and Z^ai1 = Z_k1, Z_k2, …, Z_km.

Since t is invariant, we can assume without loss of generality that the labels k₁,…, k_m are defined such that $Z_j^{ai1}=1$ for j = 1, …, M₁; $Z_j^{ai1}=0$ otherwise; and $Y_j^{ai1}\ge Y_k^{ai1}$ if j ≤ k and $Z_j^{ai1}=Z_k^{ai1}$. In other words, the elements of Z^ai1 are in descending order and the elements of Y^ai1 are in descending order within fixed levels of Z^ai1. Similarly define the labels l₁, …, l_m such that ${\mathit{Y}}_1^{ai}\cup {\mathit{Y}}_0^{ai}[1:M_0]=\{Y_{l_1}^{\mathit{obs}},\dots ,Y_{l_m}^{\mathit{obs}}\}$. Let $Y^{ai2}=(Y_{l_1}^{\mathit{obs}},Y_{l_2}^{\mathit{obs}},\dots ,Y_{l_m}^{\mathit{obs}})$ and define Z^ai2 analogously. Assume the labels l₁, …, l_m are defined similar to k₁, …, k_m such that Z^ai2 = Z^ai1 and $Y_j^{ai2}\ge Y_k^{ai2}$ if j ≤ k and $Z_j^{ai2}=Z_k^{ai2}$.

Note the first M₁ elements of Y^ai1 and Y^ai2 are the same, such that if $Z_j^{ai1}=1$, then $Y_i^{ai2}=Y_i^{ai1}$. On the other hand, if $Z_i^{ai}=0$, then $Y_i^{ai2}\ge Y_i^{ai1}$ because (i) Y^ai2 and Y^ai1 are both in descending order within fixed levels of Z^ai2 = Z^ai1 and (ii) Y^ai2 contains the M₀ largest values of { $Y_i^{\mathit{obs}}:Z_i=0,S_i^{\mathit{obs}}=1$}. This implies $(Y_j^{ai1}-Y_j^{ai2})(2Z_j^{ai}-1)\ge 0$ for j = 1, …, m. Since t is an effect increasing statistic, it follows t(Z^ai1, Y^ai1) ≥ t(Z^ai2, Y^ai2), which implies $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0^{ai}[1:M_0])\ge p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0)$.

Proof of Proposition 3

Proof

Fix γ and α. Let Z denote a randomly selected treatment assignment vector and let $p_{\gamma }^{ai}$ denote the resulting PSET p-value. By Proposition 2, there exists an m̃ ∈ C_γ such that $p_{\gamma }^{ai}-\gamma =p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0[1:(\stackrel{\sim }{m}-M_1)])$. Similar to the proof of Proposition 2, define the labels l₁,…, l_m̃ such that ${\mathit{Y}}_1^{ai}\cup {\mathit{Y}}_0[1:(\stackrel{\sim }{m}-M_1)]=\{Y_{l_1}^{\mathit{obs}},\dots ,Y_{l_{\stackrel{\sim }{m}}}^{\mathit{obs}}\}$. Let ${\mathit{Y}}^{ai\stackrel{\sim }{m}}\equiv (Y_{l_1}^{\mathit{obs}},Y_{l_2}^{\mathit{obs}},\dots ,Y_{l_{\stackrel{\sim }{m}}}^{\mathit{obs}})$ and define Z^aim̃ analogously. Let ${\mathit{y}}_{\mathbf{0}}^{ai\stackrel{\sim }{m}}\equiv (y_{l_1}(0),\dots ,y_{l_m}(0))$ be the vector of potential outcomes if individuals l₁, …, l_m were all assigned control. Note if z_lk= 1 then l_k ∈ 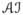and thus $Y_{l_k}^{\mathit{obs}}=y_{l_k}(1)\ge y_{l_k}(0)$ under (1) or (9). On the other hand, by construction the l_k element of Y^aim̃ and the l_k element of ${\mathit{y}}_{\mathbf{0}}^{ai\stackrel{\sim }{m}}$ are equal if z_lk = 0. Because t is effect increasing, it follows $t({\mathit{Z}}^{ai\stackrel{\sim }{m}},{\mathit{Y}}^{ai\stackrel{\sim }{m}})\ge t({\mathit{Z}}^{ai\stackrel{\sim }{m}},{\mathit{y}}_{\mathbf{0}}^{ai\stackrel{\sim }{m}})$ when either (1) or (9) hold. Therefore

$$\sum _{\mathit{z}\in {\mathrm{\Omega }}_{\stackrel{\sim }{m}}^{ai}}I[t(\mathit{z},{\mathit{Y}}^{ai\stackrel{\sim }{m}})\ge t({\mathit{Z}}^{ai\stackrel{\sim }{m}},{\mathit{Y}}^{ai\stackrel{\sim }{m}})]{\left(\begin{array}{c}\stackrel{\sim }{m}\\ M_1\end{array}\right)}^{-1}\le \sum _{\mathit{z}\in {\mathrm{\Omega }}_{\stackrel{\sim }{m}}^{ai}}I[t(\mathit{z},{\mathit{Y}}^{ai\stackrel{\sim }{m}})\ge t({\mathit{Z}}^{ai\stackrel{\sim }{m}},{\mathit{y}}_{\mathbf{0}}^{ai\stackrel{\sim }{m}})]{\left(\begin{array}{c}\stackrel{\sim }{m}\\ M_1\end{array}\right)}^{-1}$$ (14)

The left side of (14) equals $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0[1:(\stackrel{\sim }{m}-M_1)])$ under H_A where as the right side of (14) equals $p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0[1:(\stackrel{\sim }{m}-M_1)])$ under H₀. Therefore

$$Pr[p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0[1:(\stackrel{\sim }{m}-M_1)])<\alpha -\gamma \mid H_A]\ge Pr[p({\mathit{Y}}_1^{ai},{\mathit{Y}}_0[1:(\stackrel{\sim }{m}-M_1)])<\alpha -\gamma \mid H_0]$$

which implies $Pr[p_{\gamma }^{ai}<\alpha \mid H_A]\ge Pr[p_{\gamma }^{ai}<\alpha \mid H_0]$, i.e., the probability of rejecting the null is at least as likely given (9) as compared to given (1).

Proof of Proposition 4

Proof

Let δ₀ be the true (unknown) value of the principal stratum direct effect. Fix γ ∈ [0, 1] and α ∈ [0, 1]. If γ > α then the PSET does not reject (11) for any choice of δ. Therefore, $Pr[{\delta }_0\notin [{\mathrm{\Delta }}_{\gamma }^{\alpha },{\delta }_{\mathit{max}}]]=Pr[{\delta }_0\notin [{\delta }_{\mathit{min}},{\delta }_{\mathit{max}}]]=0\le \alpha$. If γ ≤ α then

$$\begin{array}{l}Pr[{\delta }_0\notin [{\mathrm{\Delta }}_{\gamma }^{\alpha },{\delta }_{\mathit{max}}]]=Pr[{\delta }_0\notin [{\mathrm{\Delta }}_{\gamma }^{\alpha },{\delta }_{\mathit{max}}],m\in C_{\gamma }]+Pr[{\delta }_0\notin [{\mathrm{\Delta }}_{\gamma }^{\alpha },{\delta }_{\mathit{max}}],m\in {\overline{C}}_{\gamma }]\\ \le Pr[{\delta }_0\notin [{\mathrm{\Delta }}_{\gamma }^{\alpha },{\delta }_{\mathit{max}}],m\in C_{\gamma }]+Pr[m\in {\overline{C}}_{\gamma }]\\ \le Pr[{\delta }_0<{\mathrm{\Delta }}_{\gamma }^{\alpha },m\in C_{\gamma }]+\gamma \\ \le Pr[p_{\gamma ,{\delta }_0}^{ai}\le \alpha ,m\in C_{\gamma }]+\gamma \\ \le \alpha -\gamma +\gamma =\alpha \end{array}$$

where the 3^rd inequality follows from the definition of ${\mathrm{\Delta }}_{\gamma }^{\alpha }$ (i.e., ${\delta }_0<{\mathrm{\Delta }}_{\gamma }^{\alpha }$ implies $p_{\gamma ,{\delta }_0}^{ai}\le \alpha$) and the 4^th inequality follows for reasons analogous to the proof of Proposition 1.