Denisova Admixture and the First Modern Human Dispersals into Southeast Asia and Oceania

Abstract

It has recently been shown that ancestors of New Guineans and Bougainville Islanders have inherited a proportion of their ancestry from Denisovans, an archaic hominin group from Siberia. However, only a sparse sampling of populations from Southeast Asia and Oceania were analyzed. Here, we quantify Denisova admixture in 33 additional populations from Asia and Oceania. Aboriginal Australians, Near Oceanians, Polynesians, Fijians, east Indonesians, and Mamanwa (a “Negrito” group from the Philippines) have all inherited genetic material from Denisovans, but mainland East Asians, western Indonesians, Jehai (a Negrito group from Malaysia), and Onge (a Negrito group from the Andaman Islands) have not. These results indicate that Denisova gene flow occurred into the common ancestors of New Guineans, Australians, and Mamanwa but not into the ancestors of the Jehai and Onge and suggest that relatives of present-day East Asians were not in Southeast Asia when the Denisova gene flow occurred. Our finding that descendants of the earliest inhabitants of Southeast Asia do not all harbor Denisova admixture is inconsistent with a history in which the Denisova interbreeding occurred in mainland Asia and then spread over Southeast Asia, leading to all its earliest modern human inhabitants. Instead, the data can be most parsimoniously explained if the Denisova gene flow occurred in Southeast Asia itself. Thus, archaic Denisovans must have lived over an extraordinarily broad geographic and ecological range, from Siberia to tropical Asia.

Introduction

The history of the earliest arrival of modern humans in Southeast Asia and Oceania from Africa remains controversial. Archaeological evidence has been interpreted to support either a single wave of settlement¹ or, alternatively, multiple waves of settlement, the first leading to the initial peopling of Southeast Asia and Oceania via a southern route and subsequent dispersals leading to the peopling of all of East Asia.² Mitochondrial DNA studies have been interpreted as supporting a single wave of migration via a southern route,^3–5 although other interpretations are possible,^6,7 and single-locus studies are unlikely to resolve this issue.⁸ The largest genetic study of the region to date, based on 73 populations genotyped at 55,000 SNPs, concluded that the data were consistent with a single wave of settlement of Asia that moved from south to north and gave rise to all of the present-day inhabitants of the region.⁹ However, another study of genome-wide SNP data argued for two waves of settlement¹⁰ as did an analysis of diversity in the bacterium Helicobacter pylori.¹¹

The recent finding that Near Oceanians (New Guineans and Bougainville Islanders) have received 4%–6% of their genetic material from archaic Denisovans¹² in principle provides a powerful tool for understanding the earliest human migrations to the region and thus for resolving the question of the number of waves of settlement. The Denisova genetic material in Southeast Asians should be easily recognizable because it is very divergent from modern human DNA. Thus, the presence or absence of Denisova genetic material in particular populations should provide an informative probe for the migration history of Southeast Asia and Oceania, in addition to being interesting in its own right. However, the populations previously analyzed for signatures of Denisova admixture¹² comprise a very thin sampling of Southeast Asia and Oceania. In particular, no groups from island Southeast Asia or Australia were surveyed. Here, we report an analysis of genome-wide data from an additional 33 populations from south Asia, Southeast Asia, and Oceania; analyze the data for signatures of Denisova admixture; and use the results to infer the history of human migration(s) to this part of the world.

Material and Methods

SNP Array Data

We analyzed data for modern humans genotyped on Affymetrix 6.0 SNP arrays. We began by assembling previously published data for YRI (Yoruba in Ibadan, Nigeria) West Africans, CHB (Han Chinese in Beijing, China) Han Chinese and CEU (Utah residents with Northern and Western European ancestry from the CEPH collection) European Americans from HapMap 3;¹³ Onge Andaman “Negritos”;¹⁴ and New Guinea highlanders, Fijians, one Bornean population, and Polynesians from seven islands.¹⁰ We also assembled data including two aboriginal Australian populations: one from the Northern Territories¹⁵ and one from a human diversity cell line panel in the European Collection of Cell Cultures. The data also include nine Indonesian populations: four from the Nusa Tenggaras, two from the Moluccas, one from Borneo, and two from Sumatra. Finally, the data include three Malaysian populations (Temuan and Jehai [a Negrito group] both from the Malay peninsula, and Bidayuh from Sarawak on the island of Borneo), two Philippine populations (Manobo and a Negrito group, the Mamanwa), six aboriginal Taiwanese populations, one Dravidian population from southern India, and San Bushmen from southern Africa from the Centre d'Étude du Polymorphisme Humain (CEPH)-Human Genome Diversity Panel.¹⁶ All volunteers provided informed consent for research into population history and the approval of appropriate local ethical review boards was obtained. This project was approved by the ethical review boards of the University of Leipzig Medical Faculty and Harvard Medical School. The genotype data that we analyzed for this study are available from the authors on request.

Merging Genotyping Data with Chimpanzee, Denisova, and Neandertal

We merged the SNP array data from modern humans with genome sequence data from chimpanzee (CGSC 2.1/PanTro2¹⁷), Denisova,¹² and Neandertal.¹⁸ We eliminated A/T and C/G SNPs to minimize strand misidentification. After removing SNPs with low genotyping completeness, we had data for 353,143 autosomal SNPs.

Removal of Outlier Samples

We carried out principal components analysis by using EIGENSOFT.¹⁹ We removed samples that were visual outliers relative to others from the same population on eigenvectors that were statistically significant by using a Tracy-Widom statistic (p < 0.05),¹⁹ resulting in the removal of three YRI, two CHB, five Polynesians, one New Guinea highlander, two Jehai, and three Mamanwa.

Sequencing Data

We prepared DNA sequencing libraries with 300 bp insert sizes from a Papua New Guinea highlander (SH10) and Mamanwa Negrito (ID36) individual by using a previously described protocol.¹² The two libraries were sequenced on an Illumina Genome Analyzer IIx instrument with 2 × 101 + 7 cycles according to the manufacturer's instructions for multiplex sequencing (FC-104-400x v4 sequencing chemistry and PE-203-4001 cluster generation kit v4). Bases and quality scores were generated with the Ibis base caller,²⁰ and the reads were aligned with the Burrows-Wheeler Aligner (BWA) software ²¹ to the human (NCBI 36/hg18) and chimpanzee (CGSC 2.1/pantro2) genomes with default parameters. The resulting BAM files were filtered as follows: (1) a mapping quality of at least 30 was required; (2) we removed duplicated reads with the same outer coordinates; and (3) we removed reads with sequence entropy < 1.0, calculated by summing −p·log₂(p) for each of the four nucleotides. The sequencing data are publicly available from the European Nucleotide Archive (Project ID ERP000121), and summary statistics are provided in Table S1, available online.

Estimating Denisova p_D(X), Near Oceanian p_N(X) and Australian p_A(X) ancestry

We define the frequency of one of the alleles at a SNP i as $z_x^i$. We can then compute three statistics for a given population X that are informative about admixture:

$$p_D\left(X\right)=\frac{\sum _{i=1}^n\left(z_{Outgroup}^i-z_{Archaic}^i\right)\left(z_{EastAsian}^i-z_x^i\right)}{\sum _{i=1}^n\left(z_{Outgroup}^i-z_{Archaic}^i\right)\left(z_{EastAsian}^i-z_{NewGuinea}^i\right)}=\frac{f_4\left(Outgroup,Archaic;EastAsian,X\right)}{f_4\left(Outgroup,Archaic;EastAsian,NewGuinea\right)}$$ (Equation 1)

$$p_N\left(X\right)=1-\frac{\sum _{i=1}^n\left(z_{Outgroup}^i-z_{Australia}^i\right)\left(z_x^i-z_{NewGuinea}^i\right)}{\sum _{i=1}^n\left(z_{Outgroup}^i-z_{Australia}^i\right)\left(z_{EastAsia}^i-z_{NewGuinea}^i\right)}=1-\frac{f_4\left(Outgroup,Australia;X,NewGuinea\right)}{f_4\left(Outgroup,Australia;EastAsia,NewGuinea\right)}$$ (Equation 2)

$$p_A\left(X\right)=1-\frac{\sum _{i=1}^n\left(z_{Outgroup}^i-z_{NewGuinea}^i\right)\left(z_x^i-z_{Australia}^i\right)}{\sum _{i=1}^n\left(z_{Outgroup}^i-z_{NewGuinea}^i\right)\left(z_{EastAsia}^i-z_{Australia}^i\right)}=1-\frac{f_4\left(Outgroup,NewGuinea;X,Australia\right)}{f_4\left(Outgroup,NewGuinea;EastAsia,Australia\right)}$$ (Equation 3)

The right side of each equation shows that these statistics can also be expressed as ratios of f₄ statistics,¹⁴ which provide unbiased estimates of admixture proportions even in the absence of populations that are closely related to the analyzed populations (Appendix A). For the ancestry estimates reported in Table 1, we use Outgroup = YRI (West Africans), Archaic = Denisova, and East Asian = CHB (Han Chinese). Table S2 and Table S3 demonstrate that consistent values are obtained when we replace these choices with a variety of distantly related populations. Further details are provided in Appendix A.

Table 1.

Estimates of Denisovan and Near Oceanian Ancestry from SNP Data

Population Information				pD(X): Denisovan Ancestry as % of New Guinea			pN(X): Near Oceanian ancestry			p value for Difference
Broad Grouping	Detailed	Code	N	Estimated Ancestry	Standard Error in the Estimate	Z Score	Estimated Ancestry	Standard Error in the Estimate	Z Score	pN(X) − pD(X)
New Guinea	Highlander	SH	24	100%	0%	n/a	100%	0%	n/a	n/a
Australian	all		10	103%	6%	17.1	n/a	n/a	n/a	n/a
	Northern Territories	AU1	8	103%	6%	16.6	n/a	n/a	n/a	n/a
	Cell Cultures	AU2	2	103%	7%	14.1	n/a	n/a	n/a	n/a
Fiji	Fiji	FI	25	56%	3%	17.7	58%	1%	94.6	0.38
Nusa Tenggaras	all		10	40%	3%	12.8	38%	1%	54.7	0.34
	Alor	AL	2	51%	6%	8.3	49%	1%	35.6	0.69
	Flores	FL	1	40%	8%	5.0	37%	2%	19.8	0.68
	Roti	RO	4	27%	4%	6.4	27%	1%	29.4	0.85
	Timor	TI	3	50%	5%	9.8	45%	1%	41.7	0.29
Philippines	all		27	28%	3%	8.2	6%	1%	10.6	3.4 × 10−10
	Mamanwa (N)	MA	11	49%	5%	9.2	11%	1%	11.4	1.5 × 10−12
	Manobo	MN	16	13%	3%	4.2	4%	1%	5.7	0.0018
Moluccas	all		10	35%	4%	10.1	34%	1%	46.0	0.59
	Hiri	HI	7	35%	4%	9.0	32%	1%	38.4	0.36
	Ternate	TE	3	36%	5%	7.2	38%	1%	33.7	0.67
Polynesia	all	PO	19	20%	4%	5.1	27%	1%	34.8	0.052
	Cook		2	16%	6%	2.5	24%	1%	17.3	0.21
	Futuna		4	28%	5%	5.3	29%	1%	26.9	0.87
	Niue		1	27%	8%	3.3	30%	2%	16.3	0.72
	Samoa		5	13%	5%	2.6	24%	1%	23.3	0.024
	Tokelau		2	22%	6%	3.5	31%	1%	23.8	0.14
	Tonga		2	17%	7%	2.5	31%	1%	22.5	0.027
	Tuvalu		3	21%	6%	3.6	28%	1%	22.8	0.28
Andamanese	Onge (N)	AN	10	10%	6%	1.6	3%	1%	1.8	0.27
Taiwan	all	TA	12	4%	3%	1.2	1%	1%	1.5	0.35
	Puyuma		2	4%	6%	0.6	2%	1%	1.8	0.79
	Rukai		2	0%	6%	0.0	2%	1%	1.6	0.74
	Paiwan		2	5%	6%	0.8	3%	1%	2.2	0.67
	Atayal		2	−5%	5%	−0.9	0%	1%	0.3	0.34
	Bunun		2	12%	6%	2.1	−2%	1%	−1.6	0.01
	Pingpu		2	7%	6%	1.2	1%	1%	1.1	0.30
Malaysia	all		18	5%	3%	1.4	0%	1%	−0.2	0.16
	Jehai (N)	JE	8	7%	5%	1.4	1%	1%	0.8	0.21
	Temuan	TM	10	3%	4%	0.8	−1%	1%	−0.9	0.32
Sumatra	All		17	4%	3%	1.4	0%	1%	0.3	0.17
	Besemah	BE	8	5%	3%	1.5	1%	1%	0.9	0.20
	Semende	SM	9	3%	4%	0.9	0%	1%	−0.3	0.31
Borneo	all		49	1%	2%	0.6	1%	1%	1.3	0.79
	Bidayuh	BI	10	6%	4%	1.7	1%	1%	1.4	0.80
	Barito River	BO	23	0%	3%	0.2	1%	1%	1.7	0.18
	Land Dayak	DY	16	0%	3%	−0.1	0%	1%	0.2	0.94
India	Dravidian	SI	12	−7%	5%	−1.5	n/a	n/a	n/a	n/a

We provide each population's estimated ancestry, the standard error in the estimate, and the Z score for deviation from zero (Z). Negrito populations are marked with (N). The New Guinea highlanders by definition have 100% Denisovan and 100% Near Oceanian ancestry because they are used as a reference population for computations. Results are not provided for Australians and Dravidians for whom the phylogenetic relationships do not allow the estimate (n/a). The last column reports the two-sided p value for a difference based on a block jackknife and a Z test.

Block Jackknife Standard Error and Statistical Testing

We used a block jackknife^22,23 to compute standard errors, dropping each nonoverlapping five cM stretch of the genome in turn and studying the variance of each statistic of interest to obtain an approximately normally distributed standard error.^12,18 To test whether p_D(X), p_N(X), p_A(X), and p_D(X) − p_N(X) are statistically consistent with zero for any tested population X, we computed the statistics along with a standard error from the block jackknife, and then used a two-sided Z test that computes the number of standard errors from zero. To implement the 4 Population Test¹⁴ for whether an unrooted phylogenetic tree ([A,B],[C,D]) relating four populations is consistent with the data, we computed the statistic f₄(A,B;C,D) and assessed the number of standard errors from zero.

Results

Quantifying Denisova Admixture from Genome-wide SNP Data

To investigate which modern humans have inherited genetic material from Denisovans, we assembled SNP data from 33 populations from mainland East Asia, island Southeast Asia, New Guinea, Fiji, Polynesia, Australia, and India, and genotyped all of them on Affymetrix 6.0 arrays. After removing samples that were outliers with respect to their own populations (reflecting admixture in the last few generations or genotyping error), we had data from 243 individuals (Table 1). We restricted the analysis to autosomal SNPs with high genotyping completeness and with data from the Denisova genome, leaving 353,143 SNPs.

To quantify the proportion of Denisova genes in each population X, we computed a statistic p_D(X), which measures the proportion of Denisova genetic material in a population as a fraction of that in New Guineans. Our main analyses in Figure 1 and Table 1 compute p_D(X) as a ratio of two f₄ statistics,¹⁴ each of which measures the correlation in allele frequency differences between the two populations used as outgroups (Yoruba and Denisova) and two East or Southeast Asian populations (Han and X = tested population). If Han and X descend from a single ancestral population without any subsequent admixture from Denisova, then the allele frequency differences between Han and X must have arisen solely since their separation from their common ancestor, and the two frequency differences should be uncorrelated; thus, the f₄ statistic has an expected value of zero. However, if population X inherited some of its ancestry from an archaic population related to Denisovans, then the allele frequency differences between Han and X will be correlated, the higher the admixture from the archaic population, the higher the correlation. Because the f₄ statistic in the numerator uses X as the test population, and the f₄ statistic in the denominator uses New Guinea as the test population, the ratio p_D(X) estimates a quantity proportional to the percentage of Denisova ancestry q_X; that is, the Denisova admixture fraction in X divided by that in New Guinea, q_X/q_{New Guinea} (Appendix A).

Figure 1.

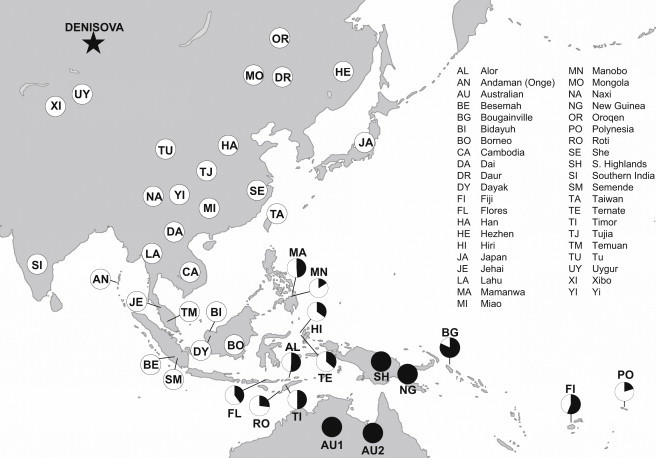
Denisovan Genetic Material as a Fraction of that in New Guineans

Populations are only shown as having Denisova ancestry if the estimates are more than two standard errors from zero (we combine estimates for populations in this study with analogous estimates from CEPH- Human Genome Diversity Panel populations reported previously¹²). No population has an estimate of Denisova ancestry that is significantly more than that in New Guineans, and hence we at most plot 100%. The sampling location of the AU2 population is unknown and hence the position of this population is not precise.

We computed p_D(X) for a range of non-African populations and found that for mainland East Asians, western Negritos (Jehai and Onge), or western Indonesians, p_D(X) is within two standard errors of zero when a standard error is computed from a block jackknife (Table 1 and Figure 1). Thus, there is no significant evidence of Denisova genetic material in these populations. However, there is strong evidence of Denisovan genetic material in Australians (1.03 ± 0.06 times the New Guinean proportion; one standard error), Fijians (0.56 ± 0.03), Nusa Tenggaras islanders of southeastern Indonesia (0.40 ± 0.03), Moluccas islanders of eastern Indonesia (0.35 ± 0.04), Polynesians (0.020 ± 0.04), Philippine Mamanwa, who are classified as a “Negrito” group (0.49 ± 0.05), and Philippine Manobo (0.13 ± 0.03) (Table 1 and Figure 1). The New Guineans and Australians are estimated to have indistinguishable proportions of Denisovan ancestry (within the statistical error), suggesting Denisova gene flow into the common ancestors of Australians and New Guineans prior to their entry into Sahul (Pleistocene New Guinea and Australia), that is, at least 44,000 years ago.^24,25 These results are consistent with the Common Origin model of present-day New Guineans and Australians.^26,27 We further confirmed the consistency of the Common Origin model with our data by testing for a correlation in the allele frequency difference of two populations used as outgroups (Yoruba and Han) and the two tested populations (New Guinean and Australian).The f₄ statistic that measures their correlation is only |Z| = 0.8 standard errors from zero, as expected if New Guineans and Australians descend from a common ancestral population after they split from East Asians, without any evidence of a closer relationship of one group or the other to East Asians. Two alternative histories, in which either New Guineans or Australians have a common origin with East Asians, are inconsistent with the data (both |Z| > 52).

To assess the robustness of these estimates of Denisova admixture proportion, we recomputed p_D(X) for diverse choices of A (YRI, San, and chimpanzee), B (Denisova, Neandertal, and chimpanzee), C (CHB and Borneo) and X (17 different populations). For any population X, we obtain consistent estimates of the archaic mixture proportion, regardless of the choice of A, B, and C. Thus, the method is robust to the choice of comparison populations, suggesting that the underlying model of population relationships (Appendix A) provides a reasonable fit to the data and that our p_D(X) ancestry estimates are reliable. For our main estimates of admixture proportion, we report results for A = YRI, B = Denisova and C = CHB because Table S2 shows that the standard errors are smallest (in part because of larger sample sizes).

To test whether our estimates of p_D(X) are robust to ascertainment bias—the complex ways that SNPs were chosen for inclusion on genotyping arrays originally designed for medical genetics studies—we also estimated Denisova admixture by using sequencing data. For this purpose, we generated new shotgun sequencing data from a Philippine Mamanwa individual (∼1×) and a New Guinea highlander (∼3×, from a different New Guinean group than the one sampled in the Human Genome Diversity Panel¹⁶). We merged these with data from Neandertal, Denisova, chimpanzee, and 12 present-day humans analyzed as part of the Neandertal and Denisova genome sequencing studies.^12,18 We then computed the same p_D(X) statistics for the sequencing as for the genotyping data, replacing YRI with a Yoruba (HGDP00927), CHB with a Han (HGDP00778), and New Guinea with a Papuan sample (Papuan2; HGDP00551). Both the full sequence data and the SNP data produce consistent estimates of p_D(X) (Table 2), suggesting that ascertainment bias is not influencing the p_D(X) estimates from genome-wide SNP data.

Table 2.

Denisovan Admixture p_D(X) Estimated from Sequencing versus Genotyping Data

Sample	HGDP ID for Sequence Data	Sequencing Data			Genotyping Data
		Estimated Ancestry	Standard Error in the Estimate	Z Score	Estimated Ancestry	Standard Error in the Estimate	Z Score
Papuan	HGDP00542	105%	9%	11.8	100%	n/a	n/a
New Guinea Highlander		104%	9%	11.7	100%	n/a	n/a
Bougainville	HGDP00491	83%	10%	8.3	82%	5%	15.9
Mamanwa		28%	10%	2.9	49%	5%	9.2
Cambodian	HGDP00711	19%	9%	2.0	−3%	3%	−0.8
Karitiana	HGDP00998	9%	12%	0.7	4%	6%	0.7
Mongolian	HGDP01224	−6%	12%	−0.5	3%	3%	1.1

For the sequencing data, we present the ratio f₄(Yoruba, Denisova; Han, X)/f₄(Yoruba, Denisova; Han, Papuan2), estimating the proportion of Denisova ancestry in a population X as a fraction of that in the Papuan2 sample (for the first line, the Papuan sample in the numerator is Papuan1 HGDP000551). For the genotyping data, we present the ratio f₄(YRI, Denisova; CHB, X)/f₄(YRI, Denisova; CHB, Papuan). No standard errors are given for the genotyping-based estimates in the first two rows because the Papuans and New Guineans are the reference populations, and so by definition those fractions are 100%.

Near Oceanian Ancestry Explains Denisovan Genes Outside of Australia and the Philippines

A parsimonious explanation for the Denisova genetic material that we detect in the non-Australian populations is the well-documented admixture that has occurred in many Southeast Asian and Oceanian groups between (1) Near Oceanian populations related to New Guineans and (2) populations from island Southeast Asia related to mainland East Asians, who are the primary populations of Taiwan and Indonesia today.^28–31 Thus, many groups might have Denisova admixture as an indirect consequence of their history of Near Oceanian admixture. For those populations whose Denisova ancestry is explained in this way, their fraction of Denisovan ancestry is predicted to be exactly proportional to their fraction of Near Oceanian ancestry.

To test this hypothesis, we designed a second statistic, p_N(X), to estimate the fraction of a population's Near Oceanian ancestry, defined here as the proportion of its ancestry inherited from a population that is more closely related to New Guineans than to Australians (Appendix A). A virtue of p_N(X) is that it provides an unbiased estimate of a population's Near Oceanian ancestry proportion even without access to close relatives of the ancestral populations (Appendix A), whereas previous estimators^10,30 depend on the accuracy of the surrogate contemporary populations used to approximate the ancestral populations. We compared p_D(X) and p_N(X) for all relevant populations (Table 1, Figure 2, and Figure S1) and found that, allowing for sampling error, they occur in a one-to-one ratio for the populations from the Nusa Tenggaras, Moluccas, Polynesia, and Fiji. Common ancestry with Near Oceania thus can account for the Denisova genetic material in these groups.

Figure 2.

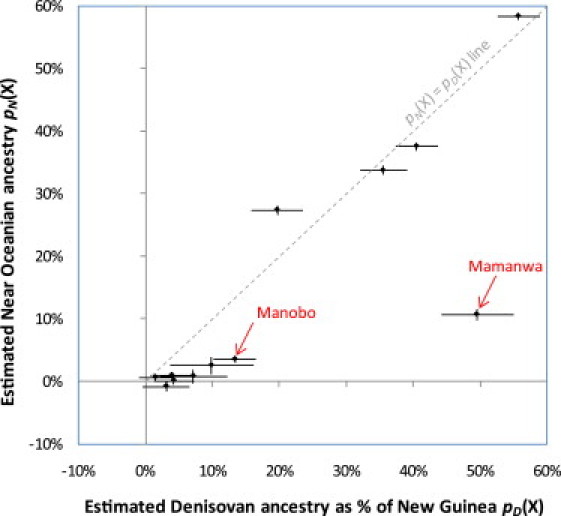
Denisovan and Near Oceanian Ancestry Are Proportional Except in the Philippines

We plot p_D(X), the estimated percentage of Denisova ancestry as a fraction of that seen in New Guineans, against the estimated percentage of Near Oceanian ancestry p_N(X) by using the values from Table 1 (horizontal and vertical bars specify ±1 standard errors). The Mamanwa deviate significantly from the p_D(X) = p_N(X) line, indicating that their Denisova genetic material does not owe its origin to gene flow from a population related to Near Oceanians. A weaker deviation is seen in the Manobo, who live near the Mamanwa on the island of Mindanao.

A striking exception is observed in the two Philippine populations, neither of which conforms to this relationship: p_D(Mamanwa) = 0.49 ± 0.05 versus p_N(Mamanwa) = 0.11 ± 0.01 (p = 1.5 × 10⁻¹² for the difference) and p_D(Manobo) = 0.13 ± 0.03 versus p_N(Manobo) = 0.04 ± 0.01 (p = 0.0018) (Figure 2). An alternative hypothesis that could account for the Denisovan genetic material in the Philippines is common ancestry with Australians.^32,33 We thus computed a third statistic, p_A(X), that estimates the relative proportion of Australian ancestry (Appendix A). However, Australian ancestry cannot explain these patterns either: p_D(Mamanwa) = 0.49 ± 0.05 versus p_A(Mamanwa) = 0.13 ± 0.01 and p_D(Manobo) = 0.13 ± 0.03 versus p_A(Manobo) = 0.05 ± 0.01. The estimates of p_N(X) and p_A(X) are consistent for a variety of outgroups (Appendix A and Table S3). Thus, the Denisova genetic material in Mamanwa, as well as the smaller proportion in their Manobo neighbors, cannot be due to common ancestry with Near Oceanians or Australians after the two groups diverged from one another. In the following section, we focus on the Mamanwa because they have a higher proportion of Denisova genetic material and allow us to study the pattern at a higher resolution.

Modeling Denisova Admixture and Population History

To test whether the patterns observed in the Philippine populations might reflect a history of Denisova gene flow into a population that was ancestral to New Guineans, Australians, and Mamanwa, followed by separation of the Mamanwa first and then divergence of the New Guineans from Australians, we fit f statistics summarizing the allele frequency correlations among all possible sets of populations to admixture graphs.¹⁴ Admixture graphs are formal models of population relationships with the important feature that simply by specifying a topology of population relationships, admixture proportions, and genetic drift values on each lineage, they produce precise predictions of the values that will be observed at f₄, f₃, and f₂ statistics (Appendix B). These predictions can then be compared to the empirically observed values (with standard errors from a block jackknife) to assess the fit to the data.¹⁴ The best-fitting admixture graph for seven populations (Neandertal, Denisova, Yoruba, Han Chinese, Mamanwa, Australians, and New Guineans) specifies Denisova gene flow into a population ancestral to New Guineans, Australians, and Mamanwa, followed by the splitting of the ancestors of the Mamanwa and much more recent admixture between them and populations related to East Eurasians (Figure 3 and Figure S2). For this model, the admixture graph predicts the values of 91 allele frequency correlation statistics (f statistics) relating the seven analyzed populations, and only one f statistic has an observed value more than three standard errors from the prediction (Appendix B).

Figure 3.

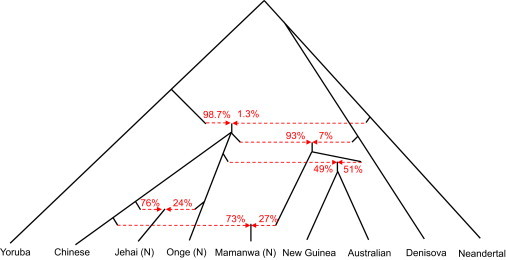
A Model of Population Separation and Admixture that Fits the Data

The admixture graph suggests Denisova-related gene flow into a common ancestral population of Mamanwa, New Guineans, and Australians, followed by admixture of New Guinean and Australian ancestors with another population that did not experience Denisova gene flow. We cannot distinguish the order of population divergence of the ancestors of Chinese, Onge/Jehai, and Mamanwa/New Guineans/Australians, and hence show a trifurcation. Admixture proportion estimates (red) are potentially affected by ascertainment bias and hence should be viewed with caution. In addition, although admixture graphs are precise about the topology of population relationships, they are not informative regarding timing. Thus, the lengths of lineages should not be interpreted in terms of population split times and admixture events.

Encouraged by the fit of the admixture graph to the data from the seven populations, we extended the model to include two additional populations—Andaman Islanders (Onge) and Negrito groups from Malaysia (Jehai)—both of which have been hypothesized to descend from the same migration that gave rise to Australians and New Guineans^4,5 (Figure 3 and Figure S3). This analysis provides overwhelming support for common ancestry for the Onge and Jehai: an admixture graph specifying such a history is an excellent fit to the joint data in the sense that only one of the 246 possible f statistics is more than three standard errors from expectation (Appendix B). The analysis also suggests that after their separation from the Onge, the Jehai received substantial admixture (about three-quarters of their genome) from populations related to mainland East Asians (Appendix B). In contrast, a model in which the Onge have no recent East Asian admixture is a good fit to the data, providing further evidence that the Onge have been unadmixed (at least with non-South Asians⁸) since their initial arrival in the region.¹⁴

A striking finding that emerges from the admixture graph model fitting is the evidence of an episode of additional gene flow into Australian and New Guinean ancestors—after their ancestors separated from those of the Mamanwa—from a modern human population that did not have Denisova genetic material. A model in which this admixture accounts for half of the genetic material in Australians and New Guineans is an excellent fit to the data (Figure 3, Figures S2 and S3, and Appendix B). Admixture graphs that do not model a second admixture event are much poorer fits, producing 11 f statistics at |Z| > 3 standard errors from expectation (Appendix B). Our analysis further suggests that the modern humans who admixed with the ancestors of Australians and New Guineans were closer to Andamanese and Malaysian Negritos than to mainland East Asians (Figure 3), although this is a weaker signal (1 f statistic with |Z| > 3 versus 3) (Figure S3). This suggests that populations with Denisova admixture could have been in proximity to the ancestors of the Onge and Jehai during the earliest settlement of the region but provides no evidence for ancestors of present-day East Asians in the region at that time (Appendix B). Thus, these findings suggest that the present-day East Asian and Indonesian populations are primarily descended from more recent migrations to the region.

Discussion

This study has shown that Southeast Asia was settled by modern humans in multiple waves: One wave contributed the ancestors of present-day Onge, Jehai, Mamanwa, New Guineans, and Australians (some of whom admixed with Denisovans), and a second wave contributed much of the ancestry of present-day East Asians and Indonesians. This scenario of human dispersals is broadly consistent with the archaeologically-motivated hypothesis of an early southern route migration leading to the colonization of Sahul and East Asia² but also further clarifies this scenario. In particular, our data provide no evidence for multiple dispersals of modern humans out of Africa, as all non-Africans have statistically indistinguishable amounts of Neandertal genetic material.^12,18 Instead, our data are consistent with a single dispersal out of Africa (as proposed in some versions of the early southern route hypothesis¹) from which there were multiple dispersals to South and East Asia.

This study is also important in providing a clue about the geographic location of the Denisova gene flow. Given the high mobility of human populations, it is difficult to use genetic data from present-day populations to infer the location of past demographic events with high confidence. Nevertheless, the fact that Denisova genetic material is present in eastern Southeast Asians and Oceanians (Mamanwa, Australians, and New Guineans), but not in the west (Onge and Jehai) or northwest (the Eurasian continent) suggests that interbreeding might have occurred in Southeast Asia itself. Further evidence for a Southeast Asian location comes from our evidence of ancient gene flow from relatives of the Onge and Jehai into the common ancestors of Australians and New Guineans after the initial Denisova gene flow (Figure 3); this suggests that ancestors of both of these groups (but not of East Asians) were present in the region at the time. Although some of the observed patterns could alternatively be explained by a history in which there was initially some Denisova genetic material throughout Southeast Asia—which was subsequently displaced by major migrations of people related to present-day East Asians—such a history cannot parsimoniously explain the absence of Denisova genetic material in the Onge and Jehai. Our evidence of a Southeast Asian location for the Denisovan admixture thus suggests that Denisovans were spread across a wider ecological and geographic region—from the deciduous forests of Siberia to the tropics—than any other hominin with the exception of modern humans.

Finally, this study is methodologically important in showing that there is much to learn about the relationships among modern humans by analyzing patterns of genetic material contributed by archaic humans. Because the archaic genetic material is highly divergent, it is easily detected in a modern human even if it contributes only a small proportion of the ancestry; this makes it possible to use archaic genetic material to study subtle and ancient gene flow much as a medical imaging dye injected into a patient allows the tracing of blood vessels. A priority for future research should be to obtain direct estimates for the dates of the Denisova and Neandertal gene flow, as these will provide a better understanding of the interactions among Denisovans, Neandertals, and the ancestors of various present-day human populations.

Appendix A: Statistics Used for Estimating Admixture Proportions

p_D(X) Statistic Used for Estimating Denisova Admixture Proportion

We first discuss the p_D(X) statistic that we use for estimating the Denisova admixture proportion in any population X. Define the frequency of allele i in a sample from population Y as $z_Y^i$. Then p_D(X) is defined as in Equation 1.

The rightmost part of Equation 1 shows that p_D(X) can also be expressed as a ratio of f₄ statistics, which we introduced previously¹⁴ to measure the correlation in allele frequency differences between pairs of populations. We previously reported simulations showing that the expected values of f₄ statistics are in practice robust to ascertainment bias (how the polymorphisms are chosen for inclusion in an analysis), making them useful for learning about history with SNP array data.¹⁴

The expected values of f₄ statistics can be understood visually by following the arrows through the phylogenetic trees with admixture relating sets of samples, assuming that these are accurate models for the relationships among the populations.¹⁴ Figure 4 illustrates how the ratio of f₄ statistics computed in Equation 1 estimates an admixture proportion. Both the numerator and denominator can be viewed as a correlation of two allele frequency differences:

Figure 4.

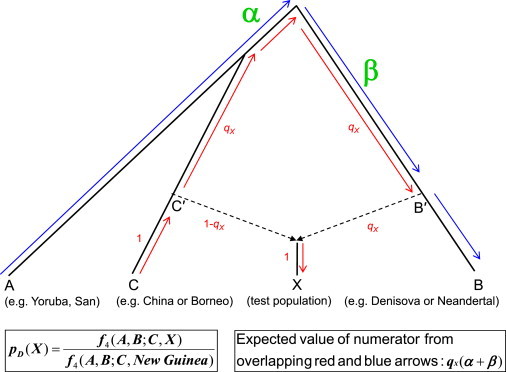
Computation of the Estimate of Denisovan Ancestry p_D(X)

The black lines show the model for how populations are related that is the basis for the p_D(X) ancestry estimate. Population X arose from an admixture of a proportion (1 − q_X) of ancestry from an ancestral non-African population C′ and (q_X) from archaic population B′ (C and B are their unmixed descendants). The expected value of f₄(A,B;C,X) is proportional to the correlation in the allele frequency differences A − B and C − X, and can be computed as the overlap in the drift paths separating A − B (blue arrows) and C − X (red arrows). These paths only overlap over the branches α and β, in proportion to the percentage q_X of the lineages of population X that are of archaic ancestry and so the expected value is q_X(α + β). When we compute the ratio p_D(X), (α + β) cancels from both the numerator and denominator, and we obtain q_X/q_{New Guinea}, the fraction of archaic ancestry in a population X divided by that in New Guinea. This provides unbiased estimates of the mixture proportion even if populations C and B have experienced a large amount of genetic drift since splitting from their ancestors, that is, even if we do not have good surrogates for the ancestral populations. This robustness arises because the genetic drift on the branches B→B′ and C→C′ does not contribute to the expectations.

$z_A^i-z_B^i$ is the correlation in the allele frequency difference between an Outgroup “A” that did not experience admixture and an Archaic group “B” hypothesized to be related to the admixing group (e.g., A = {chimpanzee, Yoruba, or San} and B = {Denisova or Neandertal}). This follows the blue arrows in Figure 4.

$z_C^i-z_X^i$ is the correlation in the allele frequency difference between a modern non-African population “C” and a test population “X” (e.g., C = {Chinese or Bornean}). This follows the red arrows in Figure 4.

If populations C and X are sister groups that descend from a homogeneous non-African ancestral population, then the allele frequency differences are expected to have arisen entirely since the split from that common ancestral population, and thus the correlation to A and B is expected to be zero (no overlap of the arrows). In contrast, if population X has inherited some proportion q_X of its lineages from an archaic population, then the expected value of the product of the frequency differences is proportional to q_X times the overlap of the paths of A and B and C and X in Figure 4, which corresponds to genetic drift α + β. While we do not know the value of α + β, when we take the ratio of the numerator and denominator to compute the p_D(X) statistic, this unknown quantity cancels, and we obtain q_X/q_{New Guinea}, the proportion of archaic ancestry in a population as a fraction of that in New Guineans (Figure 4).

Two issues merit further discussion. First, Figure 4 is an oversimplification in that it does not show two archaic gene-flow events (corresponding to Denisovans and Neandertals). However, we have previously reported that the data are consistent with the same amount of Neandertal gene flow into the ancestors of East Asians (C, such as CHB) and populations with Denisovan ancestry (X).^12,18 As a result, the same genetic drift terms are added to the numerator and denominator, which then cancel in the ratio p_D(X) so that they do not affect results. Second, p_D(X) is expected to provide an unbiased estimate of the admixture proportion even if the genetic drift on various lineages has been large. This contrasts with previous methods for estimating admixture, which have required accurate proxies for the ancestral populations.¹⁰

p_N(X) and p_A(X) Statistics for Estimating Near Oceanian and Denisova Admixture

We next discuss the statistics that we use for estimating the New Guinean p_N(X) or Australian p_A(X) mixture proportion in any East Eurasian or island Southeast Asian population X, which are defined in Equations 2 and 3, respectively.

Figure 5 shows the admixture graph corresponding to the computation of p_N(X). Both the numerator and the denominator are of the form f₄(A,Australia; X,New Guinea). The first term measures the correlation in allele frequency differences between (A − Australia) and (X − New Guinea). If X and New Guinea descended from a common ancestral population since the split from Australians, then they are perfect sister groups, and the expected value of f₄ is zero (the sample is consistent with 100% Near Oceanian ancestry). On the other hand, if X has a proportion (1 − q_X) of non-Near Oceanian ancestry, then the two terms will have a nonzero correlation, which as shown in Figure 5 is proportional to the genetic drift shared between the two population comparisons and has an expected value of (1 − q_X)[(1 − p_X)β + γ] (the proportions of ancestry flowing along various genetic drift paths times the genetic drift on each of these lineages, indicated by the overlap of the red and blue arrows). When we take one minus the ratio p_N(X) = 1 − f₄(A,Australia; X,New Guinea)/f₄(A,Australia; CHB,New Guinea), the complicated term on the right side of this expectation cancels, and we obtain E[p_N(X)] = q_X. As with Figure 4, we do not show the independent Neandertal admixture because the effect of this term is to cancel from the numerator and denominator.

Figure 5.

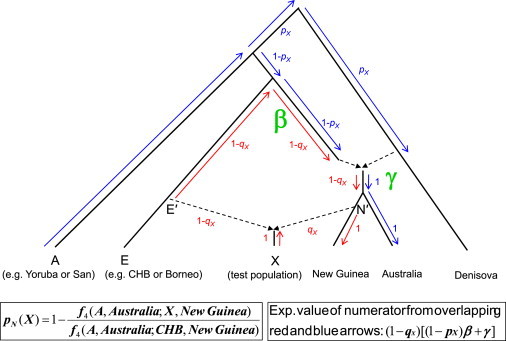
Computation of the Estimate of Near Oceanian Ancestry p_N(X)

The test population X is assumed to have arisen from a mixture of a proportion (1 − q_X) of ancestry from ancestral East Asians E′ and (q_X) of ancestral Near Oceanians N′. The Near Oceanians are, in turn, assumed to have received a proportion p_X of their ancestry from the Denisovans (E and New Guinea are assumed to be unmixed descendants of these two). The expected value of f₄(A,Australia; X, New Guinea) can be computed from the correlation in the allele frequency differences A − Australia (blue arrows) and X − New Guinea (red arrows). These paths only overlap along the proportion (1 − q_X) of the ancestry of population X that takes the East Asian path, where the expected shared drift is (1 − p_X)β+γ as shown in the figure. Thus, the expected value of the f₄ statistic is (1 − q_X)(1 − p_X)β+γ. Because q_X = 0 for the denominator of p_N(X) (no Near Oceanian ancestry), the ratio of f₄ statistics has an expected value of (1 − q_X) and E[p_N(X)] = q_X.

In Table S3 we report the p_N(X) estimates for diverse choices of outgroup populations A (Yoruba, San, and chimpanzee) and E (China and Borneo). The estimates are consistent whatever the choice of A and E, suggesting that our inferences are robust. (We do not report p_N(X) estimates in Table S3 for the Australians because this population is not expected to conform to the population relationships shown in Figure 5; indeed, the p_N(X) estimates for Australians, when we do compute them, are significantly greater than 1.) Further evidence for the usefulness of the p_N(X) estimates comes from the fact that it is consistent with the p_D(X) estimate for nearly all the populations in Table 1 (except for the Philippine populations, in which the Denisova ancestry does not appear to be explainable by Near Oceanian gene flow as described in the main text).

We also computed a statistic p_A(X) that is identical to p_N(X) except for the transpositions of the positions of Australia and New Guinea in the statistics (Equations 2 and 3). Once again, we obtain consistent inferences of p_A(X) in Table S3 regardless of the choice of outgroup populations. Because New Guinea and Australia are sister groups, descending from a common ancestral population, the justifications for the two statistics are very similar.

The only problem we found with the estimation of p_N(X) procedure is that when X is any non-African population known to have West Eurasian ancestry (e.g., Europeans or South Asians), we often obtained negative p_N(X) statistics. Two hypotheses could be consistent with this observation: (1) In unpublished data, we have attempted to write down a model of population separation and mixture analogous to that in Figure 3 that jointly fits the genetic data comparing eastern and western Eurasian populations and have so far not succeeded in developing a model that passes goodness-of-fit tests. This suggests that the population relationships between eastern and western Eurasians might be more complex than we have been able to model to date, and therefore we cannot use them in the p_N(X) computation. (2) An alternative possibility is that the negative p_N(X) statistics reflect an artifact of ascertainment bias on SNP arrays. Ascertainment bias is likely to be particularly complex with regard to the joint information from Europeans and East Asians because these populations were heavily used in choices of SNPs for medical genetics arrays. Thus, it might be difficult to make inferences using populations from both regions together with data from conventional SNP arrays developed for medical genetic studies.

Whatever the explanation, we have some reason to believe that estimates of Near Oceanian admixture by using data from populations with West Eurasians might be unreliable. Thus, we have excluded West Eurasians from the estimates reported in Table 1.

Appendix B: Admixture Graphs

Overview of Admixture Graphs

A key finding from this study is that there is Denisova genetic material in the Mamanwa, a Negrito group from the Philippines, which cannot be explained by a history of recent gene flow from relatives of New Guineans (Near Oceanians) or Australians. To further understand this history, we use the admixture graph methodology that we initially developed for a study of Indian genetic variation¹⁴ to test whether various hypotheses about population relationships are consistent with the data. Specifically, we tested the hypothesis of a single episode of Denisovan gene flow into the ancestors of New Guineans, Australians, and Mamanwa, prior to the separation of New Guineans and Australians.

Admixture graphs refer to generalizations of phylogenetic trees that incorporate the possibility of gene flow. Like phylogenetic trees, admixture graphs describe the topology of population relationships without specifying the timing of events (such as population splits or gene-flow events), or the details of population size changes on different lineages. While this can be a disadvantage in that fitting admixture graphs to data does not allow inferences of these important details, it is also an advantage in that one can fit genetic data to an admixture graph without having to specify a demographic history. This allows for inferences that are more robust to uncertainties about important parameters of history. Once the topology of the population relationships is inferred, one can in principle use other methods to make inferences about the timing of events and population size changes. This makes the problem of learning about history simpler than if one had to simultaneously infer topology, timing, and demography.

An admixture graph makes precise predictions about the patterns of correlation in allele frequency differences across all subsets of two, three, and four populations in an analysis, as measured for example by the f₂, f₃, and f₄ statistics of Reich et al.¹⁴ Given n populations, there are n(n − 1)/2 f₂ statistics, n(n − 1)(n − 2)/6 f₃ statistics, and n(n−1)(n−2)(n−3)/24 f₄ statistics. To fit an admixture graph to data, one first proposes a topology, then identifies the set of admixture proportions and genetic drift values on each lineage (variation in allele frequency corresponding to random sampling of alleles from generation to generation in a population of finite size) that are the best match to the data under that model. The admixture graph topology, admixture proportions, and genetic drift values on each lineage together generate expected values for the f₂, f₃ and f₄ statistics¹⁴ that can be compared to the observed values—which have empirical standard errors from a block jackknife—to assess the adequacy of the best fit under the proposed topology. As we showed previously,¹⁴ the topology relating populations in an admixture graph can be accurately inferred even if the polymorphisms used in an analysis are affected by substantial ascertainment bias. The software that we have developed for fitting admixture graphs carries out a hill-climb to find the genetic drift values and admixture proportions that minimize the discrepancy between the observed and expected f₂, f₃, and f₄ statistics for a given topology relating a set of populations.

A complication in fitting admixture graphs to data is that we do not know how many effectively independent f statistics there are, out of the [n(n − 1)/2][1 + (n − 2)/3 + (n − 3)/12] that are computed. These statistics are highly correlated, and in fact can be related algebraically to each other; for example, all the f₃ and f₄ statistics are a linear combinations of the f₂ statistics. Although we believe that it is possible to construct a reasonable score for how well the model fits the data by studying the covariance matrix of the f statistics—and indeed a score of this type is the basis for our hill-climbing software—we have not yet found a formal way to assess how many independent hypotheses are being tested, and thus we do not at present have a goodness-of-fit test. Instead, we simply compute all possible f statistics and search for extreme outliers (e.g., Z scores of 3 or more from expectation). A large number of Z scores greater than 3 are not likely to be observed if the admixture graph topology is an accurate description of a set of population relationships.

Denisova Gene Flow into Mamanwa/New Guinean/Australian Ancestors

We initially fit an admixture graph to the data from Mamanwa, New Guineans, Australians, Denisova, Neandertal, West Africans (YRI), and Han Chinese (CHB), basing some of the proposed population relationships on previous work that hypothesized a model of an out-of-Africa migration of modern humans, Neandertal gene flow into the ancestors of all non-Africans, and sister group status for Neandertals and Denisovans.¹² A complication in fitting an admixture graph to these data is that because of the low coverage of the Neandertal and Denisova genomes, we could not accurately infer the diploid genotype at each SNP. Thus, we sampled a single read from Neandertal and Denisova to represent each site and (incorrectly) assumed that these individuals were homozygous for the observed allele at each analyzed SNP. This means that the estimates of genetic drift on the Neandertal and Denisova branches are not reliable (the genetic drift values are overestimated). However, these sources of error do not introduce a correlation in allele frequencies across populations and hence are not expected to generate a false inference about the population relationships.

Figure S2 shows an admixture graph that proposes that the Mamanwa, New Guineans, and Australians descend from a common ancestral population; the Mamanwa split first and the New Guinean and Australian ancestors split later. This is an excellent fit to the data in the sense that only one of 91 f statistics is more than three standard errors from zero (|Z| = 3.4). An interesting feature of this admixture graph is that it specifies an additional admixture event, after the Mamanwa lineage separated, into the ancestors of Australians and New Guineans that contributed about half of their ancestry and involved a population without Denisova admixture. A model that does not include such a secondary admixture event is strongly rejected (see below).

The estimated proportion of Neandertal ancestry in all non-Africans from the admixture graph fitting in Figure 3, at 1.3%, is at the low end of the 1%–4% previously estimated from sequencing data.¹⁸ Similarly, we infer a proportion of Denisova ancestry in New Guineans of 3.5% = 6.6% × 53%, which is lower than the 4%–6% previously estimated based on sequencing data but not significantly so when one takes into account the standard errors quoted in that study.¹² These low numbers could reflect statistical uncertainty from the previously reported analyses of sequencing data or in the admixture graph estimates (the latter possibility is especially important to consider because we do not at present understand how to compute standard errors on the admixture estimates derived from admixture graphs). Another possible explanation for the low estimates of mixture proportions is ascertainment bias affecting the way SNPs were selected, which can affect estimates of mixture proportions and branch lengths (while having much less impact on the inference of topology). Further support for the hypothesis that ascertainment bias might be contributing to our lower estimates of mixture proportions comes from the fact that in unpublished work we have found that the polymorphisms most enriched for signals of archaic admixture are those in which the derived allele is present in the archaic population, absent in West Africans, and present at low minor allele frequency in the studied population. In our admixture graph fitting, we filtered out this class of SNPs, as the f statistics used in the admixture graph have denominators that require frequency estimates from a polymorphic reference population, and we used YRI as our reference. Thus, when we refitted the same admixture graph with CHB instead of YRI as the reference population, we obtained the same topology but the Neandertal mixture proportion increased to 1.9%. We have chosen to use YRI as the reference population in all of our reported admixture graphs because they are a better outgroup for the modern populations whose history we are studying than the CHB (populations related to the Chinese were directly involved in admixture events in Southeast Asia).

Adding Onge and Jehai

The Andamanese Negrito group (Onge) and Malaysian Negrito group (Jehai) have been proposed to share ancient common ancestry with Philippine Negritos (e.g., Mamanwa). The fact that neither the Onge nor the Jehai have evidence of Denisova genetic material, however, suggests that any common ancestry must date to before the Denisova gene flow into the ancestors of the Mamanwa, New Guineans, and Australians. To explore the relationship between the Onge and Jehai and the other populations, we added them into the admixture graph. The only family of admixture graphs that we could identify as fitting the data have the Onge as a deep lineage of modern humans, with the Jehai deriving ancestry from the same lineage but also harboring a substantial additional contribution of East Asian related admixture (Figure S3).

A striking feature of the family of admixture graphs shown in Figure S3 is that both the Jehai and Mamanwa are inferred to have up to about three-quarters of their ancestry due to recent East Eurasian admixture, which is not too surprising given that these populations have been living side by side with populations of East Eurasian ancestry for thousands of years. Moreover, both Y-chromosome and mtDNA analyses strongly suggest recent East Asian admixture in the Mamanwa.^32,34 In contrast, the genome-wide SNP data for the Onge are consistent with having no non-Negrito admixture within the limits of our resolution, perhaps reflecting their greater geographic isolation.

We next sought to resolve how the lineage including Onge and Jehai ancestors, the mainland East Asian (e.g., Chinese), and the eastern group (including Mamanwa, Australian and New Guinean ancestors) are related. Three relationships are all consistent with the data. Specifically, for all three of the admixture graphs shown in Figure S3, only one of the 246 possible f statistics has a score of |Z| > 3. Thus, we cannot discern the order of splitting of these three lineages and represent the relationships as a trifurcation in Figure 3. The actual estimates of mixture proportions are similar for all three figures as well.

Perturbing the Best-Fitting Admixture Graph to Assess the Robustness of Our Inferences

To assess the robustness of the admixture graphs, we perturbed Figure S3 (in practice, we perturbed Figure 3A, but given the fact that the graphs are statistically indistinguishable we expected that results would be similar for all three). First, we considered the possibility that after the initial Denisova gene flow into the ancestors of Mamanwa, New Guineans, and Australians, the New Guinean and Australian ancestors did not experience an additional gene-flow event with a population without Denisovan admixture. However, when we try to fit this simpler model to the data, we find that instead of one f statistic that is |Z| > 3 standard errors from expectation, there are now 11, and all but one of them involve the Mamanwa, suggesting that this population is poorly fit by such a model. Thus, an additional admixture event in the ancestry of New Guineans and Australians (resulting in a decrease in their proportion of Denisova ancestry) results in a major improvement in the fit.

Second, we considered the possibility that the secondary gene-flow event into the ancestors of Australians and New Guineans came from relatives of Chinese (CHB) rather than western Negritos such as the Onge. However, when we fit this alternative history to the data, we find three f statistics (rather than one) with scores of |Z| > 3, a substantially worse fit. We conclude that the modern human population with which the ancestors of Australians and New Guineans interbred was likely to have been more closely related to western Negritos than to mainland East Asians.

Web Resources

The URLs for data presented herein are as follows:

• Burrows-Wheeler Aligner, http://bio-bwa.sourceforge.net/index.shtml

• CEPH-Human Genome Diversity Cell Line Panel, http://www.cephb.fr/en/hgdp/diversity.php

• EIGENSOFT, http://genepath.med.harvard.edu/∼reich/Software.htm

• European Collection of Cell Cultures, http://www.hpacultures.org.uk/pages/Ethnic_DNA_Panel.pdf

• European Nucleotide Archive (Project ID ERP000121), http://www.ebi.ac.uk/ena/

• Ibis, http://bioinf.eva.mpg.de/Ibis/

• SAMtools, http://samtools.sourceforge.net/