Skip to main content
PMC home page
British Journal of Cancer logoLink to British Journal of Cancer
. 2011 Jul 26;105(5):682–686. doi: 10.1038/bjc.2011.276

Objective assessment of tumour response to therapy based on tumour growth kinetics

E Mehrara 1,*, E Forssell-Aronsson 1, P Bernhardt 1
PMCID: PMC3188932  PMID: 21792200

Abstract

Background:

Current standards for assessment of tumour response to therapy (a) categorise therapeutic efficacy values, inappropriate for patient-specific and deterministic studies, (b) neglect the natural growth characteristics of tumours, (c) are based on tumour shrinkage, inappropriate for cytostatic therapies, and (d) do not accommodate integration of functional/biological means of therapeutic efficacy assessed with, for example, positron emission tomography or magnetic resonance imaging, with data from anatomical changes in tumour.

Methods:

A quantity for tumour response was formulated assuming that an effective treatment may decrease the cell proliferation rate (cytostatic) and/or increase the cell loss rate (cytotoxic) of the tumour. Tumour response values were analysed for 11 non-Hodgkin's lymphoma patients treated with 131I-labelled anti-B1 antibody and 12 prostate cancer patients treated with a nutritional supplement.

Results:

Tumour response was found to be equal to the logarithm of the ratio of post-treatment tumour volume to the volume of corresponding untreated tumour. Neglecting the natural growth characteristics of tumours results in underestimation of treatment effectiveness based on currently used methods. The model also facilitates the integration of data from tumour volume changes, with data from functional imaging.

Conclusion:

Tumour response to therapy can be assessed with a continuous dimensionless quantity for both cytotoxic and cytostatic treatments.

Keywords: tumour, response, therapy, growth kinetics, cytotoxic, cytostatic

Assessment of tumour response (TR) to therapy is necessary for evaluation of the efficacy of novel anticancer drugs in clinical trials. Furthermore, response evaluation with high individual precision may facilitate individualised therapy rather than standardised treatment regimen in daily clinical practice.

Tumour shrinkage has been traditionally used as a measure of treatment efficacy. For example, the response evaluation criteria in solid tumours (RECIST) is currently adopted by academic and industrial groups (Miller et al, 1981; Therasse et al, 2000), where response to therapy is categorised as follows: complete response (CR), the disappearance of all target lesions; partial response (PR), at least a 30% decrease in the sum of the longest diameter of all target lesions; progressive disease (PD), at least a 20% increase in the sum of the longest diameter of all target lesions or the appearance of one or more new lesions; and stable disease (SD), neither sufficient shrinkage to qualify for PR nor sufficient increase to qualify for PD (Therasse et al, 2000; Eisenhauer et al, 2009). Appropriateness of RECIST criteria, for example, whether the change in tumour size is a proper end point for response assessment, has been widely discussed (Barnacle and McHugh, 2006; Tuma, 2006; Twombly, 2006; Eisenhauer, 2007). The specific criteria have been developed for different types of cancers, for example, prostate cancer (Scher et al, 2008) and malignant lymphoma (Cheson et al, 2007). However, this study was focused only on quantification of TR to therapy, regardless of the type of tumour and clinical measures other than tumour response.

The following limitations can be identified in current standards for quantification of TR to therapy:

(1) Traditional standards may not be appropriate to assess the efficacy of emerging numbers of cytostatic agents, which do not result in tumour regression to a point of PR or CR. Proposals of a general means of assessment of both cytocidal and cystostatic effects must be developed (Michaelis and Ratain, 2006; Gwyther and Schwartz, 2008).

(2) The natural growth rate of tumour is not considered. A certain treatment that kills the same ratio of tumour cells in two different tumour types will give different results if the natural proliferation rates of tumour cells are different.

(3) Adopting the current standards will convert a continuous variable, as TR, into a discrete variable, resulting in the loss of information. This will make comparison of individual, or combination of, treatments less accurate. Furthermore, attempts to relate treatment efficacy to molecular or cellular characteristics of tumours, for example, by systems biology approach, will be rather difficult when data are categorised. Karrison et al (2007), based on suggestions by Lavin (1981), demonstrated that clinical trial designs that treat change in tumour size as a continuous variable are feasible (Karrison et al, 2007). They used the logarithm of the ratio of tumour volume after therapy to that at baseline as an end point for quantification of TR, denoted as LR (log ratio) (Karrison et al, 2007).

(4) Many studies have shown that the effect of treatment on tumours can be assessed by means of changes in tumour characteristics other than size, for example, estimated by positron emission tomography (PET) or magnetic resonance imaging or spectroscopy (MRI/MRS) (Padhani and Miles, 2010). Available standards do not accommodate mathematical integration of physiological or functional imaging modalities into anatomical changes in tumour and new methods must evolve (Jaffe, 2008).

The aim of this study was to develop a mathematically accurate and biologically relevant method for assessment of TR to any type of treatment.

Materials and methods

Kinetics of tumour growth

Volumetric growth rate of tumours can be quantified with specific growth rate (SGR), described as relative volume change per time unit. Quantification of growth rate with SGR is mathematically more accurate and biologically more relevant than the widely used parameter tumour volume doubling time (DT) (Mehrara et al, 2007, 2009). The SGR of a tumour during time period from t0 to t can be calculated from tumour volumes at the start and at the end of this period, V0 and V, respectively:

graphic file with name bjc2011276e1.jpg

More rapidly growing tumours have higher SGR values, SGR=0 represents non-growing tumours, and negative SGR values can be assigned to tumour regression. Specific growth rate is constant for exponentially growing tumours; however, if SGR is time dependent, as for non-exponentially growing tumours, the above equation can be rewritten as follows:

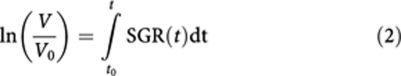graphic file with name bjc2011276e2.jpg

where SGR(t) is the SGR at time t. The value of SGR(t) depends on the level of cell proliferation rate, CPR(t), and cell loss rate, CLR(t), at time t:

graphic file with name bjc2011276e3.jpg

TR to therapy

If the natural growth of tumour is interrupted by therapy, an effective therapeutic agent may increase the CLR (cytotoxic effect) and/or decrease the CPR (cytostatic effect) of tumour. Specific growth rate will then decrease to SGR′ regardless of the mechanism of the therapeutic effect:

graphic file with name bjc2011276e4.jpg

where ΔSGR(t) is the effect of treatment at time t. Temporal variation of SGR′ depends on all factors that naturally affect tumour growth as well as the effect of therapy. Readjustment and integration of the above equation over time gives:

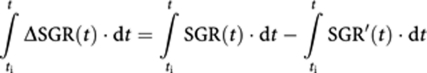graphic file with name bjc2011276e5.jpg

where ti and t are the time of therapy initiation and efficacy assessment, respectively. The right side of the above equation can be replaced using Equation (2), which gives:

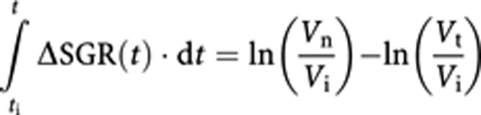graphic file with name bjc2011276e6.jpg

where Vi is tumour volume at the time of therapy initiation, and Vt and Vn are the volume of treated and corresponding (hypothetical) non-treated tumour at the time of efficacy assessment, respectively. The left side of the above equation is the overall effect of treatment during time from treatment initiation to time of efficacy assessment, and can be denoted as TR. Since ln(Vn/Vi)−ln(Vt/Vi)=−ln(Vt/Vn):

graphic file with name bjc2011276e7.jpg

TR is a general continuous dimensionless quantity for tumour response to both cytotoxic and cytostatic therapeutic effects. TR can thus be calculated by the logarithm of the ratio between the post-treatment volume of tumour and the volume that the tumour would have had (at the time of efficacy assessment) if the growth was not influenced by therapy. The value of Vn cannot be defined, but only estimated based on the natural growth model of tumour.

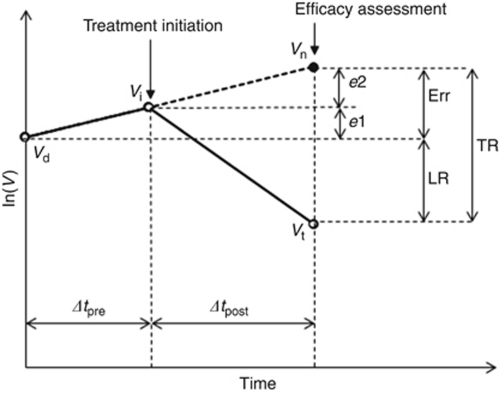
To estimate Vn the following assumptions were used (cf. Figure 1): (1) tumour volume at first diagnostic investigation is Vd; (2) therapy is initiated at a time point Δtpre after measurement of Vd; (3) tumour grows exponentially with a constant SGR(t)=SGR0 during the studied time period and tumour volume at the time of therapy initiation is Vi; (4) tumour response is assessed at a time point Δtpost after therapy initiation and tumour volume at the time of efficacy assessment is Vt; and (5) tumour would continue to grow with SGR0 if the growth was not interrupted and its volume would be Vn at the time of efficacy assessment.

Figure 1.

Figure 1

Open in a new tab

Definition of the parameters used in the study. Vd, Vi, and Vt are tumour volumes at diagnosis, therapy initiation, and time of efficacy assessment, respectively. Tumour volume would increase to Vn at the time of efficacy assessment if therapy was not started. TR=tumour response value derived in this study, LR=log ratio measure for quantification of treatment effectiveness, e1 and e2=underestimation of TR if pretreatment or post-treatment growth of tumour is neglected, respectively. Err=overall underestimation of TR if pretreatment and post-treatment growth of tumour are neglected (TR=LR+e1+e2).

Application to patient data

Tumour response values were calculated for treatment of non-Hodgkin's lymphoma patients with 131I-labelled anti-B1 antibody, where data were retrieved from a previously published article (Sgouros et al, 2003). The study was selected based on the availability of tumour volumes and the time of pretreatment and post-treatment volume estimations in each patient, information necessary for TR calculation. Total tumour burden was assessed by drawing contours around all lymphoma lesions identified on whole-body CT or MRI. Two more patients are included in the original article, where tumours disappeared after treatment. Those data were excluded in this study. Average post-treatment re-growth of tumour volumes used as an estimation of the natural growth rate of non-Hodgkin's lymphomas in this study.

Another set of data were retrieved from the literature, where prostate-specific antigen (PSA) increase rates before and after treatment with a nutritional supplement were available in 12 prostate cancer patients (Guess et al, 2003). Tumour response values were calculated using PSA levels before and after treatment for assessment of treatment efficacy.

Tumour response values were calculated for non-Hodgkin's lymphoma patients using total tumour burden as reference and for prostate cancer patients using PSA level as reference, respectively. On the basis of the calculated mean and standard deviation of TR and LR in each group of patients, frequency distribution of TR and LR were approximated with corresponding normal distribution with the same mean and standard deviation values in each group, respectively.

Results

When the tumour response model developed in this study (Equation (5)) is applied to an exponentially growing tumour, TR is related to tumour volume and growth rate as follows (Figure 1):

graphic file with name bjc2011276e8.jpg

The first term on the right-hand side of the above equation, LR, is the treatment effectiveness where the natural growth of tumour is neglected and is equivalent to the LR measure suggested by Karrison et al (2007). LR values less than −0.5, between −0.5 and +1, and larger than +1 correspond to progressive disease, stable disease, and partial response according to RECIST, respectively. The second term, e1, and the third term, e2, represent tumour growth before and after treatment initiation, respectively. The overall effect of tumour growth from the time of diagnosis to the time of efficacy assessment, Δt, sums up as follows:

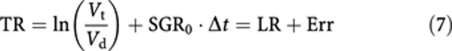graphic file with name bjc2011276e9.jpg

The above equation indicates that evaluation of treatment effectiveness by comparing the volume of treated tumour with pretreatment tumour volume underestimates the effect of therapy by Err.

If a therapeutic drug has pure cytostatic effect, that is, the drug inhibits tumour growth, but does not destroy existing tumour cells, and if the drug can completely block tumour growth, the tumour volume at the time of efficacy assessment will be the same as the tumour volume at the time of treatment initiation, Vi. The cytostatic efficacy of treatment is then e2=ln(Vn/Vi) (Figure 1). If the drug can partially control tumour growth, the tumour volume at the time of efficacy assessment will be larger than Vi (closer to Vn) and the treatment efficacy will be less than e2 in Figure 1. Note that tumour volume at the time of efficacy assessment is, however, larger than tumour volume at the time of diagnosis, Vd. According to RECIST, a Vt of more than 1.73Vd (20% increase in diameter) will be considered as progressive disease. For a tumour with DT shorter than 27 days (SGR >2.6% per day) and a treatment that completely blocks tumour growth, the drug will be considered without any effect and be categorised as progressive disease according to RECIST.

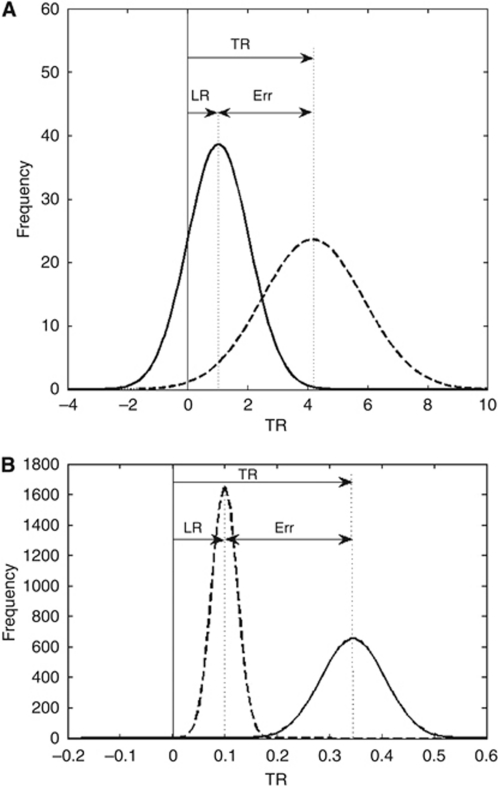
The frequency distributions of TR and LR are shown in Figures 2A and B for non-Hodgkin's lymphoma and prostate cancer patients, respectively. The results show that LR largely underestimates tumour response compared to TR.

Figure 2.

Figure 2

Open in a new tab

Frequency distributions of TR and LR based on treatment results of (A) 11 non-Hodgkin's lymphoma patients and (B) 12 prostate cancer patients. The mean and standard deviation values were obtained for each group and the corresponding normal distributions were drawn. TR: mean=4.16 and 0.35, s.d.=1.69 and 0.06; LR: mean=1.02 and 0.1, s.d.=1.03 and 0.02 for non-Hodgkin's lymphoma and prostate cancer patients, respectively. TR and LR values were calculated from changes in tumour volume and PSA level in non-Hodgkin's lymphoma and prostate cancer patients, respectively.

Discussion

Traditional quantification methods used in oncology can give contradictory results to mathematically accurate and biologically relevant methods (Mehrara et al, 2007, 2009). In this article, we present a dimensionless continuous quantity for objective assessment of TR, regardless of tumour type, clinical measures other than tumour response, and the mechanism of the effect of therapy on tumour: cytotoxic and/or cytostatic. Studies have shown that tumour growth rate is a valuable parameter for, for example, prediction of recurrence after surgery (Cucchetti et al, 2005) and survival of patients (Blankenberg et al, 1995), and the change in tumour growth rate can serve as a surrogate end point for determination of therapy response (Haney et al, 2001). In this study, a simplified formula was derived based on the effect of therapy on kinetics of tumour growth. Tumour response was measured by the logarithm of the ratio of post-treatment tumour volume to the volume of tumour (at the time of efficacy assessment) if therapy was not initiated. TR=0 indicates no effect, and the larger TR value the more effective therapy. A negative TR value indicates post-treatment tumour swelling or growth enhancement.

TR values are larger than corresponding LR values, which were used by Karrison et al (2007). The value of LR is calculated as the logarithm of the ratio of post-treatment tumour volume to the pretreatment tumour volume. The natural growth of tumour during diagnosis and therapy initiation as well as after therapy is neglected in the LR value. There might be a few weeks or longer delay between tumour diagnosis and initiation of therapy due to practical limitations or necessity of further evaluations. Tumours continue to grow during this period. As an example, the volume of a tumour with DT of 70 days will increase 23% during 3 weeks. Repopulation of tumour cells during therapy, for example, between cycles of chemotherapy, is also an important factor that should not be neglected (Davis and Tannock, 2000; Kim and Tannock, 2005). The overall underestimation of treatment effectiveness by LR (Err) is larger when tumour is rapidly growing or the time between pretreatment and post-treatment volume assessments is long. The relative importance of Err also depends on dose–response relation, that is, for a more effective drug LR is less affected by this error.

The generally used methods when comparing the post-treatment volume of tumour with the pretreatment volume will thus result in underestimation of treatment effectiveness. It has already been shown that RECIST underestimates the effect of imatinib on metastatic gastrointestinal stromal tumour (Choi et al, 2007). The fact that treatment effectiveness is underestimated by LR or RECIST has important implications on assessing the efficacy of new anticancer drugs or combinations of therapies.

It has been demonstrated that clinical trial designs based on LR are feasible (Karrison et al, 2007), which suggests that TR can also be used for such studies. The main difference between TR and LR is the reference volume of tumour for efficacy assessment, which is the volume of corresponding untreated tumour or pretreatment volume of tumour for TR and LR, respectively. The statistical aspects of using such continuous variables in clinical trials, for example, handling extreme cases as complete disappearance of lesions in two patients in this study, are discussed elsewhere (Karrison et al, 2007). Here we discuss the advantages and limitations of using TR as a quantity for tumour response.

The main limitation with using TR, compared to LR, is the estimation of the volume of an untreated tumour at the time of TR evaluation, which needs the natural growth model of tumour. In this study, we assumed an exponential model for natural growth of tumours. However, the presented formula for calculation of TR (Equation (5)) can be used for any growth model, provided that the non-exponential growth characteristics of tumour and Vn can be estimated.

The natural growth rate of tumours can be estimated by appropriate techniques according to the available data in each study. Owing to lack of information, we estimated the growth rate of untreated non-Hodgkin's lymphoma tumours from the average re-growth rate of tumours after therapy, which might be different from the true growth rate of tumours before treatment. However, these data were used only for demonstration, and no clinical interpretation of the results should be made. If tumour volumes at two occasions before start of therapy are available, for example, having two CT scans at diagnostic investigation and an investigation just before therapy initiation, natural SGR of tumour and consecutively Vn can be calculated using Equation (1). Taking both inter- and intra-operator as well as inter-scan variability into account, an increase of the measured volume by more than 25% is needed for a 95% likelihood of being a true growth, rather than measurement inaccuracy. For an exponentially growing tumour, increase of the measured volume will be more than 25% if the measurement time interval between two investigations is longer than 0.32 DT.

If tumour volume before treatment is only available at one occasion, for example, the first diagnostic imaging, tumour volume at the time of therapy initiation can be estimated by back-extrapolation of volume regression curve during therapy, which might be described by exponential model (Stein et al, 2008). That measure together with the first tumour volume available can be used for estimation of the natural SGR of tumour.

However, we used PSA level as reference, instead of tumour volume, for calculation of TR and LR in prostate cancer patients and the results were similar to when tumour volume was used for calculations in non-Hodgkin's lymphoma patients. This indicates that TR values calculated based on tumour marker level can be used for quantification of treatment efficacy in some types of tumours. Measurement of tumour marker level before the initiation of treatment is usually more practical in clinical research and practice. However, other factors that may affect tumour marker level, for example, PSA decline due to dedifferentiation of the tumour as it becomes anaplastic, must be considered, when post-treatment changes of tumour marker level is studied.

Tumour structure can be rather non-homogeneous, consisting of, for example, different clones of cancer cells (with different sensitivities to an anticancer agent), stroma and necrotic areas. The value of SGR of the tumour may then be obtained from the spatial distribution of SGR within tumour, sgr(x,y,z):

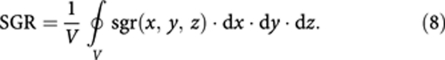graphic file with name bjc2011276e10.jpg

An effective treatment can reduce sgr(x,y,z) differently in different parts of the tumour depending on, for example, pharmacokinetics and dose–response of a systemically used agent. This will accordingly cause a reduction in SGR of tumour as was used in the presented model (Equation (4)). Studies have shown that functional imaging variables might be correlated with tumour growth rate, for example, using PET (Duhaylongsod et al, 1995; Tann et al, 2008). Further developments in this field can facilitate tumour SGR estimation by functional imaging before treatment as well as integration of TR data based on anatomical changes in tumour with other means of tumour response assessment by functional imaging with MRI (Chenevert et al, 1997) or PET (Stroobants et al, 2003; Boss et al, 2008).

In this study, we assumed that TR is evaluated at a specific occasion after treatment, as it is usually done in clinical studies. However, temporal changes of tumour SGR after treatment can also give valuable information such as progression due to the resistant clones of tumour, which can be identified with the point that SGR starts rising. However, this remains to be studied.

Time to event, for example, time to progression (TTP) or progression-free survival (PFS), is an end point that is also recommended for assessment of therapeutic efficacy (Scher et al, 2008; Eisenhauer et al, 2009). An interesting aspect of the presented method in this study is that Equations (1) and (5) imply that TTP is linearly related to TR. It should be noted that in this context, the TTP refers to the progression of the tumour(s) under study, whereas from a clinical perspective, appearance of new metastatic lesions may be considered as disease progression. However, the metastases might have been settled before the start of treatment or the effect of treatment might be different on the primary tumour and metastases.

In conclusion, a number of flaws can be identified in quantification methods of TR used in available standards, for example, neglecting the natural growth rate of tumour, which leads to underestimation of treatment effectiveness. The logarithm of the ratio of treated tumour volume (tumour marker level) to the volume (tumour marker level) of corresponding non-treated tumour is a general continuous quantity for tumour response to both cytostatic and cytotoxic agents. It can also accommodate integration of data from anatomical changes of tumour with data from changes in other biological characteristics of tumour after therapy. These results are valuable for clinical studies, revision of current standards for assessment of TR, and also a deterministic approach for individualised therapy in oncology.

Acknowledgments

This study was supported by grants from the Swedish Cancer Society (4956), the Assar Gabrielsson Foundation (FB 07-69), and the King Gustav V Jubilee Clinic Cancer Research Foundation, Göteborg, Sweden. We thank Professor Ragnar Hultborn, Department of Oncology, Gothenburg University, Professor George Sgouros, Johns Hopkins University, USA, and Associate Professor Magnus Båth, Department of Medical Physics and Engineering, Sahlgrenska University Hospital, Sweden.

References

  1. Barnacle AM, McHugh K (2006) Limitations with the response evaluation criteria in solid tumors (RECIST) guidance in disseminated pediatric malignancy. Pediatr Blood Cancer 46(2): 127–134 [DOI] [PubMed] [Google Scholar]
  2. Blankenberg FG, Teplitz RL, Ellis W, Salamat MS, Min BH, Hall L, Boothroyd DB, Johnstone IM, Enzmann DR (1995) The influence of volumetric tumor doubling time, DNA ploidy, and histologic grade on the survival of patients with intracranial astrocytomas. Am J Neuroradiol 16(5): 1001–1012 [PMC free article] [PubMed] [Google Scholar]
  3. Boss DS, Olmos RV, Sinaasappel M, Beijnen JH, Schellens JH (2008) Application of PET/CT in the development of novel anticancer drugs. Oncologist 13(1): 25–38 [DOI] [PubMed] [Google Scholar]
  4. Chenevert TL, McKeever PE, Ross BD (1997) Monitoring early response of experimental brain tumors to therapy using diffusion magnetic resonance imaging. Clin Cancer Res 3(9): 1457–1466 [PubMed] [Google Scholar]
  5. Cheson BD, Pfistner B, Juweid ME, Gascoyne RD, Specht L, Horning SJ, Coiffier B, Fisher RI, Hagenbeek A, Zucca E, Rosen ST, Stroobants S, Lister TA, Hoppe RT, Dreyling M, Tobinai K, Vose JM, Connors JM, Federico M, Diehl V (2007) Revised response criteria for malignant lymphoma. J Clin Oncol 25(5): 579–586 [DOI] [PubMed] [Google Scholar]
  6. Choi H, Charnsangavej C, Faria SC, Macapinlac HA, Burgess MA, Patel SR, Chen LL, Podoloff DA, Benjamin RS (2007) Correlation of computed tomography and positron emission tomography in patients with metastatic gastrointestinal stromal tumor treated at a single institution with imatinib mesylate: proposal of new computed tomography response criteria. J Clin Oncol 25(13): 1753–1759 [DOI] [PubMed] [Google Scholar]
  7. Cucchetti A, Vivarelli M, Piscaglia F, Nardo B, Montalti R, Grazi GL, Ravaioli M, La Barba G, Cavallari A, Bolondi L, Pinna AD (2005) Tumor doubling time predicts recurrence after surgery and describes the histological pattern of hepatocellular carcinoma on cirrhosis. J Hepatol 43(2): 310–316 [DOI] [PubMed] [Google Scholar]
  8. Davis AJ, Tannock JF (2000) Repopulation of tumour cells between cycles of chemotherapy: a neglected factor. Lancet Oncol 1: 86–93 [DOI] [PubMed] [Google Scholar]
  9. Duhaylongsod FG, Lowe VJ, Patz Jr EF, Vaughn AL, Coleman RE, Wolfe WG (1995) Lung tumor growth correlates with glucose metabolism measured by fluoride-18 fluorodeoxyglucose positron emission tomography. Ann Thorac Surg 60(5): 1348–1352 [DOI] [PubMed] [Google Scholar]
  10. Eisenhauer EA (2007) Response evaluation: beyond RECIST. Ann Oncol 18(Suppl 9): ix29–ix32 [DOI] [PubMed] [Google Scholar]
  11. Eisenhauer EA, Therasse P, Bogaerts J, Schwartz LH, Sargent D, Ford R, Dancey J, Arbuck S, Gwyther S, Mooney M, Rubinstein L, Shankar L, Dodd L, Kaplan R, Lacombe D, Verweij J (2009) New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1). Eur J Cancer 45(2): 228–247 [DOI] [PubMed] [Google Scholar]
  12. Guess B, Jennrich R, Johnson H, Redheffer R, Scholz M (2003) Using splines to detect changes in PSA doubling times. Prostate 54(2): 88–94 [DOI] [PubMed] [Google Scholar]
  13. Gwyther SJ, Schwartz LH (2008) How to assess anti-tumour efficacy by imaging techniques. Eur J Cancer 44(1): 39–45 [DOI] [PubMed] [Google Scholar]
  14. Haney SM, Thompson PM, Cloughesy TF, Alger JR, Frew AJ, Torres-Trejo A, Mazziotta JC, Toga AW (2001) Mapping therapeutic response in a patient with malignant glioma. J Comput Assist Tomogr 25(4): 529–536 [DOI] [PubMed] [Google Scholar]
  15. Jaffe CC (2008) Response assessment in clinical trials: implications for sarcoma clinical trial design. Oncologist 13(Suppl 2): 14–18 [DOI] [PubMed] [Google Scholar]
  16. Karrison TG, Maitland ML, Stadler WM, Ratain MJ (2007) Design of phase II cancer trials using a continuous endpoint of change in tumor size: application to a study of sorafenib and erlotinib in non small-cell lung cancer. J Natl Cancer Inst 99(19): 1455–1461 [DOI] [PubMed] [Google Scholar]
  17. Kim JJ, Tannock IF (2005) Repopulation of cancer cells during therapy: an important cause of treatment failure. Nat Rev Cancer 5(7): 516–525 [DOI] [PubMed] [Google Scholar]
  18. Lavin PT (1981) An alternative model for the evaluation of antitumor activity. Cancer Clin Trials 4(4): 451–457 [PubMed] [Google Scholar]
  19. Mehrara E, Forssell-Aronsson E, Ahlman H, Bernhardt P (2007) Specific growth rate versus doubling time for quantitative characterization of tumor growth rate. Cancer Res 67(8): 3970–3975 [DOI] [PubMed] [Google Scholar]
  20. Mehrara E, Forssell-Aronsson E, Ahlman H, Bernhardt P (2009) Quantitative analysis of tumor growth rate and changes in tumor marker level: specific growth rate versus doubling time. Acta Oncol 48(4): 591–597 [DOI] [PubMed] [Google Scholar]
  21. Michaelis LC, Ratain MJ (2006) Measuring response in a post-RECIST world: from black and white to shades of grey. Nat Rev Cancer 6(5): 409–414 [DOI] [PubMed] [Google Scholar]
  22. Miller AB, Hoogstraten B, Staquet M, Winkler A (1981) Reporting results of cancer treatment. Cancer 47(1): 207–214 [DOI] [PubMed] [Google Scholar]
  23. Padhani AR, Miles KA (2010) Multiparametric imaging of tumor response to therapy. Radiology 256(2): 348–364 [DOI] [PubMed] [Google Scholar]
  24. Scher HI, Halabi S, Tannock I, Morris M, Sternberg CN, Carducci MA, Eisenberger MA, Higano C, Bubley GJ, Dreicer R, Petrylak D, Kantoff P, Basch E, Kelly WK, Figg WD, Small EJ, Beer TM, Wilding G, Martin A, Hussain M (2008) Design and end points of clinical trials for patients with progressive prostate cancer and castrate levels of testosterone: recommendations of the prostate cancer clinical trials working group. J Clin Oncol 26(7): 1148–1159 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Sgouros G, Squeri S, Ballangrud AM, Kolbert KS, Teitcher JB, Panageas KS, Finn RD, Divgi CR, Larson SM, Zelenetz AD (2003) Patient-specific, 3-dimensional dosimetry in non-Hodgkin's lymphoma patients treated with 131I-anti-B1 antibody: assessment of tumor dose–response. J Nucl Med 44(2): 260–268 [PubMed] [Google Scholar]
  26. Stein WD, Figg WD, Dahut W, Stein AD, Hoshen MB, Price D, Bates SE, Fojo T (2008) Tumor growth rates derived from data for patients in a clinical trial correlate strongly with patient survival: a novel strategy for evaluation of clinical trial data. Oncologist 13(10): 1046–1054 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Stroobants S, Goeminne J, Seegers M, Dimitrijevic S, Dupont P, Nuyts J, Martens M, van den Borne B, Cole P, Sciot R, Dumez H, Silberman S, Mortelmans L, van Oosterom A (2003) 18FDG-positron emission tomography for the early prediction of response in advanced soft tissue sarcoma treated with imatinib mesylate (Glivec). Eur J Cancer 39(14): 2012–2020 [DOI] [PubMed] [Google Scholar]
  28. Tann M, Sandrasegaran K, Winer-Muram HT, Jennings SG, Welling ME, Fletcher JW (2008) Can FDG-PET be used to predict growth of stage I lung cancer? Clin Radiol 63(8): 856–863 [DOI] [PubMed] [Google Scholar]
  29. Therasse P, Arbuck SG, Eisenhauer EA, Wanders J, Kaplan RS, Rubinstein L, Verweij J, Van Glabbeke M, van Oosterom AT, Christian MC, Gwyther SG (2000) New guidelines to evaluate the response to treatment in solid tumors. European Organization for Research and Treatment of Cancer, National Cancer Institute of the United States, National Cancer Institute of Canada. J Natl Cancer Inst 92(3): 205–216 [DOI] [PubMed] [Google Scholar]
  30. Tuma RS (2006) Sometimes size doesn’t matter: reevaluating RECIST and tumor response rate endpoints. J Natl Cancer Inst 98(18): 1272–1274 [DOI] [PubMed] [Google Scholar]
  31. Twombly R (2006) Criticism of tumor response criteria raises trial design questions. J Natl Cancer Inst 98(4): 232–234 [DOI] [PubMed] [Google Scholar]

Articles from British Journal of Cancer are provided here courtesy of Cancer Research UK

RESOURCES