Abstract
In therapeutic ultrasound, the presence of shock waves can be significant due to the use of high intensity beams, as well as due to shock formation during inertial cavitation. Although modeling of such strongly nonlinear waves can be carried out using spectral methods, such calculations are typically considered impractical, since accurate calculations often require hundreds or even thousands of harmonics to be considered, leading to prohibitive computational times. Instead, time-domain algorithms which generally utilize Godunov-type finite-difference schemes are commonly used. Although these time domain methods can accurately model steep shock wave fronts, unlike spectral methods they are inherently unsuitable for modeling realistic tissue dispersion relations. Motivated by the need for a more general model, the use of Gegenbauer reconstructions as a postprocess tool to resolve the band-limitations of the spectral methods are investigated. The present work focuses on eliminating the Gibbs phenomenon when representing a steep wave front using a limited number of harmonics. Both plane wave and axisymmetric 2D transducer problems will be presented to characterize the proposed method.
INTRODUCTION
Shock waves can often be observed in therapeutic ultrasound, due to its use of high intensity acoustic sources. It is well known that this type of wave profile can be extremely hard to model by frequency-domain methods,1 since the Fourier expansion of a shock wave has a slow convergence rate. Therefore, to model a shock wave using the frequency-domain approach, the spectral components typically have to include hundreds or even thousands of harmonics, resulting in intolerable computation time. The same rule also holds for modeling short pulses which carry ample frequency components. To solve this dilemma, a time-domain model has emerged,2 where the computation time increases linearly to the number of harmonics. Nevertheless, this preliminary study considers the use of an implicit solution of Burgers’ equation which is not conservative and not suitable for shock wave modeling.3 Consequently, more sophisticated schemes which involve Godunov’s method were proposed.3, 4, 5, 6 Shock waves can then be accurately approximated through the scheme’s internal viscosity. During the fast development of time-domain algorithms, the effort of improving the frequency-domain approach never ceased. Christopher and Parker proposed a harmonic-limited scheme where excess absorptions were added into high frequency components.1 However, this scheme is approximate in the sense that it highly distorts the shock wave front. Asymptotic values for high frequency amplitudes have also been used both in the algorithm of modeling nonlinear propagation of shocks, and in the post-numerical waveform reconstruction.7, 8, 9 While this method works well for one-dimensional cases containing one shock wave, it becomes rather complex when two- or three-dimensional waves containing multiple shock waves are considered.9, 10 Particularly, when pistons are modeled (focused or unfocused), edge waves are present and may result in formation of two shocks per waveform. The asymptotic method relies on the assumption that there exists only one shock per cycle.10
The goal of this study is to introduce an approach that can reduce harmonic representations for shock waves during the numerical implementations. This approach integrates artificial attenuations in modeling of nonlinear wave propagation and a so-called Gegenbauer reconstruction method (or reprojection method) as a post-numerical procedure. The artificial attenuations are used to stabilize the frequency-domain algorithm by reducing the errors at points away from the discontinuity. The Gegenbauer reconstructions are used as a final step to recover the accuracy of the sound field everywhere including the discontinuity. The focus of this paper is the Gegenbauer reconstructions, which were originally introduced by a series of papers11, 12, 13, 14 and have been applied to engineering problems, e.g., the propagation of electromagnetic waves.15 The general idea is to take the Fourier expansions of a piecewise smooth function which is generally contaminated by the Gibbs noise, and project them onto another basis with Gegenbauer polynomials. This basis is Gibbs complementary to the family of the Fourier expansions,11, 12, 13, 14 so that the new expansions converge exponentially. Gegenbauer reconstructions further require the location of the discontinuity a priori, which necessitates an edge-detection algorithm. It is noted that the Gegenbauer reconstruction method is designed to suppress the Gibbs noise, not specifically for either a frequency- or time-domain method, thus it has general usages in complementing both methods. It is noted that Gibbs-type phenomena sometime also occur in time-domain algorithms.16 However, this study concentrates on the frequency-domain method where reducing the number of harmonics is more imperative.
The paper is structured as follows. In Sec. 2, the theory of Gegenbauer reconstructions is briefly revisited. Section 3 discusses simulation results for plane wave and some axisymmetric beam problems. Here, the validity of the Gegenbauer reconstructions in the context of nonlinear acoustics is verified. Section 4 concludes the paper.
GEGENBAUER RECONSTRUCTION
Suppose a nonperiodic function f(x) on [–1, 1] has a discontinuity at x = x0, and the first 2N + 1 Fourier expansion coefficients are known as F(k), where |k|≤N. Then the Fourier partial sum approximation yields
| (1) |
This reconstructed function fN(x) suffers from the Gibbs phenomenon: first order convergence away from the jump discontinuity with nonuniform oscillations as the jump discontinuity is approached.
To improve the convergence rate, a conventional approach is to introduce artificial attenuation to the algorithm. For example, in the Westervelt equation, it is straightforward to add an artificial attenuation which grows quadratically with frequency.17
The main purpose of the artificial attenuation is to stabilize the algorithm. Since this is essentially an excess-absorption scheme, while it maintains the accuracy of low frequency, it reduces the accuracy of the high frequencies and inevitably distorts the shock fronts.1, 9 Fortunately, recent studies on Gegenbauer reconstructions11, 12, 13, 14 show that if the function under test is piecewise analytic∕smooth, high frequency components can be recovered by essentially using only the low frequency components and the Gibbs effect can be completely removed. This is realized by reconstructing a rapidly converging series based on the expansions in Gegenbauer polynomials.
We now briefly introduces the underlying theory of the Gegenbauer reconstruction following previous literatures.11, 12, 13, 14, 18 The Gegenbauer partial sum expansion, which converges exponentially for a smooth function f(x) defined in [–1,1], is given by11, 12, 13, 14
| (2) |
where are the Gegenbauer coefficients
| (3) |
The Gegenbauer polynomials, , are orthogonal under the weight function (1–x2)λ–1∕2 with
| (4) |
where δk,n is the Kronecker δ.
The Gegenbauer polynomials can be calculated by a recurrence relation19
| (5) |
with and
It is assumed that f(x) is a piecewise smooth function that is analytic in the subinterval [a, b]. A local variable ξ is defined such that x(ξ) = ɛξ + η, where ɛ=(b-a)∕2 and η=(b+a)∕2, the Gegenbauer partial sum expansion of f(x) in [a, b] can be obtained as
| (6) |
where the Gegenbauer coefficients yield
| (7) |
Based on the Fourier partial sum approximation Eq. 1, an approximation to can be written as
| (8) |
This approximation replaces in the computation of the Gegenbauer partial sum to reconstruct the function f(x) in an exponentially accurate way in [a, b] as
| (9) |
It has been mathematically demonstrated that, if both λ and m grow linearly with N, and λ = γm where γ is an arbitrary positive, the error introduced by Eq. 9 is exponentially small.11, 12, 13, 14
SIMULATIONS
Algorithm
Frequency-domain method
In this section, the aforementioned methods are numerically verified through shock wave modeling using a recently developed frequency-domain method.20 This method is based on the Westervelt equation which is written as
| (10) |
where p is the sound pressure, c0 is the sound speed, δ is the diffusivity, β is the nonlinearity coefficient, and ρ0 is the ambient density.
Fourier transformation of the x, y, and t dimensions yields an ODE in the wave-vector frequency-domain:
| (11) |
where
| (12) |
| (13) |
with ω being the angular frequency; kx, ky being the wave numbers; and ⊗ representing the convolution in terms of kx, ky, and ω. It is noted that the frequency-dependent absorption and dispersion are considered in K.
While the exact solution to Eq. 11 has been found, it is not suitable for numerical implementations. An approximate solution to Eq. 11 is therefore used and can be written as20
| (14) |
where
| (15) |
It is noted that the first term on the right hand side of the equation represents the linear term and the second term represents the nonlinear term. This solution is numerically evaluated via the left-hand Riemann sums. In general, the initial pressure distribution on the surface of a transducer can be predetermined, and the sound field is then projected step by step to the desired plane along the z-axis. Details of the algorithm follow a previous description by Jing et al.20 A previous study has already shown the validity of this frequency-domain method. It will be demonstrated in this paper how the Gegenbauer reconstructions can be used as a post modeling procedure along with this frequency-domain method to model shock wave propagation.
Artificial attenuation and Gegenbauer reconstruction
The Gibbs effect occurs when shock waves are represented by insufficient harmonics. The errors, which are typically manifested as high frequency oscillations near the discontinuity, become amplified while undergoing the planar projection. This causes algorithm instability, and in some cases, produces overflow errors. Therefore, artificial attenuations which grow quadratically with the frequency are introduced into the frequency-domain algorithm during each step of the projection. Artificial attenuation for shock wave modeling is a well established approach. Even for shocks of 60–80 MPa it is possible to obtain accurate results with about 500 harmonics.17 For example, an artificial absorption that has a dependence on the axial coordinate was introduced in the algorithm locally around the focus to suppress strong gradients appear in the transverse spatial field.17
For the relevant model equation, this can be easily accomplished by adding a small value to the sound diffusivity δ in Eq. 11. This small value should be chosen carefully to prevent excessive signal noise and to stabilize the algorithm. This could, for example, be done by starting with a very small value to test for stability and noise levels, and then progressively increasing the attenuation to determine the minimum acceptable value. Clearly, if an overly high value is used, essential lower-frequency components of the signal might also be artificially reduced by a significant amount, thereby reducing the efficacy of the Gegenbauer reconstructions, which assume the low frequencies are reasonably accurate.11, 12, 13, 14
Recalling the Gegenbauer reconstructions, which are understood to have exponential convergence for a smooth function on [a, b] [element] [–1,1] (see Sec. 2. for details), the first task is to locate the discontinuity. It is noted that, the number of shocks can be less or more than 2 (at a and b), as will be shown in the simulation section. For example, if the discontinuities are at –1, a, b, c, 1, the subintervals are [–1, a], [a, b], [b, c], and [c, 1]. The time-domain waveform used to find the discontinuities was obtained from the inverse FFT with respect to frequency.
In shock wave modeling, assuming shocks are ideally discontinuous, the discontinuities are then at a and b. However, these discontinuities are usually unknown. Although there are sophisticated edge detection procedures21, 22 for Gegenbauer reconstructions, they limit the edge to a certain grid point, which may be not sufficiently accurate, as this edge does not necessarily correspond to a sampling point especially when a small number of harmonics are used. The present study considers several common problems in acoustic shock waves, and proposes empirical methods to locate the edge that are specific to each problem. These methods will be discussed in detail along with the presentation of numerical results. In general, the edge corresponds highly with the location of the first order derivative (∂f∕∂x) maximum.
Once the edge of the function is known, the reconstruction can be implemented according to Sec. 2 with the parameters λ and m, which are function dependent and need to be carefully determined. The optimum relation between the parameters and other factors has been considered analytically.23 However, these analytical results are not sufficient for providing a practical algorithm. There is also need for further numeric experimentation.15 As will be verified, once the optimized parameters are chosen, the smooth portion of the signal away from the discontinuity can be accurately reconstructed. This verification is achieved by comparing the reconstructed curve with the original curve on the portion where the contamination is not overwhelming (i.e., even though the curve is contaminated by the Gibbs noise, typically there is a portion of the curve away from the discontinuity that has only negligible oscillation). A more accurate but less straightforward method of comparison considers the frequency spectrum of the reconstructed shock wave with the original, where good agreement should be observed for the low frequency region.
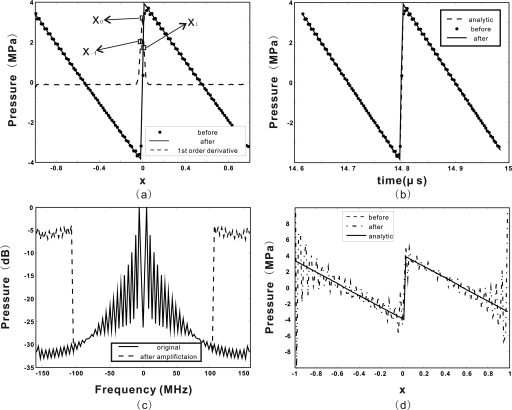
An example is shown here to demonstrate the Gegenbauer reconstruction process. The Fay solution to Burgers’ equation was used, which is valid for sinusoidal waves after the propagation distance is larger than 3σ, where σ is the shock formation distance, and the diffusivity is sufficiently small. For the numerical implementation, the projection distance Δz on the z-axis was chosen as 1∕16 of the wavelength at the center frequency, the temporal resolution dt for the sinusoidal source was 1∕(64fc), where fc is the center frequency, indicating 32 harmonics were used. The center frequency was 5 MHz, the initial pressure amplitude was 8 MPa, the speed of sound was 1500 m∕s, the density was 1000 kg∕m3, the nonlinearity coefficient was 3.5, and the diffusivity was 5 × 10–6 m2 s–1. An artificial diffusivity of δ = 4 × 10–5 m2 s–1 was employed to prevent overflow error. Results at a distance of σ = 5.2 before Gegenbauer reconstructions are shown in Fig. 1a (dots). For the present case, if no artificial attenuation was introduced, about 50 harmonics were required to obtain stable results and 150 harmonics to obtain results nearly free of Gibbs noise. To indicate the edge location, the first order derivative is also plotted. It is initially considered that the signal peak indicates the discontinuity, and that the shock wave consists of two smooth subintervals above and below the discontinuity. However, since the analytic solution indicates that the shock wave is not ideally discontinuous (the shock front includes at least one point), results after Gegenbauer reconstruction would be erroneous at grid points very close to the real edge. Thus, it is decided to divide the function into three intervals. The location of the first order derivative maximum is defined as x0, and the two neighboring grid points as x−1 and x1, from left to right. Similarly, x–n and xn indicate positions n points away from x0. Note that subinterval boundaries do not have to coincide with grid points. For one-dimensional continuous wave propagation, the best results have been found using the subintervals: (1) -1 to (x-1+x0)∕2; (2) (x-1+x0)∕2 to (x0+x1)∕2; (3) (x0+x1)∕2 to 1, in some cases providing more accurate results than defining interval boundaries as the neighboring points, i.e., x1 and x–1. It is believed this is because the width of the shock front is usually overestimated when modeling using a limited harmonics. In this example, since the second and third discontinuities are close, the subinterval in between is very short. However, this is not generally the case, as will be shown in Sec. 3. It is also noted that, the factor 2 here is only an approximate number that keeps the edge somewhere between, for example, x–1 and x0. In other words, the results are not sensitive to this factor. Again, the value of fN on any arbitrary point, not necessarily a grid point, can be calculated by using Eq. 1.
Figure 1.
Profiles of shock waves produced from an initial sinusoidal wave at a distance σ1 = 5.2. (a) Numerical simulations before and after the Gegenbauer reconstructions, as well as the first order derivative. (b) Numerical simulations before and after the Gegenbauer reconstructions, as well as the analytic solution. (c) Frequency spectrums before and after the amplification. (d) Numerical simulations before and after the Gegenbauer reconstructions. The frequency spectrums after the amplification were used.
As discussed below in Sec. 3, although shock waves are rarely ideally discontinuous, assuming discontinuity and applying the Gegenbauer reconstructions still yield accurate results for cases where the shock fronts are very sharp. For example, when modeled by 30–100 harmonics and including artificial attenuation, only 0–4 points were observed on the shock front.
Initially, the values of λ and m were set identically for each subinterval (λ = 4, m = 2), and then increased separatively until a satisfactory result was found. It is noted that the choices of λ and m could be different for each subinterval, however, for simplification, they remain the same in this study. For most one-dimensional problems, where diffraction was not taken into account, the initial values themselves were observed to yield accurate results. Especially increasing λ does not significantly change the results. Figure 1b shows results after reconstruction (solid line) using this setting, indicating that Gegenbauer reconstructions successfully recovers the shock front. To quantify the agreement with the analytic solution, the least-square error was used and was defined as
| (16) |
where ∥p(t)∥ is the least-square norm.
The least-square errors were 0.0659 and 0.0072 for before and after the Gegenbauer reconstructions, respectively, indicating a reduction of almost a factor of 10.
When λ less than 4 was chosen, the Gegenbauer reconstructions generally did not yield satisfactory results. The Gegenbauer reconstructions were designed for problems where a limited number of Fourier coefficients for a discontinuous function are known and correct. However, when modeling shock wave with a limited number of harmonics, the spectrum at high frequencies is inaccurate due to the incomplete description of harmonic interaction and corresponding reflections from the high frequency boundary of the spectral window.
Fortunately, for a relatively large λ, such as 4 used in this study, the weight of the reprojection basis (1-ξ2)λ-1∕2 reduces quickly to zero at its boundaries. The smooth function on [a, b] that requires reconstruction is multiplied by this weighting function when calculating the Gegenbauer coefficient, such that oscillations at high frequencies that corresponds to the points on or near the boundaries are tapered to zero by the weighting function. In other words, as long as the Gibbs noise is not spread over a significant range of the frequency spectrum, the Gegenbauer reconstructions work, because they essentially utilize only the lower portion of the frequency spectrum.
To demonstrate this point, results before reconstruction were amplified by a factor of 20 at frequencies above 100 MHz [Fig. 1c]. Gegenbauer reconstructions were then applied to this signal. Figure 1d shows that even in this case where the frequency spectrum is highly inaccurate near the frequency boundaries, the Gegenbauer reconstructions still can recover the correct signal.
For a subinterval which is expected to be approximately a flat line, it is found that m should be small, e.g., 2. On the other hand, if the subinterval is a highly variant function, which is typically seen when diffraction is considered, then m must be relatively large, e.g., 8 or even larger. As mentioned above, there is no direct method to calculate or select the exact m and λ, but rather it is problem-specific and numeric experimentations are typically required to obtain the optimal parameters.
The CPU time for computing the Gegenbauer reconstructions has been shown to increase mainly with N and m.15 Processing time was less than one second for all the cases tested in this paper, when implemented using Matlab on a XP 64-bit operating system. The hardware consisted of four dual-core 2.67 GHz Xeon processors, and 24 GB of RAM.
To close this section, the procedure is summarized as follows.
Step 1: After the location of the discontinuity is determined, the whole time window of the numerical solution breaks down to a few (depending upon the number of discontinuities) subintervals.
Step 2: For one subinterval, compute the Gegenbauer coefficients by using Eq. 8.
The integral is numerically evaluated. Point values fN in the integral are calculated using Eq. 1. m and λ are obtained through numeric experimentations.
Step 3: Construct the Gegenbauer finite sum by using Eq. 9.
Step 4: Repeat steps 2–3 for other subintervals.
Results
One-dimensional cases
To verify the model, we then studied the case of N waves, with the initial wave written as
| (17) |
where p0 is 5 MPa and T0 is 0.3 × 10–6. The analytic solution for this case is available,24 and is not repeated here. In general, as the N wave propagates, the peak amplitude reduces and the width increases.
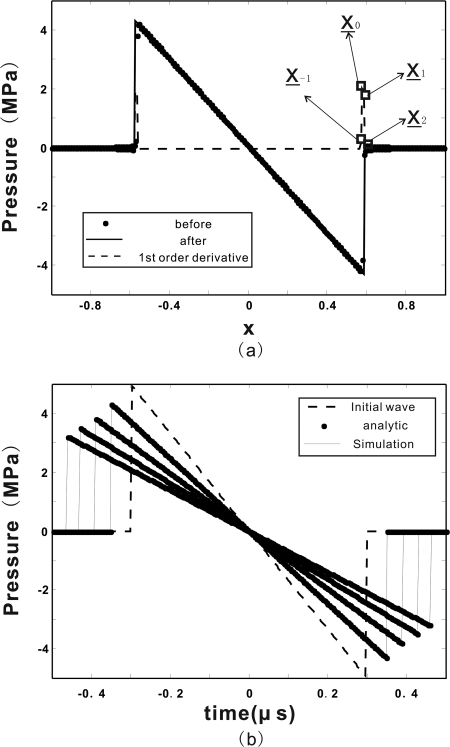
For the numerical implementations, the nonlinearity was 3.5 and 150 sampling points were used across the initial N shock wave. The step size Δz was 18.75 μm. The medium diffusivity was set to zero, however, an artificial diffusivity δ = 1 × 10–5 m2 s–1 was used. Empirically, good results can be acquired when the N shock wave was assumed to consist of three smooth subintervals: (1) -1 to (x-1+x0)∕2; (2) (3) . The underline denotes the point on the right side of the N wave. Occasionally, the first order derivative on x–1 only differs from the one on x0 by a small amount, e.g., less than 10%. In this case, the first subinterval becomes −1 to (x–2 + x–1)∕2, and the second subinterval will need to change accordingly. A similar rule holds for the right side of the N wave, i.e., if the first order derivative on only differs from the one on by a small amount, then the third subinterval becomes . This rule of finding the edge for the N waves is based on the fact that modeling the N wave using a limited number of harmonics usually underestimates the total width of the N wave. Figure 2a shows the results at a distance of 20 mm. In this specific case, the edge on the right side is at .
Figure 2.
(a) Profiles of shock waves produced from an N wave. Two results are presented at a distance of z = 20 mm, one before the Gegenbauer reconstructions, one after. The first order gradient is shown to indicate approximately where the edge is. (b) Simulation results after the Gegenbauer reconstructions are compared with the analytic solution at various distances 20, 40, 60, and 80 mm, where the longer the distance, the lower the peak pressure.
λ and m were again chosen to be 4 and 2, respectively. Figure 2b shows the comparisons between the simulation with Gegenbauer reconstructions and the analytic solution for portions of the shock wave at distances of 20, 40, 60, and 80 mm. To calculate, for example, the result at 40 mm, the result at 20 mm before the reconstructions (rather than after) was projected to 40 mm, where the reconstructions were applied. This is important, as even in the “worst case” scenario where the edge was misidentified by one grid point after the reconstructions, this error would not accumulate during propagation. Again, the Gegenbauer reconstructions successfully recovered the high frequency components that were overly reduced by the artificial attenuation. The least-square errors were found to be rather small, being 0.000187, 0.000248, 0.000261, and 0.000259 for distances at 20, 40, 60, and 80 mm, respectively. For comparison, the least-square errors before the reconstructions were 0.176, 0.099, 0.159, 0.071.
The second case tests the algorithm with multi-cycle tone bursts that generally contain several shocks of different amplitudes formed at different distances. A Gaussian-modulated sinusoidal pulse with a center frequency of 5 MHz, and a bandwidth of 2.5 MHz was selected. Peak amplitudes were varied from 12 to 8 MPa at increments of 2 MPa. The medium properties remained the same except the diffusivity was set at 5 × 10–6 m2 s–1. Travel distances corresponded to 7.9σ, 6.5σ, and 5.2σ, respectively, as referenced to a 5 MHz continues wave signal. For the simulation, the projection distance Δz was 1∕16 of the wavelength at center frequency, and 32 harmonics were used with an artificial diffusivity of 3 × 10–5 m2 s–1. To assess the accuracy of the simulation, the benchmark solution was obtained by considering 256 harmonics and no artificial attenuation. The results were later interpolated to have the same sampling frequency with 32 harmonics.
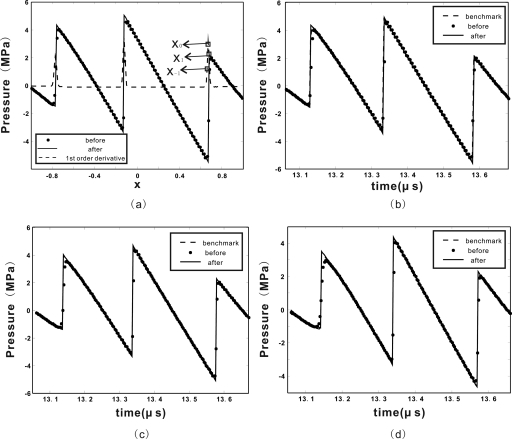
To locate the edges, three maximum first order derivatives were identified first, see Fig. 3a. Taking the one on the rightmost as an example, the best results were found when the edge is assumed to be located at (x±1 + x0)∕2, where x±1 is either x–1 or x1, dependent upon which coordinate had a higher first order derivative. In the specific case shown in Fig. 3a, x±1 = x1 in that specific case. The same rule was found to hold when searching for other edges. Occasionally the first order derivatives on x–1 and x1 only differ by less than 10%. In this special case, the edge is assumed to be at x0. Last, λ and m were 4 and 2, respectively.
Figure 3.
(a) Portions of the profile of a shock wave produced from a Gaussian-modulated sinusoidal wave. Two results are presented at a distance of 7.9σ, one before the Gegenbauer reconstructions, one after. The first order gradient is also shown. Simulation results after the Gegenbauer reconstructions are compared with the benchmark solution at distances of (b) 7.9σ, (c) 6.5σ, and (d) 5.2σ.
Figures 3b–3d show the results at different distances, where Gegenbauer reconstructions are shown to be valid. The least square errors for results after the reconstructions were 0.0396, 0.0101, and 0.0179, respectively. The errors before the reconstructions were 0.149, 0.151, and 0.157.
Axisymmetric cases
This section presents axissymmetric cases, which are relevant to therapeutic ultrasound. The advantage of the proposed approach is that there is no essential difference between dealing with a one-dimensional problem and an axissymmetric problem. The acoustic field is propagated by the frequency-domain method, and the Gegenbauer reconstructions are applied at the last step to the time-domain signal that is of interest.
The first case considers the field due to a spherically concave transducer (single element) with an aperture radius of 3 mm and a 20 mm focal distance. The initial time-domain signal was a continuous wave. The center frequency was 5 MHz and the initial peak pressure was 1 MPa. For the medium, water was modeled, as the attenuation is rather small and the Gibbs phenomenon is more pronounced. The sound speed was 1500 m∕s, density was 1000 kg∕m3, nonlinear parameter was 3.5, and attenuation coefficient α∕f2 was 25 × 10–15 Np∕m/Hz2.
Two numerical implementations were conducted separately. The first considered 50 harmonics, the second considered 250 harmonics. The latter was used roughly as a reference to assess the accuracy of the Gegenbauer reconstructions when fewer harmonics are considered. The step sizes Δz were 18.75 and 1.25 μm, respectively. On the radial axis, the spatial resolution was 37.5 μm, where convergence for the results on the axis was observed. An artificial attenuation of 8 × 10–6 m2 s–1 was added to the algorithm.
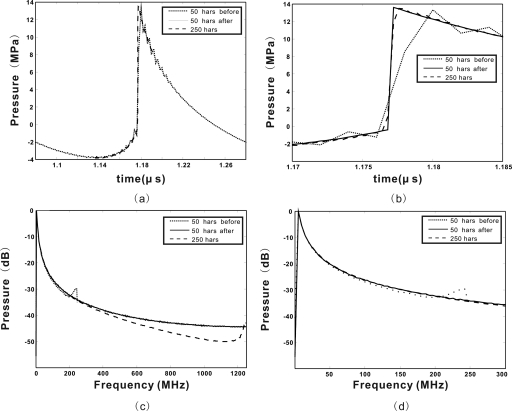
To locate the edge, the same rule in the one-dimensional Gaussian pulse case was used. Therefore, the shock wave was divided into two parts: (1) −1 to (x±1 + x0)∕2; (2) (x±1 + x0)∕2 to 1. λ and m were chosen to be 4 and 8, respectively. As explained above, a larger m was used because the two subintervals, instead of being straight lines, are quite curvy, see Fig. 5a. It is worth pointing out that the result is insensitive to the choice of λ if the difference is within 1.
Figure 5.
Profile of a shock wave produced from a focused circular transducer. Simulation results before and after Gegenbauer reconstructions with 50 harmonics are compared with the result before the Gegenbauer reconstructions with 250 harmonics at a distance of 15 mm on the axis. The 50 harmonics results after Gegenbauer reconstructions are resampled to include in total 250 harmonics. (a) Depicts a full cycle. (b) Depicts the shock fronts. Corresponding spectral results. (c) Spectrums for the first 250 harmonics. (d) Spectrums for the first 60 harmonics.
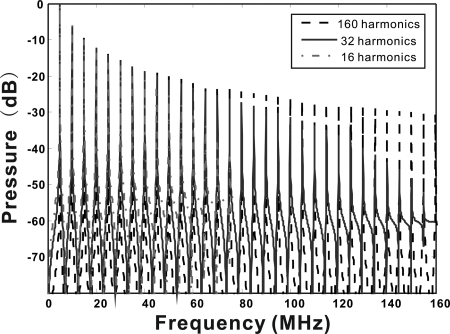
It is further noted that, according to Eq. 9, once the Gegenbauer coefficients are calculated, the waveform can be reconstructed everywhere on the time-domain. In other words, even though the algorithm started with only 50 harmonics, during the Gegenbauer reconstructions, the number of harmonics can be increased by enlarging the sampling frequency. In this case, 200 harmonics were added to the original 50 harmonics according to the procedure described above. As a matter of fact, it is found that if only 50 harmonics were considered, the frequency spectrum close to the 50th harmonics would not be accurate. As more harmonics are added, the frequency spectrum close to the 50th harmonics would converge and become much more accurate. To demonstrate this, we took the Fay solution to the one-dimensional continuous wave problem discussed above (Sec. 3), and compare the frequency spectrum up to the 32th harmonics when considering 16, 32, and 160 harmonics. Figure 4 shows that, even though all the results are analytic solutions in the time domain, their frequency spectrums could be different toward the end of the spectrum. The procedure of adding harmonics during the Gegenbauer reconstructions were not done in the one-dimensional cases, because the same sampling frequency was used when comparing the results.
Figure 4.
(Color online) Frequency spectrums for the Fay solution to the one-dimensional continuous problem discussed in Sec. III A 2. Three results are shown, one with 16 harmonics, one with 32 harmonics, and one with 160 harmonics. Only the results up to the 32th harmonics are presented.
Figure 5a shows four results: a shock wave profile predicted by using 50 harmonics without Gegenbauer reconstructions and with Gegenbauer reconstructions (two and three subintervals), shock wave profile predicted by using 250 harmonics at a distance of 15 mm on the axis. All the results are over a full cycle. When only 50 harmonics are used, severe artifacts are observed as expected. Gegenbauer reconstructions eliminated these artifacts and produced a curve that is indistinguishable from the one generated by using as many as 250 harmonics. Figure 5b shows only the shock fronts, and indeed the shock front is reconstructed. Figures 5c, 5d show the corresponding spectral results for different frequency ranges. The result before Gegenbauer reconstructions clearly show high frequency noise at the end. The result after Gegenbauer reconstructions agrees fairly well with the one carrying 250 harmonics for the first 60 harmonics, but different beyond this range. Nevertheless, it is recalled that the initial signal only carries 50 harmonics, and the Gegenbauer reconstructions have produced an accurate spectrum at least up to this range. For higher harmonics, i.e., up to 60 harmonics, even though accurate results are obtained, they are actually not being modeled in the propagation and are extrapolated results. Their diffraction and absorption are not accounted for and should be treated with cautions. Future study is expected to verify the results beyond the harmonics considered in the propagation algorithm at more locations.
In the first case, only one shock wave is observed in a cycle. The second case considers the field due to an unfocused circular transducer (single element) where two shock waves within one cycle have been found in the near field10 due to the propagation of edge waves. The aperture radius is 23.5 mm. The initial time-domain signal was again continuous wave. The center frequency was 1 MHz and the initial peak pressure in water was 1.43 MPa.
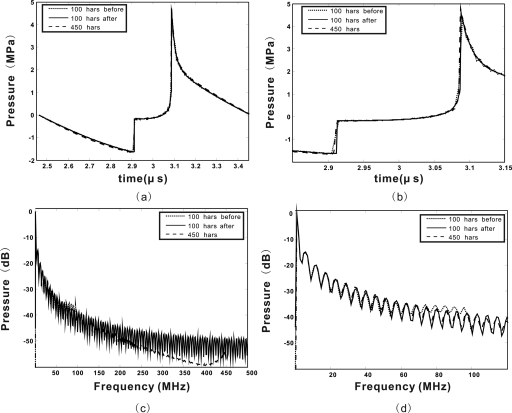
Again, two numerical implementations were conducted separately. The first considered 100 harmonics, the second considered 450 harmonics. The step sizes Δz were 25 and 5 μm, respectively. On the radial axis, the spatial resolution was 187.5 μm. The artificial attenuation was 3 × 10−6 m2 s−1. This shock wave, which contains two shock fronts, was assumed to consist of three parts, and the rule for finding the edges follows the one in the one-dimensional Gaussian pulse problem. For the 100 harmonics simulation, 400 harmonics were added during the reconstructions. λ and m were 4 and 12, respectively.
Figure 6a shows three results: shock wave profile predicted by using 100 harmonics without Gegenbauer reconstructions and with Gegenbauer reconstructions, shock wave profile predicted by using 450 harmonics at a distance of 255 mm on the axis. All the results are in a full cycle. Numerical oscillations can be observed near the edges when only 100 harmonics are used. Gegenbauer reconstructions were able to suppress these oscillations.
Figure 6.
Profile of two shock waves produced from an unfocused circular transducer. Simulation results before and after Gegenbauer reconstructions with 100 harmonics are compared with result before the Gegenbauer reconstructions with 450 harmonics at a distance of 255 mm on the axis. The 100 harmonics results after Gegenbauer reconstructions are resampled to include in total 500 harmonics. (a) Depicts a full cycle. (b) Depicts the shock fronts. Corresponding spectral results. (c) Spectrums for the first 500 harmonics. (d) Spectrums for the first 120 harmonics.
Figure 6b shows only the shock fronts. Figures 6c, 6d show the corresponding spectral results for different frequency ranges. The spectrum decays much like a sinc function rather than following the 1∕n asymptotic behavior which occurs in shock waves containing one shock front.9 The result after Gegenbauer reconstructions shows good agreement to the result with 450 harmonics for the first 120 harmonics, while the results before Gegenbauer reconstructions overestimate the values after about 80 harmonics.
CONCLUSIONS
In conclusion, this paper proposes combining artificial attenuation in the modeling of shock wave propagation with the Gegenbauer reconstruction method as a post-numerical procedure. Conventional frequency-domain methods are not suitable for shock wave modeling due to the large number of harmonics required. The spectrum of a shock wave decays slowly, and a truncation at a relatively low frequency introduces numerical errors. The present method takes the Fourier spectral projection and projects it onto another basis; in this case, the basis is the Gegenbauer polynomials. By knowing the location of the discontinuity using empirical ways proposed in this paper, one can reconstruct a rapidly converging series based on the expansions in Gegenbauer polynomials. Simulations have shown for both one-dimensional and axisymmetrical problems that the Gegenbauer reconstructions are able to successfully recover the high frequency spectrum of a shock wave, even when multiple shock fronts are present. These high frequency details are very significant to the absorption of the shock front and thus the associated heating rate and radiation force of the propagation. These features are expected to be studied in a future paper.
The present study concentrated on improving reconstruction at a fixed position. However, the method may also prove useful in the progressive problem, where reconstructions could be applied periodically along the beam path to maintain stability and accuracy. Although not considered here, the conditions and extent to which such efforts could be applied is proposed as a future topic of study.
Finally, the underlying diffractive complexity off-axis (for example, the “fingers” in a transverse beam plot), which requires a very fine grid, could provide additional harmonic complexity to the shock waves. It is possible to use the Gegenbauer reconstructions for this type of spatial discontinuity. The three-dimensional Gegenbauer reconstructions are not available at this moment to the best of our knowledge. However, the available two-dimensional Gegenbauer reconstructions15 may be useful for axisymmetrical problems.
ACKNOWLEDGMENTS
The authors would like to thank three anonymous reviewers for constructive comments. The authors also thank Dr. Vera Khokhlova, Dr. Ted Christopher, and Dr. Robin Cleveland for helpful discussions. This work was supported by NIH Grant No. U41RR019703.
References
- Christopher P. T. and Parker K. J., “New approaches to nonlinear diffractive field prop agation,” J. Acoust. Soc. Am. 90, 488–499 (1991). 10.1121/1.401274 [DOI] [PubMed] [Google Scholar]
- Lee Y.-S. and Hamilton M. F., “Time-domain modeling of pulsed finite-amplitude sound beams,” J. Acoust. Soc. Am. 97, 906–917 (1995). 10.1121/1.412135 [DOI] [Google Scholar]
- Pinton G. F. and Trahey G. E., “Modeling of shock wave propagation in large amplitude ultrasound,” Ultrasonic Imaging 30, 44–60 (2008). [DOI] [PubMed] [Google Scholar]
- Bakhvalov N. S., Zhileikin Y. M., and Zabolotskaya E. A., Nonlinear Theory of Sound Beams (American Institute of Physics, New York, 1987), pp. 1–184. [Google Scholar]
- Averianov M., Khokhlova V., Cleveland R., Sapozhnikov O., and Blanc-Benon P. “Parabolic equation for nonlinear acoustic wave propagation in inhomogeneous moving media,” Acoust. Phys. 52, 725–735 (2006). [Google Scholar]
- Averiyanov M., Yuldashev P., Blanc-Benon P., and Khokhlova V., “Comparison of time and frequency domain approaches to simulate propagation of weak shocks,” J. Acoust. Soc. Am. 125, 2601 (2009). [Google Scholar]
- Pishchal’nikov Y. A., Sapozhnikov O. A., and Khokhlova V. A., “A modification of the spectral description of nonlinear acoustic waves with discontinuities,” Acoust. Phys. 42, 362–367 (1996). [Google Scholar]
- Curra F. P., Mourad P. D., Khokhlova V. A., Cleveland R. O., and Crum L. A., “Numerical simulations of heating patterns and tissue temperature response due to high-intensity focused ultrasound,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 47, 1077–1089 (2000). 10.1109/58.852092 [DOI] [PubMed] [Google Scholar]
- Christopher T., “Reduced harmonic representation for continuous wave, shock-producing focused beams,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56, 859–863 (2009). 10.1109/TUFFC.2009.1109 [DOI] [PubMed] [Google Scholar]
- Khokhlova V. A., Souchon R., Tavakkoli J., Sapozhnikov O. A., and Cathignol D., “Numerical modeling of finite-amplitude sound beams: Shock formation in the near field of a cw plane piston source,” J. Acoust. Soc. Am. 110, 95–108 (2001). 10.1121/1.1369097 [DOI] [Google Scholar]
- Gottlieb D., Shu C.-W., Solomonoff A., and Vandeven H., “On the Gibbs phenomenon I: Recovering exponential accuracy from the Fourier partial sum of a nonperiodic analytic function,” Math. Comput. 64, 1081–1095 (1995). [Google Scholar]
- Gottlieb D. and Shu C. W., “Resolution properties of the Fourier method for discontinuous waves,” Computer Meth. Appl. Mech. Eng. 116, 27–37 (1994). 10.1016/S0045-7825(94)80005-7 [DOI] [Google Scholar]
- Gottlieb D. and Shu C.-W., “On the Gibbs phenomenon IV: Recovering exponential accuracy in a subinterval from a Gegenbauer partial sum of a piecewise analytic function,” Math. Comput. 64, 1081–1095 (1995). [Google Scholar]
- Gottlieb D. and Shu C.-W., “On the Gibbs phenomenon and its resolution,” SIAM Rev. 39, 644–668 (1997). 10.1137/S0036144596301390 [DOI] [Google Scholar]
- Min M.-S., Lee T.-W., Fischer P. F., and Gray S. K., “Fourier spectral simulations and Gegenbauer reconstructions for electromagnetic waves in the presence of a metal nanoparticle,” J. Comput. Phys. 213, 730–747 (2006). 10.1016/j.jcp.2005.06.025 [DOI] [Google Scholar]
- Averkiou M. A. and Cleveland R. O., “Modeling of an electrohydraulic lithotripter with the KZK equation,” J. Acoust. Soc. Am. 106, 102–112 (1999). 10.1121/1.427039 [DOI] [PubMed] [Google Scholar]
- Yuldashev P. V. and Khokhlova V. A., “Simulation of three dimensional nonlinear fields of ultrasound therapeutic arrays,” Acoust. Phys. 57, 337–347 (2011). 10.1134/S1063771011030213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jerri A. J., Advances in The Gibbs Phenomenon with Detailed Introduction (Sampling Publishing, Potsdam, NY, 2007), Chap. 7, pp. 1–25. [Google Scholar]
- Abramowitz M. and Stegun I. A., Handbook of Mathematical Functions (Dover, New York, 1970), pp. 771–802. [Google Scholar]
- Jing Y., Tao M., and Clement G., “Evaluation of a wave vector frequency domain method for nonlinear wave propagation,” J. Acoust. Soc. Am. 129, 32–46 (2011). 10.1121/1.3504705 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelb A. and Tadmor E., “Detection of edges in spectral data,” Appl. Comput. Harmonic Anal. 7, 101–135 (1999). 10.1006/acha.1999.0262 [DOI] [Google Scholar]
- Gelb A. and Tadmor E., “Detection of edges in spectral data II: Nonlinear enhancement,” SIAM J. Numer. Anal. 38, 1389–1408 (2000). 10.1137/S0036142999359153 [DOI] [Google Scholar]
- Jackiewicz Z., “Determination of optimal parameters for the Chebyshev–Gegenbauer reconstruction method,” SIAM J. Sci. Comput. 25, 1187–1198 (2003). 10.1137/S1064827503423597 [DOI] [Google Scholar]
- Hamilton M. F. and Blackstock D. T., Nonlinear Acoustics (Academic Press, San Deigo, CA, 1998), pp. 421–440. [Google Scholar]