A cocktail party model of spatial release from masking by both noise and speech interferers

Abstract

A mathematical formula for estimating spatial release from masking (SRM) in a cocktail party environment would be useful as a simpler alternative to computationally intensive algorithms and may enhance understanding of underlying mechanisms. The experiment presented herein was designed to provide a strong test of a model that divides SRM into contributions of asymmetry and angular separation [Bronkhorst (2000). Acustica 86, 117–128] and to examine whether that model can be extended to include speech maskers. Across masker types the contribution to SRM of angular separation of maskers from the target was found to grow at a diminishing rate as angular separation increased within the frontal hemifield, contrary to predictions of the model. Speech maskers differed from noise maskers in the overall magnitude of SRM and in the contribution of angular separation (both greater for speech). These results were used to develop a modified model that achieved good fits to data for noise maskers (ρ = 0.93) and for speech maskers (ρ = 0.94) while using the same functions to describe separation and asymmetry components of SRM for both masker types. These findings suggest that this approach can be used to accurately model SRM for speech maskers in addition to primarily “energetic” noise maskers.

INTRODUCTION

Listeners can use differences in source directions to perceptually separate a target speech signal from one or more interfering sources (Hirsh, 1950; Cherry, 1953). This can result in an improvement (i.e., decrease) in speech reception thresholds or an increase in percent correct performance at a fixed signal-to-noise ratio. This benefit of spatial separation of masker(s) from the target is known as spatial release from masking (SRM) and is the subject of a large body of auditory research (for reviews, see Zurek, 1993; Yost, 1997; Bronkhorst, 2000; Darwin, 2008). A mathematical formula to estimate SRM for maskers arrayed in the horizontal plane would be useful as a simpler alternative to computationally intensive approaches (e.g., Beutelmann and Brand, 2006; Beutelmann et al., 2010; Lavandier and Culling, 2010) and may contribute to an improved understanding of mechanisms underlying binaural hearing. In addition, existing models may not be suitable for predicting SRM across multiple masker types: some models are not designed for use with speech maskers (e.g., Bronkhorst, 2000) or include a step in which speech maskers or targets are replaced with noise prior to calculating outputs (e.g., Beutelmann et al., 2010, Lavandier and Culling, 2010).

The task of describing SRM with a single mathematical formula is complicated by the great number of contributing factors. These include, but are not limited to, room acoustics (Culling et al., 2003; Marrone et al., 2008; Beutelmann et al., 2010) and the measurement paradigm used (Bronkhorst, 2000) as well as numerous parameters of the interfering sound(s) such as the number of interfering sounds (Peissig and Kollmeier, 1997; Hawley et al., 2004; Cullington and Zeng, 2008), their physical configuration (Plomp and Mimpen, 1981; Bronkhorst and Plomp, 1992; Peissig and Kollmeier, 1997), and their similarity to the target (Brungart et al., 2001). Two studies that examined effects of reverberation offer an illustration of how complex and parameter-dependent the contributions of these factors can be. Culling et al. (2003) found that the advantage of spatially separating a single masker spoken by a female talker from a target spoken by a male talker was completely eliminated under highly reverberant conditions, whereas Marrone et al. (2008) found an advantage of spatial separation in excess of 8 dB in reverberant conditions in three-talker experiments in which the target and both maskers were all spoken by male talkers. The challenge for a model of SRM is to capture many complex effects well enough to yield accurate predictions while providing a fairly straightforward description that can potentially offer insight into basic mechanisms.

In the existing literature, SRM is frequently represented as a sum of components. Such “additive” descriptions of SRM have been used with some success even though masking itself need not be additive (e.g., Green, 1967; Lutfi, 1983; Moore, 1985). One well-known approach divides SRM into distinct monaural and binaural elements: (1) the benefit of a more favorable signal-to-noise ratio (SNR) at the “better ear” due to head shadow and (2) binaural unmasking (Zurek, 1993; Hawley et al., 2004). Although a division of SRM into monaural and binaural elements has been applied successfully in the computational algorithm described by Beutelmann and colleagues (2006, 2010) and in the prediction method described by Lavandier and Culling (2010), the suitability of this approach for use in a model that distills SRM down to a single equation has not been demonstrated for conditions where more than one interferer is present.

A different allocation of SRM into additive “separation” and “asymmetry” components is used in Bronkhorst’s model (2000), which provides a formula to calculate SRM for any configuration of noise maskers in the horizontal plane. This model was created by a multiple regression fit of data from three published studies that reported intelligibility of a speech target in the presence of one or more noise maskers (Plomp and Mimpen, 1981; Bronkhorst and Plomp, 1992; Peissig and Kollmeier, 1997).1 The model is given by the following equation, which can be used to estimate SRM in decibels for a speech target presented from 0° azimuth and elevation amid one or more noise interferers arrayed in the horizontal plane:

$$\mathit{SRM}=C[\alpha (1-\frac{1}{N}\sum _{i=1}^N\cos {\theta }_i)+\beta \frac{1}{N}\left|\sum _{i=1}^N\sin {\theta }_i\right|]$$ (1)

In this model, N is the number of masker sources, where all maskers have the same long-term average level, θ_i is the azimuth of the ith interfering source (i = 1,…, N), and C is an overall scaling coefficient that reflects differences among testing paradigms.2 The values of the regression coefficients were found to be α = 1.38 and β = 8.02. Despite the numerous challenges in modeling SRM that were noted in the preceding text, there was a high correlation between SRM predicted by this relatively simple equation and the data (ρ = 0.92). The model in Eq. 1 has two components: a cosine term that was interpreted as the contribution to SRM of angular separation of interferer(s) from the target and a sine term that was understood to be the contribution of the asymmetry of the masker array (Bronkhorst, 2000). Equation 1 can therefore be expressed in the following, simpler form, which will be used in the derivation of equations underlying the experiment reported herein:

$$\mathit{SRM}={\mathit{SRM}}_{\mathit{separation}}+{\mathit{SRM}}_{\mathit{asymmetry}}$$ (2)

In the following text, the “contributions of angular separation” and the “contributions of asymmetry” to SRM are to be understood in terms of the SRM_separation and SRM_asymmetry terms of Eq. 2.

One question of great interest is whether this model is also applicable to speech maskers. A single model describing SRM for both noise and speech maskers could provide useful insight into the cocktail party problem. Culling et al. (2004) found that their data with triplets of speech maskers were predicted fairly well by the Bronkhorst model. However, it is possible that this result is specific to three-masker configurations as the number of maskers can be an important factor in speech-on-speech masking (Brungart et al., 2001; Hawley et al., 2004; Cullington and Zeng, 2008). Moreover, there was limited variation in the degree of asymmetry in the masker configurations tested by Culling et al. Thus, it is unknown whether the Bronkhorst model is also applicable to speech maskers.

Masking of speech targets by speech interferers differs from masking by noise interferers in both the amount of masking and the types of masking involved. Masking of speech targets by speech maskers, but not noise maskers, can give rise to “informational masking” (Freyman et al., 1999; Brungart, 2001). At present, any discussion of this type of masking necessarily involves definitional issues, and there are ongoing efforts to improve existing definitions of informational masking, which is frequently associated with target-masker similarity and∕or uncertainty (Durlach et al., 2003; Watson, 2005). Informational masking is typically defined as any masking beyond the “energetic” component of masking, where energetic masking results primarily from overlapping excitation patterns created by the target and masker(s) at the auditory periphery. When a speech target is masked by speech interferers, the amount of informational masking varies depending on such factors as the number of talkers, the similarity of targets and maskers, and trial-to-trial uncertainty about the location of the target (Brungart et al., 2001; Freyman et al., 2004; Kidd et al., 2005; Brungart and Simpson, 2007). Spatial separation of masker(s) from the target is an effective way to counteract informational masking (Kidd et al., 1998; Freyman et al., 1999, Arbogast et al., 2002). As a result, when the target is speech, the magnitude of SRM with speech maskers can be quite large relative to noise maskers, particularly under conditions that lead to high informational masking such as when targets and maskers are spoken by talkers of the same gender or by the same talker (Brungart et al., 2001et al.,; Balakrishnan and Freyman, 2008). Thus, a model of SRM for both noise and speech maskers would have to be flexible enough to accommodate key differences between these types of maskers.

Although the Bronkhorst model as a whole has been evaluated by comparing model predictions to measured SRM, it would also be worthwhile to examine the validity of the individual components. One can determine the contribution to SRM of angular separation by measuring SRM for bilaterally symmetric two-masker configurations in which one masker is θ degrees left of the target and the other masker is θ degrees right of the target. In the remainder of this article, such bilaterally symmetric two-masker arrays are denoted as “−θ∕+θ” configurations, where θ is the separation angle from the target in degrees; negative angles between −180 and 0 are understood to be left of the midline; and positive angles between 0 and 180 are right of the midline. Because the asymmetry component is zero for a − θ∕+θ configuration [sin(−θ) = −sin(θ)], SRM of a − θ∕+θ configuration consists of the separation component only. That is,

$${\mathit{SRM}}_{\mathit{separation}}(-\theta ∕+\theta )=\mathit{SRM}(-\theta ∕+\theta )$$ (3)

The contributions of asymmetry can then be examined by measuring SRM in asymmetric masker configurations of the form +θ∕+θ, in which two maskers are presented from the same location. For these configurations, the contributions of angular separation and asymmetry can be computed from SRM(−θ∕+θ) and SRM(+θ∕+θ) as follows:

$${\mathit{SRM}}_{\mathit{separation}}(+\theta ∕+\theta )=\mathit{SRM}(-\theta ∕+\theta )$$ (4)

$$\begin{array}{c}{\mathit{SRM}}_{\mathit{asymmetry}}(+\theta ∕+\theta )=\mathit{SRM}(+\theta ∕+\theta )-\mathit{SRM}(-\theta ∕+\theta )\end{array}$$ (5)

Equation 4 follows from Eq. 3 and from the fact that the cosine term that defines SRM_separation is an even function, i.e., cos(−θ) = cos(θ). Equation 5 is derived by rearranging Eq. 2 and then applying Eq. 4. Thus, tests with −θ∕+θ and +θ∕+θ configurations can be used to assess the validity of the components of the Bronkhorst model.

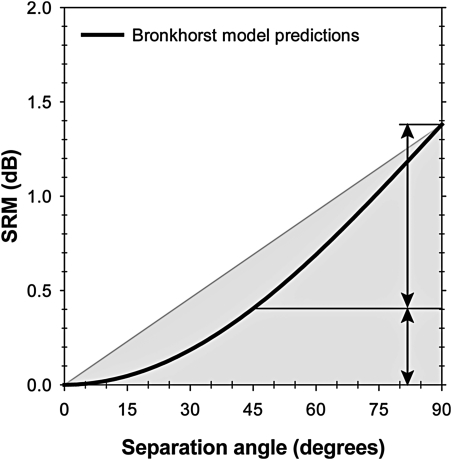
Bronkhorst found that his model was able to predict SRM for noise maskers rather well (see preceding text), but it may give an inaccurate description of at least one key mechanism. Consider, for example, Fig. 1, which shows the SRM predicted by the Bronkhorst model for −θ∕+θ configurations as the separation angle, θ, increases from 0° to 90°. In the Bronkhorst model, the function that describes SRM for these −θ∕+θ configurations (see Fig. 1) has a very low slope in the region from 0° to 45° and becomes increasingly steep as the separation angle approaches 90°. The lower of the two arrows near the right edge of Fig. 1 indicates that the benefit of the first 45° of angular separation is a mere 0.4 dB, which is appreciably smaller than the ∼1-dB predicted growth of SRM as angular separation is increased by another 45°, i.e., from a separation angle of 45° to 90°. To put it another way, the model suggests less sensitivity to changes in angular separation near the front (target location) than near the left and right ears.

Figure 1.

The plot above shows spatial release from masking (SRM) predicted by the Bronkhorst model for bilaterally symmetric two-masker configurations of the form −θ∕+θ as θ, the angular separation of the maskers from the target, is increased from 0 to 90. The arrows and horizontal lines near the right edge of the plot indicate model predictions concerning SRM in the −45∕+45 configuration and the anticipated growth of SRM among these bilaterally symmetric two-masker arrays as angular separation is increased from 45° to 90°. The fact that the curve is concave-upward and lies in the shaded region of the plot indicates that listeners’ sensitivity to changes in angular separation is predicted to be greatest when maskers are located by the left and right ears. A concave-downward curve that lies above the shaded region would predict greatest sensitivity to changes in masker angle when the maskers are located near the target location (front).

The shape of the function plotted in Fig. 1 suggests a strikingly different pattern than was indicated by results in both anechoic and reverberant environments with speech maskers in −θ∕+θ configurations reported by Marrone et al. (2008). In that study, each subject’s data could be fitted with rounded exponential (“roex”) functions that began to approach a horizontal asymptote at angular separations between 15° and 45° and had near-zero slope between 45° and 90°. Moreover, Jones and Litovsky (2008) reported SRM for speech maskers in a −45∕+45 configuration that was such a large proportion of the maximum SRM they measured in the frontal hemifield as to be incompatible with the growth of SRM predicted by the Bronkhorst model. Given that the work of Marrone et al. and of Jones and Litovsky was conducted with speech maskers, one possible explanation for the differences between their results and the predictions of the Bronkhorst model is that growth of SRM_separation as a function of angular separation may have a different trajectory for speech maskers than for noise maskers. Alternatively, it is possible that for both noise and speech maskers, SRM in the −θ∕+θ configurations exhibits a pattern somewhat akin to the minimum audible angle (Mills, 1958) in which sensitivity to changes in angle is greatest near 0°.

Bronkhorst (2000) identified two data points for which there were relatively large differences between the model predictions and measured SRM. One of these two data points was from a −θ∕+θ configuration (−90∕+90) for which the model prediction of 1.4 dB SRM was 3.2 dB lower than the measured SRM of 4.6 dB. The other such data point was from a 0∕+105 configuration in which one masker was collocated with the target and the other masker was near one ear. The model prediction for this configuration was 4.0 dB, which was 2.9 dB higher than the measured SRM of 1.1 dB. Thus, these two types of masker configurations are of particular interest in the evaluation of the model.

In the experiment reported in this article, SRM was determined for several two-masker configurations. The maskers were speech, unmodulated speech-shaped noise, and envelope-modulated speech-shaped noise. Key aims of the experiment were to delineate the respective contributions of angular separation and asymmetry to SRM and to test whether the Bronkhorst model can be extended to include speech maskers. To provide a strong test of the model and its components, masker configurations similar to the two problematic data points from the fitting of the Bronkhorst model were included in the experiment. It was hypothesized that there would be diminishing growth of SRM_separation with increasing angular separation in the frontal hemifield. The results supported this hypothesis and, moreover, suggested a greater contribution of angular separation to SRM for speech maskers than for noise maskers. Based on the results of this experiment, a revised model is proposed to describe SRM for both speech and noise maskers.

SRM IN SOUND-FIELD PRESENTATION

Methods

Listeners

Listeners were 10 university students (10 females, 18-22 yr of age), who were paid for their participation. Only native English speakers from households in which no language other than English was spoken were recruited. Audiograms were measured on each potential subject, and pure tone thresholds of 20 dB hearing level (HL) or better at the octave frequencies from 250 to 8000 Hz were required.

Stimuli

Speech stimuli were recorded by a male talker trained to speak at constant levels and rates. The targets were from a closed set of 40 spondees with equivalent intelligibility as determined by pilot testing. The maskers were of three types: speech, steady-state speech-shaped noise (SSN), and modulated speech-shaped noise (MSSN). The same talker was recorded reading the spondee targets and Harvard IEEE sentences (Rothauser et al., 1969). The recordings were low-pass filtered at 10 kHz and saved at a sampling rate of 44.1 kHz. The recorded sentences were edited to reduce opportunities for “listening in the gaps” between individual words and sentences as described previously (Jones and Litovsky, 2008). Briefly, silent gaps between consecutive words were edited out manually, and both ends of each recorded sentence were edited using an iterative, automated algorithm. The algorithm works from each end of the sentence and removes 10-ms segments until it finds a segment the root mean square amplitude (RMS) of which is within 12 dB of the RMS of the whole sentence at which point it identifies a zero crossing near the end of the sentence and makes the final cut there. The automated editing caused six of the recorded sentences to sound unnatural, and these six sentences were discarded. The edited sentences had a rapid cadence of about 250 words per minute but were judged by both experimenters and by the listeners to be natural and were readily understandable. Pairs of sentences were concatenated to create two-sentence maskers with durations of 3.5 to 3.7 s.3 This masker duration, which was longer than was strictly necessary for the current study, reflected the needs of a companion study with which this experiment had four data points in common. Each speech masker was then used to create two noise maskers. First, for each speech masker, a steady-state noise masker was created by filtering Gaussian noise to match the long-term spectrum of the speech masker from which it was generated. Second, an envelope-MSSN masker was created with the same long-term spectrum and envelope as the speech masker from which it was derived. The speech envelope was extracted using a method similar to that described by Festen and Plomp (1990), in which a rectified version of the waveform is passed through a first-order low-pass Butterworth filter with a 3-dB cutoff at 40 Hz. On every trial the maskers consisted of two independently generated, randomly selected maskers of the same type: i.e., two speech maskers, two unmodulated speech-shaped noise maskers, or two MSSN maskers.

Procedures

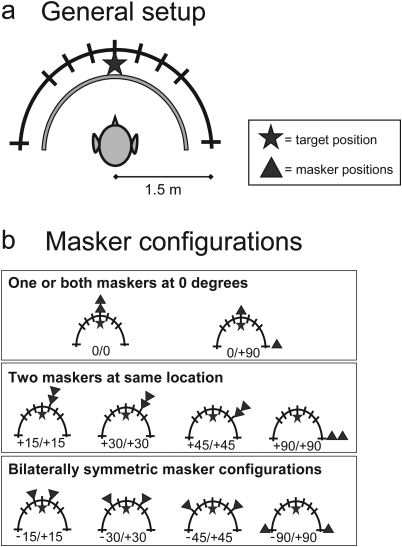
A schematic overview of the experimental setup is shown in Fig. 2a. Testing was conducted in a small room (2.9 m ×3.6 m) with a reverberation time (RT₆₀) of approximately 250 ms. The subject was at the center of a hemispheric loudspeaker array with a radius of 1.5 m and seated on a chair on a platform that could be raised or lowered so that the opening of the ear canal was within 4 cm of the horizontal plane. The platform, walls, and ceiling were covered by 8-cm deep acoustically absorbent foam. This experiment used nine loudspeakers at 0° elevation at the following locations from left to right: −90°, −45°, −30°, −15°, 0°, +15°, +30°, +45°, and +90°. The positions of the loudspeakers were concealed from the subjects by a visually opaque, acoustically transparent curtain.

Figure 2.

A schematic view of the setup used in this experiment is shown in panel (a). Subjects were seated at the center of a 1.5 m loudspeaker array with loudspeakers at 0° elevation at the following locations from left to right: −90°, −45°, −30°, −15°, 0°, +15°, +30°, +45°, and +90°. The positions of the loudspeakers were concealed by a curtain. Ten two-masker configurations with the target at 0° were used in this experiment (b).

Software for stimulus presentation and data collection was written in Matlab (Mathworks Inc.). Target and masker stimuli were upsampled from 44.1 kHz using the resample command in Matlab, digitally summed (where necessary), and played at a sampling rate of 48.8 kHz using 16-bit, digital-to-analog conversion. Speaker switching and amplification were controlled through Tucker Davis Technologies (TDT) System III hardware (RP2, PM2, SA1) in conjunction with a PC host. The outputs of individual speakers were calibrated with a sound level meter prior to each day of testing. The combined level of the maskers was 57 dB(A), and the levels of the two maskers were equal to one another. The level of the target was varied adaptively as described in the next paragraph. A cosine squared window with 2 ms rise and fall times was applied to each signal; this was done prior to upsampling to reduce resampling distortion.

The 40 spondee targets were displayed in alphabetical order reading down the columns of an 8 × 5 grid, and subjects were asked to verbally identify the target word on each trial using words from the list in a 40-alternative forced choice task. They were instructed to guess if they could not identify the target word. The responses were entered into a computer by a tester, who was monitoring the experiment via closed-circuit TV. Subjects were informed that the target would always be presented from straight ahead, and the 0° location was visually marked on the curtain. No other information was given about the positions of the loudspeakers. Subjects were instructed to face straight ahead with the nose pointing at the 0° loudspeaker, and they were monitored throughout each testing session to ensure they maintained proper head position.

Ten two-masker configurations were used in the experiment [see Fig. 2b]. In two of the masker configurations, 0∕0 and 0∕+90, one or both maskers were at 0°. The 0∕0 configuration is the baseline for all SRM calculations. The 0∕+90 configuration was included due to its similarity to the 0∕+105 configuration that was one of the two data points for which a relatively large difference was noted between predicted and measured SRM in the data fitting of the Bronkhorst model. The remaining eight masker configurations, four −θ∕+θ configurations and four +θ∕+θ configurations, were used to examine the respective contributions of angular separation and asymmetry to SRM, as described in Sec. 2A4 [see also Eqs. 3 through 5 in the introduction]. Within this subset of the tested masker configurations, the angular separation and asymmetry parameters were varied orthogonally. This was done as follows: (1) the angular separation of maskers from the target was 15°, 30°, 45°, or 90° and (2) the array was either asymmetrical (with both maskers presented from the same loudspeaker) or symmetrical (with the two masker locations mirrored across the midline). It is important to note that two independently generated, randomly selected maskers were presented on each trial. The computer program that ran the experiment specifically prevented the random generator from selecting two copies of the same masker for presentation within a single trial. This is in contrast with previous research that has examined spectral benefits of spatial separation in the special case where two identical or highly correlated maskers are presented in a bilaterally symmetrical configuration (Ter-Horst et al., 1993). This approach also differs from the experiments of Marrone et al. (2008) with the coordinate response measure (CRM) corpus in which the content of all stimuli is based on a common template that differs in designated keywords.

The target and two maskers were randomly selected for each trial. At the beginning of each trial, the subject was prompted with the word “Ready?” from the 0° loudspeaker. The prompt was a recording spoken by the same talker as the targets and maskers, and there was a silence of 0.6 ± 0.1 s between the prompt and masker onset. The onset of the target was delayed relative to the onset of the maskers by a mean of 0.1 s with 0.1 s jitter. Subjects were familiarized with the task during an initial visit for hearing screening and in a 5-min practice before the start of each testing session.

Testing with each subject was organized into 60 blocks of trials such that each combination of the factors masker type (3 levels) and masker configuration [10 levels, see Fig. 2b] was tested twice. The order of blocks was balanced across subjects in an incomplete Latin Square design, and the two repetitions of each combination of masker type and masker configuration were always on separate visits. The 60 blocks of trials were run concurrently with a separate study (not reported here) over three approximately 2-hr visits.

In each block, the speech reception threshold (SRT) was determined based on a fit of psychometric functions to data from an adaptive procedure with four reversals. This paradigm has been used reliably with both pediatric and adult populations (Litovsky, 2005; Johnstone and Litovsky, 2006; Garadat and Litovsky, 2007; Jones and Litovsky, 2008), although it should be noted that the algorithm was modified slightly here. An adaptive tracking method was used to vary the level of the target signal from an initial level of 63 dB(A), such that correct responses result in level decrement and incorrect responses result in level increment. The algorithm includes the following rules: (1) Level is initially reduced in steps of 8 dB following each correct response. (2) Following the first incorrect response, a 3-down∕1-up rule is used, whereby level is decremented following three consecutive correct responses and level is incremented following a single incorrect response. (3) Following each reversal, the step size is halved. (4) A step size that has been used twice in a row in the same direction is doubled. For instance, if the level was decreased from 40 to 36 dB (step size = 4 dB) and then again from 36 to 32 dB, a set of three consecutive correct responses at 32 dB would result in an 8-dB drop to 24 dB. (5) Testing is terminated following four reversals. Data collected using this algorithm were fitted to a logistic function by a constrained maximum-likelihood estimation (MLE) method (Wichmann and Hill, 2001a, b). The 3-down∕1-up method converges to the 79.4% correct point (Levitt, 1971).

Data analysis

The lower bound of the psychometric function was set to the chance level of performance, 0.025. The sampling scheme and lapses in listener attention can introduce biased estimates of threshold. The bias introduced by attentional lapses was overcome by limiting the upper bound of the psychometric function to the range [0.95,1] (Wichmann and Hill, 2001b). Threshold was calculated as the 80% point on the fitted psychometric function.

For each subject, the SRT for each masker configuration was calculated as the average of thresholds from two adaptive tracks. For each masker configuration in which one or both maskers were spatially separated from the target, SRM was calculated by subtracting the SRT for that configuration from the SRT for the 0∕0 configuration. Analyses of variance (ANOVAs) were performed on SRM values. Planned comparisons to evaluate possible differences as a function of masker angle and masker type were conducted using paired t-tests. The criterion for statistical significance was P < 0.05. In t-tests, the criterion for significance was corrected for the number of comparisons. The 95% confidence intervals for group mean SRM data were calculated using a t-distribution with 9 degrees of freedom. The components of SRM were calculated by using Eqs. 3, 4 to determine contributions of angular separation to SRM and Eq. 5 to compute contributions of asymmetry to SRM.

Results

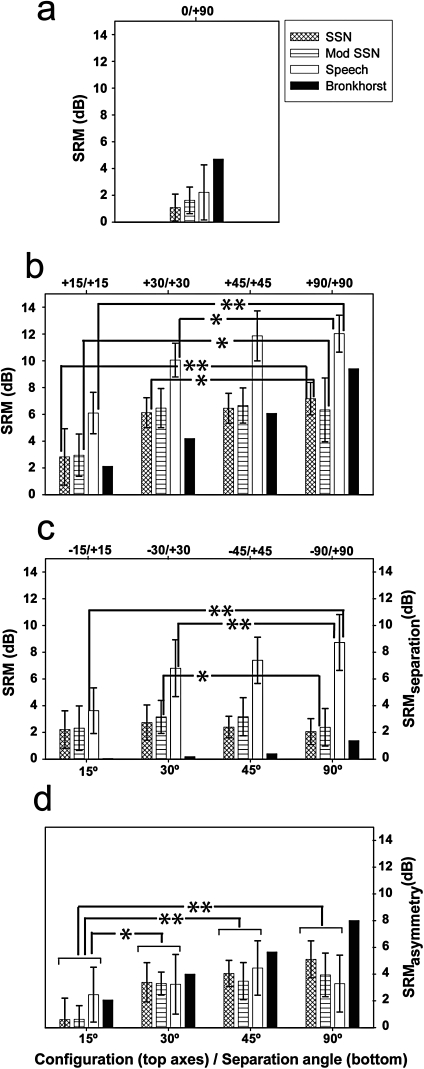
Figure 3 shows group mean SRM [left y axis labels of Figs. 3a through 3c] in the masker configurations with at least one masker separated from the target as well as a breakdown of SRM into SRM_separation and SRM_asymmetry [right y axis labels of Figs. 3c, 3d]. The error bars show 95% confidence intervals. The hatched and white bars show data for the three tested masker types, and the black bars show predictions of the Bronkhorst model. The data for the 0∕+90 configuration [Fig. 3a] indicate smaller SRM than predicted by the Bronkhorst model for all three masker types. The results of a one-way ANOVA did not show an effect of masker type on SRM in this configuration [F(2,18) = 0.9; P > 0.05]. However, differences were observed among masker types in the +θ∕+θ and −θ∕+θ configurations [Figs. 3b, 3c]. A three-way ANOVA was calculated on SRM values in the asymmetric +θ∕+θ configurations and the symmetric −θ∕+θ configurations for the following factors: angular separation (four levels: 15, 30, 45, 90), symmetry (two levels: symmetric, asymmetric), and masker type (three levels: steady-state noise, modulated noise, speech). There were main effects of all three factors (angular separation: [F(3,27) = 69.4; P < 0.001]; symmetry: [F(1,9) = 155.8; P < 0.001]; masker type: [F(2,18) = 29.0; P < 0.001]) as well as significant two-way interactions between the factors angular separation and masker type [F(6,54) = 8.3; P < 0.001] and between angular separation and symmetry [F(3,27) = 26.8; P < 0.001]. SRM in the +θ∕+θ and −θ∕+θ configurations was significantly greater for speech maskers than for noise maskers that were unmodulated (P < 0.0001) or modulated (P < 0.0001). Moreover, the amount of SRM with noise maskers was not significantly affected by modulation of the masker envelopes (P > 0.05). Comparison of group mean SRM with model predictions reveals that measured SRM generally exceeded Bronkhorst model predictions for speech maskers in the +θ∕+θ configurations [Fig. 3b] and for all masker types in the bilaterally symmetric −θ∕+θ configurations [Fig. 3c].

Figure 3.

Group means for SRM are shown for three types of maskers (hatched and white bars) along with predictions of the Bronkhorst model (black bars) for the 0∕+90 configuration (a), the +θ∕+θ configurations (b), and the −θ∕+θ configurations (c). Data in c also give the separation component of SRM for angular separations of 15°, 30°, 45°, and 90°. (d) shows the asymmetry component of SRM for these angular separations. x-axis labels at the top of a plot show masker configurations; labels at the bottom of a plot show angular separation of maskers from the target. y-axis labels on the left side of plots (a)—(c) report SRM for masker configurations. y-axis labels on the right side of a plot report SRM_separation (c) or SRM_asymmetry (d). The error bars show 95% confidence intervals. *, P < 0.05; **, P < 0.002.

Figure 3c serves two different roles. In addition to reporting SRM in the −θ∕+θ configurations (left y axis labels), (c) also gives estimates, per Eqs. 3, 4, of SRM_separation (right y axis labels) as a function of separation angle. The separation component of SRM [Fig. 3c] exceeded the model predictions for all masker types, and the difference is particularly large for speech. SRM_separation with noise maskers was not significantly greater at a separation angle of 90° than at separation angles as small as 15° (P > 0.05 for both modulated and unmodulated noise). This observation is consistent with the hypothesis of diminishing growth of SRM_separation with increasing angular separation, which is tested and discussed in the following text. SRM_asymmetry in the +θ∕+θ configurations [Fig. 3d] was calculated using Eq. 5, which shows that SRM_asymmetry in these configurations is the difference between data in Figs. 3b, 3c. A two-way ANOVA showed a significant effect of masker angle [F(3,27) = 16.5; P < 0.001] on SRM_asymmetry but did not show an effect of masker type [F(2,18) = 0.5; P > 0.05] or an interaction between the factors [F(6,54) = 1.3; P > 0.05]. Post hoc Tukey tests in which values of the asymmetry component were collapsed across masker types indicated that SRM_asymmetry was significantly smaller at an angular separation from the target of 15° than at angular separations of 30° (P < 0.005), 45° (P < 0.001), and 90° (P < 0.001). Significant differences in the asymmetry component of SRM were not found in pairwise comparisons among angular separations of 30°, 45°, and 90°. Within each masker type changes in SRM_separation [Fig. 3c] and SRM_asymmetry [Fig. 3d] were generally small as angular separation was increased beyond about 30°.

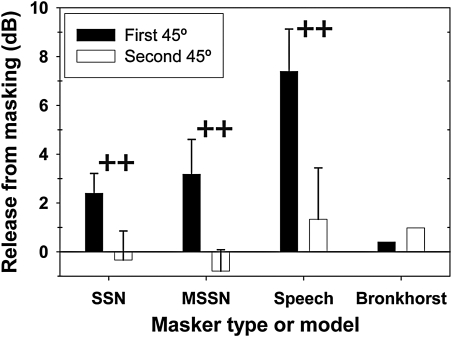
Figure 4 shows the release from masking due to increasing target∕masker separation by 45° in two different regions of the frontal hemifield. The comparison of interest here is between the black bars, which show the benefit of the first 45° angular separation from the target, and the white bars, which show the release from masking that results from further increasing angular separation from 45° to 90°. In contrast with the predictions of the Bronkhorst model, for both noise and speech maskers, the benefit of the first 45° angular separation from the target was greater than the benefit of increasing angular separation from 45° to 90°. t-tests with a Bonferroni correction confirmed that this difference was significant for unmodulated noise (P < 0.005), envelope-modulated noise (P < 0.001), and speech maskers (P < 0.001). Thus, the hypothesis of diminishing growth of SRM_separation with increasing angular separation in the frontal hemifield was supported across masker types.

Figure 4.

This plot shows the release from masking that results from the first 45° angular separation from the target (black bars) and the release from masking due to further increasing angular separation from 45° to 90° (white bars). Data are shown for three types of maskers along with predictions of the Bronkhorst model. ++, P < 0.0167.

Discussion

The current experiment examined the relationships among masker type, angular separation, and the symmetry or asymmetry of the masker array as they relate to SRM. The overall magnitude of SRM and the contribution of angular separation to SRM were both greater for speech maskers than for noise maskers. Across masker types, the contribution to SRM of angular separation of maskers from the target was found to grow at a diminishing rate as angular separation increased within the frontal hemifield. Because the finding of diminishing growth of SRM_separation with increasing separation angle within the frontal hemifield is at odds with the description provided by the Bronkhorst model, it suggests a need to replace the negative cosine function in the Bronkhorst model with a function of a very different character. In contrast with the separation component, the SRM_asymmetry data are generally consistent with predictions of the Bronkhorst model [Fig. 3d]. A small disparity is evident between 45° and 90° where in contrast with the modest growth of the sine function used in the model (black bars), the SRM_asymmetry data had a flat pattern (hatched and white bars). Nevertheless, considering that SRM_asymmetry is calculated indirectly [see Eq. 5 in the introduction], the match between model and data was considered to be acceptable. Finally, it should be noted that the largest SRM measured in the frontal hemifield with noise maskers in this experiment was smaller than has been measured in anechoic rooms (e.g., Zurek, 1993). Reverberation may have limited the benefit of spatial separation of noise maskers from the target in the current experiment, which was conducted in a sound-treated, but not anechoic, room. With speech maskers, however, SRM can be quite robust even in reverberant rooms (e.g., Marrone et al., 2008) and was up to 12 dB in the sound-treated room used in the current experiment.

The observation of greater SRM with multiple speech maskers than with noise maskers is consistent with existing reports (e.g., Hawley et al., 2004). The finding that greater SRM with speech maskers was due to larger SRM_separation is consistent with results in the existing literature indicating that separation of masker(s) from the target is an effective way to counteract informational masking (Kidd et al., 1998; Freyman et al., 1999; Arbogast et al., 2002; Noble and Perret, 2002). The observation of no effect of masker type on SRM_asymmetry in the current experiment is similar to the finding of Hawley et al. (2004) that monaural advantage was about equal across masker types. This raises the possibility that there may be substantial overlap between “better ear” advantages and benefits of asymmetry even though one is typically measured monaurally and the other was determined based on experiments performed binaurally. In addition, the interaction in the SRM data between masker type and angular separation is similar to findings of Noble and Perret (2002) and Hawley et al. (2004). At present, however, not enough is known to draw definitive conclusions about whether the division of SRM into separation and asymmetry components has significant parallels with the division of SRM into “better ear” and “binaural unmasking” components.

The results with the 0∕+90 configuration were unique among the tested masker arrays [compare Fig. 3a to Figs. 3b, 3c]. In this configuration, SRM was lower than predicted by the Bronkhorst model for all masker types. In addition, there was no effect of masker type on SRM in the 0∕+90 configuration. One interpretation of this result is that there is a strong effect of presenting a masker at the target location that may outweigh differences that are otherwise observed between speech and noise maskers. Another interpretation, which was suggested by Bronkhorst (2000), is that the model may overestimate SRM when the combination of a masker at the target location and masker(s) near 90° are presented.

A REVISED MODEL OF SRM

In the following text, we present a modified model that is built on a framework similar to that of the Bronkhorst model, but with changes to allow the inclusion of speech maskers in the model, to improve the representation of SRM_separation and to better predict SRM in configurations with at least one masker at the target location. Given the fairly good match between the data for SRM_asymmetry and the model, the asymmetry component of SRM is represented in the revised model by the same sine function as in the Bronkhorst model. Based on examination of the data [Fig. 3c], the function representing SRM_separation should rise rather steeply from 0 and then have a relatively slower rate of growth over a large range of angular separations up to 90°. Specifically, these data are described well by hyperbolic tangent functions of the form tanh(cθ) when c is a small number on the order of 2 to 5. One limitation of a separation component of this type, however, is that it does not adequately model front∕back differences. In the model presented in the following text, this is overcome by including a distinct front∕back component consisting of a sigmoidal function that is 0 in the frontal hemifield and asymptotically approaches its maximum value at angular separations ≥120°. When combined with the sine and hyperbolic tangent functions described in the preceding text, the addition of this front∕back component results in an equation for calculating SRM that peaks between 110° and 120°, which is comparable to reports in the literature (Plomp and Mimpen, 1981; Peissig and Kollmeier, 1997). In addition to the shape of the function that describes the relationship between masker angle(s) and SRM, there are differences in the magnitude or scale of the SRM function that depend on such factors as reverberation, masker type, the measurement paradigm, the number of maskers (when the maskers are speech), and target-masker similarity (Bronkhorst, 2000; Brungart et al., 2001; Hawley et al., 2004; Marrone et al., 2008). This can be modeled by including a scaling factor, D, that plays a similar role to that of the overall scaling factor in Eq. 1. The full model, which can be used to estimate SRM in decibels when a speech target at 0° azimuth and 0° elevation, is presented amid one or more noise or speech maskers, is as follows:

$$\begin{array}{c}\mathit{SRM}=D[\alpha \frac{1}{N}\sum _{i=1}^N\tanh (3{\theta }_i^{*})+\beta \frac{1}{N}|\sum _{i=1}^N\sin {\theta }_i|+\gamma \frac{1}{N}\sum _{i=1}^N\frac{1}{1+e^{-0.5*(|{\theta }_i|-110)}}]\end{array}$$ (6)

$${\theta }_i^{*}=\{\begin{array}{cc}\left|{\theta }_i\right|& -90\le {\theta }_i\le 90\\ \left|{\theta }_i-180\right|& 90\le {\theta }_i\le 180\\ \left|{\theta }_i+180\right|& -180\le {\theta }_i\le -90\end{array}$$ (7)

In this model, N is the number of masker sources, where all maskers have the same long-term average level, θ_i is the azimuth of the ith interfering source (i = 1,…, N), and ${\theta }_i^{*}$ is the angular separation of the ith masker from the midline. Thus ${\theta }_i^{*}$ is between 0 and 90 for each masker angle θ_i. For noise maskers, the model is defined for the entire horizontal plane (−180 ≤  θ_i ≤ 180 for all i), and the regression coefficients are α = 0.23, β = 0.75 and γ = 0.15 (see next paragraph for their derivation). In the case of speech maskers, where the model is currently defined for maskers in the frontal hemifield only (−90 ≤ θ_i ≤ 90 for all i), the regression coefficients are α = 0.60 and β = 0.41, with γ = 0. The tanh, sine, and reciprocal exponential functions in Eq. 6 determine SRM_separation, SRM_asymmetry, and SRM_back, respectively. The larger value of α for speech maskers (0.60) than for noise maskers (0.23) is consistent with the greater SRM_separation for speech maskers than for noise maskers described in the preceding text [Fig. 3c]. The overall scaling factor “D” will be discussed in detail in the following text.

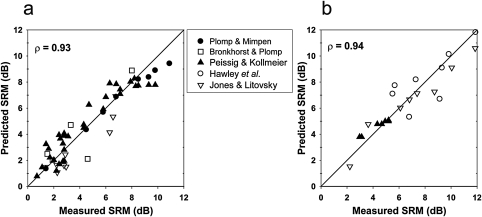
The noise-masker version of the model was fitted by conducting multiple regression analyses on the same data sets that were used in the fit of the Bronkhorst model plus the data for noise maskers from the current study, giving in total 55 data points. The regression coefficients were significant for the separation (P < 0.0001), asymmetry (P < 0.0001), and front∕back (P < 0.005) components of SRM. A plot comparing SRM predicted by this version of the revised model with measured SRM is shown in Fig. 5a. A good fit was found between the model and the data with a correlation of 0.93 and a mean absolute prediction error of 0.81 dB. The largest absolute prediction error, 2.5 dB, was found for the data point from a −90∕+90 configuration for which an even larger discrepancy of 3.2 dB was observed in the Bronkhorst model. The mean absolute prediction error in the 10 bilaterally symmetric masker configurations from the four studies included in the fit was 0.97 dB for the revised model, which was significantly lower than the 1.60 dB for the Bronkhorst model (P < 0.005).

Figure 5.

These scatter plots compare predictions of the model of SRM presented in Eq. 6 with measured SRM for noise maskers (a) and speech maskers (b). The correlation coefficients for noise maskers and speech maskers, respectively, are displayed on each plot.

The speech-masker version of the model was fitted by conducting multiple regression analyses on data collected with one speech masker in the frontal hemifield reported by Peissig and Kollmeier (1997), data collected with one, two, or three speech maskers reported by Hawley et al. (2004), and the two-masker data for speech maskers reported in the current article, giving in total 26 data points.4 The regression coefficients were significant for both the separation and asymmetry terms (P < 0.0001 for both). A plot comparing SRM predicted by the speech masker version of the revised model with measured SRM is shown in Fig. 5b. A good fit was found between measured and predicted SRM as indicated by a correlation coefficient of 0.94 and by a mean absolute prediction error of 0.74 dB. The largest absolute prediction error was in a configuration with a single masker 60° from the target, in which measured SRM exceeded the model prediction by 2.4 dB.

The scaling factor “D” in Eq. 6 serves a similar purpose to the overall scaling factor in the Bronkhorst model. Values of D for the data sets that were used in the model fitting are provided in Table TABLE I.. In most cases, in which all maskers are spatially separated from the target, the value of D reflects the largest SRM in the frontal hemifield for a given testing paradigm. Among speech maskers, the dependence of the maximum SRM in the frontal hemifield on the number of maskers, with a peak at N = 2, is consistent with previous reports concerning the use of spatial cues when speech targets are presented amid speech maskers (e.g., Hawley et al., 2004; Freyman et al., 2004). The largest SRM in the frontal hemifield will typically occur in a masker configuration with all maskers at a single location about 90° from the target, but in light of the potential impact of statistical variation on any single measurement, some care is required in choosing the value of D for a given paradigm.5 The numerical values of D shown in Table TABLE I. were calculated by taking the average of at least two reported data points.6 For example, the value of D for the data of Plomp and Mimpen (1981) and the data of Bronkhorst and Plomp (1992) was determined to be 9 dB by averaging the SRM values for the +90 configuration reported in the two studies. The use of the same value of D for both studies is based on their use of highly similar stimulus recording and presentation.

Table 1.

The values of the overall scaling factor “D” that were used in the data fitting are given in this table along with the formula for calculating D analytically in the special case of masking arrays with one or more maskers at the target location.

Any maskers at target location?	D	Comments
Yes	10*log 10(N∕n)	N = number of maskers in array; n = number of maskers at target location (0<n≤N)
No	Speech maskers (D can vary by paradigm and number of maskers)
	7	1 masker: Hawley et al., 2004
	5	1 masker: Peissig and Kollmeier, 1997
	12	2 maskers: Hawley et al., 2004; current article
	10	Hawley et al., 2004: 3 maskers
	Noise maskers (D can vary by paradigm)
	9	Bronkhorst and Plomp, 1992; Plomp and Mimpen, 1981
	8	Peissig and Kollmeier, 1997
	7	Current article

In addition, the overall scaling coefficient, D, plays a unique role in setting the magnitude of SRM in masker configurations with one or more maskers at the target location. Namely, in the special case of masker configurations in which n of N uncorrelated maskers are collocated with the target (0 < n ≤ N), the value of the scaling factor D is calculated analytically as 10*log10(N∕n), i.e., the amount by which masking would have decreased, relative to the array with all maskers at the target location, if the spatially separated maskers had simply been turned off rather than being presented from a different location than the target.7 Thus, for example, the value of D for a two-masker array with one masker at the target location is about 3 dB. Use of this rule in the revised model resulted in low prediction errors. The absolute prediction error for the 0∕+105 configuration described in the introduction was 0.4 dB with the revised model as compared with 2.9 dB with the Bronkhorst model. The absolute predictions errors for the other three data points from configurations with one masker collocated with the target were also low with the revised model: 0.1, 0.1, and 0.7 dB.

Despite the good fit noted in the preceding text, the model of SRM for speech maskers should be applied and interpreted with some caution. First, it should be emphasized that in the case of speech maskers, the model is only defined for maskers in the frontal hemifield. Second, the amount of informational masking can depend on factors such as the number of speech maskers and the similarity of maskers and targets (Brungart et al., 2001; Hawley et al., 2004). Although the number of speech maskers did vary in the data included in the model fitting, target-masker similarity was concentrated toward the high end of the range. That is, the data fitted for the speech masker version of the model were collected under conditions that are typically associated with high informational masking, with targets and maskers spoken by the same talker (two of the three data sets) or same-gender talkers (one of the three data sets). Based on the results described in the preceding text, one would expect the relative contributions of angular separation and asymmetry to SRM, and thus the regression coefficients for the speech masker version of the model, to vary as the amount of informational masking varies. Further research is required to determine whether the regression coefficients for the speech masker version of the model are typical for release from masking of speech targets by speech interferers.

This descriptive model is limited somewhat in its explanatory power by the fact that values of the overall scaling factor, D, were based solely on empirical measurement. The value of D is likely to depend on multiple factors including room acoustics and, in the case of speech maskers, informational masking, but the way these factors determine D has not yet been specified. It is worth noting that computational approaches (Beutelmann et al., 2010; Lavandier and Culling, 2010) are being used to explore the contributions of room acoustics to speech intelligibility. Thus, such approaches might ultimately offer a way to clarify the contributions of room acoustics to the overall scaling factor in the current model. Finally, the use of a special rule for calculating the overall scaling factor in configurations with one or more maskers collocated with the target should be noted. Specification of how to calculate the scaling factor in cases of nonzero, but very small, angular separations from the target would be a useful addition to the model.

GENERAL DISCUSSION

The main motivation for this study was to test whether SRM in a cocktail party environment can be accounted for, across various types of maskers, with a computationally simple model. A primary result of this work is a model of SRM that is built on a framework similar to the model proposed by Bronkhorst (2000) but with modifications to improve characterization of the contributions of angular separation to SRM and to extend the model to include speech maskers. Of particular interest is the observation that the same mathematical functions could be used to describe the contributions of angular separation and asymmetry to SRM for both speech maskers and noise maskers, which differed only in the regression coefficients of the components.

The method that was used to examine the components of SRM in the current study appears in some respects to be the reverse of a commonly used approach in which contributions of “better ear” effects to SRM are measured directly and benefits of “binaural unmasking” are then calculated indirectly by taking the difference between binaural and monaural performance (Zurek, 1993; Hawley et al., 2004). In the current study, SRM_separation was determined for masker arrays in which there is no “better ear,” the −θ∕+θ configurations, and SRM_asymmetry was then calculated by taking the difference between +θ∕+θ and −θ∕+θ configurations per Eq. 5. Based on the goodness of fit achieved with the Bronkhorst model and with the revised model, the general approach of dividing SRM into angular separation, asymmetry, and (as needed) front∕back components appears to be a productive way to analyze this topic. The similarity of the finding of a greater contribution of angular separation to SRM in the case of speech maskers to findings in the informational masking literature offers further support for the use of this approach.

Whereas the components of the Bronkhorst model have the useful property that the sine and cosine functions are orthogonal, the angular separation and asymmetry components in the revised model have some shared variance. However, the shared variance is low for N-masker arrays with N > 1 due to the left-right cancellation inherent in the asymmetry component. This was confirmed by calculating the correlation coefficient between the angular separation and asymmetry components in each of 30 runs of a procedure in which 20 masker configurations were randomly selected at each N for N = 2, 3, 4, 5, and 6. The mean correlation coefficient (±SE) for the 30 runs was 0.21 ± 0.01. Thus, the shared variance of the angular separation and asymmetry components is less than 5% when multiple interferers are presented.

The model currently has separate versions for speech maskers and noise maskers. Moreover, the speech masker version of the model has not been fitted for configurations with four or more interferers. When the number of speech maskers is very high, one would expect masking efficiency (and SRM) to be similar to that of noise maskers. It is therefore of considerable interest to determine the number of speech maskers at which the overall scaling factor D and the regression coefficients α and β in Eq. 6 will be the same as for noise maskers and whether the transition is gradual or abrupt. The results of experiments reported by Freyman et al. (2004) suggest that as many as 10 talkers may not be sufficient to complete this transition. The authors used an experimental paradigm in which maskers are presented 60° away from a speech target and a copy of the maskers is presented from the same speaker as the target but with a 4-ms delay. This presentation paradigm, which takes advantage of the precedence effect, results in release from masking when the maskers are speech but not when the maskers are noise. The authors found that as the number of speech maskers was increased from 2 to 10, release from masking decreased but was not eliminated. Moreover, the results suggested a gradual reduction in release from masking with increasing numbers of speech maskers. Thus, the values of the regression coefficients and the overall scaling factor D in the speech-masker version of the model are expected to very slowly approach the values in the noise-masker version as the number of maskers is increased.

A key issue affecting the further development and application of the speech portion of the model is informational masking. Specifically, improved models of informational masking may contribute to improved models of spatial release from masking of speech targets by speech interferers. Gallun and colleagues (2008) raised the prospect that it may not be possible to model the role of informational masking in a simple, position-based manner. However, as Gallun et al. point out, their results in a tone detection task may not necessarily apply in other domains such as the speech intelligibility measures that were considered here. It is worth noting that in the model presented here, a good fit was achieved for speech maskers with data collected under conditions in which targets and maskers were spoken by the same talker (two of three data sets) or by talkers of the same gender (one of three data sets). Thus, the current modeling results leave open the possibility that release from both energetic and informational masking of speech targets can be expressed simply as a function of the positions of the maskers.

The results of the model fitting suggest that one can get accurate predictions of SRM using a single equation. For some applications, this may be preferable to computationally intensive approaches such as the binaural speech intelligibility model (BSIM) of Beutelmann and colleagues (2010) or the method of Lavandier and Culling (2010) for predicting binaural speech intelligibility in the presence of a noise interferer. However, it is important to emphasize differences in the uses of these models and in the degree of explanatory power that each model aims to achieve. First, the BSIM is used to account for speech intelligibility in both normal-hearing and hearing-impaired populations, whereas the model presented in this paper is currently restricted to adults with normal hearing. Second, the approach of Beutelmann et al. explicitly incorporates a model of possible neurocomputational mechanisms of the binaural system, whereas the current model does not. Third, the prediction method of Lavandier and Culling (2010) has been used for different target azimuths, whereas the current model and the BSIM have been used to model configurations with the target presented from straight ahead of the listener. On the other hand, the BSIM was tested for one-masker configurations only (Beutelman and Brand, 2006; Beutelmann et al., 2010), whereas SRM can be calculated for multi-masker arrays with the model presented herein. Moreover, the BSIM does not account for informational masking: speech maskers are replaced with noise prior to calculating outputs of the BSIM. In contrast with the BSIM, the prediction method of Lavandier and Culling has been used to predict SRTs with multiple noise maskers (Jelfs et al., 2010). A final point concerning the method of Lavandier and Culling is that it is limited to use with noise maskers. Thus, the model presented herein may be preferred in cases where a computationally simple approach is advantageous and when modeling SRM for up to three speech maskers.

APPENDIX A: LIST OF SPONDEE TARGETS

Airplane

Barnyard

Baseball

Bathtub

Bedroom

Bird nest

Birthday

Blue jay

Bus stop

Cowboy

Cupcake

Daylight

Doorbell

Drawbridge

Drugstore

Duck pond

Eardrum

Eyebrow

Grandson

Greyhound

Hairbrush

Hardware

Highchair

Horseshoe

Hotdog

Ice cream

Inkwell

Jackknife

Jump rope

Mousetrap

Necktie

Oatmeal

Padlock

Playground

Rainbow

Scarecrow

Sidewalk

Sunshine

Toyshop

Woodwork