Comparison of I-131 Radioimmunotherapy Tumor Dosimetry: Unit Density Sphere Model Versus Patient-Specific Monte Carlo Calculations

Abstract

High computational requirements restrict the use of Monte Carlo algorithms for dose estimation in a clinical setting, despite the fact that they are considered more accurate than traditional methods. The goal of this study was to compare mean tumor absorbed dose estimates using the unit density sphere model incorporated in OLINDA with previously reported dose estimates from Monte Carlo simulations using the dose planning method (DPMMC) particle transport algorithm. The dataset (57 tumors, 19 lymphoma patients who underwent SPECT/CT imaging during I-131 radioimmunotherapy) included tumors of varying size, shape, and contrast. OLINDA calculations were first carried out using the baseline tumor volume and residence time from SPECT/CT imaging during 6 days post-tracer and 8 days post-therapy. Next, the OLINDA calculation was split over multiple time periods and summed to get the total dose, which accounted for the changes in tumor size. Results from the second calculation were compared with results determined by coupling SPECT/CT images with DPM Monte Carlo algorithms. Results from the OLINDA calculation accounting for changes in tumor size were almost always higher (median 22%, range −1%–68%) than the results from OLINDA using the baseline tumor volume because of tumor shrinkage. There was good agreement (median −5%, range −13%–2%) between the OLINDA results and the self-dose component from Monte Carlo calculations, indicating that tumor shape effects are a minor source of error when using the sphere model. However, because the sphere model ignores cross-irradiation, the OLINDA calculation significantly underestimated (median 14%, range 2%–31%) the total tumor absorbed dose compared with Monte Carlo. These results show that when the quantity of interest is the mean tumor absorbed dose, the unit density sphere model is a practical alternative to Monte Carlo for some applications. For applications requiring higher accuracy, computer-intensive Monte Carlo calculation is needed.

Introduction

Radiolabeled antibody therapy, including I-131 radioimmunotherapy (RIT), has shown much success in the treatment of malignancies such as non-Hodgkin's lymphoma (NHL).^1,2 The potential exists to further improve the efficacy of these therapies by individualized, dosimetry-based treatment planning. Thus, there is much interest in the accurate assessment of the radiation absorbed dose delivered to normal organs and tumor during therapy.

Conventionally, dosimetry in internal emitter therapy has been based on the S-value formalism developed by the Medical Internal Radiation Dose (MIRD) Committee.³ Here, the absorbed dose to a target region from decays in a given source region is expressed as the product of the cumulated activity in the source region and the source-to-target S-value, which is the absorbed dose to the target region per unit cumulated activity in the source region. The total absorbed dose to a target is then calculated as the sum of contributions from self-irradiation (where target and source regions are the same) and from cross-irradiation (where target and source regions are different). The S-values for such calculations have been predetermined by Monte Carlo methods, originally for the “Reference Man” anatomy⁴ and later for stylized models representing individuals of both sexes at several ages.⁵ A major limitation of using reference S-values for absorbed dose estimation in patients is the potential for a significant difference between organ geometries of the individual patient and those of the models used to generate the S-values. In addition, the models of the human anatomy used to determine S-values do not include tumor, because tumors can be of arbitrary shape, size, and location within the anatomy.

For tumor dosimetry, the conventional approach has been based on a sphere model that assumes that tumors are isolated unit density spheres in an infinite unit density medium. This approach has been implemented in the OLINDA/EXM code,⁶ which is often used for dosimetry calculations in internal emitter therapy. For any of the radionuclides included in the program, S-values for self-irradiation of unit density spheres are available for discrete sphere masses in the range 0.01–6000 g. These S-values have been precalculated based on the most recent evaluation of electron- and photon-absorbed fractions in spheres of various sizes.⁷ Because organ-to-tumor cross-dose depends almost exclusively on the proximity of tumor relative to the organ and because tumor locations are arbitrary, organ-to-tumor S-values cannot be calculated for the general case. Therefore, dose estimates from this approach will account only for the self-dose and not for any cross-dose from any extratumor activity.

To overcome the obvious limitations of the simplistic sphere model, researchers have turned to other more patient-specific approaches to tumor dosimetry.^8–13 One such approach is the dose point-kernel method, which is based on convolving the spatial distribution of activity with tabulated dose point-kernels for a specific isotope.¹⁴ This method tends to be inaccurate when there are tissue inhomogeneities such as at tissue–air and tissue–bone interfaces.¹⁴ Loudos et al.¹⁵ have recently developed a patient-specific dosimetry method based on modifying tabulated dose point-kernels to account for the spatial variation in densities (derived from patient CTs) between source and target voxel centers. This method was not considered in this work as it was felt that the increased accuracy obtained by using a Monte Carlo-based dosimetry model outweighed the relatively modest computation time penalty incurred.

The more sophisticated of the patient-specific tumor dosimetry methods couples 3D anatomical (from MRI or CT) and functional (from SPECT or PET) images of the patient with explicit Monte Carlo radiation-transport calculations. In a recent publication, highly patient-specific tumor dose assessment results for 60 tumors in 20 NHL patients who underwent I-131 tositumomab RIT were reported.¹² Dose assessment was carried out by coupling SPECT/CT imaging data at multiple time points with the Dose Planning Method Monte Carlo (DPMMC) radiation transport algorithm.¹³ The voxel-level calculations were carried out, including deformable image registration to relate tumor voxels that are changing from one time point to another because of tumor regression or deformation. Registered tumor dose-rate maps were integrated over time to obtain the 3D dose distribution, which allowed for calculation of not only mean absorbed dose to the tumor but also other summary measures such as maximum dose and equivalent uniform dose. Such patient-specific dose assessment provides 3D dose distributions and is more accurate than a calculation based on reference S-values. However, 3D imaging data are needed, in addition to high computational requirements. With recent advances in computer power and acceleration of Monte Carlo algorithms, these calculations can be carried out in a research environment, but such calculations are still not practical for the clinic. Therefore, when the quantity of interest is the mean absorbed dose to the target, comparison of results from patient-specific Monte Carlo calculations with results using reference S-values is clinically relevant to determine the level of accuracy that can be achieved with the simpler approach. Previous reports on such comparisons have either focused on organ dosimetry or were limited to simulated tumor geometries.^16,17 The goal of the present study is to compare mean tumor absorbed dose estimates using the unit sphere model incorporated in OLINDA with dose estimates from previously reported Monte Carlo calculations for NHL patients. Unlike previous reports, the present study uses actual patient SPECT/CT imaging data and tumors of varying size, shape, and uptake relative to background for this comparison.

Materials and Methods

Patient imaging data

The imaging data came from patients undergoing 131 I-tositumomab therapy of relapsed or refractory B-cell lymphoma under an approved clinical protocol. The clinical treatment protocol¹ and the SPECT/CT imaging procedure under a research protocol^11,12 have been previously described in detail and are summarized here. The administered diagnostic (tracer) activity was 185 MBq (5 mCi) and the therapy activity ranged from 2.15 to 5.68 GBq (58–153 mCi). For the research study, patients volunteered for imaging at multiple time points on the Siemens Symbia TruePoint SPECT/CT scanner. Patients were imaged three times following the tracer (days 0, 2, and 6) and three times following the therapy (days 2, 5, and 7–9). At each time point, a nuclear medicine specialist with radiology CT training defined the tumor volumes of interests on CT, plane by plane. Data for 60 tumors in 20 patients (13 men and 7 women; age range, 33–81 years) were available for the present calculations. One of these patients (patient 17 in Table 1), who developed human anti-mouse antibodies, had too few SPECT counts to perform dosimetry, so 19 patients with a total of 57 tumors were analyzed.

Table 1.

Comparison of Different Dose Estimation Techniques for 57 Tumors Found in 19 Patients

					Tumor absorbed dose calculated using OLINDA (cGy)		Percentage of difference between doses from Monte Carlo and from OLINDA approach 2
Subject	Tumor name	Initial tumor volume (mL)	Decrease in tumor volumea(%)	Bb	Approach 1 (using baseline tumor mass)	Approach 2 (accounting for mass change)	Comparison to self-dose from Monte Carloc	Comparison to total dose from Monte Carloc
1	Pelvis	400	5	3	125	129	−5	18
2	Paraaortic	409	15	6	229	227	−8	17
3	Inguinal	140	49	7	153	231	−6	7
	Iliac	234	45	7	140	218	−9	5
4	Pelvis big	314	31	15	361	407	−7	6
	Pelvis small	39	27	14	380	387	−5	10
5	Renal	58	62	4	246	274	−5	23
	L paraaortic	34	67	4	201	243	−5	23
	Central	21	50	4	222	252	−5	27
	Hepatic	19	62	3	210	263	−5	28
	Crux	10	57	4	164	234	−4	26
6	L iliac	34	81	10	171	352	−5	9
	Paraaortic	74	65	9	160	335	−10	13
7	R inguinal up	16	42	8	147	188	−2	15
	R inguinal big	71	37	9	190	235	−5	10
	R inguinal small	24	44	4	59	84	−4	23
	L inguinal up	11	39	9	129	183	−1	12
	L inguinal big	114	43	10	187	252	−5	3
	L inguinal small	22	55	7	100	164	−3	14
8	R inguinal lateral	5	80	3	62	135	2	21
	R inguinal medial	7	73	7	175	316	0	13
	R iliac	54	77	6	161	296	−8	13
	R aorta	79	67	7	193	328	−8	10
	R anterior acetab.	34	87	7	148	332	−6	11
	R posterior acetab.	44	85	6	130	325	−6	14
	L acetabulum	31	79	7	142	355	−5	16
9	R inguinal	12	46	4	63	93	−2	18
	L inguinal	19	28	4	71	85	−3	16
	L iliac	35	31	4	81	101	−6	19
10	R anterior iliac	45	50	12	317	380	−6	8
	R posterior iliac	54	56	11	246	348	−7	14
	R inguinal	76	31	11	324	352	−7	2
11	L kidney up	7	53	11	300	503	−1	13
	L kidney down	15	34	10	386	507	−2	10
	R psoas	113	7	10	508	536	−7	5
12	Para vertebral	28	34	4	150	181	−7	26
13	Hilar spleen	7	64	5	213	283	−2	28
	L Dph	36	60	3	154	215	−5	28
	L paraaortic	84	43	4	199	233	−9	24
	L psoas	36	39	3	171	200	−8	20
	R Dph down	6	35	4	164	209	−4	31
	R Dph up	27	49	3	167	210	−5	29
	R paraaortic	97	32	4	211	250	−9	23
14	L neck up	3	20	5	175	180	−1	16
	L neck mid	2	11	7	245	255	0	13
	L neck down	2	53	8	281	308	2	13
15	Central	18	40	5	233	334	−7	27
16	Abdominal	423	18	3	144	150	−5	24
17	Speen	157	25	NA	NA	NA	NA	NA
	L pelvis	135	50	NA	NA	NA	NA	NA
	L Ex	19	66	NA	NA	NA	NA	NA
18	Lung	151	81	2	53	167	−6	30
19	L neck	12	41	4	221	354	−13	13
20	L iliac	7	42	9	235	298	−4	13
	L inguinal inferior	45	43	9	269	351	−6	7
	R iliac	12	32	19	630	670	−1	6
	R inguinal inferior	34	36	15	453	535	−3	3
	R inguinal lateral	5	30	9	263	311	2	15
	R inguinal medial	14	57	13	340	493	0	7
	R inguinal superior	5	53	7	159	246	2	17

^aPercentage of difference in tumor volume defined on first post-tracer SPECT/CT and last post-therapy SPECT/CT (a time period of approximately 15 days).

^bTumor–to–rest-of-the-body activity concentration ratio.

^cDifference calculated as 100×(Monte Carlo −OLINDA)/Monte Carlo.

Tumor time–activity curves

The 3D SPECT reconstruction and activity quantification have been previously described^11,12 and are summarized here. SPECT data were reconstructed with 35 iterations (6 subsets) of 3D ordered-subsets expectations maximization (OSEM) including triple-window-based scatter correction, CT-based attenuation correction, and compensation for 3D depth-dependent detector response. At each time point, the SPECT counts within the CT-defined tumor volume were converted to an activity using a calibration factor. Correction for partial volume effects was carried out by applying volume-dependent recovery coefficients determined from phantom experiments.¹² Tumor time–activity data were generated for both tracer and therapy administrations. For the present study, the rest-of-the-body time–activity curves were not needed, as only the self-dose is determined in the OLINDA calculation. Time–activity data were fitted using a biexponential of the form 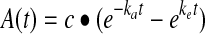.¹⁸ This function was analytically integrated over time to obtain the tumor residence time (cumulated activity divided by the administered activity) for the dosimetry calculations discussed later. The endpoint of the integration was somewhat arbitrarily chosen as 300 hours. The 300 hours time was selected, because the last imaging time point was typically about 150 hours postadministration for tracer and 190 hours postadministration for therapy and extrapolating too far from that time point could lead to greater variance in the results. The residence times when the time–activity curve was integrated to infinity were within 5% of the values obtained by integrating to 300 hours for every tumor except one (patient 11, R psoas in Table 1). The activity clearance of this tumor was unusually slow, resulting in a residence time 53% higher when integrated to infinity. The 300 hours integration is consistent with the previous study in which Monte Carlo dose-rate maps were integrated up to this time to obtain the dose map.¹²

Although much emphasis was placed on accurate SPECT activity quantification using state-of-the-art hybrid imaging and 3D OSEM reconstruction, inaccuracies can remain because of approximations made when correcting for physical factors, uncertainty in tumor volume determination, SPECT-CT misregistration, and the limited imaging time points. These inaccuracies will have a similar impact on the two absorbed dose calculation methods compared in the present work, because tumor time–activity data were generated in the same manner for both calculations.

Tumor dosimetry using the unit density sphere model

For tumor dosimetry, the unit density sphere model implemented within OLINDA was used. Here, tumors are approximated as unit density spheres with uniformly distributed activity. The precalculated OLINDA sphere-model S-factors for I-131 were obtained for all available sphere sizes ranging from 0.01 to 6000 g. These S-values were plotted vs. sphere mass and the fitted function was used to determine the S-value for any mass. The dose equation based on the MIRD formalism can be expressed as follows:

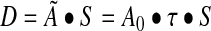(1)

Here, τ is the residence time, Ã is the cumulated activity, A₀ is the patient's administered activity, and S is the dose per unit cumulated activity.

The dosimetry calculation was carried out with and without accounting for changes in tumor size measured at the multiple imaging time points. In the first approach, the absorbed dose was estimated for a constant tumor mass corresponding to the outline defined on the day 0 post-tracer SPECT/CT (baseline mass). The tracer residence time was determined by integrating the tracer time–activity curve from 0 to 300 hours, and the therapy residence time was determined by integrating the therapy time–activity curve from 0 to 300 hours. To estimate the mean tumor absorbed dose from the tracer administration, the S-value corresponding to the baseline tumor mass and the tracer residence time were used in Equation 1. To estimate the mean tumor absorbed dose from the therapy administration, the S-value corresponding to the baseline tumor mass and the therapy residence time were used in Equation 1.

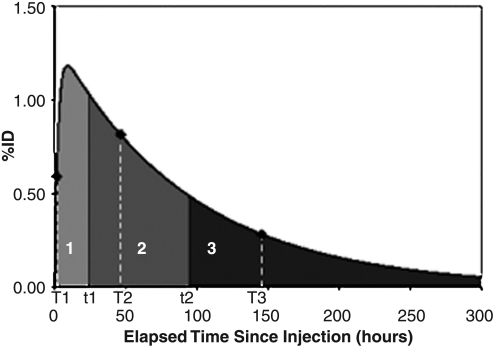
The availability of SPECT/CT imaging data and CT-defined tumor outlines at multiple time points favor splitting the OLINDA calculation over multiple time periods, which was done in the second approach. As imaging was carried out at three time points, three time periods were used for the calculation. A typical tumor time–activity curve with the three time periods (0 to t₁, t₁ to t₂, t₂ to 300 hours) is shown in Figure 1. Here, T₁, T₂, and T₃ are the three imaging time points, t₁ is the midpoint between T₁ and T₂, and t₂ is the midpoint between T₂ and T₃. The total dose was calculated as the sum of the dose delivered over each of the three periods:

(2)

FIG. 1.

A typical tumor time–activity curve showing the biexponential fit and the three time periods used for the OLINDA calculation over multiple time periods to account for the measured changes in tumor size. The %ID is the percentage of activity normalized by the injected activity.

where τ₁, τ₂, and τ₃ are the residence times for the three time periods determined by integrating the time–activity curve over each period, and S₁, S₂, and S₃ are the OLINDA S-values corresponding to the tumor masses outlined at imaging time points T₁, T₂, and T₃, respectively. This calculation was carried out separately for the tracer and the therapy imaging data.

The dosimetry results from the OLINDA calculation carried out over multiple time periods according to Equation 2 were used for the comparison to the previous Monte Carlo results as this approach is more consistent with how the SPECT/CT data were previously utilized (SPECT/CT images and tumor outlines from each of the time points were input to the DPMMC algorithm to generate corresponding tumor dose-rate maps).¹²

Results

Typical patient SPECT/CT images with tumor outlines are shown in Figure 2. The tumor dosimetry results for all tumors are given in Table 1, together with other relevant information useful for interpreting the dosimetry results. The tumor-to-background activity concentration ratio, B, is the activity per voxel in the tumor divided by the activity per voxel in the rest of the body (“rest of the body” was defined as the total body section within the SPECT camera field of view minus the tumor). Also given in Table 1 are the baseline tumor volume defined on the first SPECT/CT and the decrease in tumor volume between this time point and the last SPECT/CT time point. The study included a wide range of tumor sizes (initial volume, 2–423 mL), tumor locations, and a wide range of B-values (2–19). Hence, there was a wide range in the level of cross-irradiation. The mean tumor absorbed dose results given in Table 1 are the total delivered from both the tracer and therapy administrations. Results from the OLINDA calculation using a baseline tumor mass and results from the OLINDA calculation carried out over the multiple time periods, accounting for changes in tumor mass, are given. Tumor absorbed doses calculated accounting for the mass changes were almost always higher than the absorbed doses calculated assuming a baseline tumor mass. The difference between the two OLINDA calculations ranged from −1% to 68%, with a median difference of 22%. The mean absorbed dose accounting for mass change was significantly higher than the mean absorbed dose without accounting for this change (p<0.001, paired t-test).

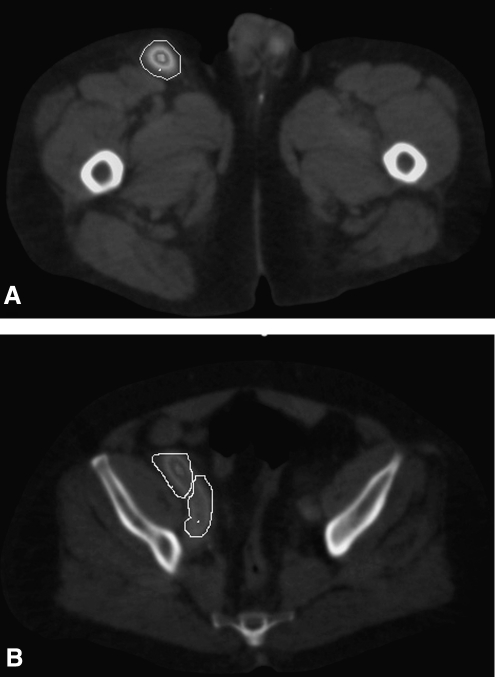
FIG. 2.

SPECT/CT images with outlines for inguinal tumor (A), anterior iliac tumor (B, upper outline), and posterior iliac tumor (B, lower outline). Images are for subject 10 in Table 1.

Next, the comparison between the mean tumor absorbed dose results from OLINDA and the previously reported Monte-Carlo-based, patient-specific calculation is presented in Table 1. (Note that results from the OLINDA calculation over multiple time periods were used for this comparison.) OLINDA results were compared with both the self-dose and the total dose (sum of self-dose and cross-dose components) from the Monte Carlo calculation. Almost always, the OLINDA results were higher than the Monte Carlo self-dose, but only slightly. Although the mean absorbed self-dose from OLINDA was significantly higher than the mean absorbed self-dose from Monte Carlo (p<0.001, paired t-test), the difference between these two calculations was small, ranging from −13% to 2%, with a median difference of only −5%. The OLINDA results were always lower than the Monte Carlo total dose, and the difference between the two ranged from 2% to 31%, with a median difference of 14%. The mean absorbed dose from OLINDA was significantly lower than the mean absorbed total dose from Monte Carlo (p<0.001, paired t-test).

Discussion

For most of the 57 tumors, significant tumor shrinkage was measured during the SPECT/CT imaging. Because of the inverse relationship between absorbed dose and mass, the OLINDA calculation carried out over multiple time periods gave significantly higher (up to 68%) absorbed doses than the calculation assuming baseline tumor masses. Conventionally, tumor dosimetry in internal emitter therapy has been carried out assuming a constant tumor mass, typically obtained from a diagnostic CT study performed before the treatment. The present results demonstrate the inadequacy of such an approach for dosimetry of malignant lymphoma, which can have dramatic shrinkage within days of the treatment.^12,19 When tumor volume information from multiple time points is available, a reasonable approach is to carry out the OLINDA calculation over multiple time periods as in the present study.

The unit density sphere model implemented within OLINDA assumes all tumors are spherical, whereas the DPM Monte Carlo calculation utilizes the actual tumor contour outlined on CT. In all cases, the DPMMC self-dose was lower than the OLINDA calculation, because in reality tumors are nonspherical (see e.g., Fig. 2) and more beta particles can escape from a nonspherical geometry without depositing all of their energy compared with a spherical geometry of the same volume. However, the relatively good agreement between the OLINDA results and the DPMMC self-dose results (see Table 1) shows that the sphere approximation is reasonable and shape effects are not a major source of error. This is due to the I-131 beta emission, which has a mean energy of 192 keV and has a short range (2.3 mm²⁰ in water) compared to the size of the tumors of the present dataset (smallest radius around 8 mm, 16 times larger than the range of the beta particle). Shape effects may lead to more errors in calculations for Y-90 RIT, which has a higher energy beta emission (mean energy of 938 keV), leading to a greater range in water (11.3 mm²⁰). In Table 1, the comparison between OLINDA results and the total DPMMC absorbed doses showed significant differences (up to 31%). As expected, the total DPMMC dose was higher, because the sphere model ignores the contribution from activity outside the sphere. In general, the difference between results of DPMMC and OLINDA increases as the tumor-to-background activity concentration ratio (B-value in Table 1) decreases because of the increasing contribution from cross-irradiation. There are, however, exceptions, because the contribution to tumor dose from cross-irradiation depends not only on the B-value but also on the size of the tumor and the proximity of the tumor to structures with significant uptake. As calculated, the B-value assumes a uniform activity distribution in the rest of the body, but in reality there is enhanced I-131 uptake in the liver, kidneys, spleen, and heart. In addition, the contribution from cross-irradiation is very much dependent on the photon energy, and hence, the trends observed in the present I-131 study may not be applicable to therapies with other radionuclides.

In a previous study, the photon contribution to tumor dose from I-131 activity outside the tumor was calculated by Monte Carlo for simulated tumors positioned in the Reference Man geometry.¹⁶ The underestimation of tumor dose due to neglecting this contribution was found to be in the range 10%–20%, which is comparable to the results of the present study. In a more recent study, focusing mainly on normal organ dosimetry Divoli et al.¹⁷ reported on the differences between results obtained using patient-specific Monte Carlo methodology and results obtained using the reference S-values implemented in OLINDA. Individual patient's CT images (total of 9 patients) were used to define the normal organs, whereas published biodistribution data were used to assign cumulated activities. When a mass correction (available in OLINDA) was used to account for differences in organ masses between the patient and the standard model, good agreement (within 5%) was demonstrated. For normal organs, agreement between the two calculations can be expected to be better than the agreement for tumor, because the cross-irradiation contribution is included in the OLINDA calculation for normal organs. The work by Divoli et al. also included tumor, but was limited to two small (7 g each) spherical tumors, artificially placed in the liver and the lung. The good agreement (<5%) between Monte Carlo and OLINDA in that reported for tumor was attributed to the limited nature of the study. Tumors of different size, shape, and varying levels of uptake relative to background were not investigated as in the present work.

Conclusions

For NHL patients treated with I-131 tositumomab RIT, the mean tumor absorbed doses determined using the unit density sphere model in OLINDA were compared with previously reported results from explicit Monte Carlo simulation using the DPMMC algorithm. SPECT/CT imaging data from multiple time points were used in both calculations. The dataset included tumors of varying sizes and shapes as well as varying uptake relative to the rest of the body. There was good agreement when the OLINDA results were compared with the self-dose component from the Monte Carlo calculation, indicating that assuming a spherical shape for the tumor was not a major source of error. However, because the sphere model ignores cross-irradiation, this calculation significantly underestimated (median 14%, range 2%–31%) the total absorbed dose compared with Monte Carlo. Although the tumor dosimetry calculation using the sphere model is much more practical than the computer-intensive Monte Carlo method, its level of accuracy may not be acceptable for some treatment planning applications.

Acknowledgments

This work was supported by grant 2R01 EB001994 awarded by the National Institutes of Health, United States Department of Health and Human Services (Bethesda, MD).

Disclaimer

The contents of this article are solely the responsibility of the authors and do not necessarily represent the official views of the funding agencies.

Conflict of Interest

The authors declare that they have no conflict of interest.