Timing molecular motion and production with a synthetic transcriptional clock

Abstract

The realization of artificial biochemical reaction networks with unique functionality is one of the main challenges for the development of synthetic biology. Due to the reduced number of components, biochemical circuits constructed in vitro promise to be more amenable to systematic design and quantitative assessment than circuits embedded within living organisms. To make good on that promise, effective methods for composing subsystems into larger systems are needed. Here we used an artificial biochemical oscillator based on in vitro transcription and RNA degradation reactions to drive a variety of “load” processes such as the operation of a DNA-based nanomechanical device (“DNA tweezers”) or the production of a functional RNA molecule (an aptamer for malachite green). We implemented several mechanisms for coupling the load processes to the oscillator circuit and compared them based on how much the load affected the frequency and amplitude of the core oscillator, and how much of the load was effectively driven. Based on heuristic insights and computational modeling, an “insulator circuit” was developed, which strongly reduced the detrimental influence of the load on the oscillator circuit. Understanding how to design effective insulation between biochemical subsystems will be critical for the synthesis of larger and more complex systems.

In biology, chemical oscillators control the timing of cellular processes and provide day-night rhythms, as in circadian clocks (1). In the past decade, synthetic clock systems with a reduced number of components have been constructed in vivo in order to study the design principles underlying oscillatory behavior (2–7). Most of these artificial gene regulatory systems are still relatively complex and difficult to understand quantitatively, as they make use of the full transcriptional and translational machinery of their host organisms. The cellular environment also puts significant limits on the types of chemistries that these oscillators can orchestrate. At the other extreme, inorganic oscillators can be quite robust, but difficult to systematically couple to a wide range of downstream processes (8, 9).

Synthetic cell-free biochemical circuits offer interesting possibilities for the design of complex molecular processes, both because of their relative simplicity and their potential applicability for controlling a wide range of in vitro chemistries (10–16). Systems whose behavior is dependent on DNA templates are particularly promising because they can be systematically rewired to obtain new functionalities. Recently, a simple oscillator based on only transcription and degradation in vitro has been demonstrated (17), raising the prospect of orchestrating the temporal expression of other synthetic chemical processes.

In the present work we demonstrate how this synthetic transcriptional circuit can be used as a molecular clock for timing biochemical processes in vitro. Specifically, we address the question of how these downstream processes influence the performance of the upstream “core oscillator,” and how this “retroactivity” (18–20) can be reduced.

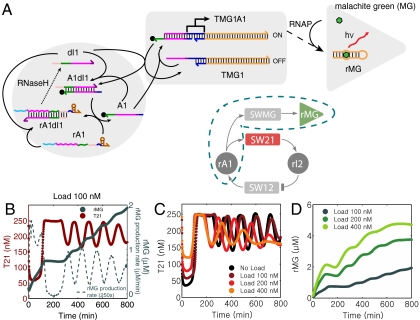
As a simple model for this general problem, we used the oscillator to drive periodic conformational changes of a DNA nanomechanical device called “DNA tweezers” (21). These tweezers, comprised of two double-helical domains connected by a hinge, have two single-stranded “hands” that can bind to a targeted oligonucleotide and thereby close the tweezers. By designing tweezer hand sequences to target different intermediate species of the transcriptional circuit, we evaluated several methods for coupling the nanodevice to the oscillator. Increasing the tweezer concentration put a load on the oscillator that considerably distorted its behavior. In order to improve the resilience of the clock with respect to the load, we developed an “insulator circuit” that put only a small load on the oscillator, yet produced a new amplified signal capable of driving larger loads. A similar architecture was employed to periodically switch on or off synthesis of a functional RNA structure, an RNA aptamer for malachite green (22).

Problem Formulation

As will be discussed in more detail below, our transcriptional circuits consist of gene templates (“genelets”), from which RNA molecules are produced by in vitro transcription reactions. These RNA molecules can act as regulators of transcription from other genelets. Thus, several genelets may be coupled together to form simple molecular circuits. Before introducing the molecular details of our experimental system we first illustrate a model problem, which will help to highlight the challenges that arise when coupling dynamical molecular systems.

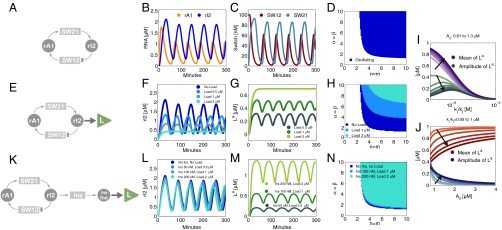
A simple oscillator motif is shown in the diagram of Fig. 1A. Genelets SW21 and SW12 are coupled via inhibiting and activating RNA species, rI2 and rA1, respectively. The major features of the dynamical behavior of this circuit can be captured by the following simple model, which was proposed previously in (17):

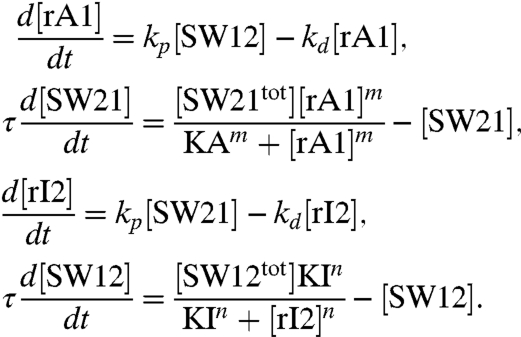Fig. 1.

Circuits and simulations for a simple oscillator system coupled to a load. Unless otherwise noted, the parameters used for all simulations in Fig. 1 are: k_p = 0.05/s, k_d = 0.002/s, KA = KI = 0.5 μM, [SW21^tot] = [SW12^tot] = 100 nM, m = n = 5, τ = 500 s, k_r = 0.006/s, k_f = 7.9·10³/M/s. For the insulating gene, the RNA output production rate is 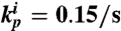, and the RNA degradation rate is 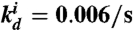. The binding rates of the insulator RNA output and the load are chosen as 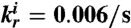and 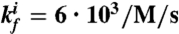. (A): Diagram for the simple model for the oscillator. (B): Time traces for the oscillator species rA1 and rI2. (C): Time traces for the oscillator species SW12 and SW21. (D): Oscillatory domain of the simple model as a function of the nondimensional parameters α = β and m = n. (E): Oscillator scheme with consumptive load coupled to rI2. (F, G): Time traces for the oscillator and load for consumptive coupling on rI2. (H): The oscillatory domain shrinks as a function of [L^tot] for the consumptive coupling to rI2. (I): Mean and amplitude of the active load [L^a] as a function of the ratio of k_r and k_f, when the driving input is [rI2] = A₀ + A₁ sin ωt, with A₀ varying between 0.81 (light color) and 1.3 μM, and A₁ = .8 μM, ω = 0.001 rad/s. (J): Mean and amplitude of the active load signal [L^a] as a function of the baseline A₀ for the input oscillating signal, for ratios k_r/k_f varying between 0.05 and 1 μM. For (I) and (J), [L^tot] = 1μM (K): Oscillator scheme with consumptive insulating circuit and consumptive load. (L, M): Time traces for the oscillator and load when the insulating genelet is used to amplify rI2. (N): The perturbation of the oscillatory domain is reduced by using a small amount of an additional genelet (insulator) that amplifies the oscillatory signal.

RNA molecules rA1 and rI2 are produced from active switches with rate k_p and degraded with rate k_d. The effectiveness of the RNA species in activating or repressing the switches is modeled by Hill functions with the thresholds KA and KI, and Hill exponents m and n. The relaxation constant τ scales the speed of the switches’ dynamics. The concentration of each species oscillates for suitable choices of the parameters (Fig. 1 B and C). The existence of an oscillatory solution can be shown to be equivalent to the instability of the sole equilibrium point for the system (SI Appendix, Section 23.1). By linearizing the dynamics around the equilibrium, and by examining the eigenvalues of the Jacobian, it is possible to numerically assess the oscillatory domain. In particular, this domain is defined by the Hill exponents m and n, by the ratio of time constants k_d·τ (which must be of order unity), and by the lumped parameters β = (k_p/k_d)[SW21^tot]/KI and α = (k_p/k_d)[SW12^tot]/KA. Fig. 1D shows the numerically computed oscillatory domain when m = n and α = β.

We will now use one of the oscillator component species to bind to a “load” molecule L, driving the periodic formation of an “active” complex L^a. We assume that [L^tot] = [L] + [L^a]. A distinction will be made as to whether the oscillator component driving the load is irreversibly consumed or not by binding to the load. As an example, we will consider the case where the species rI2 is coupled to the load L (cf. Fig. 1E). The active form of the load is produced according to the second order reaction: , and in the consumptive case it decays to its inactive form via 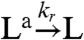. If the mass of the oscillator species rI2 is not consumed, the previous reaction is replaced by 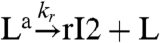. In both cases, the concentration dynamics for L are:

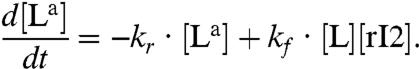[1]

The rI2 concentration dynamics are perturbed by the new reactions:

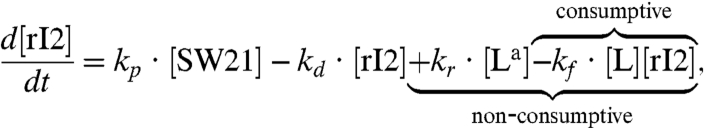[2]

where the braces highlight the additional terms appearing in the consumptive and nonconsumptive coupling cases.

To simplify the discussion, we assume that the kinetics described in Eq. 1 are much faster than the oscillator period, and [L^a] can be replaced by a quasi steady-state concentration

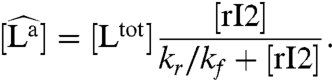[3]

Numerical simulations show that for typical parameters the quasi steady-state solution Eq. 3 is a very good approximation of the full load dynamics.

We are now interested in two aspects of the coupled system: (i) how well can the load be driven by the oscillator? (ii) how strongly are the dynamics of the core oscillator affected by the presence of the load? As can be seen from Eq. 3, the load signal depends on [rI2] and the parameters k_r and k_f. Suppose [rI2](t) ≈ A₀ + A₁ sin ωt: then, the amplitude and mean of the load signal vary with k_r/k_f and A₀ as shown in Fig. 1 I and J. For [rI2] ≪ k_r/k_f, only a small amount of load can be driven, whereas for A₀ - A₁≫k_r/k_f the mean value of the driven load is high, but the amplitude is low. For a given A₀ and A₁, the optimum ratio of k_r and k_f is given by , for which the amplitude of the load oscillations is maximum.

Under the assumption that the load dynamics are well approximated by Eq. 3, we can write new expressions for the perturbed dynamics of rI2. For the consumptive case we have: 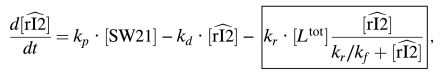4 where the box highlights the quasi steady-state perturbation term. This term is bounded by the constant k_r[L^tot], and converges to it for large values of 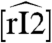. Loosely speaking, adding the load is similar to introducing a new degradation term in the rI2 dynamics, directly proportional to the total load amount. In effect, this reduces the magnitude of parameters α, β that define the oscillatory domain of the system.

While the approximated trajectory Eq. 4 provides qualitative insight on the system behavior, in Fig. 1 F and G we display the full numerical simulations of the five ordinary differential equations describing the oscillator with load, which shows the rI2 and load trajectories for increasing [L^tot]. The oscillatory domain of the system shrinks with increasing load as shown in Fig. 1H. For the nonconsumptive case, the sum of the perturbation terms is equal to zero (this is the quasi steady-state assumption). Therefore, in this approximation the dynamics of the oscillator are actually unaffected by the presence of the load. This conclusion is also supported by numerical simulations (SI Appendix, Fig. S50).

Our results on load coupling obtained with the simple model may be summarized as follows: in order to drive a large amount of load at a high amplitude, the core-oscillator species to which the load is coupled should be present at a high concentration with a comparably high amplitude. Furthermore, the coupling should occur with appropriately fast binding rates. If the load is coupled consumptively, the dynamics of the core oscillator are perturbed by an additional effective degradation term that drives the system out of its oscillatory domain—typically resulting in lower oscillation amplitudes. If the load is coupled nonconsumptively to the oscillator, and rates k_r, k_f are large enough to ensure quasi steady-state behavior, there is no detrimental back-action of the load. These conclusions—though made under slightly different assumptions—are consistent with the results of a theoretical analysis of the problem (19), where it was shown that the retroactivity of a load to its source can be minimized by choosing appropriately fast binding rates and by reducing the total load amount.

In practical cases it may be impossible to couple a signaling molecule to the desired load nonconsumptively. It may also not be possible to adjust the binding rates arbitrarily to provide small retroactivity and good signal transmission. If we fall in the consumptive load coupling case with limited freedom in tuning k_f and k_r, Eq. 4 shows that the only way to bound the perturbation on rI2 is to reduce [L^tot]. We can overcome this limitation by using rI2 to activate another genelet, whose RNA output amplifies the oscillator signal and can drive larger amounts of [L^tot] (Fig. 1K). The genelet effectively acts as an insulator and will be denoted as Ins. We assume that the genelet Ins binds to rI2 consumptively: 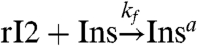, 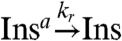. The active genelet Ins^a produces an RNA output as the oscillator switches: 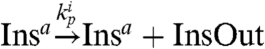. We finally assume that the RNA output, which in practice amplifies the oscillatory signal, in turn activates the desired load by the usual consumptive binding mechanism: 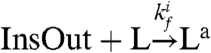, 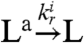. The RNA output is also degraded as the other RNA species in the system, with a rate constant 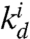. (The full set of dynamic equations are reported in the SI Appendix, Section 23.3).

As shown in Fig. 1 L and M, by using a small amount of insulator genelet it is possible to drive large amounts of load introducing negligible perturbations. The oscillatory domain of the system is virtually unaffected by the load (Fig. 1N).

Molecular Implementation of the Oscillator

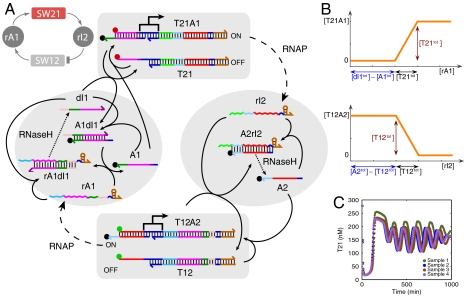
An in vitro biochemical implementation of the abstract oscillator scheme of Fig. 1A is shown in Fig. 2. Building on earlier work on transcriptional circuits (23–25), the oscillator (17) utilizes in vitro transcription by T7 RNA polymerase (RNAP) from double-stranded DNA templates (genelets) with a T7 promoter sequence (Fig. 2A). Switch SW21 is realized as a genelet whose noncoding strand contains a nick in the promoter region and is extended by a short single-stranded “toehold” on the 3′ end. This part of the promoter—the activator strand A1—can be displaced from the template by branch migration (21, 26, 27) using a complementary DNA or RNA molecule. Transcription from the remaining promoter fragment only occurs with low efficiency (24, 28). In this way, transcription can be switched on and off by addition or removal of promoter fragment A1, respectively. Switch SW12 works analogously, with A2 as an activator strand.

Fig. 2.

(A): Operation scheme of the transcriptional oscillator system. Colors indicate complementary DNA and RNA domains. Sequences are given in SI Appendix, Section 1. When switch SW21 is turned on, RNA polymerase (RNAP) transcribes regulatory RNA (rI2) from the genelet template T21. RNA strand rI2 inhibits transcription from switch SW12 by removal of DNA strand A2 from template T12, resulting in an incomplete promoter region. On the other hand, RNA species rA1, which is transcribed from SW12, activates transcription from SW21 by releasing A1 from the A1·dI1 complex. RNA levels in the system are controlled by RNase H-mediated RNA degradation. By fluorescently labeling strand T21 with Texas Red or TYE665 (red dot), strand T12 with TAMRA or TYE563 (green dot), and activation strands A1 and A2 with Iowa Black RQ quenchers (black dots), the genelet states can be monitored by fluorescence measurements—high signals correspond to low transcription activity. (B): Thresholds are set by adding threshold strands dI1 and A2 in excess over A1 and T12, respectively. In a typical experiment, the concentrations were [T21^tot] = 250 nM, [A1^tot] = 250 nM, [dI1^tot] = 700 nM, [T12^tot] = 120 nM, [A2^tot] = 500 nM. (C): Oscillator traces showing T21 levels for typical oscillations obtained in several, separate experiments. Note the good reproducibility of the oscillations from trial to trial, although different enzyme batches yield somewhat different core oscillator behavior. T12 has lower amplitude oscillations and is not shown; see SI Appendix, Section 9.

The feedback coupling between SW21 and SW12 is achieved as follows: the transcript of genelet SW21—RNA species rI2—is designed as the complement of the downstream genelet’s activator strand A2, and hence deactivates transcription from SW12. On the other hand, the transcript of SW12—RNA species rA1—activates SW21 via an indirect mechanism: genelet SW21′s activator strand A1 is initially sequestered by the partially complementary DNA oligonucleotide dI1. Strand rA1 can displace dI1 from the duplex A1·dI1, which releases the activator strand A1, and therefore switches on transcription from SW21.

In order to obtain dynamical behavior from the circuit, RNA signals must be degraded as well as produced. This function is served by Escherichia coli ribonuclease H (RNase H), which selectively degrades the RNA part of DNA-RNA hybrids occurring in the network. Hence, the system is based on the action of only two essential enzymes: RNAP is responsible for RNA production, and RNase H controls degradation.

As indicated by the phase diagrams for the simple model in Fig. 1, oscillations require inhibition and activation with high Hill exponents—or thresholding with a steep response function. Experimentally, thresholding is realized using an ultrasensitive mechanism (29, 30). To this end, dI1 and A2 are added in excess over their complementary counterparts A1 and T12, respectively. By way of pathways and energetics, RNA activator strands rA1 then prefer binding to free dI1 over binding to the same strand within the complex A1·dI1. Similarly, given the choice between free A2 and A2 bound to template T12, inhibitor strands rI2 will preferentially bind to the free DNA species. As indicated schematically in Fig. 2B, the concentrations of dI1 and A2 can therefore be used to set the activation/inhibition thresholds for the transcriptional switches SW21/SW12, which crucially influence the dynamical behavior of the feedback network.

The activation states of the oscillator templates T12 and T21 are read out using fluorescent probes attached to the 5′ end of their regulatory domains. When an activator strand (A1 or A2, respectively) labeled with a quencher is bound to the template (forming transcriptionally active complexes T12·A2 or T21·A1), fluorescence is quenched. Low fluorescence therefore corresponds to an active genelet, whereas high fluorescence corresponds to an inactive genelet. A series of typical oscillatory fluorescence traces are shown in Fig. 2C.

Depending on the choice of parameters, such as DNA strand concentrations, the circuit displays stable or oscillatory behavior. Large oscillations typically are slow, whereas faster oscillations usually have a smaller amplitude swing. The frequency and amplitude of the oscillations can also be influenced by changing the RNAP and RNase H concentrations, which set the time scales for RNA production and degradation. In the experiments described here, an “operating point” was chosen at which the oscillator typically exhibits 4–6 large amplitude oscillations (cf. Fig. 2C). The batch reaction eventually collapses, presumably due to exhaustion of rNTPs and build-up of waste products. The oscillations are started in an initial state where genelet SW12 is active and SW21 is switched completely off—corresponding to a large initial fluorescence signal from this genelet. The system typically goes through a lag phase, during which RNA activator rA1 is produced until SW21 is activated sufficiently and the oscillations begin.

Driving a DNA Nanodevice with the Oscillator

In order to study the coupling of the oscillator to a load process, we used it to clock the motion of a simple DNA-based nanodevice, the well known DNA tweezers system (21). DNA tweezers are a nanomechanical structure, which consists of two rigid double-stranded “arms” of 18 bp length connected by a 4 nt long single-stranded molecular “hinge.” Hybridization of single-stranded extensions of these arms—the “hands”—with a complementary “effector” strand brings the tweezers into a “closed” conformation. The sequences of the tweezer hands can be chosen freely to target any selected nucleic acid strand as the effector. Removal of the effector strand by a complementary strand via branch migration restores the original configuration of the device. Alternating addition of effector and antieffector results in a cyclical motion of the tweezers.

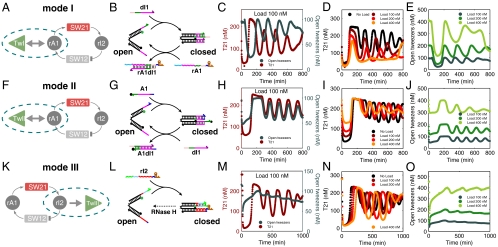
Several possibilities for coupling the tweezers to the oscillator system were explored (Fig. 3 and SI Appendix Figs. S3–S6). Three coupling modes use DNA strands for closing the tweezers: coupling mode I uses dI1 to close the tweezers, and RNA strand rA1 to open them (Fig. 3A). Mode II utilizes strand A1 for closing and strand dI1 for opening (Fig. 3F), while mode II* (reported in the SI Appendix, Figs. S4 and S41) uses strand A2 for closing and RNA rI2 for opening the tweezers. Other possibilities are to close the tweezers with RNA species rI2 (mode III, Fig. 3K) or rA1 (mode IV, see SI Appendix, Figs. S6 and S43) and open them by RNA degradation by RNase H. The various coupling mechanisms differ with respect to the concentration levels and dynamics of their effector strands (i.e., mean A₀ and amplitude A₁ in the simple model), in the extent and potency of spurious binding due to sequence similarity, or in the degree of desired and undesired interactions with enzymes.

Fig. 3.

Three different ways of coupling a load to the oscillator. (A): In the simple model scheme, mode I couples to the rA1 node. Dashed line encloses the subcircuit whose mechanistic details are provided to the right. (B): Molecularly, mode I uses dI1 to close the DNA tweezers, and rA1 to open them. (C): Oscillator traces (T21 levels) and mode I tweezers oscillations superimposed for a load of 100 nM tweezers. (D): Load dependence of the core oscillator (load 0–400 nM). (E): Corresponding oscillations of the tweezers load. (F): In the simple model scheme, mode II also couples to the rA1 node. (G): On the molecular level, mode II uses A1 to close the tweezers and dI1 to open them. (H): Oscillator traces and mode II tweezers oscillations superimposed for 100 nM load. (I, J): Oscillations of the core oscillator and the tweezers load for different load concentrations. (K): In the simple model, mode III couples to the rI2 node. (L): Mode III uses rI2 to close the tweezers and RNase H to open them. (M): Oscillator traces and mode III tweezers oscillations superimposed for 100 nM load. (N, O): Oscillations of the core oscillator and the mode III tweezers signal for different load concentrations.

As in previous experiments (21, 31), the tweezers are also labeled with a distinct fluorophore-quencher pair—open tweezers display a high fluorescence, whereas closed tweezers exhibit low fluorescence—allowing tweezer and genelet state to be measured simultaneously. (See SI Appendix, Sections 3 to 9 for information on sample preparation and normalization of fluorescence traces to estimate species’ concentrations). As can be seen from the fluorescence traces shown in Fig. 3 C and H, coupling modes I and II can indeed be used to drive the motion of the DNA tweezers. The different phase relationships between the tweezers and T21 oscillator signals in modes I and II are easily explained. In mode I, the tweezers are opened whenever rA1 is abundant. In the oscillator circuit, however, rA1 displaces A1 from the A1·dI1 duplex, and therefore activates switch SW21. High tweezers fluorescence (open state) therefore corresponds to low SW21 fluorescence (on state), and vice versa, resulting in a phase shift by a half period of the oscillator. In mode II, an abundance of rA1 releases A1 molecules in the same way as in mode I. In this case, however, A1 is used to close the tweezers and therefore low tweezers fluorescence coincides with low fluorescence of SW21.

In contrast, modes III and IV (Fig. 3M, SI Appendix Figs. S42 and S43) do not lead to a satisfactory opening and closing motion—the tweezers remain almost fully open. Concerned that RNase H could only partially degrade RNA fuel strands when complexed with the DNA device, resulting in “poisoned” DNA tweezers that are always open, we examined interactions between enzymes and tweezers in the absence of the core oscillator (SI Appendix, Section 19). Surprisingly, several (if not all) tweezers designs served as substrates for promiscuous RNAP activity that caused tweezers opening. In the case of modes I and II, RNase H eliminated this effect and restored function to the DNA closing strand. However, in the presence of RNase H, the RNA closing strands for modes III and IV were not fully effective, helping to explain the poor performance of these modes when driven by the oscillator circuit. In addition to partial degradation of RNA closing strands, it was found in Kim and Winfree (17) that even in the core oscillator, RNase H leaves partial degradation products that can accumulate to reach micromolar concentrations; these are predicted to have sequences complementary to one hand of the tweezers for both modes III and IV.

Mode II* tweezers also failed to satisfactorily open and close in response to the core oscillator (SI Appendix Fig. S41). In this case we could attribute the lack of function to the concentration dynamics of the oscillator. At our operating point rI2 concentrations are high, presumably sequestering A2 most of the time (in fact, on average only 20 nM of SW12 are active, cf. SI Appendix, Fig. S19). Hence, the closing strand concentrations are simply too low in this mode to actuate tweezers efficiently.

Influence of Load on the Oscillator’s Performance

In order to investigate the influence of the load on the core oscillator, we studied the behavior of the coupled system for increasing load concentrations. As can be seen in Fig. 3, increasing the load generally affects both amplitude and frequency of the oscillator. Superficially, the influence on the oscillations is smaller for coupling mode II (Fig. 3I) than for coupling mode I (Fig. 3D). However, a smaller fraction of the total tweezers population is actually switched in this coupling mode, as can be judged from the small amplitude of the oscillations (Fig. 3J). In mode I, a larger fraction of the DNA nanodevice is actuated by the oscillator (Fig. 3E), which is accompanied by a stronger distortion of the oscillator dynamics. This behavior is related to the fact that in mode I the tweezers are coupled to oscillator species dI1, which has a higher abundance than A1 used for mode II.

Even though coupling modes III and IV do not lead to a satisfactory oscillatory actuation of the tweezers, the dynamics of the oscillator itself are strongly affected by the presence of the DNA device (Fig. 3N, SI Appendix, Figs. S42 and S43). This finding is consistent with the hypothesis that partially degraded transcripts bind to one hand, keeping the tweezers open, while the other hand is still active in binding new transcripts and serving as a substrate for RNase H.

As explained in detail in the SI Appendix, Section 16, due to the specific concentration dynamics of the core-oscillator strands, mode IV affected the oscillations more drastically than all other modes. For a similar reason, mode II* had only a negligible effect, but also resulted in very inefficient load coupling.

Heuristically, much of the behavior of the oscillator under load can be understood in terms of changes of threshold strand concentrations [A2] and [dI1]. For instance, in mode I, tweezers are closed by dI1 and opened in a strand displacement reaction by rA1 (cf. Fig. 3B). As can be seen from the reaction scheme in Fig. 2A, in the core-oscillator strand A1 is similarly bound by dI1 and freed by a strand displacement reaction with rA1. An increase in the concentration of mode I tweezers therefore roughly mimics an increase in [A1], which in turn corresponds to an effective reduction of the threshold set by [dI1]. By contrast, in mode II (Fig. 3G) a fraction of activator strands A1 is bound to the tweezers rather than to template T21. Dynamically, the effective reduction in [A1] should therefore be analogous to an increase in threshold [dI1]. Finally, an increase of tweezers concentrations in mode III (Fig. 3L) is similar in effect as an increase in [A2], as rI2 interacts with A2 in the core oscillator. We experimentally confirmed this heuristic argument by changing the concentrations of threshold strands in the core oscillator and found that indeed this reproduces most of the general trends in amplitude and period observed also in Fig. 3 D, I, N (see SI Appendix, Section 21 and Fig. S38). Similar reasoning can be applied to all other coupling modes.

Referring to the simplified oscillator model, our observations on load coupling may—with some caution—be interpreted as follows: the amplitude of the load oscillations strongly depends on the mean value A₀ and amplitude A₁ of the oscillator species to which the load is coupled, and also the effective coupling constant k_r/k_f. In this respect mode I (high A₀, A₁) appears to work better than mode II (medium A₀, A₁), which in turn is better than mode II* (low A₀, A₁). Regarding retroactivity of the load, several factors can be considered: in terms of the simplified model, an effective change of thresholds as discussed above will change parameters α, β, and also the steepness of the response functions (cf. Fig. 2B) that define the oscillatory domain of the system. Furthermore, coupling rates k_r and k_f in practice may not be high enough to ensure effective time-scale separation as required for low retroactivity. Finally, spurious binding events, incomplete RNase H degradation and promiscuous RNAP activity (as present in all modes) result in “consumptive” processes that permanently remove oscillator species from the system.

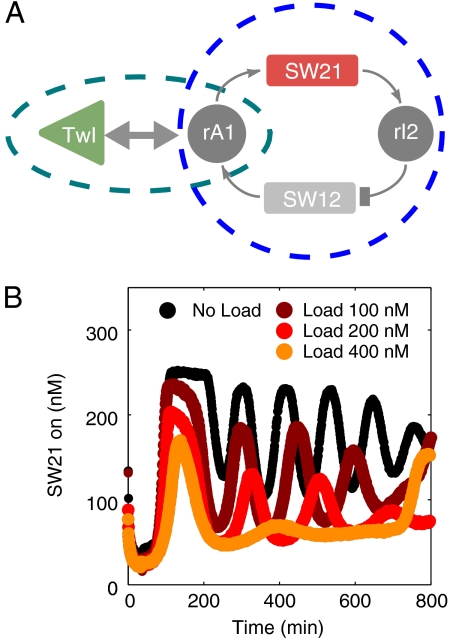
An Insulator Circuit

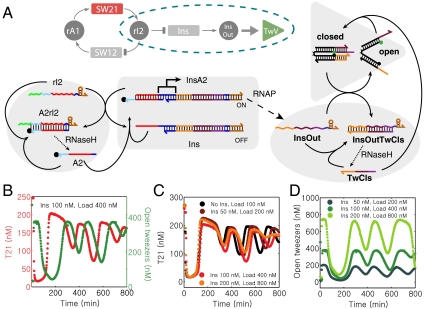
As already indicated from our simulations of the simple model in Fig. 1, it is possible to reduce retroactivity effects of the load by the isolation of source components from downstream loads using buffering and amplification stages. A simple implementation of this strategy (termed mode V) for our oscillator system is displayed in Fig. 4.

Fig. 4.

An insulator circuit (mode V coupling). (A): Insulator genelet Ins is operated in parallel with SW12. The genelet is activated by A2 and deactivated by rI2. Transcription of Ins results in RNA signal InsOut which opens tweezers previously closed by DNA strand TwCls. (“Load” for mode V is defined as closed tweezers with a 50 nM excess of TwCls, in contrast to modes I–IV where the load consists only of open tweezers.) The RNA part of hybrid duplex TwCls·InsOut is degraded by RNase H, resulting in free TwCls. This operation principle is analogous to mode I tweezers. (B): Oscillator (red) and tweezers (green) traces for 100 nM insulator genelet and 400 nM tweezers load. (C): Core-oscillator traces for 0 nM Ins and 100 nM tweezers load (black), and 200 nM (dark red), 400 nM (red), and 800 nM (orange) tweezers load and a 4∶1 ratio of tweezers:Ins. (D): Tweezers signal for 200 nM (dark green), 400 nM (green), and 800 nM (light green) tweezers load.

The insulator genelet is operated in parallel with oscillator switch SW12, i.e., it is activated by A2 and deactivated by rI2 (Fig. 4A). The insulator is used to produce a new RNA species InsOut, which in turn acts as the opening strand for DNA tweezers that were previously closed by DNA strands TwCls. Fig. 4 C and D shows load experiments where tweezers and insulator genelet are added in a ratio of 4∶1. Transcription from the insulator genelet acts as an amplifier stage: a small increase in the concentration of the insulator genelet (which incurs a small disruption of the core-oscillator dynamics) results in a large increase in the RNA available to drive the tweezers. Furthermore, this design effectively isolates tweezers operation from oscillator dynamics; even when there are more tweezers than can be effectively driven, the absence of specific interactions between the tweezers and the core-oscillator strands leaves the core-oscillator dynamics relatively intact (SI Appendix, Fig. S44). These features allow mode V to drive much larger loads than the direct coupling modes discussed previously.

As can be seen from Fig. 4C, even excessive loading of the circuit with 800 nM tweezers (and, hence, 200 nM insulator genelet) does not affect the oscillator dynamics significantly. At the same time, insulated DNA tweezers exhibit undistorted conformational switching (Fig. 4D). This behavior is in stark contrast compared to the mode I and II tweezers discussed above (Fig. 3 D and E and I–J), where both core oscillator and tweezers oscillations are already strongly affected at much lower load concentrations.

Temporal Control of RNA Aptamer Synthesis

Naturally occurring biochemical clocks control the timely production of proteins needed, e.g., at a particular phase of the cell cycle. As a simple analogue to this situation, we also utilized the transcriptional oscillator for the clocked synthesis of RNA molecules. To this end, the insulator circuit architecture was used to produce a functional RNA molecule rather than tweezer-opening RNA (Fig. 5). As functional RNA, we chose an RNA aptamer for the chromophore malachite green (MG) (22). When MG is bound to the aptamer, it becomes highly fluorescent (32). As can be seen from the scheme in Fig. 5A, MG aptamer production runs in parallel with the production of the inhibitory RNA strand rI2. However, the aptamer is not degraded by RNase H as it is not complexed with a DNA molecule. Thus, the MG aptamer fluorescence signal increases, whenever SW21 is on and therefore is proportional to the “integral” of the state of SW21 (Fig. 5B). We here also studied the influence of load by adding increasing amounts of aptamer genelet SWMG—i.e., template TMG1 without additional A1. The oscillations of the core system are similarly affected as in mode II (compare Fig. 5C with Fig. 3I), while the total MG aptamer production increases sublinearly with increasing [SWMG] (Fig. 5D). Apparently, MG does not affect enzyme and nucleic acid hybridization reactions.

Fig. 5.

Clocked production of a MG aptamer. (A): Operation scheme of SWMG. SWMG is operated in parallel to switch SW21, but is used to produce a functional RNA molecule—the MG aptamer rMG—instead of regulatory RNA species rI2. When MG is bound to the aptamer, it becomes highly fluorescent. (B): The MG aptamer is not degraded by RNase H, and hence accumulates over time. The MG fluorescence signal grows whenever SW21 is on. Shown is the concentration of T21 (dark red) and MG aptamer (dark green) as well as the derivative of the MG signal at 100 nM SWMG concentration. (C): Oscillator time traces in the presence of 0 nM (black), 100 nM (dark red), 200 nM (red), 400 nM (orange) SWMG. (D): Corresponding fluorescence signals (converted to aptamer concentration) recorded from the MG aptamer.

Model Description of the Oscillator Under Load

Even though the simple model of Fig. 1 introduced as a motivation for our work qualitatively shows many of the major features of our oscillator system, it is not capable of a faithful description of all experimental observations. One of the advantages of synthetic in vitro transcriptional circuits, however, is the level of control over the components of the system. This feature enables us to establish mechanistic numerical models describing the major chemical processes involved. Indeed, with a more detailed model our main experimental results could be semiquantitatively reproduced using physically reasonable rate parameters.

We began by establishing parameters for a model of the core oscillator that semiquantitatively reproduced the behavior of the oscillator when changing the threshold strand concentrations [dI1] and [A2]. This modeling helped ensure that the oscillator was placed in the “correct” region of its dynamical phase space. Starting with the mass-action chemical kinetics model and parameters from prior work (17), parameters were optimized to minimize a least-squares criterion for matching fluorescence trajectories and oscillation amplitude, frequency, and damping coefficients (as described in SI Appendix, Sections 24 and 25). The resulting fits reproduce several trends observed when changing the concentrations of DNA thresholds (SI Appendix, Section 21): reduction of dI1 concentrations decreases the amplitude, frequency, and mean level of oscillations; increasing dI1 concentrations also decrease amplitude, but increase the frequency and mean level of oscillations; decreasing A2 similarly decreases amplitude while increasing frequency and mean level; increasing A2 increases amplitude while decreasing frequency and mean level. Overall, frequency, amplitude, and mean level were adequately reproduced in most cases (SI Appendix, Fig. S54).

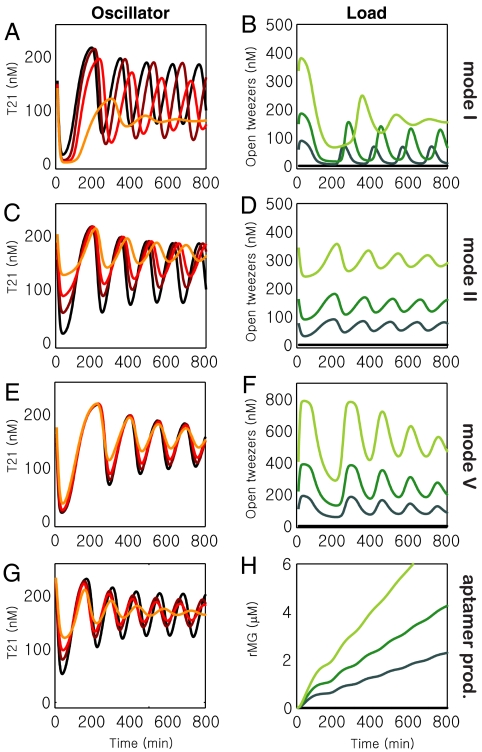
For a description of the oscillator under load, the core-oscillator model was expanded to incorporate reactions modeling the opening and closing of tweezers and the operation of additional genelets, where appropriate (see SI Appendix, Sections 26 through 31). These model extensions introduced two new fitting parameters (tweezer opening and closing) for modes I, II, and V; another six parameters for modes V and MG (k_cat and KM for RNAP for the new switches’ ON and OFF states, and their hybridization rates for switching ON and OFF); and an additional three for mode V (k_cat and KM for RNase H degradation of the new transcript and a hybridization rate for the new transcript directly binding to the tweezer closing strand). Physically plausible rate constants for these new reactions could be found, without changing the core-oscillator parameters, that semiquantitatively reproduced our experimental observations (cf. SI Appendix, Section 33). The amplitude, frequency, and mean signal levels of both the tweezers and the core oscillator are generally captured well, including the different behaviors in the initial phase of the oscillations (Fig. 6 A–H).

Fig. 6.

Simulations of the core oscillator and oscillator driven loads, using the mechanistic mass-action model described in the SI Appendix, Sections 24–33, for initial DNA concentrations identical to those in several experiments. (A, B): cf. Fig. 3 D and E. (C, D): cf. Fig. 3 I and J. (E, F): cf. Fig. 4 C and D. (G, H): cf. Fig. 5 C and D.

One notable discrepancy is that, experimentally, the magnitude of frequency change is much greater in mode I than in mode II, whereas in simulation they are roughly the same (see SI Appendix, Section 32). The model confirms the experimentally observed similarity between the effect of an increasing load with tweezers mode I and a decreasing amount of dI1. In both cases, the amplitude is damped, the oscillation frequency is reduced, and the mean level of T21 decreases. Furthermore, in addition to matching amplitude and mean level trends, the model calculations reproduce the experimental decrease in frequency for an increasing amount of tweezers mode II, while they correctly (though only slightly) show an increase in frequency for increasing [dI1]. The effectiveness of mode V and the behavior of mode MG was also semiquantitatively reproduced.

It is quite interesting to note that even though we aimed to include all major reactions occurring in our system, we were not able to find perfect agreement between the numerical model and the experiments. This deviation may be attributed to a variety of potential side reactions that are difficult to quantify. One major source of uncertainty comes from the two enzymes in the system: RNAP and RNase H. For instance, it is not clear how the activity of RNAP varies during the operation of the oscillator. The rate of RNA synthesis for the first reaction turnover is generally believed to be faster than the following turnovers (“burst phase”) (33). After termination, T7 RNAP is assumed to be in a initiation-incompetent conformation and has to revert to a competent state first (“recycling”) (34). Additional degradation mechanisms such as oxidation of Cys residues of T7 RNAP can lead to a continually decreasing activity over time (35, 36). Apart from these effects, we also did not consider the influence of abortive transcription, resulting in short RNA molecules with incomplete sequences, or unwanted interactions between RNAP and DNA tweezers (SI Appendix, Section 19). In addition, RNase H degrades RNA only partially, starting from the 3′ side and typically leaving a short RNA fragment that thermally dissociates from the RNA-DNA duplex (37). This effect is heuristically accounted for in the model, and it turns out to be essential for capturing the dynamics of the system more faithfully (cf. SI Appendix, Section 24). The build-up of short RNA waste products by the latter processes can also be expected to influence DNA hybridization kinetics in a complicated manner. In principle, short RNA waste products could be removed by introduction of an additional RNase (e.g., RNase R). However, addition of yet another enzyme would considerably increase the complexity the system.

A second major source of uncertainty in the model comes from spurious modes of hybridization—not only those involving incompletely characterized RNA waste products, but also several types of inevitable interactions between designed components that we did not initially anticipate (SI Appendix, Figs. S2–S10). The tweezers design itself exhibits some undesirable behaviors, such as forming a subpopulation of dimers when the closing strand is added (21) or potentially binding two closing strands simultaneously (38).

Discussion and Conclusion

We have shown that a synthetic transcriptional oscillator can be utilized as a “master clock” for timing a variety of biochemical processes in vitro such as the control of a DNA nanodevice or the production of an RNA aptamer. The oscillator is based on a negative feedback circuit that contains two genelets producing regulatory RNA molecules, one activating and one inhibiting species (rA1 and rI2), and three DNA species (A1, A2, dI1) that switch the genelets and set activation/inhibition thresholds. We attempted to couple load processes to each of these single-stranded RNA and DNA molecules, resulting in a variety of different “coupling modes:” mode I (coupling to dI1), mode II and mode MG (coupling to A1) , mode III (rI2), mode II* (A2), mode IV (rA1). These modes differ both in their coupling efficiency and in their influence on the oscillator dynamics itself. Efficient coupling is achieved when the load is coupled to an oscillator species that itself undergoes sufficiently strong oscillations, and when the coupling kinetics are fast enough for the load to follow the oscillations. In this respect, mode I turned out to be the best coupling mode for our particular choice of parameters.

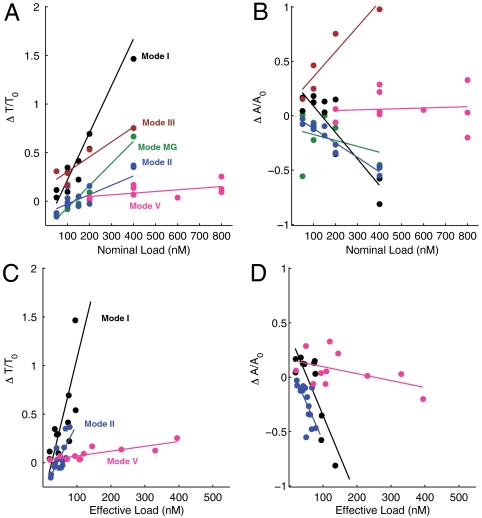
The most striking results of the retroactivity of the load on the core oscillator—the change in amplitude and period of the oscillations—are summarized in Fig. 7. In all coupling modes the oscillations tend to get slower with increasing load (Fig. 7A). This behavior can be attributed to the fact that the system parameters (without load) were initially optimized for fast oscillations. Hence, any perturbation typically moves the oscillator away from these optimum settings. For modes I and II the amplitude of the oscillations decreases with increasing load, while for mode III the amplitude increases (Fig. 7B). While mode I seems to affect the oscillator dynamics most strongly, one has to recognize that in this mode a larger fraction of the load is driven than in mode II (compare also amplitudes in Fig. 3 E and J). We therefore also plotted the period and amplitude change with respect to the “effective load”—the maximum amplitude swing induced in the tweezers. When only the influence of the effective load is considered, modes I and II affect the oscillator similarly (Fig. 7 C and D). One of the most important results of our work is the implementation of an insulator genelet (mode V). The insulator acts as an amplifier that diverts a small amount of an oscillator species and amplifies it to drive downstream load processes. As can be seen from Fig. 7, the insulator renders the system almost insensitive with respect to load.

Fig. 7.

Analysis of the influence of load on the oscillation amplitude and period. (A, C): Relative period change as a function of the nominal (A) and effective (C) load concentrations. (B, D): Relative amplitude change as a function of the nominal (B) and effective (D) load concentrations. A complete overview of the effects of all coupling modes is found in the SI Appendix, Section 16.

Many of the general features of our system can be understood already on the basis of a simple theoretical model for the oscillator that only accounts for the basic feedback circuit and makes some generic assumptions about the nature of the load coupling. For instance, this simple model shows how coupling efficiency depends on mean value and amplitude of the oscillating species, it predicts that the oscillatory domain of the system will shrink in the presence of a load process, and it can be used to demonstrate that retroactivity can be remedied by an insulator concept. Our simple model cannot offer a quantitative description of the experiments, however. A much more detailed understanding has therefore been attempted with a mechanistic numerical model that accounts for all major reactions occurring in the system. Satisfyingly, this detailed model was able to semiquantitatively reproduce all of the experimental data with a single set of physically reasonable parameters.

Nevertheless, it is interesting to note that a synthetic gene regulatory system with only two enzymes and a handful of DNA oligonucleotides already results in considerable complexity. Major uncertainties originate from the enzyme-catalyzed reactions. For instance, experimentally one has to cope with enzyme activities varying considerably from batch to batch, an issue which is extensively discussed in the SI Appendix, while numerically it is difficult to account for all side reactions and the accumulation of waste products. The complexity of potential molecular interactions (folding, degradation, combinatorial assembly of complexes, polymerization, etc.) quickly overwhelms brute-force attempts to design, analyze, and experimentally characterize molecular systems. Instead, combinatorial models used for nucleic acids (39, 40) and rule-based models used for combinatorial protein interactions (41, 42) may be necessary for formulating detailed models with tractable numbers of experimentally measurable parameters.

For synthetic biology, one would like to engineer systems that either avoid unwanted side reactions and waste products, or that are constructed in a robust and fault-tolerant manner. In the case of the transcriptional oscillator, one first step towards such robustness has here been demonstrated by the insulator circuit. The next step would be to construct an improved system whose behavior does not depend too sensitively on enzyme activities and therefore provides a stable rhythm regardless of the source or age of the enzyme batch used, or to construct an improved insulator subcircuit that can drive dynamically changing loads.

In summary, the oscillator system under load represents one of the first realizations of an in vitro molecular clock that is used to drive other molecular processes. The oscillator may therefore serve as a model system for the study of modularity, coupling of subcircuits, and robustness in biochemical networks. In the future, in vitro oscillators could be used to orchestrate more diverse downstream processes, could be modified to effect more complex and conditional regulation (as in the cell cycle), and could be embedded in artificial vesicles as part of the quest to construct an artificial cell (12, 43).

Materials and Methods

DNA Oligonucleotides and Enzymes.

DNA and RNA sequences were designed to minimize secondary structure and unwanted cross-hybridization. Oligonucleotides were purchased from IDT DNA, IBA and biomers.net . The sequences and modifications are given in the SI Appendix. RNase H and T7 Megashortscript kits were purchased from Ambion/Applied Biosystems, and used for the data presented in the main text. T7 RNA polymerase and reagents from Epicentre were used for an additional set of experiments shown in the SI Appendix, Section 4. Concentrations of nucleic acids were determined by absorption measurements (Nanophotometer and Nanodrop 2000c, Thermo Scientific), using sequence dependent extinction coefficients.

Sample Preparation.

In order to ensure constant DNA concentrations for all experiments, all oscillator sequences were premixed in a DNA stock solution. To maintain constant enzyme concentration ratios, T7 RNAP and RNase H were premixed once for each dataset. For the experiments performed at Technische Universität Müchen (TUM), the final concentrations of the oscillator strands were: T12 (120 nM), T21 (250 nM), dI1 (700 nM), A1 (250 nM), A2 (500 nM). Transcription buffer, as part of the kit, was 0.8× of the concentration suggested by the supplier. rNTPs were used at a 1.5× concentration. The MgCl₂ concentration was adjusted by adding additional 15 mM to balance with the increased rNTP concentration. For the experiments performed at Caltech, the final concentrations of the oscillator strands were: T12 (120 nM), T21 (250 nM), dI1 (650 nM), A1 (300 nM), A2 (550 nM) unless otherwise noted. Transcription buffer and rNTPs were 1× of the concentration suggested by the supplier, and the MgCl₂ concentration was not adjusted. Tweezers, insulator genelets, MG aptamer genelet (TMG1) and malachite green were added separately to each corresponding sample.

Fluorescence Measurements.

All fluorescence experiments were performed on a Horiba Jobin Yvon Fluorolog 3 system in 60 μL cuvettes. Fluorescence emission from labeled DNA strands was recorded every minute or two, depending on the dataset. A sample temperature of 37 °C was either maintained using a Peltier element (for single samples) or a water circulation thermostat (using a four position sample changer). First, excitation and emission spectra were recorded for each dye separately to check for bleed-through of any of the dyes into another channel. For the experiments performed at TUM, the following excitation and emission lines were used to receive the best spectral separation of the dyes: 515/540 nm (rhodamine green/BHQ1 labeled tweezers), 557/570 nm (TAMRA/Iowa Black labeled SW12), 595/610 nM (Texas Red/Iowa Black labeled SW21), 630/655 nm (MG channel). The MG signal was further processed in order to correct for excitation and emission of Texas Red in the MG channel. A different set of dyes and accordingly different excitation and emission spectra were used for the experiments done at Caltech: 504/531 nm (rhodamine green/BHQ1 labeled tweezers), 549/563 nm (TYE563/Iowa Black labeled SW12), 645/665 nM (TYE665/Iowa Black labeled SW21). To convert fluorescence data into concentrations, relative open/closed tweezers or off/on state switches, corresponding to the maximum and minimum fluorescence intensity levels, were determined by titration in the absence of enzymes; the experimental fluorescence data were normalized with respect to these signal ratios determined off-line.

For further information on data processing and modeling, refer also to the SI Appendix.