Melanoma and seborrheic keratosis differentiation using texture features

Abstract

Purpose

To explore texture features in two-dimensional images to differentiate seborrheic keratosis from melanoma.

Methods

A systematic approach to consistent classification of skin tumors is described. Texture features, based on the second-order histogram, were used to identify the features or a combination of features that could consistently differentiate a malignant skin tumor (melanoma) from a benign one (seborrheic keratosis). Two hundred and seventy-one skin tumor images were separated into training and test sets for accuracy and consistency. Automatic induction was applied to generate classification rules. Data analysis and modeling tools were used to gain further insight into the feature space.

Result and Conclusions

In all, 85–90% of seborrheic keratosis images were correctly differentiated from the malignant skin tumors. The features correlation_average, correlation_range, texture_energy_average and texture_ energy_range were found to be the most important features in differentiating seborrheic keratosis from melanoma. Overall, the seborrheic keratosis images were better identified by the texture features than the melanoma images.

The main objective of this research is to find the texture features or a combination of features to consistently classify a skin tumor. Classification rules, using the ID3 algorithm (1), were generated in this endeavor. A classification rule is deemed consistent with respect to a given set of class-based features if it correctly classifies the set (2). We consider classification rules defined by a combination of features for consistent and accurate classification. The proposed approach aims to yield a reduction of misclassified tumors, relating the classification process to a clustering property of the features. In this endeavor, second-order histogram features are used to develop a consistent classification rule.

Introduction

Malignant melanoma is a lethal form of skin cancer that claims many lives. Over the past few years, its incidence rate has increased considerably. Since melanoma can be cured if detected early, accurate and early detection is extremely important for the survival of the patient. When diagnosed in the early stages, melanoma is relatively easy to treat. Additionally, if benign tumors can be distinguished from malignant ones, the cost of unnecessary biopsies can be reduced (3).

The problem of differentiating melanoma from seborrheic keratosis (seb ker) is important, since these tumor types are often confused by existing methods. If a reliable method is found to differentiate these two diagnoses, it will greatly enhance the automatic classification schemes. Additionally, it is believed that this will lead to a greater understanding of the visual features, which can be used to differentiate between melanoma and seb ker.

The cost of misclassifying malignant melanoma as benign is much greater than misclassifying a benign tumor as malignant. In the former case the patient dies, whereas in the latter case the patient is subjected to temporary mental tension. A texture-based method is presented that uses second-order histogram features to generate classification rules. These new classification rules can be used to train medical students and primary health care providers. The most predictive features are sought by the automatic induction software to classify a tumor.

Materials and Methods

Equipment and tools

Hardware

The images used in this research were digitized from 35-mm color photographic slides and photographs. The digital images had a spatial resolution of 512×512 pixels, and a gray scale resolution of 8 bits per pixel per color band, giving 256 possible intensity levels. Thus, the color images thus obtained had a resolution of 24 bits per pixel, with each pixel having one of 16,777,216 possible colors. A border image was manually determined by the dermatologist to find where the tumor was located in the image. The tumor images and the border images were both in PPM and TIF format. The data type was BYTE and the format was REAL. The data range was 0–255.

The database currently contains 173 melanoma, 98 seb ker images and an equal number of their borders. These are clinical images from private dermatological practices and from university archives (4, 5). The database is still growing and will eventually contain a few thousands of digitized images of skin tumors. The experiments were initially carried out with subsets of the database, and then extended to the entire database.

Software

The software package computer vision and image processing tools (CVIPtools) was used for the texture feature extraction. CVIPtools is an excellent research tool with more than 170 functions and algorithms that explore imaging with minimal programming skills required (6). The first-class Fusion expert system development software (7) was used as an automated induction engine for the development of classification rules. The data analysis and modeling software package Partek (8) was used for data analysis and visualization. All the experiments were performed on a SUN-SPARC station operating on a SUN-SOLARIS platform.

Feature Files

Feature information for each tumor was generated using the CVIPtools software. The texture features were extracted using the tumor image (9), in conjunction with its border image, so that texture information was extracted based solely on the tumor than on the surrounding skin. The texture features were obtained for varying pixel distances. The pixel distance is the distance that is used in calculating the co-occurrence matrix (10, 11) (similar to second-order or joint histogram, which approximates the joint probability distribution). This distance defines which pairs of pixels are used to determine the co-occurrence matrix. A larger distance will define a coarser structure, while a smaller distance will define a finer texture. For these texture features, the software performs a luminance transform on the image before extracting the features. It extracts features for four different orientations (specifically, angles of 0°, 45°, 90° and 135°) and returns the average and the range for each feature. These feature files provide a database, which can be used for testing the success of any feature identification rule.

Training/Test Set Paradigm

The training/test set paradigm is used extensively in statistical studies (3). Data are separated into two distinct sets: one used for training or developing the algorithms and the other used for testing the algorithms. This allows for unbiased testing of algorithm performance. If the same set is used to train and test an algorithm, the algorithm performance on other independent data is not predictable. Most of the experiments were performed with equal sizes of training and testing sets.

Texture Features

Texture is the arrangement of elements or objects. The essential characteristic of a texture is the presence of fine detail within surfaces perceived as belonging to a given object. In this endeavor, to provide consistent and accurate classification, a statistical method based on local gray-level statistics has been adopted. The set of 10 texture features used in this experiment are also known as second-order histogram features (10). The following features were used:

1. Texture_energy_average: A feature indicating the average distribution of gray levels, i.e. it is a measure of the brightness of the texture.

2. Texture_energy_range: A feature indicating the variation of energy along the four orientations.

3. Inertia_average: A feature indicating the average contrast of the texture.

4. Inertia_range: A feature indicating the variation of inertia along four directions.

5. Correlation_average: A feature indicating the average measure of similarity between adjacent pixels.

6. Correlation_range: A feature indicating the variation of correlation along four directions.

7. Inverse_difference_average: A feature indicating the average local homogeneity of the texture.

8. Inverse_difference_range: A feature indicating the variation of homogeneity along four directions.

9. Texture_entropy_average: A feature indicating the average information content of the texture.

10. Texture_entropy_range: A feature indicating the variation of entropy along four directions.

Automatic Induction

Induction is the process of generating a general classification algorithm from a set of specific examples. It is a reasoning process that allows human beings to formulate theories from limited and specific experience that can be used to predict future events, such as the results of an experiment. Here, induction was used to generate a classification rule. The mechanism used by the software is based on an algorithm known as ID3. The ID3 algorithm is the induction engine, which operates by generating decision trees based on input examples. ID3 was specifically designed to handle large masses of data, with the processing time growing linearly with the size of the data (1, 12).

The classification rules thus generated were analyzed, and the primary features used by the induction software in generating the rules were selected for further experimentation. The following example illustrates this point. In the sample rule shown below, the features corr_a (correlation_average) and tex_energy_a (texture_energy_average) are the first and foremost features used in this rule. Note also that correlation_range and texture_energy_range (corr_r, tex_energy_r) are used, and that inertia_range is all that is required to differentiate melanoma from seb ker fully, for this experiment.

---- Start of rule ----
1: CORR_A??
2:   <0.91992: ----------------------------------------------- melanoma
3:   >0.91992: TEX_ENERGY_A??
4:                 <307.469: --------------------------- seb ker
5:                 >307.469: CORR_R??
6:                         <0.17054: --------------------------- melanoma
7:                         >0.17054: TEX_ENERGY_R??
8:                             <244.965: INERT_R??
9:                                          <0.002118: ------- seb ker
10:                                         >0.002118: ------- melanoma
11:                                >244.965: --------------seb ker
---- end of rule ----

Rules

In the experiments described below, the rules generated using first-class induction software (7) are based on two methods: (1) Optimize and (2) Left–Right. This was primarily done to facilitate comparison between the two methods.

The Optimize method attempts to produce the smallest possible rule tree (7). It creates compact decision trees by choosing the ‘best’ features in the proper sequence. In this method, the ID3 algorithm selects the features that will make the most progress towards completing the decision tree. It discards irrelevant and redundant features. It is easy, fast and efficient. The Optimize method can find simple rules underlying complex data. Sometimes, the rule the Optimize method builds provides useful information by itself. The Left–Right method processes the features in left to right order as they appear on the definition screen. It does this by discarding the irrelevant features. This method is especially useful when we would like to force certain features to be used first in generating classification rules.

Texture Analysis Experiments

As a first step towards consistent classification, the texture features for the two diagnoses, melanoma and seb ker, were extracted for varying pixel distances (i.e. 2, 3 and 5). The idea was to compare the results for different pixel distances to determine which one serves the purpose the best. The rules were generated and tested for their accuracy.

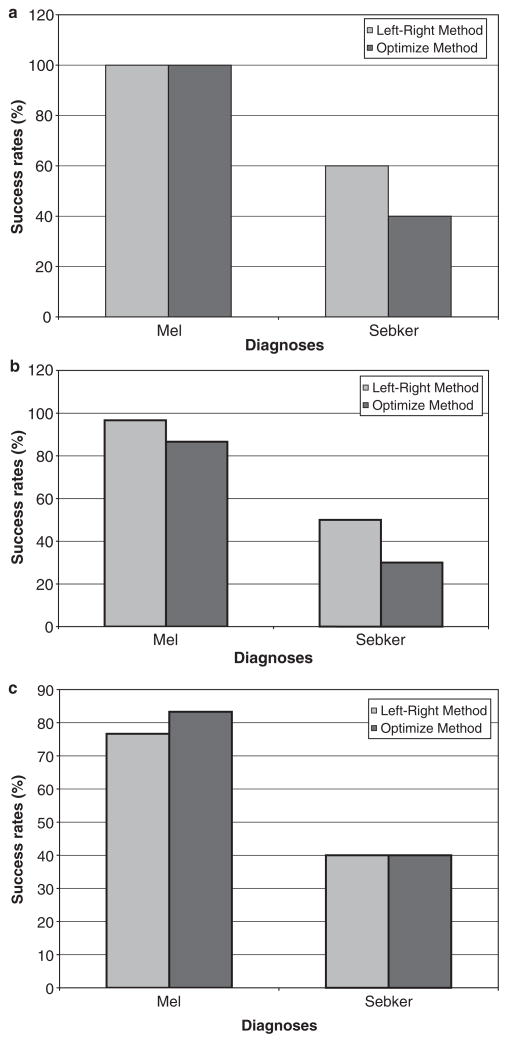
The initial experiments were carried out with three pixel distances (using both the Left–Right and Optimize methods). The results are tabulated in Tables 1 and 2 and depicted in Fig. 1. The relative consistent results obtained in the experiments with melanoma and seb ker led us to the conclusion that texture features with a pixel distance of two are good features to identify melanoma. Moreover, the features correlation and texture_energy seem to be the most promising in detecting melanoma since these were the main distinguishing features in the rules generated. Correlation is the measure of similarity between adjacent pixels, while texture_energy is the measure of brightness distribution of the texture. Additionally, Fig. 1 illustrates that the Left–Right method is best for rules generation.

TABLE 1.

Success rates in the diagnosis of melanoma and seb ker using the Left–Right method for pixel distances 2, 3 and 5

Diagnoses	2		3		5
	Melanoma	Seb ker	Melanoma	Seb ker	Melanoma	Seb ker
Training set (43)	27	16	27	16	27	16
Test set (40)	30	10	30	10	30	10
Detected	30	6	29	5	23	4
Success rate (%)	100.00	60.00	96.66	50.00	76.66	40.00

TABLE 2.

Success rates in the diagnosis of melanoma and seb ker using the Optimize method for pixel distances 2, 3 and 5

Diagnoses	2		3		5
	Melanoma	Seb ker	Melanoma	Seb ker	Melanoma	Seb ker
Training set (43)	27	16	27	16	27	16
Test set (40)	30	10	30	10	30	10
Detected	30	4	26	3	25	4
Success rate (%)	100.00	40.00	86.60	30.00	83.33	40.00

Fig. 1.

(a–c)Success rates for the two methods as a function of the two diagnoses (melanoma and seb ker) for pixel distances 2, 3 and 5, respectively.

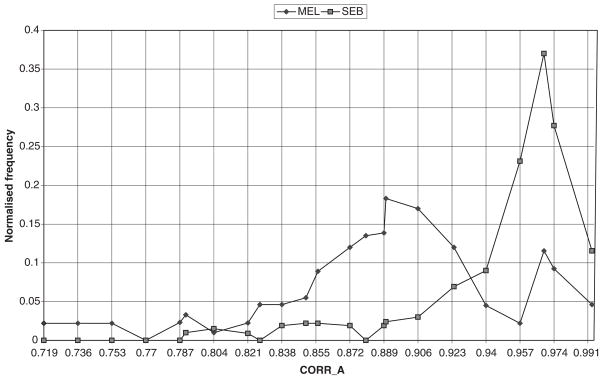
Subsequent experiments involved attempting to improve the success for seb ker by using the same set of features. In these experiments, visual analysis tools (8), i.e. 1D-histogram and scatter plots, were plotted with the data and visually analyzed. Scatter plots are statistical tools that show how much one variable is affected by another (13). The 1D-histogram plots depict how one independent variable affects each class of data. The feature correlation_average provided some plots with distinct peaks for the two diagnoses (Fig. 3), which shows that this feature is useful for differentiating melanoma from seb ker. This feature was also found to be the most promising feature in classifying melanoma by the induction software.

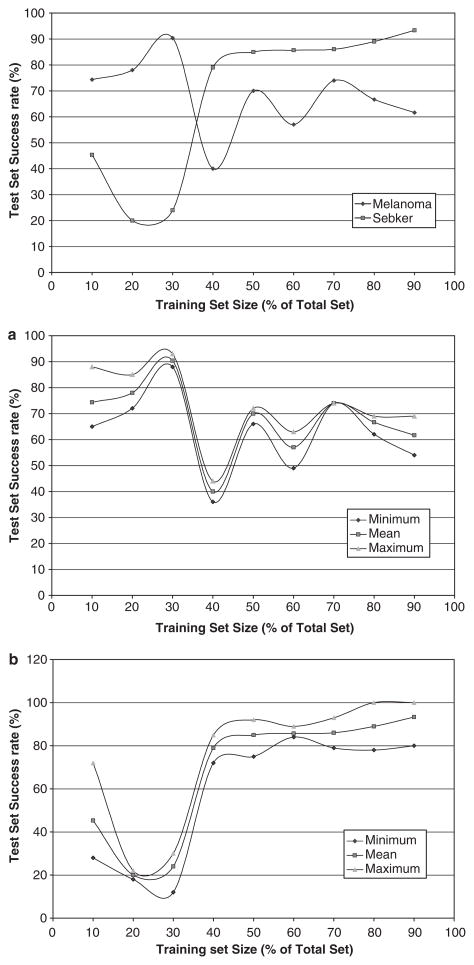
Fig. 3.

Success rates of melanoma and seb ker for varying training set sizes as a percentage of total images database size. (a, b) Minimum, mean and maximum success rates of melanoma and seb ker, respectively, for varying training set sizes as a percentage of total images database size.

The variable selection and discriminant analysis modeling tools yielded some useful results. The variable selection tool is an important technique for reducing the dimensionality in multivariate predictive classification (14). The variable selection tool was used to train the data and the discriminant analysis tool was used for testing. The discriminant analysis tool is a statistical tool that looks at all the features and works out which combinations of features are the most characteristic of a class (15). As the modeling tools assume a Bayesian distribution of the data (Gaussian distribution and zero mean), the data were preprocessed using the standardization method. While training the data, the quadratic discriminant classifier was used as the evaluation criteria, and the forward selection and backward elimination methods were used as the search methods. The forward selection method starts with an empty subset to which is added one variable at a time – the one that most reduces the error. The backward elimination method starts with the full subset from which one variable is removed at a time – the one that least increases the error. With the backward elimination method, the best results for seb ker were obtained with three variables (of which correlation was one) with a success rate of 88%. On the other hand, with the forward selection method the best results for seb ker were obtained with one variable with a success rate of 96%. In a group of similar experiments, the forward selection method produced better results than the backward elimination method.

As the number of seb ker images was smaller than the melanoma image set, a unique method was adopted to compare the results. The variable selection tool was used to train the data and the discriminant analysis tool was used for testing, using all the 10 texture features. While training the data, the quadratic discriminant classifier was used as the evaluation criteria and the forward selection method was used as the search method. The training set was gradually increased from 10% of the total images to 90% of the total images, and was tested with the remaining images. Three readings were taken at each size and the mean was calculated. The results were plotted with the training set size as a percent of the total size on the x-axis and the test set success rate on the y-axis (Fig. 4). The plot shows that as the training set size increases, the success rate of seb ker also increased considerably (except for the first reading, which shows that 10% for the total seb ker, which is five images, was not sufficient to train the data properly). On the other hand, the success rates of melanoma showed no unique trend.

Fig. 4.

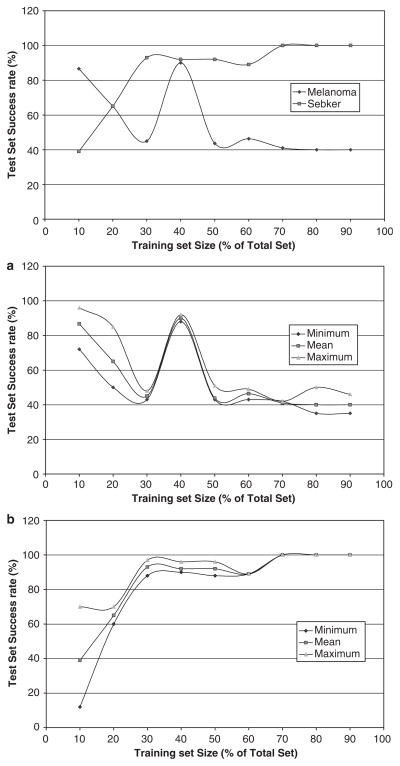
Success rates of melanoma and seb ker for varying training set sizes as a percentage of total image database size, with success rate for each experiment. The training set includes only four features, namely correlation_average, correlation_range, texture_energy_average and texture_energy_range. (a, b) Minimum, mean and maximum success rates of melanoma and seb ker, respectively, for varying training set sizes as a percentage of total image database size. The training set includes only four features namely, correlation_average, correlation_ range, texture_energy_average and texture_energy_range.

Next, four features – correlation_average, correlation_range, texture_energy_average and texture_energy_range – were selected and the above experiment was repeated. These four features were found to be the primary features for classifying melanoma in the rules generated in the preliminary experiments carried out using melanoma and seb ker. The results are plotted in Fig. 5. As expected, the success rate for seb ker increased with the training set size, but for melanoma there was no specific trend. The high and almost constant success rates for seb ker are clearly suggestive of the fact that the features texture_energy and correlation are good indicators of seb ker. Few discrepancies in the results (like the success rates at training set size 50% was greater than the success rate at training set size 60%) suggest the need to increase the image set sizes.

Fig. 5.

Success rates of melanoma and seb ker for varying training set sizes as a percentage of total image database size for all the 10 texture features.

The image database was expanded by including two image sets from private dermatological practices (Menzies (4) and Marghoob (5)). The database was split into two equal halves randomly called the training set and the test set, each consisting of 86 melanoma and 49 seb ker images. The experiments were performed with the discriminant analysis tool. First, one of the sets was used for training and the second set was used for testing. The tests were repeated for varying prior probabilities with the training sets and test sets and the sets being swapped; the results are tabulated in Tables 3 and 4, respectively. The results showed, with the same prior probability but for different training sets and test sets, that the success rates are nearly consistent. These results imply that the two seb ker sets are similar and complete. For melanoma, the success rates for the first experiment vary from 39% to 65%, and for the second they vary from 65% to 86%. These disjoint success rates imply that the two melanoma sets are not similar and complete.

TABLE 3.

Success rates of melanoma and seb ker for varying prior probabilities using the discriminant analysis tool

Prior probabilities		Success rates (%)
Melanoma	Seb ker	Melanoma	Seb ker
0.1	0.9	65	73
0.2	0.8	70	71
0.3	0.7	70	71
0.4	0.6	72	71
0.5	0.5	77	71
0.6	0.4	78	69
0.7	0.3	80	69
0.8	0.2	80	65
0.9	0.1	86	51

TABLE 4.

Success rates of melanoma and seb ker for varying prior probabilities using the discriminant analysis tool (with the training and test sets swapped from Table 3)

Prior probabilities		Success rates (%)
Melanoma	Seb ker	Melanoma	Seb ker
0.1	0.9	39	71
0.2	0.8	44	69
0.3	0.7	45	69
0.4	0.6	48	69
0.5	0.5	49	63
0.6	0.4	52	63
0.7	0.3	56	61
0.8	0.2	63	59
0.9	0.1	65	57

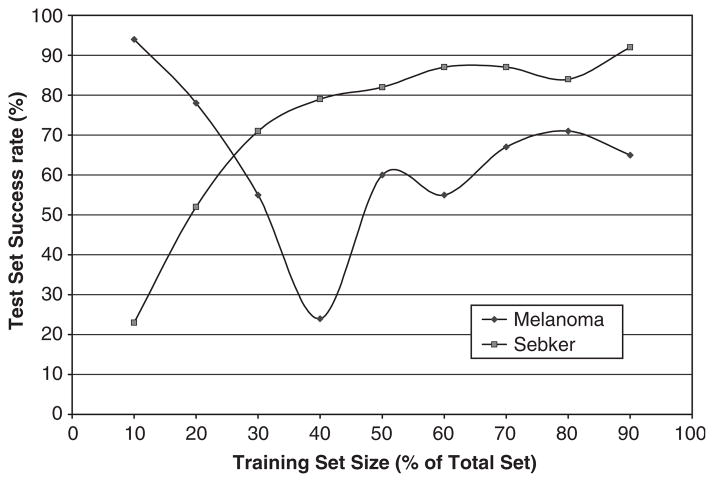
Since the prior probability of 0.9 for seb ker and 0.1 for melanoma showed higher success rates for seb ker (from Tables 3 and 4), further experiments were performed to maximize seb ker success. Using these prior probabilities, experiments were carried out by increasing the training set size gradually from 10% of the total size to 90%, and the corresponding success rates have been plotted. The success rates for seb ker increased gradually as the training set size increased, whereas for melanoma no specific trend was observed. These results further support our conclusion that melanoma sets are incomplete.

These experiments were followed by a principal component analysis (PCA) or principal components transformation (16). The experiments with PCA were performed on all the images in the database as a single set. The PCA scatter plot showed two clusters of seb ker that were separated by a cluster of melanoma (however, there were a few outliers). The PCA performs a linear transform of the 10 texture features to produce a three-dimensional plot with the three axes containing the new features with the largest variance. These new features are found by using the eigenvectors of the covariance matrix of the data set. The orthogonal basis of the covariance matrix can be found by calculating the eigenvalues and eigenvectors. By ordering the eigenvectors in the order of descending eigenvalues (largest first), one can create an ordered orthogonal basis with the first eigenvector having the direction of the largest variance of the data. In this way, we can find the directions in which the data set has the most significant amounts of energy.

The original vector was projected on the coordinate axes defined by the orthogonal basis. The original vector was then reconstructed by a linear combination of the orthogonal basis vectors. Instead of using all the eigenvectors of the covariance matrix, we may represent the data in terms of only a few basis vectors of the orthogonal basis. By comparing the values of the eigenvalues to the total sum of eigenvalues, we can get an idea as to how much of the energy is concentrated along the particular eigenvector.

From the experiment, it has been determined that the first three components have a contribution of 79.32%. The eigenvector contributions were found to be: U1, 39.52%; U2, 24.68%; U3, 15.12%. The component correlations with the original variables are provided in Table 5. This table indicates that texture_energy, correlation, and inverse_difference are good indicators of seb ker because of their contributions to the eigenvalues–other features had much smaller contributions. This helps to confirm results obtained from the induction software which indicated that correlation and texture_energy are good indicators of seb ker.

TABLE 5.

Percentage of texture features present in the eigenvalues U1, U2 and U3

Texture features	U1	U2	U3
Texture_energy_average	0.4442	0.6079	0.52179
Texture_energy_range	0.5772	0.5669	0.4377
Correlation_average	−0.8763	−0.84 709	0.3855
Correlation_range	−0.7621	0.7229	−0.6333
Inverse_difference_average	0.8592	0.2597	−0.4901
Inverse_difference_range	0.7117	0.3092	−0.3930

Results and Discussion

These results clearly suggest that the texture features can serve as good classifiers of seborrheic keratosis. Of these, the features texture_ energy_average, texture_energy_range, correlation_ average and correlation_range serve the purpose the best. Also, the pixel distance 2 gave good results when compared with other pixel distances, i.e. 3 and 5.

The experiments carried out by varying the training set size as a percent of the total set size yield some useful results. Fig. 4 shows that the texture features are good identifiers of seb ker. This is confirmed by the increasing success rates for seb ker as the training set size is increased. The results obtained in Fig. 5 clearly show that the features correlation and texture_energy are the primary features that distinguish seb ker from melanoma. This could be concluded from the nearly consistent and increasing success rates for seb ker.

The results from the experiments were performed with the discriminant analysis tool by varying the prior probabilities further confirm the above results. It was observed that seb ker showed consistent success rates over varying prior probabilities. Moreover, for the same prior probability (i.e. 0.5 for melanoma and 0.5 for seb ker), the success rate for seb ker (71%) and for melanoma (77%) was reasonably good. Fig. 6 shows the usefulness of the texture features in identifying melanoma. The results obtained from PCA (tabulated in Table 5) once again confirm the fact that the features texture_energy and correlation contribute the most in the correct classification of seb ker. The results obtained from the experiments performed by the texture features, in Table 6, are useful in classifying seb ker.

TABLE 6.

Percentage of texture features present in the eigenvalues U1, U2 and U3

Texture features	U1	U2	U3
Texture_energy_average	0.6712	0.5234	0.2653
Texture_energy_range	0.6052	0.6339	0.2916
Correlation_average	−0.7372	−0.3053	0.2722
Correlation_range	0.5751	0.4612	0.2963

Overall, the ID3 algorithm produced results that favored the Left–Right method over the Optimize method. Even though the Optimize method resulted in more compact and general rules, its success rate was considerably low. On the other hand, the Left–Right method generated rules with distributed clusterings, but with much more consistent results than the Optimize method.

Conclusion

This research has shown that the texture features extracted from color skin tumor images can be good discriminators of malignant tumors from benign ones: specifically, malignant melanoma from seborrheic keratosis. The reliability was demonstrated by the consistent success rates with different testing sets in the case of melanoma and seborrheic keratosis.

Of the 10 texture features considered, texture_ energy_average, texture_energy_range, correlation_average and correlation_range were shown to be the best features in the accurate and consistent classification of seborrheic keratosis. These features were first shown to be useful by the automatic induction software and were later confirmed by data analysis tools. Specifically, discriminant analysis and principal component analysis showed the importance of these features in differentiating melanoma from seb ker. In all, 85–90% of seborrheic keratosis images were correctly differentiated from the malignant skin tumors.

Fig. 2.

Histogram depicting the texture feature correlation. Melanoma, –●–●–●–, clusters and peaks around 0.89, while seborrheic keratosis, –■–■–■–, clusters and peaks around 0.96.