Detection of pigment network in dermatoscopy images using texture analysis

Abstract

Dermatoscopy, also known as dermoscopy or epiluminescence microscopy (ELM), is a non-invasive, in vivo technique, which permits visualization of features of pigmented melanocytic neoplasms that are not discernable by examination with the naked eye. ELM offers a completely new range of visual features. One such prominent feature is the pigment network. Two texture-based algorithms are developed for the detection of pigment network. These methods are applicable to various texture patterns in dermatoscopy images, including patterns that lack fine lines such as cobblestone, follicular, or thickened network patterns. Two texture algorithms, Laws energy masks and the neighborhood gray-level dependence matrix (NGLDM) large number emphasis, were optimized on a set of 155 dermatoscopy images and compared. Results suggest superiority of Laws energy masks for pigment network detection in dermatoscopy images. For both methods, a texel width of 10 pixels or approximately 0.22 mm is found for dermatoscopy images.

1. Introduction

Malignant melanoma is a lethal form of skin cancer that has claimed many lives in recent years. Over the past decade the number of people affected by this disease has doubled in most parts of the world. In the United States alone, around 53,600 new cases of melanoma are estimated in 2002 [1]. The number of deaths estimated from this deadly disease is around 7400 in 2002 [1]. Since melanoma can be cured if detected early, accurate and early detection is extremely important for the survival of the patient.

Epiluminescence microscopy (ELM), also known as skin-surface microscopy, dermatoscopy or dermoscopy, was described in 1921 [2] and later in 1987 [3]. It is a non-invasive tool to improve the early diagnosis of malignant melanoma. Initially, it was designed to be used with complex microscopic equipment. However, ELM now is used in a general clinical setting with an inexpensive hand-held otoscope-like unit [4]. ELM combines oil immersion with standard magnifying optics and incident surface lighting to permit in vivo visualization of features of pigmented melanocytic neoplasms that are not discernable by examination with the naked eye. ELM offers a completely new range of visual features such as the pigment network, solid pigment, radial streaming, globules, blue/gray veil, etc., to aid the diagnostic process.

The procedure consists of first applying alcohol or mineral oil to the pigmented skin lesion. A transparent material is then pressed against the lesion after which it is examined under tangential illumination with magnification. This technique reduces the reflected light from the irregular surface of the stratum corneum and thus makes the epidermis more transparent so that structures at the dermal–epidermal junction and upper dermis may be visualized [4]. The use of ELM can increase experts’ diagnostic accuracy for pigmented lesions, assisting in clinically differentiating melanoma from its benign simulators [3,5].

Texture analysis is the attempt to quantify texture notions such as ‘fine’, ‘rough’ and ‘irregular’ and to identify, measure, and utilize the differences between them [6]. A point has no texture; only a region can have a texture. The most prominent feature that discriminates between textured and non-textured images is their coarseness, or the size of textural primitives. Coarseness of an image is not absolute but depends on the scale at which the image is processed or viewed. Reducing the size of the image makes a textured image seem smoother, while magnifying the image brings forward the rough structure of the surface. Textural features and texture analysis methods can be loosely divided into two categories: statistical and structural. Statistical methods define texture in terms of local gray-level statistics that are constant or slowly varying over a textured region. Different textures can be discriminated by comparing the statistics computed over different sub-regions. Structural texture models try to determine the primitives of which the texture is composed. While statistical features measure gray value variations in an image neighborhood, structural features explicitly characterize properties of textural primitives, such as their size and shape [7]. This study develops a statistical technique for detecting pigment network.

An excellent set of techniques is presented in Ref. [8] by Fleming and co-authors. Structural analysis is performed based on a line extraction algorithm developed by Steger. Asymmetrical line contrast is corrected and holes are identified. Gaps are filled with dynamic contour or snake modeling. Additional pre- and post-processing to segment lesions and identify hairs and bubbles was needed. This series of algorithms, although computationally intensive, produced a mean network line width and mean hole area that correlated well with malignant melanoma. Our hypothesis is that a simple texture-based network identification method is needed for a global pigment network assessment. Many benign lesions have large structureless areas, with virtually no regular pigment network. Other benign lesions such as spindle-cell nevi may lack repeating lines but instead present with a cobblestone or follicular pattern. However, previously reported methods, as they are not texture-based, find only line-based patterns and not dot or globular textures. Our goal is to map the presence or absence of pigment network on a block-by-block basis, so that spatial analysis of the network such as asymmetric network can be reported, and to do this regardless of the specific type of network present, as long as it presents with a recurring pattern that yields an identifiable texture.

Two approaches were analyzed for detecting the pigment network. The first method is the neighboring gray-level dependence matrix (NGLDM) developed by Sun and Wee [9] and the second method uses the lattice aperture waveform set (LAWS) developed by Laws [10]. The first method is described in Ref. [9] and the application of that method to skin texture determination is discussed in Ref. [11]. The NGLDM and LAWS methods are discussed in the following sections. Our hypothesis is that both methods can detect pigment network with good accuracy. The purpose of this paper is to present optimized results for each method and to determine which is superior for determination of pigment network.

2. Laws energy masks

Laws [10] investigated many local measures of texture (called ‘micro-features’) in combination with a number of global ‘macro-statistics’. His two-tier approach combined co-occurrence, correlation and statistical moment methods with a variety of data aggregation steps and compiled both inter- and intra-method comparisons using principal component analysis. He incorporated the best concepts from these methods into a new model that convolves the image with 3 × 3, 5 × 5 or 7 × 7 masks and computes the energy of the results as texture attributes [10]. The following analysis was performed using the Laws methodology.

Fig. 1 shows the one-dimensional convolution masks, called LAWS, of orders three and five, that can be used to create the two-dimensional masks used in this study. The vectors are weighted toward the center and are either symmetric or antisymmetric. All but the Level vector are zero-sum. The vectors in each set are independent, but not orthogonal to each other.

Fig. 1.

One-dimensional Laws masks of size 3 and 5.

The higher order masks can be generated from the third-order set by convolution. For example, the fifth order mask L5 can be generated by convolving L3 with itself. The two-dimensional masks are created by convolution of a vertical vector with a horizontal vector. It can be seen that a vector of size N can give rise to N² different masks. Each mask represents a characteristic feature that can be detected such as Level, Edge, Spot, Wave, Ripple, Undulation and Oscillation [6]. Laws determined that the variance or standard deviation was the best single transform to extract texture information from the filtered images. Since circular convolution with a zero-sum mask gives rise to a zero-mean field, the variance will be the average of the squared-filtered values and represents the energy of a filtered image [6]. Laws approximated the standard deviation by the average absolute value of the filter pixels and accepted the caveat that a dark field with bright spots is indistinguishable from a bright field with dark spots.

3. Neighboring gray-level dependence matrix (NGLDM)

This is a rotation-invariant texture determination method developed by Sun and Wee [9] that we have found to be the best of three texture determination methods for analysis of smoothness in skin tumors [12]. This method defines a matrix that considers the relation between a pixel and all its neighbors instead of just in one direction, eliminating angular dependency. Sun and Wee defined five texture attributes: small number emphasis, large number emphasis, number nonuniformity, second moment, and entropy.

The NGLDM entries record, for the (i,j)th position in the NGLD matrix, the number of pixels (these are called index pixels) in the image that have gray level i and have j neighboring pixels (1) within a predetermined distance d of the index pixel, and (2) within a predetermined range a of the gray level of the index pixel. For example, for a distance of one, the NGLDM has all zero entries after the eighth column, as a pixel has at most eight neighbors. We empirically varied a and d to find the optimal a and d for this domain of a = 4 and d = 5. The large number emphasis index which Sun and Wee called N2 was found to be a useful index, as it appears to measure the coarseness of visual pigment texture. Screening the entire image to find areas with a large enough N2 successfully found pigment network candidates.

4. Methods

4.1. Images and pre-processing

One hundred fifty-five dermatoscopy images, 62 malignant melanomas and 93 benign lesions (nevocellular nevi and dysplastic nevi), were digitized at a resolution of 512 × 480 in full 24-bit color. Images were acquired with a Heine Dermaphot camera and Fujichrome film.

Because dermatologists differ in their assessment of pigment network irregularity as well as other dermatoscopic features, a gold standard for presence of pigment network, especially the extent to which it is present on the lesion, does not exist. It would be desirable to study detection rates using a formal classifier, but we feel this type of study is more meaningful when the pigment network is included with other features for a formal classifier for pigmented lesions. In this study, we therefore are comparing blocks of images, with the entire image scored by a dermatologist for presence or absence of pigment network, with empirically determined classification algorithms.

Dullrazor [13] was applied to all images to remove hair. For each of the 155 tumor images, for each 64 × 64 block, 49 per image, a dermatologist (WVS) scored the block for pigment network presence or absence: full (entire block contains pigment network), partial (pigment network exists in a portion of the block), or none. Boundary blocks incompletely contained within the tumor were not included in the analysis. Luminance images were calculated from the RGB (red, green, blue color space) color images by the equation: luminance = 0.29R + 0.59G + 0.11B.

Two algorithms, namely the NGLDM numbers and the Laws energy masks, were used for the detection of the pigment network. Our reason for choosing these and not other texture measures is based on earlier work by Harris [6] which showed that Laws energy masks and NGLDM indices were superior to fractal and symmetric autoregression measures in this domain and work by Chang [14] and Cheng [15] which showed inability of orthogonal masks and wavelet analyses to improve on the NGLDM and Laws results in the domain of pigmented skin lesions. The performance and results of the two algorithms we have chosen are discussed in the sections that follow.

4.2. Methods for NGLDM numbers

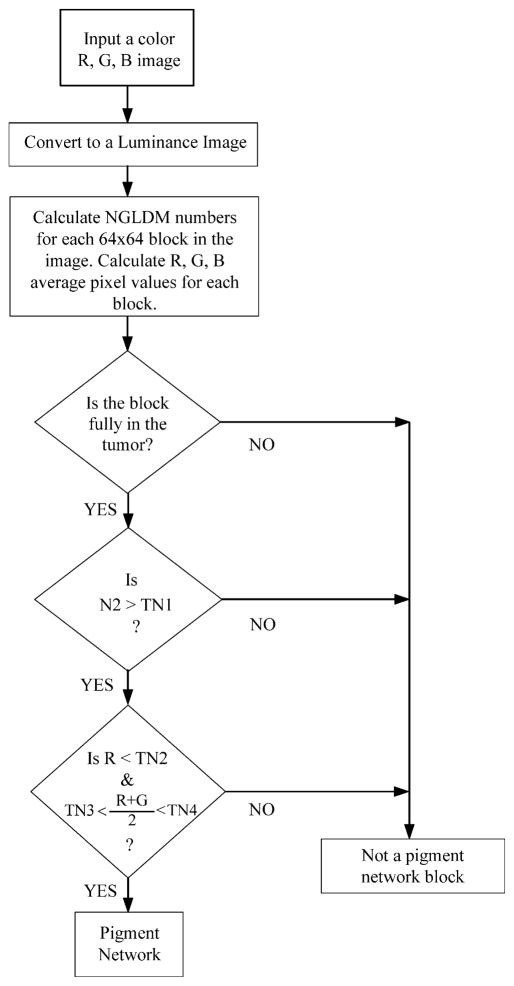
The NGLDM large number emphasis was also used for detecting the pigment network. The algorithm makes use of a two-step process. Image blocks of 64 × 64 size are used as input to the algorithm and a threshold of 5800 is set. All the blocks that are above this threshold are considered for the color filtering stage. The red color component is averaged over a block. The average of the red and the green components is also taken because it was observed in some cases that the green component of the image shows the pigment pattern more prominently than the red component. A blue check was done similar to the one carried out in the Laws analysis (see Section 4.3). The flow chart in Fig. 2 shows the steps involved in detecting the pigment network.

Fig. 2.

Flow chart illustrating steps for detecting pigment network using NGLDM numbers (Thresholds TN1 = 5800, TN2 = 80, TN3 = 0, and TN4 = 150 worked well, as did TN1 = 5800, TN2 = 235, TN3 = 100, and TN4 = 200).

4.3. Methods for laws energy masks

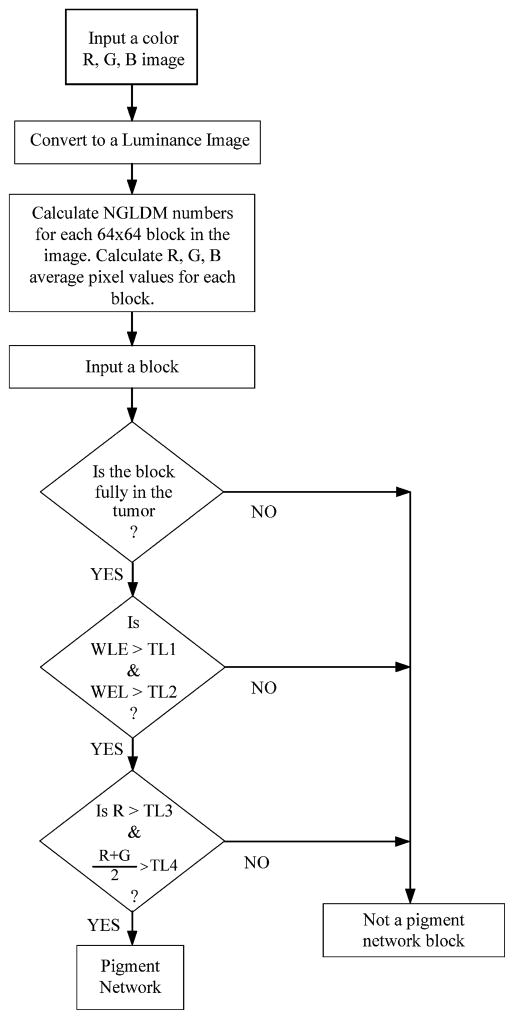
For 512 × 480 dermatoscopy images, Laws energy masks smaller than 9 × 9 or larger than 13 × 13 were not as effective at measuring the pigment network. All the Laws energy measures are calculated for the luminance image on masks of size 9 × 9, 11 × 11 and 13 × 13, as these were the scales at which the texture content was mainly concentrated. The masks used were LxEx and ExLx. Here x can take values 9, 11 and 13. LxEx and ExLx are formed by convolving Level and Edge one-dimensional vertical masks with the one-dimensional horizontal masks. The luminance image was divided into 64 × 64 blocks and the mask was convolved with the image blocks. The resultant convolved image elements were squared, added and averaged over the size of the block. This process was carried out for all the blocks in the image and for masks of sizes 9 × 9, 11 × 11 and 13 × 13. The results were stored in data files. These energy measures were used for the first stage of detection of pigment network. A threshold was set and only those blocks whose energy values were greater than the threshold are considered for the color filtering stage. In the color filtering stage the blocks that have the red component greater than a threshold and the average of the red and the green components greater than a threshold were used for deciding the presence of pigment network. These thresholds were optimized for best results. Also excessive blue content in the image is checked. If a block exists with a blue color component exceeding a third threshold then that block is ignored, as it is likely a blue veil. Throughout the analysis only blocks that are fully enclosed within the tumor are considered. This is done to avoid the edge effects caused by the partial blocks. The flow chart in Fig. 3 shows the steps involved in the detection of pigment network. Most features in the image are detectable in the 9 × 9 and 11 × 11 scale.

Fig. 3.

Flow chart for detecting pigment network using Laws energy filters, where WLE is the weighted combination of L9E9 and L11E11 and WEL is the weighted combination of E9L9 and E11L11. (Thresholds TL1 = TL2 = 30,000, TL3 = 130, and TL4 = 180 worked well).

5. Results

5.1. Results using laws energy masks

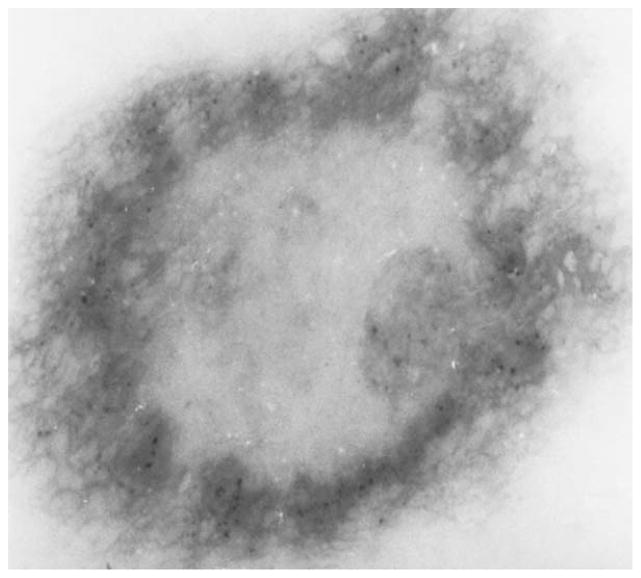
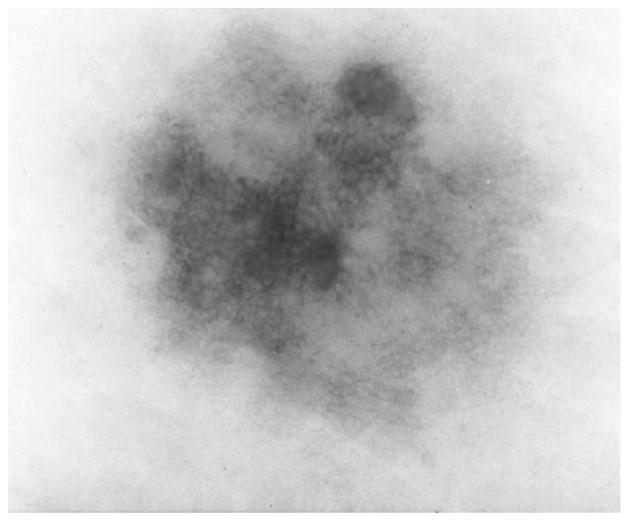
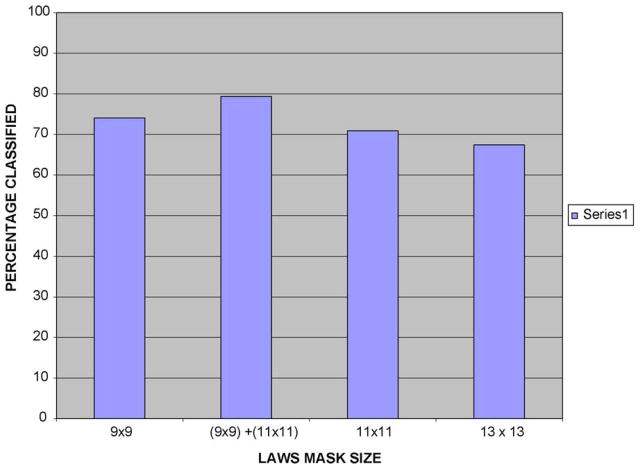
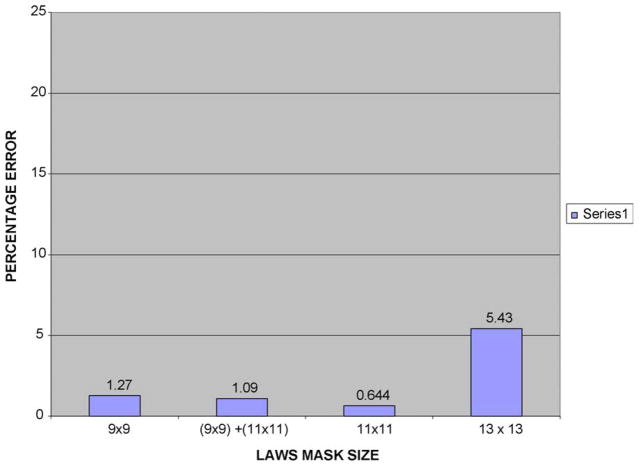
Note that pigment network can exist in both benign and malignant lesions. We chose to demonstrate the results using an image that well illustrates the differences in the algorithms. This image happened to be benign. Figs. 4–6 show the original image and the result of the pigment network finder at scales 9 × 9 and 11 × 11, respectively. These were the two scales that allowed the best results. In order to get best results from both scales, a weighted sum of the above masks was formed. This weighted sum was determined empirically to optimize results over combinations of two weights that summed to 100%. The 9 × 9 mask was weighted 40% and the 11 × 11 mask was weighted 60%. It can be seen from Fig. 7 that for the same image the weighted sum classifies better than either the 9 × 9 mask or the 11 × 11 mask. Note that although partial blocks are shown, these are not included in the analysis. Figs. 8 and 9 are examples showing the performance of the pigment network detection algorithm. The comparison of the performance of the various mask sizes on the image in terms of percentage classified and percentage error is shown in Figs. 10 and 11, respectively. It can be seen that for the combination of the 9 × 9 and 11 × 11 masks, the percentage classified is the maximum. The error in classification is less for the combined mask when compared to the 9 × 9 mask but slightly greater than for the 11 × 11 mask. The standard deviation of the different methods were high and hence a two-sample T test was conducted and the results proved the hypothesis that the combination of the 9 × 9 and 11 × 11 masks was better than the individual masks.

Fig. 4.

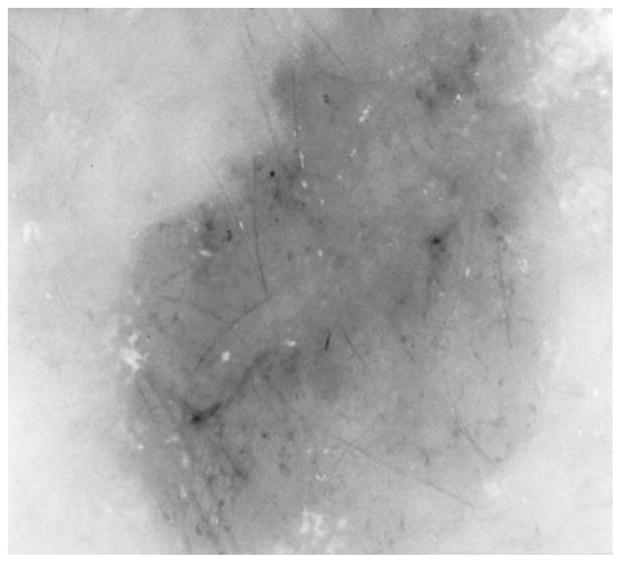
Dermatoscopy image of dysplastic nevus tumor having net-like pigment pattern at the periphery.

Fig. 6.

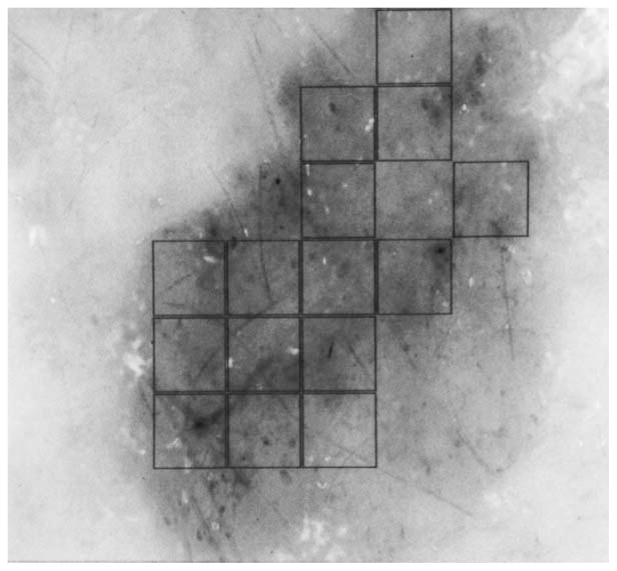
Result of pigment network finder using 11 × 11 mask.

Fig. 7.

Result of pigment network finder using the weighted combination of 9 × 9 and 11 × 11 masks.

Fig. 8.

Dermatoscopy image of benign nevus (108) with a relatively light pigment network covering nearly the entire tumor.

Fig. 9.

Result of pigment network finder.

Fig. 10.

Performance of Laws masks of different sizes on various images (percentage classified correctly).

Fig. 11.

Performance of Laws masks of different sizes on various images (percentage error).

For our 155-image set, a total of 2037 full blocks were tested. Fifteen blocks were classified as pigment network by the algorithm and not by the dermatologist. Four blocks were classified as having pigment network by the dermatologist and not having any network by the algorithm. The source of errors (success rate of considerably less than 100%) as shown in Fig. 10 is the presence of partial blocks.

Partial blocks, where pigment network is present over part of the 64 × 64 block, create a problem. Approximately 20% of all blocks have partial pigment network by either dermatologist or algorithm. It is this disagreement that leads to a success rate of around 80% shown in Fig. 10.

5.2. Results using NGLDM numbers

Fig. 12 shows the result of applying the NGLDM algorithm to the same image used to illustrate the previous algorithm in Fig. 8.

Fig. 12.

Result of pigment network finder using NGLDM numbers on benign nevus in Fig. 8.

5.3. Comparison of algorithms

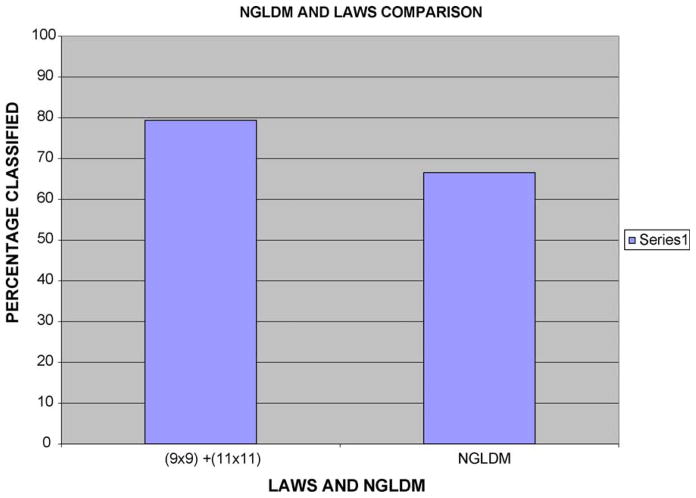
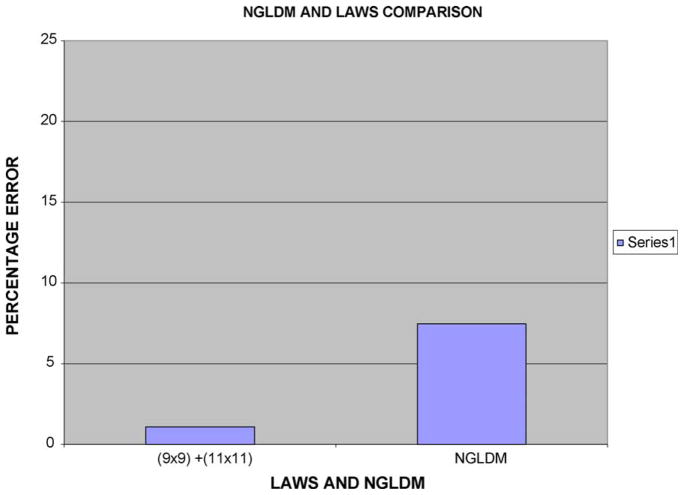
Both the algorithms were tested on the same set of 155 images and the results were compared with pigment network presence as determined by the dermatologist (WVS), scoring the whole lesion for presence or absence of pigment network. Figs. 13 and 14 show the performance in terms of the percentage classified, using algorithms shown in Figs. 2 and 3, and the percentage error, respectively. It can be seen that Laws energy masks did significantly better than the NGLDM. This was also proved using the two-sample T test. However, the Laws method fails on some cases as shown in Figs. 15 and 16 where the residue of Dullrazor [12], a hair removal program, causes an error in texture measure, leading to misclassification.

Fig. 13.

Comparison of algorithms using Laws and NGLDM numbers (percentage classified correctly).

Fig. 14.

Comparison of algorithms using Laws and NGLDM numbers (percentage error).

Fig. 15.

Dermatoscopy image of dysplastic nevus tumor with residual hair.

Fig. 16.

Result of pigment network finder showing erroneous classification.

6. Discussion

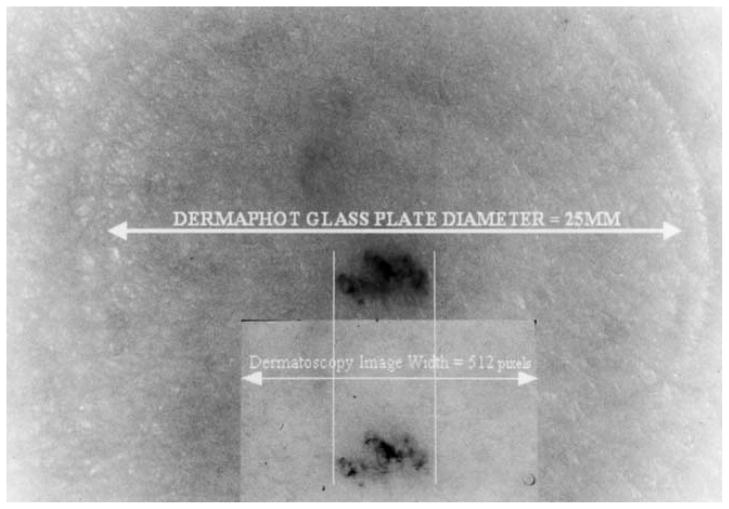
The NGLDM large number emphasis and Laws energy masks were used for the detection of the pigment network. It was observed that the pigment network finder using a combination of 9 × 9 and 11 × 11 masks did better than the NGLDM large number emphasis and the individual masks. The factors d and a used in calculating NGLDM numbers were chosen as optimum by experimentation. The fact that d = 5 optimizes the NGLDM measure implies a texture ‘unit’ width of about 10 pixels or 0.22 mm. Similarly the Laws filter dimensions appear to be optimized between 9 × 9 and 11 × 11. (The Laws filters must have an odd dimension by definition.) This again implies a repeating pigment texture unit or texel of 10 pixels or approximately 0.22 mm. Fig. 17 shows a clinical image taken after a dermatoscopy image was taken of the same lesion. The large circle seen is the imprint on the skin of the dermaphot glass plate used in taking the dermatoscopy image. It has a known diameter of 25 mm. The smaller rectangle shows the width of the dermatoscopy image, illustrating that the 512-pixel width of the dermatoscopy image corresponds to 11.9 mm, confirming the 10-pixel texel width of 0.22 mm.

Fig. 17.

Clinical image showing location of dermatoscopy image allowing scale factor of 512 pixels = 11.9 mm. Ten pixels, approximately 0.22 mm, correspond to optimal repeating texture unit by both Laws and NGLDM analysis.

The significance of the pigment network is in its association with a benign lesion. The pigment network is disrupted when malignant melanoma is present. We were able to observe three general patterns for benign lesions.

1. The pigment network is present over most of the lesion. The pattern was observed to be strongly correlated with a benign diagnosis (Figs. 7,9 and 12).

2. The pigment network is present in the center of the lesion. Often a lighter periphery is observed.

3. There is solid pigment in the center and pigment network at the periphery. This pattern is often present with dysplastic nevi. Fig. 4 shows the center-pigment-absent variety.

A skin lesion is typically benign if the network is present over most of the area of the lesion or if a light net exists or if there is network in the center or if there is solid pigment in the center and network in the periphery of the tumor. For early malignancy, the pigment pattern appears in only one portion of the tumor and is generally asymmetric.

7. Summary

The pigment network is an important feature of dermatoscopy images. A number of variants of the pigment network are critical in diagnosing malignant melanoma. In this study, two statistical texture determination methods are compared in detecting the pigment network, using the dermatologist’s determination of the pigment network as the gold standard. One hundred fifty-five dermatoscopy images were analyzed, including 62 malignant melanomas and 93 benign lesions. All digitized images were divided into 64 × 64 pixel blocks, and all blocks were classified as having no pigment network, partial or full pigment network. For the 155 images, a total of 49 × 155 or 7595 blocks were included in the study. Two experiments were performed. The first experiment (Section 4.3) was in optimizing results for the Laws energy filters. Using 7 × 7, 9 × 9, 11 × 11 and 13 × 13 masks, the optimal results were obtained between 9 × 9 and 11 × 11 masks. The best classification was obtained with the Laws method using a weight of 40% for the 9 × 9 masks and 60% for the 11 × 11 masks. For the 2037 full pigment blocks, four blocks were erroneously classified as having network by the dermatologist and not by the best Laws algorithm. For the 4585 blocks lacking pigment as classified by the dermatologist, all but fifteen are correctly classified by the algorithm using Laws energy masks. Approximately 20% were incorrectly classified because of determination of a full block or empty texture block as a partial block and vice versa. The second experiment (Section 4.2) compared the various NGLDM (neighborhood gray level dependence matrix) indices N1 through N5 and optimized the distance and intensity parameters d and a. It was found that the best results were obtained with the NGLDM large number emphasis (N2). These results were not as successful as those noted for the best Laws algorithm. It was noted that the optimal parameters for both methods implied a texture unit of about 10 pixels in the dermatoscopy images, which corresponds to a repeating texel of about 0.22 mm.

We have hypothesized that application of texture analysis can allow detection of the pigment network. Our work is somewhat different to the approach of other investigators, who identified and measured irregularities in the pigment network [8]. Instead of identifying irregularities, our method identifies grossly any pigment network that is present, as defined by texture measures, and therefore is not directly comparable to this previous work. We have shown that the NGLDM method and the LAWS developed by Laws can both detect the pigment network with reasonable accuracy, with somewhat better results obtained by the latter.

Fig. 5.

Result of pigment network finder using 9 × 9 mask. Note that the network finder requires a complete block and this misses some peripheral areas with incomplete blocks.

Biographies

Anantha Murali received his BE from the University of Mysore in Electrical Engineering and MSEE from the University of Missouri-Rolla. He is presently working with D2 Technologies. He interests include image processing, signal processing and computer vision.

Randy H. Moss received the BSEE and MSEE in Electrical Engineering from the University of Arkansas and the PhD from the University of Illinois at Urbana-Champaign, where he was a National Science Foundation graduate fellow. He is Professor of Electrical and Computer Engineering at the University of Missouri-Rolla where he has developed a machine vision course and laboratory. He is especially interested in medical applications of image processing and pattern recognition, vision systems for industrial robots, and automated inspection systems.

William V. (Van) Stoecker received the B.S. degree in Mathematics in 1968 from the California Institute of Technology, the M.S. in Systems Science in 1971 from the University of California, Los Angeles, and the M.D. in 1977 from the University of Missouri, Columbia. He is Adjunct Assistant Professor of Computer Science at the University of Missouri-Rolla and Clinical Assistant Professor of Internal Medicine-Dermatology at the University of Missouri-Columbia. He is past president of the International Society for Digital Imaging of the Skin (ISDIS). His interests include computer-aided diagnosis and application of computer vision to dermatology.