Using network properties to predict disease dynamics on human contact networks

Abstract

Recent studies have increasingly turned to graph theory to model more realistic contact structures that characterize disease spread. Because of the computational demands of these methods, many researchers have sought to use measures of network structure to modify analytically tractable differential equation models. Several of these studies have focused on the degree distribution of the contact network as the basis for their modifications. We show that although degree distribution is sufficient to predict disease behaviour on very sparse or very dense human contact networks, for intermediate density networks we must include information on clustering and path length to accurately predict disease behaviour. Using these three metrics, we were able to explain more than 98 per cent of the variation in endemic disease levels in our stochastic simulations.

1. Introduction

Recent global outbreaks of infectious diseases such as SARS, avian influenza and H1N1 influenza have illustrated the need for tools that allow public health officials to predict disease dynamics. Quantitative models offer such tools provided that they account for those elements of human contact structure and disease behaviour that most strongly impact disease dynamics. Traditional disease models, such as the ubiquitous susceptible–infected–recovered (SIR) model [1,2], assume that the host population is homogeneously mixed, meaning that each member of the population is equally likely to come into contact with every other member. This approach ignores the heterogeneous nature of human contact since we know that, in general, individuals only interact with a subset of the total population. Human social networks tend to be highly clustered [3,4] in the sense that any two of your friends are more likely to be friends themselves than two individuals chosen at random. This structure creates a non-uniform probability of interacting with an infected individual and a violation of the assumption of homogeneous mixing. Although homogeneous-mixing models have been surprisingly useful for increasing our understanding of disease dynamics generally [1], their utility diminishes as the contact network increases in heterogeneity.

There has been increasing recognition among disease modellers that the nuances of the contact structure among hosts in a population can have profound impacts on the spread of disease, which cannot be predicted by traditional homogeneous-mixing models [5–11]. This has led to an explosion in the use of modelling approaches based on graph theory that allow contacts between all individuals in a population to be modelled explicitly [12,13]. A graph consists of a set of nodes and a set of edges between those nodes. In this framework, contact networks are represented by graphs where nodes represent individuals and an edge between two nodes represents a contact between the individuals that would allow for disease transmission.

While graph theoretic approaches allow the incorporation of realistic contact structure, they are more complicated to implement because the status of individuals and their interactions must be explicitly modelled, resulting in complex models with many parameters that must be estimated [13]. Thus, network-based approaches typically do not lend themselves to straightforward analyses as do SIR-type models. Several studies have sought to address this problem by seeking correlations between easily measured properties of network structure and disease dynamics on the network. They ultimately seek to use these network properties to modify SIR models so as to incorporate the effects of structure [5,6,10,14,15]. This approach seeks to get the best of both worlds: the incorporation of important contact structure plus the analytic tractability of traditional SIR models.

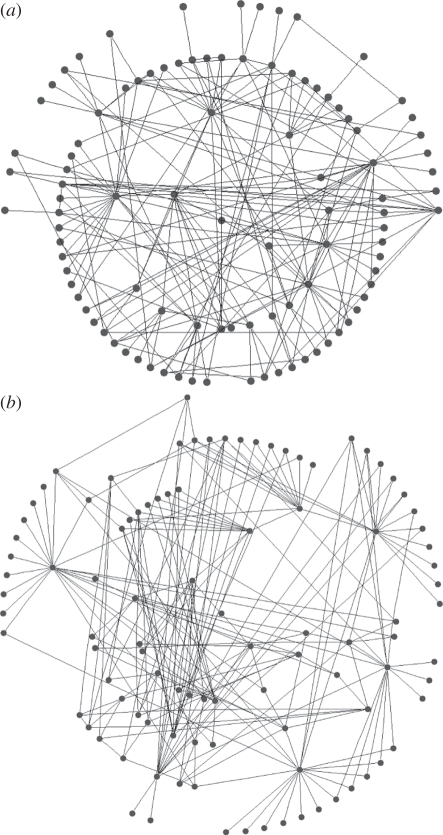
Contact networks are typically characterized by their associated degree distribution. The degree of an individual is the number of contacts, and the degree distribution of the network is the frequency distribution of the degrees of individuals in the network. Since two networks with identical degree distributions can differ structurally [16,17] (figure 1), focusing only on degree distribution may prove problematic if disease is influenced by elements of network structure other than degree distribution. In particular, models that fail to account for these structural elements may provide inaccurate predictions.

Figure 1.

An example of a 100 node (a) Bansal network and (b) Asano network that have identical exponential degree distributions, but differ substantially in other elements of network structure. Notice that the Asano network has most individuals with a single contact connected to just a few individuals; however, individuals with a single contact are more dispersed in the Bansal network.

Several studies have suggested that structural characteristics such as the level of clustering, mean degree and/or path length of the contact network (§2) should affect disease dynamics in certain classes of theoretical networks, such as random [8,18–20], small-world [4,19], scale-free [7,20] and lattice networks [18,20].

It has recently been demonstrated that the empirical human contact networks available in the literature are best described as having exponential degree distributions [6]. Despite this, very little is specifically known about the effects of network structure on diseases or exponential contact networks. Our study therefore focuses only on networks with exponential degree distributions because of their relevance to disease dynamics on human contact networks.

In this paper, we investigate how the structure of an exponential contact network impacts the spread of disease. To this end, we ask three pertinent questions. (i) Is degree distribution sufficient, by itself, to accurately predict disease behaviour, or are other measures of contact network structure required? (ii) Under what conditions do other measures of structure matter? (iii) What measures of network structure can improve predictions of disease outcomes? To answer these questions, we compare the outcomes of disease processes on pairs of networks that have identical exponential degree distributions but, by construction, differ with respect to other structural attributes. We show that these structural differences profoundly impact the dynamics of a disease process on human contact networks for diseases spread by close contact and endemic dynamics.

2. Methods

To assess the effect of contact structure on disease dynamics, while controlling for the effect of degree distribution, we generated pairs of networks such that each had an identical degree distribution but differed in other elements of structure. The first network in each pair was generated using an algorithm of Bansal et al. [6] and will hereafter be referred to as a Bansal network. This method involves generating an uncorrelated random network and then rewiring randomly selected edges until the network has an exponential degree distribution (see appendices A and C of [6]). The second network of the pair is generated using the algorithm of Asano [21] and will hereafter be referred to as an Asano network. The Asano algorithm takes as input the degree distribution of the Bansal network and deterministically generates another network that has the same exact degree distribution. An artefact of the Asano algorithm, which we exploit for our purposes, is that the resulting network is structurally different from the associated Bansal network (as noted below). Thus, the resulting network pairs have the same degree distribution, but differ substantially in other measures of structure, which we discuss in more detail below (figures 1 and 2). There are other algorithms (e.g. [22]) that can generate pairs of graphs with identical degree distributions that differ structurally, but we chose the Bansal and Asano algorithms because they were straightforward to implement and worked for our purposes. For this study, we consider only static, connected networks. In other words, the connections between individuals were fixed for the duration of the simulation, and every individual was connected to every other via at least one path. For each mean degree (3–16), we used 10 network pairs, with each network consisting of 10 000 individuals. This range of mean degrees is representative of empirical contact networks available in the literature [6].

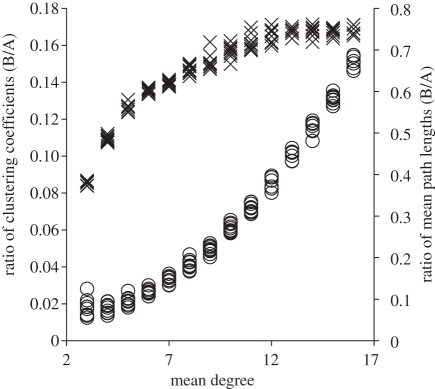
Figure 2.

The ratios of clustering coefficient and mean path length (Bansal network/Asano network) as a function of mean degree. Circles, clustering coefficient; crosses, mean path length.

For any given communicable disease, the absolute number of infected individuals at equilibrium tends to be higher on a dense contact network (i.e. a network with a large mean degree) than for a sparse network. In order to make reasonable comparisons of the differences in network attributes and model output between network pairs with different mean degrees, we looked at the ratio of the Bansal network value of a particular attribute to the Asano network value of that attribute. This gives a measure of the relative difference in magnitude between the networks in a pair that is comparable across mean degrees. If the value of the network attribute or measure of disease behaviour is similar for both networks in the pair, this ratio will be approximately 1. Systematic deviations of this ratio from 1 are indicative of structural differences affecting disease spread.

For each network, we measured a series of structural attributes (see the electronic supplementary material for details) related to clustering and distance across the network because these attributes have previously been shown to be important with respect to other classes of contact networks [3,4,17,18,23,24]. We measured two forms of clustering at the graph level. The first, transitivity, is the probability that two contacts of a node are themselves directly connected, averaged over the whole graph [24,25]. The second, called the clustering coefficient, removes effects of degree correlations from transitivity [26]. We found that the transitivity and clustering coefficient of the networks in our study were virtually identical, and their values were one to two orders of magnitude smaller for the Bansal networks than for the Asano networks (figure 2). Thus, individuals in the Asano contact networks were much more clustered than those in the corresponding Bansal contact networks.

To determine the size of the network in terms of the ‘distance’ across the contact network from the perspective of a spreading pathogen, we measured three related network attributes. We started by calculating the set of minimum path lengths between each pair of individuals in the network. The mean path length of the network is the mean of this set. The maximum of this set is the diameter of the network. If, for each individual in the network, we find the longest minimum path length to another individual, the minimum value across all individuals is the radius of the network. When comparing the Bansal networks with Asano networks, we found that the ratios of diameter (Bansal/Asano) remained relatively constant across mean degrees (mean = 0.73, s.d. = 0.06), and the ratio of radii was similar (mean = 0.79, s.d. = 0.07). The story is slightly more complicated for the mean path length. The ratio increases with mean degree until saturating near 0.75 for mean degrees above 10 (figure 2). Together, these measures demonstrate that the average distance a pathogen must travel from one member of the population to another arbitrary individual is much larger for the Asano networks than for the Bansal networks.

Based on the systematic differences in both the clustering and distance metrics, it is clear that although each graph in a pair shares an identical degree distribution, they differ markedly in key elements of structure. Admittedly, the graphs may also differ in other, unmeasured aspects of structure. However, different network statistics often capture similar aspects of structure and can be highly correlated with one another. Thus, we have focused on network characteristics that are common in other studies.

The disease process was simulated using a stochastic version of an SIRS model [1]. In this version of the SIR model, there are susceptible, infected and recovered classes, but recovered individuals lose immunity, becoming susceptible again. Also, there are no birth or death processes incorporated in the model. Because of this, there is a constant population and contact structure for the duration of the simulation. The underlying deterministic model is described by:

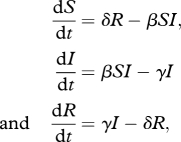where β is the rate at which susceptible individuals contract the disease when exposed to infection, γ is the rate at which infected individuals recover from the disease and δ is the rate at which recovered individuals lose immunity and become susceptible again. Since these parameters describe important epidemiological properties of diseases, varying these parameters is equivalent to examining a range of different diseases. We used Gillespie's direct algorithm [27] to implement a stochastic version of the SIRS model on each network. We ran 200 realizations of the disease process on each network using randomly selected sets of 20 initial infected individuals for each realization. Each realization ran until the transient behaviour ended. Subsequently, we used the last 200 iterations of the model to evaluate the result of the disease process at stochastic equilibrium.

To measure the performance of a disease for a particular contact network, we used the average number of infected individuals at stochastic equilibrium (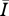). As with the aforementioned network attributes, we consider the ratio of Bansal network 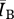to the Asano network 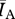to derive a metric comparable across network pairs. We refer to this ratio as 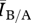. As before, systematic deviations of this ratio from one indicate that differences in network structure impact disease behaviour.

For each network in the study, we also measured the basic reproductive number, R₀ [1], for a range of parameter sets, in order to determine whether the differences in structure between networks had an appreciable impact on the transient phase of disease spread. These parameter values were chosen empirically because they resulted in the greatest difference in disease outcomes between network types and were qualitatively representative of the behaviour across the range of parameters tested. We started with an entirely susceptible population, chose a random individual to infect and then counted the number of secondary cases resulting from contact with the original infected individual. We repeated this process 1000 times for each contact network in the study, using a different randomly selected individual for each realization. We used the average number of secondary cases across all 1000 realizations as the R₀ value for each contact network. A thousand realizations were empirically determined to be more than sufficient for the mean to converge to its average value.

3. Results

(a). Network structure and R₀

The R₀ values measured on our networks ranged from an average of 0.74 for networks of mean degree 3 to an average of 12.24 for networks of mean degree 16. R₀ increased linearly with mean degree for both Asano and Bansal networks, with all networks with mean degree 4 and higher having R₀ > 1. We found that there was no identifiable trend in the ratio of R₀ (Bansal/Asano), but the mean of 0.975 was statistically different from 1 (two-sided t-test, p < 0.0001). Although this suggests that R₀ for Bansal networks is slightly lower, it is not clear that this is biologically relevant rather than an artefact of the stochastic simulation. R₀, as we have measured it, should be largely determined by the degree distribution, so we would expect the ratio (Bansal/Asano) to be close to 1. For each network, we averaged the measured R₀ for 1000 different nodes. Because of this, the resulting R₀ measure can be influenced by the random selection of many highly and/or weakly connected nodes. This may explain why the ratio was extremely close to, but not quite, 1.

The range of R₀ values we measured on our networks is consistent with ranges of R₀ values measured from empirical data for other human diseases spread by close contact, such as measles (4.4–11 [28]), H1N1 influenza (2.68 [29]), SARS (0.54–2.65 [30]) and smallpox (1.66–1.42 [30]). A more rigorous comparison with empirical R₀ values may not be appropriate since empirical studies rarely incorporate information on network structure, although other results from our study (below) suggest that network structure can be unimportant in some contexts.

(b). Is degree distribution sufficient to accurately predict disease behaviour?

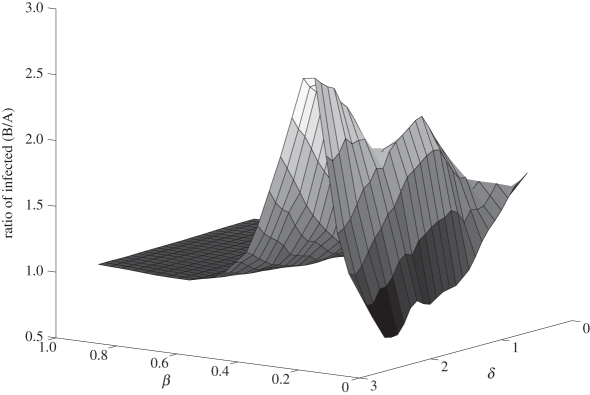
If degree distribution were a sufficient measure of network structure for predicting disease outcomes, then we would expect that the same disease should behave similarly on two contact networks with identical degree distribution. For our model, this corresponds to the case where the ratio 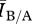≈ 1. To test this, we varied the disease parameters β, δ and γ factorially over a broad range of values (i.e. many possible diseases) for a network pair of each mean degree in order to determine the effect of network density on disease behaviour. Figure 3 shows an example for fixed γ and mean degree. For each network density, there were broad regions of parameter space where 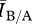at equilibrium is roughly constant and close to 1 (≈0.97), indicating a small and predictable effect from differences in structure between networks in a pair for most diseases. There were, however, significant regions of parameter space where 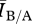was systematically larger than 1, indicating that the Bansal networks consistently have more infected individuals at equilibrium than the associated Asano networks for these types of diseases. In one case, the Bansal value of equilibrium number of infected individuals was more than five and a half times larger than the associated Asano network value. The behaviour is qualitatively similar for all graph densities, but the regions of parameter space where structure had the most impact differed slightly for each mean degree. This result demonstrates that knowledge of the degree distribution alone is generally insufficient to explain disease behaviour on contact networks.

Figure 3.

The ratio (Bansal/Asano) of the average number of infected individuals at equilibrium as a function of the disease parameters β (rate of infection) and δ (the rate of loss of immunity) for a typical graph (mean degree = 8). The rate of recovery, γ, is held constant (γ = 1.2).

(c). Under what conditions do other measures of structure matter?

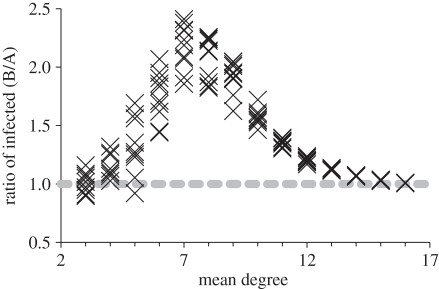
To investigate the conditions under which structure matters for a particular disease, we present an illustrative set of parameter values (β = 1.2, γ = 1.2, δ = 0.2) and associated simulations of the disease process on many network pairs of each mean degree. We examined a range of parameter sets and found the results to be qualitatively similar. In general, 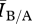was nearly always greater than 1 for the representative parameter set, indicating that the endemic level of infection was universally higher on Bansal networks than on Asano networks. We found that for intermediate densities (mean degrees between about 7 and 10), the Bansal 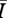was more than 50 per cent higher than that of the associated Asano network (figure 4). For low-density network pairs (mean degrees 3–4), the ratio of the values was near 1 with relatively large variance, while for higher-density networks (mean degrees greater than 12), the ratio of values was also near 1, but with relatively small variance. To give a sense of the difference in disease behaviour in absolute terms, the largest absolute difference in this set of model runs occurred for a graph pair of mean degree 10, where 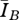= 1788 individuals and 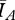= 1039 individuals. The difference (749 individuals) is 7.5 per cent of the population.

Figure 4.

The ratio (Bansal/Asano) of the average number of infected individuals at equilibrium as a function of the mean degree of the network. Systematic deviations from a ratio of 1 (grey dashed line) indicate that network structure affects disease processes.

From this result, we can see that for both relatively sparse contact networks (mean degrees 3–4) and relatively dense contact networks (mean degrees greater than 12) 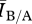≈1, implying that degree distribution alone is a sufficient predictor of disease behaviour. For intermediate densities (mean degrees 5–11), 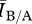is systematically greater than 1, suggesting that differences in network structure other than degree distribution are impacting disease behaviour.

(d). What measures of network structure increase prediction accuracy?

For intermediate density networks (mean degree 5–11), we must explain the relationship between the differences in disease behaviour on the Bansal and Asano networks and the structural properties of those networks. Previous studies of other network types have hypothesized that disease dynamics should be affected by the level of clustering and mean path length of the contact network [3,4,17,18,20,23,24], and we have shown that disease spread on the networks in each pair systematically differs with respect to those metrics.

For this portion of the study, we combined data from both the Bansal and Asano network simulations (for mean degrees 5–11) rather than using the pair-wise ratios so that we could determine which structural properties best explain 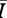across network types. We constructed a series of linear regression models using mean degree, clustering coefficient and mean path length as covariates (table 1). Using the R statistical package (R v. 2.7.0), we fitted the models and used Akaike's information criterion (AIC) [31] to select the best model from among the candidate set (table 1).

Table 1.

Regression models used to relate the network attributes mean degree (MD), mean path length (MP) and clustering coefficient (CC) to disease behaviour (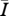) for networks of intermediate density (mean degrees 5–11 only). AIC values are provided to rank model performance, with the lowest AIC values indicating models most supported by the data.

model	R2	AIC
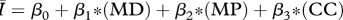	0.984	−170
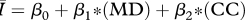	0.932	28
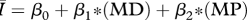	0.898	84
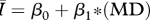	0.848	137
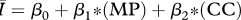	0.633	260
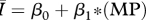	0.464	311
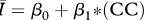	0.156	373
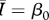	0	724

While all four of the top models (as indicated by the lowest AIC values) contain mean degree as a covariate, the model containing only mean degree has the poorest explanatory power of the four, though it still explains approximately 85 per cent of the variation. The model containing mean degree and mean path length and the model containing mean degree and clustering coefficient were also quite successful, with R² ≈ 0.90 and R² ≈ 0.93, respectively. The full model, containing mean degree, clustering coefficient and mean path length, was the top rated model (with the lowest AIC value) and was far and away the most successful predictor of 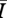, explaining more than 98 per cent of the variation.

4. Discussion

We were interested in understanding how the results of disease processes are impacted by the structure of human contact networks. Although much work has been done on the effects of structure on disease spread in many classes of networks, very little work has been done for networks with exponential degree distributions, which best describe empirical human contact networks [6]. We found that differences in network structure had no meaningful influence on the ratio of measured R₀ values across mean degrees, and thus no relationship between the ratio of R₀ values to .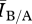

We did find that, regardless of network density, there were broad ranges of parameters (i.e. many diseases) for which the average number of infected individuals at stochastic equilibrium between pairs of networks was roughly the same, indicating a small and predictable difference in disease dynamics between these networks (figure 3).

On the other hand, we found that there were many diseases for which disease behaviour on the Asano and Bansal networks differed substantially (figures 3 and 4). Since the networks in each pair had identical degree distributions, it follows that other structural differences between networks in each pair must be driving differences in disease dynamics. The ratio of the average number of infected individuals at stochastic equilibrium is approximately 1 for low-density networks (mean degrees 3–4) and for high-density networks (mean degrees 12+), but is substantially larger than 1 for intermediate degrees (figure 4). We speculate that this humped shape is the result of multiple competing processes, such as the relative importance of global or local connectivity.

For the relatively dense networks (mean degree 12+), the convergence of 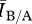to 1 is the result of the finite size of the contact network. For a fixed number of individuals (n), as the mean degree increases toward n, a network approaches a complete graph, which is a network where every individual is directly connected to every other. From the perspective of the pathogen, there are more pathways to spread, and the distance between any two individuals is shorter. In effect, the pathogen is better able to take advantage of the global connectivity of the network. As density increases and the networks approach a complete graph, the networks become so highly connected that most individuals are connected to a sufficient number of other individuals for the network to appear homogeneously mixed to the pathogen. In these cases, the high level of connectivity overrides the effects of the other elements of structure.

For relatively sparsely connected networks (mean degree 3–4), there are so few connections between individuals that there are few opportunities for the disease to spread. The two graphs in each pair structurally differ in terms of clustering and path length (figure 2), but these are global properties of the whole network. It is important to recognize that individuals in these sparse networks have so few connections that the two networks are very similar at the local level, making it hard for the disease to ‘see’ the global properties of the network. In other words, from the perspective of the disease, the two networks appear locally identical, resulting in similar behaviour. This is confirmed by the fact that the R₀ values, a measure of local spread, for networks with the same degree distribution were roughly the same, regardless of other differences in structure. The larger variance in 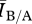associated with sparse networks compared with denser networks (figure 4) is probably the result of disease behaviour being dependent on highly connected individuals being initially infected.

In the cases of both very low- or relatively high-density networks, other local and global processes, respectively, overshadow the effects of structure, such as clustering or path length. This trade-off between local and global network properties has been shown in a number of different types of networks [32]. This is good news for those wishing to use models that assume a homogeneously mixed population. Relatively high-density and low-density networks represent cases where modifications to SIR models based on measures of degree distribution alone (such as mean degree) probably will be successful at representing pathogen dynamics in these populations. In a spatial context, there have been several cases where disease dynamics for an empirical contact network have been successfully modelled without needing to incorporate fine-scale network structure (e.g. fast-spreading farm animal disease such as foot-and-mouth [33]; or plague [34]), probably because of the mean degree of these empirical networks.

In the case of intermediate density networks, where structure impacts disease behaviour, we showed that the variation in disease performance is almost entirely explained by mean degree, mean path length and clustering coefficient (table 1). This strongly suggests that some combination of these terms can be used to correct an SIR model to account for the structure of the network. Studies on other network types have shown that degree variance is important for predicting disease behaviour on those networks [23]. With an exponential distribution the variance is the square of the mean, so they are functionally related, and this may explain why we did not need to include it for these networks. Given that mean degree can explain 85 per cent of the variance in 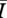for intermediate density networks, and can explain nearly all the variation for very sparse and very dense networks, it is fair to ask why one might go to the trouble of incorporating other contact network structure.

We have shown that, for certain diseases, we can explain an additional 14 per cent of the variation in disease behaviour by using the mean path length and clustering coefficient of the network. It is also worth noting that the second best model contains mean degree and clustering coefficient (table 1). These two properties should be relatively straightforward to estimate empirically by sampling members of the network (with interviews) since they depend only on local information. Underestimating the impact of a disease can lead to an inadequate public health response, while overestimations can lead to misallocation of limited public health resources. By incorporating additional structure, we can significantly improve our predictions of endemic levels of the disease and thereby improve our public health response.

Our results are consistent with a number of studies on different classes of networks that have found that network structural properties such as clustering and path length impact the spread of disease [4,7,8,18–20]. They are also consistent with the more recent work of Boily et al. [35] on scale-free networks, which demonstrated that macro-scale measures of structure (e.g. degree distribution) are insufficient, by themselves, for understanding disease outcomes on those networks. For exponential networks we have gone further and quantitatively analysed the conditions under which degree distribution is or is not sufficient to describe the outcome of disease processes, and linked this with an intuitive explanation based on global and local connectivity. We expect that the specific effects of structure such as clustering would be different for other types of network degree distributions. We have focused on exponential degree distributions exclusively since they have been shown to best describe empirical human contact networks available in the literature [6].

Depending on the nature of the disease in question, the outcome of disease processes may be very different for two human contact networks that have identical exponential degree distributions but that differ with respect to other structural properties. Our results show that, for very sparse or very dense networks, knowledge of the degree distribution of a contact network is generally sufficient to predict disease behaviour on the network. For networks of intermediate density, different structural attributes have a profound impact on disease behaviour. By including the clustering coefficient and mean path length along with the mean degree of the contact network, we can reduce the uncertainty of our model predictions of disease performance (by nearly 14%).