Abstract
Background and Aims
Girdling, or the removal of a strip of bark around a tree's outer circumference, is often used to study carbon relationships, as it triggers several carbon responses which seem to be interrelated.
Methods
An existing plant model describing water and carbon transport in a tree was used to evaluate the mechanisms behind the girdling responses. Therefore, the (un)loading functions of the original model were adapted and became a function of the phloem turgor pressure.
Key Results
The adapted model successfully simulated the measured changes in stem growth induced by girdling. The model indicated that the key driving variables for the girdling responses were changes in turgor pressure due to local changes in sugar concentrations. Information about the local damage to the phloem system was transferred to the other plant parts (crown and roots) by a change in phloem pressure. After girdling, the loading rate was affected and corresponded to the experimentally observed feedback inhibition. In addition, the unloading rate decreased after girdling and even reversed in some instances. The model enabled continuous simulation of changes in starch content, although a slight underestimation was observed compared with measured values.
Conclusions
For the first time a mechanistic plant model enabled simulation of tree girdling responses, which have thus far only been experimentally observed and fragmentally reported in literature. The close agreement between measured and simulated data confirms the underlying mechanisms introduced in the model.
Keywords: Feedback inhibition, girdling, loading, mechanistic plant modelling, phloem turgor, photosynthesis, Quercus robur L., stem diameter variations, transport model, unloading
INTRODUCTION
Girdling, or the complete removal of a strip of bark around a tree's outer circumference, is often used as a practical application to promote flowering, to improve fruit-set/growth (Williams and Ayars, 2005; Mahouachi et al., 2009) and as a means to fell the tree (Reque and Bravo, 2007). In addition, girdling is used as a research tool (1) to study apical dominance (Wilson and Gartner, 2002), (2) to quantify xylem and phloem flow towards growing fruits (Fishman et al., 2001; Morandi et al., 2007), (3) to study the hydraulic properties of the wood (Wilson and Gartner, 2002; Zwieniecki et al., 2004; Salleo et al., 2006; Domec and Pruyn, 2008), (4) to quantify the different contributions of several components to soil respiration (Hogberg et al., 2001, 2009; Johnsen et al., 2007; Chen et al., 2010) and (5) to study the processes involving bark regeneration (Mwange et al., 2003; Pang et al., 2008). Girdling is also the ideal research tool to investigate tree carbon relationships, because this destructive manipulation triggers several carbon-related responses: (1) a decrease in photosynthesis due to a feedback inhibition (e.g. Iglesias et al., 2002; Urban and Alphonsout, 2007; Cheng et al., 2008; Rivas et al., 2008; De Schepper et al., 2010), (2) an increase of starch and sugars in the leaves (Myers et al., 1999; Iglesias et al., 2002; Cheng et al., 2008; Mahouachi et al., 2009) and in the bark above the girdled zone of trees with little or no fruits (Daudet et al., 2005; Cheng et al., 2008; De Schepper et al., 2010), (3) an increase and decrease of respiration above and below the girdled zone, respectively (Wang et al., 2006; Johnsen et al., 2007), and (4) a change in stem growth (an increase of growth above the girdled zone and a decrease of growth below the girdled zone). All these carbon-related responses occur simultaneously after girdling and appear to be interrelated. As dynamic process-based models allow us to study such complex and integrated systems, they are useful to investigate the mechanisms underlying these correlated girdling responses. In this study, we therefore used a mechanistic plant model describing the water and carbon transport in a single tree (De Schepper and Steppe, 2010) to evaluate some of the mechanisms underlying and/or triggering the set of above-mentioned girdling responses. These mechanisms are often difficult to confirm experimentally, because variables, such as phloem turgor and (un)loading rates, are extremely demanding and difficult to measure.
MATERIALS AND METHODS
Plant material and experimental set-up
A 3-year-old oak tree (Quercus robur L.) was used as a model plant. The tree, growing in a 50-litre container, was placed in a growth chamber at the Laboratory of Plant Ecology (Ghent University, Belgium) with dimension 2 × 1·5 × 2 m (height × width × length). At the beginning of the measurements, the tree was 1·8 m high and had a stem diameter of 21·4 mm at soil surface. The growth chamber allowed us to control radiation and air temperature, while relative humidity of the air fluctuated freely depending on radiation, air temperature and the transpiration rate of the tree. The tree was watered every 2–3 d to ensure that the potting mixture remained adequately watered, with the average soil water potential being –0·004 MPa. During a first experimental period, from 26 to 28 August [day of year (DOY) 239–241], no manipulations were performed on the tree, representing non-stressed well-watered conditions. On 29 August (DOY 242) the tree was girdled. Two 3-cm-wide bands were carefully detached from the xylem at a height of 27 and 36 cm above the soil surface, respectively. The thickness of the bark layer was approximately 1·2 mm. This manipulation divided the stem into three parts. The part between the two girdled bands is of no interest for the present modelling study, in which we focused only on the two remaining stem parts. Hereafter, the stem part positioned above the upper girdled zone will be referred to as the upper stem zone (U) and the stem part positioned below the lower girdled zone as the lower stem zone (L) (De Schepper et al., 2010). After girdling, the xylem tissue was covered with aluminium foil to prevent dehydration. On 7 September (DOY 251), the aluminium foil was lifted to remove the wound tissue formed. Hence, two manipulations were performed during the experiment: girdling at DOY 242 and wound tissue removal at DOY 251.
Plant and microclimate measurements
Leaf net photosynthesis of the oak tree was continuously measured with a branch bag connected to an infrared gas analyser (IRGA-225-MK3 CO2; ADC, Hertfordshire, UK). Air from the growth room was blown into the branch bag at a rate of 0·8 L min−1. Every hour the incoming and outgoing air of the branch bag was measured. These hourly measurements were further corrected for a zero measurement, taking possible drifts of the zero point readings of the IRGA into account. The branch bag was installed at a first-order branch at a height of 128 cm and contained a leaf area of 68·5 cm2. More technical details about this measurement can be found in De Schepper et al. (2010).
Transpiration was estimated with a sap flow sensor based on the heat balance principle (SGA10; Dynamax Inc., Houston, TX, USA), following the approach of Steppe et al. (2005). The sensor was thermally insulated with several layers of aluminium foil. Sheath conductance of the gauge was recalculated daily using the minimum value observed during the dark period between 0000 and 0600 h. This sensor was installed at the main stem with a thickness of 1·4 cm and at a height of 130 cm.
Variations in stem diameter were continuously measured with linear variable displacement transducers (LVDTs) (model DF5·0; Solartron Metrology, Leicester, UK). One LVDT was installed above the girdled zone in U at a height of 40 cm, while a second LVDT was installed below the girdled zone in L at a height of 28 cm. Both LVDTs were supported by a custom-made stainless steel frame. No temperature correction was needed for this support system (Steppe and Lemeur, 2004).
The microclimate around the tree was characterized by continuous measurements of photosynthetic active radiation (Li-190S; Li-COR, Lincoln, NE, USA), soil water potential (SWT6; Delta-T, Cambridge, UK), relative air humidity (Hygroclip S; Rotronic, AG Schweiz, Bassersdorf, Switzerland) and air temperature (copper–constantan thermocouple; Omega, Amstelveen, the Netherlands). All sensor signals were logged at 10-s intervals and 5-min means were stored using a data logger (DL2; Solartron Metrology, Leicester, UK).
Measurements of starch content were performed on bark samples. The removed band of bark was collected on the day of girdling and two samples, a sample in U and a sample in L, were collected at the end of the experiment. All samples were immediately frozen in liquid nitrogen and stored at –80 °C. The bark samples were ground and treated with ethanol at 45 °C to extract the soluble sugars, which were analysed using high pH anion-exchange chromatography with pulsed amperometric detection (Dionex, Sunnyvale, CA, USA; CarboPac MA1 column with companion guard column; eluent: 50 mm NaOH, 22 °C). The remaining ethanol-insoluble material was washed and treated with 1 m HCl for 2 h at 95 °C to hydrolyse starch. Starch content was determined spectrophotometrically at 340 nm by the enzymatic reduction of NADP+ (UV-vis, Biotek Uvikon XL, Winooski, VT, USA).
Three similar experiments are reported and extensively discussed in De Schepper et al. (2010). The experiment in the present modelling study shows the typical expected behaviour of a tree after girdling. In addition, continuous measurements are available during the entire experimental period. For these reasons, the experiment was selected as a benchmark example.
MODEL DESCRIPTION
Original model
An existing model describing the water and carbon transport in a single tree (De Schepper and Steppe, 2010) was used to simulate the girdling event. Besides water and carbon transport, this model simulates stem diameter variations, respiration and starch conversion. The model incorporates the main concepts of leading water and carbon transport models in the literature (Daudet et al., 2002; Hölttä et al., 2006; Steppe et al., 2006; De Pauw et al., 2008; Lacointe and Minchin, 2008).
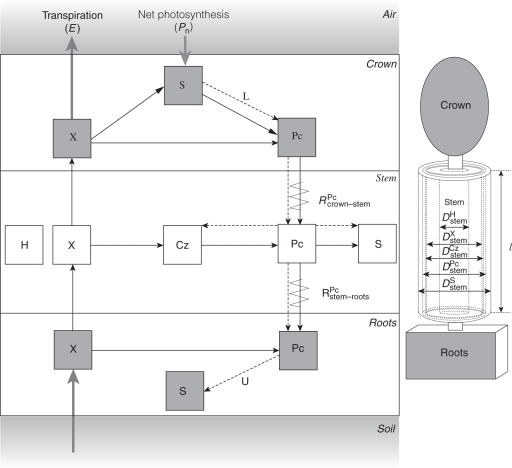
The model tree is divided into three vertical main compartments (Fig. 1): crown, stem and roots. Each main compartment is divided into several radial sub-compartments representing different tissues. Both the crown and the root compartment consists of three sub-compartments: xylem vessels (X), phloem tubes (Pc) and storage cells (S). The stem compartment has five sub-compartments: heartwood (H), conductive xylem vessels (X), cambial zone (Cz), conductive phloem (Pc) and cortex with a storage function (S). These stem tissues are modelled as five coaxial cylinders (Fig. 1). Each sub-compartment is separated from its radial adjacent sub-compartment by a virtual semi-permeable membrane, while no membranes are involved between vertical adjacent compartments, as X contains perforation plates and Pc sieve plates.
Fig. 1.
Diagram with model compartments (X, conductive xylem; Pc, conductive phloem; S, storage cells; Cz, cambial zone) and water (full line) and sugar (dotted line) transport. This transport can occur in both directions: the flow is considered positive when it is in the direction of the arrow and negative when it is in the opposite direction. The stem consists of five coaxial cylinders with length l and with diameter D. Each cylinder represents a stem tissue: heartwood (H), conductive xylem (X), cambial zone (Cz) and conductive phloem (Pc) and storage cell, e.g. cortex (S). DstemS is equal to the total stem diameter. The coaxial cylinders are separated from each other by virtual membranes. RPccrown–stem and RPcstem–roots represent the phloem resistances which are changed during the girdling experiment.
Transpiration is used as input variable for the water transport sub-model, because it starts a chain of water movement events throughout the entire tree. Water is moving vertically between the main compartments along xylem and phloem pathways (Fig. 1). As no membranes need to be crossed, this vertical flow is driven by differences in pressure potential. In the case of radial flow (Fig. 1) where membranes prevail, the radial flow is driven by differences in total water potential.
Net photosynthesis is used as input for the carbon transport sub-model. In the phloem tubes, dissolved sugars are transported by flowing water according to the principle of mass flow. Loading and unloading functions are defined to be dependent on the sucrose concentration. Sugar and starch amounts are described by sucrose equivalents.
The concurrent water and carbon transport causes changes in water content in the different tissues. In the stem compartment, these changes are converted to volume and corresponding diameter changes (Fig. 1) from which the total stem diameter is calculated. Stem diameter variations are considered to consist of two components: reversible and irreversible variations (Steppe et al., 2006). Reversible stem diameter variations are described according to Hooke's law and represent mainly fluctuations in water content, while irreversible growth is based on Lockhart's equation (Lockhart, 1965). According to the latter equation, a threshold value must be exceeded before growth occurs.
Finally, respiration and starch conversion are taken into account in order to close the carbon balance. Respiration is the sum of two components: maintenance respiration, which is concentration dependent, and growth respiration, which is a function of the magnitude of growth. The conversion of excess sucrose into starch is driven by a target sucrose concentration. More details about the model description and its equations can be found in De Schepper and Steppe (2010).
Model adaptations
First, the sugar loading function of the original water–carbon transport model (De Schepper and Steppe, 2010) was modified to enable simulation of the girdling event. Feedback inhibition of photosynthesis could not be simulated with the original model, as loading was only a function of the sugar concentration in the leaves and not of the sink strength (Patrick et al., 2001). Therefore, a new loading equation was defined, which is a function of the turgor pressure in the phloem tubes (Daie, 1989; Patrick, 1994; Lalonde et al., 2003):
| (1) |
| (2) |
where rL is the loading rate (mg sucrose s−1), CScrown is the sucrose concentration in the storage tissue of the crown (mg m−3), Vmax,L (mg sucrose s−1) and KM,L (mg m−3) are kinetic parameters, b is a scaling factor (dimensionless), Γ2 is a threshold turgor (MPa) and PPccrown is the phloem turgor pressure in the crown compartment (MPa). This function is based on the experimental observations of Patrick (1994) showing that a minimal turgor pressure (Γ2) must be exceeded to make the release of photosynthates proportional to the turgor deviation from this minimal turgor set point (Γ2). When the phloem turgor is below the threshold turgor Γ2, the loading function (eqn 1) equals the loading function of the original model.
Secondly, the unloading function of the original model was changed to allow a bidirectional unloading rate. Depending on the tissue where the sucrose concentration is highest, sucrose will flow from the phloem tubes towards the root storage tissues or from the root storage tissues towards the phloem tubes, according to:
| (3) |
where rU is the unloading rate (mg sucrose s−1), kU is a kinetic parameter (m3 s−1), CPccrown is the sucrose concentration in the root phloem tubes (mg m−3) and CSroots the sucrose concentration in the root storage tissue (mg m−3). rU can be considered as (facilitated) diffusion, which is a common transport pathway when symplastic unloading takes place (Patrick et al., 2001).
Lastly, the axial resistance in the phloem tubes (RPc), which was a parameter in the original model, became an input variable. This allowed us to change the value of RPc at the days of manipulation (DOY 242 and 251).
Model simulations
The model is implemented in a self-written modelling and simulation software package STACI to solve the model equations numerically (Steppe et al., 2008; De Schepper and Steppe, 2010). The simulations are calculated with a fourth-order Runge-Kutta numerical integrator with adaptive step size (integrator settings: accuracy = 1 × 10−6 and maximum step size = 0·1 s) and the simulation results are plotted with time steps of 5 min, which is equal to the measurement frequency of the sensors used.
Initial values of tree-specific variables were derived from measurements of the tree dimensions (De Schepper and Steppe, 2010). Parameter values of the original model were obtained by fitting the measured and simulated stem diameter variations in a period before the girdling experiment (DOY 231–235). The calibration procedure and results are described in detail in De Schepper and Steppe (2010). The values of the new parameters (b, Γ2 and kU) and the input variable RPc were determined by manual model calibration using stem diameter variations. The values of RPc are given in Table 1 and the values of b, Γ2 and kU were set to 0·09, 0·4 MPa and 1·1 × 10−9 m3 s−1, respectively. The value of Γ2 is in the same order of magnitude as reported observations (Patrick, 1994).
Table 1.
Phloem resistance (RPc), which was an input variable, obtained after manual calibration, in the upper (U) and lower (L) stem zones
| Before girdling (DOY 238–240) | After girdling (DOY 241–250) | After wound tissue removal (DOY 250–254) | |
|---|---|---|---|
| Simulation of U | |||
| RPccrown–stem | 0·2 | 0·2 | 0·2 |
| RPcstem–roots | 0·2 | 1·45 | 13·2 |
| Simulation of L | |||
| RPccrown–stem | 0·2 | 1015 | 1015 |
| RPcstem–roots | 0·2 | 0·2 | 0·2 |
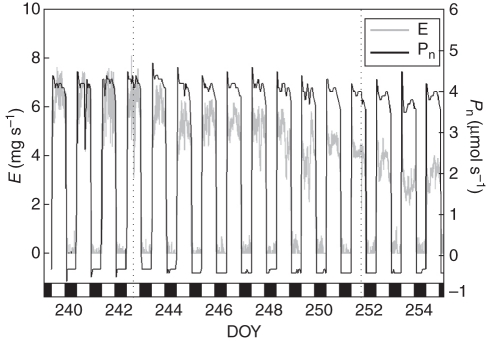
Results of the girdling experiment were simulated twofold: simulation of stem behaviour above and below the girdled zone, respectively. In the first simulation, the phloem resistance between stem and crown was considered constant and equal to the initially calibrated resistance, while the phloem resistance between stem and roots was increased dramatically after the girdling event (Table 1). Hence, the upper stem part became isolated from L and the root compartment after girdling (initial root part acted as L + roots during this simulation). During simulation of the stem part below the girdled zone, the phloem resistance between stem and roots remained unchanged, while the phloem resistance between stem and crown increased at both manipulations, causing the stem to be isolated from U and the crown compartment (initial crown part acted as crown + U during this simulation; Table 1). The results of the two simulations described the girdling responses as a whole. Figure 2 shows the input variables of the model: transpiration and photosynthesis. Note the controlled and constant conditions in the growth room.
Fig. 2.
Transpiration rate (E) and net leaf photosynthesis rate (Pn) used as input variables in the water–carbon transport model. The dotted lines indicate the time of manipulation: at day of the year (DOY) 242 girdling was performed and at DOY 251 wound tissue formed was removed. Black boxes on the axis correspond to the dark periods.
RESULTS AND DISCUSSION
Changes in stem growth
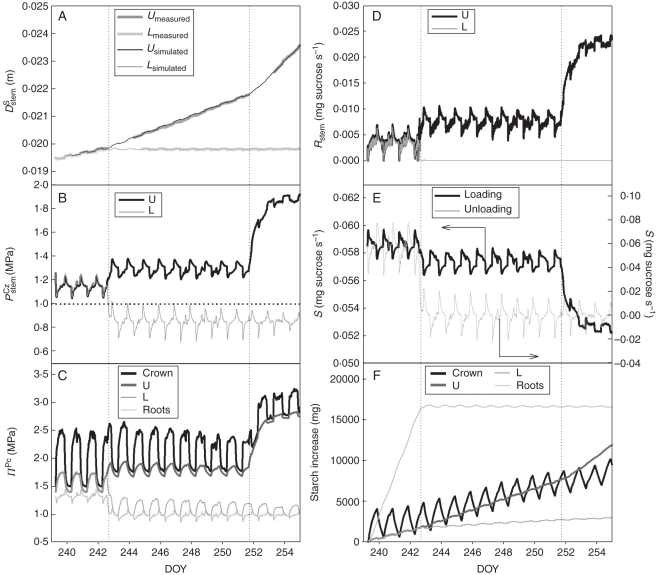
The adapted water–carbon transport model successfully simulated the measured changes in stem diameter variations before and after the girdling event (Fig. 3A). After girdling, simulated and measured stem growth accelerated in U and ceased in L. The simulated turgor pressure increased in the cambial zone of U after girdling. Modelled growth accelerated in U, because the pressure difference between simulated turgor pressure and the threshold pressure increased. In contrast, turgor pressure in L dropped below the threshold pressure causing growth to stop (De Schepper and Steppe, 2010; Fig. 3B). Gould et al. (2004) experimentally observed a similar increase in phloem turgor pressure above the cold block during cold-girdling. According to our model, this increased pressure in U after girdling is caused by an expected accumulation of sugars in the phloem tubes above the girdled zone, as sugars could no longer be transported towards the root sinks. Due to the modelled lateral exchange of sugars between phloem tubes and the cambial zone, the simulated cambial osmotic pressure increased correspondingly after girdling (Fig. 3C). Therefore, more water was drawn into the cambial zone causing a higher pressure and, hence, simulating accelerated growth. Because respiration was modelled as the sum of growth and maintenance respiration, simulated respiration changed in parallel to changes in growth rate after girdling (Fig. 3D): an increased respiration in U was observed, while a complete cessation occurred in L. In L, growth respiration diminished after girdling, resulting in a low respiration that equalled maintenance respiration. Similar changes in respiration were experimentally determined by Johnsen et al. (2007).
Fig. 3.
Model simulations of the oak tree responses before girdling, after girdling and after wound tissue removal (three periods are indicated by the vertical dotted lines): (A) comparison between simulated and measured data of total stem diameter (DSstem) for both the lower (L) and upper (U) stem zone; (B) simulated turgor pressure in the cambial stem zone (PCzstem) for the lower (L) and upper (U) stem zone – the horizontal dotted line represents the threshold turgor needed for growth; (C) simulated osmotic pressure of the phloem tubes (ΠPC) in the lower (L) and upper (U) stem zone, in the crown and in the roots; (D) simulated stem respiration (Rstem) in the lower (L) and upper (U) stem zone; (E) simulated sugar flow (S) represented as loading and unloading rates (the arrows indicate the corresponding y-axis scale); and (F) simulated starch content in the lower (L) and upper (U) stem zone, in the crown and in the roots (DOY: day of year).
Changes in (un)loading rate
In the period after girdling, the modelled loading rate gradually decreased in response to the increased turgor pressure in the crown phloem tubes (Fig. 3E). The decreasing loading rate caused an accumulation of sugars and starch in the leaves (Fig. 3F), which can explain the observed feedback inhibition in photosynthesis. This feedback inhibition can also be noted in the measured transpiration rate, and to a lesser extent in the photosynthesis data, indicating stomatal closure (Fig. 2; De Schepper et al., 2010). The inhibition became more pronounced after wound tissue removal (DOY 251). The simulated unloading rate decreased sharply after girdling and even reversed at some instances (Fig. 3E). This reversed unloading occurred because the sucrose concentration in the phloem tubes dropped below the sucrose level in the root storage tissue (eqn 3). Consequently, sugars from the roots became available for the stem in L. This was confirmed experimentally by the formation of new shoots and leaves in L (De Schepper et al., 2010).
Changes in starch content
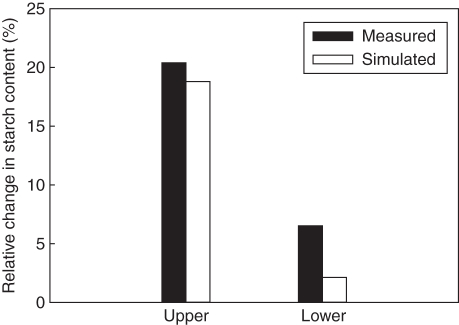
An increase in bark starch was simulated in U after girdling (Fig. 3F). In U, modelled sugar concentrations, and corresponding osmotic pressures, increased after girdling (Fig. 3C). These higher sugar concentrations caused a higher conversion of sugars into starch. According to the model, starch accumulation slowed down in the bark of L, but did not entirely stop. Immediately after girdling, the sugar concentration in the phloem tissue decreased, causing a reversed unloading in the roots. Due to this reversed unloading, sugar concentrations in the phloem were maintained at a higher concentration compared with those in the stem storage tissue. Therefore, sugar continued to leak from the phloem into the stem storage tissues where it was partially converted into starch. Hence, a slight increase in starch content of the bark was simulated in L. The simulated changes in bark starch content were compared with those measured by De Schepper et al. (2010) (Fig. 4). To estimate the measured increase 11 d after girdling, a linear increase in starch content with time was assumed. The initial mass of starch in the bark was calculated from the measured starch content before girdling and from the tree dimensions. Given this assumption regarding linearity, the model slightly underestimated the measured values, particularly in L (Fig. 4), but yielded realistic results. A similar change in sugar concentration has been experimentally observed in several girdling experiments (Daudet et al., 2005; Cheng et al., 2008; De Schepper et al., 2010).
Fig. 4.
Comparison between simulated and measured values of the relative change in starch content after girdling, compared with before girdling, in the upper and lower stem zone.
Information exchange
The first simulated response after girdling was the change in sucrose concentration in the direct vicinity of the manipulated zone. This caused a change in phloem turgor pressure, which was transferred to the other plant parts (crown and roots) by interconnecting phloem. Hence, phloem turgor pressure can be seen as a medium that transfers information between different plant parts. Thompson and Holbrook (2003) similarly concluded that pressure concentration waves function as a signal transfer in the phloem.
Effect of wound tissue
Interestingly, the simulated responses (Fig. 3) were less pronounced after the girdling event (DOY 242) compared with the action of wound tissue removal (DOY 251). After the first manipulation, the tree probably invested considerable energy and carbon in the formation of wound tissue in order to reconnect L and U. This wound tissue hence served as an alternative sink for carbon and as such partially substituted the root sink. Following the second manipulation, the physical reconnection between L and U disappeared together with the wound tissue. As new wound tissue did not reform, it could no longer function as a carbon sink nor as a connection between U and L. This behaviour is mathematically translated as higher RPc values during the period after wound tissue removal (Table 1).
Furthermore, the phloem resistances of the girdled zones have different calibrated values for simulations of U and L (Table 1), because the stem was girdled twice instead of once. As mentioned in the Materials and methods, the middle stem part enclosed by these two girdled zones was excluded from the current modelling study. However, this middle stem part is the reason why RPc values need to be different in the two simulations. Indeed, wound tissue formed where the bark was removed in order to reconnect the different stem zones (De Schepper et al., 2010). Due to this wound tissue formation, some sugars of U could still reach the middle and lower stem part after girdling, but the amount finally reaching the lower and middle stem part is not necessarily the same and depends on the amount of wound tissue formed and the buffering capacity of the middle stem part. Therefore, the amount of sugars transported downwards out of the upper stem part is higher than the amount of sugars received by the lower stem part. Hence, RPc during simulation of the upper stem part represents the girdling band between U and the middle stem part, while RPc during simulation of the lower stem part represents both girdling bands (the band between U and the middle stem part and the band between the middle stem part and L).
Conclusions
For the first time, a mechanistic plant model assessed the experimentally observed and previously published dispersed responses induced by girdling. To this end, an unloading and a loading rate, which are functions of the phloem turgor pressure, needed to be formulated. Once adapted, the water–carbon transport model (De Schepper and Steppe, 2010) could be used successfully to explain all responses by continuous simulating variables which are often difficult to measure experimentally (phloem pressure, sugar concentrations, etc.). By bringing together experimental knowledge of girdling responses, the model gives an integrated and more complete view of whole-tree-system behaviour related to water and carbon transport. Furthermore, the model confirms some underlying mechanisms that are difficult to estimate experimentally, such as turgor-dependent loading and information exchange by changes in phloem turgor. Our study therefore highlights that the combination of easy-to-perform plant measurements and mechanistic plant modelling is necessary to further improve our knowledge about tree functioning and that approaches embracing this combination will foster new and unique opportunities in plant science.
ACKNOWLEDGMENTS
We thank the Research Foundation – Flanders (FWO) for the PhD funding granted to V.D.S. We are also indebted to Philip Deman and Geert Favyts of the Laboratory of Plant Ecology for their accurate and enthusiastic technical support.
LITERATURE CITED
- Chen DM, Zhang Y, Lin YB, Zhu WX, Fu SL. Changes in belowground carbon in Acacia crassicarpa and Eucalyptus urophylla plantations after tree girdling. Plant and Soil. 2010;326:123–135. [Google Scholar]
- Cheng YH, Arakawa O, Kasai M, Sawada S. Analysis of reduced photosynthesis in the apple leaf under sink-limited conditions due to girdling. Journal of the Japanese Society for Horticultural Science. 2008;77:115–121. [Google Scholar]
- Daie J. Turgor-regulated sugar release from the source leaves of sugarbeet (Beta-Vulgaris L) Plant and Cell Physiology. 1989;30:1115–1121. [Google Scholar]
- Daudet FA, Lacointe A, Gaudillére JP, Cruiziat P. Generalized Münch coupling between sugar and water fluxes for modelling carbon allocation as affected by water status. Journal of Theoretical Biology. 2002;214:481–498. doi: 10.1006/jtbi.2001.2473. [DOI] [PubMed] [Google Scholar]
- Daudet FA, Ameglio T, Cochard H, Archilla O, Lacointe A. Experimental analysis of the role of water and carbon in tree stem diameter variations. Journal of Experimental Botany. 2005;56:135–144. doi: 10.1093/jxb/eri026. [DOI] [PubMed] [Google Scholar]
- De Pauw DJW, Steppe K, De Baets B. Identifiability analysis and improvement of a tree water flow and storage model. Mathematical Biosciences. 2008;211:314–332. doi: 10.1016/j.mbs.2007.08.007. [DOI] [PubMed] [Google Scholar]
- De Schepper V, Steppe K. Development and verification of a water and sugar transport model using measured stem diameter variations. Journal of Experimental Botany. 2010;61:2083–2099. doi: 10.1093/jxb/erq018. [DOI] [PubMed] [Google Scholar]
- De Schepper V, Steppe K, Van Labeke MC, Lemeur R. Detailed analysis of double girdling effects on stem diameter variations and sap flow in young oak trees. Environmental and Experimental Botany. 2010;68:149–156. [Google Scholar]
- Domec JC, Pruyn ML. Bole girdling affects metabolic properties and root, trunk and branch hydraulics of young ponderosa pine trees. Tree Physiology. 2008;28:1493–1504. doi: 10.1093/treephys/28.10.1493. [DOI] [PubMed] [Google Scholar]
- Fishman S, Genard M, Huguet JG. Theoretical analysis of systematic errors introduced by a pedicel-girdling technique used to estimate separately the xylem and phloem flows. Journal of Theoretical Biology. 2001;213:435–446. doi: 10.1006/jtbi.2001.2442. [DOI] [PubMed] [Google Scholar]
- Gould N, Minchin PEH, Thorpe MR. Direct measurements of sieve element hydrostatic pressure reveal strong regulation after pathway blockage. Functional Plant Biology. 2004;31:987–993. doi: 10.1071/FP04058. [DOI] [PubMed] [Google Scholar]
- Hogberg P, Nordgren A, Buchmann N, et al. Large-scale forest girdling shows that current photosynthesis drives soil respiration. Nature. 2001;411:789–792. doi: 10.1038/35081058. [DOI] [PubMed] [Google Scholar]
- Hogberg P, Bhupinderpal S, Lofvenius MO, Nordgren A. Partitioning of soil respiration into its autotrophic and heterotrophic components by means of tree-girdling in old boreal spruce forest. Forest Ecology and Management. 2009;257:1764–1767. [Google Scholar]
- Hölttä T, Vesala T, Sevanto S, Perämäki M, Nikinmaa E. Modeling xylem and phloem water flows in trees according to cohesion theory and Münch hypothesis. Trees. 2006;20:67–78. [Google Scholar]
- Iglesias DJ, Lliso I, Tadeo FR, Talon M. Regulation of photosynthesis through source: sink imbalance in citrus is mediated by carbohydrate content in leaves. Physiologia Plantarum. 2002;116:563–572. [Google Scholar]
- Johnsen K, Maier C, Sanchez F, et al. Physiological girdling of pine trees via phloem chilling: proof of concept. Plant Cell and Environment. 2007;30:128–134. doi: 10.1111/j.1365-3040.2006.01610.x. [DOI] [PubMed] [Google Scholar]
- Lacointe A, Minchin PEH. Modelling phloem and xylem transport within a complex architecture. Functional Plant Biology. 2008;35:772–780. doi: 10.1071/FP08085. [DOI] [PubMed] [Google Scholar]
- Lalonde S, Tegeder M, Throne-Holst M, Frommer WB, Patrick JW. Phloem loading and unloading of sugars and amino acids. Plant Cell and Environment. 2003;26:37–56. [Google Scholar]
- Lockhart JA. An analysis of irreversible plant cell elongation. Journal of Theoretical Biology. 1965;8:264–275. doi: 10.1016/0022-5193(65)90077-9. [DOI] [PubMed] [Google Scholar]
- Mahouachi J, Iglesias DJ, Agusti M, Talon M. Delay of early fruitlet abscission by branch girdling in citrus coincides with previous increases in carbohydrate and gibberellin concentrations. Plant Growth Regulation. 2009;58:15–23. [Google Scholar]
- Morandi B, Rieger M, Grappadelli LC. Vascular flows and transpiration affect peach (Prunus persica Batsch.) fruit daily growth. Journal of Experimental Botany. 2007;58:3941–3947. doi: 10.1093/jxb/erm248. [DOI] [PubMed] [Google Scholar]
- Mwange KN, Hou HW, Cui KM. Relationship between endogenous indole-3-acetic acid and abscisic acid changes and bark recovery in Eucommia ulmoides Oliv. after girdling. Journal of Experimental Botany. 2003;54:1899–1907. doi: 10.1093/jxb/erg204. [DOI] [PubMed] [Google Scholar]
- Myers DA, Thomas RB, DeLucia EH. Photosynthetic responses of loblolly pine (Pinus taeda) needles to experimental reduction in sink demand. Tree Physiology. 1999;19:235–242. doi: 10.1093/treephys/19.4-5.235. [DOI] [PubMed] [Google Scholar]
- Pang Y, Zhang J, Cao J, Yin SY, He XQ, Cui KM. Phloem transdifferentiation from immature xylem cells during bark regeneration after girdling in Eucommia ulmoides Oliv. Journal of Experimental Botany. 2008;59:1341–1351. doi: 10.1093/jxb/ern041. [DOI] [PubMed] [Google Scholar]
- Patrick JW. Turgor-dependent unloading of photosynthates from coats of developing seed of Phaseolus-Vulgaris and Vicia-Faba – turgor homeostasis and set points. Physiologia Plantarum. 1994;90:367–377. [Google Scholar]
- Patrick JW, Zhang WH, Tyerman SD, Offler CE, Walker NA. Role of membrane transport in phloem translocation of assimilates and water. Australian Journal of Plant Physiology. 2001;28:695–707. [Google Scholar]
- Reque JA, Bravo F. Viability of thinning sessile oak stands by girdling. Forestry. 2007;80:193–199. [Google Scholar]
- Rivas F, Fornes F, Agusti M. Girdling induces oxidative damage and triggers enzymatic and non-enzymatic antioxidative defences in Citrus leaves. Environmental and Experimental Botany. 2008;64:256–263. [Google Scholar]
- Salleo S, Trifilo P, Lo Gullo MA. Phloem as a possible major determinant of rapid cavitation reversal in stems of Laurus nobilis (laurel) Functional Plant Biology. 2006;33:1063–1074. doi: 10.1071/FP06149. [DOI] [PubMed] [Google Scholar]
- Steppe K, Lemeur R. An experimental system for analysis of the dynamic sap-flow characteristics in young trees: results of a beech tree. Functional Plant Biology. 2004;31:83–92. doi: 10.1071/FP03150. [DOI] [PubMed] [Google Scholar]
- Steppe K, Lemeur R, Dierick D. Unravelling the relationship between stem temperature and air temperature to correct for errors in sap-flow calculations using stem heat balance sensors. Functional Plant Biology. 2005;32:599–609. doi: 10.1071/FP04242. [DOI] [PubMed] [Google Scholar]
- Steppe K, De Pauw DJW, Lemeur R, Vanrolleghem PA. A mathematical model linking tree sap flow dynamics to daily stem diameter fluctuations and radial stem growth. Tree Physiology. 2006;26:257–273. doi: 10.1093/treephys/26.3.257. [DOI] [PubMed] [Google Scholar]
- Steppe K, De Pauw DJW, Lemeur R. A step towards new irrigation scheduling strategies using plant-based measurements and mathematical modelling. Irrigation Science. 2008;26:505–517. [Google Scholar]
- Thompson MV, Holbrook NM. Scaling phloem transport: water potential equilibrium and osmoregulatory flow. Plant Cell and Environment. 2003;26:1561–1577. [Google Scholar]
- Urban L, Alphonsout L. Girdling decreases photosynthetic electron fluxes and induces sustained photoprotection in mango leaves. Tree Physiology. 2007;27:345–352. doi: 10.1093/treephys/27.3.345. [DOI] [PubMed] [Google Scholar]
- Wang WJ, Zu YG, Wang HM, Li XY, Hirano T, Koike T. Newly-formed photosynthates and the respiration rate of girdled stems of Korean pine (Pinus koraiensis Sieb. et Zucc.) Photosynthetica. 2006;44:147–150. [Google Scholar]
- Williams LE, Ayars JE. Water use of Thompson Seedless grapevines as affected by the application of gibberellic acid (GA(3)) and trunk girdling – practices to increase berry size. Agricultural and Forest Meteorology. 2005;129:85–94. [Google Scholar]
- Wilson BF, Gartner BL. Effects of phloem girdling in conifers on apical control of branches, growth allocation and air in wood. Tree Physiology. 2002;22:347–353. doi: 10.1093/treephys/22.5.347. [DOI] [PubMed] [Google Scholar]
- Zwieniecki MA, Melcher PJ, Feild TS, Holbrook NM. A potential role for xylem-phloem interactions in the hydraulic architecture of trees: effects of phloem girdling on xylem hydraulic conductance. Tree Physiology. 2004;24:911–917. doi: 10.1093/treephys/24.8.911. [DOI] [PubMed] [Google Scholar]