Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2011 Jun 17;108(6):1085–1096. doi: 10.1093/aob/mcr119

NEMA, a functional–structural model of nitrogen economy within wheat culms after flowering. I. Model description

Jessica Bertheloot 1,*, Paul-Henry Cournède 2, Bruno Andrieu 3
PMCID: PMC3189836  PMID: 21685431

Abstract

Background and Aims

Models simulating nitrogen use by plants are potentially efficient tools to optimize the use of fertilizers in agriculture. Most crop models assume that a target nitrogen concentration can be defined for plant tissues and formalize a demand for nitrogen, depending on the difference between the target and actual nitrogen concentrations. However, the teleonomic nature of the approach has been criticized. This paper proposes a mechanistic model of nitrogen economy, NEMA (Nitrogen Economy Model within plant Architecture), which links nitrogen fluxes to nitrogen concentration and physiological processes.

Methods

A functional–structural approach is used: plant aerial parts are described in a botanically realistic way and physiological processes are expressed at the scale of each aerial organ or root compartment as a function of local conditions (light and resources).

Key Results

NEMA was developed for winter wheat (Triticum aestivum) after flowering. The model simulates the nitrogen (N) content of each photosynthetic organ as regulated by Rubisco turnover, which depends on intercepted light and a mobile N pool shared by all organs. This pool is enriched by N acquisition from the soil and N release from vegetative organs, and is depleted by grain uptake and protein synthesis in vegetative organs; NEMA accounts for the negative feedback from circulating N on N acquisition from the soil, which is supposed to follow the activities of nitrate transport systems. Organ N content and intercepted light determine dry matter production via photosynthesis, which is distributed between organs according to a demand-driven approach.

Conclusions

NEMA integrates the main feedbacks known to regulate plant N economy. Other novel features are the simulation of N for all photosynthetic tissues and the use of an explicit description of the plant that allows how the local environment of tissues regulates their N content to be taken into account. We believe this represents an appropriate frame for modelling nitrogen in functional–structural plant models. A companion paper will present model evaluation and analysis.

Keywords: Rubisco turnover, remobilization, functional–structural plant model, nitrogen, light acclimation, senescence, wheat, Triticum aestivum, root uptake, common pool

INTRODUCTION

Nitrogen (N) availability regulates numerous aspects of plant growth. Nitrogen is involved in the expansion of organs that capture resources (meristematic activity and cell extension), as well as in their photosynthetic activity. Up to 75 % of reduced N in cereal leaves is involved in photosynthetic processes, mainly as Rubisco, and the rate of light-saturated photosynthesis is linearly correlated with specific N mass (Evans, 1989a). Nitrogen is also involved in the quality of harvested organs since it is a component of proteins (Ourry et al., 2001). In monocarpic species such as wheat (Triticum aestivum), N is remobilized from vegetative organs to fill growing grains after flowering, leading to the progressive death of the vegetative tissues.

The increasing use of N fertilizers played a considerable role in increasing yield and production quality in the last century (Tilman, 1999; Cassman et al., 2003; Hirel et al., 2007), but resulted in unsustainable environmental and economic costs (Wallsgrove et al., 1983; Tilman, 1999; Cassman et al., 2003). Reducing N inputs while maintaining high yields of high quality requires novel practices, in which N acquisition and use by plants is maximized and N losses are minimized. Optimum N management practices should closely respect plant requirements and should be combined with breeding for specific traits.

Numerical models simulating crop growth and yield from environmental variables are potentially efficient tools for designing improved agricultural practices and identifying useful traits for cultivars. Models offer the possibility to predict plant responses to changes in management practices, cultivar traits and climate. In recent decades, many crop models have been developed (for a review, see Jeuffroy et al., 2002) including the model of Sinclair and Amir (1992), STICS (Brisson et al., 1998), CERES (Jones and Kiniry, 1986; Gabrielle et al., 1998a, b), Sirius (Jamieson and Semenov, 2000; Martre et al., 2006) and ORYZA2000 (Bouman and Laar, 2006). In this type of model, a few compartments are accounted for (typically roots, reproductive organs and vegetative organs). These models capture the main processes governing N economy of crops and are able to simulate mean plant behaviour observed under intensive conditions, for which they have been developed; however, even if several crop models have a solid mechanistic basis, they also include teleonomic components and/or equations that approximate observed crop behaviour rather than expressing the physiological processes from which this behaviour emerges. This raises difficulties when the model is used as a tool for understanding how N economy is regulated at the plant scale and when addressing current needs to simulate how novel management practices and cultivars can impact N economy.

It has been proposed that the predictive ability of these models is mainly hampered by the use of the concept of plant demand for resources in teleonomic approaches (Thornley, 1998b). Before flowering, N content of the vegetative compartment is calculated from a demand in N, that would result from the difference between a target N concentration and the real one. Defining such demand is difficult, because it is not linked to a physiological process. Consequently, the quantification of N deficiency and its effect on leaf area expansion and photosynthesis by comparing N demand and supply also raise difficulties. The calculation of N remobilization after flowering also uses a target-driven approach: most models use the approximation that all N present in the vegetative compartments at flowering will have migrated to the reproductive compartment at maturity (Sirius, ORYZA2000 and CERES). This assumption cannot account for the stay-green behaviour of some cultivars, which is characterized by a significant percentage of vegetative tissues that are still photosynthetic at maturity (Borrell et al., 2001) and is often associated with high yields (Benbella and Paulsen, 1998; Borrell et al., 2000; Hafsi et al., 2000). Finally, N mass in vegetative organs is often considered to decrease at a constant rate during grain filling even though it has been observed first to remain stable – or even show a transient increase – in the case when N fertilization is carried out at flowering (for wheat, see Triboï and Triboï-Blondel, 2002).

We hypothesize that to use models as comprehensive tools, to make them more flexible and to enable them to elucidate what could happen under novel conditions, plant functioning should not be formalized by demand-driven rules defined at the whole plant or crop scale, but rather be simulated as the result of mechanisms described at a finer scale. Such mechanisms will then be more faithful to physiological processes, which increases the realism of simulation and paves the way for adapting the model according to ongoing progress in our knowledge of physiology. The functional–structural approach is one possible way to develop more mechanistic models (Prusinkiewiz, 2004; Godin and Sinoquet, 2005; Dingkuhn et al., 2006; Luquet et al., 2006; Bertheloot et al., 2008a; Fourcaud et al., 2008; de Reffye et al., 2008). It explicitly represents plant botanical structure, so that the main functional processes can be formalized at the organ or tissue scale while accounting for the effect of the local environment (Chelle, 2005).

Until now, functional–structural models mainly focused on carbon (C) acquisition and distribution within the aerial parts of plants (Fournier and Andrieu, 1998, 1999; Allen et al., 2005; Luquet et al., 2006; de Reffye et al., 2008). The first model accounting for N fluxes was GRAAL-CN (Drouet and Pagès, 2007), which was developed for maize plants (Zea mays) before flowering. GRAAL-CN simulates the distribution of N and C mass within the plant which is represented as an assembly of connected modules, each characterized by a botanical type (i.e. lamina, sheath, internode and root segment) and a position within the plant. However, C and N fluxes are modelled following a demand-driven approach, which raises the difficulty of quantifying this demand, as in crop models. Moreover, remobilization rates are independent of the environment and of the plant N status. A more mechanistic approach is used for N acquisition from the soil, based on the formalization of the activities of two known major transport systems for nitrate, HATS (high affinity transport system), which functions at a low soil nitrate concentration, and LATS (low affinity transport system), which functions at a high soil nitrate concentration (for reviews, see Glass and Siddiqi, 1995; Daniel-Vedele et al., 1998). GRAAL-CN accounts for an up-regulation of these transport systems by carbohydrate availability, and a down-regulation by plant N content. This is in accordance with physiological and molecular studies (Delhon et al., 1996; Forde and Clarkson, 1999; Touraine et al., 2001; Gojon et al., 2009; Masclaux-Daubresse et al., 2010) that demonstrated that the expression and/or activity of root N uptake systems is down-regulated by reduced N metabolites and up-regulated by sugar signals; besides, sugar is a source of energy required for mineral N assimilation.

We previously proposed a mechanistic alternative to the demand-driven approach for modelling the N fluxes between leaf laminae of wheat after flowering (Bertheloot et al., 2008a). The N content of each lamina is regulated by the turnover of Rubisco, whose synthesis depends on light intercepted by the lamina and the availability of mobile N (representing mainly amino acids and nitrate). We demonstrated that N contents could be accurately simulated by assuming all organs share a common pool of mobile N, but differ in their light environment. The role of light intercepted by a leaf is to increase the rate of protein synthesis. The mechanism behind is the effect of light on the transpiration flux that carries both mobile N and cytokinin towards the leaf (Pons and Bergkotte, 1996; Pons et al., 2001); cytokinin is a hormone involved in the synthesis of photosynthetic proteins (Kusnetsov et al., 1994; Aloni et al., 2005). In addition, light provides the sugar required for nitrate assimilation to leaf tissues. Phloem transport was left aside, but this simplification did not hamper calculations, probably because at the stage of development concerned, phloem transport is mostly only directed toward grains. Still, the model lacked a predictive capacity because it focused on a system consisting of laminae and grains, the N mass of other organs being forced to follow experimental data.

This paper proposes a comprehensive process-based model of N economy for wheat plants after flowering, as a step forward in the development of a model spanning the full growth cycle. During the post-flowering period, N economy is driven by N acquisition from the soil and by N remobilization from vegetative tissues for grain filling, because the vegetative structure (roots and aerial parts) has mainly completed its development. The objective of the study is to propose an alternative to the demand-driven approach to model, from N available in the soil and incident light, the N fluxes within the aerial structure of plants and their impact on dry matter acquisition and allocation to grains. The model, called NEMA (Nitrogen Economy Model within plant Architecture), extends the turnover model proposed earlier (Bertheloot et al., 2008a) to all photosynthetic organs (i.e. laminae, sheaths, internodes and chaff) and links it to a model of N acquisition from the soil based on the formalization of transport systems. The present paper describes the model and discusses the reasons and expected consequences of the modelling choices. In a companion paper (Bertheloot et al., 2011), we describe parameter fitting, model evaluation and a study of model behaviour involving a sensitivity analysis that aims to understand how N acquisition from the soil and the effect of N on total dry mass and N content of grains are regulated at the whole plant scale.

MODEL DESCRIPTION

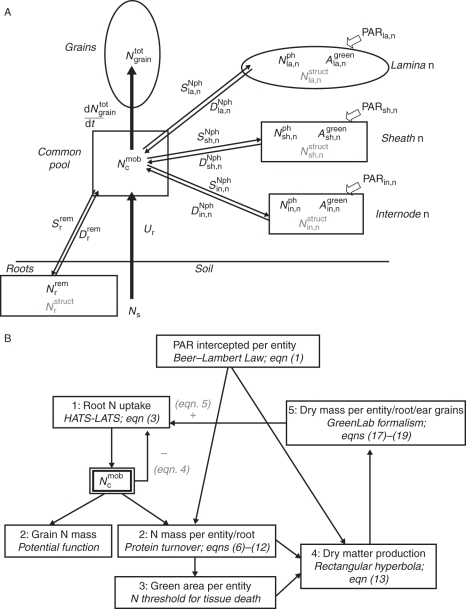
After flowering, each culm has its own root system, and translocation of assimilates between the culms in the same plant is very low (Williams, 1964); consequently, in NEMA, the crop is seen as a population of individual culms of density Densc (culms m−2). Processes are described at the scale of one culm and, for the sake of simplicity, all culms are considered to be identical. This work focuses on N distribution within aerial parts, while roots are represented by a single compartment. NEMA predicts with a daily time step, for a culm free of disease or water stress, the acquisition of N and of total dry mass as well as their distribution between leaf laminae, sheaths, internodes, peduncle, chaff, ear grains and roots. The distribution of photosynthetic area between photosynthetic modules is also predicted. The distribution of total dry mass is modelled according to GreenLab formalism, i.e. following a demand-driven approach (Kang et al., 2008). Obviously N is part of the total dry mass but represents a small fraction (0·5–2 %); so, for the sake of simplicity, we keep the calculations for total dry mass distribution independent of those of N. On the other hand, the calculation of total dry mass distribution contributes to the calculation for the fluxes of N, which is partly transported with carbohydrates. The inputs are: (a) a complete plant description at flowering (i.e. for each organ: N mass, total dry mass, photosynthetic and total areas); (b) soil N concentration at flowering; and (c) the daily time course of photosynthetically active radiation (PAR) above the canopy. Culm characteristics and density enable calculation of the tissue area density and thus the vertical light profile. Soil N only changes as a function of N acquisition by roots to keep the calculation simple and to focus on the modelling of N in aerial parts. The model consists of sub-modules formalizing N and total dry mass acquisition, storage and translocation within the plant, as well as tissue death following N remobilization. Calculations are detailed below, and the general principle of the model is presented in Fig. 1.

Fig. 1.

Fig. 1.

Open in a new tab

Overview of the model of N economy within a wheat (Triticum aestivum) culm after flowering. (A) Structure and functioning of N acquisition and distribution within a culm. Each lamina (la), sheath (sh) and internode (in), all chaff, all grains (grain), all roots (r) and the peduncle are represented by different modules, but only the uppermost phytomer (n), grains and roots are shown on the figure. Symbols in black represent the N-related model variables: PAR intercepted by each entity, photosynthetic N mass (Nph) and area (Agreen), remobilizable N mass in roots (Nrrem) and total N mass in grains (Ngraintot); Nstruct, the structural N mass, shown in grey, is constant throughout the grain-filling period. A supplementary module describes the mobile N pool (Ncmob), which is enriched by root N uptake and assimilation (Ur) and Nph, Nrrem degradation (DNph, Drrem), depleted by grain N filling (dNtotgrain/dt) and Nph, Nrrem synthesis (SNph, Srrem). N fluxes between modules are represented by arrows. (B) Calculations within one model time step. Each box represents one meta-process, with the calculation principle indicated as well as the numbers of the equations; the number in the box corresponds to the calculation step; the dependence between one meta-process and the others is indicated by arrows. In addition, the common pool of Ncmob is explicitly represented because of its central role in the regulation of N fluxes. The PAR intercepted by each entity is calculated once at flowering.

Plant structure

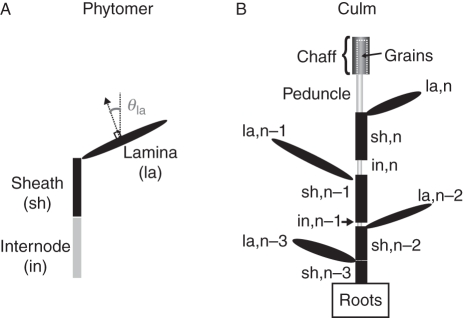
Roots are represented by a single compartment, while the botanical and functional organization of the aerial part of the culm is explicitly represented (Fig. 2). The aerial part of the culm is an assembly of phytomers, each consisting of three types of entities: from the bottom to the top, internode (in), sheath (sh) and lamina (la); the upper vegetative internode is surmounted by the peduncle (ped), which bears the ear consisting of chaff (pooled in a single compartment denoted chaff) and grains (pooled in a single compartment denoted grain). All the entities except grains are exposed to light and are photosynthetic. They are defined by their type (denoted tp), and vegetative entities are numbered acropetally according to the phytomer they belong to (denoted i).

Fig. 2.

Fig. 2.

Open in a new tab

Botanical structures of a phytomer (A) and a culm (B) in wheat after flowering as implemented in the model. Laminae are defined by planar shapes characterized by their orientation, θla; sheaths and internodes are represented by vertical cylinders. Parts of internodes are surrounded by sheaths, and grains are surrounded by chaff; enclosed parts are represented by dotted lines. Phytomers are numbered according to their rank from the top of the culm, n being the uppermost phytomer.

Each photosynthetic entity is characterized by its length (Ltottp,i; m) and area (Atottp,i; m2). The exposed length (Lexptp,i; m) and exposed area (Aexptp,i; m2) of sheaths and internodes are also specified, since part of these entities is hidden by the sheath of the phytomer below. Laminae are approximated as planar shapes, so that their orientation can be characterized by the two angles defining the unit vector normal to the plane: (1) the azimuth angle, i.e. the angle between the projection of the normal vector on a horizontal plane and the north; and (2) the zenith angle, i.e. the angle between the normal vector and the vertical (θla; radians). Calculation of light intercepted by the lamina of a given rank was done using the Beer–Lambert approximation: light corresponds to the mean expected value for that rank, assuming that the zenith angle was identical for all plants and all phytomer ranks and that the azimuth angle followed a random uniform distribution. All structural characteristics were assumed to remain constant over time; only the photosynthetic active area of each entity (Agreentp,i; m2) decreased following N remobilization. Structural characteristics and the PAR above the canopy (PAR0; J m−2 d−1) were used to calculate the PAR incident on each entity (PARtp,i; J m−2 d−1; calculation detailed below). Following our previous observations (Bertheloot et al., 2008b), both senescent and photosynthetic tissues were taken into account to calculate PAR extinction and were assumed to have an identical effect on PAR extinction. Consequently, PARtp,i was only affected by variations in PAR0 between days.

Grains were characterized by their total dry mass (Mtotgrain; g) and their N mass (Ntotgrain; g). For photosynthetic entities and roots, two forms of dry matter and N were distinguished: structural N and dry mass (Nstructtp,i, Mstructtp,i for an entity of type tp and rank i; Nstructr, Mstructr for roots; g), which were assumed to be constant for the period after flowering, and remobilizable N and dry mass (Nphtp,i, Mremtp,i for an entity of type tp and rank i; Nremr, Mremr for roots; g), that can be synthesized or degraded. Remobilizable N mass of photosynthetic entities was assumed to consist only of N associated with the photosynthetic apparatus.

All modules are connected to a common pool of mobile N (Nmobc; g), which is the N form involved in the transport, i.e. mainly amino acids and nitrate. Total N mass of a module was calculated as the sum of its structural, remobilizable and mobile N masses. The mass of mobile N within each plant module was calculated from the mass of mobile N in the whole culm (Nmobc) by assuming that the distribution of mobile N paralleled that of the remobilizable N mass, as in Bertheloot et al. (2008a). Total dry masses of photosynthetic entities (Mtottp,i; g) or roots (Mtotr; g) are sums of their structural and their remobilizable dry masses.

The effect of temperature on the rate of processes leading to the distributions of N and dry mass is accounted for by expressing time as thermal time with a base temperature of 0 °C, as widely accepted for wheat. The number of degree days (°Cd) within day t is denoted Δ(t). Variables are listed in Table 1 and parameters are listed in Table 2.

Table 1.

Model variables: their symbols, definitions and units.

Symbol Definition Unit
Δ(t) Thermal time within 1 d °Cd
t Time days (d)
tp,i Indices for an entity of type tp and rank i
PAR interception
Aexptp,i Exposed area of entity tp,i m2
Atottp,i Total area of entity tp,i m2
AItp,i Cumulative area index above entity tp,i m2 m−2
Densc Density of culms in the field Culm m−2
kcanopy Canopy extinction coefficient m2 m−2
ktp Extinction coefficient of entity tp m2 m−2
Lexptp,i Exposed length of entity tp,i m
Ltottp,i Total length of entity tp,i m
PAR0 Photosynthetic active radiation above the canopy J m−2 d−1
PARtp,i Photosynthetic active radiation incident on entity tp,i J m−2 d−1
N mass, dry mass and photosynthetic active area
Agreentp,i Photosynthetic area of entity tp,i m2
Nmobc Mobile N mass in the common pool g
[N]mobc Mobile N mass concentration g g−1
Nphtp,i Photosynthetic N mass of entity tp,i g
Nremr Root remobilizable N mass g
NrstructNstructtp,i Structural N mass of roots, entity tp,i g
NtotgrainNtotrNtottp,i Total N mass of grains, roots, entity tp,i g
Mgreentp,i Photosynthetic tissues dry mass of entity tp,i g
MremrMremtp,i Remobilizable dry mass of roots, entity tp,i g
MstructrMstructtp,i Structural dry mass of roots, entity tp,i g
MtotgrainMtotrMtottp,i Total dry mass of grains, roots, entity tp,i g
N fluxes, dry mass fluxes and tissue death
DMremrDMremtp,i Remobilizable dry matter degradation rate for roots, entity tp,i g d−1
DNphtp,i Photosynthetic N degradation rate for entity tp,i g d−1
DNremr Remobilizable N degradation rate for roots g d−1
EC(t) EN(t) Effect of C and N availability within the culm on root N uptake Dimensionless
[N]s Soil N concentration g m−3
Ptp,i Dry mass production by entity tp,i g d−1
qrqgqtp,i Sink strengths of grains, roots, entity tp,i Dimensionless
Qtp,0 Normalizing factor for the beta function Dimensionless
SMremrSMremtp,i Remobilizable dry matter synthesis rate for roots, entity tp,i g d−1
SNremr Remobilizable N synthesis rate for roots g d−1
SNph,phloemtp,i Photosynthetic N synthesis rate from phloem N for entity tp,i g d−1
SNph,xylemtp,i Photosynthetic N synthesis rate from xylem N for entity tp,i g d−1
ttinitgrainttinitrttinittp,i Thermal time at which grains, roots, entity tp,i begin to grow °Cd
Ur Root N uptake rate per unit root mass g g−1 d−1
Open in a new tab

Table 2.

Model parameters: their symbols, definitions and units

Symbol Definition Unit
PAR interception
θla Angle between the vertical and the normal vector to the lamina plane Radians
kvertical PAR extinction coefficient for vertical entities m2 m−2
Root N uptake
βC βN Coefficient for C and N availability effect on root N uptake Dimensionless
kr,l Constant of the Michaelis function reflecting HATS activity g m−3
kr,2 Rate constant of the linear function reflecting LATS activity g m−3 °Cd−1
(SMremr)min Minimum threshold of dry matter influx into roots to sustain root N uptake g d−1
Ur,max Theoretical maximum N acquisition at saturating soil N concentration g m−3 °Cd−1
N fluxes
δNr δNtp Relative degradation rates of remobilizable N for roots, entities tp °Cd−1
γ Relative rate of potential grain N filling during cell division °Cd−1
ktp,1ktp,2 Michaelis–Menten constants defining photosynthetic N synthesis associated with xylem influx for entities tp g g−1, J m−2 d−1
prptp,i Proportion coefficient for N influx following dry mass influx into roots, entities tp,i Dimensionless
σNphtp,i Relative rate of photosynthetic N synthesis associated with xylem influx for entities tp,i g g−1 °Cd−1
Death of photosynthetic active tissues and photosynthesis
dtp Proportion of maximum specific N mass at which tissues die for entities tp Dimensionless
ωtp Proportion coefficient linking photosynthesis at saturating PAR and N mass per unit photosynthetic area d−1
ɛtp Photosynthetic efficiency g J−1
Dry matter fluxes
αgrain – βgrain; αr – βr; αtp – βtp Two parameters determining the shape of the beta function for grains, roots, entities tp Dimensionless
δMr δMtp Relative degradation rates of remobilizable dry mass for roots, entities tp °Cd−1
σMgrain σMr σMtp,i Relative sink strength of grains, roots, entities tp,i Dimensionless
ttMaccgrainttMaccrttMacctp Period during which grains, roots, entities tp can accumulate dry mass °Cd
Open in a new tab

Photosynthetically active radiation intercepted by a photosynthetic entity

The PAR intercepted by an entity was estimated by multiplying the area of the entity by the PAR intercepted per unit area, the latter being calculated for the position corresponding to the middle height of the entity. For entities which are partly hidden, such as sheaths, this calculation was done for the exposed part of the entity. PAR intercepted by an entity was estimated from PAR above the canopy using Beer–Lambert's law (Monsi and Saeki, 2005), as:

graphic file with name mcr119eqn1.jpg (1)

where ktp (m2 m−2) is the PAR extinction coefficient associated with entities of type tp, kcanopy is the mean extinction coefficient of the canopy, and AItp,i (m2 m−2) is the cumulated area index above the middle height of the entity exposed part.

The effect of entity orientation on PAR interception was accounted for by varying the extinction coefficient from 1 for horizontal entities to kvertical for vertical entities. The lamina extinction coefficient kla was calculated with the following function of lamina orientation:

graphic file with name mcr119eqn2.jpg (2)

kcanopy was calculated as the mean of the extinction coefficients of all entities weighted by their exposed areas.

AItp,i was calculated as the product between culm density, Densc, and the exposed areas above the middle of the height of the entity tp,i exposed part, whose distance from the top of the canopy was calculated from the plant structure described in Fig. 2. Following the usual calculation of PAR by Beer–Lambert's law, only half the exposed areas of the cylinders representing sheaths and internodes were considered.

Nitrogen uptake by roots and assimilation

The calculation of N acquisition by the culm is based on that of GRAAL-CN. Processes of N uptake by transport systems and of N assimilation into reduced N (that enriches the common pool) are not distinguished in that formalization. Nitrogen acquisition within a time step is modelled as the product of a rate of acquisition per unit root mass (Ur; g g−1 d−1) and the mass of the root compartment. Ur is described as a potential rate that depends on the nitrate concentration in the soil ([N]s; g m−3), modulated by two dimensionless functions, EC(t) and EN(t), which express the positive and negative effects of culm C and N availability, respectively, on N acquisition. The potential rate is described as the sum of (1) a Michaelis–Menten function of [N]s, corresponding to the activity of the HATS transport system, and (2) a linear function of [N]s, corresponding to LATS activity:

graphic file with name mcr119eqn3.jpg (3)

where Ur,max (g g−1 °Cd−1) is the theoretical maximum reduced N influx per gram of roots at the soil saturation concentration of N, kr,1 (g m−3) is the Michaelis constant and kr,2 (g m−3 °Cd−1) is the rate constant for the linear component.

Nmobc, which represents circulating amino acids and nitrate, was used to account for the known negative feedback of circulating N on N uptake by transport systems. EN(t) is assumed to be negatively related to the mobile N concentration (i.e. total mobile N mass divided by the total dry mass of green tissues in the culm; [N]mobc; g g−1) following an exponential function:

graphic file with name mcr119eqn4.jpg (4)

where βN (dimensionless) is a parameter.

Dry mass import by roots (SMremr; g d−1) was used to account for the positive effect of carbohydrate availability on N acquisition by the culm. Below a given threshold (SMremr)min of dry mass influx into roots (calculation is detailed below), N acquisition was assumed to be null; above, EC(t) was assumed to be exponentially related to SMremr, as:

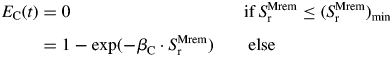graphic file with name mcr119eqn5.jpg (5)

where βC is a dimensionless parameter.

Nitrogen storage and translocation

The modelling of N accumulation in grains follows that of Bertheloot et al. (2008a) and Martre et al. (2003): at any time step, N influx into grains follows a potential rate if sufficient Nmobc is available in the common pool; otherwise it corresponds to the mass of mobile N available at that time step. The potential rate is a parametric function of the thermal time, with two successive stages corresponding respectively to cell division and to rapid protein storage: the rate is an affine function of thermal time in the first stage characterized by the parameter γ, and is constant thereafter. All N entering grains is assumed to be permanently stored.

For roots and photosynthetic entities, remobilizable N mass fluxes were calculated as the difference between a synthesis rate (SNremr, SNphtp,i; g d−1) and a degradation rate (DNremr, DNphtp,i for roots and photosynthetic entities, respectively; g d−1). Synthesis and degradation rates for an entity were assumed to match the fluxes of mobile N from the common pool into the entity and from the entity into the common pool, respectively. For grains and roots, N was assumed to come only from the phloem following the osmotic gradient generated by C transport (Münch, 1930). After ligulation, laminae do not import C from other organs, so N can only come from the transpiration stream. Concerning other photosynthetic entities, no information could be found in the literature and mobile N was assumed possibly to come from both phloem and xylem. Synthesis rates were calculated differently according to the origin of the mobile N, as given in eqns 10–12. The variation in N mass of respectively the roots and the different photosynthetic modules was written as:

graphic file with name mcr119eqn6.jpg (6)
graphic file with name mcr119eqn7.jpg (7)

The degradation of photosynthetic N produces amino acids that enrich the pool of mobile N; degradation is described by first-order kinetics as in Bertheloot et al. (2008a), in accordance with conclusions of Irving and Robinson (2006):

graphic file with name mcr119eqn8.jpg (8)

where δNtp (°Cd−1) is the relative rate of photosynthetic N degradation for entities of type tp.

Similarly, for roots:

graphic file with name mcr119eqn9.jpg (9)

where δNr (°Cd−1) is the relative rate of remobilizable N degradation in roots.

The N influx rate from the phloem into the roots was modelled as proportional to both [N]mobc and the dry mass influx into roots SMremr:

graphic file with name mcr119eqn10.jpg (10)

where pr is a dimensionless parameter.

Dry mass influx into photosynthetic entities was calculated as the difference between the rate of increase in dry mass for that entity (SMremtp,i; g d−1) and the increase in dry mass due to its own photosynthesis (Ptp,i; g d−1); consequently, the N influx rate from the phloem into an entity is written as:

graphic file with name mcr119eqn11.jpg (11)

SMremtp,i and Ptp,i calculations are detailed in subsequent sections.

The N influx rate through the xylem into photosynthetic entities is expressed, following Bertheloot et al. (2008a), as a function of the PAR intercepted, the mass of photosynthetic tissues (Mgreentp,i, g) and [N]mobc:

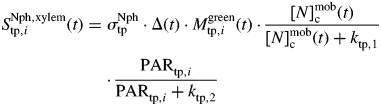graphic file with name mcr119eqn12.jpg (12)

where σNphtp (g g−1 °Cd−1) is the relative rate of Nphtp,i synthesis associated with xylem influx, and ktp,l (g g−1) and ktp,2 (J m−2 d−1) are Michaelis constants.

Photosynthesis and dry mass production

The production of total dry mass per unit area of photosynthetic tissue was modelled as a function of the daily PAR intercepted according to a rectangular hyperbola (Thornley, 1998a). This approximation proved satisfactory when assessed using instantaneous light response curves of photosynthesis, measured for a range of leaf N statuses (data not shown).

Dry mass production of a photosynthetic entity was calculated as:

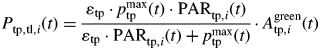graphic file with name mcr119eqn13.jpg (13)

where ɛtp (g J−1) is the photosynthetic efficiency and pmaxtp (g m−2 d−1) is photosynthesis at saturating light.

Photosynthetic efficiency varies mainly with long-term adaptation to light climate and was assumed to be independent of leaf N (Hirose and Werger, 1987; Schieving et al., 1992). Photosynthesis at saturating light is limited by the amount of Rubisco, which is the main form of leaf N storage (Evans, 1989b). Accordingly, pmaxtp was assumed to be proportionally related to photosynthetic N mass per unit area, with the coefficient ωtp (d−1) (Hirose and Werger, 1987; Thornley, 1998a):

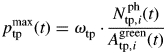graphic file with name mcr119eqn14.jpg (14)

In each photosynthetic entity, a given fraction of tissues die when photosynthetic N mass per unit photosynthetic area drops below a threshold, which was expressed as a fixed fraction (dtp; dimensionless) of entity N mass per unit photosynthetic area at flowering. The photosynthetic dry mass of an entity was calculated by a cross product depending on its total dry mass, total area and photosynthetic active area

Dry mass distribution within the plant

Photosynthetic entities and roots lose dry mass by remobilization (DMremr, DMremtp,i; g d−1), which was assumed to follow first-order kinetics of remobilizable dry mass (Drouet and Pagès, 2007):

graphic file with name mcr119eqn15.jpg (15)
graphic file with name mcr119eqn16.jpg (16)

where δMtp and δMr (°Cd−1) are relative rates of remobilization for an entity of type tp and roots, respectively.

At any given time step, the mobile dry mass available within the culm is the dry mass produced by photosynthesis during that time step, plus the remobilized dry mass. It is distributed among modules following the GreenLab model (de Reffye et al., 2008): the increase in dry mass of one entity, the root compartment or grain compartment, is the product of the dry mass available at the culm scale and the demand in dry mass of the module. This demand is defined as the sink strength of the module, which is a dimensionless function [qtp,i(t), qr(t) and qgrain(t) for an entity, roots and grains, respectively], expressed relative to the sum of the sink strength of all modules. Below is the equation for an entity of type tp and rank i:

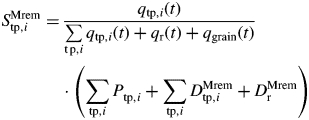graphic file with name mcr119eqn17.jpg (17)

For one module, sink strength was modelled from a relative sink strength parameter (denoted σMtp,i for entity tp,i, σMr for roots and σMgrain for grains), which corresponds to its potential sink strength, and a normalized beta function, which indicates the pattern of change in sink strength during its life. For entity tp,i, the equation is written as:

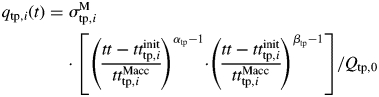graphic file with name mcr119eqn18.jpg (18)

where ttinittp,i (°Cd) is the thermal time at which the entity begins to grow, ttMacctp,i (°Cd) is the duration of the period in which the module can accumulate dry mass and Qtp,0 is a normalizing factor calculated so that the relative sink strength parameter corresponds to the maximal value of the sink strength. It is calculated as:

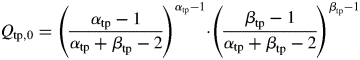graphic file with name mcr119eqn19.jpg (19)

Model implementation

The model was implemented in C ++. The daily time step was sub-divided into four sub-steps in order to avoid mistakes in solving differential equations due to a too long time step. Above four sub-steps, there were no longer any significant changes in model predictions.

Model initialization method

Model initialization corresponds to a description of the state variables of the different modules at flowering. One difficulty is to be able to quantify the different forms of N and dry matter; however, they can be indirectly estimated from measurements of total dry mass and N mass in each entity at flowering and maturity, if (a) it is assumed that the matter remaining in dead tissues at maturity corresponds to structural matter and (b) the mean percentage of mobile N in an entity is known (see Bertheloot et al., 2008a). This method is used in a companion paper (Bertheloot et al., 2011) to calibrate the model.

DISCUSSION

NEMA predicts the acquisition and distribution within wheat plants after flowering of both dry matter and N, using soil N concentration and the daily time courses of temperature and of PAR above the canopy as driving variables. The originality of the model is that it proposes, thanks to an explicit description of plant botanical structure, a mechanistic alternative to the conventional demand-driven approach for modelling N fluxes within the aerial parts of plants. On the other hand, like other models at the whole plant scale, NEMA uses much simplified descriptions of the processes with the aim of simulating relevant plant behaviours without multiplying the number of parameters. The choices we made were the following: N content and remobilization in each photosynthetic organ is simulated from the formalization of Rubisco degradation and synthesis, which depends on the PAR intercepted by the organ and the amount of mobile N. While individual organs differ in their PAR intercepted, they are assumed to share identical amounts of internal resources; mobile N is represented by a common pool shared by all plant organs in accordance with suggestions by several authors (Cooper and Clarkson, 1989; Kull and Kruijt, 1999; Thornley, 2004). The amount of mobile N varies according to the fluxes of N from and to plant organs: it is enriched by root uptake and assimilation or organ remobilization, and depleted by grain accumulation or protein synthesis. This modelling of N fluxes within the plant was associated with a previous model of N acquisition (Devienne-Barret et al., 2000; Malagoli et al., 2004; Drouet and Pagès, 2007) that integrates the activities of transport systems in response to soil availability and the feedbacks linked to plant nutrient status (for reviews, see Glass and Siddiqi, 1995; Daniel-Vedele et al., 1998).

The present version of NEMA does not include a realistic description of root architecture or of soil: such developments will be required, for example, to compare cultivars differing in root architecture or to define optimum agricultural practices, since practices may affect N forms and their spatial distribution in the soil. The present implementation should, however, be sufficient to respond to the objective of testing the validity of the new concepts implemented and gain new insights into N economy regulation in the aerial parts of the plant. In contrast to N, few efforts have been made here to model C acquisition and distribution mechanistically within the plant. Nitrogen distribution, together with PAR, regulates photosynthesis, but it is not C metabolism, but the increase in total dry mass that is directly modelled. This simplification is valid since C has a much higher contribution to dry mass than N. Moreover, the modelling of total dry mass distribution between plant parts follows the conventional demand-driven approach. A more elaborate model for C transfer to wheat grain was proposed, for instance, by Bancal and Soltani (2000) or Minchin and Lacointe (2005). Coupling this type of model with the N model proposed in this study will be considered in a future step; however, we believe that, given the determining role of N metabolism for C production at the whole plant scale and the fact that C fluxes are mainly directed towards grains after flowering, the present implementation will already provide new insights into the regulation of N economy within the plant after flowering, which is fundamental for more efficient N management practices or cultivars.

The simulations we presented in Bertheloot et al. (2008a) showed that it is possible to accurately simulate the gradient of photosynthetic N that exists between the top and the bottom leaves of a dense wheat canopy by considering mobile N as a pool equally accessible to all laminae and by relating the protein synthesis rate to the PAR intercepted by laminae. Functional acclimation of the lamina photosynthetic apparatus to PAR intensity has been demonstrated in different studies (Prioul et al., 1980a, b; Grindlay, 1997; Terashima et al., 2005). The relationship between PAR intensity and the transpiration stream is likely to be the origin of this acclimation (Pons and Bergkotte, 1996; Pons et al., 2001) as the transpiration stream supplies nitrate and circulating amino acids as well as cytokinins, known to be involved in the synthesis of the photosynthetic apparatus (Aloni et al., 2005). NEMA assumes that N of all photosynthetic tissues can be modelled in a unified way and extends the assumption of acclimation to PAR light to all plant organs. The observation that entities of the same type but located at different depths in the canopy followed similar patterns of N concentration depletion (Bertheloot et al., 2008b) is in accordance with this assumption. Time courses of these vertical gradients were similar for leaf laminae and sheaths on the one hand, and for internodes and chaff on the other hand, but differed between the two groups. This suggests that, if the processes involved are the same, the relationship of organ N content to light climate depends on the type of organ; this would imply different parameter values for synthesis and/or degradation.

The central role of PAR light interception in N dynamics within the plant implies being able to estimate it accurately. In the present version, Beer's law was implemented and is used in a companion paper to calibrate the model and study its behaviour (Bertheloot et al., 2011). This law has the advantage of allowing rapid calculations and of only requiring a simple description of plant structure. However, for a detailed investigation on how plant architecture impacts N economy or for analysing plant–plant interactions, the next step will be to couple it with a model of radiative transfer based on surfacic approaches (Chelle and Andrieu, 1998), as in Evers et al. (2010). To investigate these questions, one interesting feature of NEMA is to formalize N economy for an individual plant. Moreover, structure is an input of the model, so that it would be easy to include variability in the structure of culms constituting the field.

NEMA also extends our previous model (Bertheloot et al., 2008a) in that organ N is assumed to come not only from the xylem but also from the phloem. The two transport paths involve different driving forces: N influx into an entity follows the transpiration stream when it originates from the xylem, while, when it originates from the phloem, it is driven by a mass flow mechanism following the carbohydrate gradient that exists between sources and sinks for C (Münch, 1930). Thus, the formalization of N influx into an entity and N synthesis rate differ depending on the transport path. On the other hand, the two synthesis paths are assumed to have access to the same circulating N, which is considered as a single pool. Consequently, the formalization implicitly assumes that N concentrations in xylem and phloem are correlated with each other. This is probably because transfers of amino acids between xylem and phloem take place throughout the vascular system (for reviews, see Feller and Fischer, 1994; Delrot et al., 2001).

It is likely that, similar to what is known for leaves (Bregard and Allard, 1999; Turgeon, 2006), other mature photosynthetic tissues cannot import C from other plant parts, so that the role of phloem in N import is negligible for such tissues. By allowing N to be imported through both the xylem and phloem for non-leaf tissues, the model will enable analysis of their possible contributions. In contrast, growth of young organs still hidden in the whorl or having a small transpiration area depends on phloem for import of both C and N. It will thus be important to take into account the role of phloem when adapting the model to the pre-flowering period.

The response of grain N accumulation to N fertilization at flowering was simulated with the simple approximation that the N flux from the common pool of mobile N to the grains follows a potential function of thermal time, but occurs only when mobile N is available in the common pool. Thus, the process by which N influx towards grains is driven by the osmotic gradient created by the differences in carbohydrate concentration (Münch, 1930) is not explicitly formalized. This choice was made because of its simplicity and the good predictions obtained with contrasted treatments (Bertheloot et al., 2008a). It appeared to be sufficient in usual agronomic conditions, when N availability, rather than carbohydrate transport and sink limitation, limits the import of N into the ear (Dingkuhn et al., 2007; Bancal, 2009); a more exact formulation may be required in a context of strong carbohydrate limitation, due to light starvation, for example.

Photosynthetic tissues were assumed to die when photosynthetic N mass per unit area fell below a critical value. The threshold value is known to vary according to N fertilization, for example (Hirel et al., 2005). In a preliminary version, we implemented the frequently used assumption (Ackerly and Bazzaz, 1995; Ackerly, 1999) that tissue death occurs when C net assimilation by tissues is null. This however led to the prediction of an earlier tissue death for the lowest leaves (data not shown) compared with that observed, which may be due to inaccuracy in the calculation of net photosynthesis. Using this assumption would probably require an appropriate account of respiration costs under conditions of low light and low N. Consequently, the N threshold for tissue death was defined empirically as a fraction of entity N content at flowering, similar to that in the original model (Bertheloot et al., 2008a). When this threshold is reached, leaves have a low impact on plant C and N economy, so the lack of a mechanistic approach is unlikely to hamper the use of the model.

The formalization of N acquisition by roots follows that proposed earlier based on nitrate uptake by transport systems and its subsequent assimilation (Devienne-Barret et al., 2000; Malagoli et al., 2004; Drouet and Pagès, 2007). Nitrate is the mineral form brought by fertilization and the main form assimilated in wheat. Changes would be required for the case of a wider range of N forms. The rate of N acquisition by roots is expressed as the sum of a Michaelis–Menten function of soil N concentration, which reflects the saturable character of HATS, and a linear function of soil N concentration, which reflects the non-saturable character of LATS [Cacco et al. (2002) for wheat; Malagoli et al. (2004) for oilseed rape; Siddiqi et al. (1990) for barley]. The well-known positive dependence of N acquisition, mainly N assimilation into reduced N, on carbohydrate availability (e.g. Delhon et al., 1996) as well as the negative feedback of reduced N (Forde and Clarkson, 1999; Touraine et al., 2001) on transport system activities were also accounted for by the use of specific functions. Regulation by C availability was based on dry mass influx into roots, which may not accurately reflect carbohydrate availability. This difficulty could probably be overcome by developing a more mechanistic module for C metabolism. In contrast, to account for N negative feedback, the formalization of a common pool of circulating N is an original and interesting feature in the model. In a previous study (Bertheloot et al., 2008a), it proved to be a reliable variable to regulate leaf N dynamics and grain N filling. For regulation of root N uptake, it provides a physiological state variable, whereas previous models used indicators that do not have a causal effect on physiological activities. The functions implemented in the model are adapted from Drouet and Pagès (2007) and Cardenas-Navarro et al. (1999). However, there is no strong support for the choice made: more work is needed to define mathematical functions that actually reflect the regulation of N acquisition by mobile N.

In conclusion, a functional–structural model of N economy for wheat after flowering is described in the present paper which accounts for physiological activities governing N acquisition and distribution within the aerial part of the plant and, in a simplified manner, for C–N interactions. This model is a mechanistic – yet still simple – alternative to the teleonomic approaches usually used to model N economy, based on the idea expressed by different authors that Rubisco turnover plays a central role in the regulation of N fluxes within the aerial part of the plant (Thornley, 1998a, 2004; Gallais et al., 2006; Hirel and Gallais, 2006). Our motivation comes from the assumption that the integration of processes governing N metabolism at the whole plant scale will provide insights into the regulation of N acquisition and the effect of N on yield by environment (light and soil N) and genotype, which is fundamental for the design of more efficient cultivars and practices as mentioned by Hammer et al. (2010). The use of the model as a comprehensive tool is investigated in a companion paper (Bertheloot et al., 2011). The model proposed here illustrates the potentialities offered by the functional–structural approach to integrate physiological knowledge at the scales of the whole plant and field, and thus to link physiology, ecophysiology and agronomy. The generality of the processes formalized should make the model adaptable to species other than wheat and, as an individual plant type model, suitable for plurispecific crops provided it is coupled with an appropriate model of radiative transfer. This will be one of the next steps. Another step will be to use the model proposed here as the basis for a model dealing with the more complex pre-flowering period. This will require the mechanistic formalization of both C and N metabolism and of their effects on the plant structure dynamic.

ACKNOWLEDGEMENTS

We thank T. Guyard (DigiPlante team, MAS laboratory) for his valuable technical help, and Daphne Goodfellow for her assistance with the editing. This work was supported by INRIA, DigiPlante Project, and conducted in the MAS laboratory of the Ecole Centrale of Paris.

LITERATURE CITED

  1. Ackerly D. Self-shading, carbon gain and leaf dynamics: a test of alternative optimality models. Oecologia. 1999;119:300–310. doi: 10.1007/s004420050790. [DOI] [PubMed] [Google Scholar]
  2. Ackerly DD, Bazzaz FA. Leaf dynamics, self-shading and carbon gain in seedlings of a tropical pioneer tree. Oecologia. 1995;101:289–298. doi: 10.1007/BF00328814. [DOI] [PubMed] [Google Scholar]
  3. Allen MT, Prusinkiewicz P, DeJong TM. Using L-systems for modeling source–sink interactions, architecture and physiology of growing trees: the L-PEACH model. New Phytologist. 2005;166:869–880. doi: 10.1111/j.1469-8137.2005.01348.x. [DOI] [PubMed] [Google Scholar]
  4. Aloni R, Langhans M, Aloni E, Dreieicher E, Ullrich CI. Root-synthesized cytokinin in Arabidopsis is distributed in the shoot by the transpiration stream. Journal of Experimental Botany. 2005;56:1535–1544. doi: 10.1093/jxb/eri148. [DOI] [PubMed] [Google Scholar]
  5. Bancal P. Decorrelating source and sink determinism of nitrogen remobilization during grain filling in wheat. Annals of Botany. 2009;103:1315–1324. doi: 10.1093/aob/mcp077. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bancal P, Soltani F. Source–sink partitioning. Do we need Münch? Journal of Experimental Botany. 2002;53:1919–1928. doi: 10.1093/jxb/erf037. [DOI] [PubMed] [Google Scholar]
  7. Benbella M, Paulsen GM. Efficacy of treatments for delaying senescence of wheat leaves: II. Senescence and grain yield under field conditions. Agronomy Journal. 1998;90:332–338. [Google Scholar]
  8. Bertheloot J, Andrieu B, Fournier C, Martre P. A process-based model to simulate nitrogen distribution in wheat (Triticum aestivum) during grain-filling. Functional Plant Biology. 2008a;35:781–796. doi: 10.1071/FP08064. [DOI] [PubMed] [Google Scholar]
  9. Bertheloot J, Martre P, Andrieu B. Dynamics of light and nitrogen distribution during grain filling within wheat canopy. Plant Physiology. 2008b;148:1707–1720. doi: 10.1104/pp.108.124156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bertheloot J, Wu Q, Cournède P-H, Andrieu B. NEMA, a functional–structural model of nitrogen economy within wheat culms after flowering. II. Evaluation and sensitivity analysis. Annals of Botany. 2011;108:1097–1109. doi: 10.1093/aob/mcr125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Borrell AK, Hammer GL, Henzell RG. Does maintaining green leaf area in sorghum improve yield under drought? II. Dry matter production and yield. Crop Science. 2000;40:1037–1048. [Google Scholar]
  12. Borrell A, Hammer G, van Oosterom E. Stay-green: a consequence of the balance between supply and demand for nitrogen during grain filling? Annals of Applied Biology. 2001;138:91–95. [Google Scholar]
  13. Bouman BAM, Laar HHv. Description and evaluation of the rice growth model ORYZA2000 under nitrogen-limited conditions. Agricultural Systems. 2006;87:249–273. [Google Scholar]
  14. Bregard A, Allard G. Sink to source transition in developing leaf blades of tall fescue. New Phytologist. 1999;141:45–50. [Google Scholar]
  15. Brisson N, Mary B, Ripoche D, Jeuffroy MH, et al. STICS: a generic model for the simulation of crops and their water and nitrogen balances. I. Theory and parameterization applied to wheat and corn. Agronomie. 1998;18:311–346. [Google Scholar]
  16. Cacco G, Sidari M, Gelsomino A, Orsega EF. An attempt to model the induction and feedback inhibition of nitrate uptake in wheat seedlings. Journal of Plant Nutrition. 2002;25:17–25. [Google Scholar]
  17. Cardenas-Navarro R, Adamowicz S, Gojon A, Robin P. Modelling nitrate influx in young tomato (Lycopersicon esculentum Mill.) plants. Journal of Experimental Botany. 1999;50:625–635. [Google Scholar]
  18. Cassman KG, Dobermann A, Walters DT, Yang H. Meeting cereal demand while protecting natural resources and improving environmental quality. Annual Review of Environment and Resources. 2003;28:315–358. [Google Scholar]
  19. Chelle M, Andrieu B. The nested radiosity model for the distribution of light within plant canopies. Ecological Modelling. 1998;111:75–91. [Google Scholar]
  20. Cooper HD, Clarkson DT. Cycling of amino-nitrogen and other nutrients between shoot and roots in cereals – a possible mechanism integrating shoot and root in the regulation of nutrient uptake. Journal of Experimental Botany. 1989;40:753–762. [Google Scholar]
  21. Daniel-Vedele F, Filleur S, Caboche M. Nitrate transport: a key step in nitrate assimilation. Current Opinion in Plant Biology. 1998;1:235–239. doi: 10.1016/s1369-5266(98)80110-6. [DOI] [PubMed] [Google Scholar]
  22. Delhon P, Gojon A, Tillard P, Passama L. Diurnal regulation of NO3− uptake in soybean plants. 4. Dependence on current photosynthesis and sugar availability to the roots. Journal of Experimental Botany. 1996;47:893–900. [Google Scholar]
  23. Delrot S, Rochat C, Tegeder M, Frommer WB. Amino acid transport. In: Lea PJ, Morot-Gaudry JF, editors. Plant nitrogen. Berlin: Springer-Verlag; 2001. pp. 213–235. [Google Scholar]
  24. Devienne-Barret F, Justes E, Machet JM, Mary B. Integrated control of nitrate uptake by crop growth rate and soil nitrate availability under field conditions. Annals of Botany. 2000;86:995–1005. [Google Scholar]
  25. Dingkuhn M, Luquet D, Kim H, Tambour L, Clement-Vidal A. EcoMeristem, a model of morphogenesis and competition among sinks in rice. 2. Simulating genotype responses to phosphorus deficiency. Functional Plant Biology. 2006;33:325–337. doi: 10.1071/FP05267. [DOI] [PubMed] [Google Scholar]
  26. Dingkuhn M, Luquet D, Clement-Vidal A, Tambour L, Kim HK, Song YH. Is plant growth driven by sink regulation? In. In: Spiertz JHJ, Struik PC, VanLaar HH, editors. Scale and complexity in plant systems research: gene–plant–crop relations. Dordrecht: Springer; 2007. pp. 157–170. [Google Scholar]
  27. Drouet JL, Pagès L. GRAAL-CN: a model of GRowth, Architecture and ALlocation for Carbon and Nitrogen dynamics within whole plants formalised at the organ level. Ecological Modelling. 2007;206:231–249. [Google Scholar]
  28. Evans J. Photosynthesis and nitrogen relationships in leaves of C3 plants. Oecologia. 1989a;78:9–19. doi: 10.1007/BF00377192. [DOI] [PubMed] [Google Scholar]
  29. Evans JR. Partitioning of nitrogen between and within leaves grown under different irradiances. Australian Journal of Plant Physiology. 1989b;16:533–548. [Google Scholar]
  30. Evers J, Vos J, Yin X, Romero P, van der Putten E, Struik P. Simulation of wheat growth and development based on organ-level photosynthesis and assimilate allocation. Journal of Experimental Botany. 2010;61:2203–2216. doi: 10.1093/jxb/erq025. [DOI] [PubMed] [Google Scholar]
  31. Feller U, Fischer A. Nitrogen metabolism in senescing leaves. Critical Reviews in Plant Sciences. 1994;13:241–273. [Google Scholar]
  32. Forde BG, Clarkson DT. Nitrate and ammonium nutrition of plants: physiological and molecular perspectives. Advances in Botanical Research. 1999;30:1–90. [Google Scholar]
  33. Fourcaud T, Zhang X, Stokes A, Lambers H, Korner C. Plant growth modelling and applications: the increasing importance of plant architecture in growth models. Annals of Botany. 2008;101:1053–1063. doi: 10.1093/aob/mcn050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Fournier C, Andrieu B. A 3D architectural and process-based model of maize development. Annals of Botany. 1998;81:233–250. [Google Scholar]
  35. Fournier C, Andrieu B. ADEL-maize: an L-system based model for the integration of growth processes from the organ to the canopy. Application to regulation of morphogenesis by light availability. Agronomie. 1999;19:313–327. [Google Scholar]
  36. Gabrielle B, Denoroy P, Gosse G, Justes E, Andersen MN. Development and evaluation of a CERES-type model for winter oilseed rape. Field Crops Research. 1998a;57:95–111. [Google Scholar]
  37. Gabrielle B, Denoroy P, Gosse G, Justes E, Andersen MN. A model of leaf area development and senescence for winter oilseed rape. Field Crops Research. 1998b;57:209–222. [Google Scholar]
  38. Gallais A, Coque M, Quillere I, Prioul JL, Hirel B. Modelling postsilking nitrogen fluxes in maize (Zea mays) using N-15-labelling field experiments. New Phytologist. 2006;172:696–707. doi: 10.1111/j.1469-8137.2006.01890.x. [DOI] [PubMed] [Google Scholar]
  39. Glass A, Siddiqi M. Nitrogen absorption by plant roots. In: Srivastava HS, Singh RP, editors. Nitrogen nutrition in higher plants. New Delhi, India: Associated Publishers; 1995. pp. 21–56. [Google Scholar]
  40. Godin C, Sinoquet H. Functional–structural plant modelling. New Phytologist. 2005;166:705–708. doi: 10.1111/j.1469-8137.2005.01445.x. [DOI] [PubMed] [Google Scholar]
  41. Gojon A, Nacry P, Davidian JC. Root uptake regulation: a central process for NPS homeostasis in plants. Current Opinion in Plant Biology. 2009;12:328–338. doi: 10.1016/j.pbi.2009.04.015. [DOI] [PubMed] [Google Scholar]
  42. Grindlay DJC. Towards an explanation of crop nitrogen demand based on the optimization of leaf nitrogen per unit leaf area. Journal of Agricultural Science. 1997;128:377–396. [Google Scholar]
  43. Hafsi M, Mechmeche W, Bouamama L, Djekoune A, Zaharieva M, Monneveux P. Flag leaf senescence, as evaluated by numerical image analysis, and its relationship with yield under drought in durum wheat. Journal of Agronomy and Crop Science. 2000;185:275–280. [Google Scholar]
  44. Hammer GL, Oosterom Ev, McLean G, et al. Adapting APSIM to model the physiology and genetics of complex adaptive traits in field crops. Journal of Experimental Botany. 2010;61:2185–2202. doi: 10.1093/jxb/erq095. [DOI] [PubMed] [Google Scholar]
  45. Hirel B, Andrieu B, Valadier MH, et al. Physiology of maize II: identification of physiological markers representative of the nitrogen status of maize (Zea mays) leaves during grain filling. Physiologia Plantarum. 2005;124:178–188. [Google Scholar]
  46. Hirel B, Gallais A. Rubisco synthesis, turnover and degradation: some new thoughts on an old problem. New Phytologist. 2006;169:445–448. doi: 10.1111/j.1469-8137.2006.01641.x. [DOI] [PubMed] [Google Scholar]
  47. Hirel B, Le Gouis J, Ney B, Gallais A. The challenge of improving nitrogen use efficiency in crop plants: towards a more central role for genetic variability and quantitative genetics within integrated approaches. Journal of Experimental Botany. 2007;58:2369–2387. doi: 10.1093/jxb/erm097. [DOI] [PubMed] [Google Scholar]
  48. Hirose T, Werger MJA. Nitrogen use efficiency in instantaneous and daily photosynthesis of leaves in the canopy of a Solidago altissima stand. Physiologia Plantarum. 1987;70:215–222. [Google Scholar]
  49. Irving LJ, Robinson D. A dynamic model of Rubisco turnover in cereal leaves. New Phythologist. 2006;169:493–504. doi: 10.1111/j.1469-8137.2005.01584.x. [DOI] [PubMed] [Google Scholar]
  50. Jamieson P, Semenov M. Modelling N uptake and redistribution in wheat. Field Crops Research. 2000;68:21–29. [Google Scholar]
  51. Jeuffroy MH, Ney B, Ourry A. Integrated physiological and agronomic modelling of N capture and use within the plant. Journal of Experimental Botany. 2002;53:809–823. doi: 10.1093/jexbot/53.370.809. [DOI] [PubMed] [Google Scholar]
  52. Jones CA, Kiniry JR, editors. CERES-Maize. A simulation model of maize growth and development. Collegs Station, TX: Texas A&M University Press; 1986. [Google Scholar]
  53. Kang MZ, Evers JB, Vos J, De Reffye P. The derivation of sink functions of wheat organs using the GREENLAB model. Annals of Botany. 2008;101:1099–1108. doi: 10.1093/aob/mcm212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Kull O, Kruijt B. Acclimation of photosynthesis to light: a mechanistic approach. Functional Ecology. 1999;13:24–36. [Google Scholar]
  55. Kusnetsov VV, Oelmuller R, Sarwat MI, et al. Cytokinins, abscisic acid and light affect accumulation of chloroplast proteins in Lupinus luteus cotyledons without notable effect on steady-state mRNA levels. Specific protein response to light/phytohormone interaction. Planta. 1994;194:318–327. [Google Scholar]
  56. Luquet D, Dingkuhn M, Kim H, Tambour L, Clement-Vidal A. EcoMeristem, a model of morphogenesis and competition among sinks in rice. 1. Concept, validation and sensitivity analysis. Functional Plant Biology. 2006;33:309–323. doi: 10.1071/FP05266. [DOI] [PubMed] [Google Scholar]
  57. Malagoli P, Laine P, Deunff El, Rossato L, Ney B, Ourry A. Modeling nitrogen uptake in oilseed rape cv Capitol during a growth cycle using influx kinetics of root nitrate transport systems and field experimental data. Plant Physiology. 2004;134:388–400. doi: 10.1104/pp.103.029538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Martre P, Porter JR, Jamieson PD, Triboï E. Modeling grain nitrogen accumulation and protein composition to understand the sink/source regulations of nitrogen remobilization for wheat. Plant Physiology. 2003;133:1959–1967. doi: 10.1104/pp.103.030585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Martre P, Jamieson PD, Semenov MA, Zyskowski RF, Porter JR, Triboï E. Modelling protein content and composition in relation to crop nitrogen dynamics for wheat. European Journal of Agronomy. 2006;25:138–154. [Google Scholar]
  60. Masclaux-Daubresse C, Daniel-Vedele F, Dechorgnat J, Chardon F, Gaufichon L, Suzuki A. Nitrogen uptake, assimilation and remobilization in plants: challenges for sustainable and productive agriculture. Annals of Botany. 2010;105:1141–1157. doi: 10.1093/aob/mcq028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Minchin PEH, Lacointe A. New understanding on phloem physiology and possible consequences for modelling long-distance carbon transport. New Phytologist. 2005;166:771–779. doi: 10.1111/j.1469-8137.2005.01323.x. [DOI] [PubMed] [Google Scholar]
  62. Monsi M, Saeki T. On the factor light in plant communities and its importance for matter production. Annals of Botany. 2005;95:549–567. doi: 10.1093/aob/mci052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Münch E. Die stoffbewegungen in der Pflanze. Jena: Fisher; 1930. [Google Scholar]
  64. Ourry A, Mcduff JH, Volenec JJ, Gaudillère JP. Nitrogen traffic during plant growth and development. In: Lea PJ, Morot-Gaudry JF, editors. Plant nitrogen. Berlin: Springer-Verlag; 2001. pp. 255–273. [Google Scholar]
  65. Pons TL, Bergkotte M. Nitrogen allocation in response to partial shading of a plant: possible mechanisms. Physiologia Plantarum. 1996;98:571–577. [Google Scholar]
  66. Pons TL, Jordi W, Kuiper D. Acclimation of plants to light gradients in leaf canopies: evidence for a possible role for cytokinins transported in the transpiration stream. Journal of Experimental Botany. 2001;52:1563–1574. doi: 10.1093/jexbot/52.360.1563. [DOI] [PubMed] [Google Scholar]
  67. Prioul JL, Brangeon J, Reyss A. Interaction between external and internal conditions in the development of photosynthetic features in a grass leaf. 1. Regional responses along a leaf during and after low-light or high-light acclimation. Plant Physiology. 1980a;66:762–769. doi: 10.1104/pp.66.4.762. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Prioul JL, Brangeon J, Reyss A. Interaction between external and internal conditions in the development of photosynthetic features in a grass leaf. 2. Reversibility of light-induced responses as a function of developmental stages. Plant Physiology. 1980b;66:770–774. doi: 10.1104/pp.66.4.770. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Prusinkiewiz P. Modeling plant growth and development. Current Opinion in Plant Biology. 2004;7:79–83. doi: 10.1016/j.pbi.2003.11.007. [DOI] [PubMed] [Google Scholar]
  70. de Reffye P, Heuvelink E, Barthélémy D, Cournède P-H. Plant growth models. In: Jorgensen SE, Fath B, editors. Ecological models. Oxford: Elsevier; 2008. pp. 2824–2837. [Google Scholar]
  71. Schieving F, Werger MJA, Hirose T. Canopy structure, nitrogen distribution and whole canopy photosynthetic carbon gain in growing and flowering stands of tall herbs. Vegetatio. 1992;102:173–181. [Google Scholar]
  72. Siddiqi MY, Glass ADM, Ruth TJ, Rufty TW. Studies of the uptake of nitrate in barley. 1. Kinetics of 13NO3− influx. Plant Physiology. 1990;93:1426–1432. doi: 10.1104/pp.93.4.1426. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Sinclair TR, Amir J. A model to assess nitrogen limitations on the growth and yield of spring wheat. Field Crops Research. 1992;30:63–78. [Google Scholar]
  74. Terashima I, Araya T, Miyazawa SI, Sone K, Yano S. Construction and maintenance of the optimal photosynthetic systems of the leaf, herbaceous plant and tree: an eco-developmental treatise. Annals of Botany. 2005;95:507–519. doi: 10.1093/aob/mci049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Thornley JHM. Dynamic model of leaf photosynthesis with acclimation to light and nitrogen. Annals of Botany. 1998a;81:421–430. [Google Scholar]
  76. Thornley JHM. Modelling shoot:root relations: the only way forward ? Annals of Botany. 1998b;81:165–171. [Google Scholar]
  77. Thornley JHM. Acclimation of photosynthesis to light and canopy nitrogen distribution: an intrepretation. Annals of Botany. 2004;93:473–475. doi: 10.1093/aob/mch051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  78. Tilman D. Global environmental impacts of agricultural expansion: the need for sustainable and efficient practices. Proceedings of the National Academy of Sciences, USA. 1999;96:5995–6000. doi: 10.1073/pnas.96.11.5995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Touraine B, Daniel-Vedele F, Forde BG. Nitrate uptake and its regulation. In: Lea PJ, Morot-Gaudry JF, editors. Plant nitrogen. Berlin: Springer-Verlag; 2001. pp. 1–36. [Google Scholar]
  80. Triboï E, Triboï-Blondel AM. Production and grain or seed composition: a new approach to an old problem – invited paper. European Journal of Agronomy. 2002;16:163–186. [Google Scholar]
  81. Turgeon R. Phloem loading: how leaves gain their independence. Bioscience. 2006;56:15–24. [Google Scholar]
  82. Wallsgrove RM, Keys AJ, Lea PJ, Miflin BJ. Photosynthesis, photo-respiration and nitrogen metabolism. Plant, Cell and Environment. 1983;6:301–309. [Google Scholar]
  83. Williams RD. Assimilation and translocation in perennial grasses. Annals of Botany. 1964;28:419–426. [Google Scholar]

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES