NEMA, a functional–structural model of nitrogen economy within wheat culms after flowering. II. Evaluation and sensitivity analysis

Abstract

Background and Aims

Simulating nitrogen economy in crop plants requires formalizing the interactions between soil nitrogen availability, root nitrogen acquisition, distribution between vegetative organs and remobilization towards grains. This study evaluates and analyses the functional–structural and mechanistic model of nitrogen economy, NEMA (Nitrogen Economy Model within plant Architecture), developed for winter wheat (Triticum aestivum) after flowering.

Methods

NEMA was calibrated for field plants under three nitrogen fertilization treatments at flowering. Model behaviour was investigated and sensitivity to parameter values was analysed.

Key Results

Nitrogen content of all photosynthetic organs and in particular nitrogen vertical distribution along the stem and remobilization patterns in response to fertilization were simulated accurately by the model, from Rubisco turnover modulated by light intercepted by the organ and a mobile nitrogen pool. This pool proved to be a reliable indicator of plant nitrogen status, allowing efficient regulation of nitrogen acquisition by roots, remobilization from vegetative organs and accumulation in grains in response to nitrogen treatments. In our simulations, root capacity to import carbon, rather than carbon availability, limited nitrogen acquisition and ultimately nitrogen accumulation in grains, while Rubisco turnover intensity mostly affected dry matter accumulation in grains.

Conclusions

NEMA enabled interpretation of several key patterns usually observed in field conditions and the identification of plausible processes limiting for grain yield, protein content and root nitrogen acquisition that could be targets for plant breeding; however, further understanding requires more mechanistic formalization of carbon metabolism. Its strong physiological basis and its realistic behaviour support its use to gain insights into nitrogen economy after flowering.

INTRODUCTION

Developing novel practices and genotypes to minimize nitrogen (N) release in the environment and maximize N use by plants is a major challenge (Tilman, 1999), which requires understanding N economy at the plant and crop scales.

An important feature of N economy in monocarpic species such as winter wheat (Triticum aestivum) is competition in the post-flowering period between (a) remobilization of N to growing grains, which determines their protein content, and (b) storage of N in green tissues, which determines their photosynthesis and dry mass acquisition by the plant and the grains (Masclaux-Daubresse et al., 2010). Up to 75 % of the reduced N in cereal leaves is involved in photosynthetic processes, mainly as Rubisco (Evans, 1989). In dense canopies, one main determinant of photosynthesis is vertical N distribution: theoretical studies have suggested that canopy photosynthesis would be maximized if N is preferentially allocated to the more illuminated leaves and if N distribution follows the light gradient (Field, 1983; Hirose and Werger, 1987).

Nitrogen remobilization can be delayed – and hence carbon (C) acquisition prolonged – when fertilization at flowering allows high post-flowering N uptake by roots, which also increases the final N content of the grains (Triboï and Triboï-Blondel, 2002; Bancal, 2009; Masclaux-Daubresse et al., 2010). However, if N remaining in the straw at maturity is high, N fertilizers would have been used inefficiently. Post-flowering fertilization may also be inefficient if N fertilizers are applied too late, since N uptake efficiency rapidly declines after flowering (Barneix, 2007). Such a decline is usually assumed to result from limited photosynthesis in aerial parts, but regulatory mechanisms remain unclear.

Models which account for these interactions and predict root N uptake, grain yield and protein content from environmental variables would help identify traits or processes that are potential targets for breeding and predict how novel practices would impact whole plant N economy. Numerous models have been developed in recent decades (Jeuffroy et al., 2002) but they were developed for intensive agricultural conditions and, even if several crop models have a solid mechanistic basis, the integrated scale at which equations are formalized make them far from physiological processes occurring at the tissue scale (Fourcaud et al., 2008; Bertheloot et al., 2010). In a companion paper (Bertheloot et al., 2011), we describe the model NEMA (Nitrogen Economy Model within plant Architecture) for wheat plants after flowering which formalizes processes governing N acquisition by roots, remobilization from vegetative organs and distribution for each organ of the aerial parts of the plant based on physiological knowledge. The impact of N distribution on dry matter acquisition by the plant and grains is also included. Carbon metabolism is not explicitly modelled, but rather its consequence on dry mass, whose major contribution is from C and not N, and dry matter is allocated to organs according to the conventional demand-driven approach (GreenLab formalism; Kang et al., 2008).

NEMA predicts N and dry matter acquisition and distribution from (a) the soil N concentration and the time courses of (b) photosynthetically active radiation (PAR) above the canopy and (c) air temperature, and (d) a realistic description of the structure of the aerial part of the culm. Processes are formalized at the scale of each organ (i.e. lamina, sheath, internode, peduncle and chaff) as a function of its local PAR – calculated following Beer–Lambert's law (Monsi and Saeki, 2005) – and internal resources. Resources are assumed to be equally available to all plant organs, and a common pool of mobile N (i.e. amino acids and nitrate) is explicitly represented. This pool is enriched by root acquisition and N depletion from vegetative organs, and depleted by grain N accumulation and protein synthesis in photosynthetic organs. The N content of all photosynthetic organs and its remobilization are driven by a single process, Rubisco turnover, modulated by mobile N and PAR intercepted by the organ. Photosynthetically active radiation is a substitute for the role of the transpiration stream in the xylem, which is the main way for mature laminae to obtain N. Given the lack of information in the literature about organs other than laminae, the model also accounts for a possible role for phloem in N influx into organs by setting two different equations for N influx: one for protein synthesis from N coming from xylem, which depends on PAR intercepted; and the other one for protein synthesis from N coming from phloem, which depends on dry mass influx into the organ to account for the role of C influx in transport of resources in the phloem (according to Münch, 1930). In addition, root N acquisition is formalized from the activities of transport systems [corresponding for nitrate to HATS (high affinity transport system) and LATS (low affinity transport system); for a review, see Glass and Siddiqi (1995)], with feedbacks linked to plant C and N status (Drouet and Pagès, 2007).

In this study, NEMA is evaluated for its capacity to simulate accurately the dynamics of root N acquisition rate, N distribution between aerial organs, grain N and dry mass, and tissue death after flowering, as well as their response to three N fertilization treatments at flowering. The model variables were initialized using measurements made at flowering for the three N treatments, while parameter values were estimated using information in the literature when available, or otherwise by fitting simulations to measurements. To better understand the regulation of N economy at the whole plant scale and N distributions observed in the field, the response of NEMA to N fertilization was analysed and sensitivity analysis of model parameters was undertaken. This should enable the identification of factors limiting root N acquisition, grain N and dry mass accumulation.

MATERIALS AND METHODS

In the present work, NEMA describes the field as a population of identical culms. The density (culms m⁻²) and tissue area profile of the culms are used to calculate light attenuation within the canopy. Measurements on median culms that are representative of the field were used to calibrate and validate NEMA, and simulations were done for one median culm.

Experimental data for model calibration and evaluation

NEMA was calibrated on the experiment (expt 1) undertaken in Clermont-Ferrand, France, in 1994, described in Martre et al. (2003) and Bertheloot et al. (2008a, b). The cultivar Thésée was grown in dense stands with high N fertilization before flowering and received either 0 (H0), 3 (H3) or 15 g N m⁻² (H15) at flowering. Crops were rain fed, and pests and diseases were chemically controlled. The number of culms within 1 m² was counted and three replicates of 15 median culms were selected from plants harvested at regular intervals from flowering to crop maturity. For each replicate, N mass and dry mass of each lamina rank (four were still green at flowering), stem (sheaths, internodes and ear peduncle pooled), chaff and grains, as well as total lamina and photosynthetic area were quantified. Mean air temperature and PAR were recorded daily by a weather station. Thermal time was calculated as the accumulated daily temperature above 0 °C. NEMA was evaluated in expt 1 for its capacity to simulate accurately, using a single set of parameter values, the time courses of N mass and dry mass observed for individual laminae, the stem compartment, chaff and grains in the three treatments H0, H3 and H15.

A second experiment (expt 2) was performed to complement the data from expt 1. This was required to initialize the model with estimates of N mass, dry mass and area of individual sheaths and internodes, as sheaths and internodes had been pooled in a single stem compartment in expt 1. Thus expt 2 was used to assess the contribution of each individual botanical entity of the stem to the whole stem compartment; however, only N measurements made in expt 1 were used for model validation. Experiment 2 was carried out at Grignon, France; cultivar Soissons, which has a stature similar to Thésée, was sown on 27 October 2005 at a density of 250 seeds m⁻² in a deep silt soil, and cultivated on five adjacent plots (plot size = 1·6 × 35 m; row spacing = 17·5 cm; gap between adjacent plots = 0·2 m). Cultural practices are similar to those in expt 1. Plants received high N fertilization before flowering (5 and 7 g N m⁻² applied at tillering and at the beginning of stem elongation, respectively; mineral soil N at the end of winter = 9 g N m⁻² in the 0·9 m deep soil profile). Plots were rain fed with complementary irrigation from mid-May to the end of June and were kept disease free by chemical treatment. Three replicates of five median culms each were selected at flowering from 0·2 m² samples (two rows × 50 cm) in three different plots. Four laminae were still green at flowering. The following measurements were made on each lamina, sheath and internode of the four upper phytomers, on the peduncle, and on chaff. Plant parts were scanned to measure their lengths and projected areas (RGB colour images, 300 dpi resolution, Epson Perfection 2400 Photo). The developed areas of sheaths, internodes, peduncles and chaff were calculated as for cylinders, by multiplying the projected areas by π. Dry masses were determined after oven drying at 80 °C until constant mass. Samples were then ground and total N mass per unit dry mass (%N) was determined by the Dumas method using an NA 1500 CN analyser (Fisons Instruments, France). Ten other culms were fixed on a vertical board and digital pictures were taken to estimate lamina orientation.

Initialization of model state variables at flowering

The model was initialized similarly for the three N treatments in expt 1, since plants had been grown under similar conditions until flowering. These variables and their values at flowering are listed in Table 1. The density of culms was given the mean value measured in expt 1: 410 culms m⁻².

Table 1.

Variables describing the culm at flowering: their symbols, definitions and values

Definition	Symbol	Unit	Value	Definition	Symbol	Unit	Value
Density of culms	Densc	Culm m−2	410	(b) Roots
Mobile N mass in the common pool	Ncmob	mg	2·4	Remobilizable N mass	Nrrem	mg	1·10
(a) Grains				Structural N mass	Nrstruct	mg	10·00
Total N mass	Ngraintot	mg	2·4	Remobilizable dry mass	Mrrem	mg	56
Total dry mass	Mgraintot	mg	120	Structural dry mass	Mrstruct	mg	504
Thermal time at which grains begins to grow	ttgraininit	°Cd	0	Thermal time at which roots begin to grow	ttrinit	°Cd	–1000

(c) Photosynthetic entities
			Lamina				Sheath				Internode
Definition	Symbol	Unit	n	n–1	n–2	n–3	n	n–1	n-2	n–3	n	n–1	n–2	n–3	Peduncle	Chaff
Total length	Ltp,itot	cm	17·4	22·7	21·1	18·2	14·5	14·0	12·5	11·0	18·6	12·8	8·6	5·0	21·9	9·0
Total area	Atp,itot	cm2	34·6	34·0	22·8	16·0	6·0	5·0	4·0	2·0	15·0	4·0	2·5	1·0	24·0	7·5
Photosynthetic N mass	Ntp,iph	mg	5·30	2·90	1·20	0·09	1·80	0·66	0·18	0·02	1·23	0·28	0	0	2·53	3·68
Structural N mass	Ntp,istruct	mg	1·02	0·83	0·53	0·38	0·68	0·21	0·11	0·12	0·85	0·33	0·14	0·05	1·30	1·07
Remobilizable dry mass	Mtp,irem	mg	40	40	20	0	22	15	9	2	41	39	33	9	56	50
Structural dry mass	Mtp,istruct	mg	140	90	50	40	103	69	43	9	188	180	154	43	257	210
Thermal time at which entities begin to grow	tttp,iinit	°Cd	–390	–480	–570	–660	–240	–330	–420	–510	–220	–310	–400	–490	–130	–400

tp stands for ‘entity type’ (either lamina, sheath, internode, peduncle or chaff), r for roots and °Cd for cumulative degree days after flowering.

Only the four upper laminae were still green at flowering in both experiments and only the four upper phytomers had elongated internodes. The culm at flowering is thus represented as an assembling of four laminae, fours sheaths, four internodes plus the internode surmounted by chaffs and ear grains. Variables for chaff, grains and individual laminae were initialized using measurements from expt 1, except chaff total area and the length of each entity (i.e. lamina, sheath, internode, peduncle and chaff), which were set to the mean values in expt 2. Each lamina total and photosynthetic area and total dry and N masses were set to the means measured over the three treatments. For each lamina and chaff, structural dry mass and N mass were given by the lowest values observed during the grain-filling period over all treatments. Remobilizable dry mass was calculated as the difference between total dry mass and estimated structural dry mass. Remobilizable plus mobile N mass allocated to a module was estimated as the difference between total N mass and structural N mass. Mobile N mass was estimated as in Bertheloot et al. (2008a), assuming that it represented 10 % of the remobilizable N mass.

Variables for sheaths, internodes and the peduncle were initialized using expt 1 and expt 2. From expt 1, total and structural N mass and dry mass of the stem compartment (N_stem^tot, N_stem^struct, M_stem^tot and M_stem^struct, respectively) were initialized as described above for laminae and chaff. From expt 2, allometric ratios were calculated for each phytomer between the dry mass of the sheath and that of the lamina. Each sheath dry mass in expt 1 was then estimated as the product of the allometric ratio and the dry mass of the lamina measured in expt 1. The same principle was used to estimate the dry mass of individual internodes in expt 1. For the peduncle, the allometric ratio was calculated relative to the upper lamina. Finally, similar calculations were done for structural dry mass and N mass, and for total N mass.

Grain dry mass and N mass at flowering were set to 120 and 2·4 mg, respectively (Bertheloot et al., 2008a); root dry mass was set to 15 % of the total dry mass of the culm aerial part following observations of Siddique et al. (1989) in different wheat cultivars. The ratio between root N and dry mass was assumed to be equal to that of the culm aerial part: 0·02. The remobilizable fraction of total N mass was set to 0·10 like that estimated for forage grass (Tabourel-Tayot and Gastal, 1998b). The same value was set for the remobilizable fraction of total dry mass (Drouet and Pagès, 2007). The concentration of soil N available for plants was calculated from the amount of N fertilizer supplied at flowering, assuming that it was located in the top metre of the soil.

Parameter estimation

The experimental data set was not sufficient to estimate all parameters directly or by model inversion; our objective was to give realistic references for the sensitivity analysis and to assess whether the model could reproduce the main differences observed among the treatments H0, H3 and H15. We used the literature as the primary source for estimation and we assumed that the parameter values describing a given process were identical for all phytomers, i.e. were independent of the position in the plant. We also considered that, in the absence of clear contradictory evidence, parameter values should be identical between entity types. To simplify the estimation of parameter values, parameters were grouped according to the meta-processes listed below; then each group of parameters was estimated successively with an order corresponding to the calculation order in NEMA and thus reflecting an increasing dependency of the meta-processes on previous ones: (1) PAR interception; (2) root N acquisition; (3) N distribution within the culm; (4) tissue death; (5) dry mass production; and (6) dry mass distribution within the culm. Taking identical parameter values for all entity types provided good simulations of observed behaviours, except for the relative synthesis rate of photosynthetic N from the xylem, whose value had to be divided by 5 for chaff (parameter σ_chaff^Nph). In a previous work (Bertheloot et al., 2008b), similar patterns of N depletion were observed for chaff and internodes, which differed from those for laminae and sheaths. Accordingly, the relative synthesis rate of photosynthetic N from the xylem for internodes (σ_in^Nph) was set equal to that for chaffs. This significantly improved model prediction of the time course of N mass within the stem compartment.

Parameter values and the method used for their estimation are presented in Table 2. The angle between the vertical and the vector normal to the lamina plane (θ_la) was estimated from photographs of the Soissons cultivar in expt 2. The extinction coefficient for vertical entities (i.e. the sheath and internodes), k_vertical, was set according to figure 15·5 in Campbell and Norman (1998). Values for rates are often expressed per day in the literature and were converted to per degree day using the mean air temperature of 20·5 °C observed in expt 1. In most cases, the process quantified in the literature did not exactly match the formalization made in the model, and parameter values from the literature were modified to simulate the differences observed between treatments: this was the case for parameters defining the activities of transport systems (i.e. U_r,max, k_r,1 and k_r,2) or parameters defining dry mass production by a photosynthetic entity (i.e. ω_tp and ɛ_tp). When no data were available in the literature, different methods were used. For example, the relative rate of N remobilization for roots (δ_r^N) was considered to be identical to that for laminae and was given the value found in Bertheloot et al. (2008a); relative dry matter remobilization rates were considered to be identical to relative N remobilization rates, as done by Drouet and Pagès (2007).

Table 2.

Model parameters: their symbols, units and values used for simulation

Symbol	Definition	Unit	Value	Source for estimation
PAR interception
θla	Angle between the vertical and the vector normal to the lamina plane	Radians	0·52	Expt 2
kvertical	PAR extinction coefficient for vertical entities	m2 m−2	0·5	Campbell and Norman (1998)
Root N uptake
βC, βN	Coefficient for C and N availability effect on root N uptake	Dimensionless	2300, 130	Expt 1
kr,1	Constant of the Michaelis function reflecting HATS activity	g m−3	2·5	Siddiqi et al. (1990) + expt 1
kr,2	Rate constant of the linear function reflecting LATS activity	g m−3 °Cd−1	5 × 10−6	Siddiqi et al. (1990) + expt 1
(SrMrem)min	Minimum threshold of dry matter influx into roots to sustain root N uptake	g d−1	0·0013	Expt 1
Ur,max	Theoretical maximum N acquisition at saturating soil N concentration	g m−3 °Cd−1	1·5 × 10−4	Siddiqi et al. (1990) + expt 1
N fluxes
δrN, δtpN	Relative degradation rates of remobilizable N for roots, entities tp	°Cd−1	0·008	Drouet and Pagès (2007), Bertheloot et al. (2008a)
γ	Relative rate of potential grain N filling during cell division	°Cd−1	0·0055	Bertheloot et al. (2008a)
ktp,1, ktp,2	Michaelis–Menten constants defining photosynthetic N synthesis associated with xylem influx for entities tp	g g−1, J m−2 d−1	0·0018, 864 000	Bertheloot et al. (2008a)
pr, ptp,i	Proportion coefficient for N influx following dry mass influx into roots, entities tp	Dimensionless	0·1	Expt 1
σtp,iNph	Relative rate of photosynthetic N synthesis associated with xylem influx for entities tp	g g−1 °Cd−1	0·00015*, 0·00003†	Bertheloot et al. (2008a) + expt 1
Death of photosynthetic active tissues and photosynthesis
dtp	Proportion of maximum specific N mass at which tissues die for entities tp	Dimensionless	0·4	Expt 1
ωtp	Proportion coefficient linking photosynthesis at saturating PAR and N mass per unit photosynthetic area	d−1	5	Marshall and Biscoe (1980) + expt 1
ɛtp	Photosynthetic efficiency	g J−1	5 × 10−6	Marshall and Biscoe (1980) + expt 1
Dry matter fluxes
αgrain, βgrain; αr, βr; αtp, βtp	Two parameters determining the shape of the beta function for grains, roots, entities tp.	Dimensionless	2,2; 2,2; 2,2
δrM, δtpM	Relative degradation rates of remobilizable dry mass for roots, entities tp	°Cd−1	0·008	Drouet and Pagès (2007)
σgrainM, σrM, σtp,iM	Relative sink strength of grains, roots, entities tp	Dimensionless	7, 1, 1 or 2‡	Expt 1
ttgrainMacc, ttrMacc, ttlaMacc, ttshMacc, ttinMacc, ttpedMacc	Period during which grains, roots, entities tp can accumulate dry mass	°Cd	700, 1700, 1090, 940, 920, 830	Expt 1

* Laminae and sheaths.

^† Internodes, peduncle and chaff.

^‡ Peduncle and chaff.

Simulation of dry mass distribution between organs with GreenLab requires defining when organs begin demanding dry mass (tt_r^init, tt_g^init and tt_tp,i^init for roots, grains and entity of type tp and rank i, respectively): they were defined as the times they begin to elongate, which is well before flowering. Roots were assumed to begin growing at plant emergence, grains at flowering, while the times photosynthetic entities begin demanding dry mass (tt_tp,i^init) were calculated assuming (a) a delay of 1000 °Cd after plant emergence and flowering (expt 2); (b) an interval of 90 °Cd between the appearance of two successive leaves (personal data); and (c) the appearance of sheath and internode 1·7 and 1·9 phyllochron later than the appearance of the lamina of the same phytomer (Fournier et al., 2005). Organ demand through thermal time was defined by beta functions, whose parameters α, β (α_grain, β_grain for grains; α_tp, β_tp for photosynthetic entities; α_r, β_r for roots) were set to 2 so as to simulate the sigmoid pattern usually observed for grain filling (Yin et al., 2009). Finally, the duration of dry mass demand (tt_r^Macc, tt_grain^Macc and tt_tp^Macc for roots, grains and entity tp, respectively) was defined so that dry matter demand of the last entity appearing, i.e. the upper one, stops at 700 °Cd after flowering, which is when grains stopped accumulating dry mass in our measurements.

Other parameters, i.e. the threshold of dry mass influx into roots that sustains N acquisition [(S_r^Mrem)_min)], the coefficients defining N fraction in dry mass influx (p_r and p_tp), the threshold for tissue death (d_tp) and the relative sink strengths for dry mass (σ_grain^M, σ_r^M and σ^M_tp,i) were adjusted empirically so that the model simulates the culm behaviour observed in expt 1.

Sensitivity analysis

In addition to the comparison of model outputs among the three N treatments, NEMA's behaviour was analysed by sensitivity analysis using the intermediate treatment H3 to identify the parameters that determine agronomic traits of interest, i.e. root N acquisition, grain N mass and dry mass. Analyses continued through the entire post-flowering period to account for the fact that outputs at maturity are the result of elaboration over time. Estimated values of parameters defining plant structure at flowering were kept constant, except for lamina orientation. Given the number of parameters, analysis was carried out in two steps as proposed by Ruget et al. (2002): first, the most important parameters were identified separately for root N uptake, N distribution within the culm, tissue death, dry mass production, and dry mass distribution within the culm; then, sensitivity to identified parameters was calculated taking all meta-processes into account.

Global approaches (as opposed to local methods; Saltelli et al., 2006; Cariboni et al., 2007; Wu and Cournède, 2010) were used to estimate the parameter effect on the output over the entire parameter space (as opposed to at specific points). It is crucial in biological models characterized by strong interactions between parameters. Each parameter was assumed to follow a uniform distribution within the interval of the reference value ± 10 %. The standardized regression coefficients (SRC) method is first used to keep a balance between computing cost and analysis reliability. The SRC method is based on a linear approximation of the model response to parameter values and uses Monte Carlo simulations to vary each parameter according to its distribution. The SRC method calculates a coefficient of determination (R²) which represents the fraction of the output variance explained by the linear approximation and produces an index (SRC_j) for each parameter, which is the fraction of the output variance explained by parameter j. The SRC method is reliable when R² >0·9 (Cariboni et al., 2007). For lower R², we turned to variance-based methods of sensitivity analysis, which consist of evaluating the contribution of the parameters to the variance of the predicted output. Sobol's method is selected here, it is model independent but time consuming. This method uses Monte Carlo simulations to vary each parameter but breaks down output variance into the contributions imputable to each individual parameter and to interactions between parameters. Such a method was already used in the crop model of Makowski et al. (2006). We chose to use the first-order sensitivity indexes produced by Sobol, S_j, measuring the relative importance of every parameter j, without the effects due to the interaction between parameters. Efficient implementation of SRC and Sobol's method in C++ adapted to a dynamic system of plant growth (Wu and Cournède, 2010) was coupled to our simulation code (also in C++). The number of simulations was set to 100 for the SRC method and to 1000 for Sobol's method, after we checked that results did not change with a larger number of simulations.

RESULTS

Photosynthetically active radiation interception

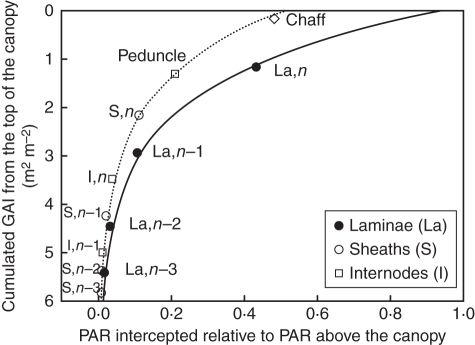
Photosynthetically active radiation interception was calculated for chaff, the peduncle and for each entity of the four phytomers bearing photosynthetic laminae at flowering (except the two lowest internodes which were fully hidden by sheaths). The mean PAR intercepted by plant tissues, expressed relative to PAR above the canopy (Fig. 1), ranged between 0·006 for the lowest sheath and 0·48 for chaff, corresponding to downward cumulative area indices (AIs) of 5·81 and 0·15, respectively. For a similar AI, the PAR intercepted per unit tissue area was always lower for vertical entities (i.e. sheath and internodes) than for laminae. Moreover, in accordance with culm structure [fig. 2 in the companion paper (Bertheloot et al., 2011) in which NEMA is described], AI increased when considering successively the lamina, the sheath and the internode of one phytomer. There was thus a strong gradient of PAR between the laminae, the sheath and the internode of each phytomer (Fig. 1).

Fig. 1.

Calculated green area index (GAI) cumulated from the canopy top vs. the predicted PAR (J m⁻² d⁻¹) intercepted by entities at flowering, expressed relative to PAR above the canopy for each type of entity. The solid line represents laminae, the dotted line vertical entities. Symbols represent values for each entity, calculated for the middle exposed height of the entity. Laminae are denoted by La, sheaths by S and internodes by I, numbered according to their rank from the top (n being the flag leaf).

Nitrogen distribution within the culm

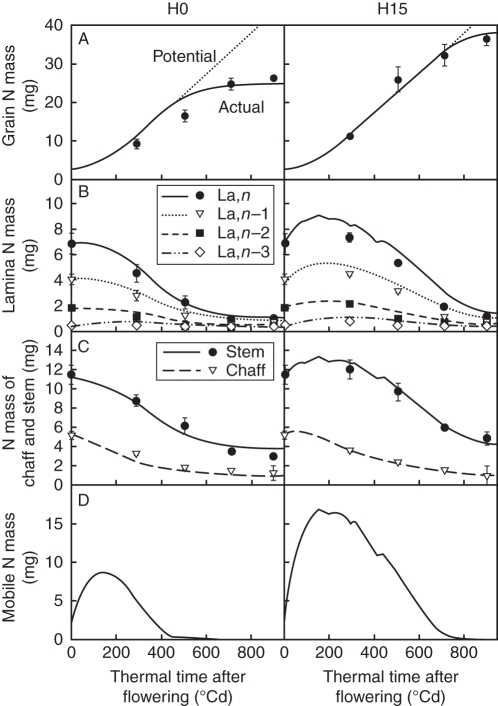
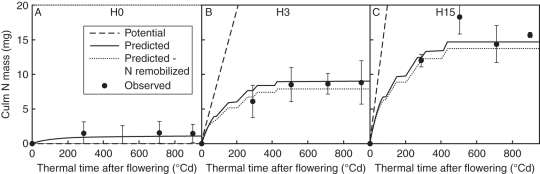
Treatments H3 and H15 resulted in similar time courses of N mass for individual laminae, the stem (i.e. sheaths, internodes and peduncle pooled) and grains, contrasting with those in treatment H0. Only treatments H0 and H15 are thus represented in Fig. 2. Final grain N mass was 39 % higher in H15 than in H0 (Fig. 2A); following N remobilization, the N mass of individual laminae or stems began decreasing around flowering in H0 and 300 °Cd later in H15 (Fig. 2B, C); N mass of chaff decreased throughout the post-flowering period in both treatments, but faster in H0 than in H15 (3·3 and 3·7 g N in chaff at 300 °Cd, respectively).

Fig. 2.

Observed (symbols) and predicted (lines) time courses of N mass for (A) grains, (B) individual laminae, (C) chaff and stem (i.e. internodes, sheaths and peduncle pooled), (D) and the common pool for treatments H0 and H15. For grains, the potential function of N mass accumulation is represented by dotted lines. Laminae are denoted La and numbered according to their rank from the top (n being the flag leaf). The observed data are means of three independent replicates. The vertical bars represent ± s.d.

Accuracy in predicting N mass dynamics in individual laminae and grains was similar to that in Bertheloot et al. (2008a) in which N mass of entities other than laminae and grains was forced to follow experimental data. Differences between treatments were interpreted through differences in mass dynamics of mobile N (Fig. 2D) linked to differences in root N acquisition. In all treatments, predicted mobile N mass first increased until 150 °Cd after flowering, reflecting a low demand by grains, and decreased to zero during grain filling in all cases. The initial increase was greater in H15 than in H0, and thus the time at which mobile N mass reached zero was later (730 °Cd vs. 450 °Cd). As a result of the longer period when mobile N was non-limiting for grain filling, (a) the predicted rate of grain N acquisition remained at potential for a longer period in H15 than in H0 (until 730 °Cd and 450 °Cd, respectively; Fig. 2A), and (b) synthesis of photosynthetic N took place at a higher rate and lasted longer in H15 [eqns 11–12 in the companion paper (Bertheloot et al., 2011)], which led to the prediction of a delay in the decrease in N masses for laminae (Fig. 2B). Finally, the increase and decrease in N mass occurred simultaneously for all lamina ranks and this was well predicted by the model, supporting the formalization of mobile N as belonging to a common pool, which implies that all plant entities have equal access to it.

The model also accurately predicted the differences observed between H0 and H15 concerning N mass dynamics in the stem compartment and chaff (Fig. 2C). These differences can be interpreted as for laminae, i.e. linked with differences in mobile N mass dynamics. In contrast to laminae, the N mass of chaff in H15 decreased after flowering without a time lag, but the final value was higher than in H0. This pattern was reproduced in the model by giving the relative synthesis rate of photosynthetic N associated with xylem influx (σ_tp,i^Nph), a value five times lower for chaff than for laminae. Values for internodes and peduncle were made identical to those for chaff because that parameterization increased the accuracy of model prediction for N mass dynamics in the stem. In all treatments and for all photosynthetic entities, only xylem influx played a significant role in N mass dynamics of photosynthetic tissues: the synthesis rate of photosynthetic N associated with phloem influx was indeed predicted to be null (data not shown). This confirmed our initial assumption that mature photosynthetic entities import N only via the xylem transpiration stream.

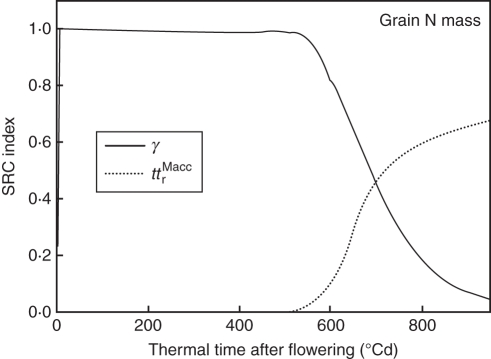
Sensitivity analysis of grain N mass showed that, until 600 °Cd, it was sensitive to the potential rate of grain N filling (γ) in accordance with simulations shown in Fig. 2A, where grain N acquisition was initially limited by its potential rate; thereafter, grain N mass became increasingly sensitive to the parameter defining how long roots are potentially able to import dry matter (tt_r^Macc; Fig. 3). Final grain N mass could be increased by 6 % by virtually extending by 50 °Cd the period during which all organs can accumulate dry mass; the increase reached 34 % when only the time for roots was extended (data not shown).

Fig. 3.

SRC index defining sensitivity of grain N mass to model parameters in treatment H1 vs. thermal time after flowering. Only parameters that had an SRC index >0·1 at least once are represented. γ (°Cd⁻¹) is the relative rate of potential grain N filling during cell division; tt_r^Macc (°Cd) is the period during which roots can accumulate dry mass.

Root N acquisition

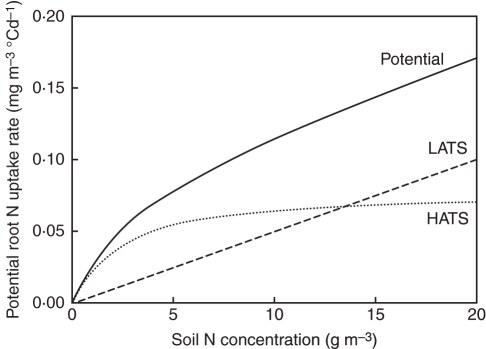
In the model, root N acquisition rate is formalized as the product of (a) a potential rate reflecting the regulation of saturable (HATS) and non-saturable (LATS) transport systems by soil N concentration only, and (b) two functions representing feedback effects of C and N availability within the roots. Figure 4 shows the response of the potential acquisition rate to soil N concentration as well as the contributions of both transport systems: below 5 g N m⁻³ in the soil, the potential increases strongly with soil N as the activities of both transport systems increase; above 5 g N m⁻³ in the soil, the rate of increase is lower since the activity of the saturable transport systems reaches a plateau.

Fig. 4.

Potential root N uptake rate as a function of N concentration available in the soil; the contributions of high and low affinity transport systems (HATS and LATS, respectively) are indicated.

Nitrogen acquisition by roots was not quantified in the experiments; reliability of model predictions was evaluated using the increase in total N mass of the aerial parts of the culm, which results from both N acquisition and remobilization from roots. Indeed, the cumulated N mass remobilized from roots over the post-flowering period was simulated to be the same for all treatments (1·1 mg; Fig. 5A–C), in accordance with the identical mass of N in roots at flowering in the three treatments and the first order kinetics followed by N release [eqn 9 in the companion paper Bertheloot et al., 2011)]. Thus, differences in the increase in observed N mass of culm aerial parts were assumed to represent differences in root N acquisition. A total of 0·0, 7·6 and 15·0 mg (average of the three last points) was estimated to be taken up by roots in H0, H3 and H15; these values are close to those simulated by the model. Simulated differences in N acquisition among treatments were mainly related to the potential response rate to soil N concentration: in H0, no N was available in the soil and the increase in culm N mass (Fig. 5A) represented remobilization of root N; between H3 and H15, the potential rate almost doubled in response to a 5-fold change in soil N concentration.

Fig. 5.

Potential, observed and predicted time courses of N mass in the aerial part of the culm, and simulated time courses of the cumulated N mass taken up by roots (dotted lines) in treatments H0, H3 and H15 (expt 1) during the post-flowering period. The cumulated N mass taken up by roots during the post-flowering period was calculated as the difference between N mass in the aerial parts of the culm and the cumulated N mass remobilized by roots. The observed data are means of three independent replicates. The vertical bars represent ± s.d.

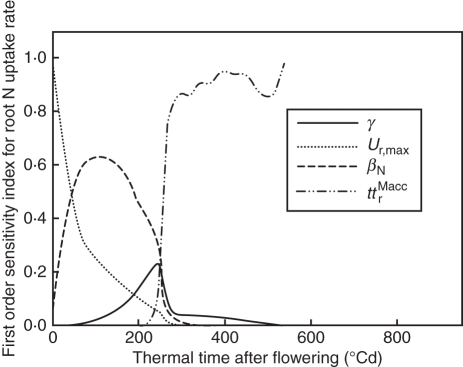
Effective N acquisition in treatments H3 and H15 were far below potential rates (dotted lines in Fig. 5B, C): 3·7 and 5·1 times lower at 150 °Cd, respectively. Until 400 °Cd, the high mobile N concentration was the only factor reducing N acquisition compared with the potential (data not shown); then, at 400 °Cd, N acquisition stopped in all treatments. At this time, dry mass accumulation in roots fell below the threshold required for root N acquisition, (S_r^Mrem)_min [0·0013 g d⁻¹; eqn 5 in the companion paper (Bertheloot et al., 2011)], which was about 60 % of the dry mass accumulation observed at flowering. In accordance with these results, sensitivity analysis showed that the N acquisition rate in H3 was initially most sensitive to the parameters defining the theoretical maximum root N acquisition rate (U_r,max) and the effect of culm N availability (β_N), and subsequently to how long roots are potentially able to import dry matter (tt_r^Macc; Fig. 6). Increasing this duration by 50 °Cd delayed the cessation of N acquisition by 300 °Cd. At around 200 °Cd, the N acquisition rate was also slightly sensitive to N demand by grains (γ).

Fig. 6.

First order sensitivity indices (Sobol's method) defining the sensitivity of the root N uptake rate to model parameters in treatment H1 vs. thermal time after flowering. Only parameters that had indices >0·1 at least once are represented. γ (°Cd⁻¹) is the relative rate of potential grain N filling during cell division; U_r,max (g m⁻³ °Cd⁻¹) is the theoretical maximum N acquisition at saturating soil N concentration; β_N (dimensionless) is the coefficient for N availability effect on root N uptake; tt_r^Macc (°Cd) is the period during which roots can accumulate dry mass.

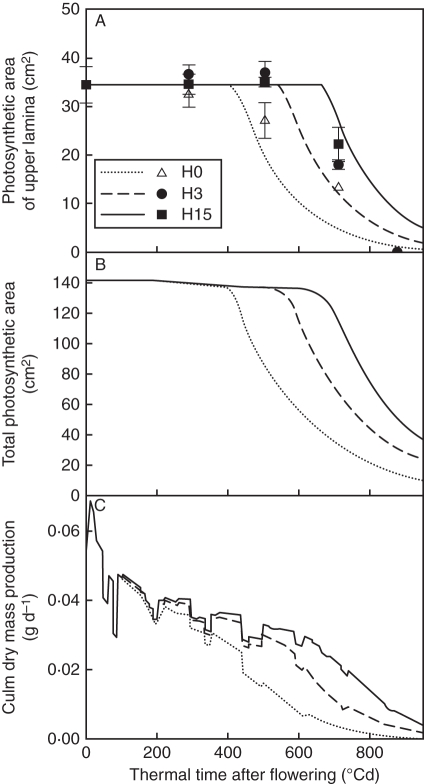
Tissue death and dry mass production

Fertilization at flowering resulted in tissues that remained photosynthetic longer, as exemplified in Fig. 7A for the flag leaf: at 700 °Cd, measured photosynthetic area was 1·36 and 1·67 times higher in H3 and H15, respectively, than in H0. The model also predicted – but overestimated – the delay in tissue death with N input at flowering. Laminae represented 80 % of the total photosynthetic area at flowering and the simulated kinetics of the total photosynthetic area approximately reflected that of laminae, with a sharp decrease starting concomitant with the onset of tissue death in laminae (Fig. 7B). Photosynthetic areas of entities other than laminae were not monitored in the field. The rate of dry mass production decreased in relation to the decrease in tissue N mass and was 40 % lower (Fig. 7C) at the onset of tissue death, after which dry mass production decreased even more dramatically. Short-term fluctuations shown on this figure reflect the fluctuations in incident PAR. In relation to the longer duration of photosynthetic area, total dry mass produced by the culm was simulated to be higher with higher N fertilization at flowering (1·21, 1·40 and 1·56 g for H0, H3 and H15, respectively).

Fig. 7.

Time courses of observed (symbols) and predicted (lines) photosynthetic area of the upper lamina (A), predicted culm photosynthetic area (B) and dry mass production at the culm scale (C) for the three N treatments H0, H3 and H15. The observed data are means of three independent replicates. The vertical bars represent ± s.d.

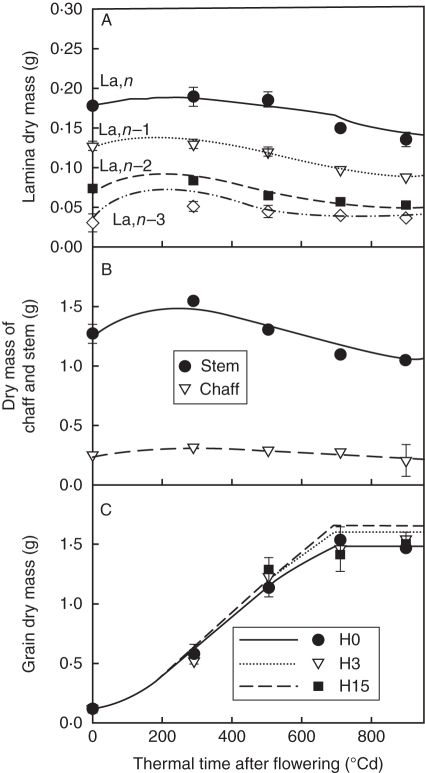
Dry mass distribution within the culm

After flowering, the main dry matter flux was directed towards grains (Fig. 8A). Nitrogen fertilization treatments did not result in significant differences in grain dry mass accumulation. Dry mass dynamics of individual laminae, the stem compartment and chaff were also similar in all N fertilization treatments, characterized by a small increase between flowering and 250 °Cd, followed by a continuous decrease until maturity, when only structural dry mass remained. The model correctly predicted dry mass kinetics for laminae, stem and chaff, but overestimated final grain dry mass for treatments H3 and H15. These differences were identical to those simulated for culm dry mass production (Fig. 7B), so this bias probably results from that already mentioned for the onset of rapid tissue death.

Fig. 8.

Observed (symbols) and predicted (lines) time courses of dry mass for (A) individual laminae, (B) chaff and stem (i.e. internodes, sheaths and peduncle pooled) and (C) grains. For laminae, stem and chaff, mean values of all treatments are represented; for grains, dry mass is represented for each treatment, H0, H3 and H15. The observed data are means of nine (A, B) or three (C) independent replicates. The vertical bars represent ± s.d.

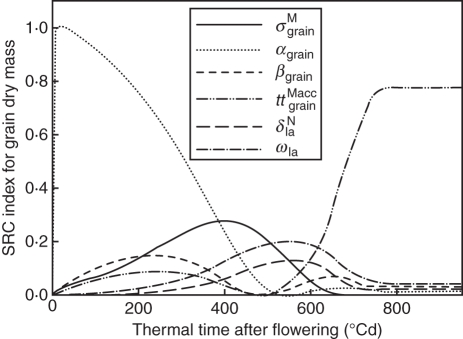
Dry mass patterns of individual plant organs are the result of a number of meta-processes: N acquisition and distribution within the plant, photosynthesis and dry mass distribution. Sensitivity analysis identified the most important processes in the elaboration of final grain dry mass. Results showed that grain dry mass depended on grain filling parameters and dry mass production, but also on parameters regulating N distribution within the culm (Fig. 9). Grain relative sink strength for dry mass and parameters α_grain, β_grain determining the form of the sink function were the most important before 500 °Cd. After 600 °Cd, grain dry mass was most sensitive to the period during which grains could accumulate dry mass (tt_grain^Macc). At the middle of the grain-filling period, the relative degradation rate of N in lamina (δ_tp^N) and the proportion coefficient relating lamina N content and dry mass production at saturating PAR (ω_la, which can be interpreted as Rubisco capacity to catalyse CO₂) were also important parameters. These two last parameters were also important in determining dry mass production at the culm scale (results of the sensitivity analysis not shown).

Fig. 9.

SRC index defining the sensitivity of grain dry mass to model parameters for treatment H1 vs. thermal time after flowering. Only parameters that had an SRC index >0·1 at least once are represented. α_grain and β_grain (dimensionless) determine the shape of the beta function indicating the pattern of change in sink strength for dry mass during grains' life; σ_grain^M (dimensionless) is grains' relative sink strength; tt_grain^Macc (°Cd) is the period during which grains can accumulate dry mass; δ_la^N (°Cd⁻¹) is the relative degradation rate of remobilizable N for laminae; ω_la (d⁻¹) is the proportion coefficient linking photosynthesis at saturating PAR and N mass per unit photosynthetic area for laminae.

DISCUSSION

In this study, the functional–structural model NEMA was parameterized for the winter wheat cultivar Thésée. The model integrates physiological knowledge on the regulation of N fluxes, coupled with a simple approach for regulating dry mass acquisition by N content of photosynthetic tissues and the conventional demand-driven approach for modelling dry mass distribution between organs (GreenLab formalism; Kang et al., 2008). The formalism simulated N mass kinetics for grains, chaff and individual photosynthetic organs under three contrasted N treatments, using a single set of parameter values. It was validated for grains, chaff, a stem compartment (i.e. sheaths, internodes and peduncle pooled) and individual laminae. NEMA's behaviour in response to N fertilization at flowering was analysed, and sensitivity analysis of outputs of agronomic interest (i.e. root N acquisition, grain N and dry matter accumulations) to model parameters was performed, providing a physiological interpretation for behaviours observed in the field and identifying factors limiting N acquisition by roots, final grain N mass and dry mass.

The validation of NEMA for individual laminae demonstrates that lamina N content can be modelled from Rubisco turnover modulated by a common pool of substrate N (representing both amino acids and nitrate) and PAR intercepted by the lamina; this supports the preliminary result we found in a first version of the model, in which N mass kinetics in organs other than laminae were forced to follow experimental data (Bertheloot et al., 2008a). We demonstrate here that a similar formalization can be used for N kinetics in chaffs, and suggest, by the validation of NEMA for the stem compartment, that the N content of all photosynthetic organs (i.e. laminae, sheaths, internodes, peduncle and chaff) can be modelled in a unified way. Acclimation to PAR is thus likely to occur in all photosynthetic tissues as in laminae, and is responsible for the vertical gradient of N observed within dense canopies for leaf laminae but also for sheaths and internodes (Grindlay, 1997; Wilhelm et al., 2002; Bertheloot et al., 2008a, b). Experimental studies have shown that high sugar concentrations in a leaf have a negative effect on the synthesis of photosynthetic proteins (Ono et al., 2001; Terashima et al., 2005); other studies rather suggested that PAR light intercepted by a leaf acts on its N content by modulating the transpiration stream in the xylem towards this leaf (Pons and Bergkotte, 1996; Pons et al., 2001). Simulations suggest that xylem is the main way for photosynthetic organs to obtain N after flowering, thus extending our knowledge on laminae (Bregard and Allard, 1999; Turgeon, 2006): N coming from phloem following C influx (theory of Münch, 1930) was almost null. The parameter value for the synthesis of proteins from N from the xylem had to be five times lower in chaff, internodes and the peduncle, than in laminae and sheaths, to reproduce the N dynamics observed for chaff and the stem compartment. Accordingly, in a previous experiment (Bertheloot et al., 2008b), the patterns of N remobilization for laminae and sheaths differed from those for chaff, peduncle and internodes. Several authors reported that chaff has a different photosynthetic function from laminae, which is closer to C₄ functioning, giving chaff a lower transpiration rate and higher tolerance to drought (for a review, see Tambussi et al., 2007).

The quantification of a mobile N pool is central in NEMA. By integrating both N release by sources and N depletion by sinks, it proved to be a reliable indicator of plant N status: it was high just after flowering when vegetative structures had finished their growth and grain filling had not yet started, then decreased due to an increase in grain N demand, and reached zero at a time which depended on the intensity of root N acquisition following N fertilization. In our study, the mobile N pool was also a reliable state variable accounting for the circulating N negative feedback on root acquisition, confirming the assumption made by different authors (Cooper and Clarkson, 1989). We have further demonstrated that it can easily regulate N accumulation in grains and storage in photosynthetic organs, as detailed below. Such a pool had been previously formalized in MecaNiCAL, a supply–demand model of C and N partitioning applied to defoliated grass (Tabourel-Tayot and Gastal, 1998a, b). As observed in our simulations, these authors reported that the amount of N in the pool was dependent on N fertilization; they also proved the ability of such a pool – as a regulator of shoot demand – to account for the dry mass ratio between shoots and roots.

Following experimental studies, root N acquisition was modelled according to the response of HATS and LATS to soil nitrate concentration (Glass and Siddiqi, 1995; Daniel-Vedele et al., 1998). This modelling has been demonstrated to fit observations in previous field studies (Devienne-Barret et al., 2000; Malagoli et al., 2004). The results of Malagoli et al. (2004) on oilseed rape stress the importance of taking into account the effects of factors related to carbohydrate availability (i.e. day/night cycle and PAR) on the HATS and LATS activities to account for root N acquisition. In the present study, the response of transport systems to soil N concentration was modulated by both plant internal carbohydrate and mobile N status according to physiological studies (Imsande and Touraine, 1994; Lejay et al., 2003; Gojon et al., 2009). This choice is further supported by the high sensitivity of the nitrogen acquisition rate to parameters regulating the negative feedback of mobile N (β_N) and the dry mass influx into roots (tt_r^Macc) used in NEMA to approximate root carbohydrate status. On the other hand, approximations were made in the calculation of N availability in the soil, which did not account for mineralization, and in the estimation of the amount of remobilizable N in the roots at flowering. Such approximations probably impacted the estimation of parameters involved in the calculation of N uptake. There is clearly a need to better estimate these parameters and investigate their variability through dedicated experiments.

A cessation of root acquisition was observed in all fertilization treatments after mid-grain filling, due to low dry matter influx into roots. Accordingly, a decrease in the rate of nitrogen acquisition was observed during the reproductive stage of many species, which is often assumed to result from the senescence of aerial parts which decreases plant photosynthesis (Imsande and Touraine, 1994; Oscarson et al., 1995). NEMA simulations showed that the root N acquisition rate became null when plant photosynthesis was still high, suggesting a lower capacity of the roots to import carbohydrates compared with that of grains, which are strong sinks for resources after flowering. At this stage, the simulated daily accumulation of dry mass in grains was more than all dry mass produced by photosynthesis (data not shown), implying net remobilization from other organs; confirmation is needed, however, by a precise quantification of the kinetics of dry mass acquisition by the culm. The period of root N acquisition could be significantly increased by delaying – even slightly – the time at which roots stop importing dry matter (by increasing parameter tt_r^Macc) compared with that of aerial organs, set by default at 700 °Cd after flowering for all organs. This would allow all dry matter produced to be allocated to roots only for a short period since demand of aerial organs would be zero. Genotypic manipulation of the duration of root capacity to import dry mass (tt_r^Macc), if possible, would thus open up interesting prospects for increasing the efficiency of N acquisition. This would require better understanding of the processes determining dry matter demand by organs.

Grain N accumulation response to an increase in root N acquisition following N fertilization could be simply simulated as the minimum between a potential rate and mobile N mass. Many authors observed, under most conditions, strong dependence between final grain N mass and N availability in the sources, i.e. soil N and N in vegetative tissues (Martre et al., 2003; Barneix, 2007; Bancal, 2009). In accordance with Martre et al. (2003), our simulations suggest that, just after flowering, N provided by the sources is not limiting: mobile N was high and N accumulated in grains at the potential rate; source limitation occurred only later when mobile N became null. This event was delayed by root N acquisition which enriched the mobile N pool, thus delaying when grain N accumulation dropped below potential, resulting in a longer period of grain N filling and higher final grain N mass. In accordance with these simulations, a high N supply increased the concentration of total amino acids in leaves of many plant species, and final grain protein content was correlated with the concentrations of free amino acids in the flag leaf during grain filling (Barneix, 2007). Consequently, increasing the duration during which roots can accumulate dry matter (tt_r^Macc) strongly increased final grain N mass due to its effect on how long root N acquisition continued, which further supports the need to include in NEMA a more mechanistic formalism for C metabolism.

Nitrogen remobilization from vegetative organs was observed and simulated as being delayed in response to N fertilization at flowering. Several authors observed antagonism between N remobilization and root N acquisition (Guitman et al., 1991; Triboï and Triboï-Blondel, 2002; Bancal, 2009), but regulatory mechanisms of N remobilization remain unclear (Barneix, 2007). Hikosaka (2005) interpreted such observations through a source–sink analysis, in which, to satisfy grain demand, if root N acquisition is increased, the other source of N, i.e. N remobilization, must decrease. NEMA allows for a more physiological interpretation: root N acquisition increases mobile N availability, which enhances protein synthesis, thus counterbalancing their degradation, and resulting in apparent non-remobilization.

In NEMA, tissue death is assumed to be completely determined by tissue N content; but more complex regulations are probably involved because differences in the onset of tissue death among treatments were overestimated by the model. Photosynthetic area together with intercepted PAR and organ N content drives dry matter acquisition, which is mainly directed towards grains after flowering. Due to overestimation of differences among treatments concerning onset of tissue death, NEMA overestimated the differences in final grain dry mass among treatments. However, this behaviour is actually observed in stay-green cultivars. These cultivars are characterized by a significant amount of tissues that are still photosynthetic at crop maturity, by high yields (Rajcan and Tollenaar, 1999; Borrell et al., 2000, 2001) and often by high root N acquisition capacity. The stay-green behaviour and origins of the high root N acquisition rate of these cultivars remain unclear. It may result from a higher intrinsic capacity of the roots to take up N. On the other hand, NEMA simulations showed that final grain dry mass was very sensitive to the rate of degradation of photosynthetic proteins in laminae. This suggests that a stay-green character may also result from a lower capacity to degrade photosynthetic proteins; one could expect that, if associated with sufficient capacity to store N in photosynthetic tissues, a low degradation rate would minimize mobile N in the plant and thus its negative feedback on root acquisition. Consequently, the Rubisco degradation rate could be a target for designing high-yielding crops. This is in addition to two better known limiting processes, also clarified by sensitivity analysis: (1) the capacity of the grains to import dry mass (Yin et al., 2009) and (2) Rubisco activity to catalyse CO₂. In accordance with the second point, Hibberd et al. (2008) suggested engineering C₄ rice or wheat.

Conclusions

In conclusion, in this paper, we demonstrated the capacity of NEMA to simulate accurately N distribution within a botanically explicit description of the aerial parts of the plant, and to account for the effect of soil N availability on N distribution. Thanks to its mechanistic formalization, NEMA helps understand the regulation of N economy after flowering based on the modulation of Rubisco turnover in each organ by intercepted light and a common pool of circulating N which indicates plant N status and regulates N fluxes. Key parameters determining root N acquisition, N and dry matter accumulations in grains were identified by sensitivity analysis. However, while the parameters for N fluxes, such as Rubisco degradation rate, are physiological and could be direct targets for the breeding of more efficient plants for N, parameters for dry matter demand by organs lack a physiological basis to help understand the limiting processes. Moreover, despite the fact that parameters of the equations that describe N fluxes have a simple physiological meaning and are measurable, values are scarce in the literature probably due to the difficulty involved in getting rid of the many factors that affect activities in vivo; combined with dedicated experiments, the model could be a tool to estimate these values. We believe that NEMA represents a basis for comprehensive mechanistic modelling of N economy at plant and crop scales and, consequently, a tool to design more efficient crop management practices and ideotypes in the way they take up N and use it for grain yield and protein content. For this, a required step is to test the concepts implemented in NEMA for the pre-flowering period. This implies accounting for C and N fluxes in a dynamic structure and expressing how they regulate the dynamics of the structure. Our hypothesis is that the quantification of a pool of mobile N in NEMA will help in formalizing response functions of the development and extension of organs to plant N status.