Abstract
Background and Aims
The relationship between Septoria tritici, a splash-dispersed disease, and its host is complex because of the interactions between the dynamic plant architecture and the vertical progress of the disease. The aim of this study was to test the capacity of a coupled virtual wheat–Septoria tritici epidemic model (Septo3D) to simulate disease progress on the different leaf layers for contrasted sowing density treatments.
Methods
A field experiment was performed with winter wheat ‘Soissons’ grown at three contrasted densities. Plant architecture was characterized to parameterize the wheat model, and disease dynamic was monitored to compare with simulations. Three simulation scenarios, differing in the degree of detail with which plant variability of development was represented, were defined.
Key Results
Despite architectural differences between density treatments, few differences were found in disease progress; only the lower-density treatment resulted in a slightly higher rate of lesion development. Model predictions were consistent with field measurements but did not reproduce the higher rate of lesion progress in the low density. The canopy reconstruction scenario in which inter-plant variability was taken into account yielded the best agreement between measured and simulated epidemics. Simulations performed with the canopy represented by a population of the same average plant deviated strongly from the observations.
Conclusions
It was possible to compare the predicted and measured epidemics on detailed variables, supporting the hypothesis that the approach is able to provide new insights into the processes and plant traits that contribute to the epidemics. On the other hand, the complex and dynamic responses to sowing density made it difficult to test the model precisely and to disentangle the various aspects involved. This could be overcome by comparing more contrasted and/or simpler canopy architectures such as those resulting from quasi-isogenic lines differing by single architectural traits.
Keywords: Crop architecture, modelling, Septoria tritici, wheat, Triticum aestivum, sowing density, 3-D virtual plant model, plant–pathogen interaction
INTRODUCTION
To limit pesticide use, one option is the use of crop architecture to promote disease escape. Several studies have shown that some architectural traits allow escape by (a) limiting pathogen contact with the host, (b) creating an unfavourable environment for pathogens or (c) limiting the ability of the pathogen to trigger the infection process (Ando et al., 2007). Indeed, architecture traits such as plant posture (Saindon et al., 1995), growth habit (Ando and Grumet, 2006) and plant height (Hilton et al., 1999) have been reported to be critical factors in determining disease incidence in several crops. Disease severity has also been shown to be influenced by the spatial distribution of leaf area in the canopy (Schwartz et al., 1978), the number of leaves (Jurke and Fernando, 2008), as well as leaf shape (Gan et al., 2007) and size (Ando et al., 2007).
For Septoria tritici, a foliar disease, wheat architecture can play a key role. Septoria tritici (sexual reproductive stage or teleomorph: Mycosphaerella graminicola) is a splash-dispersed pathogen: it progresses from the base to the top of the canopy when spores are incorporated in droplets resulting from the impact of rain drops on sporulating tissues of the lower infected leaves. The relationship between S. tritici and its host is dynamically complex and is comparable to a race between the vertical progress of the pathogen and the production of new leaves. According to Shaw and Royle (1993), opportunities of escape exist due to the long latency period of the pathogen compared with the time needed for internode extension to move leaf blades of successive phytomers sufficiently away (a phytomer is the morphological building unit of plant axes, consisting of an internode, a node, a sheath and a leaf blade). Several studies reported that tall plants were less attacked by S. tritici (Tavella, 1978; Danon et al., 1982; Camacho-Casas et al., 1995; Simon et al., 2005). It has been suggested that this could result from unfavourable environmental and epidemiological factors due to plant height (Bahat et al., 1980; Scott et al., 1985; Simon et al., 2005), or from linkage between resistance and plant height (Scott et al., 1982). A modelling study of light leaf spot, a splash-dispersed disease (caused by Pyrenopeziza brassicae) has shown that differences in leaf area distribution resulted in differences in the vertical progress of the disease (Pielaat et al., 2002). The vertical transport of the pathogen is also tightly linked to the distance between healthy and infected organs. It has been shown that the position of the healthy newly emerging leaves relative to the inoculum sources (soil or older diseased leaves) modulates S. tritici severity (Bahat et al., 1980; Eyal, 1981; Scott et al., 1985). Lovell et al. (1997) hypothesized that spore transfer to the upper leaves is affected by the rate of stem extension: during stem extension, the distance between young and old leaves increases and thus the plant may outgrow the disease. Leaf posture also influences the proximity between sources and receptors of the pathogen. For instance, the tips of leaves that bend down are further from the emerging upper leaves than those with an erect position (Lovell et al., 1997).
Cropping practices (e.g. nitrogen fertilization, sowing density and date of sowing) influence disease development in many ways, including the modification of canopy architecture. However, these effects are irregular and interpretations may be controversial. Regarding the effect of sowing density, several authors have suggested that increasing density enhanced foliar disease (Ando and Grumet, 2006; Gan et al., 2007; Jurke and Fernando, 2008). The density effect was attributed either to the establishment of a favourable microclimate such as higher relative humidity (Tompkins et al., 1993) or to modifications of canopy architecture. Pielaat et al. (2002) reported that denser canopies increase the contacts between leaves and thus facilitate the progress of the disease through the canopy. According to Broscious et al. (1985), the significant increase in wheat tiller number with higher plant density could favour M. graminicola spore deposition. However, discrepancies concerning the density effect are found in the literature. Pfleeger and Mundt (1998) found only very little effect of sowing density on disease development. Eyal (1981) reported that reduced plant densities resulted in sparser canopies, which increased the probability that raindrops impact on lower leaves, resulting in a faster disease progress by splashing in less-dense plant stand. Ultimately, there are difficulties to identify and to understand the effects of cropping practices on disease development. First, effects are irregular between years in terms of intensity and direction. Secondly, the mechanisms that are likely to be involved are complex and difficult to disentangle. A modelling approach could thus be useful to understand better the role of crop architecture in the effect of cropping practices on epidemic development.
To study the effect of crop architecture on disease dynamics, one possible tool is the use of coupled epidemic–virtual plant models. ‘Virtual Plants’ use morphogenesis rules and geometric information to simulate the time course of the three-dimensional (3-D) position of botanical entities. Room et al. (1996) proposed that by handling 3-D information on the development and growth of individual plants and activities of the organisms which live on them, these models should allow the interactions between plant architecture and pathogen or herbivore dynamics to be represented in depth. Since that time, plant models have progressed in realism and functionality (Godin and Sinoquet, 2005; Vos et al., 2010); however, a few examples exist where they have been used to investigate the interactions between plants and diseases or pests. Wilson and Chakraborty (1998) used a virtual plant model to quantify the impact of anthracnose on the branching of a pasture legume. Later, two plant models were proposed to simulate theoretical movement of insects at the individual plant and field scales (Hanan et al., 2002; Skirvin, 2004). More recently, virtual plant models were applied to two pathosystems: grape–powdery mildew (Calonnec et al., 2008) and wheat–S. tritici (Robert et al., 2008). The model of wheat–S. tritici (Septo3D) has been used to assess the influence of architectural traits on S. tritici development by varying separately each trait. This supported the view that the rate of plant development is a major factor in determining disease severity. However, until now, the model has not been validated with detailed disease measurements.
This study addresses the question whether coupled epidemic–virtual plant models can capture and help us to better understand the role of architecture in the effect of cropping practices on epidemics. Here the example of the pathosystem wheat–S. tritici is studied, focusing on the effect of sowing density. The aims are (a) to develop a method for increasing the realism of 3-D wheat reconstruction, particularly by including plant-to-plant variability, (b) to test the model for its capacity to simulate S. tritici epidemics for different sowing densities and (c) to define to what extent the level of architecture description influences disease simulations.
MATERIALS AND METHODS
Overview
A field experiment was performed in Grignon, France in 2008/09 with winter wheat (Triticum aestivum ‘Soissons’) grown at three densities. Detailed architecture and disease measurements were performed through the growing season. Plant measurements were used to calibrate the plant model while disease measurements were used to evaluate the disease dynamics simulated by the model Septo3D. Three scenarios of simulation, differing by the degree of detail with which the observed variability of architecture between plants was represented, were compared.
Modelling
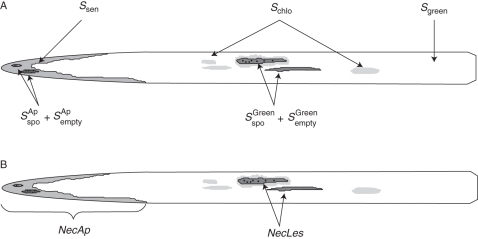
The model Septo3D (Robert et al., 2008) combines a dynamic architectural model of wheat, ADEL-Wheat (Fournier et al., 2003) with a dynamic model of S. tritici epidemic based on Rapilly and Jolivet (1974). Starting from a given initial state of infection, the model simulates the lesion development and propagation from the infected lower leaves to the healthy upper leaves in a canopy. Epidemics result from repeated successions of lesion development resulting in spore production and spore dispersal. In the model, canopy architecture influences epidemics through the amount of tissue available for lesion development, which is driven by plant development, and through its effects on rain penetration and infectious droplet distribution. Model outputs are the dynamics of green (Sgreen), apical senescent (Ssen) and diseased leaf blade areas distinguishing between incubating (Sinc), chlorotic (Schlo), sporulating (Sspo), and emptied lesion (Sempty) tissues on each leaf (Fig. 1A). To make the link with measured variables, a distinction was made between sporulating and emptied lesions located in the apical senescent part of the leaf (SspoAp and SemptyAp) from those located in the green part of the leaf (SspoGreen and SemptyGreen). The model includes three modules, which deal, respectively, with canopy development, lesion development and spore dispersal. Below, the main functioning of the three modules and changes with respect to Robert et al. (2008) are described.
Fig. 1.
Scheme of (A) simulated disease variables by Septo3D and (B) measured disease variables on a wheat leaf. NecLesGreen is calculated from model outputs as: (SspoGreen + SemptyGreen)/Sgreen where SspoGreen and SemptyGreen are, respectively, the sporulating and emptied lesions located in the green part of the leaf Sgreen.
Canopy development
Canopy simulation is based on the model ADEL-Wheat which simulates in 3-D the dynamics of appearance and extension of all vegetative organs of a wheat canopy. Several modifications have been made to the version described in Fournier et al. (2003); they allow for a more flexible and detailed parameterization of plant development and its variability in the canopy. The present version of ADEL-Wheat takes as input parameterizations of (a) the rates of leaf appearance as a function of thermal time for several types of axes, (b) the individual thermal time course of senescence progression on leaves on each axis, (c) the tillering dynamics and (d) the geometry and dimensions of mature plant organs. These parameterizations can be given in the form of numeric look-up tables so that no constraints exist in the patterns they follow. In ADEL-Wheat, the rate of leaf appearance is used to drive the extension of laminas, sheaths and internodes using co-ordination schemes (Fournier et al., 2005). The concept is extended after flag-leaf appearance by assuming that all durations are stable fractions of the phyllochron value before flag-leaf appearance (the phyllochron being the interval, expressed in thermal time, between appearance or ligulation of two successive leaves; Wilhelm and McMaster, 1995). The measured senescence dynamic of leaves can be directly used as input. Alternatively, senescence progression may be given at the shoot level, using an index of progression: the shoot senescence index (SSI) that represents the fractional number of leaves senesced on an axis. The progression of senescence within each leaf is then computed with stable functions of SSI. Tillering dynamics are simulated from measured probability of appearance and regression for primary tillers and using the principle of cohorts to extrapolate to secondary tillers. A cohort refers to the set of tillers that emerge on a plant at the same time. Tiller emergence is co-ordinated with the emergence of leaves on the main stem so that the potential number of tillers in each cohort follows precisely a Fibonacci series (Friend, 1965; Masle-Meynard and Sebillotte, 1981; Masle, 1985). These authors and others (Darwinkel, 1978) have reported that behaviour of a tiller is highly related to the time of emergence. In the model, it is assumed that tillers of a same cohort behave identically; they have the same properties of probability of emergence and disappearance, rate of growth, and dimensions.
Lesion development
This module simulates the development of a lesion after deposition of a spore-containing droplet on the leaf. Four stages are considered: infection (spore germination and penetration in the leaf), incubation, appearance and extension of chloroses, and maturation of chloroses into sporulating necrotic tissue. Infection and incubation are assumed to occur only on green tissue. In Septo3D, each leaf blade is divided into small regions called sectors in which disease development is tracked. At each time step, the model computes in each leaf sector the area allocated to each stage of the infection cycle: incubating, chlorotic and sporulating.
Spore dispersal
Dispersal occurs when drops with sufficient kinetic energy hit sporulating surfaces, and are splashed away into droplets carrying spores. In the model, splash occurs for rain events with an intensity above 0·5 mm h−1, and the kinetic energy of splashed droplets is considered too low to allow re-splashing. Sporulating lesions are considered empty after having being exposed to rain three times.
For the simulation of spore dispersal, the canopy is represented as a horizontally homogenous turbid medium and droplet transport is simulated between layers of the vegetation as a function of the distance to the source. The properties of the turbid medium are derived from the 3-D representation of the canopy. Rain penetration is computed using an analogy with light penetration in a multi-layered turbid medium, and droplet transportation and interception in analogy to light scattering. The 3-D representation of the canopy makes it possible to calculate the density and orientation of leaves in each layer and to assign, afterwards, the intercepted droplets of a layer to the appropriate leaf sector.
More precisely, taking into account the density and orientation of vegetation in each layer, the model first computes a global production of droplets per layer, proportional to the rain intercepted within that layer. The fraction of droplets that contains spores is calculated as the ratio between the sporulating area and the total area of that layer. A term of loss is subtracted, that represents the evaporation of too-small droplets. Spore-containing droplets are emitted in all directions above the leaf surface; they are assumed to move in straight line till a limited distance and then to fall down vertically. Along their trajectory, droplets may be intercepted according to density and orientation of vegetation elements. The output of the spore dispersal module is the number of spore-containing droplets that have reached green tissues and have not been washed away by the rain. Washing is calculated for each layer as a function of rain intensity and duration.
Sowing density changes the time course of vegetation density in each layer, which impacts on (a) the amount of rain intercepted in each layer and thus droplet production, (b) the interception of spore-containing droplets during their upward and downward movements and (c) the loss by washing of intercepted spore-containing droplets. For example, increasing the sowing density may reduce rain penetration resulting in fewer droplets produced in the lower leaf layers where active sporulating lesions are generally abundant; this is referred to as the ‘umbrella effect’. However, for high density, once spore-containing droplets are produced, there is a higher probability of interception and thus of successful dispersal at shorter distance. At the same time, the umbrella effect could also mean less washing of the lower infected leaf layers. These processes have contradictory effects and their relative importance will depend on rain event intensity, on the vegetation profile and on the initial contamination.
Epidemic model parameterization
Parameter values of the dispersal model and the lesion model were taken from Robert et al. (2008) (Tables 1 and 2). Only the latency period was given a slightly lower value of 310 °Cd.
Table 1.
Dates, products, active agents and doses of different agronomic applications performed on winter wheat ‘Soissons’ grown in Grignon in 2008/09 at three densities D1 (59 plants m−2); D2 (160 plants m−2) and D3 (406 plants m−2) under two fungicide treatments (T, treated; NT, non-treated)
| Treatment | Date | Product | Active agents | Dose |
|---|---|---|---|---|
| Herbicide (on T and NT) | 26 August 2008 | Roundup Max 480 | Acid glyphosat | 2·5 L ha−1 |
| 30 April 2009 | Bofix | Fluroxypyr Clopyralid | 2·5 L ha−1 | |
| Fungicide (on T only) | 2 April 2009 | Input pack | Prothioconazol | 0·8 L ha−1 |
| 5 May 2009 | Opus team | Epoxiconazol Fenpropimorph | 1·5 L ha−1 | |
| 23 June 2009 | Soleil | Bromuconazol | 1·2 L ha−1 | |
| Fertilization (on T and NT) | 9 April 2009 | Ammonium nitrate (33·5 %) | 80 kg ha−1 | |
| 6 May 2009 | Ammonium nitrate (33·5 %) | 50 kg ha−1 (D1); 120 kg ha−1 (D2, D3) |
Table 2.
Mean values and standard errors of Haun stage (HS) measured at two dates (3 and 30 April 2009) and sheath length (lsh) for main stems of winter wheat ‘Soissons’ grown in Grignon in 2008/09 at three densities D1 (59 plants m−2); D2 (160 plants m−2) and D3 (406 plants m−2) under two fungicide treatments (T, treated; NT, non-treated)
| D1 | D2 | D3 | ||
|---|---|---|---|---|
| HS: 3 April 2009 | NT | 5·33 ± 0·25a | 5·09 ± 0·35a | 4·92 ± 0·44a |
| (unitless) | T | 5·16 ± 0·3a | 5·00 ± 0·4a | 4·58 ± 0·17b |
| HS: 30 April 2009 | NT | 8·84 ± 0·23a | 8·63 ± 0·12a | 8·23 ± 0·23a |
| (unitless) | T | 9·08 ± 0·3a | 8·5 ± 0·3a | 8·2 ± 0·21a |
| lsh (6) (mm) | NT | 10·42 ± 1·18a | 10·56 ± 0·72a | 7·97 ± 0·49a |
| T | 10·17 ± 1·21a | 9·09 ± 1·43b | 7·64 ± 0·6a | |
| lsh (7) (mm) | NT | 13·03 ± 1a | 13·37 ± 1·43a | 10·61 ± 0·77a |
| T | 12·90 ± 1·02a | 11·88 ± 1·18a | 10·10 ± 0·6 b | |
| lsh (8) (mm) | NT | – | – | 13·70 ± 0·94a |
| T | – | – | 12·91 ± 0·97b |
Numbers in parenthesis following lsh correspond to the phytomer rank counted from the base of the shoot.
Numbers followed by the same superscript letter are not statistically different at the α = 10 % level across columns.
Initialization of disease in the model was the only significant change compared with the version presented in Robert et al. (2008). Here, it is assumed that initial contamination on the first lower leaves results from spore-containing droplets splashed from the soil. This was represented using two parameters: Ssposoil (m2 m−2), the fraction of soil surface covered by infectious leaf debris and Tinfsoil (°Cd), the duration during which this soil surface bears spores. Therefore, the amount and the interception of spore-containing droplets from soil are determined by the canopy architecture and the interactions with rainfall. Parameters of the initial infection conditions were adjusted so that simulated infection of the three uppermost leaves were in best agreement with field measurements and that the ranking of density treatments for infection of the lowermost simulated leaf (here leaf 6 counted from the top) was as close as possible to the observed. Thereby, Tinfsoil was fixed to 1000 °Cd and Ssposoil to 0·65 10−4 m2 m−2.
Reconstruction of individual plant architecture
The model was parameterized for simulating the architecture of wheat plants of three contrasted densities of a field experiment. Reconstructions were performed for each density and for each type of plant differing in final number of leaves (referred to Nleaf modality). Rates of appearance, growth and senescence of plant organs, tillering dynamics and dimensions of mature organs of the main stem and primary tillers were based on field measurements and those of secondary tillers were inherited from the primary tillers of the same cohort. Leaf curvature was not measured during the experiment. It was parameterized based on data from a previous field experiment carried out with the same cultivar. To compute the dates of leaf appearance on the main stem and on primary tillers, a linear model was fitted on the data of leaf collar appearance, i.e. the Haun stage (HS) which is the decimal index for the number of liguled leaves (Haun, 1973), and we considered a delay of 1·6 HS between leaf emergence and collar appearance (Fournier et al., 2005). The progression of senescence was estimated at the shoot level using the SSI and ADEL-Wheat default functions until leaf 4 (counted acropetally from the first true leaf), and using spline functions fitted to the measurements for upper leaves. The measurements of the number of active main stem tillers were used to fit a tillering dynamic model using a set of approximations derived from literature. The Fibonacci sequence was used to calculate the potential number of secondary tillers, and their probability of appearance was given the value measured for the corresponding primary tiller. The calculation was validated for the maximum number of tillers. It was assumed (and verified in the data for the first two primary tillers) that the emergence of a tiller n is synchronous with the emergence of leaf on phytomer n + 3 (Masle-Meynard and Sebillotte, 1981). The senescence of tillers was simulated assuming that (a) tiller regression takes place at a constant rate during stem extension and (b) tillers regress by cohorts, in the reverse order compared with their appearance. When a tiller starts to regress, it is still represented in the model for 400 °Cd12, without producing any new leaf, then disappears.
Canopy reconstruction with different levels of plant variability
Three scenarios of canopy reconstruction (Sref, S1 and S2) differing in the level of description of plant architecture variability were defined. In S1, the canopy is represented by cloning a mean plant without considering any variability, whereas in S2 and Sref canopies are composed of two types of plants differing in their total number of leaves (Nleaf). In Sref, the variability of timing of development between plants is also taken into account (all plants are unique). The latter scenario is the more realistic and is considered as the reference.
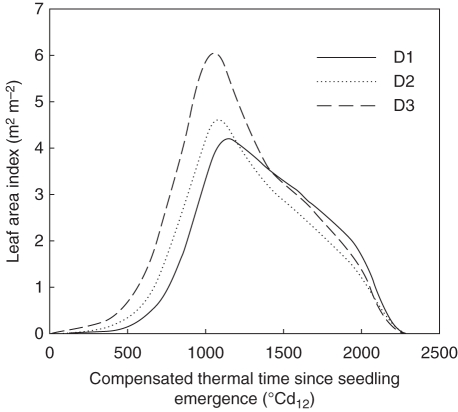
To get average values for S1, organ dimensions, rate of organ appearance and senescence were computed for each phytomer as the mean of measurements for corresponding phytomers counted from the top of the canopy. The final number of leaves on a tiller axis was given the most frequent value for that type of tiller. In scenarios S2 and Sref, the architecture of the plant representing each Nleaf modality was computed from the average of measurements for all plants that produced Nleaf leaves. Each modality was represented in the proportions observed in the field. For Sref, the plant-to-plant variability of development was represented by variability in the date of seedling emergence. It was represented as a normal distribution with standard deviation equal to that measured for HS. In the model, a population of ten plants was created to capture this variability, each plant corresponding to a decimal quartile of the normal distribution. The simulated leaf area index of the three density treatments was similar between the three scenarios (Fig. 2). Scenarios are used to test how the level of detail in the description of plant-to-plant variability of development influences epidemic simulations.
Fig. 2.
Simulated leaf area index versus compensated thermal time since seedling emergence for the canopy of winter wheat ‘Soissons’ grown at three densities: D1 (59 plants m−2); D2 (160 plants m−2) and D3 (406 plants m−2). Simulations are for the scenario that takes into account plant-to-plant variability of development and number of final phytomers (Sref).
Field experiment
Treatments and experimental design
The field experiment was carried out in 2008/09 at the research unit of INRA at Thiverval-Grignon near Paris, France (48°51'N, 1°58'E) on a silty loam soil. The previous crop was Vicia faba. Winter wheat, T. aestivum ‘Soissons’ was sown on 17 November 2008 at three sowing densities: low (D1, 77 plants m−2), standard (D2, 228 plants m−2) and high (D3, 514 plants m−2). At seedling emergence, actual plant densities were, respectively, 59, 160 and 406 plants m−2. Each density treatment was sown in three parallel plots, approx. 80 m long, spaced 0·2 m apart. Each plot was further separated into two parts 10 m apart for fungicide treatments: treated (T) and non-treated (NT). A plot consisted of nine rows of plants with an inter-row distance of 0·175 m. The two external rows on each side of the plots were not used for measurements. The soil nitrogen content was measured to be 70 kg ha−1 at the end of January, and fertilization was adjusted following recommendations for high-yielding crops (Table 1). An irrigation system was installed to complement natural rainfall when needed. Weeds were controlled by herbicide application (Table 1). Three fungicide treatments were performed on the treated part of the field 470, 860 and 1580°Cd after seedling emergence, corresponding to HS = 4 and HS = 8 for the two first applications and to grain filling for the last.
Field measurements: plant model calibration
Architectural measurements used to calibrate the plant model were performed on plants from the fungicide treatment (T). In each density treatment, 20 plants were tagged to monitor weekly the HS on the main stem and on primary tillers. On five occasions during crop growth, 15 previously tagged plants were dissected to measure the dimensions of all mature organs. Lamina images obtained with a flat-bed scanner were processed using the program Lamina2Shape (Dornbusch and Andrieu, 2010) to compute blade length (lbl), width (wbl), and area (Abl). In addition, lengths of sheaths (lsh) and internodes (lin) were measured with a ruler. Distance from the shoot base to a leaf collar (hcol) was computed as the sum of lin below the considered leaf plus the lsh of that leaf. Final leaf number on the main stem (Nleaf) and number of tillers per plant were also recorded. In addition, all the tagged plants from treated and non-treated plots (60 plants per density) were used to determine the total number of leaves per axis in each density.
Some measurements were duplicated on non-treated plants to insure that they were consistent with those of treated plants. HS was measured both on T and NT plots on 20 plants on 3 April 2009 and on 30 plants on 30 April 2009 for each density treatment. Measurements of lsh on 20 plants picked randomly from each density on NT plot were carried out on a single sampling date (11 May 2009).
Field measurements: disease and senescence
For both T and NT plots, 30 plants were tagged in each density treatment to monitor, on the true leaf rank, the dynamics of apical senescence and S. tritici necrotic lesions. Measurements began on 15 April 2009 and were performed once or twice each week, which corresponds to an interval of 80–100°Cd. Starting with leaf 5 counted acropetally, each leaf was measured at least four times during its lifespan. For each leaf of the tagged plants, the proportion of total leaf area occupied by (a) apical necrosis (NecAp) (bearing pycnidia or not) and (b) S. tritici necrotic lesions located in the green part of the leaf (NecLes) was recorded (Fig. 1B).
From these measurements, two variables were used to describe the S. tritici epidemic: the proportion of total necrotic leaf area and the proportion of lesions in the green part of the leaf (NecLesGreen). The total necrotic leaf blade area was computed as the sum of measured areas occupied by S. tritici lesions (NecLes) and of the apical necroses (NecAp). Lesion development was characterized as the proportion of lesion surface area in the green part of a leaf (NecLesGreen). Assuming that the fraction of tissue occupied by lesions was the same in the apical region as in the rest of the leaf, the proportion of lesions in the green part of the leaf was calculated as:
| (1) |
where NecLes and NecAp are the fraction of the total leaf area occupied by necrotic lesions (assessed in the green part) and by apical necrosis, respectively.
The green leaf area decreases when the leaf senesces, so that the proportion of lesions becomes increasingly difficult to estimate. The indicator NecLesGreen is reliable only as long as apical necrosis and necrotic lesions do not merge on the leaf. For that reason, only the first stage of lesion development was used to compare with simulations.
Field measurements: meteorological data
Air temperature at a height of 2 m, amount of rainfall in millimetres and relative humidity were monitored hourly over the growing season at a weather station 500 m from the field. Soil temperature (Tsoil) at 3 cm deep was measured within one row of the plots of density treatments D1 and D3, from sowing until the start of fast internode elongation. No differences were found between density treatments so measurements were averaged to represent soil temperature regardless of the density.
Data analysis
Calculation of thermal time
Linear thermal time (Γ, °Cd) based on air temperature was used to drive the dynamics of S. tritici. Linear thermal time is computed assuming a linear response to temperature above a base temperature Tb (taken as 0 °C here):
| (2) |
where i is the number of hours elapsed after seedling emergence and Tair is the hourly-averaged air temperature.
A non-linear thermal time (Γc) based on the growing zone temperature was used to drive wheat development. The growing zone temperature (Tp) was assumed to be equal to Tsoil before internode elongation then to Tair. Non-linear thermal time Γc was computed, based on a modified Arrhenius equation that describes a non-linear response F(T) of biological processes to temperature (Johnson and Lewin, 1946). Applicability of this equation to plant development was established in Parent (2009) and calibration for wheat is presented in R. Baccar et al. (unpubl. res.). Here the temperature sum is expressed in °CdTref (Tref is a reference temperature that can be chosen arbitrarily) and is calculated as:
| (3) |
where i is the number of hours elapsed after seedling emergence, Tp is the hourly-averaged plant temperature and Tref is the reference temperature. Tref = 12 °C was chosen as it is close to the average temperature during the wheat growing season.
Convention for leaf numbering
To express the kinetics of disease, the leaf numbers were counted from the top of the canopy, starting with 1 for the flag leaf.
Statistical analysis
Means and standard errors were calculated for all the measured and derived disease and architectural variables. The significance of differences in the stage of development and in sheath lengths between T and NT plants were tested using the non-parametric Mann and Whitney test for samples <30 and the Student's t-test for samples ≥30 (Georgin and Gouet, 2000).
Disease simulations and test of Septo3D
Simulations of lesion development were run with three scenarios of canopy reconstruction. The proportion of lesion in the green part of the leaves (NecLesGreen) was used to compare field measurements with model simulations. This indicator is an accurate estimate of disease in the early stages of leaf infection. As a measure for the deviation from a 1 : 1 line between measured and simulated disease variables, the root mean squared error (RMSE) was used.
RESULTS
Effect of density on plant architecture and development
Comparison between treated and non-treated plants
The mean values of HS measured on 3 and 30 April 2009 were found similar for treatments T and NT with no significant differences at the 0·1 level (Table 2). For dimensions, the average length of sheaths 6, 7 and 8 (counted acropetally) was found lower by 0·5–1·5 cm for treated plants (Table 2). These differences were in the range of the standard deviation with each treatment, and in most cases were not significant at the 0·05 level. Thus, it was considered that T and NT plants did not differ in their development or organ dimensions.
Final leaf number and phyllochron
The total number of leaves produced on the main stem (Nleaf) varied between nine and 11 among plants at all densities. The proportion of plants with a given Nleaf varied between densities (Table 3): low-density treatment D1 produced very few plants with nine leaves and similar proportions of plants with ten and 11 leaves, D2 had almost exclusively plants with ten leaves and D3 produced a majority of plants with nine leaves and a bit less than half with ten leaves. Thus the mean value for Nleaf decreased with increasing density.
Table 3.
Proportions of final leaf number on main stems of winter wheat ‘Soissons’ grown in Grignon in 2008/09 at three densities D1 (59 plants m−2); D2 (160 plants m−2) and D3 (406 plants m−2) under two fungicide treatments (T, treated; NT, non-treated)
| D1 | D2 | D3 | |
|---|---|---|---|
| Nleaf = 8 | 0·05 | ||
| Nleaf = 9 | 0·03 | 0·08 | 0·63 |
| Nleaf = 10 | 0·52 | 0·89 | 0·32 |
| Nleaf = 11 | 0·44 | 0·03 |
Total number of plants for each density = 60.
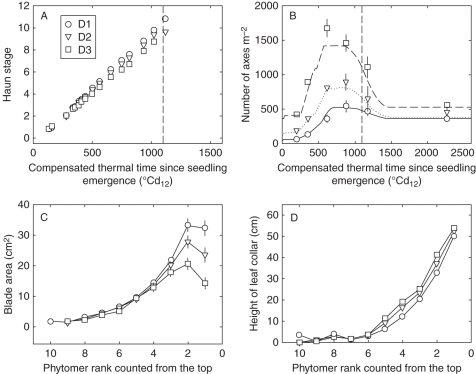
The phyllochron of a plant was negatively correlated with Nleaf (R. Baccar et al., unpubl. res.). For a given Nleaf, phyllochron did not depend on plant density. However, as the proportion of plants with high Nleaf decreased with increasing densities, the average phyllochron increased accordingly, from 98 °Cd12 in D1 to 117 °Cd12 in D3 (Fig. 3A).
Fig. 3.
(A) Mean Haun stage of main stem and (B) number of axes per square metre versus compensated thermal time since seedling emergence; (C) mean blade area and (D) height of leaf collar versus phytomer rank counted from the top. Data are for main stems with ten leaves of winter wheat ‘Soissons’ grown in Grignon in 2008/09 at three densities: D1 (59 plants m−2), D2 (160 plants m−2) and D3 (406 plants m−2). Error bars mark the 95 % confidence intervals when larger than the size of the symbol. The vertical dashed line corresponds to the date of flag leaf ligulation.
Organ dimensions
A detailed description of organ dimensions measured in this experiment is presented in Dornbusch et al. (2010). Here, these results are summarized through two synthetic variables that illustrate the differences in the shoot architecture between population density treatments: the leaf blade area (Abl) and the height of leaf collar (hcol). Both Abl and hcol varied between density treatments and between Nleaf modalities. Few or no differences were observed for lower phytomers whereas differences existed for the four upper phytomers, i.e. those with elongated internodes. For the same Nleaf, Abl was higher for lower density whereas hcol was higher for high density (Fig. 3C, D). Abl differed increasingly between density treatments with lower leaf rank counted from the top. Hence, the difference of Abl between D1 and D3 was, respectively, 3 % and 65 % for leaf 3 and leaf 1. Collar height hcol increased approximately linearly with decreasing leaf rank counted from the top and the difference between the densities was constant along the shoot (2–4 cm). For a given density, Abl and hcol increased at higher Nleaf. Only Abl of the flag leaf was reduced at high Nleaf modality. Finally these effects resulted in slightly taller plants (53 vs. 50 cm for the height of flag leaf collar) with larger blade area (100 vs. 66 cm2 for cumulated area of blades 1–4) in D1 compared with D3, with intermediate values for D2.
Tillering dynamics
In wheat the number of actively growing tillers increases up to a maximum, then remains stable and finally decreases during stem elongation. The number of actively growing tillers at the very beginning of stem extension is a good estimate of the maximum reached. Here it was, respectively, 8·2, 4·2 and 3·1 axes plant−1 for D1, D2 and D3 which corresponds, respectively, to 542, 896 and 1461 axes m−2 (measured 880 °Cd12 after seedling emergence at HS = 7·5–8). The final number of axes was estimated at harvest (2270 °Cd12) by counting the number of ears: there were 6·2, 2·5 and 1·3 axes plant−1, respectively, for D1, D2 and D3 (Fig. 3B), corresponding respectively, to 359 ± 16, 458 ± 60 and 557 ± 33 axes m−2.
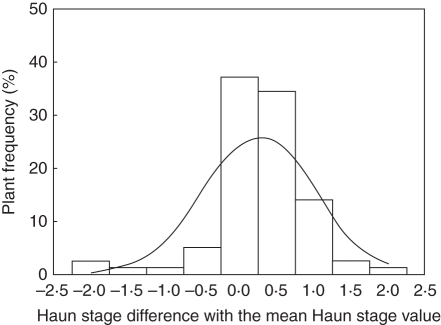
Plant-to-plant variability of development
Measurements of HS performed on 30 April 2009 on 30 plants per density treatment were used to assess the plant-to-plant variability of development and parameterize it in scenario Sref. First, data were pooled by groups of plants that produced different Nleaf, and the dispersion of HS around the mean of each group studied. Calculated standard deviations of HS were similar for all groups in all treatments (between 0·54 and 0·77). Therefore, a unique normal distribution of HS with a standard deviation of 0·65 was used in the parameterization (Fig. 4).
Fig. 4.
Frequency of classes of plant development. Each class is made of plants quasi-synchronous in development; the x-axis represents the delay (in Haun stage) between a class and the mean calculated over all plants. Measurements were performed the 30 April 2009 for winter wheat ‘Soissons’ grown in Grignon in 2008/09; plants from three density treatments D1 (59 plants m−2); D2 (160 plants m−2) and D3 (406 plants m−2) are pooled together. The line represents the normal distribution of the dispersion of Haun stage used in the parameterization of the scenario Sref.
Disease development
Pattern of total necrosis development
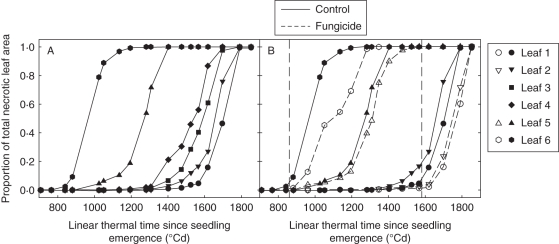
The total necrotic area within a leaf blade progressed at a low rate up to the time when 15–20 % of the blade area was necrotic, then at a fast rate, approximately constant up to total leaf death (Fig. 5A). Necrotic tissues appeared on successive leaf layers according to an acropetal sequence, from lower to upper leaves. However, the time interval between necrosis of successive leaves was much longer for lower leaves (170–270 °Cd) than for the upper leaves (70 °Cd). This pattern occurred similarly in treated and non-treated plots, but was hastened in the absence of fungicide treatment: starting from leaf layer 4 (counted from the top) in D1 and D3, and leaf layer 6 in D2, leaf life span was shortened by 50–170 °Cd in the absence of fungicide compared with treated plots (Fig. 5B). This reflects a moderate epidemic. Yield was high and similar in treated and non-treated plots (61 ± 4, 72 ± 2 and 74 ± 4 q ha−1 for, respectively, D1, D2 and D3).
Fig. 5.
(A) Total necrotic leaf area versus linear thermal time since seedling emergence, for leaves 1–6, as indicated, counted from the top of the main stem of wheat plants not treated with fungicide; (B) total necrotic leaf area versus linear thermal time for leaf 1, leaf 2, leaf 5 and leaf 6, as indicated in the key in (A), of main stem from wheat plants not treated (continuous line, closed symbols) and treated (dotted line, open symbols) with fungicide. Data are for winter wheat ‘Soissons’ grown in Grignon in 2008/09 at the intermediate density (D2, 160 plants m−2). Vertical dashed lines correspond to dates of fungicide treatment.
Effect of density treatment on lesion development
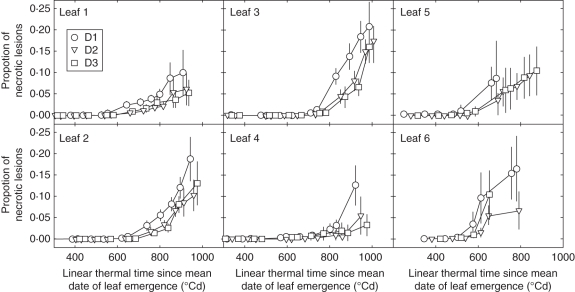
Lesion development was characterized as the proportion of lesions in the green tissue of a leaf blade. To compare between leaves of different ranks, or of same rank between plants that were not synchronous in development, the moment of leaf emergence was used as the time of origin. A leaf can be infected as soon as it emerges and the time interval between leaf emergence and lesion development reflects the timing of infections for that leaf. Comparisons between density treatments are presented first at the plot level by averaging over all plants; in this case the average lesion development measured for each leaf rank was plotted against the thermal time since the average date of leaf emergence (Fig. 6). Secondly, within each density treatment, a separation was made between plants with different final leaf number (Nleaf; Fig. 7).
Fig. 6.
Dynamic of necrotic lesions of Septoria tritici versus linear thermal time since the mean date of leaf emergence, for main stem leaves 1–6 (counted from the top) of winter wheat ‘Soissons’ grown in Grignon in 2008/09 at three densities: D1 (59 plants m−2); D2 (160 plants m−2) and D3 (406 plants m−2). Error bars mark the 95 % confidence intervals.
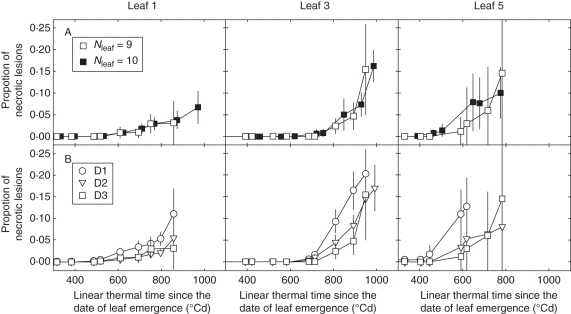
Fig. 7.
Dynamic of necrotic lesions of Septoria tritici versus linear thermal time since the date of leaf emergence, for leaves 1, 3 and 5 (counted from the top) of the main stem (A) for plants with Nleaf = 9 and Nleaf = 10, as indicated, grown at the high density (D3, 406 plants m−2) and (B) for plants with Nleaf = 10 grown at three densities: D1 (59 plants m−2), D2 (160 plants m−2) and D3 (406 plants m−2), as indicated. Data are for winter wheat ‘Soissons’ grown in Grignon in 2008/09. Error bars mark the 95 % confidence intervals.
Figure 6 shows the pattern of lesion development for the six upper leaves (numbered from the top) for the three density treatments. In each leaf layer, lesions appeared almost simultaneously in all density treatments. For leaves 6 and 5, lesions appeared starting around 400 °Cd after leaf emergence, suggesting favourable conditions of infection shortly after leaf emergence (latency period of S. tritici being around 300–400 °Cd). Lesion appearance was delayed on upper leaves (between 600 °Cd and 700 °Cd). After appearance of the first lesion on a leaf, lesion area progressed similarly in treatments D2 and D3, while the rate of development was higher in D1. Lesion development was thus similar in the three density treatments, except for the faster rate of development in the low-density treatment D1.
For each density treatment, lesion development was investigated separately for plants differing by the final leaf number on the main stem. Overall, within each density treatment, there was no noticeable difference in the pattern of lesion development between the groups of plants (Fig. 7A). Thus, differences in the date of leaf emergence, and the slightly shorter phyllochron for plants with higher number of leaves had no noticeable effect on disease progress. Lesion development was also compared between densities considering only plants with the same number of leaves (Nleaf = 10 that could be found in the three treatments; Fig. 7B). The differences between density treatments were very similar to those found when all plants were considered.
Altogether these results indicate that (a) no strong difference in lesion development between the three density treatments was observed (b) plants from the same treatment, but differing in final leaf number showed the same disease development in the upper leaves and (c) the lowest density resulted in slightly stronger disease development compared with the two other densities but this did not result from the higher number of leaves in this treatment.
Disease simulations
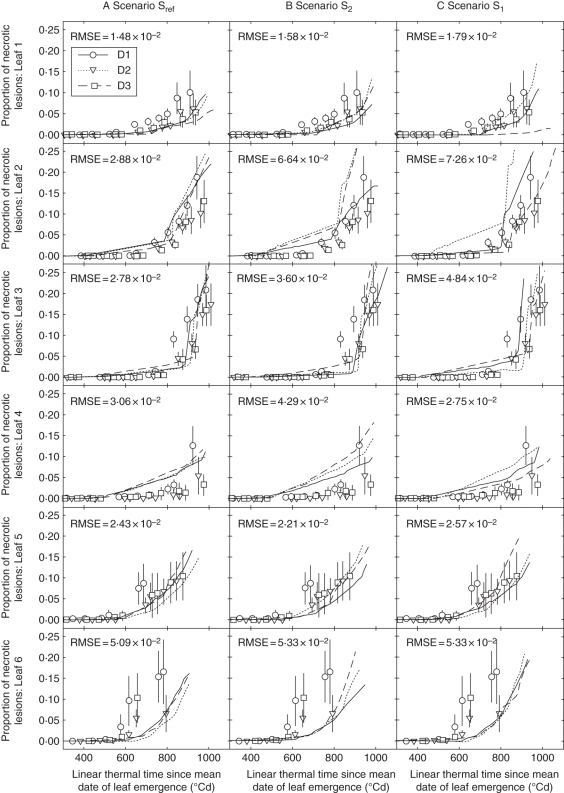
Simulations of lesion development with the reference scenario Sref
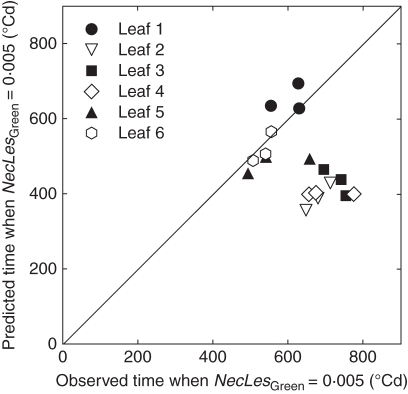
Figure 8A shows measured and simulated kinetics of lesions (NecLesGreen) for leaves 1–6 with the scenario of canopy reconstruction Sref. Simulations were similar for the three density treatments. The onset of fast lesion development was predicted to take place nearly simultaneously in all treatments, consistent with observations. The simulated increase in lesion development was consistent with field observations for the intermediate- and high-density treatments (D2 and D3, respectively). However, the model did not reproduce the higher rate at which lesions extended in treatment D1 compared with D2 and D3. Figure 9 illustrates how the model simulated the earliest detectable signal of lesion development (estimated as the time when NecLesGreen = 0·5 % of blade area). This was correctly predicted for leaves 1, 5 and 6, but was underestimated by approx. 250 °Cd for leaves 2, 3 and 4. On leaves 2 and 3, the model predicted the appearance of a small lesion area, starting 400 °Cd after leaf appearance, but increasing at a low rate. Given the latency period (310 °Cd in the model), this corresponds to a very limited infection predicted to have taken place shortly after leaf emergence. Field observations did not detect such small amounts of early necrotic lesions. This could be either because they were too small to be seen or because model prediction of an early infection was not correct. In the case of leaf 4, the simulated onset of first lesions was followed by a significant development in the simulated lesions so that here the model clearly deviated from what occurred in the field. Differences between field data and simulations were important for leaf 6; in this leaf, the timing of first lesion appearance was similar between simulations and field measurements (approx. after 500 °Cd), but the rate of lesion development was underestimated in the simulation. This difference was quantitatively stronger for the low-density treatment D1 with >10 % difference at 620 °Cd after leaf emergence. This was true also for leaf 7 (not shown since few measurements were available).
Fig. 8.
Predicted (lines) and measured (symbols) dynamic of necrotic lesions of Septoria tritici versus linear thermal time since the average date of leaf emergence of leaves 1–6 (counted from the top) for wheat main stem for three scenarios of simulation differing in the degree of architecture description: (A) scenario Sref, (B) scenario S2 and (C) scenario S1. Simulated canopy is represented by the mean plant in scenario S1, by two mean plants differing in their final leaf number in S2 and by plants differing in their final leaf number and stage of development in Sref. Data are for winter wheat ‘Soissons’ grown in Grignon in 2008/09 at three densities, D1 (59 plants m−2), D2 (160 plants m−2) and D3 (406 plants m−2), as indicated. Error bars mark the 95 % confidence intervals.
Fig. 9.
Predicted versus observed time when NecLesGreen = 0·005 for leaves 1–6, as indicated, counted from the top for the main stem of winter wheat ‘Soissons’ grown in Grignon in 2008/09 at three densities: D1 (59 plants m−2), D2 (160 plants m−2) and D3 (406 plants m−2). Time is expressed in linear thermal time (°Cd) since the average date of leaf emergence. Predictions are for the scenario that takes into account interplant variability of development (Sref). Each point corresponds to the mean value for a leaf rank in one density treatment.
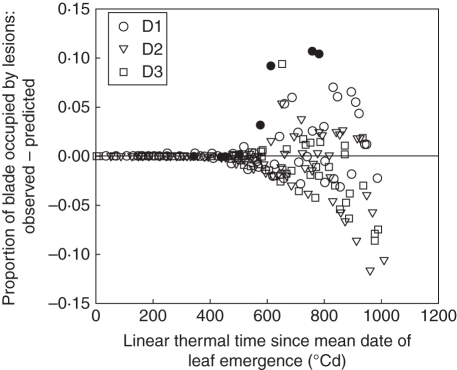
To give an overall impression of the model fit, Fig. 10 shows the difference between simulated and observed lesions (NecLesGreen) for leaves 1–6, for the three density treatments, as a function of the leaf age. The RMSE values calculated for leaves 1–6 pooled are very similar and low for the three treatments (0·029, 0·028 and 0·027 for treatments D1, D2 and D3, respectively). However, simulation errors increased for higher leaf age. This could reflect that the reduction in the amount of green tissue (due to apical senescence) results in a lower accuracy in both the simulated and measured proportion of lesions (NecLesGreen) in these tissues. Moreover, during fast lesion development a small error in the predicted timing of development corresponds to a large difference in the amount of lesions at a given time. The comparison is most meaningful before 900 °Cd, when there is >50 % of green tissue. During this period, the points for treatments D2 and D3 are centred on zero, indicating that there is no overall bias, whereas for treatment D1 the model underestimates the disease.
Fig. 10.
Differences between observed and predicted proportions of blade occupied by Septoria tritici necrotic lesions versus linear thermal time since leaf emergence. Predictions are simulated with scenario Sref (that takes into account interplant variability of development) for leaves 1–6 counted from the top of the main stem of winter wheat ‘Soissons’ grown in Grignon in 2008/09 at three densities, D1 (59 plants m−2), D2 (160 plants m−2) and D3 (406 plants m−2), as indicated. Data for leaf 6 at the low density (D1) are shown in closed symbols.
Effect of the canopy reconstruction scenarios on the disease simulation
The model run with the three scenarios of canopy reconstruction Sref, S2 and S1 (Fig. 8A–C) showed differences in simulated epidemics mostly on the two upper leaves and mostly between the two extremes Sref and S1, i.e. when comparing between taking into account the interplant variability of development and cloning a same mean plant without any variability. Besides, small differences in the timing of lesion appearance were observed between the three scenarios.
Simulations with S2 did not show much change compared with Sref. It is noticeable, however, that the ranking of the treatments with regards to the epidemics was changed: in Sref the ranking of simulated necrotic development was D1 ≥ D2 ≥ D3, whereas in S2, the model simulated a slightly higher level of necrotic development in D2 compared with D1 and D3.
More important differences were observed between Sref and S1. In S1, differences between density treatments in the simulated lesion development increased and became large for leaves 1 and 2. For these leaves, S1 resulted in a strong hierarchy of lesion development between density treatments, (D2 > D1 > D3) that did not match the field observations. It is noticeable that S1 even predicted that the disease will not reach leaf 1 in the high-density treatment D3. Scenario S1 also yielded stair-shaped curves.
DISCUSSION
In this study, the capacity of a coupled virtual wheat-Septoria tritici epidemic model (Septo3D) was tested to simulate S. tritici progress on the different leaf layers for three contrasted sowing density treatments. To do this, first the plants were experimentally characterized to parameterize their description in the model. Then, the simulated and observed epidemics were compared. Despite the contrasted canopy structures, there were few differences in disease progress between treatments: only the low-density treatment resulted in a higher rate of lesion development. Simulating lesion development using the canopy reconstruction that includes plant developmental variability (Sref) yielded the best agreement with field measurements. In particular, the model predicted lesion onset on each layer to take place simultaneously on all treatments which was consistent with observations. However, simulations did not reproduce the higher rate at which lesions developed in the low-density treatment.
Originalities of the field experimental design
One of the originalities of our experiment is the high level of detail with which both plant architecture and disease dynamics were measured. It resulted in the acquisition of an original dataset. Compared with the few existing similar studies (Evers et al., 2005), architecture characterization here included two novel aspects: (a) the characterization not only of axis development but also of tiller regression and leaf senescence and (b) the characterization of plant-to-plant variability in terms of seedling emergence, number of axes, number of phytomers and correlations with the size of mature phytomer components. The development of S. tritici was also monitored in detail on each leaf. It is not always possible in the field to distinguish necrosis due to the lesions (that show pycnidia) from those due to monocarpic senescence (Royle et al., 1986; Robert, 2003). In the literature, two types of assessments can be found, based either on the lesions containing pycnidia (Shaw and Royle, 1993; Lovell et al., 2004b) or on the total area of necrotic tissues (Robert et al., 2004; Bancal et al., 2007). Here, the area of necrotic lesions in the green part of the leaf blade is used, which allowed for an accurate characterization of the early stage of infection of each layer.
Density effect on architecture
The three sowing densities resulted in varied architecture dynamics. The effects observed are in line with those described in previous studies on the effect of sowing density for wheat (Ljutovac, 2002; Evers et al., 2005). Changing sowing density was partially compensated by regulation in (a) the number of tillers, (b) the dimensions of leaf blades in upper phytomers and (c) the lower total number of leaves formed on an axis for higher densities. However, compensation took place progressively and was not complete even at flowering. At the onset of stem extension, the total number of axes per square metre was, respectively, 542 and 1461 for D1 and D3. At flowering, it was, respectively, 359 and 557. Thus, the environment of development of individual plants and pathogen differed between treatments.
Density effect on epidemics
Irregular intervals between kinetics of total necrotic lesions were observed for successive leaf layers for the three density treatments. Robert et al. (2004) reported that the death of successive wheat leaves infected by S. tritici occurred at regular intervals, corresponding to one phyllochron. This regularity result from very favourable climatic conditions that caused infection of leaves just after their emergence. In the present experiment, the unfavourable environment could have resulted in irregular timing of infection of successive leaves.
Contrasted effects of sowing density on foliar diseases have been reported: increasing densities may enhance epidemics (Tompkins et al., 1993; Ando and Grumet, 2006; Gan et al., 2007; Jurke and Fernando, 2008); have little effect (Pfleeger and Mundt, 1998); or even reduce epidemics (Eyal, 1981). For S. tritici, several authors have reported that increasing plant density enhances epidemics (Broscious et al., 1985; Tompkins et al., 1993; Ansar et al., 1996; Ansar and Leitch, 2009). However, S. tritici increased only up to some threshold in plant density, above which either no further effect (Ansar et al., 1996), or a decrease in disease severity was observed, even to a level below that observed at the lowest density (Ansar and Leitch, 2009). In a field trial carried out by Broscious et al. (1985), only five out of 13 trials showed a significant sowing rate effect on S. tritici severity, one of which was a decrease. In the present experiment, the different density treatments resulted in similar epidemics, except for a slightly higher rate of lesion development at the low density. This higher rate of development was observed from leaf 6, a rosette leaf, and persisted throughout the season on the upper leaves, suggesting that the density effect resulted partly from interaction between architecture and climate during the winter, i.e. the rosette stage. The potential importance of the winter period for the resulting epidemic may possibly be linked to two characteristics of the present experiment: (1) the late sowing date reduced the duration during which rosette leaves could be infected; and (2) the rather unfavourable environmental conditions for S. tritici during stem extension may have given strong importance to differences established in the rosette leaves.
Two processes may have contributed to the higher disease development observed in the rosette leaves in the low-density treatment. The sparser canopy may have (1) induced a higher rain penetration and thus a stronger contamination from the soil and (2) resulted in a higher number of spores deposited per unit of leaf area. Assuming that during a rain event spores on the soil are splashed until they are deposited on a leaf, an equal amount of spores is then divided by a smaller leaf area for less dense vegetation. This is consistent with Eyal (1981) who reported that the raindrop-splashing effect was increased in less dense crops leading to earlier and faster pathogen progress.
Finally, it is also possible that the physiological status of the leaves and, in particular, the leaf nitrogen content played a role in the difference in disease development between the density treatments. This effect is suggested because, on the one hand, leaf nitrogen dynamics likely differed between density treatments, as the content of nitrogen usually decreases rapidly in leaves and shoots of seedlings grown at high density (Sasaki and Toriyama, 2006; Ansar and Leitch, 2009) and, on the other hand, foliar lesion development has been found to be influenced by the leaf nitrogen content (Leitch and Jenkins, 1995; Lovell et al., 1997).
Within a density treatment, no difference was observed in disease development on upper leaves between plants with different numbers of leaves. This was checked because differences in final leaf number implies differences in phyllochron and date of leaf emergence (R. Baccar et al., unpubl. res.), which is known to influence leaf infection by S. tritici (Shaw and Royle, 1993; Moreau and Maraite, 1999). A possible hypothesis is that the variability in plant development in the field (in part due to variability in the date of seedling emergence) was strong enough to mitigate the effect of the variability between plants due to different leaf number.
Modelling canopy variability and its effect on epidemics
One of the originalities of the present architecture reconstruction is to address the modelling of interplant variability. Most of the time, a mean plant is reconstructed, and random variability is added on the top of this base (Fournier and Andrieu, 1999; Fournier et al., 2003; Evers et al., 2005). Here, two sources of variability were quantified experimentally and the impact of taking into account each of them on disease simulation was tested. The first source of variability is that related to differences in total number of leaves produced on the main stem, which are linked to various architectural variables (dimensions, development and senescence) on main stems and tillers. This variability was taken into account by integrating separately in the model architectural variables of each group of plants with the same number of leaves and by representing the observed proportions of each group of plants in the reconstructed canopy. The second source of variability is linked to delays in the date of plant emergence. The variability in development between plants at two dates was characterized and, from this, the variability in the date of emergence that was introduced in the simulation was estimated. The level of variability included in the canopy reconstruction influenced the simulated disease dynamics. Reducing the variability of plant development increased the difference between the density treatments, leading to unrealistic differences when all plants were taken as identical. In addition, taking into consideration the plant-to-plant variability of development (i.e. in scenario Sref) resulted in realistic kinetics with smooth curves of lesion development. Scenarios S2 and mostly S1 yielded stair-shaped curves reflecting the simultaneous response of the same type of plants to a single infection event. Simulating a canopy of identical plants introduces the risk of missing the infection of an entire leaf layer if the predicted leaf emergence happens to be just after a rare but important rain event.
New parameterization of initial infection conditions improved triggering the disease
Septo3D requires an initialization of disease. In the previous version of the model (Robert et al., 2008), initial infection was parameterized by infecting directly the three first rosette leaves. In the present version, the rosette leaves are infected by splashes from spores on the ground as in Audsley et al. (2005). The parameters for initial conditions are the period during which infection can occur, taken as infinite here as in Audsley et al. (2005), and the area of sporulating surface on the ground. Using this new parameterization, the three densities responded differently to varying initial conditions, showing that the infection of the rosette leaves does now respond to architecture.
Capacity of the model to simulate S. tritici epidemics
For scenario Sref, the most realistic architecture description, simulations of lesion development displayed little difference between the three density treatments. For the five upper leaves, the simulations were consistent with field data (within the 95 % confidence intervals, RMSE above 3·06 10−2 of the proportion of necrotic lesions) particularly for high and intermediate density treatments. The model simulated consistently the onset of lesion development in leaves 6, 5 and 1 (numbered from the top). Three main discrepancies were found between simulations and observed epidemics.
The model underestimated disease progress on leaf 6, especially strongly for the low density. Two known mechanisms of infection: ascospore deposition (Shaw and Royle, 1989; Hunter et al., 1999) and contamination by direct contact between leaves (Lovell et al., 2004b) are currently lacking in Septo3D, which may explain the disease underestimation on the rosette leaves.
The model did not reproduce the higher rate at which lesions developed in the low-density treatment compared with intermediate and high-density treatments. The underestimation observed on leaf 6 for all densities, was subsequently observed on all upper leaves only for the low density. This suggests that the underestimation on rosette leaves did not affect the simulation of the higher leaves for intermediate and high density, whereas it did for the low density. In this treatment, the underestimation of the infection of rosette leaves may have resulted in a simulated inoculum sufficiently low to hamper the simulated disease progress and thus in the underestimation of the infection of higher layers.
On leaves 2 and 3 the model predicted the appearance of small, slowly extending, lesions largely before the date the first lesions were observed. This also occurred for leaf 4 and, in this case, it resulted later in a significant development of the simulated disease sooner than observed in the field. One possible explanation is that a fixed duration of the latency period (310 °Cd) we used, whereas the latency period may be much longer when conditions of temperature and humidity hamper fungus development (Shaw, 1990, 1991; Lovell et al., 2004a).
Difficulties of validation of coupled architecture–epidemic models
Testing the model predictions appeared to be quite a challenge. Septoria tritici epidemics turned out to be low in the present experiment: the assessed disease severity was below 20 % for all leaves and yields were similar in the treated and non-treated plots. Therefore, density effects were less likely to be expressed or detectable. Moreover, lesions can only be identified in green tissue, meaning that in the case of a slow-developing epidemic, such as here, the progress of monocarpic senescence hampers the completeness of the description of lesion extension.
Using sowing-density treatments to vary canopy architecture and test the model was a complex task for two reasons: (1) despite using extreme ranges of densities, the plasticity of wheat resulted in the compensation of differences between the three densities at canopy level over time and introduced complex effects within a single density; and (2) the phenotypic response of the plants to density is complex and raises important challenges for a realistic reconstruction of the canopy. To overcome these difficulties, a possible solution could be to test the model with field experiments using more contrasted and/or simpler canopy architectures such as monoculm wheat canopies avoiding thus compensation by tillering, different Rht-gene lines allowing strong differences in stem height, or modified plant architectures, e.g. clipping an entire leaf layer.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge Fabrice Duhamel and Maxime Marques for their excellent technical assistance, and Valérie Bontemps for her high degree of commitment in the characterization of S. tritici epidemics. The Unité Expérimentale of Centre INRA, Versailles-Grignon, headed up the agronomic work. The work was funded by INRA, Department of Environnement et Agronomie and by ARVALIS, Institut du végétal.
LITERATURE CITED
- Ando K, Grumet R. Evaluation of altered cucumber plant architecture as a means to reduce Phytophthora capsici disease incidence on cucumber fruit. Journal of the American Society for Horticultural Science. 2006;131:491–498. [Google Scholar]
- Ando K, Grumet R, Terpstra K, Kelly JD. Manipulation of plant architecture to enhance crop disease control. CAB Review. Perspectives in Agriculture, Veterinary Science, Nutrition and Natural Resources. 2007 No. 2. [Google Scholar]
- Ansar M, Leitch MH. The effect of agronomic practices on the development of Septoria Leaf Blotch and its subsequent effect on the yield and yield components of wheat. American-Eurasian Journal of Sustainable Agriculture. 2009;3:57–67. [Google Scholar]
- Ansar M, Leitch MH, Jenkins PD, Hayden NJ. Effect of nitrogen fertilizer, crop density and development of Septoria tritici on components of growth and yield of winter wheat in the UK. In: Braun H-J, Altay F, Kronstad WE, Beniwal SOS, McNab A, editors. Wheat: Prospects for Global Improvement. Proceedings of the 5th International Wheat Conference. Heidelberg: Springer; 1996. pp. 270–272. 10–14 June 1996, Ankara, Turkey. [Google Scholar]
- Audsley E, Milne A, Paveley N. A foliar disease model for use in wheat disease management decision support systems. Annals of Applied Biology. 2005;147:161–172. [Google Scholar]
- Bahat A, Gelernter I, Brown MB, Eyal Z. Factors affecting the vertical progression of Septoria leaf blotch in short-statured wheats. Phytopathology. 1980;70:179–184. [Google Scholar]
- Bancal MO, Robert C, Ney B. Modelling wheat growth and yield losses from late epidemics of foliar diseases using loss of green leaf area per layer and pre-anthesis reserves. Annals of Botany. 2007;100:777–789. doi: 10.1093/aob/mcm163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broscious SC, Frank JA, Frederick JR. Influence of winter wheat management practices on the severity of powdery mildew and Septoria blotch in Pennsylvania. Phytopathology. 1985;75:538–542. [Google Scholar]
- Calonnec A, Cartolaro P, Naulin JM, Bailey D, Langlais M. A host–pathogen simulation model: powdery mildew of grapevine. Plant Pathology. 2008;57:493–508. [Google Scholar]
- Camacho-Casas MA, Kronstad WE, Scharen AL. Septoria tritici resistance and associations with agronomic traits in a wheat cross. Crop Science. 1995;35:971–976. [Google Scholar]
- Danon T, Sacks JM, Eyal Z. The relationships among plant stature, maturity class, and susceptibility to Septoria leaf blotch of wheat. Phytopathology. 1982;72:1037–1042. [Google Scholar]
- Darwinkel Patterns of tillering and grain production of winter wheat at a wide range of plant densities. Netherlands Journal of Agricultural Science. 1978;26:383–398. [Google Scholar]
- Dornbusch T, Andrieu B. Lamina2Shape – an image processing tool for an explicit description of lamina shape tested on winter wheat (Triticum aestivum L.) Computers and Electronics in Agriculture. 2010;70:217–224. [Google Scholar]
- Dornbusch T, Baccar R, Watt J, et al. Plasticity of winter wheat modulated by sowing date, plant population density and nitrogen fertilisation: dimensions and size of leaf blades, sheaths and internodes in relation to their position on a stem. Field Crops Research. 2010;121:116–124. [Google Scholar]
- Evers JB, Vos J, Fournier C, Andrieu B, Chelle M, Struik PC. Towards a generic architectural model of tillering in Gramineae, as exemplified by spring wheat (Triticum aestivum) New Phytologist. 2005;166:801–812. doi: 10.1111/j.1469-8137.2005.01337.x. [DOI] [PubMed] [Google Scholar]
- Eyal Z. Integrated control of Septoria diseases of wheat. Plant Disease. 1981;65:763–768. [Google Scholar]
- Fournier C, Andrieu B. ADEL-maize: an L-system based model for the integration of growth processes from the organ to the canopy. application to regulation of morphogenesis by light availability. Agronomie. 1999;19:313–327. [Google Scholar]
- Fournier C, Andrieu B, Ljutovac S, Saint-Jean S. ADEL-wheat: a 3D architectural model of wheat development. In: Hu B-G, Jaeger M, editors. Plant Growth Modeling and Applications. Proceedings of 2003 International Symposium. Beijing: CHN Tsinghua University Press/Springer Verlag; 2003. pp. 54–63. [Google Scholar]
- Fournier C, Durand JL, Ljutovac S, Schaufele R, Gastal F, Andrieu B. A functional-structural model of elongation of the grass leaf and its relationships with the phyllochron. New Phytologist. 2005;166:881–894. doi: 10.1111/j.1469-8137.2005.01371.x. [DOI] [PubMed] [Google Scholar]
- Friend DJC. Tillering and leaf production in wheat as affected by temperature and light intensity. Canadian Journal of Botany. 1965;43:1063–1076. [Google Scholar]
- Gan Y, Gossen BD, Li L, Ford G, Banniza S. Cultivar type, plant population, and ascochyta blight in chickpea. Agronomy Journal. 2007;99:1463–1470. [Google Scholar]
- Georgin P, Gouet M. Statistiques avec Exel 2000. Paris: Eyrolles; 2000. [Google Scholar]
- Godin C, Sinoquet H. Functional–structural plant modelling. New Phytologist. 2005;166:705–708. doi: 10.1111/j.1469-8137.2005.01445.x. [DOI] [PubMed] [Google Scholar]
- Hanan J, Prusinkiewicz P, Zalucki M, Skirvin D. Simulation of insect movement with respect to plant architecture and morphogenesis. Computers and Electronics in Agriculture. 2002;35:255–269. [Google Scholar]
- Haun JR. Visual quantification of wheat development. Agronomy Journal. 1973;65:116–119. [Google Scholar]
- Hilton AJ, Jenkinson P, Hollins TW, Parry DW. Relationship between cultivar height and severity of Fusarium ear blight in wheat. Plant Pathology. 1999;48:202–208. [Google Scholar]
- Hunter T, Coker RR, Royle DJ. The teleomorph stage, Mycosphaerella graminicola, in epidemics of Septoria tritici blotch on winter wheat in the UK. Plant Pathology. 1999;48:51–57. [Google Scholar]
- Johnson FH, Lewin I. The growth rate of E. coli in relation to temperature, quinine, and coenzyme. Journal of Cellular and Comparative Physiology. 1946;28:239–251. doi: 10.1002/jcp.1030280104. [DOI] [PubMed] [Google Scholar]
- Jurke CJ, Fernando WGD. Effects of seeding rate and plant density on sclerotinia stem rot incidence in canola. Archives of Phytopathology and Plant Protection. 2008;41:142–155. [Google Scholar]
- Leitch MH, Jenkins PD. Influence of nitrogen on the development of Septoria epidemics in winter wheat. Journal of Agricultural Science. 1995;124:361–368. [Google Scholar]
- Ljutovac S. Coordination dans l'extension des organes aériens et conséquences pour les relations entre les dimensions finales des organes chez le blé. 2002 Thèse de Docteur, Ingénieur, Institut National Agronomique Paris-Grignon, Paris. [Google Scholar]
- Lovell DJ, Parker SR, Hunter T, Royle DJ, Coker RR. Influence of crop growth and structure on the risk of epidemics by Mycosphaerella graminicola (Septoria tritici) in winter wheat. Plant Pathology. 1997;46:126–138. [Google Scholar]
- Lovell DJ, Hunter T, Powers SJ, Parker SR, van den Bosch F. Effect of temperature on latent period of septoria leaf blotch on winter wheat under outdoor conditions. Plant Pathology. 2004a;53:170–181. [Google Scholar]
- Lovell DJ, Parker SR, Hunter T, Welham SJ, Nichols AR. Position of inoculum in the canopy affects the risk of Septoria tritici blotch epidemics in winter wheat. Plant Pathology. 2004b;53:11–21. [Google Scholar]
- Masle J. Competition among tillers in winter wheat : consequences for growth and development of the crop. In: Day W, Atkin RK, editors. Wheat growth and modelling. New York, NY: Plenum Press; 1985. pp. 33–44. [Google Scholar]
- Masle-Meynard J, Sebillotte M. Study of the heterogeneity of a winter wheat stand. II. Origin of the different sorts of individuals in the stand: factors allowing description of its structure. Agronomie. 1981;1:217–223. [Google Scholar]
- Moreau JM, Maraite H. Integration of knowledge on wheat phenology and Septoria tritici epidemiology into a disease risk simulation model validated in Belgium. Information Technology for Crop Protection. 1999 No. 55, 1–6. Harpenden, UK. [Google Scholar]
- Parent B. Leaf development in rice and maize: framework of analysis, compared responses to temperature and growth regulation under water deficit. 2009 PhD thesis, Montpellier Supagro, Montpellier. [Google Scholar]
- Pfleeger TG, Mundt CC. Wheat leaf rust severity as affected by plant density and species proportion in simple communities of wheat and wild oats. Phytopathology. 1998;88:708–714. doi: 10.1094/PHYTO.1998.88.7.708. [DOI] [PubMed] [Google Scholar]
- Pielaat A, van den Bosch F, Fitt BDL, Jeger MJ. Simulation of vertical spread of plant diseases in a crop canopy by stem extension and splash dispersal. Ecological Modelling. 2002;151:195–212. [Google Scholar]
- Rapilly F, Jolivet E. Construction d'un modèle (episept) permettant la simulation d'une épidémie de Septoria nodorum BERK sur blé. Revue de statistiques appliquées. 1974;3:31–60. [Google Scholar]
- Robert C. 2003 Etude et modélisation du fonctionnement d'un couvert de blé attaqué par le complexe parasitaire Puccinia triticina–Mycosphaerella graminicola. Institut National Agronomique de Paris-Grignon, Paris, France. [Google Scholar]
- Robert C, Bancal MO, Nicolas P, Lannou C, Ney B. Analysis and modelling of effects of leaf rust and Septoria tritici blotch on wheat growth. Journal of Experimental Botany. 2004;55:1079–1094. doi: 10.1093/jxb/erh108. [DOI] [PubMed] [Google Scholar]
- Robert C, Fournier C, Andrieu B, Ney B. Coupling a 3D virtual wheat (Triticum aestivum) plant model with a Septoria tritici epidemic model (Septo3D): a new approach to investigate plant–pathogen interactions linked to canopy architecture. Functional Plant Biology. 2008;35:997–1013. doi: 10.1071/FP08066. [DOI] [PubMed] [Google Scholar]
- Room P, Hanan J, Prusinkiewicz P. Virtual plants: new perspectives for ecologists, pathologists and agricultural scientists. Trends in Plant Science. 1996;1:33–39. [Google Scholar]
- Royle DJ, Shaw MW, Cook RJ. Patterns of development of Septoria nodorum and S. tritici in some winter wheat crops in Western Europe, 1981–83. Plant Pathology. 1986;35:466–476. [Google Scholar]
- Saindon G, Huang HC, Kozub GC. White-mold avoidance and agronomic attributes of upright common beans grown at multiple planting densities in narrow rows. Journal of the American Society for Horticultural Science. 1995;120:843–847. [Google Scholar]
- Sasaki R, Toriyama K. Nitrogen content of leaves affects the nodal position of the last visible primary tiller on main stems of rice plants grown at various plant densities. Plant Production Science. 2006;9:242–248. [Google Scholar]
- Schwartz HF, Steadman JR, Coyne DP. Influence of Phaseolus-vulgaris blossoming characteristics and canopy structure upon reaction to Sclerotinia. Sclerotiorum Phytopathology. 1978;68:465–470. [Google Scholar]
- Scott PR, Benedikz PW, Cox CJ. A genetic study of the relationship between height, time of ear emergence and resistance to Septoria nodorum in wheat. Plant Pathology. 1982;31:45–60. [Google Scholar]
- Scott PR, Benedikz PW, Jones HG, Ford MA. Some effects of canopy structure and microclimate on infection of tall and short wheats by Septoria nodorum. Plant Pathology. 1985;34:578–593. [Google Scholar]
- Shaw MW. Effects of temperature, leaf wetness and cultivar on the latent period of Mycosphaerella graminicola on winter wheat. Plant Pathology. 1990;39:255–268. [Google Scholar]
- Shaw MW. Interacting effects of interrupted humid periods and light on infection of wheat leaves by Mycosphaerella graminicola (Septoria tritici) Plant Pathology. 1991;40:595–607. [Google Scholar]
- Shaw MW, Royle DJ. Airborne inoculum as a major source of Septoria tritici (Mycosphaerella graminicola) infections in winter wheat crops in the UK. Plant Pathology. 1989;38:35–43. [Google Scholar]
- Shaw MW, Royle DJ. Factors determining the severity of epidemics of Mycosphaerella graminicola (Septoria tritici) on winter wheat in the UK. Plant Pathology. 1993;42:882–899. [Google Scholar]
- Simon MR, Perello AE, Cordo CA, Larran S, van der Putten PEL, Struik PC. Association between Septoria tritici blotch, plant height, and heading date in wheat. Agronomy Journal. 2005;97:1072–1081. [Google Scholar]
- Skirvin DJ. Virtual plant models of predatory mite movement in complex plant canopies. Ecological Modelling. 2004;171:301–313. [Google Scholar]
- Tavella CM. Date of heading and plant height of wheat varieties, as related to Septoria leaf blotch damage. Euphytica. 1978;27:577–580. [Google Scholar]
- Tompkins DK, Fowler DB, Wright AT. Influence of agronomic practices on canopy microclimate and Septoria development in no-till winter wheat produced in the Parkland region of Saskatchewan. Canadian Journal of Plant Science. 1993;73:331–344. [Google Scholar]
- Vos J, Evers JB, Buck-Sorlin GH, Andrieu B, Chelle M, de Visser PHB. Functional–structural plant modelling: a new versatile tool in crop science. Journal of Experimental Botany. 2010;61:2101–2115. doi: 10.1093/jxb/erp345. [DOI] [PubMed] [Google Scholar]
- Wilhelm WW, McMaster GS. Importance of the phyllochron in studying development and growth in grasses. Crop Science. 1995;35:1–3. [Google Scholar]
- Wilson PA, Chakraborty S. The virtual plant: a new tool for the study and management of plant diseases. Crop Protection. 1998;17:231–239. [Google Scholar]