A functional–structural model for radiata pine (Pinus radiata) focusing on tree architecture and wood quality

Abstract

Backgrounds and Aims

Functional–structural models are interesting tools to relate environmental and management conditions with forest growth. Their three-dimensional images can reveal important characteristics of wood used for industrial products. Like virtual laboratories, they can be used to evaluate relationships among species, sites and management, and to support silvicultural design and decision processes. Our aim was to develop a functional–structural model for radiata pine (Pinus radiata) given its economic importance in many countries.

Methods

The plant model uses the L-system language. The structure of the model is based on operational units, which obey particular rules, and execute photosynthesis, respiration and morphogenesis, according to their particular characteristics. Plant allometry is adhered to so that harmonic growth and plant development are achieved. Environmental signals for morphogenesis are used. Dynamic turnover guides the normal evolution of the tree. Monthly steps allow for detailed information of wood characteristics. The model is independent of traditional forest inventory relationships and is conceived as a mechanistic model. For model parameterization, three databases which generated new information relating to P. radiata were analysed and incorporated.

Key Results

Simulations under different and contrasting environmental and management conditions were run and statistically tested. The model was validated against forest inventory data for the same sites and times and against true crown architectural data. The performance of the model for 6-year-old trees was encouraging. Total height, diameter and lengths of growth units were adequately estimated. Branch diameters were slightly overestimated. Wood density values were not satisfactory, but the cyclical pattern and increase of growth rings were reasonably well modelled.

Conclusions

The model was able to reproduce the development and growth of the species based on mechanistic formulations. It may be valuable in assessing stand behaviour under different environmental and management conditions, assisting in decision-making with regard to management, and as a research tool to formulate hypothesis regarding forest tree growth and development.

INTRODUCTION

Being able to predict the quality and value of forest products is much desired by the timber industry. Models can help in this regard.

Most models of radiata pine (Pinus radiata), the main industrial forest species in New Zealand, Australia and Chile, are robust empirical models of growth but with little physiological basis. They predict yield in terms of gross timber volume and selected wood product per hectare and may include the effects of management practices (Prodan et al., 1997). However, the final price and quality of the wood is largely determined by knots, internode length and wood density (Carson and Inglis, 1988; Mezzano, 1997; Todoroki et al., 2001). Wood quality also determines pulp and paper properties (Wimmer et al., 2002). To model wood quality a good understanding of crown architecture is needed, and if the goal is to develop a functional model, the eco-physiological behaviour of the species must be better understood.

Pinus radiata modelling is being used to gain a better understanding of the physiology and crown characteristics of the tree, especially by researchers in countries where the species is an economically important resource, such as New Zealand, Australia and Chile.

In terms of tree architecture, that of P. radiata corresponds to Rauh's model, with a rhythmic pattern of development, the axes showing indeterminate growth, with lateral flowering. Female flowering occurs on axis order 1 (the stem) as differentiated from axes of order 2, and on axes of order 2 (Fernández, 1994). The rhythmic growth pattern of development as given by Hallé et al. (1978) describes alternating periods in which the axis of a tree elongates with periods in which it remains in a resting state. This has been substantiated for radiata pine by Jacobs (1937), Fielding (1960), Pawsey (1964), Doran (1974), Bollmann and Sweet (1976), Jackson et al. (1976) and Tennent (1986). Nevertheless, there are some indications by Bollmann and Sweet (1976) and Tennent (1986) that, depending on environmental conditions, the species does not undergo a true period of rest. This is relevant because it may be an opportunistic strategy for growth, so that the species may take advantage of occasionally favourable environmental circumstances in otherwise generally adverse conditions. A growth unit consists of an internode and the following section of stem containing a cluster of lateral structures (branches, and/or cones or buds). A growth unit develops during an uninterrupted period of extension (Hallé et al., 1978). P. radiata normally produces several growth units per annual shoot on the main stem and some usually vigorous branches. Therefore, it is considered to be a polycyclic species, as shown by Jacobs (1937), Fielding (1960), Bannister (1962), Bollmann and Sweet (1976), Fernández (1994) and Fernández et al. (2007). However, some trees in some years occasionally produce only one growth unit in the main axis, so the model also has to include some type of switch or activating signal elicited by particular environmental factors (temperature, photoperiod, water balance). The first growth unit of an annual shoot in a mature polycyclic individual is typically a reproductive one bearing female strobili and small branches, if any (Jacobs, 1937; Bannister, 1962; Bollmann and Sweet, 1976; Fernández, 1994). The ensuing growth units may also carry female reproductive units. The last growth unit, however, normally does not bear female strobili but strong branches instead; the latter develop during the following season. It is also possible to observe in some annual shoots one or more growth units without female strobili between the growth unit with female strobili and the last growth unit of the whole annual shoot (Fernández et al., 2004). Bannister (1962), referring to the development of the main axis, indicates that the number of growth units per annual shoot varies continuously. Fernández et al. (2007) have corroborated this phenomenon during the juvenile stage, and have shown a strong effect of the phase change from the juvenile to the mature stage on the architecture of the main stem of the tree, becoming stabilized after the first flowering. Fernández et al. (2007) also observed that despite the fact that flowering took place at different times in stands of otherwise similar characteristics at different sites, it occurred when the trees had ‘accumulated’ approximately the same number of branches in the main axis, 89 on average. This suggests the operation of genetic labels that promote the irreversible change from the juvenile (no cone formation) to the mature phases. As branch number, position and size are important features of eco-physiological modelling focused on wood quality, a structural–functional model must take into account variables that relate to branch development and production.

Jackson and Gifford (1974) and Jackson et al. (1976) were some of the first researchers to show and elaborate on the close relationship between environmental variables and growth of radiata pine. Subsequently, basic physiological phenomena such as photosynthesis and respiration and structural features such as canopy conductance and solar radiation interception and use efficiency have been studied and introduced into functional models. The influence of atmospheric carbon dioxide, soil nitrogen and phosphorus supply, and water deficits have been incorporated and given rise to useful model parameters that have broadened our knowledge of the growth of P. radiata (McMurtrie et al., 1992; Sheriff and Mattay, 1995; Medlyn, 1996; Ryan et al., 1996; Sheriff, 1996; Teskey and Sheriff, 1996; Dewar, 1997; Walcroft et al., 1997; Miller et al., 1998; Bown et al., 2007). Carbon partitioning among various structural units and its relationship to the nitrogen status, water deficit and stand age of P. radiata have been studied by Beets and Whitehead (1996) and by Rodríguez et al. (2003).

Further developments in modelling are illustrated by more integral or process-based models of P. radiata. Photosynthesis, respiration, carbon allocation and net primary productivity algorithms have been developed for the species and existing models have been parameterized and tested under different site, management or climate scenarios. Sheriff et al. (1996) tested the climate effect on annual net carbon gain, stem biomass and annual transpiration with BIOMASS. Arneth et al. (1998) modelled net ecosystem productivity and carbon allocation with a biochemically based and environmentally constrained model. Kirschbaum (1999) parameterized and tested the model CenW. The model realistically simulated water use, foliage production and turn-over, foliar nitrogen dynamics, wood production and stand architecture (not tree architecture) across a wide range of responses under variable water and nitrogen supply in controlled experimental conditions and natural variations in rainfall. Sands et al. (2000) parameterized the model PROMOD. The model focuses on stand growth following canopy closure and predicts closed-canopy leaf area index, annual biomass production and stand water use. The model was calibrated to predict peak mean annual stem-volume increment of a plantation following canopy closure, and is used in combination with a conventional empirical model to predict stand development (Sands et al., 2000). In general terms, it is a practical model for productivity assessment. Magnani et al. (2004) parameterized and tested the model HYDRALL which give rise to stand-level results in terms of biomass production and biomass allocation between compartments.

On a broader scale, basic process-based models such as 3PG have been used to predict P. radiata growth at a landscape scale using satellite data as input (Coops, 1999).

In summary, a large number of models and related information is already available for radiata pine. But, as far as we are aware, no functional–structural model specifically developed for P. radiata, or parameterized for P. radiata, has been developed. The detailed information necessary for this required a better understanding and a more comprehensive view of the species to incorporate more physiological and structural relationships that underlie the development and growth of the tree. Our basic aim here was to provide a connection between tree biomass production, tree architecture (branches and knots) and wood ring characteristics to establish a practical link between the forest and industry. The present functional–structural model has been elaborated, implemented and validated in order to relate the environmental and management conditions of plantations to final industrial products through their influence on tree growth and architecture, wood density and number, position and size of knots.

METHODS

Description of the model

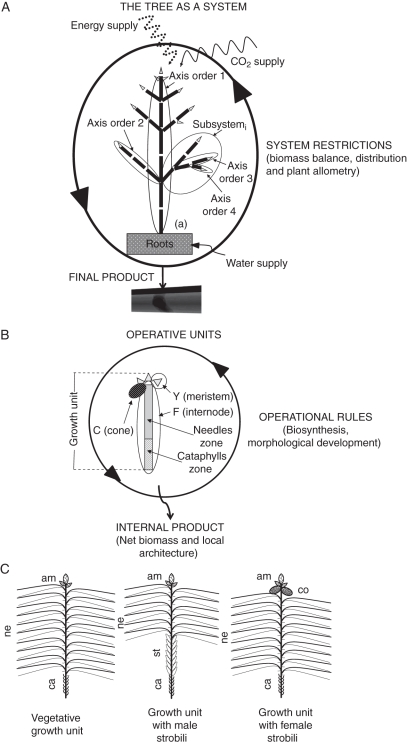
This is a single-tree model (Figs 1 and 2) composed of productive or operative units connected to one another so that fluxes of raw materials and metabolites take place among them. Each unit obeys operational rules, as in a cellular automata system. The raw materials are water, minerals from the soil and atmospheric CO₂. Energy sources are solar radiation, air temperature and wind momentum. Tree system activity is regulated by, and subjected to, constraints that lead to balanced growth. The productive units are organized so as to comply with the peculiar architecture of the species and perform three main tasks: (1) determining the morphological changes of the tree (apical meristems); (2) generating metabolites (photosynthesis) necessary for growth and respiration and maintenance of structures (internodes with needles); and (3) consuming metabolites in respiration and growth (cones, roots and internodes with and without needles). The balance between photosynthesis and consumption is distributed among the different structures of the system.

Fig. 1.

Model structure. (A) The tree is a productive system, comprising operative units organized in axes that consist of subsystems starting from a branching point. Roots are treated as a single entity. The whole system receives energy and supplies for its functioning. System restrictions such as biomass balance, distribution and plant allometry ensure a harmonic growth. (B) Operative units consist of apical meristems, internodes and cones; each operative unit obeys its operational rules and generates internal products as net biomass and local architecture. (C) P. radiata presents three types of growth units: a vegetative growth unit with cataphylls zone (ca), needles zone (ne) and lateral and terminal vegetative meristems (am); a growth unit with male strobili (st) in the zone between cataphylls (ca) and needles (ne); and a growth unit with female strobili (co) as modified branches in the lateral meristems.

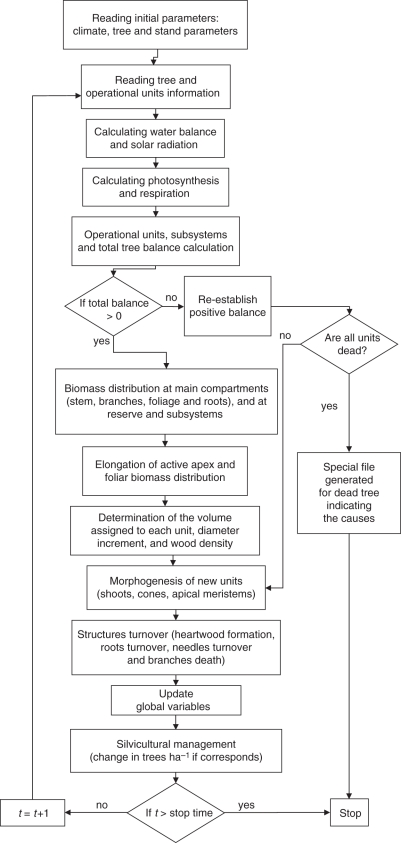
Fig. 2.

Main flowchart of the model.

The onset of flowering, quiescence, senescence and death of structures are modulated through time, leading to the overall expression of growth and development of the tree. The general constraints of the system are: (1) distribution of net biomass production is such that a balance among producers, consumers and supporting structures is maintained, and (2) there are limits to the size structures may attain so that the architecture and the allometry of the species are satisfied. The simulation has a monthly step. The growth of the tree is monitored through a monthly feedback evaluation of the conditions of every operating unit. These time lapses produce monthly increments in stem and branch diameter (ring width) that lead to intra-annual ring variations. Different processes are addressed in the simulation through sub-models (Fig. 2).

Model programming

The model uses the Lindenmayer system, which produces three-dimensional (3-D) images of plant development and growth (Prusinkiewicz and Lindenmayer, 1990). All routines, including the L-Systems rotation matrix, were programmed in Basic using Visual Studio (Release 2008; Microsoft), generating topological, morphological and physiological characteristics of each operating unit. The subsets of topological and morphological outputs are visualized in Autocad (Release 10; Autodesk, San Rafael, CA, USA) by means of the Autolisp programming language. Insertion points of branches maintain their original positions, and therefore they become knots inside the stem. At the end of a simulation run a virtual sawing of the wood reveals the pattern of rings and the presence and character of knots. Operating units are hierarchically organized and permit access to a multi-scale level of information.

Variables and parameters units

If not indicated, units of variables and parameters are: length, cm; surface area, cm²; volume, cm³; weight, g; time, months; temperature, °C; precipitation and evapotranspiration, mm; radiation, cal cm² min⁻¹; wind speed, m s⁻¹; biomass, g dry matter; balances, g CO₂ month⁻¹; photosynthetic and respiration rate, g CO₂ cm⁻² min⁻¹; resistance to the flux of carbon dioxide, min cm⁻¹; specific leaf area, cm² (g dry matter)⁻¹; and nitrogen content, g N (g dry matter)⁻¹.

Attributes of operational units

Four operational units are defined: apical meristems (Y) for each branch order, cones (C), internodes (F) and roots (R). The first three structures and their state variables are identified with subscripts ijt (i.e. F_ijt), i indicating order of axis and j an ordinal number to indicate that it is the jth unit of order i, present at time t. In the remaining text these subscripts are shown only if necessary. An internode is the part of a shoot free of branches or lateral structures, and normally produced during one growing flush. A growth unit is an internode and the upper lateral structures such as branches, cones and/or meristems (this upper part of the growth unit is normally called the cluster or whorl in forestry terms). All the structures are characterized by hierarchical, morphological, physiological and topological attributes. Common attributes are: order (o), 1 being the main axis, 2 being branches stemming from the latter, etc.; age (a_ge) and month they come about (m); age of heartwood (a_geh, in months); p, indicating whether they are dead or alive; and elongation (e) indicating whether the internode is in a primary growing condition or only in a secondary growth. The canopy is divided into 20-cm strata, so an attribute s identifies the canopy stratum into which the operational unit is located, based on its z point at the middle of the unit. The apical meristem (Y) has an initial diameter (d), which is also the initial diameter of internodes. As P. radiata branches appear in clusters with acrotony (Pont, 2001), a relative vigour attribute (v_g) (0 to 1) is assigned to every apical meristem relative to the others in the same cluster. The same relative value is maintained by the corresponding branch for biomass allocation. The morphology of the internode (F) is defined by its diameter (d), total length (l), the diameter of heartwood (d_h), length of the sterile zone of cataphylls at the base of the internode (l_c), length covered by needles (l_n), total foliar area (f), projected leaf area (f_p), total cross-section area (a) and total volume (v). The diameter of heartwood (d_h) is related to heartwood cross-section area (a_h) and heartwood volume (v_h). The variables a, v and v_h can be calculated from d, l and d_h. The difference between total cross-section area and heartwood cross-section area is the sapwood cross-section area or conductive area (a_s). Sapwood volume (v_s) is the difference between total volume and heartwood volume.

Other morphological traits refer to variables of standing biomass. Distinctions are made between living (and respiring) and non-living biomass for calculation of total balance. Attributes of biomass are total structural biomass (b_t), sapwood biomass (b_s), functional and respiring biomass as a fraction of sapwood biomass (b_a), heartwood biomass (b_h) and foliar biomass (b_f). The attributes B_f, B_a and B_t are, respectively, the sum of leaf, live woody biomass (structural biomass) and total structural biomass on all internodes supported by and including F. Width and wood density of monthly rings are r and δ, respectively. Another variable of the internode is s_ii, the Surface Interception Index of the unit. This is the projected surface area of the internode itself plus the projected surface area of its foliage. It is used to compute solar radiation extinction in the canopy, which is affected not only by foliage but also by branches. Once photosynthesis (p_h) and respiration (r_p) in every internode are computed their balance is evaluated (b_al). Every internode also has a cumulative balance of all structures borne by it (B_al).

Cones (C) or female strobili are modified branches. Therefore, they develop along with branches in the cluster, typically in a low position thereon. In P. radiata they are only order 2 and 3, being attached to the main stem or to branches of order 2. Once a cone is differentiated, it grows continuously until it reaches maturity after 36 months (Griffin, 1982) and dies. Morphological attributes of cones are also diameter (d), length (l) and structural biomass (b_c).

The root system is described as a single overall unit, only in terms of a living biomass attribute (B_R). Attributes are summarized in the Appendix, Table A1.

Environmental resources

Environmental variables are incorporated and evaluated through a water balance and water restriction factor and solar radiation sub-models. Detailed models are presented in the Supplementary Data (available online).

Biosynthesis and biomass balance

Biosynthesis is obtained by photosynthesis and respiration models that are detailed in the Supplementary Data.

Biomass distribution and growth

Sub-models in this module distribute the available matter to growing leaves and non-leaf structures among various subsystems and units within subsystems. Then, elongation of units, needle development and increase in diameter are computed.

Biomass distribution

If a positive balance is achieved the surplus biomass is distributed among four main compartments: trunk plus bark, branches, foliage and roots, as dictated by allometric relationships. Research indicates that allometric values may vary with time, environment and management (Madgwick et al., 1977; Beets and Whitehead, 1996; Ryan et al., 1996; Arneth et al., 1998; Rodríguez et al., 2003; Muñoz et al., 2005). However, a distinction should be made between live and dead biomass, especially in adult trees. The trunk of trees accumulates wood, part of which progressively becomes heartwood. So, the biomass of the trunk of older trees becomes an increasing proportion of the total biomass of the entire tree and the ratio of trunk biomass to biomass of other structures progressively widens. In this model it is living, and not total biomass that is considered in allometric relationships among of the four compartments. Sapwood is the main water-transporting tissue for leaves, so sapwood biomass is used for biomass allocation computations. Cone biomass is included in branch biomass because cones are considered to be modified branches. Also, structural changes take place at different growth stages because of leaf decay, root turnover, branch elimination, death of part of the tissues in the trunk and branches (heartwood), or loss of structures due to pruning. It is therefore necessary to keep track of the state of equilibrium among the various compartments. If not in balance, biomass is first allocated so as to restore it, after which it is allocated to growth of compartments.

The distribution pattern of photosynthates follows Kozlowski and Pallardy (1997): (1) a tree is an integrated system of consumers and producers competing for a common pool of metabolites; (2) transport occurs without restrictions to direction or distance; (3) the route and rate of translocation are regulated by the strength of sinks; (4) the demand of upper apical meristems is stronger than lower apical meristems; (5) fruits or cones are powerful consumers and often monopolize resources and may inhibit vegetative development if resources are limited; (6) in pine species that grow practically year-round, a large proportion of carbohydrates are used for axis elongation; (7) clusters in the upper part of conifers are the main source of photosynthates for cambial growth (diameter expansion) and consequently diameter increment is relatively larger in the crown zone than further down the trunk; and (8) lower branches of widely spaced trees are an important source of photosynthates for the lower part of the tree. As lower branches become progressively shaded, their capacity to provide carbohydrates to the trunk diminishes. This means that a low branch gradually changes from a net producer to a net consumer. This circumstance is considered in the overall balance at the branch level.

Distribution of metabolites to the four compartments (foliage, stem, branches and roots) begins by first checking the ongoing proportions of each one to the total functional biomass of the tree at time t. The compartments are: B_F, total foliar biomass; B_SA, total living sapwood biomass of stem; B_BA, total living sapwood biomass of branches; and B_R, total living root biomass. These proportions are compared with the expected allometric values (p_f, p_sa, p_ba, p_r) corresponding to the proportion of foliar, stem, branch and root living biomass, respectively. If they are not satisfied, part of total tree balance B_AL is distributed so as to match them. Once the proportionality of the four compartments is restored, the remaining balance B_AL is then distributed between the compartments to generate new growth, and thus the balance designated to foliage will be B_{AL_F} = B_AL· p_f, to stem B_{AL_S} = B_AL· p_sa, to branches B_{AL_B} = B_AL· p_ba, and to roots B_{AL_R} = B_AL· p_r. Foliar biomass is held by stems or branches, so if no biomass is available for these latter structures and only for leaves, the foliar biomass is retained in the reserve pool.

Structural biomass distribution in subsystem levels

The assignment of structural biomass to branches (B_{AL_B}) is done in successive cycles, first allotting the total available amount to branches of order 2. Cones have priority and they are the first recipients, according to Kozlowski and Pallardy (1997). According to Griffin (1982) a cone is assumed to attain a given final biomass (b_c) at maturity when it is 30 months old. Therefore, every month a growing cone will receive a fraction b_c/30. The same rate is applied to length and diameter expansion.

Once cone demands are met the remaining matter available to branches is distributed under the conditions set by Kozlowski and Pallardy (1997). A Biomass Distribution Index (B_DI) was developed to assign due quantities to branches of order 2. This index establishes a relative capacity of branches to incorporate biomass. The Biomass Distribution Index of the subsystem of basal unit F, is

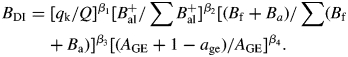(1)

The first term of eqn (1) is the ratio of solar radiation incident on the terminal meristem of the branch ij, q_k, to the solar radiation incident upon the tree crown, Q. It is assumed that this ratio relates directly to growth hormone activity, thus stimulating a corresponding demand of biomass for the growing branch.

The second term of eqn (1) is the ratio of the branch balance to the sum of balances of all branches competing for the same supply. This procedure favours delivery of resources to the most productive branches in the system. Some branches may end up with negative balance. In this case, all the cumulative balances of branches are made positive by adding the absolute value of the largest negative value. This yields a temporary positive B_al⁺ for each order 2 branch, permitting its use in eqn (1). Thus,

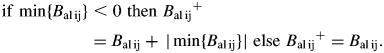(2)

The third term of eqn (1) is the ratio of the live biomass (foliar B_f and structural living wood B_a) of an order 2 branch to the sum of biomass of the same variable of all branches of order 2. This concept states that larger living branches have priority as recipients. A larger size, if accompanied by a positive balance, is interpreted as a greater capacity of the branch to occupy a larger space and therefore to expose itself to more sunlight. So, branches of similar age with meristems of similar exposure to sunlight will obey the relative vigour values in any given cluster.

The fourth term of eqn (1) relates the age of the branch a_ge (equivalent to the age of the supporting internode) to the age of the whole tree, A_GE. It assumes that young branches that have only a small positive balance are nevertheless benefited with a biomass supply to make up for this natural initial low productivity. Exponents β₁, β₂, β₃ and β₄ are relative weighting parameters.

Total net balance for branches (B_{AL_B}) is distributed in a given branch (B_{al_b}) according to

(3)

Following the same procedure, B_{al_b} of a branch of order 2 is distributed among its branches of order 3, and so on.

Proportion of structural biomass used in elongation and in diameter increment

Prior operations will have assigned separate amounts of biomass to the axis and its ramifications. The computed overall biomass available for growth in each subsystem (stem or branches) is split between elongation and diameter expansion. Studies by Fielding (1960), Pawsey (1964), Cremer (1973), Doran (1974), Jackson et al. (1976) and Tennent (1986) indicate that: (1) height increment anticipates that of diameter, and declines before the diameter does; and that (2) the pattern of growth is influenced more by environmental conditions than by a genetic command for a dormant period, so that the tree stem can increase in height and diameter during any time of the year if conditions are favourable.

To simulate allotment of biomass destined to relative increases in length and diameter of stem and branches, it is assumed that the proportion between them follows the seasonal cycle of solar radiation:

(4)

where p_diam is the proportion of available biomass used in diametric expansion and p_elong is the proportion employed in elongation. The coefficient α_d adjusts the equation to ensure a minimum amount to diameter increment. The variables Q_min and Q_max correspond to the upper and lower limit of the solar radiation of the locality under study. So, annual solar radiation will oscillate between these limits. Thus, the proportions of biomass allotted to the stem to be used in elongation (B_{AL_S_e}) and in diameter increment (B_{AL_S_d}) are:

(5)

In the same way, the proportion of biomass allotted to a certain branch (B_{al_b}) of any order is partitioned for elongation (B_{al_b_e}) and for diameter increment (B_{al_b_d}).

Elongation growth in active apex

After the distribution of growth to every axis (of order 1, 2, 3 and 4) for elongation has been established, a growing cylinder with an initial diameter of the apical meristem (d_m) is generated with such a length as to create the volume to accommodate the allotted biomass. This requires the definition of an initial pith density (δ_p), usually around 0·3 g cm⁻³. Thus, the new elongation is

(6)

where B_{al_b_e} (or B_{AL_S_e} for the stem) is the allotted balance for elongation of a particular branch of order i, α_cb is a conversion factor of g CO₂ to g dry matter and l is length.

Foliar biomass distribution to new elongated structures

After computing elongation of units F, a value Δl will have been generated in every elongating unit, so that total foliar biomass available to the tree, ΔB_F = B_{AL_F}·α_cb, is distributed among all those structures. Every unit length of elongated structure is capable of sustaining a certain amount of leaf biomass according to its order and is given by the parameter b_fcm, leaf biomass per unit length of order i (eqn 7):

(7)

where f_cm is foliar area per unit of length of the corresponding axis, S_LA is specific leaf area, n_a is needle area, n_n is needle number per fascicle (particular case for conifers) and n_fas is number of fascicles per unit length. Following Grace (1987) we assume that the fascicle is a tube made up (in the particular case of P. radiata) of three equal sections, and thus the needle area n_a is

(8)

where n_d is needle diameter and n_l is needle length. An allometric relationship between needle length and diameter was derived from Beets (1977). As needle length is easier to measure, the relationship permits the estimation of needle diameter:

(9)

A relative value was considered, between needle length of order 2, 3 and 4 in relation to needle length of order 1. Thus, n_li = n_l1·ζ_i, where ζ_i is a scaling factor with value less or equal to one. So, assigning in each step (via a stochastic Monte-Carlo process) a value of needle length to needles of order 1, needles of order 2, 3 and 4 are assigned length, diameter and area. Also, the number of fascicles per unit length (n_fas) is different for the different axis orders. So, a relative value of n_fas for the different orders in relation to needles of order 1 is also used. Thus, n_fasi = n_fas1·η_i, where η_i is a scaling factor (0–1). Therefore, the required leaf biomass demand (B_{F_dem}) at the tree level and assuming total coverage of elongated surface is given by

(10)

Where available leaf biomass is larger than demand, the new leaf biomass of unit ij (Δb_f) will cover the whole of the new elongated stem giving rise to only a needle zone (Δl_n). By contrast, when leaf demand is not completely satisfied by available biomass to completely cover the elongated axis, a partial needle zone (Δl_n) and a cataphylls zone (Δl_c) are created. If leaf biomass production exceeds demand the excess is placed in the reserve pool.

Structural biomass distribution for ring growth

The structural biomass employed every month in diameter increase is spread as a cylindrical mantle forming the annual growth ring. The width and density of this mantle is not uniform, as it has to comply with water, mineral and metabolite transport properties to satisfy leaf biomass demands (Mäkelä, 2002), which vary throughout the tree and individual branches. This condition poses three problems: (1) How much biomass to deliver to individual growth so that as a whole they form the wood mantle around the trunk or branches. (2) Once this is resolved, which is the new conducting area necessary to satisfy transport requirements? And (3) what is the density of the new wood matter?

Let B_t be the total size (in terms of living biomass) of the above-ground portion of the tree at time t and B_max the maximum size it may attain during its whole life period. Assuming the operation of the general law of growth (Lotka, 1956) the rate of increase in size in a given time period will be proportional to the actual size times the degree of increase that it can still attain, thus

(11)

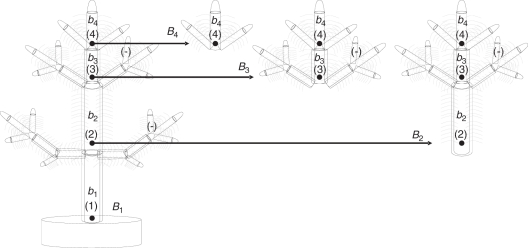
where ΔB′t is the potential biomass (if available) that the tree should increase during Δt, and α_B is a proportionality constant. On integration this statement gives rise to the logistic growth curve (Salisbury and Ross, 1992). Let b₁, b₂, b₃ and b₄ be the sizes, in terms of live leaf and non-leaf biomass, of internodes 1, 2, 3 and 4, respectively (with b_i = b_fi + b_ai) (Fig. 3); let B₁ be the live leaf and non-leaf total cumulative biomass from internode 1 upwards, i.e. the sum of all biomass of units supported by F₁ and B₂, B₃ and B₄ cumulative biomass over F₂, F₃ and F₄, respectively. Then, following the same law of growth, but at partial levels of the tree:

(12)

The value of Δb′_nt can be considered as the potential biomass that the structure should receive. The amount of biomass available for diameter increment at time t, ΔB_{S_d} = B_{AL_S_d}·α_cb, with B_{AL_S_d} (corresponding to the balance available for diameter growth in the stem and α_cb the conversion factor from g CO₂ units to g dry matter units), is not sufficient for the demand of all the structures. In this case the real biomass that each unit n will receive, Δb_nt, corresponds to the proportion of its demand and the sum of the demands of all the units in the corresponding axis. Thus,

(13)

Fig. 3.

Sketch of live foliar and structural biomass of growth units of the tree (b₁, b₂, b₃, b₄) on a given axis and total live biomass accumulated from each unit upwards (B₁, B₂, B₃, B₄). The biomass assigned to a certain growth unit i is the difference between the biomass assigned to B_i and the biomass assigned to B_(i+1).

Diameter increment and wood density

Once the allocation of structural biomass for growth ring formation in every internode has been determined the next question to resolve is the resulting density of wood and the width it will attain. This new monthly ring is related to the new cross-section that will participate in the transport of water and minerals.

The available biomass to be deposited in internode F is used as a basis to determine the width and density of the new growth ring assuming that there is an allometric relationship between leaf biomass (water-demanding structure) and the cross-sectional area that contributes to that biomass (Mäkelä, 2002). Also, it is assumed that the density of wood is negatively correlated with the conductive property of the cross-sectional area (Santiago et al., 2004; Bucci et al., 2004). Considering both conditions, the relevant allometric relationship occurs between the whole leaf biomass alive at time t (old and new needles) and the effective conducting area of the section (i.e. the sections of active cell lumen), corresponding to older rings and the new monthly ring under construction.

As primary growth precedes secondary growth, determination of the area needed for transport is based on total leaf biomass, i.e. the existing leaf biomass plus the newly generated one. Let A_t be the total active conductive cross-sectional area of wood (sapwood area) of internode F. This area comprises an effectively conducting area A_fluxt and an area of solid wood A_wt (cell walls). Then,

(14)

An allometric relationship is assumed to exist between the effective conducting area and leaf biomass (B_ft) above this area:

(15)

where ω₁ is a scaling coefficient and ω₂ a scaling exponent (parameters). Likewise, the total area is made up of an old area (A_t–1) and an increment during time t (ΔA_t); similarly, the woody area (A_wt) is made up of an old area (A_w(t-1)) and a new increment during same time t (ΔA_wt).Thus, the increment in total area is

(16)

(17)

An alternative expression can be derived for the area of solid wood (cell walls, A_wt) based on the volume of solid wood (V_wt) of the internode, the length of the internode (l_t), the biomass of solid sapwood wood (b_st) and its density, i.e. wall cell density (δ_w), which is about 1·53 g cm⁻³ (Domec and Gartner, 2002). Thus

(18)

Therefore, the increase of the total cross-sectional area is

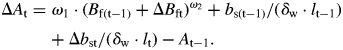(19)

The increase in total volume of the internode (ΔV_t) is

(20)

and the basic density of wood (dry matter/fresh volume, δ_t) for the recently formed monthly wood ring is

(21)

The model does not define a priori the newly formed wood as earlywood or latewood. The resulting annual ring density profile based on the monthly rings can be analysed to determine the limit between early and latewood.

Morphological development

There is a change from the juvenile phase to the mature phase of the tree, the threshold of which is recognized by the onset of the first female flower and is accompanied by changes in the stem architecture (Barthélémy et al., 1997; Fernández et al., 2007). Fernández et al. (2007) showed that the transition in P. radiata takes place when a critical number (n_br = 89) of order 2 branches had been reached. This observation has been incorporated in the model. Also, the transition from juvenile to mature state causes the value of certain parameters to change, as explained below.

Signals for the generation of a new growth unit

There is ample evidence in the field of agronomy (Chang, 1968; Faust, 1968) that the generation and the time of development of organs are closely related to heat or temperature accumulation. Our analysis of data provided by Bollmann and Sweet (1976) also suggests an influence of temperature, and eventually also of photoperiodism on P. radiata organogenesis. We used the concept of chron (γ) or physiological day as the unit of plant development within a given range of temperatures, and of tautochron (τ) as the total sum of physiological days required to complete the phase of development (Norero, 1987). We used Norero's proposal of a general Gomperz-type of equation for the phenological response of plants to temperature. This function requires two parameters for cardinal temperatures, a minimum value (φ_min) below which there is no reaction to temperature and an optimal value (φ_opt) at which the reaction attains is fastest rate. Accumulation of physiological time of development driven by environmental temperature is express as γ. Based on architectural data analysis of the species in different environments (Fernández, 2008) a variation was introduced, so that thermal accumulation is gradually limited by water deficit or drastically modified by high temperature stress. Thus,

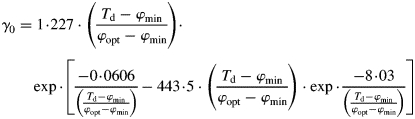(22)

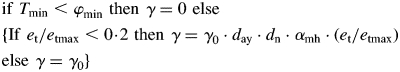where e_t/e_tmax is a water deficit factor (see Suplementary Data for details), d_ay is day duration, d_n is the number of days per month and α_mh is conversion factor of minutes to hours. Then, f(γ) is the accumulation of physiological time as f(γ) = ∑γ. An apical meristem remains inactive as long as f(γ) < τ. When the thermal accumulation exceeds the tautochron value, f(γ) ≥ τ the apical meristem starts generating a new ensemble of lateral and terminal meristems that later elongate to become new internodes. Once the process to create a new internode has been triggered at time t, the accumulation of physiological days for each particular meristem continues according to f(γ)_t+1 = f(γ)_t – τ so as to deduct the chrons involved in the generation of the previous meristem ensemble.

Once an internode has been generated, it begins its own thermal accumulation f(γ). The elongation of the internode ends when the accumulation exceeds the critical value τ_stop = α_stop·τ, with α_stop being larger or smaller than 1. Values larger than 1 generate a simultaneous enlargement of growth units in a given axis, giving rise to a generally smoother growth curve.

The value of tautochron of axis of order 1 is different during the juvenile (τ_j = τ_j1) and reproductive (τ_m = τ_m1) stages of development (Appendix, Table A2). Also, values of tautochron for branches of order 2, 3 and 4 are proportional to the values of the order 1 axis, thus for orders 2, 3 and 4, τ_j = τ_j1·σ_j and τ_m = τ_m1·σ_m, with σ_j = 1·5, 1·8 and 2·0 for orders 2, 3 and 4, respectively, and σ_m = 2 for all the orders. These gradients mean that axes of order 1 and 2 have greater possibilities of exhibiting policyclism than axes of order 3 or 4.

Number of lateral meristems and differentiation of reproductive structures

The number of lateral meristems generated is probably under strong genetic command. The eventual success of these meristems to become branches, cones or continue in an inactive state or even die out depends on environmental conditions. An average value of lateral structures of vegetative growth units or units that bear cones are used (λ) to feed a Poisson simulation procedure; λ_t is the total number of structures (cones and branches) in flowering clusters, λ_v is the number of vegetative structures in vegetative clusters and λ_c is the number of cones in flowering clusters. Cone production is only possible in a cluster originated from order 1 or order 2 meristems. Also, cone production is possible only if the tree has reached maturity, i.e. if the transitional limit of branch number n_br has been reached. Based on data of Bollmann and Sweet (1976), a critical day length (c_l) was established as an environmental signal to stimulate the differentiation of a meristem into a cone, when a new cluster is formed. Thus, the polycyclic pattern of P. radiata with vegetative and reproductive clusters (Fielding, 1960; Bannister, 1962; Bollmann and Sweet, 1976) can be simulated.

Phyllotaxis and size relationships of branches in a cluster

Branches of P. radiata that develop into clusters normally show acrotony (Barthélémy et al., 1997; Pont, 2001), i.e. the vigour of the first branch to appear in a cluster is lowest and increases progressively to the largest value in the last branch. To incorporate this phenomenon in the model, each lateral meristem in a new cluster receives a relative vigour value (υ, 0–1), corresponding to its ratio in relation to the largest meristem in the cluster (with value 1). The relative vigour of lateral meristems in the cluster is characterized by a Markov chain of first order (Guédon, 1997) whose states are: state 1 (E₁, υ [1, 0·8)), state 2 (E₂, υ [0·8, 0·6)), state 3 (E₃, υ [0·6, 0·4)), state 4 (E₄, υ [0·4, 0·2)) and state 5 (E₅, υ [0·2, 0·0)). The transition matrix is defined as the probabilities p_ij of changing from state E_i to state E_j subject to the condition that p_ij = 0 if i > j, as meristems are ranked from larger to smaller sizes. Therefore, starting with the distal branch 1 with υ = 1, the transition matrix indicates the probability that the following branch will have the same or a lower vigour, and so on. These relative acrotonic indices are used to distribute available biomass to growing branches in a new cluster. An example of a transition matrix for a cluster of n = 6 lateral structures can be seen in the supplementary material.

The diameter of the largest meristem of order i in the cluster is given an initial value proportional to the size of the meristem of order (i – 1) from which it sprang, and thus for each meristem of order i Y_i d_i = α_YY· d_i-1 with α_YY [0,1]. In the same way, every apical meristem as it evolves according to the sequential enlargement of its axis will have a diameter proportional to the preceding internode F, i.e. d_Y/d_F = α_YF, d_Y being the meristem diameter and d_F the supporting internode diameter.

An angle of ω = 137·5 is used to obtain a spiral phyllotactic pattern (Prusinkiewicz and Lindenmayer, 1990), and an angle α_ins is used for the insertion angle between contiguous axes.

Structural turnover: heartwood formation

As growth rings age they undergo a gradual process leading to the formation of heartwood (Bamber and Burley, 1983). Heartwood formation was calculated by assuming a linear relationship between cambium age of the internode and the number of rings of heartwood, according to Gjerdrum (2005): a_geh = c_h1·a_ge + c_h2 where a_geh is age of heartwood and a_ge is the age of the internode (also cambial age). Successive internodes on a given axis are of different age, the lowermost ones being the oldest, so a heartwood gradient becomes manifest.

Needle turnover

A logistic function was elaborated to describe the probability of needles in a given internode being alive (π_a). This depends on the age of needles (a_ge) and on their position or depth in the crown (H_tree – H_Fi, in cm), related to the degree of shading of leaves. The latter is the difference between the height of the tree (H_tree) and the height at which the internode of order 1 bearing the subsystem of branches under analysis is located (H_Fi). The logistic model is

(23)

Coefficient values for the different axis orders are given in the supplemmentary material.

When needles die a proportion of their biomass (α_T) is redistributed in the system and held as a global reserve. If the whole internode disappears because the bearing branch is eliminated a certain amount of leaf biomass is also translocated to the trunk.

Turnover of roots

To maintain a reasonable root–shoot ratio of the species (Evans, 1975) it is assumed that a reduction of root biomass is concurrent with the reduction of leaf biomass. The model does not consider variations in the root to shoot ratio, as determined by Magnani et al. (2002) or Mokany et al. (2006). This will be an important aspect to include in the future.

Branch elimination: self-pruning

Dead branches are commonly observed in shaded zones of the canopy of trees of densely populated stands or within exuberant crowns of individual trees. A compensation procedure to eliminate branches when the general balance of the tree is negative was presented. However, vigorous trees that may never run into negative balances may also exhibit a natural decay of branches that become inactive in the overall metabolic system. To simulate an elimination process of branches of order 2, branches that simultaneously exceed an age limit (m_lim) and a given number of months with consecutive negative balances (m_neg) (parameter) are eliminated, i.e. when they have become systematically inefficient to the system (but excluding young branches from this elimination process), in spite of their initial, low productive efficiency.

DATABASES

Most input parameters for the model were obtained from three original databases.

Database 1. This is a tree crown architecture database of 188 individuals, 5–6, 15–16 and 23 years old, from four different geographical and environmental conditions in Chile (Fernández and Norero, 2006; Fernández et al., 2007; Fernández, 2008). Two contrasting sites were used for validation purposes: Los Alamos, with a site index value of 34 (height when 20 years old) almost without water deficit, and La Granja, with a site index of 27, frequently exposed to water deficit stress in low-fertility soils. Sampling design and methodology followed Barthélémy et al. (2002) and Fernández et al. (2004). Relevant measured parameters were tree height, diameter at breast height (dbh), length and base diameter of every growth unit, number of branches per growth unit, cones and lateral meristems per cluster, diameter and length of lateral branches, length of zone with needles and length of cataphylls or sterile zone of internodes, length of the needles in all four axis orders, annual ring widths measured at the basal discs, and discs of growth units at different heights.

Database 2. This consists of magnetic resonance images of 21 fresh discs of ten different trees of different sites, ages and heights scanned and analysed with a 0·5-T MRI (General Electric) at the Centro de Imágenes Biomédicas at the Pontificia Universidad Católica de Chile. Images were obtained according to a proton density protocol suited for detecting water in wood (Morales et al., 2004) to detect contrast in internal structures. This database was used for heartwood formation analysis.

Database 3. This consists of values for the number of needle fascicles per linear centimetre of all order branches randomly taken from five 6-year-old trees of P. radiata from a plantation in the Region VI of Chile.

DEFINITION OF INPUT PARAMETERS

Table A2 (see Appendix) lists the parameters of the model, the values used for simulation and their sources. If derived from databases, the average, standard deviation, sample size and confidence interval at 95 % level are also given. If values are taken from the literature, the range when available is also indicated.

SIMULATION AND VALIDATION PROCEDURE

Modelling starting conditions

The model starts operations with a 1-year-old seed tree in the field, i.e. 21 months post-germination (including 9 months at the nursery plus 12 months in the field). The characteristics of this tree are measured values of a 1-year-old plantation: height 65 cm, basal diameter 0·6 cm, two growth units of order 1, and stem, branch, leaf and root biomass of 4·7, 1·2, 5 and 5 g dry matter, respectively, and corresponds to an average tree in the stand. Time intervals are monthly steps. Month number 1 is July, assuming that the biological year starts at the winter solstice (June 21 in the southern hemisphere). Initial stand density was 1100 trees ha⁻¹.

Due to memory restrictions, runs were limited to age 81 months (9 months in the nursery plus 72 months in the field, 6 × 12 months). Hereafter we give years from planting, as it is usually used in the forestry sector; i.e. when trees are referred as 6 years old, this means 6 years after plantation plus 9 months in the nursery (81 months). Graph axes notation includes the 9 months in the nursery. Graphical representation does not show needles.

To validate the model two different environmental conditions were evaluated, as represented by the Los Alamos and La Granja sites. And 80 % of the database from those sites was used for parameter acquisition [tautochron, needle length and number of lateral units (i.e. branches and cones) per growth unit] and 20 % was set apart for the validation process. The validation process compares the output variables of the model (tree height and diameter, growth unit lengths, and basal diameter of branches of order 2) with the same variables in the validation dataset. Actual data for local climatic and soil conditions corresponding to the real growth period of stands were used. According to Cochran (1980), optimal sample size calculation and a prior sampling variance (assuming a 20 % error), a total of 14 runs for the Los Alamos and 11 runs for La Granja were performed.

A comparison was made between three different stand initial densities (400, 1100 and 1800 trees ha⁻¹). Only the growth curves were compared.

Statistical analysis

Mean, standard error, and minimum and maximum values were computed for statistical evaluation of the simulated and validation results. Wilcoxon's rank sum test was applied to compare mean values and the Kolmogorov–Smirnov adjustment fitness test was used to determine if both results belong to the same distribution. Comparisons of time series of height and diameter were performed by using the Kolmogorov–Smirnov non-parametric adjustment fitness test, as suggested by Barrales et al. (2004).

RESULTS

As the model was built mainly on physiological and morphological functions, simulated values were checked against known forest inventory data, with crown architecture data related to wood quality, internode length and basal diameter of branches of order 2.

Table 1 presents a comparison of average values of height and basal diameter (without bark) between simulation and actual measurements in two sites.

Table 1.

Average values for the total height and basal diameter without bark of 6-year-old trees of the simulations and validation samples in two contrasting sites.

	Good site: Los Alamos		Regular site: La Granja
	Simulation results	Validation database	Simulation results	Validation database
Height (cm)
Mean (s.e.)	692·8 (25·9)	654·8 (29·9)	443·3 (21·8)	402·3 (27·7)
Sample size	14	4	11	4
Range	541·2–846·9	596–738	369·7–568·0	314·3–490·2
Basal diameter (cm)
Mean (s.e.)	15·7 (0·74)	12·5 (1·7)	18·2 (0·66)	14·5 (1·2)
Sample size	14	4	11	4
Range	12·7–23·2	7·8–15·6	15·4–22·6	12·1–17·5

According to Wilcoxon rank tests simulated and real diameter and height data were not significantly different at either Los Alamos (P = 0·505 and 0·157, respectively) or La Granja (P = 0·0264 and 0·279).

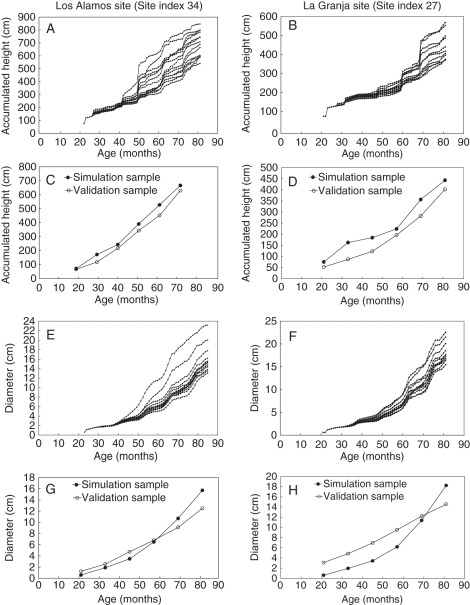
Figure 4(A, B) show the height evolution and Fig. 4(E, F) the diameter evolution of the simulated samples at the two sites. The growth spurts correspond to seasons of better growing conditions. As the trees form, the stochastic assignation of the number of branches per cluster produces divergences between the growth and development of the trees. A larger number of branches imply a larger crown, a greater photosynthetic capacity and a higher rate of growth. Evolution of the average values from the simulations is compared with the average values of the validation samples. These are shown in Fig. 4(C, D) for height and Fig. 4(G, H) for diameter.

Fig. 4.

Evolution of cumulated height and diameter at Los Alamos (A, E) and La Granja (B, F); average simulated height and data for Los Alamos (C) and La Granja (D), and simulated diameter and data for Los Alamos (G) and La Granja (H).

The evolution of height of simulated and experimental data for Los Alamos (Fig. 4C) is rather similar, with a slight overestimation of the simulated values. The evolution of simulated diameters (Fig. 4G) underestimates the real values over the first few years but tends to overestimate them later on. The Kolmogorov–Smirnov non-parametric adjustment fitness test (Barrales et al., 2004) of the series of data corresponding to t = 33, 45, 57, 69 and 81 months indicated that height and diameter were not significantly different (P = 0·99 in both cases).

At La Granja comparisons yielded similar results: the average value of height simulations overestimates database values (Fig. 4D). Simulated evolution of diameter underestimates the true diameter during the first few years but overestimates it later on (Fig. 4H). Nevertheless, the Kolmogorov–Smirnov non-parametric adjustment fitness for t = 33, 45, 57, 69 and 81 months (Fig. 4D, H) indicated that differences for height (P = 0·873) or for diameter evolution (P = 0·99) were not significant.

Table 2 presents the average values for growth unit lengths in the stem. The growth unit length includes the internode (F) length plus the length of the cluster of lateral structures.

Table 2.

Average values for growth unit length (cm) of order 1 at two sites

	Good Site: Los Alamos		Regular Site: La Granja
	Simulation results	Validation database	Simulation results	Validation database
Mean (s.e.)	57·3 (2·5)	54·1 (3·5)	40·3 (2·9)	45·2 (5·9)
Sample size	156	69	97	31
Range	13·3–172·9	14–166	4·6–167·2	10–127

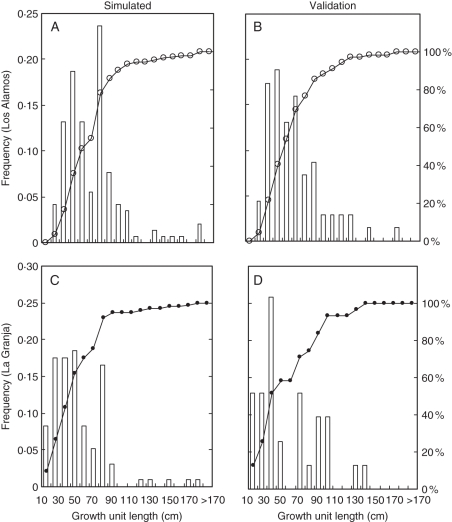
Comparison of averages for Los Alamos and La Granja (Wilcoxon rank sum test) indicated that there were no significant differences (P = 0·438 and 0·802, respectively) between growth unit lengths of the simulated and validation data. The Kolmogorov–Smirnov adjustment fitness test indicated that there were also no significant differences between simulated and validation set distributions (Fig. 5) for Los Alamos (P = 0·09) and for La Granja (P = 0·212).

Fig. 5.

Histograms of simulated growth unit length (cm) and of the validation data for Los Alamos (A and B, respectively) and for La Granja (C and D, respectively).

Basal diameter of order 2 branches

Knot size is relevant to timber quality, and consequently the basal diameter of order 2 branches is important to validate. A sub-sample of order 2 branches was taken from a database of 48-month-old trees at Los Alamos and compared with the order 2 branches of the 14 simulated trees at the same age (see Table 3).

Table 3.

Basal diameter (cm) of branches of order 2 in Los Alamos

	Simulation results (cm)	Validation database (cm)
Mean (s.e.)	1·87 (0·72)	1·2 (0·73)
Sample size	566	1669
Range	0·47–5·28	0·1–10

Mean diameter of branches differed significantly between simulated and real values (Wilcoxon rank sum test; P < 0·0001). Also, distributions differed at least in one point (Kolmogorov-Smirnov test, P < 0·0001). Therefore, the model overestimated the basal diameter of order 2 branches, and consequently the size of knots. There were no data series for the diameter of branches in 6-year-old trees at La Granja, so this comparison was not made.

Figure 6 presents different views of real and simulated 3-D structures of the species. A visual comparison of the two sites trees is also shown. The variable growth unit lengths, as in real trees, can be observed.

Fig. 6.

(A, B) Main apex and lateral branches; (C, D) detail of the main apex; (E, F) close-up of an order 2 branch apex; (G, H) whorl of branches; and (I) two simulated 5-year-old trees from La Granja (left) and from Los Alamos (right). Margins of branches are not shown.

Effect of initial density of stands

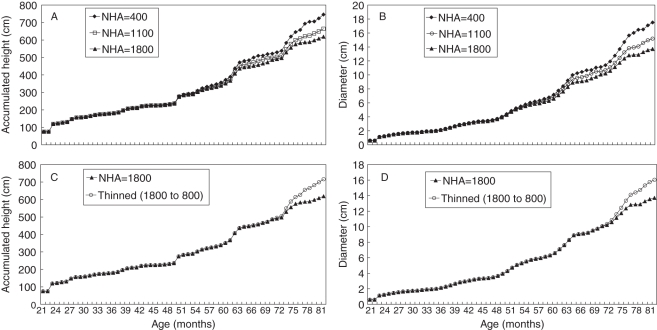
Figure 7(A) shows the evolution of simulated height and Fig. 7(B) of simulated diameter of an average tree growing under three different initial stand densities (400, 1100 and 1800 trees ha⁻¹). At 60 months the divergence of the curves illustrates the beginning of competition for supplies, particularly because of shading between the trees.

Fig. 7.

(A) Cumulative height and (B) diameter under initial stand densities of 400, 1100 and 1800 trees ha⁻¹ for an average tree. Effect of thinning at 5 years after planting on (C) height and (D) diameter; initial stand density was 1800 trees ha⁻¹ and after thinning was 800 trees ha⁻¹.

At both sites the model generated a tree whose height and diameter 6 years after planting were less at higher stand densities. The lower values at higher stand densities were probably due to competition for light and water as the predicted height and diameter were similar at all stocking until 52–54 months, approximately the time of canopy closure, a condition that significantly alters the solar radiation and water balance parameters.

To compare the behaviour of the model under thinning and non-thinning practices, the following simulation was made: initial plantation density was 1800 trees ha⁻¹ and thinning was performed after 5 years of planting (9 months nursery plus 5 × 12 months in the field = 69 months), decreasing the stand to 800 trees ha⁻¹. Figure 7(C) shows height evolution under the two situations and Fig. 7(D) for basal diameter without bark.

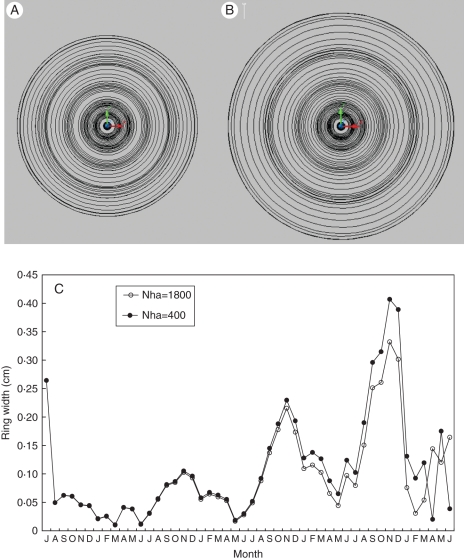
Figure 8(A, B) sketches monthly rings under high and low initial stand densities. Figure 8(C) reveals neat seasonal cycles. Narrower monthly rings are formed during less favourable growing periods.

Fig. 8.

Sketch of widths of monthly rings for a stand density of (A) 1800 trees ha⁻¹ and of (B) 400 trees ha⁻¹. (C) Monthly wood profiles showing ring width peaks and depressions.

Wood density

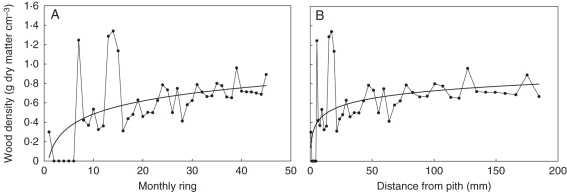
The density of the simulated timber could not be validated, as there were no suitable experimental data available. However, the expected behaviour of the simulated wood density was not quite fulfilled. In some growth units, wood density tended to increase (Fig. 9) from pith to bark, whereas in others it tended to decrease. Ranges of density values did not hold to expectations. Therefore, this part of the model needs to be reviewed.

Fig. 9.

Wood density profile in a growth unit 1·3 m high: (A) based on monthly rings, (B) based on distance from the pith (mm). Measured data and fitted curves are shown.

Visual evaluation of the resulting wood

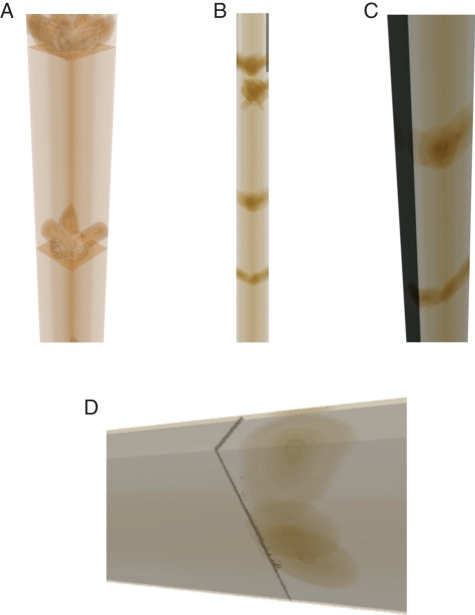
A central objective of this model was to relate tree development and growth to the quality of the timber. An advantage of 3-D models is that the resulting simulated timber can be virtually sawn and evaluated. Figure 10 shows a virtual slab and a series of 3-inch-thick planks from different points of view. The slabs are from virtual logs cut up to a useful diameter over or equal to 10 cm. The images of monthly thinner rings of branches (knots) contrast with the wider rings of stem wood.

Fig. 10.

Details of simulated slab and planks with knots. Fairly realistic monthly rings are observed.

DISCUSSION

The usual parameters of diameter and height of trees have been adequately simulated by the model when applied to quite different environmental conditions. This might imply that the assumed photosynthesis and respiration functions, the allocation rules of metabolite supplies and the allometric relationships are reasonably adequate to mimic the functioning of the tree. However, simulation runs were limited to trees up to 6 years old and it remains to be shown whether they hold for older trees.

Predicted growth unit lengths are also of interest. P. radiata typically produces long and short internodes in any given growing season depending on the prevailing environmental conditions. In the model this pattern is achieved as a result of a thermal accumulation command for initiation of units and of currently available metabolites (Fig. 5). Comparison of the distributions reveals close similarity. A considerable plasticity regarding this phenomenon is attained in the model by the simultaneous superposition of two or more growing internodes. The influence of temperature and water deficits in the thermal control of the rate of development is in line with factors involved in cellular expansion (Taiz and Zeiger, 2010). The present model structure allows for further refinements of the mechanisms of cellular extension and internode elongation incorporating known controlling factors (Vaganov et al., 2006; Hölttä et al., 2010).

The diameter of order 2 branches was overestimated by the model. One reason for this may be that the allometric function that relates foliar biomass to cross-section area of order 1 branches differs from order 2 (parameters ω₁ and ω₂). This is reasonable; although branches and trunks behave in a similar way they do not do so in an identical manner. Another reason may be that simulated branches continue vigorous growth longer than real branches and consequently they reach larger diameters.

In spite of some image imperfections and neglecting the absence of needles and the rigid representation of branches, the simulated 3-D evolution of the growth of trees were at both sites largely visually correct. Another logical outcome of the model was indicated by a better individual tree development under lower initial stand density and thinning conditions.

The monthly ring patterns shown in Fig. 7 matched the expected narrower rings in January, February and March as a result of less water availability and higher respiration rates. The same occurred during June and July, this time due to lower temperatures and to shorter days in the southern hemisphere. Interestingly, the model was able to generate the twin peaks pattern of diameter increment observed in P. radiata by Pawsey (1964), first during spring conditions and later at the beginning of autumn.

The simulation of wood density values of modelled logs was not satisfactory. Nevertheless, the changes in density were in line with changes in environmental conditions.

The relationship between foliar biomass and cell lumen sections needs to be improved, and efforts to this end are presently under way at our laboratory incorporating more refined approaches.

The simulated 3-D images of wood pieces produced under different environmental and management conditions are reasonably realistic and emphasize the potential of 3D modelling of L-Systems. This three-dimensionality allows for better description of radiation distribution in the crown and also for estimating the quality of the resulting timber. There are already cut-optimizers and log quality evaluator programs, such as WoodSim (VTT, Finland), to do this. These programs may be fed by modelled logs of variable size, internode length and knots, and can carry out virtual sawings for economical evaluation of the final wood products.

CONCLUSIONS

Pinus radiata is a forest species of complex development and high plasticity, and thus is a good species to evaluate the quality and plasticity of the model. The central objective of the functional–structural model elaborated for this tree species has in a gross sense generally been met, especially with respect to the usual diameter and height variables and wood quality variables. The results of simulations lend support to the idea that most model assumptions are acceptable and basically robust as they reflect general laws of plant development. Various applications of this model may be envisaged: as a virtual laboratory to evaluate relationships among species, site and management; to aid in silvicultural design and decision-making processes; as a tool in genetic improvement programmes of clonal silviculture to analyse the potential behaviour of different genetic lines according to the specific morphological and physiological parameters of genetic dependence; and to evaluate the probable quality of the wood produced under various environmental and management conditions and consequently strengthening the links between forest practices and industrial processes.

At present the model generates an average tree of a stand. A more realistic approach would be to extend model capabilities to generate a stand of many different trees, a common situation in commercial P. radiata plantations. However, it seems likely that large forest companies will work with clonal material that will diminish considerably intra-population variability. Under that scenario research could be directed to the characterization and measurement of model parameters of potential genotypes of productive interest.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and give full details of the models used in relation to environmental resources, and biosynthesis and biomass balance.

APPENDIX

Table A1.

Hierarchical, morphological, physiological and topological attributes of apical meristems (Y), internodes (F), cones (C) and roots (R)

Attribute	Meaning	Units	Value
Hierarchical attributes
o	Axis order of Y, F and C	integer	1, 2, 3, 4
Morphological attributes
d	Total diameter of Y, F and C	cm
l	Total length of the Y, F and C	cm
lc	Length with cataphylls in F	cm
ln	Length of the F covered with needles	cm
a	Total cross-section area of F	cm2
v	Total volume of F	cm3
dp	Diameter of pith of F	cm
dh	Diameter of heartwood section of F	cm
ah	Heartwood cross-section area of F	cm2
vh	Total heartwood volume of F	cm3
as	Sapwood cross-section area of F	cm2
vs	Sapwood total volume of F	cm3
f	Total foliar area of F	cm2
fp	Total projected foliar area of F	cm2
sii	Surface Interseption Index calculated for the unit Fij	adimensional
bt	Total structural biomass of F	g dry matter
bs	Sapwood or conductive biomass of F	g dry matter
ba	Functional and respiring structural biomass as a fraction of bs of F	g dry matter
bh	Heartwood biomass of F	g dry matter
bf	Foliar biomass in F	g dry matter
bc	Cone biomass	g dry matter
Bf	Sum of all foliar biomass on all internodes supported by and including F	g dry matter
Ba	Total structural functional biomass on all internodes supported and including F	g dry matter
Bt	Total structural biomass (functional and non-functional) supported and including F	g dry matter
BF	Total foliar biomass of the tree	g dry matter
BSA	Total living sapwood biomass of the stem	g dry matter
BBA	Total living sapwood biomass of branches	g dry matter
BR	Total living root biomass	g dry matter
r	Monthly ring width of F	cm
δ	Monthly ring density of F	g cm−3
vg	Vigour of Y when the cluster is generated	adimensional	0–1
Physiological attributes
age	Age of Y, F and C	months	Correlative between years
m	Month of creation of Y, F and C	months	Integer, correlative between years
p	Living state of Y, F and C	adimensional	0 if dead, 1 if alive
e	Elongation signal for F indicating if it is in primary growth or only in secondary growth stage	adimensional	0 if not elongating, 1 if elongating
τ	Thermophysiological function at Y for a new growth unit generation	adimensional
ageh	Heartwood age of Fij at time t	months
ph	Photosynthesis of foliar structures of F	g CO2 month−1
rp	Respiration of foliar and structural biomass of F	g CO2 month−1
bal	Photosynthesis and respiration balance of F	g CO2 month−1
Bal	Photosynthesis and respiration balance of all of the structures supported and including F	g CO2 month−1
AGE	Age of the whole tree	months
BAL	Photosynthetic and respiration balance at tree level	g CO2 month−1
BAL_F	Portion of the total balance destined to foliage	g CO2 month−1
BAL_S	Portion of the total balance destined to stem	g CO2 month−1
BAL_B	Portion of the total balance destined to branches	g CO2 month−1
BAL_R	Portion of the total balance destined to roots	g CO2 month−1
Topological attributes
(x1, y1, z1)	3-D basal point	cm
(x2, y2, z2)	3-D distal position	cm
s	Position in the kth foliage stratum	integer	k = 1 to n

Table A2.

Parameters of the model

Type of atribute*	Name	Meaning	Units	Value	Confidence interval (95 %)	Source	Value at validation process	Equations†
E	K	Extinction coefficient of radiation (Beer's law)	adimensional	0·5		Jarvis et al. (1976)	0·5	(S3), (S6), (S8)
E	cv	Vegetation coverage coefficient	adimensional	1·05		Pedrero (2005)	1·05	(S5)
P	αp, αS	Plant and soil albedo	adimensional	0·15; 0·1			0·15; 0·1	(S8)
E	θ	Carbon dioxide concentration in the air		6·5 × 10−7			6·5 × 10−7	(S9)
P	q10	Respiration factor (quotient between respiration at T °C and T – 10 °C)	adimensional	2–2·5		Ryan et al. (1996)	2·5	(S10) (S21) (S25)
P	rb	Basic respiration per nitrogen unit	g CO2 g N−1 h−1	0·2–0·23		Norero (1987), and derived from Dewar (1996)	0·23	(S22)
M	SLA	Specific leaf area (ratio between total foliar area and foliar biomass)	cm2 g−1	62·5–600		McMurtrie et al. (1992), Walcroft et al. (1997), Warren and Adams (2000), Rodríguez et al. (2003), De Lucia et al. (2003)	300	(S12) (S16)
P	fn0	Proportion of foliar N on needles	g N (g dry matter)−1	0·0128		Adapted from Ryan et al. (1996)	0·0128	(S13)
M	SLAP	Specific leaf area based on projected leaf area	cm2 g−1	19·9–191		McMurtrie et al. (1992),Walcroft et al. (1997), Warren and Adams (2000), Rodríguez et al. (2003), De Lucia et al. (2003)	95·5	(S14)
M	psa	Proportion of functional stem biomass on the total (in g CO2)	adimensional	0·39–0·67		After several authors	0·35
M	pba	Proportion of functional branches biomass on the total (in g CO2)	adimensional	0·09–0·27		After several authors	0·43
M	pf	Proportion of functional foliage biomass on the total (in g CO2)	adimensional	0·04–0·15		After several authors	0·08
M	pr	Proportion of functional roots biomass on the total (in g CO2)	adimensional	0·20–0·23		After several authors	0·14
M	bc	Final biomass of a female cone	g dry matter	191·2 (59·4), n = 25	167·9–214·5	C. Gantz, Forestal MININCO, Chile, pers. comm.	191·2
P	β1	First exponent related to radiation in BDI (Biomass Distribution Index)	adimensional			Iterated	4	(1)
P	β2	Second exponent in BDI related to balance	adimensional			Iterated	0·3	(1)
P	β3	Third exponent in BDI related to accumulated biomass	adimensional				0·01	(1)
P	β4	Fourth exponent in BDI related to branch age	adimensional				0·1	(1)
P	αd	Coefficient in model of elongation/diameter ratio	adimensional	(0–1)			0·4	(4)
M	nfas1	Fascicle number per unit of length (cm) for order i = 1	integer	5·2 (1·57), n = 12	4·2–6·19	Database 3 analysis	6	(7)
M	nl1	Needles length for order i = 1	cm	13·7 (2·57), n = 148	13·28–14·11	Database 1 analysis	13·7	(8)
M	nn	Needles number per fascicle		3		Standard value for the species	3	(8,9)
M	ςi	Factor of proportionality between needles length	adimensional	(0–1)		Database 1 analysis	0·8; 0·65; 0·43 for order 2, 3 and 4, respectively
M	ηi	Factor of proportionality between number of fascicles per linear cm	adimensional	(0–1)		Database 3 analysis	1·25; 1·50; 1·73 for order 2, 3 and 4, respectively
M	αB	Proportionality constant	adimensional	(0–1)			1	(11)
M	Bmax	Maximum total living biomass reached by an adult tree	g	72 400		Deduced after several authors	72 400	(11)
	αcb	Conversion factor from g CO2 to g dry matter	g dry matter g−1 CO2	0·54 for wood; 0·61 for foliage			0·54; 0·61
P	ω1	Scaling coefficient for stem section area calculation	adimensional			Estimated	0·16	(15)
P	ω2	Scaling exponent for stem section area calculation	adimensional			Estimated	0·9	(15)
M	δw	Cell wall density	g cm−3	1·53		Domec and Gartner (2002)	1·53	(18, 19)
M	nbr	Critical cumulative number of branches produced on the stem necessary to change from juvenile to mature state		89·8 (29·3), n = 20	76·09–103·51	Fernández et al. (2007)	89
P	φmin	Cardinal minimum temperature for chron accumulation	°C	0		Deduced after Jackson and Gifford (1974), Booth and Saunders (1979), Hunter and Gibson (1984)	0	(22)
P	φopt	Cardinal optimal temperature for chron accumulation	°C	23·3		Deduced after Jackson and Gifford (1974), Booth and Sanders (1979), Hunter and Gibson (1984)	23·3	(22)
	αmh	Conversion factor from min to h	h min−1	1/60		Calculated
P	τj	Critical tautochron value for a new growth unit generation during juvenile phase for order 1	adimensional	1425·40 (300), n = 32	1317·23–1533·56	Database 1 analysis	1425·4
P	τm	Critical tautochron value for a new growth unit generation during mature phase for order 1	adimensional	785·65 (240·4), n = 32	699·02–872·37	Database 1 analysis	785·7
P	αstop	Coefficient in tautochron function for internode elongation ending	adimensional	Real, non-negative		Iterated	2·2
P	σj	Coefficient of proportionality between τj of order 1 and order 2, 3 and 4	adimensional			Estimated	1·5; 1·8; 2 for order 2, 3 and 4 respectively
P	σm	Coefficient of proportionality between τm of order 1 and order 2, 3 and 4	adimensional			Estimated	2, for order 2, 3 and 4
M	λt1	Average of total lateral structures in a cluster of order 1	adimensional	7·8 (2·23), n = 755	7·64–7·95	Database 1 analysis	7·8
M	λt2	Average of total lateral structures in a cluster of order 2	adimensional	5·91 (2·33), n = 243	5·61–6·20	Database 1 analysis	5·91
M	λv1	Average of lateral structures in a vegetative cluster of order 1	adimensional	6·26 (2·15), n = 2712	6·18–6·34	Database 1 analysis	6·26
M	λv2	Average of lateral structures in a vegetative cluster of order 2	adimensional	4·18 (2·10), n = 5286	4·12–4·23	Database 1 analysis	4·18
M	λv3	Average of lateral structures in a vegetative cluster of order 3	adimensional	2·09 (1·10), n = 1604	2·04–2·14	Database 1 analysis	2·09
M	λc1	Average of floral lateral structures (cones) in a floral cluster of order 1	adimensional	3·18 (1·57), n = 755	3·07–3·29	Database 1 analysis	3·18
M	λc2	Average of floral lateral structures (cones) in a floral cluster of order 2	adimensional	2·56 (1·52), n = 243	2·37–2·75	Database 1 analysis	2·56
P	cl	Critical day length	min	660		Deduced after Bollmann and Sweet (1976)	660
M	αYY	Coefficient of proportionality between meristems	adimensional	(0–1)			0·8
M	αYF	Coefficient of proportionality between an apical meristem and the supporting internode	adimensional	0·79 (0·12), n = 964	0·78–0·80	Database 1 analysis	0·79
M	ω	Phyllotactic angle	radians	2·400351		Corresponding to the golden angle (137·5 °)	2·400351
M	αins	Bending angle in branches	radians	0·785398			0·785398
P	ch1, ch2	Regression coefficients for heartwood age estimation	adimensional			Database 2 analysis	0·2636; –4·5731
P	μ1, μ2,μ3	Coefficients of logistic regression for needles turnover				Database 1 analysis		(23)
P	αT	Coefficient of biomass translocation	adimensional			A. Norero, unpubl.	0·25
P	mlim	Age mortality limit	months				36
P	mneg	Limit of number of consecutive months with negative balance	months				8
P	φemin	Critical minimal temperature for enzymatic activity (carboxylation)	°C	–15		Norero (1987)	–15	(S20)
P	φe	Critical optimal temperature for enzymatic activity (carboxylation)	°C	25		Norero (1987)	25	(S20)
	ε	Coefficient to transform from min to h or from s to min		1/60				(S22)
E	u20	Wind speed at 20 m height	m s−1	5		After A. Norero (unpubl.)	5	(S19)

* E, environmental parameter; M, morphological parameter, P, physiological parameter.

^† S, Supplementary Data, available online.