Simulating the grazing of a white clover 3-D virtual sward canopy and the balance between bite mass and light capture by the residual sward

Abstract

Background and Aims

The productivity and stability of grazed grassland rely on dynamic interactions between the sward and the animal. The descriptions of the sward canopies by standard 2-D representations in studies of animal–sward interactions at the bite scale need to be improved to account for the effect of local canopy heterogeneity on bite size and regrowth ability. The aim of this study was to assess a methodology of 3-D digitized canopies in order to understand the balance between bite mass and light interception by the residual sward.

Methods

3-D canopy structures of four white clover swards were recorded using a POLHEMUS electromagnetic digitizer and adapted software (POL95). Plant components were removed after digitizing to determine aerial dry matter. Virtual canopies were synthesized and then used to derive canopy geometrical parameters, to compute directional interception and to calculate bite mass. The bit masses of cattle and sheep were simulated according to their form, depth and placement on the patch, taking account of explicit sward architecture. The resulting light interception efficiency (LIE) of each organ was then calculated using a projective method applied to the virtual residual sward. This process enabled an evaluation of light interception based on Beer's law at the bite scale.

Key Results

The patterns of the vertical profiles of LAI appeared as bimodal, triangular or skewed parabolic functions. For a single bite of similar area and depth, the lowest mass was observed with half-spherical form and the highest for the cylindrical form, whatever the initial sward structure. The differences between the actual LIE and that calculated by Beer's law were marked for residual swards shorter than 8 cm. Bite mass and LIE values after grazing were more strongly affected by the initial structure of the sward than by bite form and placement.

Conclusions

3-D digitizing techniques enabled a definition of the geometry of each component in sward canopies and an accurate description of their vertical and horizontal heterogeneities. The discrepancy between Beer's law results and actual light interception was reduced when the sward regrew rapidly and if the rest period was long. Studies on the biting process would greatly benefit from this method as a framework to formulate and test hypotheses in a quantitative manner.

INTRODUCTION

The productivity and stability of grazed grassland rely on dynamic interactions between the sward and the animal. The quantity and quality of herbage removed by herbivores or cutting are strongly dependent on sward structure, and these defoliation processes determine in turn the residual architecture, which influences plant regrowth. A grazed sward is heterogeneous in both its horizontal and vertical planes. This heterogeneity is scale-dependent, displaying small grazing patterns at the bite level and large-scale grazing patterns at the canopy level (Rossignol et al., 2011). In order to analyse the dynamics of the grazed system, it is necessary to obtain a clearer understanding of plant–animal interactions at the different scales (Hodgson and Illius, 1996).

Grazing choices by a foraging animal are made at the bite level (Demment and Laca, 1993). Various bite-oriented models of herbivore–plant interactions relating the instantaneous or daily dry matter intake of animals to bite masses are available for the study of foraging strategies and depletion processes by different grazers (Ungar et al., 1992; Baumont et al., 2004; van der Graaf et al., 2006; Edouard et al., 2009). Some of these approaches link herbage consumption with herbage growth (Schwinning and Parsons, 1999; Hutchings and Gordon, 2001; Brereton et al., 2005)

Two important problems encountered when modelling animal–plant interactions concern a description of the vegetation resource (Hodgson and Da Silva, 2000) and the difference in conceptualization between the bite process and plant growth. The grazing process is treated as a discrete and instantaneous event that generates a regrowth pattern specific to each bite taken, while plant growth is conceived as a continuous process at the field scale (Parsons and Dumont, 2003). The canopy structure is therefore considered as the interface between the grazing and regrowth processes. Bite form and bite placement are highly sensitive to local sward structure (Demment and Laca, 1993), and the residual structure determines the light interception ability of the grazed site. However, sward structure is more frequently condensed into global attributes such as sward height and herbage mass (Palhano et al., 2007). An experimental determination of light interception at the bite scale is extremely difficult, and the assumptions on the size and spatial distribution of components within the sward are made to apply the Beer's law. These assumptions have often been observed at field scale for grassland (Warren Wilson, 1959; Turitzin, 1978; Nouvellon et al., 2000), but bias may be very considerable at a more detailed scale such as the bite scale.

A statistical two-dimensional description of sward structure is widely employed, even in the most sophisticated approaches (Woodward, 1998; Schulte and Lantinga, 2002). New techniques to determine 3-D structures and generate virtual plants or canopies have been developed (Sinoquet and Rivet, 1997) and applied to various species. Drouet et al. (2000) and Shibayama (2001) demonstrated the feasibility of these methods in the context of short forage canopies under field conditions.

The aim of the present study was to assess the use of a 3-D virtual canopy built from 3-D digitizing within a sward, and to simulate potential bite mass and the regrowth of the remaining sward at the same spatial scale, taking account of both vertical and horizontal heterogeneity. As an animal regulates its bite size more through bite depth than through bite area (Ungar, 1996), a constant bite area (equal to the digitized area) and different bite depths were thus assumed. The combination of such virtual plant canopies with a bite volume model and projective light model software (Adam et al., 2006) can enable the computation of potential bite mass and light interception (Sonohat et al., 2002) at the same bite scale. The assumption applied during this study was that a digitized area corresponded to one or more bites (depending on the size of the grazer), and that the plant material removed could be used to determine the dry matter of sward components.

A 3-D digitizing method was applied to field cropped white clover (Trifolium repens) in order to (a) relate the canopy structure to the balance between herbage intake and regrowth ability, (b) test the 3-D approach as a tool to assist with the modelling of bite volume and depletion and (c) assess the use of Beer's law to simulate residual light inception at a bite scale.

MATERIALS AND METHODS

Building of the virtual canopy

Two white clover (Trifolium repens L.) cultivars of different leaf size – ‘Rivendel’ (a small-leafed type) and ‘Aran’ (a large-leafed type) – were sown on 25 September 1998 at the Le Robillard experimental farm (Normandy, France; 48°59′N, 0°00′E). The soil here was 1 m deep calcosol, and the climate is of a moderate oceanic type. Plots 20 m² in size were sown using a seed drill with 0·17-m spacing. Two cutting frequencies at a height of 0·05 m were applied, corresponding to rest periods of 2 and 6 weeks (Simon et al., 2004); together with the two white clover cultivars this resulted in four different treatments. Based on these treatments, four canopies structures were selected and digitized on 29 June 1999: ‘Aran’ with a rest period of 6 weeks (S1), ‘Rivendel’ with a rest period of 2 weeks (S2), ‘Rivendel’ with a rest period of 6 weeks (S3) and ‘Aran’ with a rest period of 2 weeks (S4).

The 3-D canopy structure of the swards was recorded on small plots considered as feeding stations (bite sites) of 0·17 m × 0·10 m (A = 0·017 m²) centred on the row. A magnetic 3-D digitizer (3Space Fastrak; Polhemus, 1993) and POL95 software were used to digitize data acquisition on the plants (Adam, 1999). This device recorded the spatial co-ordinates of a pen-like sensor located in a magnetic field. The different plant components (leaflet, petiole, inflorescence and peduncle) were digitized independently and then cut after digitizing, as described by Rakocevic et al. (2000) and Sonohat et al. (2002). The organs were digitized from the top to the bottom of the canopy and then removed immediately after digitizing. For each inflorescence, four points were digitized: the distal end of the peduncle, the central point of the upper surface and the two widest points on the sides. A lamina was described from a sequential recording of ten points that included the intersection of the three petiolules, the distal tips of the leaflet midrib and the more distal points of each half-leaflet. To describe the petioles and peduncles, two to 20 points were recorded along the same generating line, depending on their length and curvature.

Plant organs were reconstructed using simple elemental geometric primitives. Two quarter-ellipses for the distal part, and two triangles for the proximal part, represented each leaflet. The petioles and peduncles were assimilated to a series of cylinders with a diameter set to their mean value. An inflorescence was considered as a sphere with a diameter set to a mean value calculated from the four points of all inflorescences on the digitized area. Details of the sward reconstruction are given in Rakocevic et al. (2000).

Structure characterization

The sward height (H_S) was approximated as the z co-ordinate of the highest leaflet within the digitized structure, and the soil level as the average height of the upper part of the stolons (these organs were digitized but the data are not shown). The area of each half leaflet was computed as the sum of the areas of its distal quarter ellipse and its proximal triangle. The area of each petiole or peduncle was computed as its half-developed area (Chen and Black, 1992). The sum of the areas of all the elements in each component (leaflet, petiole, etc.) within the digitized sward was divided by plot area (A) to calculate the area index (m² m⁻²): LAI, PetAI and TAI for, respectively, the leaflet, petiole and plant area indices.

The orientation (i.e. normal inclination and azimuth) of each half leaflet and each petiole were computed from the direction cosines of their normal (Rakocevic et al., 2000). Angle distributions were described by angle classes of each element weighted by its area. The inclination functions were discretized in nine classes of 10°, and azimuth functions in eight classes of 45°. These parameters (area index, angles, etc.) were calculated for the entire digitized structure in horizontal layers that were 0·02 m deep to obtain vertical profiles. In the further sections, these horizontal layers are referred to as ‘grazing strata’. The calculations were applied to residual structures with a different residual height H_R, obtained from virtual grazing of the virtual swards at different bite depths.

The plant material that was clipped during the digitizing procedure was separated into the components defined above. No dead material was contained within these young swards. Leaflet area was measured using an electronic leaf area meter (Li-Cor 3100; Li-Cor., Lincoln, NE, USA) and the lengths of petioles, peduncles and stolons were measured with a ruler. Their diameters were measured with a caliper rule. All fractions of the plant material were dried for 48 h at 80 °C and then weighed. The leaflet mass area ratio (m² kg⁻¹) and petiole mass length ratio (m kg⁻¹) were calculated and used to determine the dry matter (DM) of each component within the structure. Herbage mass (kg DM) was obtained from the sum of the DM of all components within the digitized volume above the basal area (A). Bulk density (BD) was expressed in kg DM m⁻³ and calculated as the ratio between DM and the sward volume (A × H_S). Bulk density was calculated for each 0·02 m horizontal layer at all residual sward heights (H_R).

Computing bite mass and light interception

The potential mass of the bite (BM, kg DM) was derived from the virtual sward image (Fig. 1) and herbage mass as an idealized rectangular bite volume defined by the product of a virtual bite depth (D) and the constant digitized surface area (0·017 m²). This area was of the same order as the reported values for the bite area of cattle, 0·012–0·022 m² (Ungar et al., 2001). The potential BM within the grazed strata during a virtual vertical depletion of a homogeneous feeding station was estimated using the concepts developed by Ungar et al. (1992). The potential BM of different grazing strata was simulated assuming that the depth of each grazing horizon was a constant fraction of the initial sward height. This fraction was taken to be 0·30, similar to the results of Milne et al. (1982) for sheep, and 0·50 which is the ‘take-half’ approximation of Ungar and Ravid (1999) for cattle. The number of grazing strata was limited to a residual height of 0·03 m. This H_R was considered as limiting for grazing by cattle and is a usual value applied in continuous grazing management (Ginnett et al., 1999).

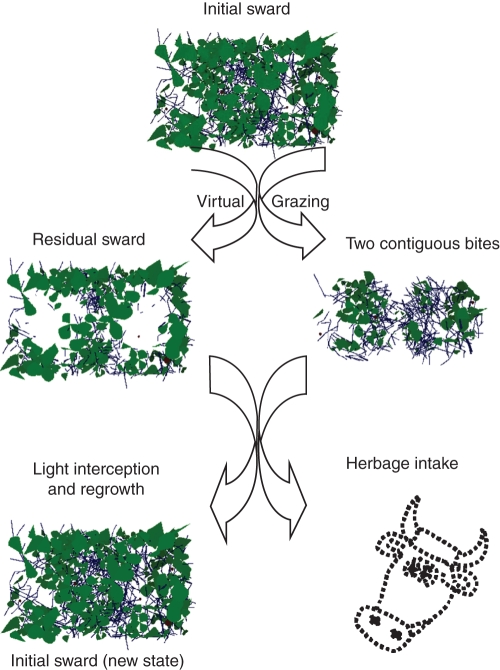
Fig. 1.

Illustration of the virtual grazing. From an initial sward canopy virtual bite is processed (contiguous bites) and light interception by the residual sward canopy is calculated.

Further simulations were run with a fixed bite area but differing in terms of bite volumes: a cylinder with a flat bottom (cylindrical bite), a half sphere (‘bowl shaped’ bite), and a rectangular bite. The cross-sectional area on the surface of the grazed strata gave the bite area, which was chosen to be equal to 50·26 × 10⁻⁴ m² (corresponding to a radius of 0·04 m for the cylindrical and half spherical bites) or 0·08 by 0·0628 m (for the rectangular bite). The bite depth was the radius of the half sphere (0·04 m), similar for the three types of bite. The BM and light interception efficiency (LIE_tot) were computed after virtual grazing on the canopy of the S1 and S4 plots with a 0·08-m-high virtual residual sward. The determination of each sward element within a given bite was derived from a geometric rule applied to the virtual canopy, and calculation of the biomass from the sum of the DM of all components within the bite volume. For each type of bite, these calculations were applied to a bite centred on the middle of the upper surface of the scene. Simulations were also made of discontinuous or contiguous bites and those with a 5 % area overlap of the placement of successive bites. An illustration of this approach is shown in Fig.1 with respect to contiguous bites.

The VegeSTAR graphic software (Adam et al., 2006) was used to visualize 3-D digitized canopies and then compute directional light interception from image processing of the virtual sward picture (Sinoquet et al., 1998). Daily light interception efficiency (LIE, defined as the fraction of incident radiation intercepted by the sward) was computed by integrating 17 directional values. These values corresponded to a sample of 17 directions of the sky vault weighted according to the radiance distribution of overcast sky, as described by Sonohat et al. (2002). Each individual scene can be duplicated several times to simulate larger areas to take account of border effects in the LIE calculation. Virtual areas 0·6 m² in size were generated. Light interception was computed for the whole canopy, and for each type of organ (a) within the whole canopy and (b) separately, i.e. when the other components had been removed virtually.

The relationships between the LIE calculated using the projective method and area indexes (LAI and TAI) were fitted to a negative exponential curve to derive an apparent extinction coefficient. Leaf-angle distribution was used to compute the average projection coefficient of plant area onto the soil surface, i.e. the extinction coefficient of the canopy assuming that phyto-elements are randomly distributed (Ross, 1981). As a result, the foliage dispersion parameter μ was calculated for each scene as the ratio between the apparent extinction coefficient derived from LIE_tot values and the average projection coefficient computed from the inclination distribution (see details in Sonohat et al., 2002).

Statistical analysis

Tukey's test (at a postulated statistical significance of P < 0·05) and regression were computed using SAS statistical procedures.

RESULTS

Initial characteristics of the structures used in the simulation

The four digitized structures differed in terms of sward height, herbage mass, bulk density and area indexes (Table 1). The relative contribution of PetAI to TAI ranged from 0·2 to 0·4. Within each structure, half leaflet azimuths were distributed uniformly at the whole sward scale, and also within each horizontal layer or vertical slice (data not shown). The mean half leaflet inclination did not differ significantly between the situations (41°), while mean petiole inclination and mean leaflet area were significantly different (Table 1). The lowest values of petiole inclinations were found in the S1 that formed the highest mean leaflet area.

Table 1.

Main structure characteristics of the digitized sward canopies S1, S2, S3 and S4

	S1	S2	S3	S4
Sward height (HS, m)	0·22	0·12	0·26	0·12
Herbage mass (kg10−3 m−2)	205	106	312	182
Local sward bulk density (BD, kg10−3 m−3)	925	887	1185	1475
Plant area index* (TAI, m2 m−2)	3·69	2·82	5·66	4·63
Lamina (leaflets) area index LAI, m2 m−2)	2·46	2·23	3·51	3·16
All petioles and peduncles area index (PetAI, m2 m−2)	1·21	0·59	2·11	1·44
Mean leaflet area (m2 10−4)	1·92a†	1·26b	1·82a	0·82c
Mean half leaflet inclination (°)	47a	39a	39a	38a
All petioles mean inclination (°)	46c	60a	50b	57a

* TAI includes laminas, petioles, peduncles and flowers.

^† Values in the same line followed by different superscript letters are significantly different under Tukey's test at P < 0·05.

Vertical and horizontal structure characteristics of the sward canopies

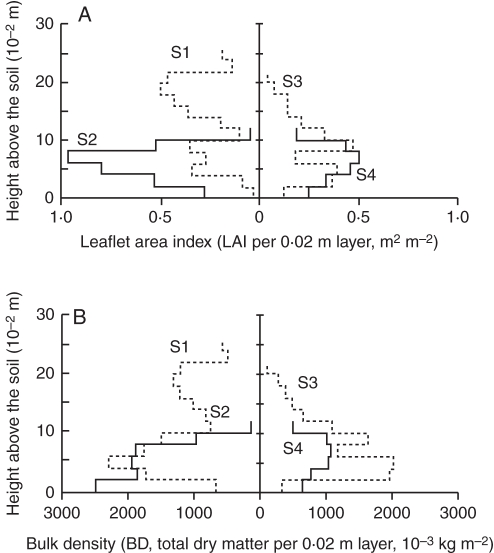
The vertical profiles of LAI and bulk density are presented in Fig. 2 (A and B, respectively). The patterns of the vertical profiles of LAI appeared as a bimodal function (S3), triangular function (S1) or skewed parabola (S2 and S4).

Fig. 2.

Vertical distribution of (A) leaflet area index (LAI, m² m⁻²) and (B) bulk density (BD, 10⁻³ kg DM m⁻³) per layer (0·02 m thick). S1 and S2 are shown on the right-hand side, while S3 and S4 are shown on the left, as indicated.

Potential bite mass estimated from virtual biting on 3-D virtual canopies

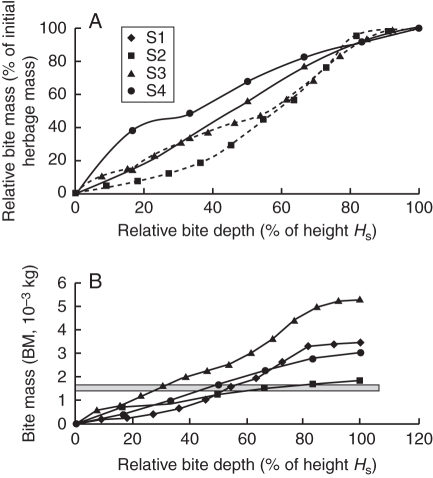
The bite mass within different grazing strata during vertical depletion is shown in Table 2. The number of grazing layers was two or three for cattle (i.e. depth of grazing strata of 50 % initial sward height) and ranged from three to six for sheep (i.e. depth of grazing strata of 30 % initial sward height), depending on the initial sward height. The BM ranged from 0·24 to 2·37 × 10⁻³ kg DM for grazing strata depths of between 0·130 m and 0·013 m. The highest BM was found in the first or second layer, depending on the canopy, the bulk density profile and stratum thickness. Bite mass relative to the initial herbage mass was not always at a similar proportion (i.e. 1/1), nor at a constant proportion of the bite depth relative to initial sward height (Fig. 3A). At 50 % relative bite depth, the relative bite mass ranged between 37 % and 68 %. Assuming a heterogeneous pasture with four types of patches investigated, a grazer might need to regulate its bite depth within the range 30–60 % of H_S to maintain a bite mass of 1·5 × 10⁻³ kg (Fig. 3B).

Table 2.

Vertical profile of the potential bite mass (BM) assuming grazing stratum thickness (GST) was (A) 50 %, or (B) 30 % of the sward canopy height (grazing was limited to 0·03 m)

	S1		S2		S3		S4
Grazing horizon	BM (10−3 kg)	GST (m)	BM (10−3 kg)	GST (m)	BM (10−3 kg)	GST (m)	BM (10−3 kg)	GST (m)
(A) Depth of grazing strata = 50 % HS
H1	1·28	0·110	2·37	0·130	1·24	0·060	1·67	0·060
H2	1·51	0·055	1·81	0·065	0·35	0·030	0·87	0·030
H3			0·88	0·032
(B) Depth of grazing strata = 30 % HS
H1	0·48	0·066	1·58	0·078	0·85	0·036	0·89	0·036
H2	0·86	0·046	0·83	0·055	0·40	0·025	0·81	0·025
H3	0·78	0·032	0·92	0·038	0·26	0·018	0·57	0·018
H4	0·74	0·023	0·97	0·027
H5	0·45	0·016	0·55	0·019
H6			0·24	0·013

Fig. 3.

(A) Relationship between relative bite mass and relative bite depth within the four sward canopies, and (B) bite mass as a function of relative bite depth. Canopy structures S1–S4 are as indicated in the key.

For a single bite of similar area and depth, the lowest mass was observed with the half-spherical form and the highest with the cylindrical form, whatever the initial sward structure (Table 3A). The lowest values obtained with a half-spherical bite resulted from the smaller volume removed. Whatever the bite form, the bite mass in the S4 sward canopy was always higher than in the S1 sward canopy. However, this no longer held true when several bites were investigated (Table 3B). For a given structure, the BM differences linked to placement remained quite small, despite the differences in the cumulated bite area (<5 % of overlap).

Table 3.

Potential bite mass, TAI of the residual sward canopy and LIE_tot after grazing for a single centred bite (0·005026 m² area and 0·04 m depth)

(A) Bite formt
	Rectangular bite	Cylindrical bite	Half-spherical bite
Structure S1
Bite mass (10−3 kg)	0·422	0·436	0·269
Residual TAI (m2 m−2)	0·966	0·952	1·124
LIEtot after grazing	0·452	0·445	0·507
Structure S4
Bite mass (10−3 kg)	0·430	0·497	0·336
Residual TAI (m2 m−2)	2·063	1·983	2·221
LIEtot after grazing	0·704	0·688	0·735
(B) Bite placement

	No grazing		Discontinuous		Contiguous		Overlapped
Sward structure	S1	S4	S1	S4	S1	S4	S1	S4
Residual DM (10−3 kg)	1·493	1·778	0·969	1·298	0·953	1·284	0·939	1·282
Mean bite mass (10−3 kg)	–	–	0·262	0·240	0·270	0·247	0·277	0·248
Residual TAI (m2 m−2)	1·391	2·743	0·844	1·983	0·830	1·942	0·816	1·955
LIEtot after grazing	0·586	0·826	0·410	0·669	0·405	0·637	0·397	0·652

The sward canopies analysed, S1 and S4, were previously defoliated at H_R = 0·08 m. In (A) there are three simulated bite geometries: rectangular, cylindrical and half-spherical. In (B) there are three simulated placements: discontinuous, contiguous and 5 % area overlapping.

Regrowth ability after virtual biting

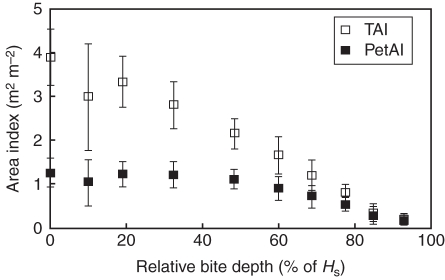
Residual TAI and PetAI values varied substantially in line with relative bite depth (Fig. 4). The LAI ranged from 1 to 1·7 after the grazing of 50 % of the H_S. For typical grazing heights of 0·08–0·03 m, the residual LAI decreased strongly and displayed marked variations between structures (data not shown). The orientation angles of remaining leaflets (inclination and azimuth distributions) were affected by neither sward height nor structure (data not shown). Petioles remained the main sward component as the height of the residual sward decreased. For example, at H_R = 0·05 m (corresponding to a relative bite depth of between 40 % and 80 %) the relative contribution of all petioles to TAI was between 0·40 and 0·75 (Fig. 4).

Fig. 4.

Total (TAI) and petiole (PetAI) area index as a function of relative bite depth. Mean values ± s.e. are presented for sward canopies.

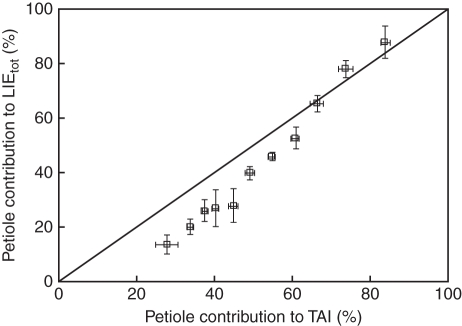
The light interception efficiency (LIE_tot) of the whole canopy was considerable, reaching 0·87 to 0·99. At a given H_R, LIE_tot varied markedly as a function of the situation; e.g. from 0·04 to 0·30 at H_R = 0·03 m (Fig. 5). The residual TAI (Fig. 5) mainly explained these variations. The contribution of petioles to the light intercepted by the whole canopy increased in line with bite depth, and consequently as H_R decreased (Fig. 4). Petiole interception was in the same proportion as their contribution to TAI, but only for the highest values of PetAI/TAI (Fig. 6).

Fig. 5.

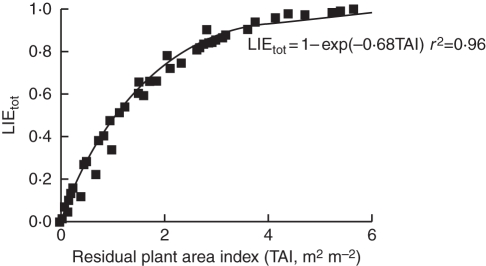
Whole-plant light interception efficiency (LIE_tot) as a function of the plant area index after grazing (TAI, m² m⁻²).

Fig. 6.

Relative contribution of petioles to LIE_tot and TAI. Mean values ± s.e. for sward canopies.

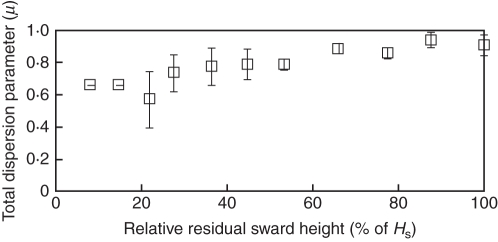
Regression analysis between TAI and LIE_tot (Fig. 5), including all the values fitted to a negative exponential, revealed an r² coefficient of 0·96 and an apparent extinction coefficient of 0·68. The discrepancy between LIE_tot calculated using Beer's law and LIE_tot computed with VegeSTAR was largely reliant on organ dispersion, as shown by the dispersion parameter μ (Fig. 7). Foliage was markedly clumped for H_R under 30 % of the initial height.

Fig. 7.

Foliage dispersion parameter (μ) as a function of relative residual sward height. Mean values ± s.e. for sward canopies.

For a single bite of a similar area and depth, the higher the residual TAI and LIE_tot, the lower the bite mass. When considering one or more simulated bites, residual TAI and LIE values were always higher in the S4 structure (Table 3). In all situations, the different placements did not lead to >5 % of variations in TAI or LIE_tot (Table 3B).

Balance between bite mass and residual light interception as a function of virtual bite depth

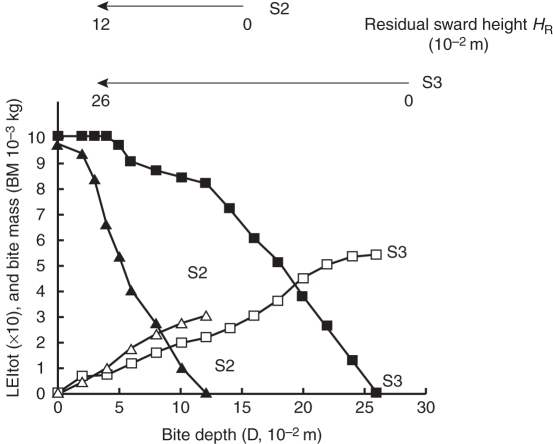
Fig. 8 represents the variations in bite mass and BM LIE_tot after grazing as a function of the residual sward height. In a low sward, LIE_tot decreased regularly with grazing depth. In a tall sward, LIE_tot decreased slightly in the first 12 cm and then fell regularly in line with bite depth. Removing the upper half of the sward increased intake from 1·24 to 2·37 × 10⁻³ kg BM (Fig. 8 and Table 2A) and the LIE_tot of the residual swards ranged from 0·45 to 0·85.

Fig. 8.

Whole-plant light interception efficiency (LIE_tot × 10; closed symbols) and bite mass (BM_, 10⁻³ kg; open symbols) as a function of bite depth D (10⁻² m) for S2 and S3, as indicated.

DISCUSSION

Simulation of the balance between bite mass and light interception

Simulated values for virtual bites showed a linear relationship between bite mass and surface sward height, as reported on white clover grazed by cattle for similar bite areas (Edwards et al., 1995). Moreover, although the mass values in the present experiment were calculated from virtual bites without animal measurements, they could be used to study the balance between herbage removal and regrowth ability.

The BM depends on the model used to characterize a virtual bite; i.e. bite depth and area. The mean bite depth of cattle ranged from 0·05 to 0·13 m as H_S varied between 0·1 and 0·30 m (Griffiths et al., 2003), which was the range of bite depth that was investigated during that study. The bite depth values that maintain 1·5 × 10⁻³ kg found in the present study are generally lower than those found in experiments with Italian ryegrasses (Barrett et al., 2003).

For a given grazer, bite area is less sensitive than bite depth to variations in sward structure but is not constant, as assumed in many grazing models. Variations in bite area have been related to sward height, and/or bulk density and/or biting force (e.g. Mitchell et al., 1991; Grifitths and Gordon, 2003). Bite depth can be considered as a constant fraction of the sward height for a given type of grazer (Ungar, 1996). The simulated data on BM under this hypothesis showed that the decrease in BM during depletion of a feeding site (Table 2) depended in part on the depth of grazed strata, with variations in bulk density between strata compensating more or less for the decrease in stratum depth, as shown by Ginnett et al. (1999). The proportionality concept between bite depth and sward height is only approximate, and a broad variability around mean values can be observed (Griffiths et al., 2003). A comparison of BM between the values shown in Table 2 illustrates the effect of these different proportionalities (30 % and 50 %).

Most experimental bite areas are average values of a number of bites, but they do not take account of any overlapping (Ungar and Griffiths, 2002) which can underestimate the actual area. As well as bite area and bite depth, the form of a bite recognized as being bowl-shaped (Ungar, 1996) may intervene. As shown in the present study, a bowl-shaped form systematically led to a smaller removed volume and bite mass. BM simulations from 3-D virtual canopies were based on the petiole and leaflet mass removed. These types of studies could also consider the biochemical characteristics of different components to simulate the nutritive and digestive qualities of the herbage removed at the same time.

Simulated LIE data in white clover were in accordance with reported values obtained in grazed swards (e.g. Rodriguez et al., 1999). The apparent extinction coefficient (K_a) deduced from fitting the simulated LIE_tot with TAI to a negative exponential curve (K_a = 0·68) was within the range 0·3–1·0 defined for white clover (Monteith, 1965; Nassiri, 1998). However, these experimental data resulted from measured transmitted PAR that took account of the light scattered by the sward components, and transmission calculated using the projective method corresponded strictly to intercepted light. The corrected K_a (0·61) was lower than the fitted value, which was in agreement with the overestimation of the projective method reported by Nouvellon et al. (2000). Typically, the experimental relationships reported in the literature only take account of LAI, whereas transmitted PAR is dependent on the light intercepted by all vegetation components. In the present study, the extinction coefficient calculated from the exponential fitting between LIE_tot and LAI was 1·03 rather than 0·68. As shown by the present data, the contribution of petioles to TAI explained a large share of the variations in the K values reported.

The four initial digitized sites were used to characterize the horizontal sward virtual heterogeneity, and the BM and LIE profiles in each situation were used to characterize its vertical virtual heterogeneity. Under the hypothesis of a grazer removing different proportions of the sward height, the BM varied 1- to 2-fold at 30 % and 1- to 3-fold at 70 %. The resulting LIE_tot varied in the same proportions. These biting scenarios caused the maintenance of horizontal heterogeneity similar to that seen initially. The sward could be grazed after mowing at a constant height to obtain a homogeneous canopy (at least in terms of surface height). Assuming this initial height to be 0·08 m, and applying a bite with a constant depth (50 % H_R), the horizontal heterogeneity of the regrown sward could be very important because the LIE_tot after grazing was highly variable (between 0·10 and 0·60). Farmers currently measure sward height to monitor herbage growth and manage stocking rates on the grazed sward. Under continuous grazing, the simplest management rule is to keep sward height at around a constant level (currently within the range 0·03–0·08 m). Assuming that the virtual sward was grazed at H_R = 0·05 m, the LIE_tot after grazing only varied between 0·25 and 0·50. However, the height of a grazed sward does not remain constant if it is maintained at a given mean H_S (Harvey and Wadge, 1994). The accuracy of sward height when managing grazing can be very important with respect to herbage regrowth. A small variation in H_R, e.g. from 0·05 to 0·03 m, may markedly reduce the LIE_tot after grazing (up to 10-fold) and cause very low recovery abilities, generating new sward heterogeneity that is independent of the initial state. Within this range of H_R values in the present study (0·05–0·03 m), there was a 2-fold decrease in LIE_tot whatever the situation, showing that the vertical heterogeneity reflected the initial sward state. Such simulations may help to analyse how the main rules of grazing management, such as sward height or rest periods, are linked to sward maintenance and potential intake.

Use of 3-D virtual canopies to assist with the modelling of grazing

Of the numerous grazing models available, only some recent ones are bite-oriented, taking the form of short-time scale models that link sward defoliation (biting) with intake and sward regrowth through the sward structure (Parsons et al., 2000; Hutchings and Gordon, 2001; Baumont et al., 2004).

Description of sward structure and bite form simulations

Stratified clipping techniques are widely employed to describe sward structure at a field scale (Rhodes and Collins, 1993) because of their simplicity of application. Nevertheless, no single component can be described in its actual situation. All sward parameters are characterized in statistical terms. Geometric structure is particularly difficult to estimate with respect to short forage species. The point quadrat method provides a better description if it is used with a combination of several needle directions (Warren Wilson, 1959). 3-D digitizing methods alone can produce an explicit spatial distribution of each element within the digitized volume of the sward. The information thus obtained allows the use of ‘classic’ LIE models (turbid medium analogy) and also of more sophisticated ones such as VegeSTAR (Adam et al., 2006) and surface models of radiative transfer (Chelle and Andrieu, 1999).

The improved description of sward structure provided by the 3-D virtual canopy can be used to test the hypothesis implied in 2-D geometric and vertical structure modelling through leaf area profiles; for example, using mean leaf inclination (Parsons et al., 1994; Schulte and Lantinga, 2002). That study showed that the planophile foliage of white clover usually reported (Ross, 1981) or modelled (Schulte and Lantinga, 2002) did not hold true. Digitizing numerous sites at the same time is not possible, so these methods rarely generate a statistically satisfactory description of sward structure at the field scale. However, a sward can be taken as an aggregation of several different patches (Schwinning and Parsons, 1999; Hutchings and Gordon, 2001). Feeding stations can be built by duplicating several similar digitized areas (up to 0·6 m² in this study). Such large virtual canopies can then be used to test bite placement modelling (Ungar et al., 2001) and enable the use of a broad range of different geometric volumes to simulate the actual bite form, as well as overlapping rules to assess different depletion patterns. The present findings show that BM and LIE after grazing are clearly dependent on bite form, even for a similar bite area and depth. They also demonstrate that the differences between bite forms were affected by sward structure.

Assessment of LIE after grazing calculated using Beer's law at the bite scale

Most models of grassland productivity apply Beer's law to the remaining structure to simulate light interception. During the present study, 3-D virtual canopies and a projective method enabled an evaluation of the simplifications and hypotheses used under these approaches. In fact, these models revealed three main sources of error in the LIE assessment: foliage dispersion is not taken into account, the contribution of petioles to TAI is not included and the lamina inclination angle is based on a midrib element.

The white clover canopies studied did not display any random foliage dispersion, as is assumed in most light interception models. Foliage was strongly clumped in the four swards, with H_R values ranging from 0·03 to 0·08 m. Such a clumped dispersion of foliage has been found elsewhere in the lowest layers of pure clover crops (Nassiri, 1998), in mixtures with tall fescue (Sonohat et al., 2002), and in various other forage species (Turitzin, 1978). Assuming a random dispersion of laminas led to an overestimation of lamina LIE ranging from 10 % to >50 % (300 % for the S3 canopy at H_R = 0·03 m) within the H_R range of 0·03–0·08 m. Under a management strategy that maintains the sward at a short height, Beer's law should therefore explicitly include a foliage dispersion parameter. The contribution of petioles to LIE_tot was generally important, and depended on the canopy structure. It was particularly high within the range H_R 0·03–0·08 m. The contribution of petioles to the carbon budget after defoliation may be an important factor in sward regrowth because of their significant photosynthetic rate (i.e. 25–35 % of the lamina assimilation rate; Woledge et al., 1990). The presence of petioles decreased the light intercepted by laminas. However, this effect was relatively limited (between 2 % and 12 %) within the current range of residual sward heights.

Light interception modelling for white clover in pure or mixed swards currently uses the mean midrib inclination for leaflets. Under the hypothesis of random leaflet dispersion, this more planophile foliage (20° vs. 41°) overestimated leaflet interception efficiency by between 6 % and 18 %, within the H_R range 0·03–0·08 m. The 3-D canopy enabled a more precise determination of half midrib inclination. Overall, the combination of the three assumptions, referred to white clover light interception modelling, leads to an underestimation of LIE_tot. The differences between actual values and those obtained using Beer's law were relatively small but only for swards with an H_R ≥0·08 m. For this reason, Beer's law should be applied with caution when simulating light interception by a short residual sward under continuous grazing. However, the discrepancy between Beer's law and actual light interception may be reduced if the sward regrows quickly and if the rest period is long enough.

Conclusions

The digitizing technique made it possible to build an explicit architecture of the bite site (feeding station or small patch). 3-D virtual images of the sward canopy made it possible to take account of the actual shape (e.g. bowl shape) of the bite in order to calculate its expected effects on intake and on the carbon balance of the residual sward.

Although it was not possible in the present study to describe different stages in the development of sward canopies, it was difficult to obtain an overview of the dynamics of the entire system. This could be achieved by using functional structure–function modelling approaches to simulate the grazing system. Although the grazing process has not yet been included in a functional structure–function model, an initial approach developed in the grass structure-function model by Verdenal et al. (2008) has been shown to take in account of plant defoliation. Moreover, most functional structure–function models are dependent on interactions between plants and environmental factors, the main one being light, to simulate photosynthetic and photomorphogenesis processes (Gautier et al., 2000; Evers et al., 2005). Thus merging these functional structure–function modelling approaches would provide an opportunity to simulate the dynamics of plant–animal interactions. This integrative approach would then enable a clearer understanding of the impact of grazers on sward dynamics.