Abstract
Background and Aims
Most studies dealing with light partitioning in intercropping systems have used statistical models based on the turbid medium approach, thus assuming homogeneous canopies. However, these models could not be directly validated although spatial heterogeneities could arise in such canopies. The aim of the present study was to assess the ability of the turbid medium approach to accurately estimate light partitioning within grass–legume mixed canopies.
Methods
Three contrasted mixtures of wheat–pea, tall fescue–alfalfa and tall fescue–clover were sown according to various patterns and densities. Three-dimensional plant mock-ups were derived from magnetic digitizations carried out at different stages of development. The benchmarks for light interception efficiency (LIE) estimates were provided by the combination of a light projective model and plant mock-ups, which also provided the inputs of a turbid medium model (SIRASCA), i.e. leaf area index and inclination. SIRASCA was set to gradually account for vertical heterogeneity of the foliage, i.e. the canopy was described as one, two or ten horizontal layers of leaves.
Key Results
Mixtures exhibited various and heterogeneous profiles of foliar distribution, leaf inclination and component species height. Nevertheless, most of the LIE was satisfactorily predicted by SIRASCA. Biased estimations were, however, observed for (1) grass species and (2) tall fescue–alfalfa mixtures grown at high density. Most of the discrepancies were due to vertical heterogeneities and were corrected by increasing the vertical description of canopies although, in practice, this would require time-consuming measurements.
Conclusions
The turbid medium analogy could be successfully used in a wide range of canopies. However, a more detailed description of the canopy is required for mixtures exhibiting vertical stratifications and inter-/intra-species foliage overlapping. Architectural models remain a relevant tool for studying light partitioning in intercropping systems that exhibit strong vertical heterogeneities. Moreover, these models offer the possibility to integrate the effects of microclimate variations on plant growth.
Keywords: Turbid medium-based models, functional–structural plant models, light interception efficiency, light partitioning, intercropping systems, grass–legume mixtures, canopy structure, Festuca arundinacea, Medicago sativa, Pisum sativum, Trifolium repens, Triticum aestivum
INTRODUCTION
The intensive and specialized agricultural systems put in place during the last 60 years are widely criticized today because of their negative environmental impacts such as nitrogen leaching, soil erosion, loss of biodiversity and high consumption of fossil-derived energy (Giller et al., 1997; Griffon, 1999; Tilman et al., 2002). Against this backcloth, research efforts have been requested to propose systems aimed to ensure sustainable agriculture. In this regard, alternative cropping systems have been explored, leading to renewed interest in crop mixtures, referred to as intercropping (Willey, 1979). Growing two or more crops simultaneously in the same area is assumed to provide high and stabilized yields in terms of quantity and quality (Ofori and Stern, 1987), to reduce the use of fertilizers and pesticides, and to enhance biodiversity conservation (for a review, see Malézieux et al., 2009). Intercropping benefits result from a trade-off between complementarity (e.g. separate root and canopy areas) and competition processes (for light, water and nitrogen) that occur between the component crops. Among the contested resources, light, and in particular its partitioning between the components, appeared to be a key factor, determining the respective proportion of each species in the stand as well as their potential yield.
In the present state of the science and the technology, and due to experimental and cost constraints, light interception of each component within an intercrop cannot be directly measured with radiation sensors (Sonohat et al., 2002), in particular for studies devoted to characterize the phylloclimate (Chelle, 2005). Thus, the only current and feasible alternative is the modelling approach. To our knowledge, most studies dealing with intercropping systems are based on statistical models founded on the turbid medium analogy (Faurie et al., 1996; Lantinga et al., 1999; Tsubo and Walker, 2002; Tsubo et al., 2005; Awal et al., 2006). In this paradigm, light transmission within a canopy is assumed to follow Beer–Lambert's law (Monsi and Saeki, 1953), i.e. an exponential decrease as a function of the downward cumulative leaf area, LAI, and leaf geometrical properties, namely the extinction coefficient k. In the case of sole crops, light interception efficiency, LIE, can be written as follows:
| (1) |
As Beer–Lambert's law deals with light transmission, i.e. non-interception probability, it cannot be directly used to compute light partitioning amongst mixed species. However, Rimmington (1984) and then Sinoquet and Bonhomme (1991) demonstrated that light interception efficiency LIEi of species i in a mixture of n components depends on the interception of the whole canopy (right-hand side in eqn 1) weighted by its extinction coefficient, ki, and its contribution to total LAI, LAIi (Sinoquet et al., 2000), such that:
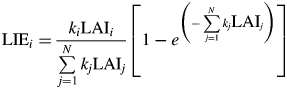 |
(2) |
One of the major assumptions underlying the turbid medium approach is that the canopy can be considered as a homogeneous and continuous medium where leaves are small and randomly distributed. Such a hypothesis could be questioned in intercropping systems which generally build up non-homogeneous canopies (Sinoquet, 1993). Indeed, these systems present several planting patterns such as mixed cropping, row intercropping, and understorey or alley intercropping, thus leading to various spatial heterogeneities. Heterogeneities may be continuous or discontinuous (foliage overlapping or empty space between species, respectively), structured or unstructured (row crops or well-mixed canopies respectively). Moreover, intercropping systems generally include various species having their own (1) morphogenesis and phenology, and (2) radiation interception ability, given by the spatial distribution of LAI and leaf geometrical features. These contrasts might lead to various inter- and intra-species patterns of leaf dispersion, either random, regular or clumped (Nilson, 1971). Light partitioning among component crops would also evolve during the growing cycle due to various dynamics of LAI establishment, thus leading to contrasted situations at canopy closure. Although the turbid medium approach has been widely used and assessed in the case of sole crops (Andrieu and Sinoquet, 1993) or trees (Chen et al., 1993; Combes et al., 2008), a major difficulty arises for the validation of such an approach applied to multispecies stands (Sinoquet and Caldwell, 1995). Indeed, due to the impossibility of carrying out direct measurements of light partitioning in mixed canopies, turbid medium-based estimations are rarely validated or only partially so through the total amount of transmitted radiation reaching the soil (Faurie et al., 1996).
Such limitations could be tackled by using surface-based approaches (Chelle and Andrieu, 1999) which model the canopy structure through realistic three-dimensional (3-D) representations in which individual plant architecture is explicitly described as a collection of interconnected phytoelements, including their geometry and optical properties (Godin, 2000). Thus, canopy heterogeneities are explicitly taken into account when simulating radiative exchanges on these architectural models. Magnetic 3-D digitizing appeared to be the most suitable technique for collecting information on plant architecture prior to in silico reconstruction (Moulia and Sinoquet, 1993). Herbaceous mixtures therefore appeared to be a relevant case for study as they are accessible to these kinds of measurements; this is particularly so for grass–legume intercrops, which are widely used because of their strong agronomical interests (Ofori and Stern, 1987; Tsubo and Walker, 2004).
The aim of the present study was to assess the ability of the turbid medium approach to accurately estimate light partitioning within mixed canopies. The turbid medium assessment was conducted on a contrasted range of grass–legume intercropping systems, which display various LAI and height ratios, at different stages of the growing cycle and with contrasted row structures. For this purpose, we considered three kinds of mixtures: (1) an annual mixture of wheat and pea (WP), and two perennial mixtures of (2) tall fescue and alfalfa (FA), and (3) tall fescue and white clover (FC). For each mixture, mini-stands were digitized to provide accurate 3-D descriptions of the canopy structure. Benchmark estimates of mixture light interception efficiencies were obtained from a radiation model based on the projective method applied on the 3-D reconstructed canopies. These reference results were then compared against the computations derived from a turbid medium model.
MATERIALS AND METHODS
Plant material and growing conditions
Some descriptors of the mixed canopies used for this study are presented in Table 1. Detailed descriptions are given below.
Table 1.
Description of the plant mixtures
| Leaf area index (m2 m−2) |
Coefficient of variation of the LAI horizontal distribution |
|||||||
|---|---|---|---|---|---|---|---|---|
| Mixture | Digitizing time (degree days, DD; or days after sowing, DAS) | Density | Designation | Grass | Legume | Grass | Legume | Mixture |
| WP | 300 DD | 30 % W-70 % P | W30-P70_300DD_1 | 0·31 | 0·15 | 0·99 | 2·49 | 0·91 |
| W30-P70_300DD_2 | 0·32 | 0·16 | 1·35 | 2·46 | 1·05 | |||
| 50 % W-50 % P in alternate rows | W50-P50A_300DD_1 | 0·48 | 0·07 | 0·70 | 2·46 | 0·62 | ||
| W50-P50A_300DD_2 | 0·48 | 0·06 | 1·14 | 2·80 | 0·98 | |||
| 50 % W-50 % P mixed on the row | W50-P50M_300DD_1 | 0·43 | 0·11 | 0·80 | 1·13 | 0·73 | ||
| W50-P50M_300DD_2 | 0·45 | 0·17 | 0·63 | 1·36 | 0·52 | |||
| 70 % W-30 % P | W70-P30_300DD_1 | 0·72 | 0·03 | 0·93 | 2·51 | 0·87 | ||
| W70-P30_300DD_2 | 0·60 | 0·03 | 1·19 | 2·60 | 1·14 | |||
| 685 DD | 30 % W-70 % P | W30-P70_685DD_1 | 0·75 | 0·54 | 1·15 | 1·25 | 0·62 | |
| W30-P70_685DD_2 | 0·65 | 0·56 | 0·94 | 0·59 | 0·59 | |||
| 50 % W-50 % P in alternate rows | W50-P50A_685DD_1 | 1·07 | 0·13 | 0·57 | 1·07 | 0·47 | ||
| W50-P50A_685DD_2 | 0·90 | 0·22 | 0·82 | 1·00 | 0·71 | |||
| 50 % W-50 % P mixed on the row | W50-P50M_685DD_1 | 1·19 | 0·40 | 0·62 | 1·18 | 0·54 | ||
| W50-P50M_685DD_2 | 1·05 | 0·60 | 0·62 | 0·76 | 0·44 | |||
| 70 % W-30 %P | W70–P30_685DD_1 | 1·54 | 0·08 | 0·75 | 1·41 | 0·66 | ||
| W70–P30_685DD_2 | 1·51 | 0·14 | 1·19 | 2·60 | 1·14 | |||
| 1100 DD | 30 % W-70 % P | W30-P70_1100DD_1 | 1·23 | 0·98 | 0·95 | 0·83 | 0·50 | |
| W30-P70_1100DD_2 | 1·12 | 1·03 | 0·88 | 1·19 | 0·59 | |||
| 50 % W-50 % P in alternate rows | W50-P50A_1100DD_1 | 2·05 | 0·34 | 0·79 | 0·71 | 0·47 | ||
| W50-P50A_1100DD_2 | 1·33 | 0·48 | 0·82 | 0·37 | 0·60 | |||
| 50 % W-50 % P mixed on the row | W50–P50M_1100DD_1 | 2·15 | 0·54 | 0·45 | 0·86 | 0·41 | ||
| W50-P50M_1100DD_2 | 1·71 | 0·98 | 0·33 | 0·82 | 0·34 | |||
| 70 % W-30 % P | W70-P30_1100DD_1 | 2·56 | 0·16 | 0·65 | 1·06 | 0·46 | ||
| W70-P30_1100D_2 | 2·56 | 0·18 | 0·62 | 1·18 | 0·54 | |||
| FA | 670 DD | 50 % F-50 % A high density | F50-A50_670DD_HD | 3·06 | 3·83 | 0·22 | 0·29 | 0·08 |
| 50 % F-50 % A low density | F50-A50_670DD_LD | 0·75 | 0·37 | 0·20 | 0·28 | 0·19 | ||
| 1150 DD | 50 % F-50 % A high density | F50-A50_1150DD_HD | 2·52 | 8·06 | 0·55 | 1·23 | 0·34 | |
| 50 % F-50 % A low density | F50-A50_1150DD_LD | 0·43 | 1·70 | 0·86 | 0·52 | 0·29 | ||
| FC | 49 DAS | NA | FC_49_1 | 2·06 | 0·05 | 0·19 | 0·12 | 0·15 |
| FC_49_2 | 1·22 | 0·24 | 0·17 | 0·34 | 0·11 | |||
| FC_49_3 | 0·60 | 0·07 | 0·29 | 0·19 | 0·17 | |||
| 62 DAS | NA | FC_62_1 | 3·37 | 0·89 | 0·43 | 0·17 | 0·36 | |
| FC_62_2 | 0·32 | 0·36 | 0·09 | 2·00 | 0·09 | |||
| FC_62_3 | 1·62 | 0·25 | 0·29 | 0·45 | 0·31 | |||
| 75 DAS | NA | FC_75_1 | 4·45 | 0·79 | 0·38 | 0·51 | 0·37 | |
| FC_75_2 | 3·62 | 0·97 | 0·44 | 0·27 | 0·39 | |||
| FC_75_3 | 2·31 | 0·87 | 0·23 | 0·28 | 0·21 | |||
Leaf area index and coefficients of variation of its horizontal distribution are given for each species belonging to wheat–pea (WP), tall fescue–alfalfa (FA) and tall fescue–clover (FC) mixtures. Sowing densities of FC mixtures were not available (NA) in the original article of Sonohat et al. (2002).
Wheat–pea mixtures
Intercropped wheat (Triticum aestivum L. ‘Apache’) and pea (Pisum sativum L. ‘Lucy’; aphylla type) were grown in 80 × 60 × 30-cm containers in a greenhouse experiment from 1 February 2010 to 15 April 2010 in Angers, France (47°27′N, 00°32′W). Containers were filled with a soil layer of 25 cm, providing 3 g m−2 of NO3−. The soil was then enriched with 3·5 g m−2 NH4NO3 at the sowing date and at 850 degree days (DD) from emergence to avoid any N-limitation for plant development. To ensure pea nodulation, each container was inoculated with a solution of Rhizobium leguminosarum P221 at 2 × 107 bacteria per plant. Plants were sown at (1) three relative densities, i.e. the percentage of each species varied so that each treatment had the same absolute density, and (2) at two different row arrangements. Each sowing pattern was repeated twice, hereafter denoted ‘_1’ and ‘_2’ as in Table 1. The first three treatments consisted of four alternative rows of wheat and pea sown at different proportions of their optimal density practised in pure stands: (1) 50 % wheat and 50 % pea (W50–P50 Alternate Row), (2) W30–P70 and iii) W70-P30. The fourth treatment also consisted of 50 % wheat and 50 % pea but, in contrast to treatment 1, plants were mixed within each row (W50–P50 Mixed Row). We considered that the optimal density was 250 plants m−2 for wheat and 90 plants m−2 for pea.
Tall fescue – alfalfa mixtures
A second mixture (FA) consisted of a 50 : 50 alfalfa (Medicago sativa L. ‘Orcha’) and tall fescue (Festuca arundinacea Schreb. ‘Noria’) mixture following an hexagonal lattice for planting, with each individual surrounded by three individuals of its own species and three of the other species (Fig. 1). Such a pattern produces a stand where all plants are equidistant and aggregated by species in rows (Harper, 1961). Two planting densities were studied corresponding respectively in the field to a crowding plant population density shortly after emergence (hereafter HD for high density, 460 plants m−2) and an old stand once self-thinning has occurred and the population density has stabilized (hereafter LD for low density, 50 plants m−2). All plants were grown outdoors at the INRA Lusignan station (46°25′N, 0°7′W, 100 m a.s.l.) from 15 April 2010 to 15 July 2010 in stands of about 1 m2 at HD and 2 m2 at LD. Each plant was in an individual pot (5 cm diameter × 40 cm high at HD; 10 cm diameter × 25 cm high at LD) filled with a medium composed of sterile potting mix, sand and brown earth soil (1 : 1 : 1, v/v). All pots were fertirrigated three times a day with a complete nutrient solution so that plants were competing for light only.
Fig. 1.

Illustration of the hexagonal lattice used for the tall fescue (open dots) – alfalfa (closed dots) mixtures. Each individual plant is neighboured by a 50 : 50 proportion of the two species.
Tall fescue–clover mixtures
Data from the tall fescue (Festuca arundinacea Schreb. ‘Barcel’) – white clover (Trifolium repens L. ‘Huia’) mixtures were obtained from a database built up following an experiment conducted and fully described by Sonohat et al. (2002). Briefly, FC mixtures were sown on a clay-loam soil near Caen, France (48°55′N, 0°0′E, 60 m a.s.l.) on 18 March 1999. Tall fescue was sown in rows of 0·17 m whereas white clover was broadcast sown.
Three-dimensional digitizing of canopies and virtual reconstructions
Canopy architecture of each mixture was digitized using a 3-D digitizer (3Space Fastrak, Polhemus Inc., Colchester, VT, USA; Polhemus, 2009). Spatial coordinates as well as each phytoelement orientation were collected with 3A software (Adam et al., 1999) and encoded as Multiscale Tree Graphs (MTG) (Godin and Caraglio, 1998). Data from digitizing were then imported into the Openalea platform (Pradal et al., 2008) where the foliage of each species was reconstructed, thus excluding the other phytoelements in light interception computations, i.e. sheaths, stems and tendrils. These 3-D mock-ups allowed us to provide accurate descriptions of the canopies structure (spatial distribution of LAI) and geometric features (leaf inclination).
Wheat–pea mixtures
Three digitizations were carried out during the growing period at 300, 685 and 1100 DD from emergence (base temperature 0°C). Wheat plants were digitized as a succession of sheaths on which lamina are branched. Then, untouched lamina were described by successive pointing out along the midribs, thus keeping their natural bearing. Pea plants were digitized as a succession of internodes on which the two-stipule orientation and dimension were measured. Wheat leaves were represented as a succession of rectangles whose widths were computed according to the current position on the midrib and the maximal leaf length (Fournier et al., 2003). For pea plants, stipules were reconstructed from a library of about 200 geometric objects stemming from photographs on which we extracted stipule shape. At the reconstruction time, geometric shapes were then (1) attributed according to the relative phytomer number of the considered stipule and (2) resized and reoriented according to the information stored during the digitization.
Tall fescue–alfalfa mixtures
For each FA stand, 3-D magnetic digitizations were performed at two stages of development (670 and 1150 DD after emergence, base temperature 4°C), corresponding to the first two cuts of the mixture at alfalfa early bloom. All plants over soil areas of about 1400 cm2 (LD) and 900 cm2 (HD) in the centre of the stand were recorded. For tall fescue, the digitization and reconstruction procedures were the same as for wheat (see above). Alfalfa plant description was also similar to pea, except that main leaf leaflets, instead of stipules, were recorded. Leaflet widths were measured on a sub-sample of phytomers of each plant only. These direct measurements were used to build up plant-specific allometric relationships considering both leaflet length and phytomer position on the stem as predictors of leaflet width.
Tall fescue–clover mixtures
Experimental data were obtained from Sonohat et al. (2002) where three plots of the FC mixture (0·17 × 0·10 m), denoted ‘_1’, ‘_2’ and ‘_3’ in Table 1, were digitized at 49, 62 and 75 d after sowing. The digitizing protocol used by the authors was similar to those described above for WP and FA mixtures; more details are given in Sonohat et al. (2002). Tall fescue virtual plants were then reconstructed in the same way as in FA mixtures. Clover leaflets were treated as for alfalfa with an adapted geometric shape.
Estimation of LIE in virtual canopies: reference model
Benchmark estimates of light interception efficiency for each stand were computed on VEGESTAR software (Adam et al., 2002), a radiation model based on the projective method, disregarding multiple scattering and assuming leaves as black bodies. Input files containing information on plant structure, were derived from the stand reconstructions obtained on the Openalea platform. Computations were performed assuming only diffuse radiations, which were approximated by a set of light sources from a sky vault discretized in 46 solid angle sectors (Den Bulk, 1989), including eight zenith angles (9·23, 10·81, 26·57, 31·08, 47·41, 52·62, 69·16 and 90°). LIEs were computed for each direction and then integrated over the sky vault by summing up the 46 directional values. The contribution of each sky sector to the incoming light energy was weighted according to the Standard Overcast sky radiation distribution where sky luminance depends only on elevation (Moon and Spencer, 1942). Thus, the weighting factor, Ra, is given by:
| (3) |
where l is the sky area altitude and Rd is the diffuse radiation integrated over the sky dome. To avoid border effects, virtual stands were virtually replicated in all directions according to their sowing pattern.
Turbid medium-based model
Light interception efficiencies estimated from the virtual plant models were then compared with the outputs of a turbid medium-based model. Numerous models using the turbid medium analogy are available in the literature, mainly contrasted by their representation of vertical structure of the canopy. In the present work, we used the turbid medium model SIRASCA (Sinoquet et al., 1990), which aims to compute light partitioning in mixed canopies. This model is assumed to provide accurate estimates of light interception and has been validated on a large range of canopies and also against other models (Sinoquet et al., 2000). This model computes light interception in multispecies canopies from the species LAI and mean leaf inclination angle. Leaf inclinations (α) are used to compute the extinction coefficients (k) by the relationship (Sinoquet et al., 2000):
| (4) |
SIRASCA was set to gradually account for vertical heterogeneity of the foliage, i.e. the canopy was described with either one, two or ten layers, which respectively correspond to the maximal height of the whole canopy, the maximal height of each species and the maximal height of the canopy divided in ten equal layers. SIRASCA inputs such as LAI and mean leaf inclination (eqn 2) for each species were extracted from the 3-D virtual stands.
Statistical analysis
Assessment of the turbid medium approach was based on two criteria: (1) the mean bias of the predictions (MBP) and (2) the root mean squared deviation of the predictions (RMSDP). For each variable, MBP was calculated as the difference between the n pairs of values predicted by (1) the virtual stand-projective method (vpp), taken as a reference, and (2) the turbid medium-based model (tmp), such that:
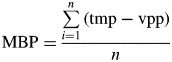 |
(5) |
Significant deviations from zero MBP were assessed based on a t-test by using the UNIVARIATE procedure of SAS 9·2 (SAS Institute, Cary, NC, USA). The RMSDP for each variable was estimated as:
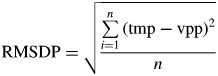 |
(6) |
RESULTS
Stand mock-ups
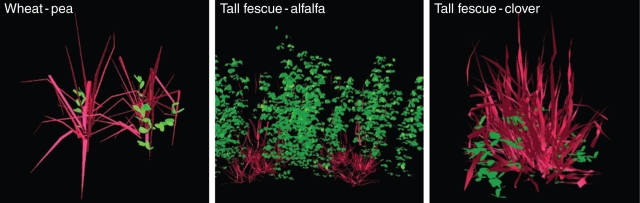
Figure 2 shows views of some reconstructed 3-D virtual mixtures presented in the horizontal direction.
Fig. 2.
Horizontal views of some reconstructed 3-D scenes of wheat–pea, tall fescue–alfalfa and tall fescue–clover mixtures. Grass species are showed in red and legumes in green.
Characterization of the mixture structures and light partitioning among component species
Spatial distribution of foliage
LAI ranged from 0·31 to 4·47 m2 m−2 for grass and from 0·03 to 8·06 m2 m−2 for legume species (Table 1). WP mixtures exhibited the smallest LAI (0·31–2·56 m2 m−2 for wheat; 0·03–1·03 m2 m−2 for pea). Highest LAI values were observed for alfalfa (maximal LAI of 8·06 m2 m−2) and for tall fescue plants in FC stands (maximal LAI of 4·47 m2 m−2).
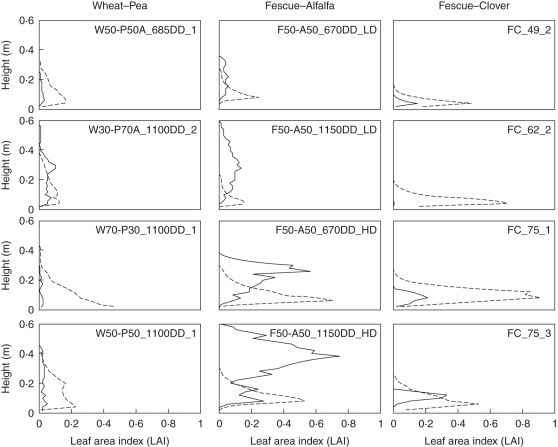
Most of the grass species belonging to the different mixtures showed a triangular vertical distribution of their LAI (Fig. 3). Two cases could be distinguished among these triangular profiles. In the first case, most of the foliage is located in the upper layers of the canopy, such as the vertical profiles of LAI exhibited by tall fescue plants (in FA and FC) where the maximal amount of leaf area is located above the middle of the stand's height. In the second case, most of the foliage is located in the lower layers of the canopy. This was particularly the case for wheat (e.g. W70–P30_1100DD_1, W50–P50A_685DD_1). The LAI of legume species within the FA stands grown at high density and the FC swards (alfalfa and clover, respectively) also followed triangular profiles with variations of LAI between layers ranging from 0·05 to 0·80 m2 m−2. In contrast, vertical distributions of alfalfa LAI grown at low density followed a rectangular pattern, as observed for pea plants within WP stands. Differences in component species height were also contrasted according to the mixtures. Height ranged from 100 to 400 mm for grass species and from 70 to 600 mm for legumes. Wheat and pea plants did not show any marked difference in height whereas in FC mixtures tall fescue plants overtopped clover by 50–100 mm. The strongest vertical stratification, however, was observed in the FA swards where (1) alfalfa largely overtopped tall fescue plants by 100–300 mm, and (2) 50–90 % of the alfalfa foliage was located in the upper layer of the canopy.
Fig. 3.
Typical vertical distribution of leaf area index (LAI) in wheat–pea, tall fescue–alfalfa and tall fescue–clover mixtures. See Table 1 for an explanation of the labels inside the individual graphs. Vertical profiles of LAI are noted for grass (dashed lines) and legume (solid lines) species.
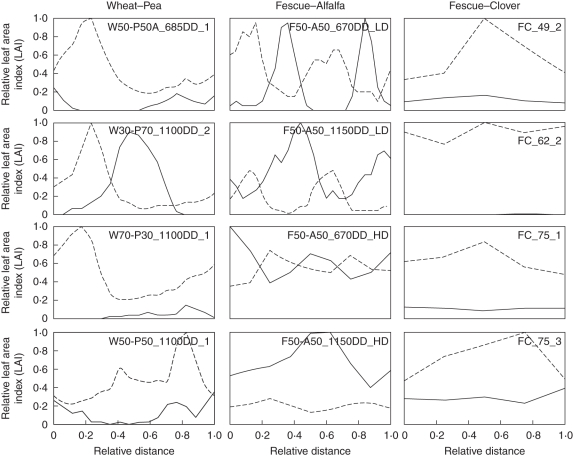
Figure 4 shows typical horizontal distributions of LAI in different mixtures. Coefficients of variation (CV) of the horizontal distribution of LAI ranged from 0·17 to 1·35 for grasses and from 0·12 to 2·80 for legumes (Table 1). Highest values of CV were observed for wheat (mean ± s.d. 0·79 ± 0·26) and for pea (1·41 ± 0·72). As a result, WP stands exhibited the most marked row arrangement as the CV of the WP mixture was 0·63 ± 0·22 (see typical profiles in Fig. 4). Similar profiles were observed in the FA swards grown at low density (mean CV = 0·70 ± 0·16 for tall fescue and 0·88 ± 0·11 for alfalfa) although their CV was lower than for the WP mixtures (0·32 ± 0·02). In contrast, horizontal heterogeneities were lower in the FA swards grown at high density (0·13 ± 0·06) as well as for the FC stands (0·27 ± 0·10).
Fig. 4.
Typical horizontal distributions of leaf area index (LAI) of the wheat–pea, tall fescue–alfalfa and tall fescue–clover mixtures. See Table 1 for an explanation of the labels inside the individual graphs. Horizontal profiles of LAI are noted for grass (dashed lines) and legume (solid lines) species where each value was normalized according to (1) the distance of the first row and (2) the maximal LAI of the overall mixture.
Mean leaf inclination
Leaf inclinations of grass species ranged from 37·1 to 58·3° while for legumes it ranged from 27·2 to 42·4°, thus reflecting the more planophile distribution of legume leaves (Table 2). Extinction coefficients (k) were 0·72–0·88 and 0·84–0·93 for grass and legume species, respectively. Within FA stands, component species exhibited distinct leaf inclination as tall fescue foliage was more erect (53·4 ± 2·0°, k = 0·76) than alfalfa (42·4 ± 6·7°, k = 0·84) regardless of density and stage of development. The most marked difference in species leaf inclination was found in the FC mixtures where mean leaf inclination was 58·3 ± 4·5° for tall fescue versus 27·2 ± 6·4° for clover, the latter therefore displaying planophile leaves (extinction coefficient reached 0·93). In contrast, the WP mixtures did not show any marked differences between the mean leaf inclination of the two component species, 37·1 ± 5·4° (k = 0·88) and 36·0 ± 3·1° (k = 0·88) for wheat and pea, respectively. Moreover, vertical profiles did not show any clear variation in mean leaf inclination as a function of canopy height (data not shown).
Table 2.
Species mean leaf inclination and extinction coefficients of wheat–pea (WP), tall fescue–alfalfa (FA) and tall fescue–clover (FC) mixtures
| Grass |
Legume |
|||
|---|---|---|---|---|
| Mixture | Mean leaf inclination (°) | Extinction coefficient | Mean leaf inclination (°) | Extinction coefficient |
| WP | 37·1 ± 5·4 | 0·87 | 36·0 ± 3·1 | 0·88 |
| FA | 53·4 + 2·0 | 0·75 | 42·4 ± 6·7 | 0·84 |
| FC | 58·3 ± 4·5 | 0·71 | 27·2 ± 6·4 | 0·92 |
Extinction coefficients were derived from eqn (4).
Species contribution to canopy LAI and light interception
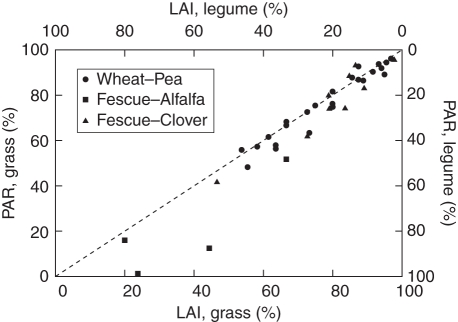
Mixtures exhibited contrasted ratios of grass/legume LAI as well as light partitioning levels, thus covering a large range of possibilities (Fig. 5), i.e. from radiation interception made at 98·69 % by legume species (constituting 76·97 % of the whole canopy) to a situation where grass species represent 96·91 % of the mixture LAI with a interception of incident light of 96·22 %. In most WP and FC stands, canopies were largely constituted by the grass species, respectively wheat and tall fescue plants, which therefore captured most of incident light, ranging from 41·93 to 96·22 % of the overall light interception. WP and FC values were distributed within this interval, depending on the species density and growth stage. In contrast, the FA swards exhibited different levels of interspecific LAI and light interception compared to WP and FC mixtures. Indeed, the contribution of the legume species (alfalfa) to total LAI ranged from 38·84 to 76·97 %, which therefore intercepted 48·18–98·69 % of incident light. In some cases, similar values of LAI were measured between the two component species. As shown in Table 1, the contribution of each component species to the overall LAI in W30–P70 at 685 and 1100 DD, F50-A50_670DD_HD and FC_62_2, was equivalent, leading to equivalent levels of light interception (grass interception ranged from 46·21 to 63·31 %).
Fig. 5.
Species contribution to leaf area index (LAI) and photosynthetically active radiation (PAR) interception. Computations were made on wheat–pea, tall fescue–alfalfa and tall fescue–clover mixtures, as indicated.
In the case of WP and FC mixtures, points were slightly distributed below the 1 : 1 line whereas most of FA points were markedly located further from this line, in particular for HD mixtures.
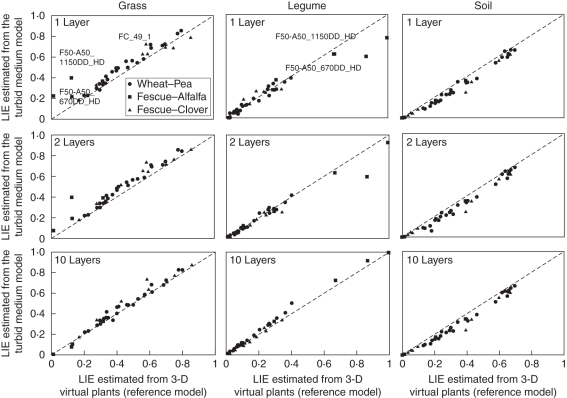
Virtual canopies vs. turbid medium approach
The ability of the turbid medium-based approach to estimate LIE of each species was assessed against a 3-D virtual plants-based approach (reference model). The turbid medium approach was set to gradually take into account the vertical distribution of the foliage by considering the canopy as a single layer (Fig. 6A) or by dividing the canopy into two (Fig. 6B) or ten horizontal layers (Fig. 6C). Figure 6 shows that the turbid medium approach was tested on a wide range of LIEs for both grass and legume species, ranging from 0·01 to 0·86 and from 0·01 to 0·99, respectively. The overall estimation of legume LIE by the turbid medium approach was unbiased whereas those for grass species were overestimated (maximal bias reaching –0·05). Predicted LIEs of the soil were significantly underestimated (maximal bias = +0·05).
Fig. 6.
Comparison between light interception efficiencies (LIE) derived from the turbid medium model and 3-D virtual plants (reference model). Values are presented for grass and legume species as well as for the soil (columns, as indicated). The turbid medium model was assessed by describing the canopy as one, two or ten layers (rows, as indicated). Estimations were made on three mixtures: wheat–pea, tall fescue–alfalfa and tall fescue–clover (as indicated in the first graph) at different densities and stages of development (see Table 1). Five outliers are highlighted.
When using the one-layered option (Fig. 6A), RMSDP was 0·08 and 0·06 for grass and legume components, respectively. For WP and FC mixtures maximal bias (Table 3) reached –0·05 for grass species (RMSDP = 0·06 and 0·07 for wheat and tall fescue, respectively) and –0·01 for legume components (RMSDP = 0·02 and 0·04 for pea and clover, respectively). Strong discrepancies were observed for the FA swards as maximal bias reached –0·16 for tall fescue (RMSDP = 0·18) and +0·14 for alfalfa (RMSDP = 0·14). Maximal deviation was observed for FA stands grown at high density as LIE of tall fescue plants was overestimated by 0·28 and 0·21 for F50-A50_670DD_HD and F50-A50_1150DD_HD, respectively. It could represent up to 17 times the LIE estimated by the reference model. For these two mixtures, alfalfa LIE was underestimated by 0·27 and 0·22, respectively.
Table 3.
Mean bias of the predictions (MBP) and root mean squared deviation of the predictions (RMSDP) for light interception efficiency estimated by the turbid medium model in wheat–pea (WP), tall fescue–alfalfa (FA) and tall fescue–clover mixtures
| Grass |
Legume |
Soil |
|||||
|---|---|---|---|---|---|---|---|
| No. of layers in SIRASCA | Mixture | MBP | RMSDP | MBP | RMSDP | MBP | RMSDP |
| 1 | WP | –0·05*** | 0·06 | 0 | 0·02 | +0·05*** | 0·05 |
| FA | –0·16* | 0·18 | +0·14 | 0·14 | +0·02 | 0·03 | |
| FC | –0·03 | 0·07 | –0·01 | 0·04 | +0·05*** | 0·06 | |
| 2 | WP | –0·05*** | 0·06 | 0 | 0·02 | +0·05*** | 0·06 |
| FA | –0·12 | 0·15 | +0·10 | 0·14 | +0·02 | 0·03 | |
| FC | –0·06*** | 0·07 | +0·01 | 0·03 | +0·05** | 0·06 | |
| 10 | WP | –0·02*** | 0·04 | –0·02*** | 0·03 | +0·05*** | 0·05 |
| FA | +0·02 | 0·03 | –0·04* | 0·04 | +0·02 | 0·03 | |
| FC | –0·05** | 0·07 | 0 | 0·01 | +0·05** | 0·06 | |
*P < 0·1, **P < 0·05, ***P < 0·01.
Considering the canopy as two layers (Fig. 6B) reduced RMSDP by 0·01. This was particularly the case for the FA swards as bias decreased by 0·04 for tall fescue (RMSDP = 0·15) and 0·05 for alfalfa (RMSDP = 0·14). This improvement in the LIE prediction of FA mixtures was particularly marked for F50-A50_1150DD_HD. In contrast, in some cases, there was no improvement in the LIE prediction compared with the one-layered model (e.g for F50-A50_670DD_HD or FC_49_1). In other cases, description of the canopy in two layers even led to a worse estimation of LIE, in particular for FC mixtures (bias = –0·06, RMSDP = 0·07; bias = +0·01; RMSDP = 0·03; for tall fescue and clover, respectively). Although these discrepancies were slight (mean deviation of 9·10 × 10−4 ± 0·001), they were observed in 42·10 % of the overall mixtures.
Discretization of the canopy into ten small layers (Fig. 6C) produced the best estimation of LIE, very close to the reference model regardless of species, density or mixture stage of development (bias ≤ |0·05|, RMSDP = 0·04). The improvement of LIE estimation was particularly marked for the FA swards as the RMSDP decreased by 80·46 and 75·81 % compared with the one- and two-layered options, respectively. The highest improvement was observed for stand F50-A50_1150DD_HD. In a few cases, however, increasing the vertical description of the canopy to ten layers did not lead to any improvement of LIE estimation, as observed for some tall fescue plants within the FC mixtures (e.g. for FC_49_1).
DISCUSSION
We assessed the turbid medium-based approach for its capacity to accurately estimate LIE of intercropped plants. We studied two different types of species, grasses and legumes, which exhibited contrasted structures and abilities to capture light. Their structural characteristics allowed us to challenge some of the turbid medium assumptions.
Variability in mixture structure, plant architecture and light partitioning among components
As reported by several authors (e.g. Sinoquet and Caldwell, 1995) vertical dominance among components of mixed crops is of upmost importance for light partitioning. In the present study, mixtures exhibited contrasted differences in the height of component species, thus leading to various levels of vertical stratification. We described canopies with equivalent height between component species as well as mixtures where one of the species overtopped the other, either the grass or the legume component. Although these mixtures were grown in controlled conditions, their structures were realistic as they represent several forms of intercropping encountered in agricultural systems. This variability can be understood based on the classification proposed by Malézieux et al. (2009) as we described a row mixture of annual crops and two other intercropping systems of perennial species with contrasted levels of row structure and vertical stratification. The FA mixture is close to structures encountered in agroforestry systems (Malézieux et al., 2009).
Variability in mixture structure also results from the vertical distribution of leaf area. Grass species, clover and alfalfa, generally exhibited triangular distributions of their leaf area, as already reported in several monospecific grass canopies (Ross, 1981) and in grass–clover mixtures (Nassiri et al., 1996; Lantinga et al., 1999; Sonohat et al., 2002). These actual vertical profiles of LAI are not in agreement with the assumption of a regular distribution commonly used in studies dealing with light interception. Such disagreements were noted by Schulte and Lantinga (2002). In contrast, regular profiles of vertical LAI distribution were observed for pea and some alfalfa plants.
In addition to the LAI distribution, leaf inclination is the second basic parameter used to characterize a plant's ability to capture light (Sinoquet and Caldwell, 1995). In the intercropping systems described, there were mixtures exhibiting equivalent leaf inclinations between their components as well as species with contrasted leaf inclination. Leaf inclinations for each species were consistent with previous studies on monospecific canopies as reported by Ross (1981), except for wheat leaves for which inclination was lower in the present study. Such differences in leaf inclinations could be the result of species plasticity in response to a multispecific environment compared with monospecific conditions.
As a result of species differences in height, foliage dispersion and inclination, various abilities for light interception and levels of competition for light were observed. Indeed, we described two canopies where the grass was the dominant species and one sward where the legume captured most of the incident light. Whatever the mixture considered, species dominance in terms of light interception was mainly the result of their contribution to overall LAI of the mixture. This was particularly the case for grass species whose lower ability for light interception, due to erectophile foliage, was counterbalanced by their aptitude to develop a large leaf area and/or by their vertical dominance (Sonohat et al., 2002). Grass–legume mixtures where the grass component is dominant have been widely described and are often considered to be more productive and stable compared with mixtures dominated by the legume component (Haynes and Brady, 1980; Louarn et al., 2010). In contrast, mixtures dominated by a legume lead to strong levels of competition for light as their vertical dominance is enhanced by their structural ability to intercept light (planophile leaves) (Chamblee and Collins, 1988; Louarn et al., 2010). This was particularly the case for the FA swards where the vertical dominance of alfalfa and its high extinction coefficient were combined to give a high stand density, thus leading to a stronger interception of light by alfalfa than its relative contribution to the LAI of the mixture (Fig. 5).
Although all the mixtures used in the present work were a case of study, their structure can highlight light partitioning features in intercropping systems where direct validation with digitizing methods is not possible.
Predicting light partitioning in intercropping systems with a turbid medium-based model
Estimating light partitioning in intercropping systems with the turbid medium approach is based on the assumption that canopies are homogeneous. Here we have shown that the turbid medium approach was in good agreement with the reference model in most of the challenging range of canopy structures. However, these mixtures included structures which could be considered as heterogeneous, such as row mixtures or open-canopies whose LAI was lower than 1 m2 m−2 and where light transmission to the soil was higher than 50 % (early growth stages). Biased estimations of LIE were therefore expected from the turbid medium approach. Similar results were reported by Sinoquet and Bonhomme (1989) in sole crops of maize sown in rows and by Tournebize and Sinoquet (1995) in heterogeneous shrub–grass mixtures whose structure allowed direct measurements of light partitioning. As mentioned by Gutschick (1991), horizontal heterogeneities, i.e. row structures, appeared to be of less importance for estimating light interception with turbid medium-based models, as mixtures with high CV did not show significant discrepancies in regard to their LIE estimates by the turbid medium model.
The two-layered model did not significantly improve LIE estimates of the overall mixtures compared with the one-layered model. In some cases, this even led to more biased estimations of LIE compared with the one-layered model. This result underlines the importance of the definition of plant height. Indeed, layers were defined according to the maximal height of each component, which therefore account for single erected laminas with small areas that generally belonged to grass species. Although many studies dealing with light partitioning within intercropping systems were based on a two-layered turbid medium model (Ofori and Stern, 1987; Sinoquet et al., 1990; Sonohat et al., 2002; Tsubo and Walker, 2002; Awal et al., 2006), no details were given on their definition of plant height. We suggest that layer boundaries should rather be delimited by a more ‘functional’ definition of plant height such as the height under which a given proportion of the foliage area may be found (e.g. 90 or 95 %). Thus, when using the turbid medium approach, leaf elements will be dispersed in a layer whose size would be closest to the actual leaf area localization.
The simplest models, with one and two layer(s), were, however, unable to estimate LIE of canopies exhibiting strong vertical stratifications combined with foliage overlapping (e.g. FA stands grown at high density). Horizontal profiles of LAI showed that in these mixtures, species appeared to be well mixed, which therefore led to high levels of interspecies foliage overlapping, referred to as between-species leaf dispersion (Sinoquet and Bonhomme, 1991). Similar conclusions could be drawn from differences of LIE estimations between species as the turbid medium model provided better estimations of legume LIE compared with grass species. Such discrepancies could be the result of contrasted within-species leaf dispersion. Indeed, legumes generally exhibit a quasi-random dispersion of their foliage (Sonohat et al., 2002), but which may vary along the vertical axis (Lantinga et al., 1999). In contrast, grass leaves tended to be more clumped (Lantinga et al., 1999; Sonohat et al., 2002) so, by using the turbid medium analogy, foliar elements of grasses are considered to be randomly dispersed, which therefore ‘artificially’ increases grass LIE. It therefore appears that light partitioning within this kind of canopy structure cannot be satisfactorily simulated by the turbid medium approach, unless a more detailed description of the canopy is provided, which improves the consideration of species height and foliage interpenetration. As a result, the ten-layered model gave predictions very close to the reference model, as the remaining bias was lower than |0·03| for grass and legume species. However, the impact of such small cumulative errors on a predictive model of biomass accumulation remains to be assessed.
Apart from the limitations discussed above, our results show that description of just the vertical stratification is enough to predict light partitioning with a turbid medium-based model in a wide range of intercropping systems and stages of development. However, these conclusions were drawn from results obtained with one of the most complex and detailed turbid medium-based models (SIRASCA) dealing with light partitioning within mixed canopies (Sinoquet et al., 2000). Moreover, increasing the vertical description of canopies (i.e. the number of horizontal layers) would require tedious and time-consuming measurements; for example, the ten-layered model used in the present paper would have required us to measure leaf area and inclination of each species every 1·5–6 cm, depending on mixture height.
Contribution of models based on explicit 3-D description of plant architecture
As reported in most studies using the turbid medium approach, canopies were characterized only by their leaf area. To compare the two models on similar canopy structures, stems (or sheaths for grass species) were therefore not taken into account for both SIRASCA and 3-D virtual plant models although they represent a significant part of the plant area. The use of structural plant models in future works would therefore allow us to quantify the interception of light by stems/sheaths while the cylindrical shape of these organs and their erected bearing require implementation of complex rules in turbid medium-based models. However, as proposed by Da Silva et al. (2008), modelling frameworks must be developed to identify a level of plant/organ description that achieves a good compromise between the amount of measurement required to describe the plant architecture (which is also associated with the computation time) and the quality of the resulting light interception model.
Light partitioning within intercropping systems is a crucial issue for studying the dynamics of the system's component species growth. These dynamics result from complex interactions involving the interception of light. In the present study, structural and static plant representations coupled to radiative transfer models were used to characterize light partitioning among component species. Moreover, these spatially explicit representations of plant architecture also offer the possibility to be dynamically coupled with functional models (e.g. photosynthetic functions) thus resulting in functional–structural plant models. As these models could be uses at several scales (stand, plant or organ level), they therefore have the ability to integrate the effects of microclimate variations on plant growth, allowing us to study feedback between plant structure, plant function and microclimate (Godin and Sinoquet, 2005; Vos et al., 2010). Apart from recent studies on a mixture of two perennial species (Sonohat et al., 2002), on an integrated legume–weed system (Cici et al., 2008) and on coconut agroforestry systems (Dauzat and Eroy, 1997; Lamanda et al., 2008), most previous works devoted to estimating light partitioning within intercropping systems used the turbid medium approach by describing the canopy in one or two horizontal layers (Faurie et al., 1996; Lantinga et al., 1999; Tsubo and Walker, 2002; Tsubo et al., 2005; Awal et al., 2006). However, due to experimental constraints inherent to multispecies canopies, these models were not directly validated. As proposed in the present study, 3-D virtual models which explicitly describe plant architecture therefore appeared to be a convenient tool for the assessment of turbid medium models dealing with light partitioning in intercropping systems. Therefore, 3-D structural models, either static or dynamic, remain a complex but efficient tool for studying light partitioning within multispecies stands in order to improve the complementarity between the mixed crops or, by contrast, to analyse/develop more competitive cultivars to improve the management of weeds (Cici et al., 2008). Moreover, such models could also be used to generate virtual experiments suitable for the assessment of the turbid medium approach on other existing intercropping systems or in the framework of theoretical and exploratory studies.
ACKNOWLEDGMENTS
This research is supported by ‘La Région Pays de la Loire’, France. We thank Arnaud Philipponneau and Cédric Perrot for their great technical assistance.
LITERATURE CITED
- Adam B, Sinoquet H, Godin C, Donès N. 3A – software for the acquisition of plant architecture. Clermont-Ferrand: UMR PIAF INRA-UBP; 1999. [Google Scholar]
- Adam B, Donès N, Sinoquet H. VegeSTAR – software to compute light interception and canopy photosynthesis from images of 3D digitised plants. Clermont-Ferrand: UMR PIAF INRA-UBP; 2002. [Google Scholar]
- Andrieu B, Sinoquet H. Evaluation of structure description requirements for predicting gap fraction of vegetation canopies. Agricultural and Forest Meteorology. 1993;65:207–227. [Google Scholar]
- Awal MA, Koshi H, Ikeda T. Radiation interception and use by maize/peanut intercrop canopy. Agricultural and Forest Meteorology. 2006;139:74–83. [Google Scholar]
- Chamblee DS, Collins M. Relationships with other species in a mixture. In: Hanson AA, Barnes DK, Hill RR Jr, editors. Alfalfa and alfalfa improvement. Madison, WI: American Society of Agronomy; 1988. pp. 439–461. [Google Scholar]
- Chelle M. Phylloclimate or the climate perceived by individual plant organs: What is it? How to model it? What for? New Phytologist. 2005;166:781–790. doi: 10.1111/j.1469-8137.2005.01350.x. [DOI] [PubMed] [Google Scholar]
- Chelle M, Andrieu B. Radiative models for architectural modeling. Agronomie. 1999;19:225–240. [Google Scholar]
- Chen SG, Impens I, Ceulemans R, Kockelbergh F. Measurement of gap fraction of fractal generated canopies using digitalized image analysis. Agricultural and Forest Meteorology. 1993;65:245–259. [Google Scholar]
- Cici SZ-H, Adkins S, Hanan J. A canopy architectural model to study the competitive ability of chickpea with sowthistle. Annals of Botany. 2008;101:1311–1318. doi: 10.1093/aob/mcn040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Combes D, Chelle M, Sinoquet H, Varlet-Grancher C. Evaluation of a turbid medium model to simulate light interception by walnut trees (hybrid NG38 × RA and Juglans regia) and sorghum canopies (Sorghum bicolor) at three spatial scales. Functional Plant Biology. 2008;35:823–836. doi: 10.1071/FP08059. [DOI] [PubMed] [Google Scholar]
- Da Silva D, Boudon F, Godin C, Sinoquet H. Multiscale framework for modeling and analyzing light interception by trees. Multiscale Modeling & Simulation. 2008;7:910–933. [Google Scholar]
- Dauzat J, Eroy MN. Simulating light regime and intercrop yields in coconut based farming systems. European Journal of Agronomy. 1997;7:63–74. [Google Scholar]
- Den Bulk JA. The interpretation of remote sensing, a feasibility study. 1989 Thesis, Wageningen. [Google Scholar]
- Faurie O, Soussana JF, Sinoquet H. Radiation interception, partitioning and use in grass–clover mixtures. Annals of Botany. 1996;77:35–46. [Google Scholar]
- Fournier C, Andrieu B, Ljutovac S, Saint-Jean S. ADEL-wheat: a 3D architectural model of wheat development. In: Hu BG, editor. International Symposium on Plant Growth Modeling, Simulation, Visualization, and their Applications. Beijing: Tsinghua University Press/Springer; 2003. pp. 54–63. [Google Scholar]
- Giller KE, Beare MH, Lavelle P, Izac AMN, Swift MJ. Agricultural intensification, soil biodiversity and agroecosystem function. Applied Soil Ecology. 1997;6:3–16. [Google Scholar]
- Godin C. Representing and encoding plant architecture: a review. Annals of Forest Science. 2000;57:413–438. [Google Scholar]
- Godin C, Caraglio Y. A multiscale model of plant topological structures. Journal of Theoretical Biology. 1998;191:1–46. doi: 10.1006/jtbi.1997.0561. [DOI] [PubMed] [Google Scholar]
- Godin C, Sinoquet H. Functional–structural plant modelling. New Phytologist. 2005;166:705–708. doi: 10.1111/j.1469-8137.2005.01445.x. [DOI] [PubMed] [Google Scholar]
- Griffon M. Développement durable et agriculture: la révolution doublement verte. Cahiers Agricultures. 1999;8:259–267. [Google Scholar]
- Gutschick VP. Joining leaf photosynthesis models and canopy photon-transport models. In: Myneni RB, Ross J, editors. Photon–vegetation interactions: applications in optical remote sensing and plant ecology. Berlin: Springer-Verlag; 1991. pp. 501–535. [Google Scholar]
- Harper JL. Approaches to the study of plant competition. In: Milthorpe FL, editor. Mechanisms in biological competition. Cambridge: Symposia of the Society for Experimental Biology; 1961. pp. 1–39. [Google Scholar]
- Haynes RJ. Competitive aspects of the grass–legume association. In: Brady NC, editor. Advances in agronomy. New York: Academic Press; 1980. pp. 227–261. [Google Scholar]
- Lamanda N, Dauzat J, Jourdan C, Martin P, Malézieux E. Using 3D architectural models to assess light availability and root bulkiness in coconut agroforestry systems. Agroforestry Systems. 2008;72:63–74. [Google Scholar]
- Lantinga EA, Nassiri M, Kropff MJ. Modelling and measuring vertical light absorption within grass-clover mixtures. Agricultural and Forest Meteorology. 1999;96:71–83. [Google Scholar]
- Louarn G, Corre-Hellou G, Fustec J, et al. Déterminants écologiques et physiologiques de la productivité et de la stabilité des associations graminées-légumineuses. Innovations Agronomiques. 2010;11:79–99. [Google Scholar]
- Malézieux E, Crozat Y, Dupraz C, et al. Mixing plant species in cropping systems: concepts, tools and models. A review. Agronomy for Sustainable Development. 2009;29:43–62. [Google Scholar]
- Monsi M, Saeki T. Über den Lichtfaktor in den Pflanzengesellschaften und seine Bedeutung für die Stoffproduktion. Japanese Journal of Botany. 1953;14:22–52. [Google Scholar]
- Moon P, Spencer DE. Illumination from a non-uniform sky. Illuminating Engineering Society. 1942;37:707–726. [Google Scholar]
- Moulia B, Sinoquet H. Three-dimensional digitizing systems for plant canopy geometrical structure: a review. In: Varlet-Grancher C, Bonhomme R, Sinoquet H, editors. Crop structure and light microclimate. Paris: INRA editions; 1993. pp. 183–193. [Google Scholar]
- Nassiri M, Elgersma A, Lantinga EA. Vertical distribution of leaf area, dry matter and radiation in grass-clover mixtures. In: Parente G, Frame J, Orsi S, editors. Grassland and land use systems. 16th meeting of the European Grassland Federation. Gorizia, Italy: ERSA; 1996. pp. 269–274. [Google Scholar]
- Nilson T. A theoretical analysis of the frequency of gaps in plant stands. Agricultural Meteorology. 1971;8:25–38. [Google Scholar]
- Ofori F, Stern WR. Cereal–legume intercropping systems. Advances in Agronomy. 1987;41:41–90. [Google Scholar]
- Polhemus. 3Space Fastrak user's manual, revision F. Colchester, VT: Polhemus Inc; 2009. [Google Scholar]
- Pradal C, Dufour-Kowalski S, Boudon F, Fournier C, Godin C. OpenAlea: a visual programming and component-based software platform for plant modelling. Functional Plant Biology. 2008;35:751–760. doi: 10.1071/FP08084. [DOI] [PubMed] [Google Scholar]
- Rimmington GM. A model of the effect of interspecies competition for light on dry-matter production. Australian Journal of Plant Physiology. 1984;11:277–286. [Google Scholar]
- Ross J. The radiation regime and architecture of plant stands. The Hague, The Netherlands: W. Junk; 1981. p. 391. [Google Scholar]
- Schulte RPO, Lantinga EA. Mechanistic simulation of the vertical structure of mixed swards. Ecological Modelling. 2002;149:229–246. [Google Scholar]
- Sinoquet H. Modelling radiative transfer in heterogeneous canopies and intercropping systems. In: Varlet-Grancher C, Bonhomme R, Sinoquet H, editors. Crop structure and light microclimate. Paris: INRA editions; 1993. pp. 229–252. [Google Scholar]
- Sinoquet H, Bonhomme R. Modelisation de l'interception des rayonnements solaires dans une culture en rangs. II: Structure geometrique du couvert et validation du modele. Agronomie. 1989;9:619–628. [Google Scholar]
- Sinoquet H, Bonhomme R. A theoretical analysis of radiation interception in a two-species plant canopy. Mathematical Biosciences. 1991;105:23–45. doi: 10.1016/0025-5564(91)90047-m. [DOI] [PubMed] [Google Scholar]
- Sinoquet H, Caldwell MM. Estimation of light capture and partionning in intercropping systems. In: Sinoquet H, Cruz P, editors. Ecophysiology of tropical intercropping. Paris: INRA; 1995. pp. 79–97. [Google Scholar]
- Sinoquet H, Moulia B, Gastal F, Bonhomme R, Varlet -Grancher C. Modeling the radiative balance of the components of a well-mixed canopy: application to a white clover-tall fescue mixture. Acta Oecologica-International Journal of Ecology. 1990;11:469–486. [Google Scholar]
- Sinoquet H, Rakocevic M, Varlet-Grancher C. Comparison of models for daily light partitioning in multispecies canopies. Agricultural and Forest Meteorology. 2000;101:251–263. [Google Scholar]
- Sonohat G, Sinoquet H, Varlet-Grancher C, et al. Leaf dispersion and light partitioning in three-dimensionally digitized tall fescue-white clover mixtures. Plant, Cell and Environment. 2002;25:529–538. [Google Scholar]
- Tilman D, Cassman KG, Matson PA, Naylor R, Polasky S. Agricultural sustainability and intensive production practices. Nature. 2002;418:671–677. doi: 10.1038/nature01014. [DOI] [PubMed] [Google Scholar]
- Tournebize R, Sinoquet H. Light interception and partitioning in a shrub/grass mixture. Agricultural and Forest Meteorology. 1995;72:277–294. [Google Scholar]
- Tsubo M, Walker S. A model of radiation interception and use by a maize–bean intercrop canopy. Agricultural and Forest Meteorology. 2002;110:203–215. [Google Scholar]
- Tsubo M, Walker S. Shade effects on Phaseolus vulgaris L. intercropped with Zea mays L. under well-watered conditions. Journal of Agronomy and Crop Science. 2004;190:168–176. [Google Scholar]
- Tsubo M, Walker S, Ogindo HO. A simulation model of cereal–legume intercropping systems for semi-arid regions: I. Model development. Field Crops Research. 2005;93:10–22. [Google Scholar]
- Vos J, Evers JB, Buck-Sorlin GH, Andrieu B, Chelle M, de Visser PHB. Functional–structural plant modelling: a new versatile tool in crop science. Journal of Experimental Botany. 2010;61:2101–2115. doi: 10.1093/jxb/erp345. [DOI] [PubMed] [Google Scholar]
- Willey RW. Intercropping – its importance and research needs. Part 1. Field Crop Abstracts. 1979;32:1–10. Competition and yield advantages. [Google Scholar]