Calibration of otoacoustic emission probe microphones

Abstract

Recently, investigators of otoacoustic emissions (OAEs) have shown interest in measuring OAEs to frequencies higher than 10 kHz. Most commercial instruments used to measure OAEs do not specify the microphone frequency response at higher frequencies, nor does their typically integrated design make it convenient to measure it. OAE probes manufactured by Etymotic Research have reasonably constant microphone sensitivity up to about 10 kHz and allow direct access to both the sound sources and microphone preamplifier output. A detailed procedure for calibrating the Etymotic Research OAE probe microphone to extend its usable frequency range to frequencies up to 20 kHz is described.

Introduction

One of the main requirements for measuring otoacoustic emissions (OAEs) is a miniature microphone with a wide bandwidth and low noise floor. Microphones commonly used for OAE measurements (e.g., ER-10B+ and ER-10C, Etymotic Research) have a reasonably flat frequency response up to about 10 kHz. Siegel1 described a procedure for extending the usable frequency range of such microphones by compensating for their actual frequency response. This paper applies Siegel’s procedure to the calibration of Etymotic OAE probe microphone using easily available hardware and software.

Siegel’s calibration procedure seems to have received little attention from OAE investigators, perhaps due to insufficient detail in the description or because most investigators have been concerned with measuring OAE only up to about 8 kHz. However, recently a number of investigators have reported OAE measurements of up to 20 kHz.2, 3, 4 Improper calibration of emission probe microphones used for these high-frequency OAE measurements can potentially lead to measurement and data interpretation errors.

Here we describe the calibration of ER-10B+ and ER-10C microphones using readily available hardware and software.

Methods

Physical setup

The calibration is performed in a hard-walled cavity of uniform cross-sectional area that has a diameter large enough to accommodate the emission probe with its foam tip and the reference microphone. The cavity should be optically transparent to allow monitoring of microphone placement. We used a 3-cm³ cutoff plastic syringe body (65 mm long and 8 mm i.d.), but any similar cylinder will suffice.

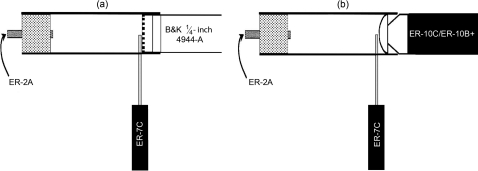
Figure 1 shows the physical setup for the calibration procedure. A sound source (ER-2, Etymotic Research) is inserted at one end of the cavity. The procedure involves two steps. In the first step [see Fig. 1a], a probe tube microphone (ER-7C, Etymotic Research) is calibrated against a reference microphone ([1∕4]-inch type 4944-A with built-in preamplifier, connected to a type 2693 conditioning amplifier, Brüel & Kjær). This reference microphone has a flat pressure spectrum up to 50 kHz. A custom sleeve (made from surgical tape) was wrapped around the reference microphone to form a stable acoustic seal and to keep the microphone in place. In the second step [see Fig. 1b], the reference microphone is replaced by the emission probe (ER-10B+ or ER-10C) and the latter is calibrated against the probe tube. The calibrated plane of the emission probe is defined as the location where the measured pressure is to be related to the pressure response of the reference microphone.

Figure 1.

Physical setup of the calibration procedure. The procedure involves two sets of measurements. In the first measurement (a), the transfer function between the reference microphone and probe tube is determined. In the second measurement (b), the transfer function between the emission probe and the probe tube is determined.

A plane progressive wave produces an instantaneous pressure that is uniform across the plane of the reference microphone. A separation of 20 mm is enough to ensure the formation of a plane wave.1 Since the reference microphone and the emission probe cannot both be placed in the cavity in the same ideal orientation at the same time, a third microphone—a probe tube—is inserted at a right angle to the length of the cavity as close as possible to the other microphone (reference or emission probe). The probe tube must be in close proximity (about 1 mm) to the other microphone so that they are both stimulated by the same sound pressure. It is also important that the probe tube not occlude the emission probe inlet.

The ER-2 sound source produces a lower sound pressure level for a constant voltage at higher frequencies compared to lower frequencies. This reduces the signal-to-noise ratio (SNR) in the measured pressure at high frequencies. To compensate for this effect, we increased the input voltage to increase the sound stimulus at high frequencies by applying preemphasis filtering (slope of 15 dB∕octave above 10 kHz) to the chirp stimulus. It is important to optimize the drive levels to achieve a satisfactory SNR, while avoiding distortion due to overloading any component of the calibration system.

Measurements and analysis

All measurements and computations were performed using SysRes,5 a software package with public access, interfaced to a high quality sound card (Layla3G, Echo Digital Audio Corporation). Use of SysRes allows for the completion of the calibration procedure of a single microphone in <5 min. A linear frequency-swept chirp of duration 21.3 ms, sampled at 48 kHz, was repeated 1024 times for signal averaging in the time-domain. There was no artifact rejection.

In the first set of measurements, the pressure frequency responses of the reference microphone P_ref(f) and probe tube P_pt1(f) are measured. The frequency transfer function of the reference microphone relative to the probe tube is

$$H_{\mathrm{ref}\mathrm{∕}\mathrm{pt}1}\left(f\right)=\frac{P_{\mathrm{ref}}\left(f\right)}{P_{\mathrm{pt}1}\left(f\right)}.$$ (1)

In the second measurement, the pressure frequency responses of the emission probe P_ep(f) and probe tube P_pt2(f) are measured. Care must be taken that the probe tube and sound source remain in the same location when swapping the reference microphone with the emission probe. The calibration plane of the emission probe has to be the same as the calibration plane of the reference microphone. The acoustic impedance of the emission probe measured at its inlet is generally different from that of the reference microphone, so the sound pressure level will now be different. This is why the response of the previously characterized probe tube is measured again. Any changes in the probe tube response are due to changes in the pressure at its inlet. However, the responses P_pt1 and P_pt2 should be generally similar. The frequency transfer function of the emission probe relative to the probe tube is computed from P_ep and P_pt2 as:

$$H_{\mathrm{ep}\mathrm{∕}\mathrm{pt}2}\left(f\right)=\frac{P_{\mathrm{ep}}\left(f\right)}{P_{\mathrm{pt}2}\left(f\right)}.$$ (2)

The frequency transfer function of the emission probe relative to the reference microphone is computed by dividing H_ep∕pt2 by H_ref∕pt1, that is:

$$H_{\mathrm{ep}\mathrm{∕}\mathrm{ref}}\left(f\right)=\frac{P_{\mathrm{ep}}\left(f\right)}{P_{\mathrm{pt}2}\left(f\right)}\times \frac{P_{\mathrm{pt}1}\left(f\right)}{P_{\mathrm{ref}}\left(f\right)}.$$ (3)

The magnitude of H_ep∕ref is a dimensionless gain. To obtain the desired physical units, H_ep∕ref must be multiplied by the sensitivity of the reference microphone (V∕Pa). Since the sensitivity is independent of frequency, the product becomes the frequency-dependent sensitivity of the emission probe in units of V∕Pa. This is the microphone sensitivity function (MSF).

Measurements of OAE made with the emission probe microphone may be corrected for frequencies greater than 10 kHz using the MSF either by multiplying the frequency response of the measured pressure by the MSF or by convolving the measured time-domain pressure with the impulse response of the MSF, obtained by inverse Fourier transform. In either case the pressure response is compensated in both magnitude and phase. The latter is often ignored when measuring sound levels, but is critical when calculating emission delays relative to the stimulus pressure at the calibrated plane of the emission probe. A decibel conversion that yields MSF with units of dB re 1 V∕Pa can be used for plotting the MSF.

Results

Examples of the calibration of six ER-10C and two ER-10B+ emission probe microphone units are presented. For each measurement of pressure required for the calibration procedure, three sets of measurements were made for each individual emission probe unit, and the individual mean pressure and standard deviation (SD) computed. The group mean and SD were also computed for the collection of emission probes.

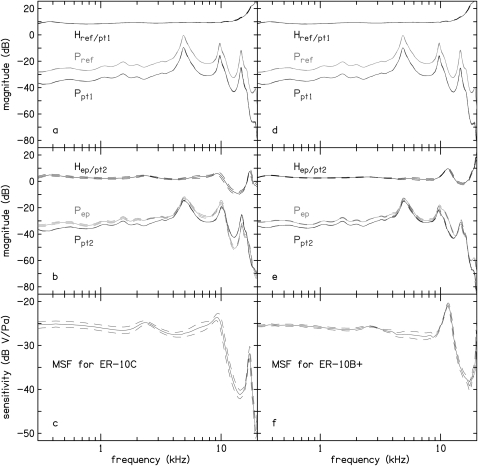
Results for the calibration of the six ER-10C emission probes are presented in the left column of Fig. 2. Figure 2a shows the group mean pressure (solid line) and mean ± SD (dashed line) for the reference microphone P_ref, probe tube P_pt1 and the transfer function H_ref∕pt1 for the first set of measurements to be used to calculate the frequency responses of the six ER-10C emission probes. For some of the measurements, the SD is very small (< 0.5 dB) that the dashed line cannot be distinguished from the solid line.

Figure 2.

(Color online) Calibration examples of ER-10C (left column) and ER-10B+ (right column) microphones. The top row (panels a and d) shows the pressure measurements (P_ref and P_pt1) used to determine the reference transfer function (H_ref∕pt1). The second row (panels b and e) shows the pressure measurements (P_ep and P_pt2) used to determine the emission probe transfer function (H_ep∕pt2). The third row (panels c and f) show the microphone sensitivity functions. Solid line: mean. Dashed line: mean ± SD.

The variation in frequency in the responses P_ref and P_pt1 represent the combined effect of the microphones, sound source and calibration cavity. The peaks in the responses P_ref and P_pt1 are the resonance frequencies of the cavity. Since the sensitivity of the reference microphone can be considered frequency-independent, the computation of H_ref∕pt1 removes all sources of frequency-dependence except for that of the probe tube. If the reference microphone and the probe tube microphone were not in close proximity so that the sound pressures at these two microphones were different, the resonance peaks of P_ref and P_pt1 would not align in frequency.

Figure 2b shows P_ep, P_pt2 and H_ep∕pt2 for the second set of measurements for the six ER-10C microphones. Again the peaks in the responses P_ep and P_pt2 are due to the resonances of the cavity, and computation of the transfer function H_ep∕pt2 has removed these peaks.

The transfer functions from the first measurement H_ref∕pt1 and the second measurement H_ep∕pt2 are used to compute the transfer function of the emission probe relative to the reference microphone H_ep∕ref using Eq. 3. This transfer function is multiplied by the sensitivity of the reference microphone (0.1 V∕Pa) to obtain the MSF. The mean MSF (solid line) and its mean ± SD (dashed line) for the ER-10C microphones are shown in Fig. 2c. The mean MSF for the ER-10C probes is nearly flat up to 10 kHz, except for a small peak at 2.4 kHz and another peak at 9.5 kHz. There is a dip of about 18 dB between 10 and 17.5 kHz. The gain of the emission probe near 19 kHz is typically as much as 30 dB lower than the nominal sensitivity at 1 kHz.

The variability in repeated measurements for the individual probes is very low; the mean SD is less than 0.7 dB in all the measurements. The maximum value of the SD for the all the measurements is in the range 0.7 dB to 5.6 dB, and typically occurs close to 20 kHz. As expected there is more variability across emission probes. However, this variability is still very low; mean SD is less than 1.2 dB, and maximum SD, occurring close to 20 kHz, is 4 dB.

Results for the calibration of the two ER-10B+ emission probes are presented in the right column of Fig. 2. Figure 2d shows mean and mean±SD of P_ref, P_pt1 and H_ref∕pt1 for the first set of measurements, and Fig. 2e shows P_ep, P_pt2 and H_ep∕pt2 for the second set of measurements. As with the ER-10C, computation of the transfer function has removed the resonance peaks due to the tube. The mean and mean ± SD for MSF for the ER-10B+ computed using the transfer functions H_ref∕pt1 and H_ep∕pt2 and the sensitivity of the reference microphone (0.1 V∕Pa) are shown in Fig. 2f. The mean MSF of the ER-10B+ is flat up to 11.5 kHz, where it has a small peak. There is a dip of about 18 dB between 12 and 18 kHz. The gain of the emission probe near 19 kHz is typically as much as 30 dB lower than the nominal sensitivity at 1 kHz.

As with the measurements for the ER-10C, the variability in the measurements for the individual ER-10B+ units is very low; the mean SD is less than 0.6 dB in all the measurements. The maximum value of the SD for all of the measurements is in the range 1 dB to 11 dB, and typically occurred close to 20 kHz. Again as expected there is more variability across emission probes. However, this variability is again still very low; mean SD for the group of units is less than 1 dB and maximum SD is 10 dB, also occurring close to 20 kHz.

Discussion and Conclusion

The low variability observed in the measurements across each set of OAE probes (see Fig. 2) demonstrates excellent repeatability of the calibration procedure.

Without calibration, the large dips of about 18 dB observed in the microphone sensitivity function of both the ER-10C and ER-10B+ (see Fig. 2) would make OAE measurements acquired with these microphones appear 18 dB lower than they actually are. This could lead to erroneous interpretations of measured data and to comparable errors for in-the-ear calibration.1

The calibration procedure produces a microphone sensitivity function that can be used in OAE acquisition hardware or software to correct the frequency response above 10 kHz, ensuring accurate measurement of acoustic signals. In addition to extending the usable frequency range of the emission probe to higher frequencies, calibrating can be used to verify that the emission probe is operating correctly.