Generalized Langevin dynamics of a nanoparticle using a finite element approach: Thermostating with correlated noise

Abstract

A direct numerical simulation (DNS) procedure is employed to study the thermal motion of a nanoparticle in an incompressible Newtonian stationary fluid medium with the generalized Langevin approach. We consider both the Markovian (white noise) and non-Markovian (Ornstein-Uhlenbeck noise and Mittag-Leffler noise) processes. Initial locations of the particle are at various distances from the bounding wall to delineate wall effects. At thermal equilibrium, the numerical results are validated by comparing the calculated translational and rotational temperatures of the particle with those obtained from the equipartition theorem. The nature of the hydrodynamic interactions is verified by comparing the velocity autocorrelation functions and mean square displacements with analytical results. Numerical predictions of wall interactions with the particle in terms of mean square displacements are compared with analytical results. In the non-Markovian Langevin approach, an appropriate choice of colored noise is required to satisfy the power-law decay in the velocity autocorrelation function at long times. The results obtained by using non-Markovian Mittag-Leffler noise simultaneously satisfy the equipartition theorem and the long-time behavior of the hydrodynamic correlations for a range of memory correlation times. The Ornstein-Uhlenbeck process does not provide the appropriate hydrodynamic correlations. Comparing our DNS results to the solution of an one-dimensional generalized Langevin equation, it is observed that where the thermostat adheres to the equipartition theorem, the characteristic memory time in the noise is consistent with the inherent time scale of the memory kernel. The performance of the thermostat with respect to equilibrium and dynamic properties for various noise schemes is discussed.

INTRODUCTION

Hydrodynamic interactions and thermal fluctuations both play important roles in determining the motion of the nanoparticle in an incompressible Newtonian stationary fluid medium. Nanoparticles undergo thermal motion in a fluid which can be simulated either using the fluctuating hydrodynamics approach or using the Langevin approach. In the fluctuating hydrodynamics approach, the nanoparticle motion incorporates both the Brownian motion and the effect of hydrodynamic force acting on its surface imparted from the surrounding fluid. Over the years, many numerical simulation schemes, such as the finite volume method,^{1, 2} the lattice Boltzmann method (LBM),^{3, 4, 5, 6, 7, 8} and the stochastic immersed boundary method,⁹ have been developed to investigate the Brownian motion of a particle using fluctuating hydrodynamics. A coarse-graining methodology has been developed to bridge molecular dynamics and fluctuating hydrodynamics simulations.^{10, 11} In our recent paper,¹² we have employed a finite element method (FEM) to determine the thermal motion of a nanoparticle in a fluid medium using fluctuating hydrodynamics approach. Even though the Brownian motion of a nanoparticle using fluctuating hydrodynamics has been extensively studied using the LBM technique,^{6, 7} the advantage of the FEM approach is that it is versatile for flow description through arbitrary geometries.¹³

In this paper, we pursue the Langevin approach, in which the thermal fluctuations from the fluid are incorporated as random forces and torques in the particle equation of motion.^{14, 15, 16, 17, 18, 19} The primary objective here is to build a robust thermostat, which preserves equilibrium distributions at constant temperatures (i.e., adheres to the equipartition theorem) and enables the evaluation of free energy landscapes of nanoparticle adhesion with surfaces in future applications. By definition, coupling to a thermostat will alter the hydrodyamics of the nanoparticle system. Hence, our objective here is to characterize the performance of the thermostat as well as how it alters the associated hydrodynamic correlations. In this respect, this study will complement our earlier investigation.¹² The results of the classical Langevin equation using the instantaneous friction law predict rapid exponential decay in the velocity autocorrelation function (VACF). Using computer simulations on a hard-sphere system, Rahman²⁰ and Alder and Wainwright²¹ found a long-tailed decay ( ∼ t^−3/2) in the VACF. Zwanzig and Bixon²² have theoretically justified the power-law decay of VACF using a frequency dependent version of the Stokes-Einstein diffusion formula. Hauge and Martin-Löf have considered the Brownian motion of particles of arbitrary shape and have shown that in the Langevin approach, the momentum equation for the nanoparticle can be appropriately modified to satisfy the generalized fluctuation-dissipation theorem.²³ Numerical schemes for studying the nanoparticle motion in a fluid must simultaneously consider the momentum (Langevin) equation for the particle and the Navier-Stokes equation for the fluid. The random force∕torque in the particle equation can then be related to the frictional force∕torque via the generalized fluctuation-dissipation theorem.^{24, 25} The implementation can occur in two ways: (i) directly adjust the variance of the random force term in the classical Langevin equation to play the role of a thermostat. In this context, Iwashita et al.^{18, 19} have considered an iterative scaling scheme within the direct numerical simulation (DNS) by adjusting the variance of the random force term in the momentum equation; such a procedure, while useful in constructing a thermostat that preserves hydrodynamic correlations, is still ad hoc in the sense that it deviates from the structure of the generalized Langevin equation. (ii) A second, more direct approach that preserves the structure of the generalized Langevin equation (GLE), is to consider the power spectrum for the variance of the random force term using a correlated or colored noise with a well defined characteristic memory time. This is the approach employed in the present study. As we show here, such a formalism simultaneously preserves the equipartition theorem and the nature of the long time hydrodynamic correlations, and proves to be a versatile thermostat. Eventually, this formalism can also easily be extended to capture (i.e., reproduce an a priori specified) the thermal force fluctuations such as those experienced by a nanoparticle due to collisions with blood cells.²⁶ This is important in intravascular nanoparticle-based targeted drug delivery (TDD)^{27, 28, 29} which is a major motivation for this study.

Here, we solve the momentum equations simultaneously for the nanoparticle and the fluid using arbitrary Lagrangian-Eulerian (ALE) based FEM to determine the thermal characteristics. The paper is organized as follows: Sec. 2 is focused on the thermostat described by a one-dimensional (1D) GLE. Section 3 describes the formulation of the hydrodynamic equations in a three-dimensional (3D) system. This includes the Galerkin finite element combined formulation for the fluid and particle momentum equations subject to thermal fluctuations. Numerical results along with validations are presented in Sec. 4 and conclusions are presented in Sec. 5.

THERMOSTAT DESCRIBED BY AN 1D GLE

1D GLE with correlated noise schemes

For a Brownian particle, the GLE in one dimension is given by

$$m\frac{dU}{dt}=-{\int }_{-\infty }^t{\zeta }^{\left(trans\right)}(t-t^{\prime })U\left(t^{\prime }\right)d{t}^{\prime }+R\left(t\right),$$ (1)

where U is the velocity of the particle, ζ^(trans)(t) is the frictional memory kernel and m is the mass of the particle. The random force R(t) is generally taken to be zero-centered and stationary Gaussian,^{24, 30} which is sampled from the correlation function,

$$\begin{array}{c}\hfill ⟨R\left(t\right)R\left(t^{\prime }\right)⟩=\mathcal{C}\left(\right|t-t^{\prime }\left|\right).\end{array}$$ (2)

The memory kernel ζ^(trans)(t) is related to the correlation function of the noise via the second fluctuation-dissipation theorem,³¹

$$\begin{array}{c}\hfill \mathcal{C}\left(\right|t-t^{\prime }\left|\right)=k_{B}T{\zeta }^{\left(trans\right)}\left(\right|t-t^{\prime }\left|\right),\end{array}$$ (3)

where, k_B is the Boltzmann constant and T is the absolute temperature. In particular, if R(t) is both Gaussian and Markovian, then Doob's theorem³² states that R(t) is necessarily an Ornstein-Uhlenbeck process,³³ with an exponential correlation function given by,

$$\begin{array}{ccc}\hfill {\zeta }^{\left(trans\right)}\left(\right|t-t^{\prime }\left|\right)& =& {\zeta }^{\left(trans\right)}\gamma \left(\right|t-t^{\prime }\left|\right),\hfill \\ \hfill \gamma \left(\right|t-t^{\prime }\left|\right)& =& \frac{1}{\tau }{e}^{-|t-t^{\prime }|∕\tau },\hfill \end{array}$$ (4)

where, ζ^(trans)( = 6πμa) is the constant friction coefficient, γ(|t − t′|) is the dissipative memory kernel, τ is the characteristic memory time, μ is the dynamic viscosity of the fluid, and a is the radius of the nanoparticle. In the limit of characteristic memory time τ → 0,

$$\begin{array}{c}\hfill \gamma \left(\right|t-t^{\prime }\left|\right)=2\delta (t-t^{\prime }),\end{array}$$ (5)

which corresponds to a white noise, non-retarded friction, and standard Brownian motion.³⁴ Zwanzig and Bixon²² have shown that for a constant friction coefficient ζ^(trans), the VACF of the particle in a simple fluid obeys

$$〈U\left(t\right)U\left(0\right)〉=\frac{k_{B}T}{m}{e}^{-{\zeta }^{\left(trans\right)}t∕m},$$ (6)

i.e., an exponential decay. Also, for the time dependent friction coefficient ζ^(trans)(t) (derived from a linearized Navier-Stokes equation), the decay of the VACF at long times obey

$$〈U\left(t\right)U\left(0\right)〉\approx \frac{\mathcal{B}{k}_{B}T}{m}{({\zeta }^{\left(trans\right)}t∕m)}^{-3∕2},$$ (7)

i.e., a power-law decay, where ⟨⟩ denotes the ensemble average, B is a constant. Rahman²⁰ and Alder and Wainwright²¹ have demonstrated using molecular dynamics simulations that the velocity autocorrelation function of the particle has a long time tail as given by Eq. 7. In the literature, pure power-law correlation functions have been employed to investigate the anomalous diffusion behavior of the particle that is related to the long time tail correlations.^{35, 36, 37, 38} Recently, Viñales and Despósito³⁹ have considered a Mittag-Leffler noise given by

$$\begin{array}{ccc}\hfill \mathcal{C}\left(\right|t-t^{\prime }\left|\right)& =& k_{B}T{\zeta }^{\left(trans\right)}\left(\right|t-t^{\prime }\left|\right)=m{k}_{B}T\gamma \left(\right|t-t^{\prime }\left|\right),\hfill \\ \hfill \gamma \left(\right|t-t^{\prime }\left|\right)& =& \frac{\gamma \left(\lambda \right)}{{\tau }^{\lambda }}{E}_{\lambda }\left[-{\left(\frac{|t-t^{\prime }|}{\tau }\right)}^{\lambda }\right],\hfill \end{array}$$ (8)

where the exponent λ taken as 0 < λ < 2, γ(λ) is the proportionality coefficient dependent on the exponent λ, and E_λ(y) is the Mittag-Leffler function defined through the series as⁴⁰

$$\begin{array}{c}\hfill E_{\lambda }\left(y\right)=\sum _{n=0}^{\infty }\frac{y^n}{\Gamma (\lambda n+1)},\lambda >0.\end{array}$$ (9)

Here, Γ denotes the Gamma function. The exponent λ is determined by the dynamics of the physical process considered. The correlation function described by Eq. 8 behaves as a stretched exponential for short times and as an inverse power-law for long times when λ ≠ 1,⁴¹ and it is non-singular at the origin due to the presence of characteristic memory time τ. For λ = 1, the function in Eq. 8 reduces to an exponential form, which describes a standard Ornstein-Uhlenbeck process given in Eq. 4 with γ(|t−t^′|)=(γ∕τ)e^{−|t−t′|∕τ}. For λ ≠ 1 and in the limit of characteristic memory time τ → 0, the function in Eq. 8 reduces to a pure power-law correlation function. It is interesting to note that the Mittag-Leffler function, E_λ( − t^λ), shows different behaviors depending on the value of exponent λ.^{41, 42}

The particle's mean velocity (i.e., VACF) and the mean square displacement (MSD) for the generalized Langevin equation with a Mittag-Leffler memory kernel are given by^{35, 39, 43}

$$\begin{array}{ccc}\hfill 〈U\left(t\right)U\left(0\right)〉& =& \frac{k_{B}T}{m}{E}_{2-\lambda }[-{\left({\omega }_{\lambda }t\right)}^{2-\lambda }],\hfill \end{array}$$ (10)

$$\begin{array}{ccc}\hfill ⟨\Delta x^2\left(t\right)⟩& =& 2\frac{k_{B}T}{m}{t}^2{E}_{2-\lambda ,3}[-{\left({\omega }_{\lambda }t\right)}^{2-\lambda }],\hfill \end{array}$$ (11)

where ${\omega }_{\lambda }^{2-\lambda }=\gamma \left(\lambda \right)$ (units of γ(λ) is s^{λ − 2}). In the short and long time regimes, the above Mittag-Leffler series reduces to a stretched (0 < λ < 1) or compressed exponential (1 < λ < 2) and an inverse power-law, respectively (see Table 1). It is well known that 1D GLE with Mittag-Leffler noise describes the motion of an anomalously diffusing particle.

Table 1.

The VACF and MSD of the particle at short and long time regimes for the generalized Langevin equation with a Mittag-Leffler memory kernel. Here, γ(λ) is a proportionality coefficient dependent on the exponent λ. We note that γ(λ) is obtained for a given λ (but is independent of time t or τ) such that the equipartition theorem is satisfied.

	Short time regime	Long time regime
VACF	${\displaystyle \frac{k_{B}t}{m}\exp \{-\chi t^{2-\lambda }\};\chi \approx \frac{\gamma \left(\lambda \right)}{\Gamma (3-\lambda )}}$	${\displaystyle \frac{k_{B}t}{m}\phi t^{\lambda -2},\phi \approx \frac{1}{\gamma \left(\lambda \right)\Gamma (\lambda -1)}}$
MSD	${\displaystyle 2\frac{k_{B}t}{m}{t}^2\exp \{-\Psi t^{2-\lambda }\};\Psi \approx \frac{\gamma \left(\lambda \right)}{\Gamma (5-\lambda )}}$	${\displaystyle 2\frac{k_{B}t}{m}\Phi t^{\lambda },\Phi \approx \frac{1}{\gamma \left(\lambda \right)\Gamma (1+\lambda )}}$

Numerical modeling of the 1D GLE

In this study, the GLE in Eq. 1 together with the correlation function in Eqs. 4 or 8 is numerically solved using a finite difference method. The time scales involved are (i) τ_b = m/ζ^(trans), the Brownian relaxation time over which velocity correlations decay in the Langevin equation, (ii) τ_d = a²ζ^(trans)/k_BT, the Brownian diffusive time scale over which the nanoparticle diffuses over a distance equal to its own radius, and (iii) τ_ν = a²/ν, the hydrodynamic time scale for momentum to diffuse over a distance equal to the radius of the nanoparticle, where ν is the kinematic viscosity of the fluid. The time scale Δt for the numerical simulation has been chosen to be smaller than all the relevant physical time scales described above. The simulations presented in this study have been carried out for long enough durations to allow for the temperature of the particle to equilibrate, i.e., if N is the number of simulated time steps then N · Δt = t ≫ τ_ν. We consider a neutrally buoyant nanoparticle of radius 50 nm, and density ρ^(p) = 10³ kg/m³, diffusing in water with viscosity, μ=10⁻³ kg ∕ms, and density, ρ^(f) = 10³ kg/m³. For a particle of radius a = 50 nm, τ_b ≈ 5.55 × 10⁻¹⁰ s, τ_ν ≈ 2.5 × 10⁻⁹ s, and τ_d ≈ 5.5 × 10⁻⁴ s and for a particle of radius a = 250 nm, τ_b ≈ 1.38 × 10⁻⁸ s, τ_ν ≈ 6.25 × 10⁻⁸ s, and τ_d ≈ 6.88 × 10⁻² s.

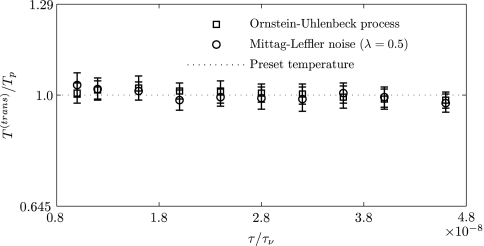
In the non-Markovian process (colored noise), the characteristic memory time τ adds a certain amount of memory from the previous history of fluctuations in the system. The value of τ is chosen such that it is much longer than the time step of integration. Figure 1 shows numerically evaluated translational temperature of the particle (T^(trans)) versus characteristic memory time for both the Ornstein-Uhlenbeck process and the Mittag-Leffler noise. The temperature of the particle is normalized with the preset temperature, T_p, of the thermostat. It is observed that the equipartition theorem is satisfied by both the colored noise schemes, validating our numerical procedure. The error bars have been plotted from standard deviations of the temperatures obtained with five different realizations, each realization computed up to 100 000 time steps.

Figure 1.

Temperature convergence for a particle of radius a = 50 nm in 1D GLE as a function of characteristic memory time using both the Ornstein-Uhlenbeck process and the Mittag-Leffler noise.

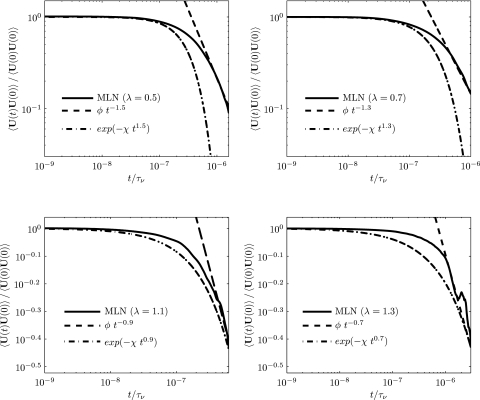
Figure 2 shows the VACF of the particle obtained from the 1D GLE simulations with Mittag-Leffler noise for various values of the power-law exponent λ. As shown, the short and long time behavior of VACF displays a stretched exponential and an algebraic decay, respectively, which depends on the exponent λ of the Mittag-Leffler noise. This is in agreement with the analytical solution presented in Table 1. We note that: (1) we have verified that the VACF for λ = 1.0 (Ornstein-Uhlenbeck process) decays exponentially and (2) for λ = 0.5 the long time decay of VACF ∼t^−3/2, and this is consistent with correlations in classical hydrodynamics of a Newtonian fluid.

Figure 2.

VACF of the particle of radius a = 50 nm for four different values of λ (holding τ fixed at 100Δt) obtained using the 1D GLE. Here, MLN stands for Mittag-Leffler Noise, ϕ and χ are given in Table 1.

FORMULATION OF HYDRODYNAMIC EQUATIONS IN THREE DIMENSIONS

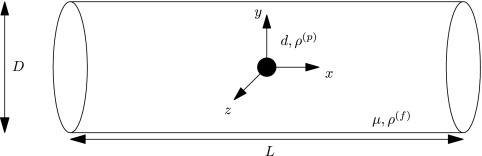
Now, we consider the thermal motion of a nanoparticle in an incompressible Newtonian stationary fluid medium in a horizontal circular vessel (see Figure 3). The fluid and particle equations are formulated in an inertial frame of reference with the origin coinciding with the center of the cylindrical vessel (Figure 3). The diameter, D, and the length, L, of the vessel are very large compared to the nanoparticle diameter, d. Initially, a nanoparticle is introduced either at the vessel centerline or at suitably chosen locations away from the center line towards the bounding wall. Initially, both the fluid and particle are at rest. No body force is assumed to be applied either on the particle or in the fluid domain. Starting at time t = 0, the nanoparticle experiences Brownian motion. The motion of the nanoparticle is determined by the hydrodynamic forces and torques acting on the particle and subject to the wall interactions.

Figure 3.

Schematic representation of a nanoparticle in a stationary fluid medium in a circular vessel (not to scale). Diameter of the vessel: D = 2R = 5 μm; length of the vessel: L = 10 μm; diameter of the nanoparticle: d = 2a = 100 or 500 nm; viscosity of the fluid: μ = 10⁻³ kg/ms; density of the fluid and the nanoparticle: ρ^(f) = ρ^(p) = 10³ kg/m³. Particle locations away from the center are not displayed in this figure.

Governing equations and boundary conditions

The motion generated in the incompressible Newtonian fluid satisfies the conservation of mass and momentum as given by

$$\begin{array}{c}\hfill \nabla ·\mathbf{u}=0,\end{array}$$ (12)

$$\begin{array}{ccc}\hfill {\rho }^{\left(f\right)}\left(\frac{\partial \mathbf{u}}{\partial t}+\left(\mathbf{u}·\nabla \right)\mathbf{u}\right)& =& \nabla ·\sigma ,\hfill \end{array}$$ (13)

where u and ρ^(f) are the velocity and density of the fluid, respectively, and σ is the stress tensor. For a Newtonian fluid, the stress tensor is given by

$$\begin{array}{c}\hfill \sigma =-p\mathbf{J}+2\mu \mathbf{D}\left[\mathbf{u}\right],\mathbf{D}\left[\mathbf{u}\right]=\frac{1}{2}[\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^T],\end{array}$$ (14)

where p is the pressure, J is the identity tensor, μ is the dynamic viscosity, and D[u] is the rate of deformation tensor.

For a rigid particle suspended in an incompressible Newtonian fluid, the translational motion of the particle satisfies Newton's second law,

$$\begin{array}{ccc}\hfill m\frac{d\mathbf{U}}{dt}& =& \mathbf{F}+\mathbf{R}\left(t\right),\hfill \end{array}$$ (15)

and the rotational motion satisfies the Euler equation,

$$\begin{array}{ccc}\hfill \frac{d\left(\mathbf{I}\omega \right)}{dt}& =& \mathbf{T}+\mathit{\Omega }\left(t\right),\hfill \end{array}$$ (16)

where m is the mass of the particle, I is its moment of inertia, and U and ω are the translational and angular velocities of the particle, respectively. The random force R and random torque Ω are added into the particle equations of motion similar to that of GLE (Eq. 1). The hydrodynamic force F and the torque T acting on the particle are given by

$$\begin{array}{ccc}\hfill \mathbf{F}& =& -{\int }_{\partial {\mathit{\Sigma }}_p}\sigma ·\widehat{\mathbf{n}}ds,\hfill \\ \hfill \mathbf{T}& =& -{\int }_{\partial {\mathit{\Sigma }}_p}\left(\mathbf{x}-\mathbf{X}\right)\times \left(\sigma ·\widehat{\mathbf{n}}\right)ds,\hfill \end{array}$$ (17)

where X is the position of the centroid of the particle, (x − X) is a vector from the center of the particle to a point on its surface, ∂Σ_p denotes the particle surface, and $\widehat{\mathbf{n}}$ is the unit normal vector on the surface of the particle pointing into the particle. The random force R and random torque Ω are assumed to be Gaussian with

$$\begin{array}{ccc}\hfill ⟨\mathbf{R}\left(t\right)⟩& =& 0,⟨\mathbf{R}\left(t\right)\mathbf{R}\left(t^{\prime }\right)⟩=\mathcal{C}\left(\right|t-t^{\prime }\left|\right)=m{k}_{B}T\alpha \left(\right|t-t^{\prime }\left|\right),\hfill \end{array}$$ (18)

$$\begin{array}{ccc}\hfill ⟨\mathit{\Omega }\left(t\right)⟩& =& 0,⟨\mathit{\Omega }\left(t\right)\mathit{\Omega }\left(t^{\prime }\right)⟩=\mathcal{D}\left(\right|t-t^{\prime }\left|\right)=\mathbf{I}{k}_{B}T\beta \left(\right|t-t^{\prime }\left|\right),\hfill \end{array}$$ (19)

where α and β are the dissipative memory kernels for force and torque, respectively. Equations 18, 19 satisfy the fluctuation-dissipation theorem.^{24, 25} The right-hand sides of Eqs. 18, 19 denote the mean and variance of the thermal fluctuations. By including this Brownian force due to the thermal fluctuations in the governing equations, the macroscopic hydrodynamic theory is generalized to include the mesoscopic scales ranging from tens of nanometers to a few micrometers.

The initial conditions for the problem are

$$\begin{array}{ccc}\hfill \mathbf{U}(t=0)& =& 0,\hfill \\ \hfill \mathbf{u}(t=0)& =& 0\text{on}{\Sigma }_0-\partial {\Sigma }_i,\hfill \end{array}$$ (20)

and the boundary conditions are given by

$$\begin{array}{ccc}\hfill \mathbf{u}& =& 0\text{on}\partial {\Sigma }_i,\hfill \end{array}$$ (21)

$$\begin{array}{ccc}\hfill \sigma ·\widehat{\mathbf{n}}& =& 0\text{on}\partial {\Sigma }_o,\hfill \end{array}$$ (22)

$$\begin{array}{ccc}\hfill \mathbf{u}& =& \mathbf{U}+\omega \times \left(\mathbf{x}-\mathbf{X}\right)\text{on}\partial {\Sigma }_p,\hfill \end{array}$$ (23)

where Σ₀ is the domain occupied by the fluid and ∂Σ_i and ∂Σ_o are the inlet and outlet boundaries, respectively. The governing equations 12, 13, 14, 15, 16 along with the initial and boundary conditions 20, 21, 22, 23 are solved numerically.

Combined fluid-solid weak formulation

Owing to the complex nature of the particle motion, finite-element techniques are particularly useful for discretizing the governing fluid equations. For this purpose, a weak formulation that incorporates both the fluid and particle equations (Eqs. 12, 13, 15, 16) is considered.^{44, 45}

Let V be the function space given by

$$\begin{array}{c}\hfill \mathbb{V}=\left\{\begin{array}{c}\mathbf{V}=(\mathbf{u},\mathbf{U},\omega )|\mathbf{u}\in H^1,(\mathbf{U},\omega )\in {\mathcal{R}}^3\hfill \\ \mathbf{u}=\mathbf{U}+\omega \times \left(\mathbf{x}-\mathbf{X}\right)\text{on}\partial {\Sigma }_p\text{,}\mathbf{u}={\mathbf{u}}_p\text{on}\partial {\Sigma }_i\hfill \end{array}\right\}.\end{array}$$ (24)

Here, H¹ corresponds to the Hilbert space defined on the fluid domain, and R³ stands for the real space for the particle velocities. The square integrable L2-functions in an L² space is chosen for the pressure and is denoted by

$$\begin{array}{c}\hfill \mathbb{P}=\left\{p\right|p\in L^2\}.\end{array}$$ (25)

The test function V (variation) is considered as follows to derive the weak formulation for the combined fluid-particle system

$$\begin{array}{c}\hfill \tilde{\mathbf{V}}=(\tilde{\mathbf{u}},\tilde{\mathbf{U}},\tilde{\Omega })\in {\mathbb{V}}_0.\end{array}$$ (26)

Here, the variational space V₀ is the same as V, except that u = 0 on ∂Σ_i. Multiplying Eq. 13 by the test function for the fluid velocity, $\tilde{\mathbf{u}}$, and integrating over the fluid domain at time t gives

$$\begin{array}{ccc}& & {\int }_{{\Sigma }_0}{\rho }^{\left(f\right)}\left(\frac{\partial \mathbf{u}}{\partial t}+\left(\mathbf{u}·\nabla \right)\mathbf{u}\right)·\tilde{\mathbf{u}}dV\hfill \\ & & +{\int }_{{\Sigma }_0}\sigma :\nabla \tilde{\mathbf{u}}dV-{\int }_{{\partial \Sigma }_p}\left(\sigma ·\widehat{\mathbf{n}}\right)·\tilde{\mathbf{u}}ds=0.\hfill \end{array}$$ (27)

It should be noted that the variations for each variable introduced above are arbitrary except on the particle surface where the no-slip boundary condition in Eq. 21 enforces the equality of variations of fluid and particle velocities given by the following relation:

$$\begin{array}{c}\hfill \tilde{\mathbf{u}}=\tilde{\mathbf{U}}+\tilde{\omega }\times \left(\mathbf{x}-\mathbf{X}\right)\text{on}\partial {\Sigma }_p.\end{array}$$ (28)

Using the equations of motion for the particles (Eqs. 15, 16), the surface integral in Eq. 27 is rewritten as follows:

$$\begin{array}{ccc}& & -{\int }_{\partial {\Sigma }_p}\left(\sigma ·\widehat{\mathbf{n}}\right)·\tilde{\mathbf{u}}ds\hfill \\ & & =-\tilde{\mathbf{U}}·{\int }_{\partial {\Sigma }_p}\left(\sigma ·\widehat{\mathbf{n}}\right)ds-\tilde{\mathit{\omega }}·{\int }_{\partial {\Sigma }_p}\left(\mathbf{x}-\mathbf{X}\right)\times \left(\sigma ·\widehat{\mathbf{n}}\right)ds\hfill \\ & & =\tilde{\mathbf{U}}·\left[m\frac{d\mathbf{U}}{dt}-\mathbf{R}\left(t\right)\right]+\tilde{\mathit{\omega }}·\left[\mathbf{I}\frac{d\mathit{\omega }}{dt}-\mathit{\Omega }\left(t\right)\right].\hfill \end{array}$$ (29)

Substituting for stress tensor σ from Eqs. 14, 29 into Eq. 27, the combined fluid-particle momentum equation for the Langevin approach is given by

$$\begin{array}{ccc}& & {\int }_{{\Sigma }_0}{\rho }^{\left(f\right)}\left(\frac{\partial \mathbf{u}}{\partial t}+\left(\mathbf{u}·\nabla \right)\mathbf{u}\right)·\tilde{\mathbf{u}}dV-{\int }_{{\Sigma }_0}p\left(\nabla ·\tilde{\mathbf{u}}\right)dV\hfill \\ & & +{\int }_{{\Sigma }_0}\left\{\mu [\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^T]\right\}:\nabla \tilde{\mathbf{u}}dV+\tilde{\mathbf{U}}·\left[m\frac{d\mathbf{U}}{dt}-\mathbf{R}\left(t\right)\right]\hfill \\ & & +\tilde{\omega }·\left[\mathbf{I}\frac{d\omega }{dt}-\mathit{\Omega }\left(t\right)\right]=0.\hfill \end{array}$$ (30)

The weak formulation for the mass conservation equation is obtained in a similar fashion. Let $\tilde{p}$ be the variation of pressure p such that $\tilde{p}\in \mathbb{P}$. Here, the function space for both $\tilde{p}$ and p are chosen to be the same. The weak form of Eq. 12 is then given by

$${\int }_{{\Sigma }_0}\tilde{p}\left(\nabla ·\mathbf{u}\right)dV=0.$$ (31)

The domain movement is handled by an ALE scheme. The details of spatial discretization, mesh movement techniques, and temporal discretization of time derivatives are discussed in Ref. 12. These details will not be repeated here for brevity. Briefly, the fluid domain is approximated by quadratic tetrahedral finite-elements (10 nodes defined per tetrahedron with 10 basis functions that are second-order polynomials). The discrete solution for the fluid velocity is approximated in terms of piecewise quadratic functions, and is assumed to be continuous over the domain (P2 elements). The discrete solution for the pressure is taken to be piecewise linear and continuous (P1 element). This P1∕P2 element for the pressure and velocity is consistent with the Ladyzhenskaya-Babuska-Brezzi or inf-sup condition and yields convergent solutions. A second order implicit time stepping scheme is used for solving Eq. 30.^{44, 45}

RESULTS AND DISCUSSION

In this section, in a stationary Newtonian fluid medium, we numerically predict (i) the translational and rotational temperatures of the nanoparticle, where the temperature calculation is carried out until thermal equilibration is obtained for the particle, (ii) the translational and rotational velocity distributions of the nanoparticle motion, (iii) the translational and rotational VACFs, (iv) the translational and rotational MSD of the particle for both ballistic and diffusive regimes, and (v) the effects of the presence of the bounding wall on a particle initially placed at various locations are evaluated for several cases. The various numerical predictions have been compared with analytical results.

A neutrally buoyant solid spherical particle of radius either a = 50 nm or a = 250 nm is initially placed either at the centerline of a cylindrical vessel (R = 2.5 μm) containing a quiescent Newtonian fluid or at suitably chosen locations away from the center line towards the bounding wall. The instantaneous flow description around the particle and the motion of the particle are fully resolved. The physical parameters used are: k_B=1.3806503×10⁻²³ kg m²∕s²K, μ = 10⁻³ kg/ms, ρ^(f) = 10³ kg/m³, and ρ^(p) = 10³ kg/m³. For a given nanoparticle of radius a, and vessel radius R, a “realization” consists of N time steps. The number of time steps, N, depends upon equilibration of particle temperature (N = 20 000), or determination of VACFs and MSD (N = 100 000). In order to ensure the uniqueness of the realizations, different initial seeds are chosen for seeding the Gaussian random number generator.

Markovian process

For the Markovian stochastic process, the dissipative memory kernel for force and torque in Eqs. 18, 19, respectively, are Dirac delta functions given by

$$\begin{array}{ccc}\hfill \alpha \left(\right|t-t^{\prime }\left|\right)& =& 2({\zeta }^{\left(trans\right)}∕m)\delta (t-t^{\prime }),\hfill \\ \hfill \beta \left(\right|t-t^{\prime }\left|\right)& =& 2({\zeta }^{\left(rot\right)}∕\mathbf{I})\delta (t-t^{\prime }),\hfill \end{array}$$ (32)

where ζ^(trans) = 6πμa and ζ^(rot) = 8πμa³ are the dissipative friction coefficients for the force and torque, respectively, and a is the radius of the particle. Here, δ(t − t′) signifies that there is no correlation between impacts at distinct time intervals.

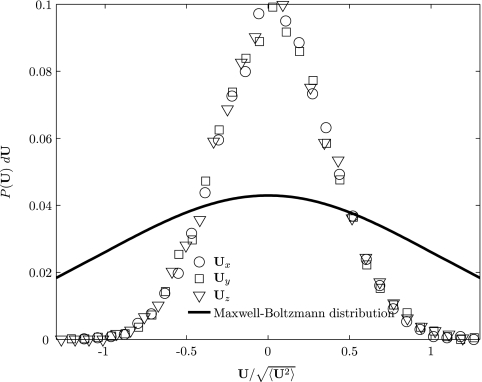
The equilibrium probability density function of the velocity of the fluctuating particle should follow the Maxwell-Boltzmann distribution (MBD),

$$\begin{array}{c}\hfill P\left(\mathbf{U}\right)=\sqrt{\frac{2}{\pi }}{\left(\frac{m}{k_{B}T}\right)}^{3∕2}⟨{\mathbf{U}}^2⟩\exp \left\{-\frac{m⟨{\mathbf{U}}^2⟩}{2k_{B}T}\right\},\end{array}$$

and by symmetry, the equilibrium statistics of the three components of U along the three coordinate directions should be independent of each other.

In Figure 4, the numerically simulated components of U (represented by three different symbols) are compared with the analytical Maxwell-Boltzmann distribution (with mean zero and variance k_BT/m). It is observed that each component of U individually follows the Gaussian distribution. However, the large deviation between the variance of the numerically determined distribution (obtained by using the uncorrelated or white noise) and that predicted by the Maxwell-Boltzmann distribution, indicates a mismatch between the average kinetic energy of the particle and the thermal energy of the system. The translational temperature of the particle obtained from its average kinetic energy is

$$\begin{array}{c}\hfill T^{\left(trans\right)}=\frac{m⟨{\mathbf{U}}^2⟩}{3k_B}.\end{array}$$ (33)

These are obtained from five different realizations in each coordinate direction. Each realization consists of N = 20 000 time steps. Thus, to evaluate the equilibration of the particle temperature with the preset temperature, we have employed 3 × 5 × 20 000 = 300 000 time steps. Furthermore, the total number of realizations for each case has been arrived such that any further increase in the number of realizations does not significantly change the prediction of temperature equilibration.

Figure 4.

Equilibrium probability of the velocity of the nanoparticle of radius a = 50 nm by using white noise.

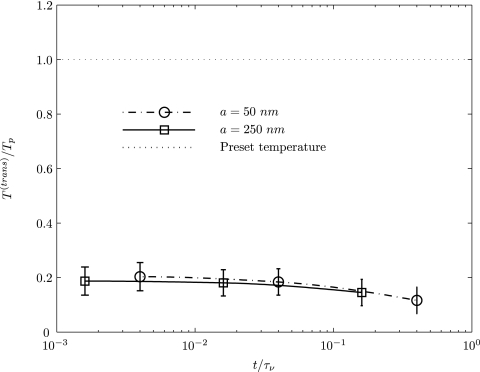
We note that Figure 5 exhibits a systematic error of ∼89% in the translational temperature of the various sizes of the particle considered . The error bars have been plotted from standard deviations of the temperatures obtained with 15 (3 × 5 = 15) different realizations.

Figure 5.

Translational temperature of the Brownian particle, T^(trans), calculated by using white noise in a cylindrical vessel of radius R = 2.5 μm.

In DNS, the frictional dissipation, or more generally the resistance offered by the surrounding fluid on the particle is time (memory) dependent. The generated fluctuations of random forces and random torques in Eq. 32, however, are uncorrelated in time. This contradicts the fluctuation-dissipation theorem from a GLE standpoint, as the random force and torque must have the power spectrum determined by the friction.^{24, 25, 30} This inequality in the systematic and random parts of the microscopic forces manifests as a lack of adherence to the equipartition theorem resulting in the large deviation between the computed velocity distribution and the Maxwell-Boltzmann distribution. This implies that a numerical scheme with white noise (Markovian) is not sufficient to serve as a thermostat within the generalized Langevin approach when the hydrodynamics is fully resolved. A noise with a well defined characteristic memory time is required.

Non-Markovian process

For a non-Markovian stochastic process, the random-noise depends on the memory effects considered through time correlations. In this case, Eqs. 18, 19 satisfy the generalized fluctuation-dissipation theorem.^{24, 25} For a time correlated Mittag-Leffler noise,^{39, 46} the dissipative memory kernel for force and torque in Eqs. 18, 19 are given by

$$\begin{array}{ccc}\hfill \alpha \left(\right|t-t^{\prime }\left|\right)& =& \frac{{\alpha }_0\left(\lambda \right)}{{\tau }^{\lambda }}{E}_{\lambda }\left[-{\left(\frac{|t-t^{\prime }|}{\tau }\right)}^{\lambda }\right],\hfill \\ \hfill \beta \left(\right|t-t^{\prime }\left|\right)& =& \frac{{\beta }_0\left(\lambda \right)}{{\tau }^{\lambda }}{E}_{\lambda }\left[-{\left(\frac{|t-t^{\prime }|}{\tau }\right)}^{\lambda }\right],\hfill \end{array}$$ (34)

respectively, where λ is the exponent taken as 0 < λ < 2, α₀(λ) (units of α₀(λ) is s^{λ − 2}) and β₀(λ) (units of β₀(λ) is s^{λ − 2}) are the proportionality coefficient dependent on the exponent λ but independent of t or τ, and E_λ(y) is the Mittag-Leffler function⁴⁰ defined through the series given by Eq. 9. When λ ≠ 1, the noise correlation function in Eq. 34 behaves as a stretched exponential for short times and as an inverse power-law in the long time limit.⁴¹

For λ = 1, the noise correlation function in Eq. 34 reduces to the Ornstein-Uhlenbeck process,^{33, 47}

$$\begin{array}{ccc}\hfill \alpha \left(\right|t-t^{\prime }\left|\right)& =& \frac{({\zeta }^{\left(trans\right)}∕m)}{\tau }{e}^{-|t-t^{\prime }|∕\tau },\hfill \\ \hfill \beta \left(\right|t-t^{\prime }\left|\right)& =& \frac{({\zeta }^{\left(rot\right)}∕\mathbf{I})}{\tau }{e}^{-|t-t^{\prime }|∕\tau }.\hfill \end{array}$$ (35)

In the limit τ → 0, the Ornstein-Uhlenbeck process, i.e., Eq. 35, reduces to the Markovian stochastic process given by Eq. 32.

For λ ≠ 1, the proportionality coefficients α₀ and β₀ are chosen such that the Mittag-Leffler noise satisfies the equipartition theorem. In our numerical simulations, initially α₀ and β₀ are dynamically optimized during the course of a trajectory according to the scheme (see, Ref. 18),

$$\begin{array}{ccc}\hfill {\alpha }_0(\lambda ,t+\Delta t)& =& {\alpha }_0(\lambda ,t)e^{1-{\mathbf{U}}^2∕⟨{\mathbf{U}}^2⟩},\hfill \\ \hfill {\beta }_0(\lambda ,t+\Delta t)& =& {\beta }_0(\lambda ,t)e^{1-{\omega }^2∕⟨{\omega }^2⟩}.\hfill \end{array}$$ (36)

We expect that for a given λ and characteristic memory time τ/τ_ν in the long time limit, α₀ and β₀ will converge to constant values, making them effectively independent of time t.

Equipartition theorem

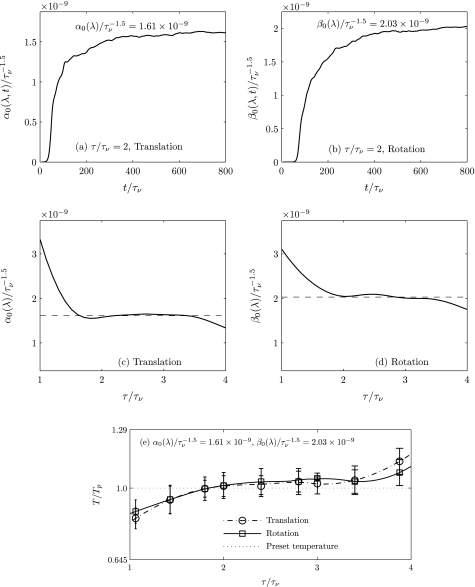
Figures 6a, 6b show that for λ = 0.5 and τ/τ_ν = 2, α₀and β₀ do converge to constant values over an ensemble average of 45 different realizations. The proportionality coefficients α₀ and β₀ are non-dimensionalized using ${\tau }_{\nu }^{\lambda -2}={\tau }_{\nu }^{-1.5}$ (for λ = 0.5). Figures 6c, 6d show α₀ and β₀ as functions of τ. For any given value of τ/τ_ν, if α₀ and β₀ are chosen from Figures 6c, 6d, respectively, then the evaluated temperature of the nanoparticle is noted to agree with the preset temperature of thermostat within 3% error. As a result, the model serves as a general thermostat for a range of the characteristic memory time τ/τ_ν.

Figure 6.

Convergence in the proportionality coefficient, (a) α₀(λ), (b) β₀(λ) for τ/τ_ν = 2; characteristic memory time as a function of proportionality coefficient (c) α₀(λ), (d) β₀(λ), and (e) translational and rotational temperatures of the nanoparticle of radius a = 50 nm by using Mittag-Leffler noise (λ = 0.5). The proportionality coefficients α₀ and β₀ are non-dimensionalized using ${\tau }_{\nu }^{\lambda -2}={\tau }_{\nu }^{-1.5}$. For a given τ/τ_ν, if α₀(λ) and β₀(λ) are chosen from (c) and (d), respectively, then the thermostat satisfies the equipartition theorem within 3% error. When ${\alpha }_0\left(\lambda \right)∕{\tau }_{\nu }^{-1.5}=1.61\times {10}^{-9}$ (a) and ${\beta }_0\left(\lambda \right)∕{\tau }_{\nu }^{-1.5}=2.03\times {10}^{-9}$ (b) are independent of τ, the thermostat satisfies the equipartition theorem in the plateau region given by (e). It is to be noted that in the same plateau region ((c) and (d)), α₀ and β₀ remain constant and agree with the values given in (a) and (b), respectively.

It is interesting to note from Figures. 6c, 6d that α₀ and β₀ remain constant (i.e., independent of τ) over a finite plateau region where the characteristic memory time τ is larger than the hydrodynamic time scale, τ_ν. The significance of this numerical result is that when τ is sampled from the interval defined by the plateau region, the values of α₀ and β₀ for which the nanoparticle translational as well as rotational temperatures agree with the preset temperature (Figure 6e) are independent of τ and t. Thus, we are able to numerically demonstrate that the characteristic memory time in the external noise has to be chosen consistent with the inherent time scale of the memory kernel, i.e., the hydrodynamic time scale, in order to adhere to the equipartition theorem within the statistical error.

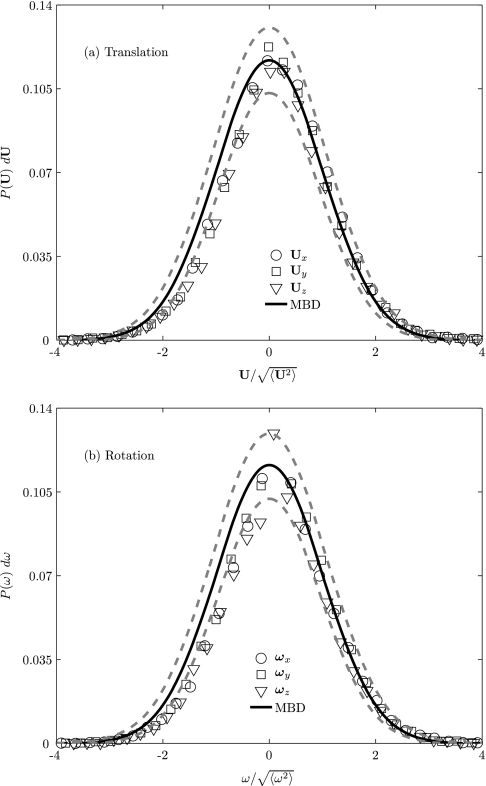
In Figure 7, we plot the velocity distributions of the particle for each component of U [Figure 7a] and ω [Figure 7b] corresponding to the plateau regions of Figures. 6c, 6d, 6e, where thermal equilibrium has been attained. These distributions agree within 5% error (see dotted line in Figure 7) with that of the analytical Maxwell-Boltzmann distribution. This agreement provides further validation in support of the correctness of the numerical procedure.

Figure 7.

Equilibrium probability of the (a) translational and (b) rotational velocities of the nanoparticle (a = 50 nm) using Mittag-Leffler noise (λ = 0.5). MBD: Maxwell-Boltzmann distribution.

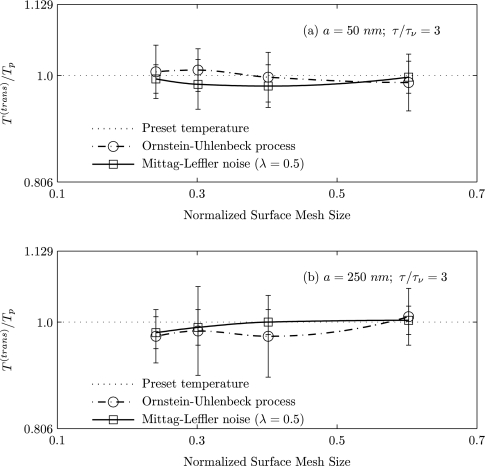
Figure 8 shows the translational temperature of the particle as a function of the normalized surface mesh (mesh length divided by particle radius) for two different radii of the nanoparticle by using the Ornstein-Uhlenbeck process and the Mittag-Leffler noise. It is observed that the temperature of the particle is independent of mesh sizes and the time step of integration, showing domain and time step convergence of our numerical protocols.

Figure 8.

Translational temperature of the nanoparticle as a function of normalized surface mesh (mesh length divided by particle radius). The non-dimensionalized characteristic memory time τ/τ_ν = 3 for radius (a) a = 50 nm and for radius (b) a = 250 nm.

Dynamics of the nanoparticle coupled to the GLE thermostat

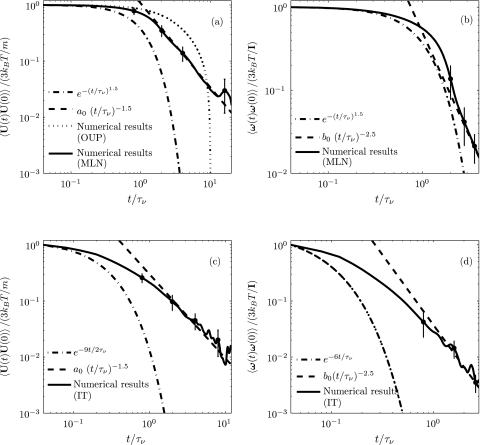
Here, we discuss, how coupling to a thermostat alters the dynamics of the nanoparticle subject to hydrodynamic interactions. The translational and rotational VACFs of the nanoparticle (a = 50 nm) in a circular vessel (R = 2.5 μm) subjected to the time correlated noise schemes are shown in Figures 9a, 9b. For determining the VACF of the nanoparticle, 45 (15 × 3 = 45) realizations have been employed with total computation of 45 × 100 000 = 4 500 000 time steps. It is observed from Figure 9a that the translational VACF of the nanoparticle using Ornstein-Uhlenbeck process (dotted line) follows an exponential decay, while it follows a stretched exponential decay (exp { − (t/τ_ν)^3/2}) and a power-law decay (a₀(t/τ_ν)^−3/2) at short and long time regimes, respectively, using Mittag-Leffler noise (solid line) for λ = 0.5. Similarly, the rotational VACF of the nanoparticle using Mittag-Leffler noise follows a stretched exponential decay (exp { − (t/τ_ν)^3/2}) and a power-law decay (b₀(t/τ_ν)^−5/2) at short and long time regimes, respectively, and this is shown in Figure 9b. The error bars have been plotted from standard deviations of the decay at particular time instants obtained with 45 different realizations. Hauge and Martin-Löf²³ have analytically shown that the decay of the translational and rotational VACFs at long time obeys a power-law,

$$\begin{array}{ccc}\hfill \frac{〈\mathbf{U}\left(t\right)\mathbf{U}\left(0\right)〉}{〈\mathbf{U}\left(0\right)\mathbf{U}\left(0\right)〉}& \simeq & \left(\frac{m{\rho }^{\left(f\right)1∕2}}{12{\pi }^{3∕2}{\mu }^{3∕2}}\right)t^{-3∕2}=\frac{1}{6\sqrt{\pi }}{\left(\frac{t}{{\tau }_{\nu }}\right)}^{-3∕2}\hfill \\ & =& a_0{\left(\frac{t}{{\tau }_{\nu }}\right)}^{-3∕2},\hfill \end{array}$$ (37)

$$\begin{array}{ccc}\hfill \frac{〈\omega \left(t\right)\omega \left(0\right)〉}{〈\omega \left(0\right)\omega \left(0\right)〉}& \simeq & \left(\frac{\mathbf{I}{\rho }^{\left(f\right)3∕2}}{32{\pi }^{3∕2}{\mu }^{5∕2}}\right)t^{-5∕2}=\frac{1}{40\sqrt{\pi }}{\left(\frac{t}{{\tau }_{\nu }}\right)}^{-5∕2}\hfill \\ & =& b_0{\left(\frac{t}{{\tau }_{\nu }}\right)}^{-5∕2},\hfill \end{array}$$ (38)

where the values of constants a₀ and b₀ are provided in Table 2.

Figure 9.

Translational (a) and (c), and rotational (b) and (d) VACFs of the Brownian particle of radius a = 50 nm through a circular vessel of radius R = 2.5 μm obtained using colored noise (a) and (b) and Iwashita's model (c) and (d). The legends are OUP: Ornstein-Uhlenbeck process; MLN: Mittag-Leffler noise for λ = 0.5; IT: Iwashita's thermostat. Solid lines in (a)–(d) and dotted line in (a) are present numerical simulation results. The error bars have been plotted from standard deviations of the decay at particular time instants obtained with 45 different realizations. The values of constants a₀ and b₀ are provided in Table 2.

Table 2.

Values of a₀ (translational) and b₀ (rotational) for long time decay of VACF.

Approach	a0	b0
Fluctuating hydrodynamics
(Hauge and Martin-Löf23)	0.094	0.014
(Virtual mass, M = m + m0/2, where m0 is the mass of the displaced fluid)
Langevin approach:
Iwashita's thermostat	0.3	0.037
Generalized Langevin approach:
Mittag-Leffler noise	1.06	0.49

For completeness, we have also compared the performance of an analogous optimization protocol that has been proposed by Iwashita et al.,¹⁸ for which the noise correlation function is given by

$$\begin{array}{c}\hfill \alpha \left(\right|t-t^{\prime }\left|\right)={\alpha }^{\left(trans\right)}\delta (t-t^{\prime }),\beta \left(\right|t-t^{\prime }\left|\right)={\alpha }^{\left(rot\right)}\delta (t-t^{\prime }).\end{array}$$ (39)

Here, α^(trans) and α^(rot) represents the noise intensity for each degree of freedom of the translational and rotational motions of the particle, respectively. They are controlled such that the variance of the translational and rotational velocities of the particle satisfy the relation,

$$\begin{array}{c}\hfill ⟨{\mathbf{U}}^2⟩=\frac{3k_{B}T}{m},⟨{\omega }^2⟩=\frac{3k_{B}T}{\mathbf{I}}.\end{array}$$ (40)

The time evolution of noise intensity is described as

$$\begin{array}{ccc}\hfill {\alpha }^{\left(trans\right)}(t+\Delta t)& =& {\alpha }^{\left(trans\right)}\left(t\right)e^{1-{\mathbf{U}}^2∕⟨{\mathbf{U}}^2⟩},\hfill \\ \hfill {\alpha }^{\left(rot\right)}(t+\Delta t)& =& {\alpha }^{\left(rot\right)}\left(t\right)e^{1-{\omega }^2∕⟨{\omega }^2⟩}.\hfill \end{array}$$ (41)

The translational and rotational VACFs of the particle for a = 50 nm are found to obey the power-law correlations (Figures 9c, 9d) with a₀ and b₀ values provided in Table 2.

The numerical results obtained by using the Mittag-Leffler noise are in accordance with the GLE presented in Sec. 2; therefore, the choice of λ = 0.5 enables our model to show long time correlations consistent with that expected from classical hydrodynamic correlations (algebraic decay). However, coupling to a thermostat does alter the dynamics of the system. In particular, we observe that the computed value of constants a₀ (translational) and b₀ (rotational) differ from those predicted by Hauge and Martin-Löf.²³ The main reason for this difference is that the short time behavior of the Mittag Leffler thermostat predicts a stretched exponential behavior as opposed to an exponential behavior. This important difference highlights how the Mittag Leffler thermostat alters the hydrodynamic correlations (and the diffusion coefficient, see below) of the nanoparticle.

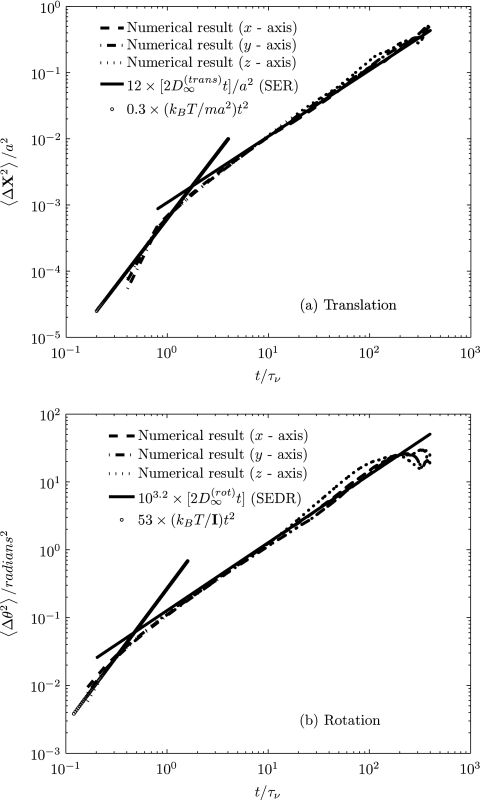
Figure 10 shows the numerically obtained translational and rotational MSDs of a neutrally buoyant nanoparticle (a = 50 nm) in a quiescent fluid medium, initially placed at the center of the vessel of radius, R = 2.5 μm, for both short and long times. For determining the MSD of the nanoparticle, 15 realizations in each coordinate direction have been employed with each realization computed up to 100 000 time steps. It is observed that in the regime where the particle's motion is dominated by its own inertia (ballistic), the translational and rotational motions of the particle follow 0.3 × (k_BT/m)t² and 53 × (k_BT/I)t², respectively. In the diffusive regime, t ≫ τ_b, the translational and rotational MSDs increase linearly in time to follow $12\times 2D_{\infty }^{\left(trans\right)}t$ and ${10}^{3.2}\times D_{\infty }^{\left(rot\right)}t$, respectively, where $D_{\infty }^{\left(trans\right)}=k_{B}T∕{\zeta }^{\left(trans\right)}$, and $D_{\infty }^{\left(rot\right)}=k_{B}T∕{\zeta }^{\left(rot\right)}$ (ζ^(r) = 8πμa³) are the translational and rotational self-diffusion coefficients. It is also observed from Figure 10 that in the diffusive regime, the translational and rotational MSDs of the particle follow Stokes-Einstein³⁰ and Stokes-Einstein-Debye⁴⁸ relations, respectively, with scaling factors of 12 and 10^3.2, respectively.

Figure 10.

The MSD of a neutrally buoyant Brownian particle (a = 50 nm) initially placed at the center of the cylindrical vessel in a stationary fluid medium using Mittag-Leffler noise for λ = 0.5. The legends are, SER: Stokes-Einstein relation; SEDR: Stokes-Einstein-Debye relation.

Hydrodynamic interactions – Wall effects

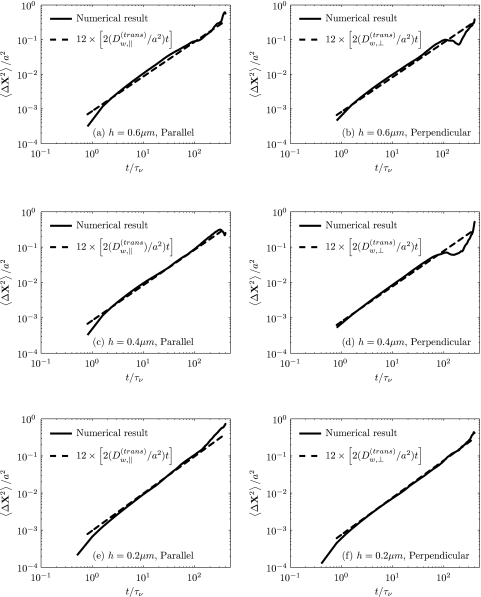
The hydrodynamic wall effects on the particle diffusivity are important for a nanoparticle thermal motion in a fluid flow that occurs in TDD and similar microparticle flows. For a particle initially located at the center of the cylindrical vessel, the wall effects play a minimal role (⩽3%, compared to an unbounded fluid domain) on the diffusion coefficient (in other words MSD) (see Figure 10).⁴⁹ When a particle of radius a is initially placed at a distance h from the tube wall to the center of the particle, h < R, the particle-wall interactions modify the particle diffusivity. For a ≪ R, in a quiescent fluid, the Brownian motion near the vessel wall is similar to that of motion in the vicinity of a plane wall (curvature effects may be neglected).^{49, 50} For a particle initially located in the near vicinity of the wall, there is reduced space for the surrounding fluid to negotiate the particle, and the corresponding drag force in a direction parallel to the wall is higher. The diffusivity of the particle in the proximity of the wall may be estimated to be

$$D_w^{\left(trans\right)}=D_{\infty }^{\left(trans\right)}\frac{{\zeta }^{\left(trans\right)}}{{\zeta }_w^{\left(trans\right)}},$$ (42)

in x, y, and z directions,⁵¹ while ${\zeta }_w^{\left(trans\right)}$ depends on the particular direction. Figure 11 shows the numerically obtained parallel (x direction) and perpendicular (y direction) MSDs of neutrally buoyant particle of radius, a = 50 nm, initially placed at various distances, h, from the tube wall, in a quiescent medium. In the diffusive regime, the translational MSD of the particle increases linearly in time and numerically obtained diffusion coefficient agrees with the prediction of Happel and Brenner⁴⁹ with a scaling factor of 12. It is to be noted that for determining the translational MSD of a nanoparticle of radius, a = 50 nm, initially placed at various distances from the tube wall, the scaling factor 12 remains unchanged.

Figure 11.

Parallel and Perpendicular MSDs of a neutrally buoyant Brownian particle (a = 50 nm) initially placed at different locations h from the wall of the cylindrical vessel in a quiescent medium using Mittag-Leffler noise for λ = 0.5.

CONCLUSIONS

An ALE based FEM is implemented to simulate the thermal motion of a nanoparticle in an incompressible Newtonian stationary fluid medium. Thermal force from the fluid is incorporated as represented by the Langevin approach, in which the thermal fluctuations are included in terms of the random force and torque in the particle equations of motion. They are assumed to follow either the Markovian process (white noise) or the non-Markovian process (Ornstein-Uhlenbeck process; Mittag-Leffler noise; Iwashita's model), and will for certain scenarios, serve as a reliable thermostat. In a quiescent fluid, at thermal equilibrium, the numerical predictions are validated by comparing with analytical results. Our findings are summarized in Tables 3, 4.

Table 3.

At thermal equilibrium, our numerical observations for velocity distribution and temperature of the nanoparticle along with the constraints obtained using various correlated and uncorrelated noise schemes. Abbreviations are MBD: Maxwell-Boltzmann distribution; OUP: Ornstein-Uhlenbeck process; MLN: Mittag-Leffler noise; IT: Iwashita's thermostat.

Thermostat Equilibrium
Thermostat	Velocity distribution and equipartition theorem	Constraints	Implementation remarks
White noise	Does not satisfy MBD and equipartition theorem	Δt < τb for stability	(i) Depends on position and shape of the particle, (ii) does not conform to GLE, and (iii) imbalance between memory and friction
OUP	Satisfies MBD and equipartition theorem	Δt < τb for stability; τ > τν for thermostat to work	(i) Depends on position and shape of the particle and (ii) approximately conforms to GLE
MLN	Satisfies MBD and equipartition theorem	Δt < τb for stability; τ > τν for thermostat to work; α0(λ) and β0(λ) are independent of τ in a small plateau region where τ ≳ τν	(i) Does not depend on position and shape of the particle and (ii) approximately conforms to GLE
IT	Satisfies MBD and equipartition theorem	Δt < τb for stability	(i) Does not depend on position and shape of the particle and (ii) does not conform to GLE

Table 4.

Our numerical observations for VACF and MSD of the nanoparticle obtained using various correlated noise schemes. Abbreviations are OUP: Ornstein-Uhlenbeck process; MLN: Mittag-Leffler noise; IT: Iwashita's thermostat.

Thermostat Dynamics
Thermostat	VACF	Diffusivity	Remarks
OUP	Follows an exponential decay at short and long times	Not considered in this study
MLN	Follows (i) an exponential decay at short times and (ii) an algebraic decay over long times (translational: t−3/2 and rotational: t−5/2)	Obeys Stokes-Einstein (translation) and Stokes-Einstein-Debye (rotation) relations, with scaling factors of 12 and 103.2, respectively	Conformed to hydrodynamic wall interactions
IT	Follows (i) an exponential decay at short times and (ii) an algebraic decay over long times (translational: t−3/2 and rotational: t−5/2)	Not considered in this study

Based on our observations presented in Tables 3, 4, a thermostat based on the Mittag-Leffler noise with an appropriately chosen characteristic memory time τ/τ_ν adheres to the equipartition theorem. Moreover, this thermostat captures the correct (long-time) hydrodynamic correlations (algebraic decay of the VACF) and normal diffusive behavior; however, given the difference in short-time behavior of VACF, the diffusion coefficient is altered by a scaling factor. The Mittag-Leffler thermostat is most useful for future applications involving computations of thermodynamic properties such as free energy landscapes of nanoparticle adhesion subject to hydrodynamic interactions (such as in a flow field).

We note that our approach in developing the Mittag-Leffler thermostat is analogous in scope to the extended Lagrangian approach for building a thermostat in molecular dynamics as described by the Nose-Hoover scheme.⁵² In the future, our thermostat can be made more versatile by introducing generalized correlated noise schemes with multiple characteristic memory times for complex physical systems. This would be in analogy with the Nose-Hoover chain approach (an extension to the Nose-Hoover thermostat) in the extended Lagrangian molecular dynamics.⁵³ Extensions of our approach to include solvation effects in addition to hydrodynamics (see Voulgarakis et al.^{10, 11}), especially in the case of hydrophobic nanoparticles can represent useful future directions of research. Finally, a computational protocol to study constant temperature properties of a nanoparticle subject to hydrodynamic interactions enables the study of more complex and biologically interactions, such as nanoparticle adhesion to cells via receptor-ligand interactions. This will also be considered in the future.