Cardiac Myocytes and Local Signaling In Nano-Domains

Abstract

It is well known that calcium-induced calcium-release in cardiac myocytes takes place in spatially restricted regions known as dyads, where discrete patches of junctional sarcoplasmic reticulum tightly associate with the t-tubule membrane. The dimensions of a dyad are so small that it contains only a few Ca²⁺ ions at any given time. Ca²⁺ signaling in the dyad is therefore noisy, and dominated by the Brownian motion of Ca²⁺ ions in a potential field. Remarkably, from this complexity emerges the integrated behavior of the myocyte in which, under normal conditions, precise control of Ca²⁺ release and muscle contraction is maintained over the life of the cell. This is but one example of how signal processing within the cardiac myocyte and other cells often occurs in small “nano-domains” where proteins and protein-complexes interact at spatial dimensions on the order of ~ 1 – 10 nanometers and at time scales on the order of nanoseconds to perform the functions of the cell. In this article, we will review several examples of local signaling in nano-domains, how it contributes to the integrative behavior of the cardiac myocyte, and present computational methods for modeling signal processing within these domains across differing spatio-temporal scales.

1. Introduction

It is becoming increasingly clear that cellular signal processing often occurs in small “nano-domains”, where proteins and protein-complexes interact at spatial dimensions ranging from 1’s to 10’s of nanometers, and on time scales of nanoseconds to microseconds. This mode of signaling in fact appears to be a common design motif in all cells, and is certainly true of the cardiac myocyte. In this article, we will present examples of the important role of such local signal processing in the cardiac myocyte. We will focus on the integration of Ca²⁺ and Na⁺ signals in and near the cardiac dyad.

Calcium-induced calcium-release (CICR) in cardiac myocytes takes place within dyads, where discrete patches of junctional sarcoplasmic reticulum (jSR) tightly associate with the t-tubule membrane. Dyad volume, diameter, and height are estimated to be ~ 3×10⁵ nm³, 100 - 200 nm, and 10-15 nm, respectively (Franzini-Armstrong et al., 1999; Hayashi et al., 2009). L-type Ca²⁺ channels (LCCs) are preferentially located in the t-tubule membrane, in close apposition to the jSR membrane. As our initial example of signal processing in nano-domains, we will consider the remarkable, recent experimental and modeling evidence indicating that LCCs are able to sense both local Ca²⁺ concentration, as well as global Ca²⁺ signals. This signal processing results from the differing temporal dynamics of conformational changes due to Ca²⁺ binding to the C- versus N-lobe of calmodulin (CaM), which is tethered to LCCs and mediates Ca²⁺-dependent inactivation. It is a compelling example of how an important regulatory signal can be sensed by a pair of molecules.

Because of the small physical dimensions of the dyad, modeling studies indicate that at any instant of time there are only a few (~ 1 - 100) Ca²⁺ ions present, and that Ca²⁺ signaling may be influenced significantly by the physical shape and size of the dyad, the relative placement of dyad proteins such as ryanodine receptors (RyRs) and LCCs, local membrane buffering of Ca²⁺ by negatively charged phospholipid headgroups, and the dyadic electric field. Our second case study will review how nano-scale models of Ca²⁺ signaling in the dyad that are based on the fundamental physical principles governing the trajectories of individual Ca²⁺ ions and their binding to RyRs, provide insights into the nature of dyadic Ca²⁺ signaling and CICR. Additional signal processing occurs in the dyad. Examples include signaling mediated by protein kinase A (PKA) and Ca²⁺/CaM-dependent protein kinase II (CaMKII). These signaling molecules are part of complex macromolecular assemblies that help guide their phosphorylation of target proteins in the dyad. These signaling molecules also exert global whole-cell level actions. Our third case study will review computational models of the actions of these important signaling molecules.

Extra-dyadic processes operating at the length-scale of 10’s to possibly 100’s of nms are also likely to influence signal processing in the dyad by establishing “boundary conditions”. Imaging studies have revealed that the Na⁺-Ca²⁺ exchanger (NCX) is localized within and/or near the dyad, and experimental evidence suggests that Ca²⁺ entry via reverse-mode NCX activity may either trigger or modulate CICR. Recent evidence also indicates that the membrane adaptor protein ankyrin-B (ANK-B) binds to NCX, the Na⁺-K⁺ ATPase (NKA), and the inositol 1,4,5-phosphate operated Ca²⁺-releasing channel (InsP₃R) in the T-tubules, creating the substrate for a macro-molecular signaling complex that may play a crucial role in modulating CICR and regulation of Na⁺ and Ca²⁺ levels in the cardiac myocyte (Mohler et al., 2005). We will review experimental data regarding the functional role of extra-dyadic Na⁺ and Ca²⁺ transporters and their possible organization into protein complexes, and suggest directions for future modeling of these systems.

Finally, as an additional example of extra-dyadic processes and their influence on dyad signal processing, we will consider the effects of close, physical approximation of mitochondria with the jSR. It is now known that mitochondria are localized within a few 10’s of nms of, and are tethered to, the jSR. Mitochondria take up Ca²⁺ via the Ca²⁺ uniporter (mCU) and extrude Ca²⁺ through the mitochondrial Na⁺-Ca²⁺ exchanger (mNCE). Recent data suggest that mCU transport in cardiac myocytes is fast, raising the possibility that positioning of mitochondria near the dyad may play a significant role in setting the boundary conditions regulating CICR and local Ca²⁺ transients on a beat-to-beat basis.

2. Signal Processing in the Cardiac Dyad

2.1 Sensing of Local and Global Ca²⁺ Signals by Calmodulin Molecules at the Site of the L-Type Ca²⁺ Channel

Ca²⁺ is a ubiquitous signaling molecule in the heart (as well as other organ systems) that plays a role in regulating a large variety of processes. In order to achieve coordinated signaling at the whole-cell level, cardiac myocytes must have mechanisms that allow for sorting of global and local Ca²⁺ signals in order to regulate processes such as gradation of contraction and heart rate (sensitive to global Ca²⁺) as well as processes involved in energy production, transcription, and cell survival (sensitive to localized Ca²⁺) (Anderson and Mohler, 2009). The cardiac dyad nano-domain is an example where a molecular Ca²⁺ sensor mediating Ca²⁺-dependent inactivation (CDI) of the L-type Ca²⁺ current (I_CaL) is positioned in very close proximity to Ca²⁺ sources (LCCs and RyRs), allowing for privileged Ca²⁺ signaling. Recent studies (Dick et al., 2008; Tadross et al., 2008) have shed new light on the function of calmodulin (CaM) as a sensor for CDI of I_CaL, demonstrating the remarkable processing of the Ca²⁺ signal that can be performed by individual molecules within the dyad in order to sense local versus global Ca²⁺.

Tadross et al (2008) used a combination of elegant models and experiments to elucidate the mechanisms underlying Ca²⁺ channel CDI, by which CaM can sense and decode local and global Ca²⁺ signals. CaM continuously complexes with LCCs and serves as the cytosolic Ca²⁺ sensor for CDI (Erickson et al., 2001). CaM is a bi-lobed protein, where both the N- and C-lobes bind Ca²⁺, but with different affinities. Despite the fact that both lobes are in very close proximity to the LCC Ca²⁺ flux (i.e. ~10 nm from the channel pore), each lobe responds selectively to either the local (brief high-amplitude spikes in [Ca²⁺]) or global (a longer lasting pedestal of [Ca²⁺]) component of the Ca²⁺ signal. The ability of the LCC to respond selectively to either of these Ca²⁺ signals was explained by interpretation of a variety of experiments using the model shown in Figure 1. This model shows the states for the association of a single lobe of CaM with a Ca²⁺ channel. Transitions from state 1 through 4 represent dissociation of apoCaM from the Ca²⁺ channel, binding of 2 Ca²⁺ ions to a lobe of CaM, and binding of Ca²⁺/CaM to the effector site for CDI. If the transitions between states 2 and 3 are slow relative to channel gating, then brief high-amplitude spikes in Ca²⁺ arising from channel gating will be sufficient to cause accumulation of channels in state 3, and subsequent transition to state 4 (CDI). This is the hypothesized mechanism for local Ca²⁺ sensing by the C-lobe of CaM. However, if the transition between states 3 and 2 is fast relative to the Ca²⁺ fluctuations associated with channel gating (in conjunction with slow transitions between states 1 and 2, and states 3 and 4), then global selectivity emerges (see Tadross et al (2008) for details). This yields a mechanism that is sensitive to fractional presence of Ca²⁺ over time (i.e. highly sensitive to weak but sustained Ca²⁺ signals), but insensitive to the intensity of the Ca²⁺ signal, and can explain N-lobe sensitivity. Furthermore, N-lobe selectivity can be switched between global and local properties by altering the function of an additional Ca²⁺/CaM binding site on the N-lobe called NSCaTE (that normally restricts CaM to respond to local Ca²⁺ in Cav1 channels) (Dick et al., 2008). This mechanism for the selective molecular sensing of local versus global Ca²⁺ signals is without question remarkable. The implications of this selective Ca²⁺-sensing mechanism on our understanding of dyadic Ca²⁺ dynamics and cardiac excitation contraction coupling (ECC) have yet to be studied within the context of models of the cardiac myocyte.

Figure 1.

Basic states for a lobe of CaM in complex with a Ca²⁺ channel (from (Tadross et al., 2008)). In state 1, apoCaM (yellow circle) is bound to the apoCaM site (round pocket). In state 2, apoCaM is a transiently dissociated. In state 3, CaM binds two Ca²⁺ ions (black dots) to become Ca²⁺/CaM (yellow square), which can then bind the Ca²⁺/CaM effector site (square pocket), yielding CDI (state 4).

2.2 Mechanisms of Ca²⁺-Induced Ca²⁺ Release in the Cardiac Dyad Nano-domain

LCCs and RyRs reside in close apposition on opposite sides of the dyadic cleft, effectively granting Ca²⁺ ions permeating an LCC privileged access to the Ca²⁺ binding sites on nearby RyRs. Importantly, the assumed structural separation of individual clefts (Franzini-Armstrong et al., 1999) suggests that released Ca²⁺ does not generally act as a trigger to RyRs in distant dyads (though recent studies suggest neighboring RyR clusters may have a functional role in ECC (Baddeley et al., 2009; Rovetti et al., 2010)). Stern’s landmark “calcium-synapse” model (Stern, 1992), in which each dyad was assumed to contain a single LCC and a single SR release channel, captured these ideas in an elegantly simple way, demonstrating that high gain and graded SR release arise from the local correlation in stochastic LCC and RyR gating due to their communication via a common local Ca²⁺ signal. This has become known as the local control theory of ECC. This idea is crucial in understanding how the microscopic properties of CICR translate into macroscopic physiologic phenomena observed in experiments. Graded Ca²⁺ release (as measured at the whole-cell level) is achieved in this model by statistical recruitment of elementary SR Ca²⁺ release events. This fundamental idea of local control of SR release has spurred a number of modeling studies, some of which are described below.

Due to the small size of the dyad, it became clear that understanding the spatial and temporal profile of dyadic Ca²⁺ concentration ([Ca²⁺]_d) would be an important step in elucidating the mechanistic details of local CICR. Langer and Peskoff (1996) developed one of the first detailed models to numerically simulate the time course of dyadic Ca²⁺. The model predicted that a single typical LCC opening led to ~ 1 mM [Ca²⁺]_d near the mouth of the LCC. The presence of sarcolemmal buffering sites slowed the decay of the local Ca²⁺ transient (such that it remained highly elevated long after LCC closure) as compared to the dynamics in the absence of buffers, a finding which was inconsistent with the idea that LCC gating imposes tight control on RyR activity. Soeller and Cannell (1997) formulated a dyad model which introduced the electrostatic effects of ion movement, and predicted that [Ca²⁺]_d actually changes more rapidly in response to LCC gating. In this model, [Ca²⁺]_d was approximately proportional to unitary LCC currents over a wide range of current amplitudes. The model yielded predictions of [Ca²⁺]_d profiles during jSR release which peaked as high as 300 μM near the center of the dyad. The decay in dyadic Ca²⁺ occurred in ~ 2 ms following termination of SR release (but this was sensitive to the dyad boundary condition). The high speed of the response of dyadic Ca²⁺ to LCC and RyR gating in this model helped to explain how tight local control of SR release by LCCs can be achieved.

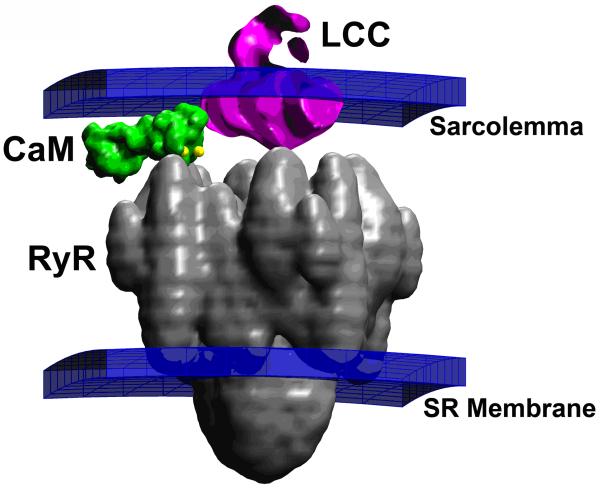
CICR occurs in the form of discrete Ca²⁺ trigger and release events that underlie the observation of Ca²⁺ sparks. These events arise as a result of the interaction of a small number of channel proteins that interact within the domain of a single cardiac dyad. The small size of the dyadic cleft (~ 4 × 10⁵ nm³ with ~ 10 - 40 RyRs) (Baddeley et al., 2009; Hayashi et al., 2009), in combination with the relatively large proteins that reside in the cleft, results in a space in which Ca²⁺ diffusion is highly restricted. Figure 2 shows a representation of an LCC, RyR, and a single CaM molecule tethered to the LCC in the dyad based directly on structural data (Serysheva et al., 2005; Wang et al., 2004a; Wilson and Brunger, 2000). Models predict that during an AP, peak Ca²⁺ concentration in the dyad ranges from 100 to 1000 μM (Langer and Peskoff, 1996; Soeller and Cannell, 1997), which corresponds to as few as 20-200 free Ca²⁺ ions (Tanskanen et al., 2007). Thus, it is clear that both feed forward and feedback signaling between RyRs and LCCs in the dyad is likely mediated by relatively few Ca²⁺ ions. Therefore, application of laws of mass-action to analysis of signaling events mediated by this relatively small number of ions may not be appropriate (Bhalla, 2004). The stochastic motion of Ca²⁺ ions in the dyad may also impart a significant amount of signaling noise between LCCs and RyRs, thereby influencing the fundamental properties of CICR (Tanskanen et al., 2007). In addition, the physical location and dimensions of dyad proteins may play a considerable role on the nature of Ca²⁺ ion motion and hence, CICR.

Figure 2.

Structure of a region of the dyad containing one LCC opposed to a single RyR, and one CaM molecule tethered to the LCC (Tanskanen et al., 2007).

To explore these issues, we recently developed a computational model of Ca²⁺ signaling in the dyad that simulates motion of Ca²⁺ ions, binding of ions to RyR receptor sites, and Ca²⁺ release from RyR. This model was developed in order to understand factors, such as those listed above, that determine properties of CICR at the level of the cardiac dyad. We addressed the following three questions: 1) what is the number of Ca²⁺ ions that are present in the dyad during CICR?; 2) how does the physical arrangement of large proteins within the dyad influence CICR?; and 3) how does “signaling noise” due to the potentially small number of Ca²⁺ ions within the dyad affect the nature of CICR? We addressed these questions by developing a molecularly- and structurally-detailed computational model of the cardiac dyad describing motions of Ca²⁺ ions, as influenced by thermal energy and electrostatic potentials.

Development of the nano-scale model is presented in detail elsewhere (Tanskanen et al., 2007). Briefly, a simplified dyad was modeled using a 200 nm × 200 nm × 15 nm lattice containing 20 RyRs arranged in a 4 × 5 matrix. Four LCCs were positioned randomly across this lattice to achieve a 5:1 RyR:LCC ratio. The geometry of each LCC and RyR protein was modeled as shown in Fig. 2, with each LCC tethering one CaM. The geometry of the Ca²⁺-accessible dyadic volume was determined by the presence, shape, and location of these proteins, which due to their large size relative to the dyad occupy a significant fraction of the dyadic volume. LCCs and RyRs were modeled using continuous-time, discrete-state Markov processes. LCC gating was simulated stochastically using a previously developed Markov model of the LCC (Greenstein and Winslow, 2002; Jafri et al., 1998) in which Ca²⁺ binding induced a shift in LCC gating dynamics into a low open probability mode representative of CDI. The LCC model incorporated a separate mechanism for voltage-dependent inactivation (VDI) as well. The gating kinetics of the RyR were described using the four-state Markov model of Stern (Stern et al., 1999; Wang et al., 2004b). CDI of an LCC required that the two C-lobe Ca²⁺ binding sites of the associated CaM were occupied. Opening of RyR required that Ca²⁺ was bound to all four activation sites. RyRs were assumed to inactivate when Ca²⁺ was bound to at least one out of four distinct inactivation sites. See Tanskanen et al. (2007) for a detailed description of how the locations of the activation and inactivation Ca²⁺-binding sites were determined. In this model, Ca²⁺ binding to the channel protein must be considered separately from the subsequent conformational change of the channel protein (steps that are typically combined in most channel models). It was assumed that a Ca²⁺-dependent state transition requires that Ca²⁺-binding sites are first occupied by Ca²⁺ ions. When a freely diffusing Ca²⁺ ion enters a lattice position adjacent to an available Ca²⁺-binding site, that Ca²⁺ ion has the opportunity to bind to the site. The relative magnitude of the binding rate compared to the rate of diffusion determines the probability that the Ca²⁺ ion either binds to the site or diffuses away. Ca²⁺-binding transitions were incorporated into the overall model of Ca²⁺ movement in the dyad (see below). Ion channel transition rates were therefore defined as functions that depend upon the occupancy of the Ca²⁺ binding sites (rather than [Ca²⁺]_d). Entry of Ca²⁺ ions into the dyad via open LCCs and RyRs was modeled as a Poisson process with rate governed by channel permeabilities measured experimentally (Rose et al., 1992). Sarcolemmal anionic sites acted as Ca²⁺ buffers and site density and Ca²⁺ binding/unbinding rates were based on the work of Langer and Peskoff (1996) and Soeller and Cannell (1997). The joint positions of Ca²⁺ ions present in the dyad were assumed to behave as Brownian motion in a potential field, where Ca²⁺ ion could interact with other Ca²⁺ ions as well as electrostatic potentials. The time-evolution of Ca²⁺ ions were therefore well described by the Fokker-Planck equation (FPE) (Risken, 1997) and we modeled the joint positions of N Ca²⁺ ions present in the dyad as a 3N-dimensional Brownian motion in a potential field, as described by the FPE. The total potential energy of the system (given as a function of Ca²⁺ ion positions) was determined within the FPE based on the assumptions that: (1) an electrostatic potential forms at each ion due to the charges on the surrounding proteins and lipids, (2) proteins within the dyad are impenetrable by Ca²⁺ ions, and (3) the Debye length for Ca²⁺ ions in the dyad is ~ 1 nm which means that two Ca²⁺ ions cannot occupy the same lattice point at the same time but otherwise have no electrostatic interaction (i.e. at distances greater than 1 nm). The lateral boundary at the interface between the dyadic volume and myoplasm was treated as an absorbing boundary for ions flowing from the dyad to the myoplasm. The multidimensional FPE describes the evolution of the probability density function for the positions of Brownian particles subject to a potential. Rather than solving the time-dependent joint probability density from the FPE, we generated the net evolution of Ca²⁺ ion positions in the dyad using an algorithm for a finite difference representation of the FPE that can be interpreted as a spatially discrete Markov process as described by Wang et al (2003) and simulated using Monte Carlo methods. The discrete description of Ca²⁺ dynamics in the dyad was coupled with the processes of Ca²⁺ binding and gating dynamics of RyRs and LCCs. The incorporation of these processes allowed the entire dyad to be simulated by a single all-inclusive Markov process (Tanskanen et al., 2007).

The peak number of free Ca²⁺ ions in the dyad has previously been estimated to be small, ~ 1 free Ca²⁺ ion at a Ca²⁺ concentration of 10 μM in a dyad of radius 50 nm (Bers, 2001). A 10-ms simulation of a model dyad containing only one LCC located at its center at a membrane potential of 0 mV generated an average of ~ 0.5 Ca²⁺ ions within a 50 nm radius of the LCC (see Fig. 8 of (Tanskanen et al., 2007)), with a minimum of zero and a maximum of 7 Ca²⁺ ions (corresponding to a maximum concentration of 98.7 μmol/L [Ca²⁺]_d). A similar protocol using a single RyR in the SR membrane (in which the RyR is initially open) generated an average of ~ 22.8 Ca²⁺ ions. The number of Ca²⁺ ions peaked at 49 during Ca²⁺ release, which corresponds to a concentration of ~ 0.7 mmol/L Ca²⁺, similar to jSR Ca²⁺ concentration (Shannon et al., 2000). RyR gating produced a high degree of variability in the number of dyadic Ca²⁺ ions (coefficient of variation of 64%), showing that the LCC-RyR signaling involved in CICR at the level of the single dyad is a noisy process mediated by tens of Ca²⁺ ions.

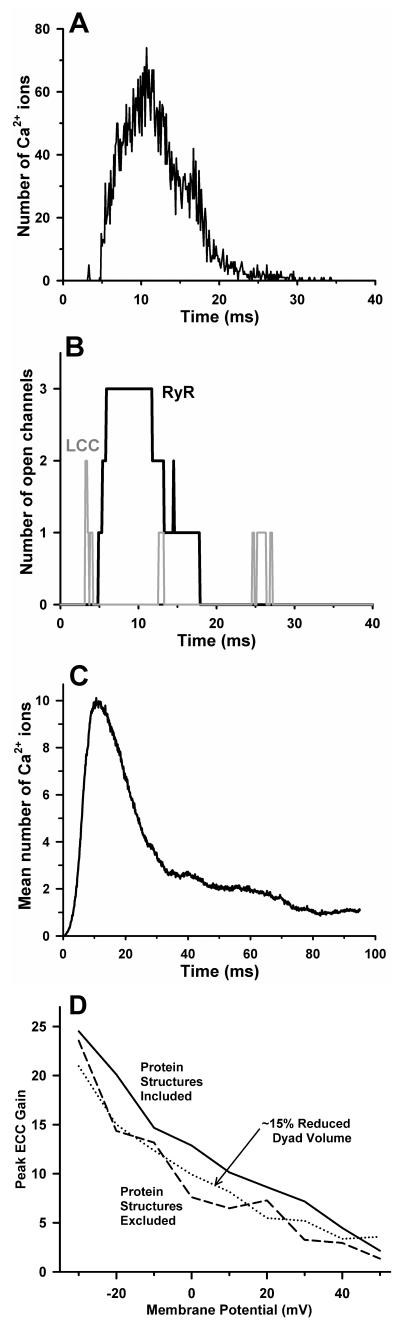
Features of a representative single dyad Ca²⁺ release event are shown in panels A and B of Fig. 3. Ca²⁺ release is evoked by a voltage clamp to 0 mV at time zero. Panel A shows the number of Ca²⁺ ions in the dyad, and panel B shows the number of LCCs (gray line) and RyRs (black line) that are open as a function of time during the release event. Two LCCs open at ~ 3 ms following the voltage clamp, and Ca²⁺ influx into the dyad triggers the opening of 3 RyRs 1-2 ms later, which inactivate after ~ 7 ms, ~ 9 ms, and ~ 13 ms, respectively. The temporal shape of the Ca²⁺ signal in the dyad (Fig. 3A) is closely correlated to the number of open RyRs (Fig. 3B). Figure 3C shows the average number of Ca²⁺ ions in the dyad based on the simulation of 1000 independent dyads. As would be expected the peak of the average signal is reduced compared to that of an individual dyad due to temporal dispersion of Ca²⁺ release events and the fact that not all dyads will exhibit a Ca²⁺ release event. The duration of the average local Ca²⁺ transient shown in Panel C is ~ 20 ms (at half-maximal amplitude), similar to that measured for Ca²⁺ spikes in myocytes (Cheng et al., 1993; Sham et al., 1998; Song et al., 2001).

Figure 3.

A CICR event in a single dyad evoked by a 0 mV voltage clamp step at time zero (from (Tanskanen et al., 2007)). (A) The number of free Ca²⁺ ions in the dyad volume as a function of time. (B) The number of open RyRs (black solid line) and the number of open LCCs (gray solid line) in the dyad during the release event depicted in panel A. (C) The average number of free Ca²⁺ ions in the dyad as calculated from 1000 independent dyads. (D) ECC gain (averaged over 400 independent dyad simulations) as a function of membrane potential for the baseline model which includes space-filling geometric models of protein structure in the dyad (solid line), for the model with protein structures excluded (dashed line), and for a modified model with dyad height reduced from 15 nm to 13 nm and protein structures excluded (dotted line).

Despite the noisy nature of dyad signaling, simulations showed that ECC gain is a robust and reproducible feature that emerges from the underlying assumptions of the model made at the nano-scale level. For a whole-cell population of dyads, the variability in gain that arises from the stochastic gating of LCCs and RyRs is small at potentials near and above 0 mV (see Fig. 11 of (Tanskanen et al., 2007)). The functional influence of protein structures on ECC is shown in Fig. 3D. Peak ECC gain (measured as the average over 400 independent dyad simulations) obtained for the baseline model (solid line) is compared to that for the model in which LCC, RyR, and CaM molecule structures were omitted (dashed line). Ca²⁺ binding site locations were the same for both simulations. Over a wide range of potentials, the peak ECC gain is decreased upon removal of the protein structures from the dyad. The protein structures occupy ~ 15% of the dyad volume. In order to show that the difference in ECC gain in the presence vs. absence of protein structures is not simply attributable to the difference in Ca²⁺-accessible dyad volume, peak ECC gain was obtained with protein structures absent and dyad volume reduced by ~ 15% (dotted line). ECC gain values for this model were clearly not increased to the level obtained in the presence of protein structures. These data indicate that the physical shape and configuration of dyad proteins influences Ca²⁺ diffusion during CICR in such a way as to enhance ECC gain. In addition, the probability of triggering a release event with protein structures intact (0.152) was 44% greater than with protein structures excluded (0.105). These data suggest that when LCCs are directly apposed to RyRs, the diffusion obstacle imposed by the structure of RyRs leads to an increase in the probability that trigger Ca²⁺ ions bind to activation sites on the RyRs, and hence increases ECC gain.

These data demonstrate that a number of features of CICR arise from mechanisms underlying the interaction of LCCs and RyRs at the level of single dyads: 1) CICR is a highly noisy process and that models based on laws of mass action may not accurately capture dyadic Ca²⁺ dynamics; 2) in ensembles of dyads, the fundamental properties of local control of CICR arise de novo as a consequence of the underlying physical structure and channel gating properties, including voltage-dependence of ECC gain; and 3) the physical shape and location of RyRs relative to LCCs is likely to have a major influence on properties of CICR.

2.3 CaMKII-dependent Modulation of Excitation-Contraction Coupling

An important Ca²⁺ cycling regulatory mechanism of recent interest is the signaling pathway involving Ca²⁺/CaM-dependent protein kinase II (CaMKII), which targets and phosphorylates LCCs and RyRs in the cardiac dyad. In addition, CaMKII targets the network sarcoplasmic reticulum (nSR) Ca²⁺-ATPase known as the SERCA pump, and phospholamban (PLB, a regulator of the SERCA pump). CaMKII also targets Na⁺ and K⁺ channels in the sarcolemma (Maier and Bers, 2007). Phosphorylation of these target proteins has multiple functional consequences. CaMKII plays a role in fine tuning ECC, and is activated when bound by Ca²⁺/CaM. Evidence suggests that CaMKII is directly associated with its target proteins (Currie et al., 2004; Hudmon et al., 2005), indicating that CaMKII signaling occurs locally in the dyadic junction. In addition, CaMKII activity is elevated in heart failure (Ai et al., 2005). Saucerman and Bers (2008) incorporated models of CaM, CaMKII, and calcineurin (CaN) into the Shannon et al (2004) model of the cardiac myocyte in order to better understand the functional consequences of the different affinities of CaM for CaMKII and CaN during action potentials (APs). The model predicted that in the cardiac dyad, Ca²⁺ levels lead to a high degree of CaM activity resulting in frequency-dependent CaMKII activation and constitutive CaN activation, whereas the lower Ca²⁺ levels in the cytosol only minimally activate CaM, which allows for gradual CaN activation, but no significant activation of CaMKII. Grandi et al (2007) developed a model of CaMKII over-expression in rabbit ventricular myocytes, including the role of CaMKII phosphorylation of fast Na⁺ channels, LCCs, and the transient outward K⁺ current (I_to1), which revealed a net effect of action potential duration (APD) reduction with CaMKII.

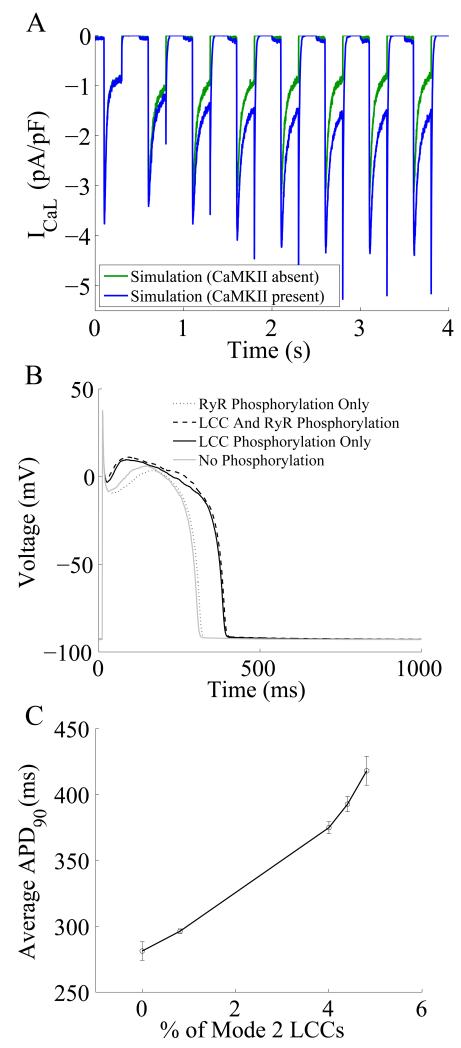
Recently, Hashambhoy et al (2009) described dynamic CaMKII phosphorylation of LCCs in an extension of the Greenstein-Winslow (Greenstein and Winslow, 2002) cardiac myocyte model. In this model, it is assumed that a single CaMKII holoenzyme is tethered to each LCC, each CaMKII monomer can transition among a variety of activity states (see Fig. 2 of Hashambhoy et al (2009)), and CaMKII monomers can catalyze phosphorylation of individual LCCs. It is a biochemically detailed, stochastic model in which the activity state of each of 12 CaMKII monomers within a CaMKII holoenzyme and the phosphorylation state of each LCC are simulated dynamically in addition to LCC voltage- and Ca²⁺- dependent gating. In this model, active CaMKII monomers can phosphorylate neighboring CaMKII monomers and/or the associated LCC. These studies demonstrated that CaMKII-dependent shifts of LCC gating patterns into high activity gating modes (where phosphorylated LCCs experience openings that are 10-20 times longer in duration than non-phosphorylated LCCs) may be the key mechanism underlying experimentally observed increases of I_CaL amplitude (Fig. 4A), the apparent macroscopic increase in the rate of recovery from inactivation, and the slowing of inactivation rate associated with I_CaL facilitation. Hashambhoy et al (2010) further expanded this model to include CaMKII-dependent regulation of RyRs in the dyad and demonstrated that under physiological conditions, CaMKII phosphorylation of LCCs ultimately has a greater effect on RyR leak flux and APD as compared with phosphorylation of RyRs (Fig. 4B). The LCC phosphorylation mediated increase in diastolic RyR leak was attributed to the augmented cytosolic (and dyadic) Ca²⁺ level resulting from increased Ca²⁺ influx via LCCs under conditions that promote high LCC activity, and hence, high open probability. APD was shown to correlate well with a CaMKII-mediated shift in modal gating of LCCs (Fig. 4C).

Figure 4.

(A) Simulated I_CaL elicited by a rapid pacing protocol in which a prepulse of −40 mV was delivered, followed by a 200 ms depolarization to 0mV (from (Hashambhoy et al., 2009)). Holding potential was −80 mV. Blue curves represent model results in the presence of CaMKII and green curves represent model results in the absence of CaMKII. (B) Simulated Results from a 1-Hz AP pacing protocol under different LCC and/or RyR phosphorylation conditions. (C) AP duration as a function of average LCC phosphorylation levels. Fully phosphorylated LCCs gate in Mode 2 which exhibit long duration openings (Hashambhoy et al., 2010).

2.4 Localized Signaling in the β-adrenergic Pathway

Cardiac ion channels as well as proteins involved in CICR and ECC are primary targets for regulation via the β-adrenergic signaling cascade. The so-called “fight or flight” response increases cardiac contractility and output via the release of neurotransmitters and hormones by the sympathetic nervous system. Norepinephrine and epinephrine bind to β-adrenergic receptors (β-ARs) on the myocyte surface. These are G-protein-coupled receptors which trigger the activation of adenylyl cyclase (AC), leading to the production of cyclic AMP (cAMP), which in turn activates protein kinase A (PKA). The numerous targets of PKA-mediated phosphorylation include LCCs and RyRs in the cardiac dyad, PLB in the nSR, the myofilament protein troponin I, and phospholemmen (a subunit of the Na⁺-K⁺ pump) (Bers, 2002; Bers, 2008; El-Armouche and Eschenhagen, 2009). Recent studies have revealed that cAMP signaling does not occur within a simple linear pathway, and this has led to the hypothesis of cAMP compartmentation, in which the cell maintains distinct localized domains of cAMP (Saucerman and McCulloch, 2006). A possible mechanisms for cAMP compartmentation is the existence of caveolae, membrane invaginations in which high concentrations of β-adrenergic signaling proteins such as β-ARs, ACs, and PKA have been found in cardiomyocytes (Ostrom et al., 2001). In addition, LCCs (a major PKA target) have been found to co-localize with caveolae (Lohn et al., 2000). A-kinase-anchoring proteins (AKAPs) may also play an important role in the compartmentalization of β-adrenergic signaling by tethering PKA near its targets. In the heart it has been shown that AKAPs target PKA to LCCs, RyRs, type 2 β-ARs, as well as mitochondria and other sites (Ruehr et al., 2004; Saucerman and McCulloch, 2006).

Early attempts to model the effects of PKA-mediated phosphorylation of its targets on the properties of CICR and the AP involved modeling the stimulated cell by altering the function of the target proteins based on the measured effects of phosphorylation. Greenstein et al (2004) developed a model of the canine ventricular myocyte in the presence of 1 μM isoproterenol (a β-AR agonist). This model could explain PKA-mediated changes in AP shape, dissected the specific effects of PKA-mediated phosphorylation of LCCs and RyRs on the voltage-dependent gain of CICR, and predicted a mechanism by which increasing levels of LCC phosphorylation could lead to increased frequency of early after depolarizations (Tanskanen et al., 2005). However, this model did not describe the dynamics of the β-adrenergic signaling pathway. Saucerman et al (2003) developed a differential-algebraic kinetic model of the β-adrenergic signaling pathway, and incorporated it into the rabbit myocyte model of Puglisi et al (2001). This model comprehensively describes the full pathway including agonist stimulation of the type 1 β-AR, activation of G_s protein, cAMP synthesis by AC, cAMP degradation by phosphodiesterase, PKA subunit activation and dissociation, phosphorylation of important target proteins PLB and LCCs, and β-AR kinase and PKA-mediated type 1 β-AR desensitization. Mobile and anchored forms of PKA and protein phosphatases were accounted for separately. A wide range of independent biochemical and physiological experimental data was used to validate the model, strengthening its ability to make mechanistic predictions, and establishing it as a core signaling model upon which others would build in future studies. This model was used to understand effects of specific molecular perturbations (e.g. expression changes in AC and β-AR density) on cAMP dynamics and contractility via changes in function of target proteins resulting from altered phosphorylation dynamics. Recently, the model of Saucerman et al (2003) was incorporated into the guinea pig ventricular model of Faber and Rudy (2000) in a study of the role of β-adrenergic agonists and antagonists in long-QT syndrome (Ahrens-Nicklas et al., 2009). The model of Saucerman et al (2003) has also been adapted in order to investigate the role of β-adrenergic signaling on Na⁺ regulation during EC coupling (Kuzumoto et al., 2008), and it was demonstrated that phospholemman has an important role in limiting the build-up of Na⁺ during β-adrenergic stimulation, a finding that was later validated experimentally (Bers and Despa, 2009; Despa et al., 2008).

Integration of signaling models of the β-adrenergic pathway with experimental techniques has recently enabled more detailed studies of cell signaling kinetics and localization. Saucerman et al (2006) combined a spatially explicit version of their model (Saucerman et al., 2003) with FRET imaging experiments to show how spatial PKA gradients could be explained by restricted diffusion of cAMP, phosphodiesterase-mediated cAMP degredation, or PKA-mediated cAMP buffering, and concluded that cAMP compartmentation likely plays an important role in limiting the rate of PKA activation (Yang and Saucerman, 2011). An approach combining mathematical modeling with FRET experiments was also used by Iancu et al (2007), in which it was demonstrated that subcellular localization of different AC isoforms (which can be either stimulated or inhibited by the G_i G-protein) can explain the mechanism by which both stimulatory and inhibitory responses in cAMP can arise in response to the same upstream stimulus (acetylcholine-mediated activation of the muscarinic M₂ receptor). While there is still much that remains unknown regarding the mechanisms underlying localization of key proteins in the β-adrenergic signaling pathway, new approaches such as this will continue to elucidate the key mechanisms for localization and regulation of this cell signaling pathway.

2.5 The Function of Extra-Dyadic Localization of Ca²⁺ and Na⁺ Channels and Transporters

Following CICR in cardiac myocytes, Ca²⁺ entering the cytosol must be removed in order to allow for mechanical relaxation and refilling of the heart. In steady state, it must be true that on each beat, Ca²⁺ that has been released from the SR via RyRs is pumped back into the SR, and Ca²⁺ that has entered the cell via LCCs is extruded from the cell. The dominant Ca²⁺ efflux mechanism in cardiac myocytes is NCX. While the primary function of NCX is to remove Ca²⁺ from the myocyte during diastole, numerous studies have indicated that NCX can operate in a so-called reverse mode in which Ca²⁺ is imported and Na⁺ is extruded, potentially providing an alternative source of Ca²⁺ influx during CICR. Given that CICR occurs in the form of discrete Ca²⁺ sparks within the dyad, functional evidence for a role of NCX in triggering SR Ca²⁺ release would suggest that NCX must be located within or near the dyad, and therefore may participate in the Ca²⁺ signaling events that occur in this nano-domain. Whether or not Ca²⁺ entry via reverse mode NCX contributes to the trigger for CICR remains controversial, as there are data that argue both for and against this mechanism. Bouchard et al (1993) measured the voltage dependence of cell shortening in rat ventricular myocytes and observed no significant effect of altering the electrochemical gradient for Na⁺ (which would alter NCX function). In addition, rapid phasic contractions were never elicited under conditions where LCC Ca²⁺ influx was blocked, suggesting NCX alone could not trigger CICR. Sham et al (1992) saw no evidence that Na⁺ influx (via fast Na⁺ channels) or its accumulation could initiate SR Ca²⁺ release. Sipido et al (1997) analyzed the characteristics of SR Ca²⁺ release triggered by reverse NCX and I_CaL in isolated guinea pig ventricular myocytes, and found that trigger efficiency for reverse mode NCX was about four times less than that for I_CaL. Moreover, they could detect no contribution of reverse mode NCX to the CICR trigger at potentials below 60 mV when I_CaL was intact, suggesting that the role of NCX in triggering CICR during the cardiac AP was negligible. In contrast to these studies, Litwin et al (1998) found that reverse mode NCX alone could not provide enough Ca²⁺ influx to activate myofilaments directly, but that the nifedipine-insensitive current carried by NCX could trigger a component of contraction that increased with voltage, suggesting reverse NCX can trigger SR Ca²⁺ release. Similarly in rat ventricular myocytes at near physiological conditions, Wasserstrom et al (1996) found that under both voltage- and AP-clamp protocols, about 50% of the elicited contraction was nifedipine-insensitive, and that this component of contraction could be blocked by Ni²⁺ (which blocks NCX), suggesting that reverse mode NCX contributes to CICR.

More recent experiments have attempted to address the controversial role of NCX in triggering SR Ca²⁺ release. Sobie et al (2008) imaged the trigger flux of Ca²⁺ across the cell membrane using a fluorescent Ca²⁺ indicator under conditions where Ca²⁺ release from the SR was disabled and found a significant contribution of reverse mode NCX to the total Ca²⁺ influx. However, NCX-mediated Ca²⁺ entry was found to be considerably smaller when measured in the absence of I_CaL, suggesting that the local elevation of [Ca²⁺] that occurs upon LCC activation is necessary to activate nearby NCX via a catalytic Ca²⁺-binding site (Hilgemann et al., 1992). Lack of NCX catalysis may explain the observation that NCX plays no role in triggering CICR in earlier studies. Neco et al (2010) have examined Ca²⁺ sparks in wild-type (WT) and cardiac specific NCX knock-out (KO) mice, and found that high sub-sarcolemmal Ca²⁺ must be maintained in KO mice for synchronous triggering of Ca²⁺ sparks resembling those of WT. In WT, NCX could prime the dyad with sufficient Ca²⁺ for normal spark triggering (so intervention to raise sub-sarcolemmal Ca²⁺ was not necessary), suggesting that the ability to generate normal Ca²⁺ sparks depends upon the presence of nearby NCX. Furthermore, Larbig et al (2010) showed that Ca²⁺ transients and SR Ca²⁺ release flux of KO mice were unaffected by inactivation (or block) of I_Na whereas those of WT were reduced by ~ 50%, and concluded that I_Na, via its effect on reverse mode NCX, modulates Ca²⁺ release in WT myocytes by enhancing the Ca²⁺ signal in the vicinity of the RyRs during CICR.

In agreement with these functional data, imaging studies indicate that up to 50-70% of NCX are located within t-tubules (Scriven et al., 2000; Thomas et al., 2003; Yang et al., 2002), and this localization is mediated by NCX binding to the membrane adaptor protein ankyrin-B (ANK-B) (Cunha et al., 2007) at ANK repeats 16 – 18 (Cunha and Mohler, 2009). As described above, the spatial distribution of NCX expression in the t-tubules, and in particular location relative to RyRs, has been a subject of great interest because of its implications for ECC processes. Using fluorescently tagged antibodies to both RyRs and NCX, Scriven et al (2000) observed virtually no co-localization of expression, suggesting that NCX is positioned in the extra-dyadic region of the t-tubules (Scriven et al., 2000). More recently, Jayasinghe et al (2009) used improved imaging techniques to show that NCX labeling in t-tubules has an approximately uniform distribution that is interrupted by local regions of more intense labeling, referred to as puncta. Many of these puncta are very close to RyR clusters, with mean distance to the nearest cluster being ~ 250 nm. If correct, these data show that NCX is not only localized in t-tubules, but may be sufficiently close to the dyad to have a significant effect on ECC.

Cardiac myocytes also express both α1 and α2 isoforms of the Na⁺-K⁺ ATPase (NKA). The α2 isoform (NKA-α2) is known to be expressed preferentially in the t-tubules (Swift et al., 2007). ANK-B binds directly to the N-terminal tail of the catalytic α-subunit of NKA (Liu et al., 2008), and both NKA-α1 and NKA-α2 expression in t-tubules is markedly reduced in haplo-insufficient ANK-B^+/− myocytes. Thus, as with NCX, ANK-B mediates localization of NKA in the t-tubule region. The fact that both NCX and NKA-α2 may require ANK-B for stable expression raises the possibility that NCX1 and NKA-α2 are co-localized in the t-tubules. This appears to be the case in several cell types. In cultured astrocytes, NKA-α2 and NCX expression is co-localized to a micro-domain between the plasma and endoplasmic reticulum (ER) membrane (Golovina et al., 2003). NKA and NCX are also co-localized in the inner segment of rod photoreceptors, and this co-localization is dependent on expression of ANK-B (Kizhatil et al., 2009). In cardiac myocytes, ANK-B co-immunoprecipitates with NCX1, NKA-α1/α2, and InsP₃Rs (Mohler et al., 2003). ANK-B is necessary for this co-localization (Mohler et al., 2005). Consistent with these data, ANK-B is known to have a binding site for InsP₃R that is distinct from those for NCX and NKA (Kline et al., 2008).

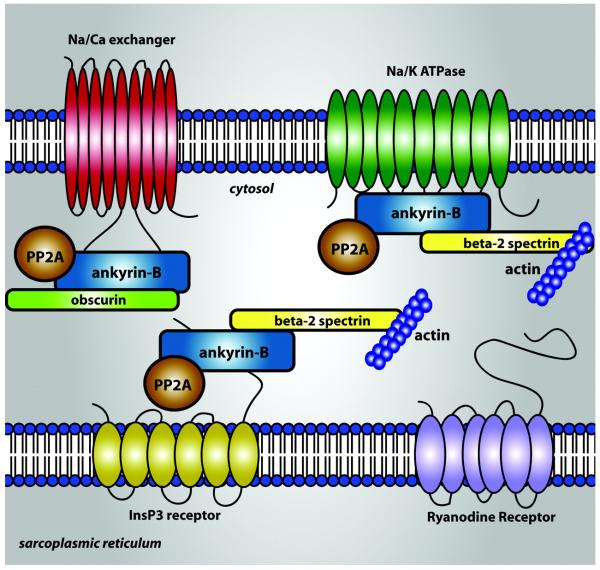
Based on these findings, Ackerman and Mohler (2010) have proposed the structural model shown in Fig. 5 of ANK-B complex formation within t-tubules (Mohler and Wehrens, 2007). This figure shows interactions between ANK-B, actin associated β2-spectrin, the cytoskeletal protein obscurin, as well as NCX, NKA, and InsP₃R. The three distinct binding sites of an ANK-B molecule are capable of binding one molecule each of NKA, NCX, and InsP₃R, configuring them into a local complex interacting over a distance of 10-20 nm. It is also possible that ANK-B can bind one or two of these molecules at a time. This raises many possibilities for local Na⁺ and Ca²⁺ signal integration. In the case of a local complex comprised of an NCX and NKA molecule bound to ANK-B, Na⁺ extrusion via NKA may quickly deplete local Na⁺ concentration, facilitating transport of Ca²⁺ out of the t-tubules via NCX, whereas inhibition of NKA, through local increase of Na⁺, may facilitate reverse mode NCX function. This close coupling of NKA and NCX activity is consistent with the observations of Terracciano (2001) and Su et al (2001) in experiments where NKA activity was rapidly inhibited, producing significantly decreased NCX-driven Ca²⁺ extrusion and increased Ca²⁺ transients, similar to the effects of oubain on NKA and SR Ca²⁺ load. The functional significance of a local complex comprised of NKA, NCX, and InsP₃R is much less clear. One hypothesis is that when this complex is localized to the extra-dyadic region of the t-tubules, InsP₃Rs can modulate CICR. InsP₃R activation may enhance the likelihood of Ca²⁺ sparks and waves through regulation of local Ca²⁺ levels. Functionally, an E1425G mutation in ankyrin-B causing dominantly inherited type 4 long-QT cardiac arrhythmia in humans leads to loss of ANK-B-associated NCX, NKA, and InsP₃R, and results in defects of intracellular Na⁺ and Ca²⁺ regulation and cellular after-depolarizations in response to catecholamines (Mohler et al., 2003). The mechanisms of such complex interactions will only be resolved through development of computational models that capture the ability of these protein complexes to integrate local Na⁺ and Ca²⁺ signals.

Figure 5.

Schematic illustration of ANK-B binding to and co-localization of NCX, NKA, and InsP₃R. ANK-B also binds the actin associated β2-spectrin, the cytoskeletal protein obscurin, and the regulatory sub-unit of protein phosphatase (PP) 2A (Ackerman and Mohler, 2010).

2.6 The Mitochondrial - JSR Local Ca Signaling Domain

Even at resting heart rates, the process of ECC consumes significant amounts of ATP. The main consumers are the myosin ATPase, NKA, and the SERCA pump. Estimates suggest that at maximal workload, the entire cellular ATP pool may be utilized over a time-course of a few seconds (Balaban, 2002). Maintaining the process of ECC therefore requires that mitochondrial ATP production be tightly controlled by myocyte workload, potentially on a beat-to-beat basis. It is therefore no wonder that understanding the mechanisms by which control is exerted has been a central theme of cardiac biology over the last several decades.

The early work of Chance and Williams indicated that energy supply and demand matching is regulated by levels of ADP and P_i through effects on the F1/F0-ATPase (Chance and Williams, 1955). This hypothesis was called into question when Balaban and colleagues (Territo et al., 2001) discovered that increased cardiac workload increased O₂ consumption without changes in the levels of ADP or P_i. This group went on to demonstrate that Ca²⁺ may play a major role in energy supply and demand matching by regulating activity of three enzymes in the tri-carboxcylate acid cycle (pyruvate, isocitrate, and a-ketoglutarate de-hydrogenase) and the F1/F0-ATPase, and that this regulation could be achieved on a time scale of ~ 100 msec (Territo et al., 2001).

In order for Ca²⁺ to be a regulator of energy supply-demand matching, sufficient Ca²⁺ must be transported into mitochondria to regulate TCA cycle enzymes and the F1/F0-ATPase. Ca²⁺ is transported into mitochondria by the mitochondrial Ca²⁺ uniporter (mCU). Careful modeling of the mCU (Dash et al., 2009) based on the experimental data of Scarpa and Graziotti (1973) shows that mCU transport rate is a sensitive function of extra-mitochondrial Ca²⁺ over the range of ~ 20 – 100 μM. These Ca²⁺ concentrations are much larger than observed in the cytosol, raising the question of how fluctuations of cytosolic Ca²⁺ can regulate ATP production. The answer may be due to the close proximity of mitochondria to the JSR and cardiac dyad. Using high-resolution optical imaging techniques, Rizutto et al (1998) showed that there appear to be numerous close contacts between mitochondria and endoplasmic reticulum in living HeLa cells. In addition, Ca²⁺ transients measured by targeting a Ca²⁺-sensitive photo-protein to the outer face of the inner mitochondrial membrane, and then evoking Ca²⁺ release through InsP₃R by application of histamine suggested that the mitochondrial surface was exposed to significantly higher Ca²⁺ concentration changes than observed in the cytosol. Subsequently, Csordas et al (2006) showed that rat liver mitochondria are connected with smooth and rough ER by structures they referred to as “tethers”. Tethers between the outer mitochondrial membrane (OMM) and smooth ER had lengths in the range of 9 – 16 nm, whereas those between OMM and rough ER had lengths 19 – 30 nm (Csordas et al., 2006). These data established a length-scale over which mitochondria and Ca²⁺ sequestering organelles may interact. In a recent elegant study, Hayashi et al (2009) showed the existence of similar electron-dense structures between the OMM and nSR/jSR in mouse ventricular myocytes, thus establishing the close proximity of cardiac mitochondria to the jSR membrane and Ca²⁺ release sites (Perkins et al., 2001) – a necessary component of the hypothesis that tight control of energy supply and demand in heart is regulated via mitochondrial sensing of local Ca²⁺ signals.

This hypothesis is also supported by predictions of local Ca²⁺ concentration in and near the cardiac dyad. Computational models predict that dyadic Ca²⁺ concentration may be as large as ~ 50 - 100 μM at the peak of the Ca²⁺ transient, and have rapid rise and decay times (< 10 ms) (Soeller and Cannell, 2004; Tanskanen et al., 2007). While these model estimates depend on many factors, they demonstrate that it is possible for the local Ca²⁺ signal near mitochondria to be large enough to activate mCU transport, and have sufficiently fast kinetics to support beat to beat regulation of mitochondrial energetics.

Tight regulation of mitochondrial energy production also requires that the mCU have sufficiently fast kinetics to respond to the local signal. Whether or not this is true remains controversial (Maack and O’rourke, 2007). Estimates of the time constant of mCU uptake differ, with some in the range of ~ 5 sec (Sedova et al., 2006), and others of ~100 ms (Territo et al., 2001). In addition, a recent study by Maack et al (2006) suggests that the mitochondrial Ca²⁺ transient always precedes the cytosolic Ca²⁺ transient, has faster mean rise time (15 ms versus 40 ms), and an average decay time of ~ 90 ms. Thus, while there remains controversy as to whether changes in mitochondrial Ca²⁺ are fast enough to follow each heart beat, there is increasing evidence that mitochondria sense Ca²⁺ in a local domain near the cardiac dyad, and that this sensing supports changes in mitochondrial Ca²⁺ over individual to 10’s of heart beats.

Implications for our understanding of both properties of ECC as well as control of mitochondrial energetics are significant. Furthermore, it is likely that mitochondria not only sense local Ca²⁺, but also regulate local Ca²⁺ by virtue of their Ca²⁺ “buffering” (i.e., Ca²⁺ uptake via mCU) properties. Accordingly, co-location of mitochondria with jSR may have an important influence on properties of ECC by helping to set the boundary conditions on Ca²⁺ flux in the vicinity of cardiac dyads. Mitochondria may also effect Ca²⁺ communication between adjacent dyads, thereby influencing cellular properties such as conduction velocity of Ca²⁺ waves. Such effects may be particularly important in light of new evidence that the nearest neighbor distance between dyadic clefts may be as small as 20 nm (Hayashi et al., 2009). For all of these reasons, computational models that incorporate close interaction between mitochondria and the cardiac dyad, and sensing of the local dyadic Ca²⁺ signal, will be necessary in order to understand properties of beat to beat regulation of cardiac energetics, and local versus more global properties of Ca²⁺ signaling. The basis for modeling these processes has been established by development of compartmental models of ATP production in cardiac mitochondria (Beard, 2005; Cortassa et al., 2003) and integration of these mitochondrial models into models of the cardiac myocyte (Cortassa et al., 2006; Cortassa et al., 2009; Matsuoka et al., 2004a; Matsuoka et al., 2004b).

3. Conclusions

We have described a variety of biophysical processes relating to CICR that involve molecular interactions over nm length- and ns time-scales. It has become clear from both experimental and modeling studies that understanding nano-scale dyanamics, whether it is the processing of the dyadic Ca²⁺ signal by LCC-tethered CaM in the cardiac dyad, the interaction among LCCs and RyRs during CICR via a small number of Ca²⁺ ions, the mechanisms of local signaling in the CaMKII and β-adrenergic pathways, functional formation and consequences of local domains defined by colocalization of Ca²⁺ and Na⁺ transport mechanisms, or the local interaction of mitochondrial Ca²⁺ transport with CICR in the dyad, provides critically important insight into cellular function. Examples of similar nano-scale interactions abound in other cells (Golovina et al., 2003; Kizhatil et al., 2009; Modchang et al., 2010; Sosinsky et al., 2005). Understanding how integrative cellular, tissue, and whole organ function emerges from a variety of subcellular component mechanisms is the goal of multi-scale modeling techniques. Modeling such complex systems will require application of careful approximations that permit model integration across a range of time- and spatial-scales. In some cases, it has been possible to build self-contained multi-scale models of a physiological system. As an example, the model of Greenstein and Winslow (2002) spans the biological scales of single channel gating to whole cell physiology in a cardiac myocyte. In other cases, it is necessary to use the knowledge obtained from a detailed model at the nano-scale, e.g. mechanisms of ECC gain in the dyad (Tanskanen et al., 2007), to constrain models that are built at a more macroscopic scale, e.g. biophysically detailed whole cell models (Greenstein et al., 2006; Saucerman and McCulloch, 2006).

We are in the early days of multi-scale modeling, and a valuable approach to building a repertoire of methods for multi-scale approximations is to work example by example. In that spirit, we offer the work of Tanskanen and Winslow (2006) as a detailed example. The starting point of this work was the nano-scale model of the dyad (Tanskanen et al., 2007), presented in Sect. 2.2, describing the motion of individual Ca²⁺ ions at nm length- and ns time-scales based on the Fokker-Planck equation. To simplify the model, it was assumed that: (1) Ca²⁺ ions are independent and do not interact; (2) the entry of Ca²⁺ ions can be described as a continuous influx of probability mass; (3) Ca²⁺ buffering by mobile buffers does not affect the steady state Ca²⁺ probability density; and (4) binding sites are in equilibrium with Ca²⁺ ion concentration. Then conditioning on a configuration of Ca²⁺ sources (RyRs and LCCs) reduced the FPE for individual ion locations and numbers to a reaction-diffusion equation (Tanskanen and Winslow, 2006). Since Ca²⁺ diffusion on nm length scales is several orders of magnitude faster than channel gating (an assumption also made by Hinch et al (2004; 2006)), Ca²⁺ ion density in the dyad equilibrates rapidly in each LCC and RyR gating state. This removed the time-dependence of the expected density of Ca²⁺ ions in the reaction-diffusion equation, yielding a Laplace equation, which under additional assumptions had an analytical solution for the spatial Ca²⁺ concentration profile (Tanskanen and Winslow, 2006). Thus, in general, the key to this multi-scale modeling approach was careful approximations regarding independence of Ca²⁺ ions (Debye length is short – under 1 nm) and successive rapid equilibrium approximations.

A more general issue, when model scalability is desired, is whether or not it is necessary to model the motion of individual signaling molecules in nano-domains, as in Tanskanen et al (2007). Under certain conditions, it is not necessary to do this, and use of reaction-diffusion equations for the spatio-temporal evolution of concentrations is appropriate. As shown elegantly by Tadross et al (2008) and Hake and Lines (2008), continuum approximations for stochastic molecular motions are appropriate when molecular flux within the nano-domain is large over the time-scale of changes in molecular conformations related to channel gating, binding of signaling molecules, or phosphorylation processes, as examples.

We believe that the examples offered above illustrate a common design motif in which proteins, protein complexes, and even organelles interact over short spatial and rapid time-scales to govern the processes of the cell. It is essential to continue efforts to understand the signal processing functions performed at these spatio-temporal scales, and to develop mathematically sound methods by which this information can be integrated to higher levels in order to understand the life of the cell.