A matching algorithm for catalytic residue site selection in computational enzyme design

Abstract

A loop closure-based sequential algorithm, PRODA_MATCH, was developed to match catalytic residues onto a scaffold for enzyme design in silico. The computational complexity of this algorithm is polynomial with respect to the number of active sites, the number of catalytic residues, and the maximal iteration number of cyclic coordinate descent steps. This matching algorithm is independent of a rotamer library that enables the catalytic residue to take any required conformation during the reaction coordinate. The catalytic geometric parameters defined between functional groups of transition state (TS) and the catalytic residues are continuously optimized to identify the accurate position of the TS. Pseudo-spheres are introduced for surrounding residues, which make the algorithm take binding into account as early as during the matching process. Recapitulation of native catalytic residue sites was used as a benchmark to evaluate the novel algorithm. The calculation results for the test set show that the native catalytic residue sites were successfully identified and ranked within the top 10 designs for 7 of the 10 chemical reactions. This indicates that the matching algorithm has the potential to be used for designing industrial enzymes for desired reactions.

Introduction

A striking feature of enzymes is their unsurpassed selectivity for chemical reactions, such as chemical selectivity, region selectivity, and stereoselectivity, which is far greater than that of chemical catalysts. Enzymes are usually active in aqueous solution and at ambient conditions of temperature and pH. Importantly, these characteristics are consistent with the criteria for environmentally sustainable industrial processing because the world is facing significant energy and environmental challenges. Enzymes are able to catalyze an increasingly broad range of reactions, and this breadth has translated into an increasing number of applications of enzymes at the industrial scale.^1–3 However, there are still three main drawbacks for currently available enzymes: too few enzymes exist to catalyze desired reactions, enzymes are often not sufficiently stable in desired media, and the development cycle to produce new and improved enzymes is too long. To tackle these issues, protein engineers have used both empirical and structure-based approaches. As an empirical approach, directed evolution techniques have been applied and have achieved numerous successes over the last decade.⁴ However, this experimental approach is costly and time consuming, and more importantly the catalytic mechanism often remains unclear, even when an efficient mutant is selected. This is because directed evolution bridges sequence and function without a mechanistic appreciation of the structure and the reaction coordinate. At the same time, since the appearance of recombinant DNA technology, rational or de novo design approaches for novel enzymes have been widely used. Examples include, catalytic antibodies designed against transition-state (TS) analogs^5,6 and a de novo O₂-dependent phenol oxidase within an artificial four-helix bundle fold, designed by Kaplan and DeGrado.⁷ Besides these efforts based on experimentation, the computational design of enzymes has been ongoing since 1991 when Hellinga and Richards devised their molecular model building computer program, DEZYMER, to provide a general method for designing enzyme active sites. Using this computational tool, Hellinga and coworkers have created several novel metalloenzymes by grafting metal-binding sites between different proteins.^8–10 Bolon and Mayo¹¹ extended their successful computational protein design tool, ORBIT, into the enzyme active-site design field and created a histidine-bearing catalyst for the hydrolysis of p-nitrophenyl acetate into p-nitrophenol. More recently, Baker and coworkers have created several artificial enzymes with appreciable activities for typical bond-breaking or -forming reactions by using the design module in their protein modeling software, ROSETTA. Specifically, Rothlisberger et al.¹² developed new enzyme catalysts for a reaction, the Kemp elimination, for which no naturally occurring enzyme exists. Jiang et al.¹³ designed novel enzyme catalysts for a retro-aldol reaction in which a carbon–carbon bond is broken in a non-natural substrate (i.e., not found in any biological system). Siegel et al.¹⁴ invented an enzyme catalyst for a stereoselective bimolecular Diels–Alder reaction using their computational enzyme design methodology.

Computational enzyme design methodology aims to identify potential new active sites in known protein structures according to the predefined catalytic geometry for a desired reaction, where the sequence and side-chain conformation are altered to optimize the binding between active site and TS of the reaction, but leaving the backbone intact. Generally, the side chains in an active site can be classified into catalytic residues, that is, the functional groups, and the binding residues, that is, those surrounding the catalytic residues that constitute the complementary surface. By virtue of this classification, the computational enzyme design process is composed of two stages to reduce the computational complexity; first, the few catalytic residues are matched onto the active pocket according to predefined catalytic geometries, and then a repacking process is run to simultaneously identify the amino acid sequence and conformations of binding residues. In this article, the first process is the focus. The complexity of this process comes from the identification of the position of each catalytic residue in the active pocket and the determination of its correct conformation to satisfy the tightly predefined catalytic geometry. To circumvent these difficulties, during the initial development of DEZYMER, Hellinga and Richards¹⁵ performed an exhaustive search using extensive divide-and-conquer heuristics on the basis of a very limited rotamer library. A discrete search was first run to determine the combinatorial placement of rotamer and ligand, and then a continuous search was used to optimize these rough combinatorial solutions. The catalytic residue matching methods presented in ROSETTA are either the inverse rotamer tree approach or the RossettaMatch approach.¹⁶ The inverse rotamer tree approach is an “inside-out” method, where an inverse rotamer tree is built up from the active site description, and the backbone coordinates of all the rotamer combinations are compared to backbone coordinates of the set of scaffolds using a geometric hashing-based algorithm. However, if full diversification of the catalytic geometric parameters or a large rotamer library was used, the inverse rotamer tree method may encounter a combinatorial explosion problem. The RosettaMatch approach is an “outside-in” method. Side-chain rotamers and the TS model are sequentially placed at all scaffold positions, and the position of the TS model is recorded in a hash table. The hash table is then scanned for TS positions that are found when placing each of the catalytic side chains independently. Because of this, the RosettaMatch method avoids the combinatorial explosion problem. However, the nature of this searching approach is still exhaustive, and it strongly depends on the discrete resolution of the catalytic geometric parameters and on the size of the rotamer library used. Fazelinia et al.¹⁷ introduced a new computational procedure, OptGraft, based on mixed integer linear programing techniques for placing a novel binding pocket onto a protein structure so that its geometry is minimally perturbed. OptGraft was used successfully to guide the transfer of a calcium-binding pocket from thermitase into the first domain of CD2. Zhu and Lai¹⁸ described a ligand-independent enzyme design method based on vector matching of key residues. This method can be used for grafting an existing active site to a scaffold. Malisi et al.¹⁹ presented an algorithm called ScaffoldSelection that is able to rapidly search large sets of protein structures for potential attachment sites of an enzymatic motif. This method first identifies pairs of backbone positions in the active pocket. Then, it combines these to complete attachment sites using a revised clique search algorithm. This method is based on rigid geometrical relationships between catalytic residues and the TS and a relatively small rotamer library.

Recently, we have extended our PROtein Design Algorithmic (PRODA) package from core redesign²⁰ into enzyme design. In our computational enzyme design methodology, the whole process is decomposed into three stages: (i) matching process for catalytic residue site selection, (ii) TS sampling based on targeted small molecule placement,²¹ and (iii) sequence selection for binding residues based on free energy minimization and hydrogen bond matching.²² In this article, the first process is described, which is a PRODA module named PRODA_MATCH.

Results

Summary of the algorithm

In this work, a novel algorithm for matching the catalytic residues onto the active pocket was developed. First, the catalytic residue site selection problem is stated by an example with the protein data bank²³ (PDB) code, 1c2t, which is a glycinamide ribonucleotide transformylase from E. coli. This enzyme has three catalytic residues: Asn106, Asp144, and His108. The TS analogy for the reaction this enzyme catalyzes is named as NHS, and the catalytic geometrical relationships between the TS and the three catalytic residues are shown in Figure 1, and the specific parameters are given in Table I. There are 21 potential residue sites determined by PRODA_ MATCH: 63, 84, 86, 87, 88, 89, 90, 91, 95, 96, 105, 107, 108, 116, 117, 136, 138, 142, 143, 144, and 145, in the active pocket of 1c2t for the three catalytic residues, Asn, Asp, and His, to satisfy the constraints of the rigorous catalytic geometrical relationships given in Table I. The total combinatorial number of the selection problem for 1c2t is only 7980 (21 × 20 × 19), if the conformation freedom of the catalytic residues and the diversification of the catalytic geometrical parameters are not taken into account. In fact, such a combinatorial optimization problem can be tackled by an exhaustive searching method. This critical finding has encouraged us to look for an efficient way to handle the conformation selection for the catalytic residues and the parameter selection for the catalytic geometrical relationship during each combinatorial searching step. The univariate optimization-based cyclic coordination descent (CCD) method, which is widely used in the protein structure prediction field for loop closure,²⁴ is developed further in this article to implement this task. The CCD step is illustrated for 1c2t in Figure 2, where the location of the first catalytic residue, Asn, has been chosen as site 105, and the second catalytic residue, Asp, is intended to be located at site 107. This particular combination of Asn105 and Asp107 holds if there are allowable conformations for Asn and Asp and suitable catalytic geometrical parameters between the TS and these two catalytic residues. All the conformation parameters and catalytic geometrical parameters of the loop starting from Ca of Asn to Ca of Asp are optimized one by one to move the Ca of Asp as closely as possible to the backbone Ca at site 107, where each parameter adjustment is done by a univariate optimization process. After all parameters of the loop are optimized once, which here is called a CCD step, and the RMSD (root-mean-standard deviation) between the moving atoms and the target atoms does not meet the predefined tolerance, the CCD step repeats until the RMSD is met or the maximal iteration number of the CCD step, N_CCD, is reached. The former termination of the CCD cycle states that the particular combination, Asn105 and Asp107, is appropriate since the loop can be closed. The site selection procedure should be continued for the remaining catalytic residues, such as for His in 1c2t, which is intended to be located at site 138 (Fig. 2). The latter termination implies that site 107 is not a suitable location for Asp and another site should be tried. Different from the existing methods for catalytic residue site selection, which always combine the combinatorial search for site enumeration and parameter optimization, the novel algorithm developed in this article has separated these two processes. As the efficiency of the CCD step is very high and the total combinatorial number for site searching is tractable, the overall matching algorithm is very efficient.

Figure 1.

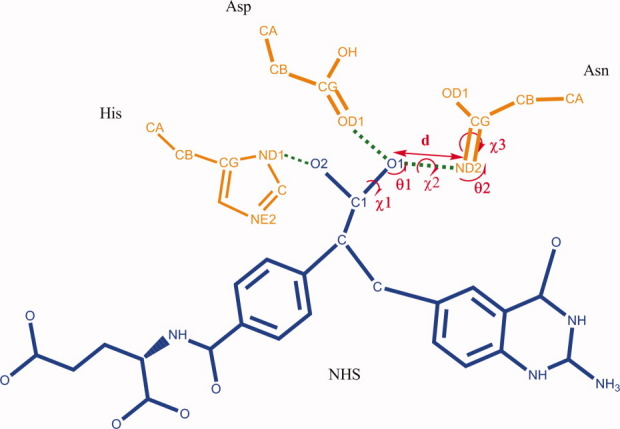
Illustration of catalytic geometrical relationships between the catalytic residues and the TS analog, for example, 1c2t. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table I.

Catalytic Geometrical Parameters, for Example 1c2t

NHS	Atom pairs	d (Å)	θ1 (°)	θ2 (°)	χ1 (°)	χ2 (°)	χ3 (°)
Asn	O1…ND2	2.8(±0.3)	120(±30)	120(±30)	Free	Free	Free
Asp	O1…OD1	2.6(±0.3)	120(±30)	120(±30)	Free	Free	Free
His	O2…ND1	2.8(±0.3)	120(±30)	109.5(±30)	Free	Free	Free

The standard values and deviations are taken from Ref.16.

Figure 2.

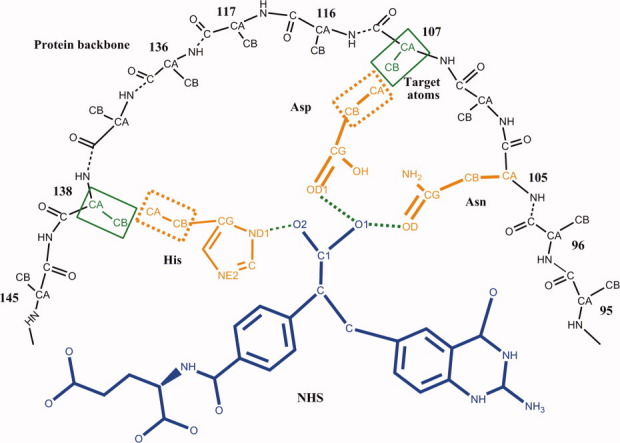
Schematic representation of the matching process in PRODA_MATCH, for example, 1c2t. The moving atoms of the loop are shown in a rectangle with dotted lines, and the target atoms on the backbone are shown in a rectangle with solid lines. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Recapitulation of native sites

The effectiveness and efficiency of the catalytic residue site selection algorithm can be validated by the recapitulation of native active sites, and the benchmark test set compiled by Zanghellini et al.¹⁶ was used to test the ability of the matching algorithm developed in this article. This test set includes 10 reactions that are catalyzed by all enzyme families except the oxidoreductases. The native catalytic site description for each corresponding reaction is taken directly from the crystal structure of the enzyme–TS analog complex or from the enzyme–inhibitor complex. The PDB codes for the 10 crystal structures in the test set are shown in Table II. The catalytic geometrical parameters relating the TS analog and the functional atoms of the catalytic residues are set to standard values based on the chemical rules described by Zanghellini et al.¹⁶ All the catalytic geometrical parameters are free to adopt a range of values, where the upper and lower bounds of the range for each parameter are determined by its degree of freedom and standard deviations. It should be noted that the parameters for the side-chain conformations,²⁵ X₁, X₂, X₃, and X₄, are simultaneously optimized in a CCD step. These parameters are always free, and inappropriate values can be discarded earlier if the intrinsic energy of the side-chain conformation is higher than the predefined tolerance.

Table II.

Recapitulation of Native Matches by PRODA_MATCH

		N = 100; R = 2.5; D = 2.5a
PDB code	Catalytic residues	Number of matches	Rankb	RMSD (Å)c
1c2t	Asn, His, Asp	41	1	0.7
1dqx	Lys, Asp, Lys, Asp	2583	31	1.8
1h2j	Glu, Glu	150	14	3.6
1jcl	Lys, Asp, Lys	62	9	1.8
1ney	Lys, His, Glu	420	2	1.4
1oex	Asp, Asp	65	8	1.1
1p6o	His, Cys, Cys, Glu	12	1	1.7
3vgc	Ser, His, Asp	88	1	1.3
4fua	His, His, His	176	1	1.1
6cpa	His, Glu, His, Glu	685	66	1.2

The catalytic geometry parameters are obtained from Ref.16.

^aAll parameters are set to the optimal values.

^bRank of native match.

^cRMSD of the TS and the catalytic residues.

The calculation results for 10 test examples in the benchmark set are summarized in Table II and were obtained by running the matching PRODA_MATCH algorithm on a single processor with a central processing unit (CPU) of 2.0 GHz and random-access memory of 8 GB on a computer cluster with 80 cores. All 10 native matches, where native match indicates a match with native catalytic residues at native sequence positions, were identified by PRODA_MATCH by virtue of the optimal algorithmic parameters. It should be noted that the novel matching algorithm succeeded in seven cases to rank the native match in the top 10 of all identified matches, including the first four. For seven cases in the top 10, PRODA_MATCH not only recapitulated the native matches but also recreated the TS model position and the side-chain conformations very well, which were confirmed by the good RMSD values shown in Table II. Two examples for enzyme active-site recapitulation are shown in Figure 3, for glycinamide ribonucleotide transformylase (1c2t) and 1-fuculose 1-phosphate aldolase (4fua), which both ranked in the top 10 of all identified matches. For the test case with PDB code, 1h2j, the RMSD is relatively high compared with those from other cases. A possible reason for this is that there are only two catalytic residues to form one loop with the TS, which cannot determine the position of the TS completely as the two catalytic side chains, Glu and Glu, are relatively small and they cannot tightly restrict the displacement of the TS. If we narrow the range of the catalytic geometrical parameters for this example, the native match will rank in the top 10 with an RMSD below 2.0 Å. The ranks for two test cases with PDB codes, 1dqx and 6cpa, are not high. A plausible explanation for this is that these two test cases both have four catalytic residues, which lead to more combinations during the site enumeration process, and the catalytic residues always have more flexible conformations, which bring about difficulties for parameter optimization of the side-chain conformations. In summary, the results for the benchmark test examples show that PRODA_MATCH can successfully find the native matches during the matching process and can accurately discriminate native and non-native matches by the scoring function. For the time requirement, PRODA_MATCH can implement one matching process in 20–30 min for a case with two or three catalytic residues, whereas 1–2 h is required for a case with four catalytic residues. Thus, the matching algorithm may potentially be used for scaffold screening.

Figure 3.

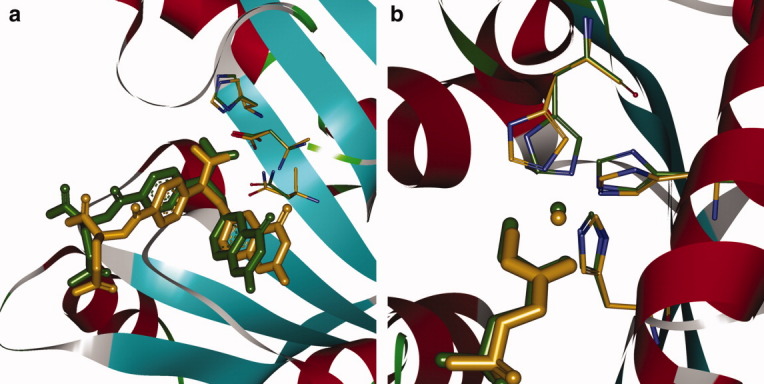
Superposition of native and predicted active sites. (a) The scaffold for the glycinamide ribonucleotide transformylase (1c2t) and (b) the scaffold for the 1-fuculose 1-phosphate aldolase (4fua). The transition state (TS) and the catalytic residues in the crystal structures are colored in orange. The predicted TS model and the catalytic residues are colored in green. The TS model is represented by thick sticks and the catalytic residues by thin sticks. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Sensitivity to parameter variation

The efficiency and effectiveness of the matching algorithm depends on the settings of the algorithmic parameters, especially the maximal iteration number of the CCD steps and the size and location of the pseudo-spheres for the binding sites. First, the influence of the settings for the maximal iteration number of CCD steps is described. As the side-chain conformation and the catalytic geometrical parameters are free to adopt a range of values, the position of the TS and the side-chain conformation of the catalytic residues are directly affected by the convergence of the CCD steps once the particular combination of the catalytic residues is determined. The matching results corresponding to the change of the maximal iteration number of the CCD steps are summarized in Table III. It is explicitly stated that the matching results approach stability when the maximal iteration number is greater than 100. Below this number, the optimization convergence is not complete. When it is set to a larger number, running times become too long and no improvement will be gained. Therefore, we set the optimal value for this parameter to 100.

Table III.

The Matching Results by Changing the Maximal Iteration Number of CCD Steps (D = 2.5, R = 2.5)

		Na = 50		N = 100		N = 200
PDB code	Catalytic residues	Number of matches	Rankb	Number of matches	Rank	Number of matches	Rank
1c2t	Asn, His, Asp	34	9	41	1	48	1
1dqx	Lys, Asp, Lys, Asp	2270	33	2583	31	3304	49
1h2j	Glu, Glu	148	13	150	14	157	13
1jcl	Lys, Asp, Lys	55	7	62	9	95	18
1ney	Lys, His, Glu	270	6	420	2	479	5
1oex	Asp, Asp	58	8	65	8	60	10
1p6o	His, Cys, Cys, Glu	11	—c	12	1	14	3
3vgc	Ser, His, Asp	73	2	88	1	95	3
4fua	His, His, His	119	1	176	1	186	2
6cpa	His, Glu, His, Glu	492	—	685	66	928	68

^aThe maximal iteration number of CCD steps.

^bRank of native match.

^cNo native match found.

The purpose of introducing the pseudo-spheres during the matching process is to simulate the true spatial environment of the active site even though the surrounding sites are truncated. If the active site of an enzyme is spacious, a larger pseudo-sphere radius is beneficial for the energy score to single out the native match from non-native ones. This is the case for 1c2t, as shown in Supporting Information Table SI and Figure 4(a). If the active site is crowded, the interactions between the pseudo-spheres and between the pseudo-spheres and the catalytic residues are pronounced. It is then advantageous to set the pseudo-sphere radius smaller; this is the case for 1dqx, 1ney, and 1p60, shown in Supporting Information Table SI and Figure 4(b–d). Here, there is an optimal value for the radius of the pseudo-sphere, and it is set to 2.5 Å according to the computing results shown in Supporting Information Table SI. As to the change of distance between the pseudo-sphere and Ca on the backbone, the matching results are presented in Supporting Information Table SII, and the same analysis as that for the pseudo-sphere radius change is true for the distance change. It should be noted that the matching algorithm failed to find the native match for the 1jcl, 4fua, and 6cpa cases shown in Supporting Information Table SII when the distance between the pseudo-sphere and Ca is set to 3.0 and 3.5 Å. This is because the large pseudo-spheres impose too many steric clashes in the active pockets. The optimal value for the distance between the pseudo-sphere and Ca is set to 2.5 Å according to the computing results shown in Supporting Information Table SII.

Figure 4.

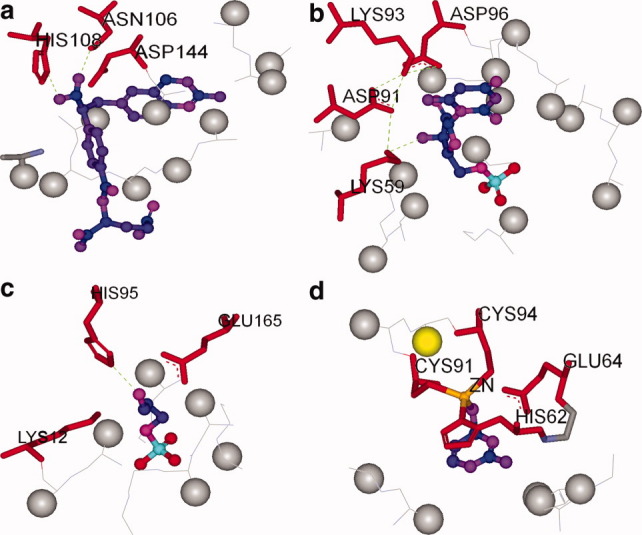
Influence of pseudo-spheres on matching results. The backbone is shown in thin line, and the pseudo-spheres representing the side chains of the binding residues are shown in gray balls. The catalytic residues are shown in red and stick mode. The TS model is shown in ball-and-stick mode. (a) The scaffold for the glycinamide ribonucleotide transformylase (1c2t), (b) the scaffold for the orotidine 5′-phosphate decarboxylase (1dqx), (c) the scaffold for the triosephosphate isomerase (1ney), and (d) the scaffold for the cytosine deaminase (1p6o). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Discussion

The existing catalytic residue site selection approaches, such as the site-search module in DEZYMER,¹⁵ the inverse-rotamer tree approach, and the Rosetta_Match approach in Rosetta_Design,¹⁶ have been used to design either metalloenzymes⁹ or artificial enzymes for organic reactions.^12–14 These de novo designs have achieved great successes based on experimental characterization, but the activities of the designed enzymes are not high enough for industrial application. Although the accurate placement of the catalytic residues cannot guarantee high activities of the designed enzymes, enzyme catalysis is commonly thought of as requiring precise structural coordination of the catalytic residues and the TS. However, there are two limitations in the existing approaches that have prevented them from positioning the catalytic residues and the TS more accurately. First, the use of a rotamer library limits the side chain to take the required conformation during the reaction coordinate. The rotamers in the library are always low-energy conformations of the corresponding amino acids statistically collected from the PDB, but the catalytic residues may take high-energy conformations during the reaction to satisfy the catalytic constraints with the TS. For example, Bolon and Mayo¹¹ designed a histidine-bearing catalyst for the hydrolysis of p-nitrophenyl acetate into p-nitrophenol by using a set of high energy state extended rotamers. Second, the discrete diversification method for the catalytic geometrical parameters restricts the searching for accurate TS positions because too fine sampling of the catalytic geometrical parameters will cause combinatorial explosion for the existing search approaches. However, sampling that is too rough will miss the accurate position of the TS during searching. The novel matching algorithm developed in this article, which is rotamer library independent, has effectively overcome these two limitations, and the side-chain conformations of the catalytic residues and the position of the TS are determined using a continuous optimization-based loop closure approach. The introduction of the pseudo-spheres for the surrounding sites has helped the algorithm to take the binding into account as early as during the matching process, and the simple energy score developed based on this can discriminate the native and non-native matches effectively. The matching algorithm is basically sequential, and its computational complexity is polynomial with respect to the number of active sites, the number of catalytic residues, and the maximal iteration number of CCD steps. The CPU time spent on the test examples with up to four catalytic residues indicates that this algorithm can potentially be used for matching problems with more catalytic sites.

We have compared the matching results obtained by PRODA_MATCH with those obtained by RosettaMatch¹⁶ for 10 benchmark test examples based on the catalytic geometrical parameters derived from chemical rules. As stated in Table IV, the matching results using PRODA_MATCH are comparable with those of RosettaMatch and are even moderately better because PRODA_MATCH ranks 7 native matches in the top 10, whereas RosettaMatch matches only 5. It should be noted that no matching results were obtained for 1dqx using RosettaMatch as an explosion of the number of files for this test case was encountered. The improved results by PRODA_MATCH come from its novelty in handling the side-chain conformation and the TS positioning by using a continuous optimization-based loop closure approach, whereas in RosettaMatch a combinatorial enumeration search based on the hash technique is used. When there are more catalytic residues concerned and, therefore, more catalytic geometrical parameters need to be diversified, the latter approach is prone to cause combinatorial explosion. In RosettaMatch, the continuous conformation optimization and full sequence design with the help of an accurate energy function are used after the matching results are obtained to make up for the drawbacks of the use of the discrete rotamer library and for the absence of the binding side chains during the matching process, but this is time consuming, although the final results are more reliable. In PRODA_MATCH, these two disadvantages are overcome by using a novel loop closure method and the introduction of the pseudo-spheres during the matching process. Moreover, the simple energy score of PRODA_MATCH for ranking design results partially represents the binding energy even without full sequence design for the surrounding sites as the introduction of the pseudo-spheres has simulated, to some extent, the true environment of the active pocket.

Table IV.

Comparison to RosettaMatch by Zanghellini et al.¹⁶

		PRODA_MATCHa		RosettaMatch by Zanghellini et al.b
PDB code	Catalytic residues	Number of matches	Rank	Number of matches	Rank after design
1c2t	Asn, His, Asp	41	1	108	1
1dqx	Lys, Asp, Lys, Asp	2583	31	—c	—c
1h2j	Glu, Glu	150	14	20,390	306
1jcl	Lys, Asp, Lys	62	9	111	8
1ney	Lys, His, Glu	420	2	36,367	79
1oex	Asp, Asp	65	8	12,808	4149
1p6o	His, Cys, Cys, Glu	12	1	72,600	1
3vgc	Ser, His, Asp	88	1	11,346	1
4fua	His, His, His	176	1	20,730	1
6cpa	His, Glu, His, Glu	685	66	21,77	17

^aThe results are identical with those shown in Table II.

^bBenchmark II results using RosettaMatch.

^cResults for 1dqx are not reported because the matching for that scaffold led to an explosion of the number of files.

Materials and Methods

Development of the matching algorithm

The atomic coordinates of the scaffolds for 10 test examples in the benchmark set are taken directly from their crystal structures, and the missed hydrogen atoms are added by virtue of the standard parameters from the CHARMM force field,²⁶ which is automatically implemented by PRODA. The sites to be selected for matching the catalytic residues in the active pocket are identified as the residues that have at least one atom within 5 Å from the TS analog or the inhibitor in the crystal structure. All the selected sites are truncated to keep only Ca and Cb atoms during the matching process, and the catalytic residues will grow from the left Ca and Cb atoms on the chosen sites. The side chains on the sites not for catalytic residue anchoring are replaced by pseudo-spheres,^27,28 the direction from Ca to the pseudo-sphere centroid is along the vector defined by Ca–Cb. The distance from Ca to the pseudo-sphere centroid and the radius of the pseudo-sphere are two adjustable parameters to simulate the true spatial environment inside the active pocket.

As to the univariate optimization in a CCD step, the torsion angles for catalytic geometrical parameters and side-chain conformation parameters are adjusted based on the method described by Canutescu and Dunbrack²⁴ for protein loop closure. Similar methods to optimize the bond angles and bond lengths for catalytic geometrical parameters are developed in this work. In Figure 5, four atoms are represented by A, B, C, and D. The bond angle θ determined by vector BC and CD is optimized to move the atom M1 as closely as possible to F1. Different from the torsion angle, the rotation axis for bond angle optimization is the vector that is perpendicular to the plane formed by atoms B, C, and D and passes atom C. The unit rotation vector is defined as 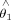, which can be obtained by the following equation,

Figure 5.

Univariate optimization of bond angle. M_o1 is the initial position of one moving atom of the loop. M₁ is the position of the moving atom after some rotation of angle θ. F₁ refers to the target atom on the backbone. O₁ is the rotating center of M₁ along the cross vector of vectors CB and CD.

(1)

The left procedures for bond angle adjustment are the same as those for torsion angle optimization.²⁴

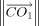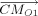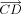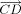As to the bond length optimization for loop closure, assume that the bond length between atoms C and D, which is shown in Figure 6, is optimized to move the atom M1 as closely as possible to F1. Note, is the projected length of the vector on the vector . Let be the unit vector of . We define d as the variation of bond length between atoms C and D. The vector 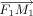is obtained by:

Figure 6.

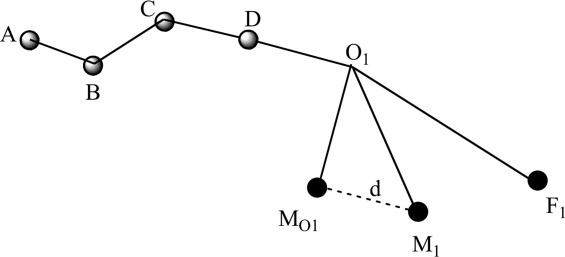
Univariate optimization of bond length. M_o1 is the initial position of one moving atom of the loop. M₁ is the position of the moving atom after some change of bond distance d. F₁ refers to the target atom of the loop. d is the bond length between atoms C and D, and Δd is its variation.

(2)

Note, 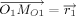, , 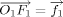and 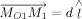. The sum of the squared distances, S, for moving atoms can be obtained by the following equation:

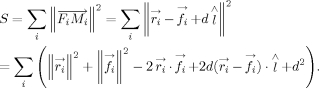(3)

The first-order derivative of S is given by

(4)

When S reaches its minimum, its first-order derivative should disappear. Therefore, we have

(5)

When the optimal value does not lie inside the range, it is identified as either the upper or lower limit of the range. The same treatment is applied to the optimization of the torsion angle and bond angle.

Description of the matching algorithm

Assume that there are m catalytic residues to match onto n sites in the active pocket, in total there are n × (n − 1) ×…×(n − m + 1) combinations and the matching algorithm enumerates all those combinations sequentially. The sequential matching algorithm starts by selecting any catalytic residue to anchor at one of the n sites and then checks if another catalytic residue can be anchored at one of the left n − 1 sites. The particular combination for these two catalytic residues will be checked by the CCD-based loop closure procedures. The loop here refers to the atom chain starting from the Ca atom of the first catalytic residue to the Ca atom of the second catalytic residue, and the loop closure means that the two Ca atoms of the chain can be overlapped with the backbone Ca atoms at the two selected sites with appropriate side-chain conformation parameters and catalytic geometrical parameters. The initial values of the loop parameters are set to the median values of their ranges. If the loop can be closed within the maximal iteration number of CCD steps, it implies that the particular combination for these two catalytic residues is suitable and this combination is recorded. Otherwise, it states that the site for the second catalytic residue is not held, and another site from the left n − 2 ones will be tried. To enhance searching efficiency, another stopping criterion for loop closure is also used to reduce the CCD iterations, that is, if the difference between the RMSD of the current CCD step with that of the preceding step is less than the predefined tolerance, the iteration will terminate. If all n − 1 sites cannot match with the second catalytic residue, the site for the first catalytic residue will be changed to a new one until all n sites are tried. If two sites are found to match with the first two catalytic residues and there are still catalytic residues left for matching, the matching process will continue. As the loop for the first two catalytic residues is recorded during the earlier matching process, the location of the TS is known. Any site from the left n − 2 sites can be selected to anchor the third catalytic residue by running the loop closure process, but the loop here starts from the functional atoms of the TS, which has a catalytic geometrical relationship with the third catalytic residue, and ends with the Ca atom of the third catalytic residue. All the left catalytic residues will be anchored in the same way as for the third catalytic residue. If all catalytic residues can be matched onto the sites in the active pocket, the particular combination constituted by these sites will be recorded as a design. The total combinatorial number for the whole matching process is n × (n − 1) × … × (n − m + 1), and in the worst case the total number of CCD steps needed for a matching problem is n × (n − 1) × … × (n − m + 1) × N_CCD. As m is usually small, up to 4 in this article, this expression can be thought of as being polynomial.

Ranking of design based on energy score

After the sequential matching process is finished, all recorded designs will be ranked by a scoring function, where only simplified van der waals interaction between atoms is considered.²² The scoring function is given by the following equation:

(6)

where r_i and r_j are van der waals radii for atoms i and j, and d_ij is the distance between these two atoms. For the sum, four energy terms are considered in this simple scoring function, as (i) the intrinsic energy of each catalytic residue; (ii) the interaction energy between any two catalytic residues; (iii) the interaction energy between each catalytic residue and the TS; and (iv) the interaction energy between each catalytic residue and the truncated backbone including the pseudo-spheres.

Glossary

Abbreviations:

CCD

cyclic coordinate descent

PDB

protein data bank

PRODA

PROtein Design Algorithmic package

RMSD

root-mean-standard deviation

TS

transition state