Causal Models for Investigating Complex Genetic Disease: II. What Causal Models Can Tell Us about Penetrance for Additive, Heterogeneity, and Multiplicative Two-Locus Models

Abstract

Background/Aims

Statistical geneticists commonly use certain two-locus penetrance models because these models are familiar and mathematically tractable. We investigate whether and under what circumstances these two-locus penetrance models correspond to models of causation.

Methods

We describe a sufficient component cause model for a hypothetical disease with two genetic causes. We then use the potential outcomes framework to determine the expected two-locus penetrances from this causal model and contrast them with commonly used two-locus penetrance models (additive, heterogeneity, and multiplicative penetrance models, as formulated by Risch [Am J Hum Genet 1990;46:222–228]).

Results

Conventional additive and multiplicative models can correspond to any two-locus causal model only when certain very specific algebraic relationships hold. The heterogeneity model corresponds to a two-locus causal model only if the model stipulates that no disease cases are caused by the combined presence of the causal genotypes at both loci (i.e. only when there is no causal gene-gene interaction). Hence the heterogeneity model provides a valid test of the null hypothesis of no gene-gene interaction, whereas the additive and multiplicative models do not.

Conclusion

We suggest that causal principles should provide the basis for statistical modeling in genetics.

‘I see no greater impediment to scientific progress than the prevailing practice of focusing all of our mathematical resources on probabilistic and statistical inferences while leaving causal considerations to the mercy of intuition and good judgment.’

Judea Pearl, Causality, p. xiv [1].

Introduction

Statistical geneticists commonly use certain two-locus penetrance models when investigating the genetic causes of disease because these models are familiar and mathematically tractable. Previous research has investigated the properties [2], uses [3], and interpretation [4,5,6,7,8] of some of these models; however, no previous study has determined whether and under what circumstances they correspond to causal models. We investigate this correspondence in this paper. As described in the first paper of this two-part series [9], the use of causal models promises new insights for applied, theoretical, or methodological statistical genetics research, as it has for other quantitative fields such as economics, social sciences, and epidemiology. Causal models can be used to determine the patterns of disease risk expected from the number and frequency of disease-causing genes, the number and frequency of non-genetic causes, and their causal interactions.

As a motivating example, consider the assumption of a multiplicative penetrance model (described in detail below) to describe the expected two-locus penetrance matrix for a disease when gene-gene interaction underlies the genetic architecture. This model is summarized by Risch [10] and is regularly applied to investigate hypotheses of gene-gene interactions (see e.g. [11,12,13,14]). However, the pattern of disease that would, in fact, result from two genes acting in concert to cause disease has not been established [5,6,7,8]. In analyses using causal models, epidemiologists have found that when two risk factors are parts of the same causal mechanism (i.e. they ‘interact’ in a causal sense), risks in individuals with both factors are predicted to be greater than those predicted by an additive model, but not necessarily consistent with those predicted by a multiplicative model [15,16]. Thus, multiplicative penetrance models might not be consistent with models of causal gene-gene interaction.

Determining the two-locus penetrances resulting from causal models of disease-causing mechanisms such as genetic heterogeneity and gene-gene interaction will inform two important applications of penetrance models: (1) the validity of different penetrance-based models (e.g. multiplicative two-locus penetrance) for inferring the biological mechanisms that lead to disease (e.g. gene-gene interaction), and (2) approaches for simulating the expected joint distribution of genes and disease under an assumed biological mechanism.

In this paper we use Rothman's sufficient component cause (SCC) model [16,17] to describe the causes of a complex genetic disease. Rothman defines a sufficient cause as a set of minimal conditions and events that inevitably produces an outcome. The SCC framework recognizes that any given cause of a disease may be, indeed usually is, neither necessary nor sufficient. If an outcome has more than one sufficient cause, then no single sufficient cause is necessary for the outcome. We postulate a SCC model that includes the causal effects of genotypes at two unlinked loci, and incorporates reduced penetrance, phenocopies, genetic heterogeneity, and gene-gene interaction, as described in our accompanying paper [9]. We then use the potential outcomes (PO) framework [18] to determine the expected two-locus penetrances from this causal model and contrast them with 3 commonly used two-locus penetrance models (additive, heterogeneity, and multiplicative penetrance models described by Risch [10]). Finally, we discuss the results and implications of this comparison.

Definitions and Assumptions

Defining the Causal (SCC) Model

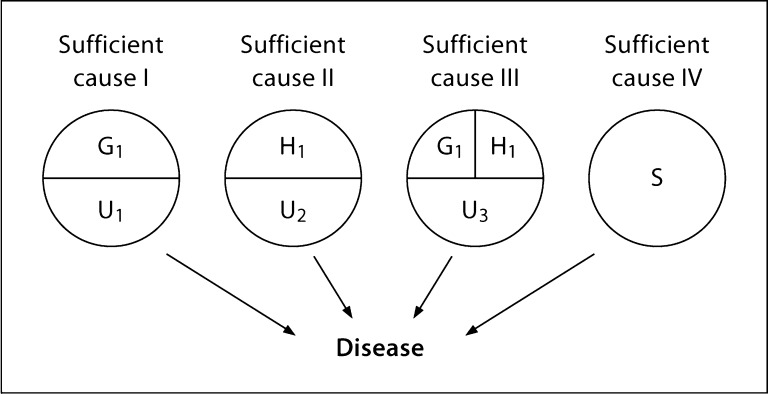
Our assumed SCC model includes two loci, G and H, where G_i and H_j denote the possible genotypes at these loci (fig. 1). We indicate the combinations of causal (a.k.a. susceptibility, predisposing, at-risk) genotypes at the respective loci with i = j = 1 and the combination of non-causal genotypes with i = j = 0. (Because this paper has considerably more mathematical development than [9], we have opted for this notation over the use of G– and H– for indicating i = j = 0 as in the first paper of this series.) Genetic heterogeneity is modeled by assuming that G₁ and H₁ participate in distinct sufficient causes (sufficient causes I and II in fig. 1), and gene-gene interaction by assuming they both participate in the same sufficient cause (sufficient cause III). As is generally assumed for complex diseases, neither locus alone or in combination is sufficient for disease, i.e. both the single- and two-locus genotypes demonstrate reduced penetrance, because each predisposing single- or two-locus genotype requires a causal partner (U₁, U₂, or U₃) for disease to occur among the causal genotype carriers. We depict another characteristic of complex diseases, ‘phenocopies,’ by specifying sufficient cause IV, consisting of the single component cause S as a cause of disease that does not include genotypes G₁ or H₁ as component causes. (We have used S to denote this component cause, rather than X which was used in our companion paper [9], to avoid confusion with the notation used later in this paper.) Note that whether or not an individual is a phenocopy depends on the genotype of interest. For example, an individual who develops disease through sufficient cause II would be considered a phenocopy with respect to G₁, whereas an individual who develops disease through sufficient cause IV would be considered a phenocopy with respect to both G₁ and H₁. U₁, U₂, U₃ and S need not be specific entities or factors, but can represent sets of random or deterministic elements. Notably, the SCC model depicted in figure 1 assumes that neither G₁ nor H₁ has preventive effects on disease (i.e. assumes monotonicity).

Fig. 1.

A SCC model depicting a disease caused by genotypes at two loci, G and H, acting independently (sufficient causes I and II) and together (sufficient cause III). Sufficient cause IV represents the causes of disease that do not involve genotypes at the G, and H loci. G₁ denotes the causal (i.e. predisposing) genotype at locus G, and H₁ denotes the causal genotype at locus H. U₁, U₂, and U₃ are the ‘causal partners’ required for the respective predisposing genotypes to cause disease (i.e. determinants of penetrance of G₁ and H₁).

Assumptions

First, we assume that the SCC model accurately describes a disease and its mechanism of causation. This assumption is required in order to use causal models as the basis for determining the expected joint distribution of genotype and disease. Second, we assume that the depictions of genetic heterogeneity and gene-gene interaction in the SCC model in figure 1 correspond to biological reality. This assumption is required to infer that comparison of predictions based on the SCC model depicted in figure 1 with those based on conventional statistical models provide valid information about measurement of underlying biological processes. To address our specific question about the expected two-locus penetrances for a disease caused by two genotypes (that may act together or separately to cause disease) and other genetic or non-genetic causes, we also assume that, taken together, these 4 sufficient causes explain the totality of disease in the population. That is, S represents the totality of sufficient causes of disease that do not include G or H as component causes. The only ways that G and H cause disease are in connection with sufficient causes I, II, and III.

We make additional assumptions that are not required to use SCC models but are often made in statistical genetics: linkage equilibrium between the two causal loci; independent distribution in the population of the component causes in the SCC model (G₁, H_1, U₁, U₂, U₃, and S); dichotomous genotypes at the susceptibility loci; dichotomous outcomes; and that the component causes depicted in figure 1 only cause disease, i.e. do not prevent disease. We will address violations of the assumptions and extensions of the model in ‘Discussion’.

Penetrances according to the SCC Model

Having posited the SCC model depicted in figure 1, we determine the corresponding probability of disease conditioned on all possible one- or two-locus genotypes specified in the causal model, i.e. the penetrance matrix. Note that although we use a SCC model, we are estimating ‘statistical penetrance’ as defined in the first paper of this series [9] – i.e. the ‘proportion of individuals with disease among those who carry a specific genotype within a defined population.’ Given the SCC model in figure 1, the disease status of a person inheriting a particular genotype (e.g. G₁) depends on two things: (1) whether the genotype completes a sufficient cause (e.g. whether U₁ is present), and (2) whether any sufficient causes not including the genotype as a component cause have been completed (e.g. whether S is present). According to an SCC model, the probability of disease conditioned on a given genotype depends on the frequency of component causes other than that genotype. We refer to the component causes other than the genotype as ‘other causes.’ The combination of other causes to which an individual is exposed determines his/her disease status given each genotype combination [19].

Using the terminology of Robins and Greenland [18] and the PO framework, we define an individual's ‘response type’ as his/her pattern of disease outcomes, given each possible genotype combination. This illustrates a unique feature of causal models, in that the model is explicitly elaborated in terms of individual disease response rather than in terms of average risk across a population.

With respect to the two-locus penetrance matrix for genotypes at loci G and H, the genotypes of interest are the 4 mutually exclusive and exhaustive combinations of the binary genotypes: G₀H₀, G₁H₀, G₀H₁, and G₁H₁. In table 1, the Response type column provides a label for each pattern of disease across these 4 possible genotype combinations [18]. The Determinants of response type columnenumerates the possible combinations of ‘other causes’ (from fig. 1) that underlie an individual's response type, and the Probability of response type column gives the probability of each combination (i.e. each response type). The P[disease ∣ response type t, G_iH_j] column describes the disease outcome for each response type given each two-locus genotype. Note that the probability of disease for any individual conditioned on his/her observed genotype and ‘other causes’ is either 1 or 0.

Table 1.

The t response types, their determinants, P[response type: t], and P[disease | response type t, G;Hj]

Response type (t)	Determinants of response type				Probability of response type: rt=V [response type t]	P[disease|response type t, GiHj]
	U1	U2	U3	S		G1H1	G0H1	G1H0	G0H0
Immune (1)	absent	absent	absent	absent	r1 = (1 – u1)(1 – u2)(1 – u3)(1 – s)	0	0	0	0
G-causal (2)	present	absent	present or absent	absent	r2 = (u1)(1 – u2)(1 – s)	1	0	1	0
H-causal (3)	absent	present	present or absent	absent	r3 = (1 – u1)(u2)(1 – s)	1	1	0	0
GH-causal (4)	absent	absent	present	absent	r4 = (1 – u1)(1 – u2)(u3)(1 – s)	1	0	0	0
Parallel (5)	present	present	present or absent	absent	r5 = (u1)(u2)(1 – s)	1	1	1	0
Inevitable (6)	present or absent	present or absent	present or absent	present	r6 = s	1	1	1	1
					Σ = 1	1	1	1	1

The ‘Immune’ row consists of individuals who do not have ‘other causes’ U₁, U₂, U₃, or S. Given the SCC model in figure 1, these individuals will not be diseased, regardless of their genotypes at loci G and H. The ‘G-causal’ row consists of individuals who have U₁ but not U₂ or S. These individuals will have disease when G₁ is present and will not have disease when G₁ is absent, regardless of their genotype at locus H, and independently of whether they have U₃ or not. The ‘H-causal’ types are defined similarly. ‘GH-causal’ types have U₃ but not U₁, U₂, or S and will have disease only when both G₁ and H₁ are present, but not when either or both are absent. ‘Parallel’ types have U₁ and U₂ (U₃ may be present or absent) but not S and will have disease when G₁ or H₁ is present, but will not have disease when both are absent. Finally, ‘Inevitable’ individuals have S, and whether or not S occurs in conjunction with U₁, U₂, or U₃, these individuals will have disease for all 4 possible combinations of genotypes at loci G and H. (The type we call ‘Inevitable’ is often called ‘Doomed’ [20]; we have replaced this term to avoid any negative connotation.)

Given our assumption that the component causes, including genotypes, are independently distributed in the population, these 6 response types will be distributed randomly among the different genotypes and vice versa. The probability of disease among individuals conditioned on their two-locus genotype is described by:

$$\text{P}\left[\hspace{0.17em}disease|G_i{H}_j\right]\hspace{0.17em}=\hspace{0.17em}\sum _{t}P\left[\hspace{0.17em}disease|response\hspace{0.17em}type\hspace{0.17em}t,\hspace{0.17em}{G}_i{H}_j\right]\hspace{0.17em}\cdot \hspace{0.17em}P\left[\hspace{0.17em}response\hspace{0.17em}type\hspace{0.17em}t\right]$$ (1)

From equation 1 and table 1, we derive the probability of disease conditioned on each two-locus genotype. These equations make up the causal model-based two-locus penetrance matrix, where the lower-case u₁, u₂, u₃, and s equal the probability that an individual has component causes U₁, U₂, U₃, and S, respectively:

$$\begin{array}{l}\text{A}\hspace{0.17em}=\hspace{0.17em}P\left[\hspace{0.17em}disease\hspace{0.17em}|\hspace{0.17em}{G}_1{H}_1\right]\hspace{0.17em}=\hspace{0.17em}{r}_2\hspace{0.17em}+\hspace{0.17em}{r}_3\hspace{0.17em}+\hspace{0.17em}{r}_4\hspace{0.17em}+\hspace{0.17em}{r}_5\hspace{0.17em}+\hspace{0.17em}{r}_6\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}-\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_3\right)\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\hfill \\ \text{B}\hspace{0.17em}=\hspace{0.17em}P\left[disease\hspace{0.17em}|\hspace{0.17em}{G}_0{H}_1\right]\hspace{0.17em}=\hspace{0.17em}{r}_3\hspace{0.17em}+\hspace{0.17em}{r}_5\hspace{0.17em}+\hspace{0.17em}{r}_6\hspace{0.17em}=\hspace{0.17em}{u}_2\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\hspace{0.17em}+\hspace{0.17em}s\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}-\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\hfill \\ \text{C}\hspace{0.17em}=\hspace{0.17em}P\left[disease\hspace{0.17em}|\hspace{0.17em}{G}_1{H}_0\right]\hspace{0.17em}=\hspace{0.17em}{r}_2\hspace{0.17em}+\hspace{0.17em}{r}_5\hspace{0.17em}+\hspace{0.17em}{r}_6\hspace{0.17em}=\hspace{0.17em}{u}_1\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\hspace{0.17em}+\hspace{0.17em}s\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}-\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\hfill \\ \text{D}\hspace{0.17em}=\hspace{0.17em}P\left[disease\hspace{0.17em}|\hspace{0.17em}{G}_0{H}_0\right]\hspace{0.17em}=\hspace{0.17em}{r}_6\hspace{0.17em}=\hspace{0.17em}s\hfill \end{array}$$ (2)

To illustrate the derivation of these probabilities, consider the quantity A. From table 1, P[disease ∣ response type t, G₁H₁] = 1 for G-causal, H-causal, GH-causal, Parallel, and Inevitable response types, which occur with probabilities r₂, r₃, r₄, r₅ and r₆, respectively, whereas P[disease ∣ response type t, G₁H₁] = 0 for the Immune response type, which occurs with probability r₁. That is, individuals with G₁ and H₁ will get disease if they represent any response type other than Immune. Thus

P[disease ∣ G₁H₁] = r₂ + r₃ + r₄ + r₅ + r₆.

But also

$$\sum _{i\hspace{0.17em}=\hspace{0.17em}1}^6{r}_i\hspace{0.17em}=\hspace{0.17em}1$$

so A = P[disease ∣ G₁H₁] = 1 – r₁ = 1 – (1 – u₁)(1 – u₂) (1 – u₃)(1 – s). Similar reasoning yields the other relationships in equation 2.

For each of the 4 probabilities in equation 2, the rightmost expression is in ‘one-minus’ form. This facilitates probabilistic interpretations in terms of the probability of not being affected. For example, B, the probability of being affected if an individual has genotype G₀H₁ can be expressed as one minus the probability of not being affected due to either U₂ or S. This deconstruction of two-locus penetrances into response-type probabilities illuminates the causal components of penetrance. As stated above, these equations satisfy the usual definition of penetrance, i.e. the probability of disease conditioned on a genotype.

Mathematical Comparisons with Commonly Used Penetrance Assumptions for Two-Locus Models

Using the causal model-based definitions of genetic heterogeneity, gene-gene interaction, proportion susceptible and phenocopy illustrated in figure 1 and explained in the first paper of this series [9], we have derived formulae that describe the relative contributions of these phenomena to two-locus penetrances. From the SCC model and equation 2, one can see that the two-locus penetrances observed in a population will vary depending on: the frequency of causes other than the 2 genotypes of interest (s); whether 2 genotypes demonstrate causal genetic heterogeneity (e.g. u₁ > 0, u₂ > 0, u₃ = 0 vs. u₁ > 0, u₂ = 0, u₃ = 0); whether 2 genetic causes demonstrate causal gene-gene interaction (u₃ > 0 vs. u₃ = 0); and whether 2 genetic causes demonstrate both causal genetic heterogeneity and causal gene-gene interaction (e.g. u₁ > 0, u₂ > 0, u₃ > 0 vs. u₁ > 0, u₂ = 0, u₃ = 0). We now compare this causal model-based penetrance matrix with the following more familiar (non-causal-based) two-locus penetrance models.

Risch presented several penetrance models for a disease given a two-locus genotype, denoted by ω_ij and defined as ω_ij = P[disease ∣ G_iH_j] [10]. He presented these models for situations in which 2 loci either act independently to cause disease (i.e. two-locus causal genetic heterogeneity) or act together to cause disease (i.e. two-locus causal gene-gene interaction).

He described the additive model for a disease with underlying two-locus causal heterogeneity. The additive model assumes that ‘penetrance factors’ or ‘summands’ x_i and y_j exist such that

$${\omega }_{ij}\hspace{0.17em}=\hspace{0.17em}{x}_i\hspace{0.17em}+\hspace{0.17em}{y}_j$$ (3)

As defined by Risch [10], the values x_i and y_j are not intended to represent single-locus or marginal penetrances. Rather, they are abstract, unobservable quantities – mathematical constructs – designed to characterize the relationships among the various penetrances. For example, the additive model necessarily implies ω₁₁ + ω₀₀ = ω₁₀ + ω₀₁, or, in our context, P[disease ∣ G₁H₁] + P[disease ∣ G₀H₀] = P[disease ∣ G₁H₀] + P[disease ∣ G₀H₁], as we will show below.

The genetic heterogeneity model is also intended to represent causal heterogeneity, and differs from the additive model by correcting for the fact that x_i + y_j can theoretically exceed 1, whereas the probability of disease given a two-locus genotype cannot. The heterogeneity formula specifies

$${\omega }_{ij}\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}-\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{x}_i\right)\left(1\hspace{0.17em}-\hspace{0.17em}{y}_j\right)\hspace{0.17em}=\hspace{0.17em}{x}_i\hspace{0.17em}+\hspace{0.17em}{y}_j\hspace{0.17em}-\hspace{0.17em}{x}_i{y}_j$$ (4)

.

The multiplicative model, described by Risch [10] for diseases with underlying two-locus causal gene-gene interaction or epistasis, specifies that ‘penetrance factors’ x_i and y_j can be defined such that

$${\omega }_{ij}\hspace{0.17em}=\hspace{0.17em}{x}_i{y}_j$$ (5)

Again, these penetrance factors are mathematical constructs.

Whether additive, heterogeneity, or multiplicative models accurately represent the patterns of disease risk that result from causal genetic heterogeneity or from causal gene-gene interaction has not been investigated before. In order to determine this, we now evaluate the correspondence between these models and the two-locus penetrances A–D when causal genetic heterogeneity (e.g. u₁ > 0, u₂ > 0) and causal gene-gene interaction (u₃ > 0) are features of the SCC model.

Additive Penetrance Models

Table 2a shows a penetrance matrix that connects the causal two-locus penetrances in equation 2 with Risch's penetrance factors in equation 3. For example, for the additive model to correctly describe the two-locus penetrances, A = ω₁₁ = x₁+ y₁, and similarly for B, C, and D. From table 2a, (A + D) and (B + C) must both equal x₁ + x₀ + y₁ + y₀. Thus, under this additive model, (A + D) must equal (B + C). In terms of component cause frequencies, this equality implies:

$$\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)u_3\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\hspace{0.17em}=\hspace{0.17em}{u}_1{u}_2\left(1\hspace{0.17em}-\hspace{0.17em}s\right)$$ (6)

Table 2.

Mathematical relationships among two-locus penetrances (A, B, C, D) and penetrance factors x_i and y_j in 3 common models

a	Additive model: ωij = yi (eq. 3)
	G1	G0
H1	x1 + y1 = A	x0 + y1 = B
H0	x1 + y0 = C	x0 + y0 = D
b	Heterogeneity model: ωij = 1 – (1 – xi)(1 – yj) (eq. 4)
	G1	G0
H1	1 – (1 – x1) × (1 – y1) = A	1 – (1 – x0) × (1 – y1) = B
H0	1 – (1 – x1) × (1 – y0) = C	1 – (1 – x0) × (1 – y0) = D
c	Multiplicative model: ωij = xiyj (eq. 5)
	G1	G0
H1	x1y1 = A	x0y1 = B
H0	x1y0 = C	x0y0 = D

Derived from the general two-locus SCC model depicted in figure 1.

The only non-trivial solution to this equation is

$$u_3\hspace{0.17em}=\hspace{0.17em}\frac{u_1{u}_2}{\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)},$$ (7)

where u₁ + u₂ ≤ 1. All other solutions would require setting both sides of equation 6 to zero, thus implying either s = 1 (i.e. everyone in the population is ‘Inevitable’ type and has the disease), and/or at least one of u₁ and u₂ equals zero, which would mean we no longer had a two-locus model. (Details are in ‘Appendix’.)

In Risch [10] and elsewhere, the additive penetrance model is used to describe the disease in the population when genetic heterogeneity is a feature of the genetic architecture, i.e. when a disease has 2 independently acting genetic causes. If sufficient causes I and II together reflect our biological concept of heterogeneity, and sufficient cause III reflects our biological concept0 of gene-gene interaction, then using the additive model to describe a disease with genetic heterogeneity requires the assumption that gene-gene interaction is also a feature of the genetic architecture.

Table 3 summarizes the sets of assumptions required to make the respective models consistent with each other. The table reveals that in order for causal heterogeneity (i.e. u₁ > 0 and u₂ > 0) to be described using an additive two-locus penetrance model, gene-gene interaction must also occur (i.e. u₃ > 0), unless all disease can be attributed either to: (1) a single-locus, meaning the disease would have happened in the absence of the causal genotype at the second locus because the entire population is susceptible to the causal genotype at the first locus (i.e. u₁ or u₂ = 1), or (2) a set of causes (other than the 2 genotypes of interest, i.e. sufficient cause IV) that produces disease in 100% of the population (i.e. s = 1). Thus, using the additive model to imply lack of interaction (or independence) in the causal sense of these words is misleading.

Table 3.

Sets of assumptions about the SCC model and the frequency of component causes Uj, U₂, U₃, and S in figure 1 that render the model consistent with additive, heterogeneity, and multiplicative two-locus penetrance models

Statistical two-locus penetrance model	Constraint on probability of component cause in population				Causal single locus	Causal genetic heterogeneity	Causal gene-gene interaction	Pheno-copies	Comments
	u1	u2	u3	s
Two-locus additive penetrance model xi + yj = ωij	-	-	-	1	allowed	allowed*	allowed*	required	entire population diseased due to S
	1	0	-	<1	required	not allowed	allowed*	allowed	fully penetrant single-locus model with or without phenocopies
	0	1	-	<1
	0	-	0	<1	allowed	not allowed	not allowed	allowed	single-locus model with or without phenocopies
	-	0	0	<1
	0 < u1 + u2 < 1		$$\frac{u_1{u}_2}{\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)}$$	<1	not allowed	required	required	allowed	causal genetic heterogeneity; requires causal gene-gene interaction with or without phenocopies; u values constrained
Two-locus heterogeneity penetrance model xi + yj – xiyj = ωij	-	-	-	1	allowed*	allowed*	allowed*	required	entire population diseased due to S
	–	1	–	<1	allowed	allowed*	allowed*	allowed	fully penetrant single-locus model with or without phenocopies (no genetic heterogeneity or gene-gene interaction)
	1	–	–	<1
	–	–	0	<1	allowed	allowed	not allowed	allowed	causal genetic heterogeneity; requires absence of causal gene-gene interaction with or without phenocopies
Two-locus multiplicative penetrance model xiyj =ωij	–	–	–	1	allowed*	allowed*	allowed*	required	entire population diseased due to S
	0	–	0	<1	allowed	not allowed	not allowed	allowed	single-locus model with or without phenocopies
	–	0	0	<1
	0	–	–	0	allowed	not allowed	allowed	not allowed	causal gene-gene interaction; requires absence of both causal heterogeneity and phenocopies
	–	0	–	0
	0 < u1 + u2 < 1		$$u_{3}s\hspace{0.17em}=\hspace{0.17em}\frac{u_1{u}_2}{\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)}$$		not allowed	required	required	required	causal gene-gene interaction; requires causal genetic heterogeneity with gene-gene interaction; u and s constrained

^*Although allowed, the mechanism does not have a ‘causal effect’, i.e. average causal effect = 0 as defined in [9]; – indicates unconstrained.

In summary, under our assumptions, the only way this additive (non-causally based) two-locus model can correspond to a causal two-locus model (aside from degenerate cases, such as when everyone in the population is affected, or when the genotype at one locus is fully penetrant) is when the proportion susceptible to the G₁H₁ genotype, u₃, has a specific algebraic relationship to the proportions susceptible to the G₁H₀ and G₀H₁ genotypes, u₁ and u₂ as defined by equation 7.

Heterogeneity Penetrance Models

Table 2b shows a penetrance matrix that connects the causal two-locus penetrances in equation 2 with Risch's penetrance factors in equation 4. From table 2b we can see that Risch's penetrance factors must satisfy a certain algebraic relationship in order to fit equations 2. The table shows that (1 – A) × (1 – D) and (1 – B) × (1 – C) must both equal (1 – x₁)(1 – y₁)(1 – x₀)(1 – y₀) and therefore must equal each other. In terms of component cause frequencies, this implies:

$$\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_3\right){\left(1\hspace{0.17em}-\hspace{0.17em}s\right)}^2\hspace{0.17em}=\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\left(1\hspace{0.17em}-\hspace{0.17em}s\right)$$ (8)

(details in ‘Appendix’).

As with the additive model, there is only one non-trivial solution – in this case, where u₃ = 0. That is, the heterogeneity model in equation 4 implies that no cases of this disease are due to causal gene-gene interaction (ruling out the trivial cases where at least one genotype is 100% penetrant or where everyone in the population is affected due to causes other than the 2 genotypes of interest). When u₃ = 0, the probabilities u₁, u₂, and s are unconstrained between 0 and 1; hence the heterogeneity model holds for any combination of values of u₁, u₂, and s. If, together, sufficient causes I and II reflect our biological concept of genetic heterogeneity and sufficient cause III reflects our biological concept of gene-gene interaction, then assuming the two-locus heterogeneity model to describe a disease with biological genetic heterogeneity with or without phenocopies also assumes that gene-gene interaction is not part of the causal model.

In summary, the only way this heterogeneity penetrance model can correspond to a causal two-locus model (aside from degenerate cases such as everyone being affected, or one fully-penetrant genotype) occurs when u₃, the proportion susceptible to G₁H₁, is zero, that is, when no cases of disease are caused by the combined presence of the causal genotypes at both loci G and H, i.e. no causal gene-gene interaction. Moreover, when some individuals in the population are GH-susceptible, i.e. u₃ > 0, the two-locus penetrance among those with both causal genotypes (i.e. Risch's ω₁₁) will exceed the two-locus penetrance predicted by the genetic heterogeneity model, x₁ + y₁ – x₁y₁. Given our assumptions, the excess penetrance will equal the proportion of GH-causal types (r₄)in the population.

Multiplicative Penetrance Models

Table 2c shows a penetrance matrix that connects the causal two-locus penetrances in equation 2 with Risch's penetrance factors in equation 5. For example, A = ω₁ = x₁y₁. For this model to describe the two-locus penetrances correctly, AD and BC must both equal x₁y₁x₀y₀ and must therefore equal each other. In terms of component cause frequencies, this becomes

$$\left[1\hspace{0.17em}-\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_3\right)\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\right]s\hspace{0.17em}=\hspace{0.17em}\left[1\hspace{0.17em}-\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\right]\left[1\hspace{0.17em}-\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\right]$$ (9)

The only non-trivial solution to this equation occurs when

$$u_{3}s\hspace{0.17em}=\hspace{0.17em}\frac{u_1{u}_2}{\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)}$$ (10)

with u₃ > 0 and u₁ + u₂ ≤ 1 (details in ‘Appendix’). Note that equation 10 differs from equation 7 only by the factor s on the left-hand side of the equality.

Our definition of causal gene-gene interaction requires u₃ > 0. Thus, equation 10 demonstrates that the multiplicative model requires the assumption that u₁, u₂, and s are all greater than zero, meaning that some individuals in the population will be susceptible to genotypes at each locus acting alone, i.e. causal genetic heterogeneity. Additionally, the proportion of individuals susceptible to one or the other of the interacting genotypes alone (i.e. due to sufficient cause I or II) must be less than unity.

In summary, under our assumptions, the only way this multiplicative model can correspond to a causal two-locus model of epistasis is for the causal parameters to satisfy the particular algebraic relationship in equation 10.

Application of the Causal Framework to Other Genetic Models

Above, we focused on Risch's models [10] because of their relative generality and because we want to illustrate the principles of using the causal framework to think about genetic models of complex diseases. These principles can also be applied to other models. For example, Vieland and Huang [4] define heterogeneity as the case in which the penetrance in individuals with both factors equals what one would expect with independent effects, i.e., in their notation, the case in which f_AB = 1 – (1 – f_A)(1 – f_B). This is just a special case of Risch's heterogeneity model, arising when (in our notation) D = 0, or when (in Risch's notation) x₀ = y₀ = 0. Some of the subsequent controversy over Vieland and Huang (especially in [21]) focused on their choice of that definition, rather than on any of the mathematical results.

Sepulveda et al. [22] present another approach for two-locus models altogether, one in which alleles act independently to influence penetrance. Within this approach, they consider several different models (‘independent action’, ‘inhibition’, and ‘cumulative’ models), with both ‘dominant’ and ‘recessive’ inheritance, although they use these terms in non-standard ways. To consider just one example, in their ‘dominant’ independent action model, we have expressed their penetrances in ‘one-minus’ form (table 4). Here, π_A and π_B represent, respectively, the penetrance component of the A (first locus) or B (second locus) allele, and π_ext represents the ‘penetrance’ of any external factors. Expressing the probabilities this way reveals that this model can readily be expressed in causal terms, with A, B, and ‘external factors’ each included in a separate causal pie (cf. our equations 2). Full exploration of all the models in Sepulveda et al. [22] is beyond the scope of the current paper, but we have shown here how to approach that task.

Table 4.

Penetrance as a function of genotype in the ‘dominant’ independent action model in Sepulveda et al. [22]

	BB	Bb	bb
AA	1 – (1 – πA)2(1 – πB)2(1 – πext)	1 – (1 – πA)2(1 – πB)(1 – πext)	1 – (1 – πA)2(1 – πext)
Aa	1 – (1 – πA)(1 – πB)2(1 – πext)	1 – (1 – πA)(1 – πB)(1 – πext)	1 – (1 – πA)(1 – πext)
aa	1 – (1 – πB)2(1 – πext)	1 – (1 – πB)(1 – πext)	1 – (1 – πext) = πext

Discussion

Additive two-locus penetrance models are frequently assumed to correspond to a causal model of genetic heterogeneity (lack of epistasis), whereas multiplicative models are assumed to correspond to a causal model of gene-gene interaction. Our results demonstrate that these assumptions are incorrect: both of these models actually correspond to a disease characterized by both causal gene-gene interaction and causal genetic heterogeneity. This suggests that neither model can be used for hypothesis testing, e.g. to reject the hypothesis of no epistasis in a complex disease.

Risch's additive two-locus penetrance model [10] corresponds to a causal model of genetic heterogeneity only under the assumptions that (1) there are individuals in the population who have disease due to the combination of genotypes at loci G and H (i.e. causal gene-gene interaction), and (2) the proportion of such individuals equals a specific algebraic function of the proportion of individuals susceptible to either locus alone, as in equation 7.

Similarly, a multiplicative two-locus penetrance model describes the two-locus penetrance for a disease with gene-gene interaction only under the assumptions that (1) there are individuals in the population who are susceptible to the causal genotype at locus G regardless of the genotype at locus H and vice versa, and (2) the proportion of such individuals equals a specific algebraic function of the proportion of individuals susceptible to the causal genotypes at loci G and H acting together and the proportion of phenocopies, as determined by equation 10.

In contrast, under the assumptions of this paper (the specified SCC model, 2 binary genotypes, a binary outcome, independent distribution of genetic and non-genetic causes, and our definitions of causal gene-gene interaction and causal genetic heterogeneity), Risch's heterogeneity penetrance model [10] perfectly describes the joint distribution of two causal genotypes in the absence of epistasis, i.e. when no individual in the population requires susceptibility genotypes at both loci for disease occurrence (u₃ = 0). This suggests that the heterogeneity penetrance model is most appropriate for testing the null hypothesis of no epistasis. Further, our finding that when u₃ > 0, the excess penetrance above that expected under the heterogeneity model is equal to the proportion of GH-causal types in the population (r₄) suggests that this model might be useful for developing a method to assess the degree to which epistasis contributes to disease susceptibility.

Likewise, Risch's heterogeneity penetrance model [10] can be used to generate simulated two-locus genotypes and disease risk for diseases with causal genetic heterogeneity or causal gene-gene interaction. Causal gene-gene interaction can be simulated by specifying a value of P[disease ∣ G₁H₁] in excess of that predicted by the genetic heterogeneity model. Specifying P[disease ∣ G₁H₁] not in excess of that predicted by genetic heterogeneity indicates no causal gene-gene interaction. On the other hand, data simulated according to additive and multiplicative models may describe causal genetic heterogeneity and causal gene-gene interaction, but only under the highly constrained conditions described above and in table 3.

The use of response types, as implemented here, provides the foundation for future investigations with different or less restrictive assumptions. For example, we assumed that all causal genotypes and other component causes were distributed independently. Relaxation of this assumption (e.g. for genetic variants in linkage disequilibrium, or genetic variants associated with specific environmental exposures) could be accommodated by changing the probabilities of the response types in table 1. Similarly, our causal model assumed that when G₁ and H₁ are in separate sufficient causes they have different causal partners. Future work could investigate a model specifying identical causal partners for G₁ and H₁.

These findings challenge the notion that ‘there is not a precise correspondence between biological models of epistasis and those that are more statistically motivated’ [5], suggesting instead that familiar models used in statistical genetics do have biological interpretations, under certain assumptions and explicit definitions. Our results suggest that causal principles, not mathematical constructs, should provide the basis of evaluating assumptions in statistical genetics research when the goal of such models is to identify the causes of diseases. Any statistical measure used to identify causes makes assumptions about the underlying causal model. Here, we have demonstrated the assumptions for additive, multiplicative, and heterogeneity penetrance models given our assumed causal model. But more generally, any statistic used in the field (e.g. recombination fraction, genotype-relative risk, recurrence risk among relatives) makes assumptions about the underlying causal model.

Causal models provide the basis of an emerging class of powerful methods in other quantitative fields and have been demonstrated to apply to concepts in human genetics [9]. We used an SCC model, which provides a single lens through which to view the effects of not only genetic heterogeneity and gene-gene interaction but also gene frequency, mode of inheritance, phenocopy frequency, and penetrance on disease risk in families and in populations.

Risch [10] also used the multiplicative and additive penetrance models, as well as an identity-by-descent distribution, as the basis for determining the magnitude of increased risk of disease among relatives (λ_R) when disease is caused by two-locus epistasis or genetic heterogeneity, respectively. His λ_R and related estimates are frequently used as the basis for power calculations. We are currently using approaches similar to those applied here to model disease risk in families, in order to derive λ_R estimates and other family-based measures from fundamental principles of causation.

Appendix

Here we derive equations 6–10, i.e. the formulas for the relationships between the causal models and the commonly used penetrance assumptions for two-locus models.

Additive Penetrance Models – Equations 6 and 7

As noted in the text, we must have A + D = B + C in order for an additive model as in equation 3 to hold. From equation 2, this implies r₂ + r₃ + r₄ + r₅ + r₆ + r₆ = r₃ + r₅ + r₆ + r₂ + r₅ + r₆; which reduces to

$$r_4\hspace{0.17em}=\hspace{0.17em}{r}_5$$ (A.1)

From table 1, substitute component cause frequencies for response-type probabilities into (A.1):

$$\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)u_3\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\hspace{0.17em}=\hspace{0.17em}{u}_1{u}_2\left(1\hspace{0.17em}-\hspace{0.17em}s\right)$$ (A.2)

.

which is equation 6. The only non-trivial solution arises when none of s, u₁, or u₂ equals unity, and neither u₁ nor u₂ equals zero. In this case, divide by (1 – s)(1 – u₁)(1 – u₂) to yield equation 7. Also note that since u₃ in equation 7 represents a probability, it cannot exceed unity, and therefore u₁ and u₂ in equation 7 must satisfy the constraint u₁u₂ ≤ (1 – u₁)(1 – u₂), i.e.

$$u_1\hspace{0.17em}+\hspace{0.17em}{u}_2\hspace{0.17em}\le \hspace{0.17em}1$$ (A.3)

To obtain the trivial solutions discussed in the text, set both sides of (A.2) to zero, and now this equation will be true (1) if s = 1; (2)if u₃ = 0 and one of (u₁, u₂) equals zero, or (3) if one of (u₁, u₂) equals zero and the other equals unity. These correspond to the trivial cases discussed in the text.

Heterogeneity Penetrance Models – Equation 8

As noted in the text, we must have (1 – A)(1 – D) = (1 – B) (1 – C) in order for a heterogeneity model as in equation 4 to hold. From equation 2, this implies

$$\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_3\right){\left(1\hspace{0.17em}-\hspace{0.17em}s\right)}^2\hspace{0.17em}=\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}s\right),$$ (A.4)

which is equation 8. The only non-trivial solution arises when none of s, u₁, or u₂ equals unity: divide through by (1 – u₁)(1 – u₂)(1 – s)² to yield 1 – u₃ = 1, i.e. u₃ = 0, as discussed in the text. To obtain the trivial solutions discussed in the text, set both sides of (A.4) to zero, and now this equation will be true if any one of s, u₁, or u₂ equals unity.

Multiplicative Penetrance Models – Equations 9 and 10

As noted in the text, we must have AB = BC in order for a multiplicative model as in equation 5 to hold. From equation 2, this implies

$$\left[1\hspace{0.17em}-\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_3\right)\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\right]s\hspace{0.17em}=\hspace{0.17em}\left[1\hspace{0.17em}-\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\right]\left[1\hspace{0.17em}-\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}s\right)\right],$$ (A.5)

which is equation 9. For ease of notation, let ν_i = 1 – u_i for all i, and let t = 1 – s. Equation A.5 becomes

$$\left(1\hspace{0.17em}-\hspace{0.17em}{v}_1{v}_2{v}_{3}t\right)\left(1\hspace{0.17em}-\hspace{0.17em}t\right)\hspace{0.17em}=\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{v}_{2}t\right)\left(1\hspace{0.17em}-\hspace{0.17em}{v}_{1}t\right)$$

Multiplying out the terms, and collecting all terms containing ν₁ν₂ on the left-hand-side, yields

$$v_1{v}_2\left[\left(1\hspace{0.17em}-\hspace{0.17em}{v}_3\right)\left(1\hspace{0.17em}-\hspace{0.17em}t\right)\hspace{0.17em}-\hspace{0.17em}1\right]t\hspace{0.17em}=\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}{v}_1\hspace{0.17em}-\hspace{0.17em}{v}_2\right)t$$ (A.6)

One solution to equation A.6 is the trivial one in which t = 0, i.e. s = 1; that is, everyone in the population is ‘Inevitable’ and has the disease. Having accounted for that solution, divide both sides by t and convert back to u-s notation:

$$\left(1\hspace{0.17em}-\hspace{0.17em}{u}_{3}s\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}-\hspace{0.17em}\left(u_1\hspace{0.17em}+\hspace{0.17em}{u}_2\right)$$ (A.7)

The only non-trivial solution arises when neither side of equation A.7 equals zero or unity. In this case, divide both sides by (1 – u₁)(1 – u₂), to yield

$$1\hspace{0.17em}-\hspace{0.17em}{u}_{3}s\hspace{0.17em}=\hspace{0.17em}\frac{1\hspace{0.17em}-\hspace{0.17em}\left(u_1\hspace{0.17em}+\hspace{0.17em}{u}_2\right)}{\left(1\hspace{0.17em}-\hspace{0.17em}{u}_1\right)\left(1\hspace{0.17em}-\hspace{0.17em}{u}_2\right)},$$

which simplifies to equation 10. Since u₃ and s in equation 10are probabilities, their product cannot exceed unity; therefore, u₁ and u₂ must satisfy the constraint in equation A.3. Trivial solutions arise (1) when both sides of equation A.7 equal zero, which occurs when u₁ + u₂ = 1 and at least one of u₁, u₂, or u₃s equals unity, or (2) when both sides of equation A.7 equal unity, which occurs when u₁, u₂, and u₃s all equal zero.