Relative Efficiency of Trend Tests with Misspecified Genetic Models in Stratified Analyses of Case-Control or Cohort Data

Abstract

Background/Aims

Genetic single-nucleotide polymorphism (SNP) data are often analyzed using trend tests that rely on a specific assumption about the way that disease frequency varies across genotypes, but the validity of this assumption is not typically known. We explore the relative efficiency of trend tests in which the assumed model may or may not correspond to the true genetic model.

Methods

We derive formulae for the asymptotic relative efficiencies (AREs) comparing tests that assume different genetic models. We consider both unstratified and stratified tests, using both case-control and cohort data. We illustrate these formulae using realistic parameters and compare the calculated AREs to simulated relative efficiencies in finite samples.

Results

The AREs are identical for unstratified tests using case-control and cohort data, but differ for stratified tests. Loss of efficiency can be substantial, given specific combinations of high-risk allele frequencies, disease frequencies, and assumed versus actual genetic models. Given reasonably large sample sizes, asymptotic calculations align well with finite sample simulations of relative efficiency.

Conclusions

ARE is a useful estimate of the relative efficiency of statistics using different underlying genetic models. ARE calculations reveal that additive gene doses, which are most commonly used, lead to large losses in power in some settings.

Introduction

The goal of many genome-wide association (GWA) studies is to identify genetic markers that are associated with a disease of interest. When single-nucleotide polymorphisms (SNPs) are used as markers, statistical inference is often based on the Cochran-Armitage (CA) test for trend, which relies on an assumption about the way that disease frequency varies across genotypes. The assumed model can be expressed as P(disease | j alleles) = H(α + βd_j), where the gene doses d_j and the function H reflect beliefs about the underlying relationship between the risk of disease and the number of alleles. The original formulations of the CA trend test [1, 2] permit the use of any gene doses d_j, so we use the label ‘CA trend test’ to refer to any choice of gene doses. But most often the additive gene doses d_j = j for; = {0,1,2} are used. For a given SNP, we do not necessarily know the true gene doses for the underlying genetic model, so assuming gene doses d_j = j may lead to a loss in power [3].

The unstratified test, based on additive gene doses d_j = j, has been shown to be locally most powerful for a broad class of alternatives with monotone and twice differentiable H functions, including the additive model [H = identity], the multiplicative model [H = exponential], and the logistic model [H = antilogit], both in the cohort setting [4] and in the case-control setting [5]. Thus using the test based on the additive gene doses will result in minimal losses in efficiency for alternatives that can be expressed as P(disease | j alleles) = H(α + βd_j). However, efficiency loss can be high when the true genetic model is dominant or recessive [3]. To obtain most powerful tests in these cases, the gene doses for j = {0,1,2} must be d_j = {0,0,1}, when the inheritance pattern is autosomal recessive, and d_j = {0,1,1}, when the inheritance pattern is autosomal dominant [5]. For the recessive and dominant inheritance patterns, the tests based on these specified gene doses are not only locally most powerful, but also minimize the sample size required to achieve prespecified type I and type II errors for any alternative [5].

Analysis of GWA studies is further complicated by the confounding effects of population stratification. Recent methods to control for this confounding have included both continuously adjusted CA trend tests [6] and stratified CA trend tests [7]. If we consider a single stratification variable as the categorization of individuals with similar risk due to a host of factors, then the stratified CA trend test can be viewed as an approximate version of the test that makes more complicated continuous adjustments. Tarone and Gart [4] investigated stratified CA trend tests for the class of alternatives using additive gene doses d_j= j and variable H functions. Their work was motivated by designed experiments, but it can also be applied to epidemiological cohort data. Once data are stratified, Tarone and Gart showed that the test based on the additive gene doses and identity H function, which together comprise the ‘additive model’, is no longer guaranteed to provide a locally most powerful test against the class of alternatives using the additive gene doses with other H functions. It is unknown how stratification affects efficiency when case-control data are used and/or when the true genetic model is dominant or recessive.

The goal of this paper is to estimate the efficiency of the stratified CA trend test when the model is misspecified. In the Methods section, we present the CA trend test and the corresponding asymptotic relative efficiencies (AREs) for both unstratified and stratified genetic models. The AREs have been derived previously for cohort data with variable H functions [4], but we extend this calculation to allow variable gene doses. We also derive AREs for stratified case-control data. We show that the unstratified tests and AREs are identical for case-control and cohort data. For stratified tests, the AREs for case-control and cohort data differ. We illustrate these AREs using parameter values that are realistic in applications. In ‘Simulations: Performance of ARE Formulae in Finite Samples’, we illustrate how closely these asymptotic calculations align with finite sample relative efficiencies. In the Discussion section, we summarize these results and suggest extensions.

Methods

Notation

Table 1 provides the notation that we use for both case-control and cohort data. The total number of subjects with disease is R, the number without disease is S, and their sum is N. The potential high-risk allele is ‘A’. The number of subjects with j ‘A’ alleles and disease is r_j, the number with j ‘A’ alleles and no disease is s_j, and their sum is n_j. The population-level genotype frequency P(j alleles) is denoted g_j and the population-level disease frequency is denoted K.

Table 1.

Unstratified data by genotype

	aa	aA	AA	Total
Disease	r0	r1	r2	R
No disease	s0	s1	s2	S
Total	n0	n1	n2	N

Case-Control Data

The total numbers of diseased and non-diseased subjects (R and S) are fixed, but the numbers of diseased and non-diseased subjects with specific genotypes are random. Using the probabilities p_j = P(j alleles | disease) and q_j = P(j alleles | no disease), the distribution of (r₀, r₁, r₂) is trinomial with parameters (R; (p₀, p₁, p₂)), and the distribution of (s₀, s₁ s₂) is trinomial with parameters (S; (q₀, q₁, q₂)).

Cohort Data

R and S are no longer fixed; instead we condition on the column totals n_j. Using the probability ${\tilde{p}}_j=\text{P}$(disease | j alleles), the distribution of r_j, is now binomial with parameters $\left(n_j;\hspace{0.17em}{\tilde{p}}_j\right)$ and Sj is the difference r_j – r_j.

Stratified Data

There is one such table for each stratum i of the I total strata. An additional subscript is added to each count to indicate stratum membership. The probability that a subject is in a given stratum is denoted v_i.

Model for Relationship between Disease and Genotype

Cohort Data, Population Model

We assume that the true model for the probability of disease in the population, given j alleles, is ${\tilde{p}}_j\hspace{0.17em}=\hspace{0.17em}L\left(\alpha \hspace{0.17em}+\hspace{0.17em}\beta d_{jL}\right)$ = L(α + βd_jL). Table 2 provides functions and gene doses for models of interest. Only the identity function is considered for dominant, recessive, and heterozygous models because when other functions are used with the same gene doses d_jL, they yield the same model. The co-dominant model, which allows arbitrary differences for heterozygotes, is not considered here because it represents a 2 degree-of-freedom alternative.

Table 2.

Functions and gene doses used to denote genetic models of interest, where $\tilde{p}$j = P(disease | j alleles) = L(α + βd_jL)

	L(x)	djL
Additive	x	j
Multiplicative	ex	j
Logistic	ex/(1 + ex)	j
Dominant	x	I[j∊{l, 2}]
Recessive	x	I[j∊{2}]
Heterozygous	x	I[j∊{l}]

Case-Control Data, Case-Control Sample Model

When case-control data are collected, investigators may sometimes assume that the true underlying model for the relationship between disease and genotype has the same structure in the case-control sample as it does in a cohort sample. Under the logistic regression model [8], the case-control sample model has the same L function, but a different intercept from the population model: P(disease j alleles, sampled) ${\tilde{p}}_j^{\left(cc\right)}\hspace{0.17em}=\hspace{0.17em}L\left(\delta \hspace{0.17em}+\hspace{0.17em}\beta d_{jL}\right)$.

Case-Control Data, Population Model

Another option for case-control data is to translate the true model relating disease and genotype in the population ${\tilde{p}}_j\hspace{0.17em}=\hspace{0.17em}L\left(\alpha \hspace{0.17em}+\hspace{0.17em}\beta d_{jL}\right)$ to the case-control sample. That is, we can write the disease probability in the case-control sample, conditional on number of alleles, in terms of the population-model parameters. This conditional probability will depend on the sampling fractions that characterize the case-control sample. We define π1 = P(sampled disease), π₀ = P(sampled | no disease), and π= π₁/π₀ We also define the function j_π to be the function of α + βd_jL that gives the true conditional probability of disease in the case-control sample using population parameters, i.e. P(disease | j alleles, sampled) = ${\tilde{p}}_j^{\left(cc\right)}\hspace{0.17em}=\hspace{0.17em}{J}_{\pi }\left(\alpha \hspace{0.17em}+\hspace{0.17em}\beta d_{jL}\right)$. The function J_π can be written in terms of the sampling fractions and the model relating disease and genotype in the population:

$$J_{\pi }\left(\alpha \hspace{0.17em}+\hspace{0.17em}\beta d_{jL}\right)\hspace{0.17em}=\hspace{0.17em}\frac{\pi L\left(\alpha \hspace{0.17em}+\hspace{0.17em}\beta d_{jL}\right)}{\pi L\left(\alpha \hspace{0.17em}+\hspace{0.17em}\beta d_{jL}\right)\hspace{0.17em}+\hspace{0.17em}{\left[1\hspace{0.17em}-\hspace{0.17em}L\left(\alpha \hspace{0.17em}+\hspace{0.17em}\beta d_{jL}\right)\right]}^{\cdot }}$$

If we have case-control data and think we have L in our data when in fact we have J_π we may be misled, as we will see in the sections that follow.

CA Trend Test

In the context of genetic association studies, CA trend tests are used to determine whether the presence of an allele of interest is related to risk of disease. Therefore the null hypothesis (H₀) of interest is β = 0. In the population, β = 0 implies that the risk of disease is the same regardless of the number of alleles present, i.e. ${\tilde{p}}_j\hspace{0.17em}=\hspace{0.17em}\tilde{p}$ for all j. In a case-control sample, β = 0 implies that the probability of having a given number of alleles is the same regardless of disease status, i.e. p_j = q_j for all j.

To emphasize that the assumed statistical model may be misspecified, we denote the model ‘m’ that is assumed to underlie the statistic of interest using the function H_m and gene doses d_jm.

Unstratified Test

To test H₀: β = 0, Tarone and Gart [4] studied the CA trend test statistic, which is the score test when the assumed model is H(α + βd_j) for differentiable function Hand linear doses dj =j. For case-control data, it is the score test under either a true population model or a true case-control sample model when H is the antilogit function. The CA trend test statistic is:

$$Z_m\hspace{0.17em}=\hspace{0.17em}\frac{N^2\hspace{0.17em}{\left[{\sum }_j{d}_{jm}{r}_j\hspace{0.17em}-\hspace{0.17em}\frac{R}{N}\hspace{0.17em}{\sum }_j{d}_{jm}{n}_j\right]}^2}{RS{\left({\sum }_j{n}_j{d}_{jm}^2\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{n}_j{d}_{jm}\right)}^2|/N\right)}^{\cdot }}$$ (1)

Note that statistic 1 does not depend on the function H_m, as all terms containing H_m cancel out in its derivation as a score statistic. The statistic has an asymptotic χ²₍₁₎ distribution under H₀ for cohort data [2] and case-control data [9],

Stratified Test

For an assumed population model denoted by m and strata indexed by i, Tarone and Gart [4] showed that the stratified score test statistic that applies to epidemiological cohort data is:

$$Z_m^{strat}\hspace{0.17em}=\hspace{0.17em}\frac{{\left[{\sum }_i\frac{N_i^2{H^{\prime }}_m\hspace{0.17em}\left({\stackrel{‸}{\alpha }}_i\right)}{R_i{S}_i}\left({\sum }_j{r}_{ij}{d}_{jm}\hspace{0.17em}-\hspace{0.17em}\frac{R_i}{N_i}{\sum }_j{n}_{ij}{d}_{jm}\right)\right]}^2}{{\sum }_i\frac{N_i^2{\left[{H^{\prime }}_m\hspace{0.17em}\left({\stackrel{‸}{\alpha }}_i\right)\right]}^2}{R_i{S}_i}\frac{1}{N_i}\left[N_i{\sum }_j{d}_{jm}^2{n}_{ij}\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{d}_{jm}{n}_{ij}\right)}^2\right]}$$ (2)

where ${\stackrel{‸}{\alpha }}_i\hspace{0.17em}=\hspace{0.17em}{H}_m^{-1}\hspace{0.17em}\left(R_i/N_i\right)$. Unlike the unstratified statistic 1, statistic 2 does depend on the assumed function H_m. This function H_m will reflect our assumption about the true population function L, when we have cohort data, or the related function J_π when we have case-control data.

Using the case-control sample model described in ‘Model for Relationship between Disease and Genotype’, a comparable derivation gives the same statistic because ${\stackrel{‸}{\alpha }}_i$ and ${\stackrel{‸}{\delta }}_i$ are both estimated by H⁻¹_m (R_i/N_i). Despite identical computations, the interpretation of these estimates differs due to the different sampling contexts. Both are estimates of disease risk under the assumption that disease does not vary with genotype (H₀), but ${H^{\prime }}_m\left({\stackrel{‸}{\alpha }}_i\right)$ estimates risk for the general population, whereas ${H^{\prime }}_m\left({\stackrel{‸}{\delta }}_i\right)$ estimates risk for a specific case-control sample that typically has a higher proportion of cases than the general population.

Examples of stratified trend tests assuming different genetic models are provided in the online supplementary materials (online supplementary Section A and online supplementary table 1, www.karger.com/doi/10.1159/000328858).

ARE of the Trend Test

Pitman ARE is the limiting ratio of the sample sizes that produces equal asymptotic power in relation to a sequence of alternative hypotheses that approach H₀ as the sample sizes become large. Using Noether's theorem [10], we can calculate the Pitman ARE as a ratio of the efficacies of two different statistics. We denote the efficacy attained by the statistic corresponding to model m under true L as e_mL. Tarone and Gart [4] calculated AREs under the assumption that one of the two statistics being compared used the true underlying L function as the function H_m in the statistic. We make three extensions to their calculations: (1) instead of using only d_j = j for all statistics, we consider statistics that use other gene doses; (2) we allow the model to be misspecified by both statistics, and (3) we compute the ARE for case-control data.

Unstratified Test

For unstratified tests performed with cohort data, the ARE comparing assumed model m to assumed model $\tilde{m}$, when data are generated from the true model L, is

ARE

$\left(m,\tilde{m}\right)$

$=\hspace{0.17em}\frac{{\left[{\sum }_j{d}_{jm}{d}_{jL}{g}_j\hspace{0.17em}-\hspace{0.17em}{\sum }_j{d}_{jm}{g}_j\hspace{0.17em}{\sum }_j{d}_{jL}{g}_j\right]}^2\hspace{0.17em}\left[{\sum }_j{d}_{j\tilde{m}}^2{g}_j\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{d}_{j\tilde{m}}{g}_j\right)}^2\right]}{{\left[{\sum }_j{d}_{j\tilde{m}}{d}_{jL}{g}_j\hspace{0.17em}-\hspace{0.17em}{\sum }_j{d}_{j\tilde{m}}{g}_j\hspace{0.17em}{\sum }_j{d}_{jL}{g}_j\right]}^2\hspace{0.17em}\hspace{0.17em}\left[{\sum }_j{d}_{jm}^2{g}_j\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{d}_{jm}{g}_j\right)}^2\right]},$

which reduces to the following when the true gene doses d_jL equal

$$=\frac{{\left[{\sum }_j{d}_{jm}{d}_{j\tilde{m}}{g}_j\hspace{0.17em}-\hspace{0.17em}{\sum }_j{d}_{jm}{g}_j{\sum }_j{d}_{j\tilde{m}}{g}_j\right]}^2}{\left[{\sum }_j{d}_{j\tilde{m}}^2{g}_j\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{d}_{j\tilde{m}}{g}_j\right)}^2\right]{\left[{\sum }_j{d}_{jm}^2{g}_j\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{d}_{jm}{g}_j\right)}^2\right]}^{\cdot }}$$ (3)

Note that if the gene doses d_j are equal in the two statistics being compared, and if they are correctly specified, then the ARE reduces to 1 regardless of the true H function.

The ARE of unstratified tests performed with case-control data is the same as the one given in equation 3. Note that under H₀, the genotype frequency in the case-control sample g^(cc)_j is equal to the population genotype frequency. The disease risk, conditional on number of alleles, cancels out under both the population model and the case-control sample model, so it does not matter which of these two models is the true one.

Stratified Test, Cohort Data, Population Model

The AREs for stratified tests are also calculated with Noether's theorem [10]. However, the efficacies are now sums of stratum-specific quantities. This procedure leads to the following expression for stratified ARE in cohort-study data: ARE$\left(m,\tilde{m}\right)$

$$\begin{array}{c}=\frac{{\left[{\sum }_i{v}_i\frac{{H^{\prime }}_m\hspace{0.17em}\left(H_m^{-1}\hspace{0.17em}\left(L\left({\alpha }_i\right)\right)\right)L^{\prime }\hspace{0.17em}\left({\alpha }_i\right)}{L\hspace{0.17em}\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}L\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{jm}{d}_{jL}{g}_{ij}\hspace{0.17em}-\hspace{0.17em}{\sum }_j{d}_{jm}{g}_{ij}{\sum }_j{d}_{jL}{g}_{ij}\right]\right]}^2}{{\left[{\sum }_i{v}_i\frac{{H^{\prime }}_{\tilde{m}}\hspace{0.17em}\left(H_{\tilde{m}}^{-1}\hspace{0.17em}\left(L\left({\alpha }_i\right)\right)\right)L^{\prime }\hspace{0.17em}\left({\alpha }_i\right)}{L\hspace{0.17em}\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}L\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{j\tilde{m}}{d}_{jL}{g}_{ij}\hspace{0.17em}-\hspace{0.17em}{\sum }_j{d}_{j\tilde{m}}{g}_{ij}\hspace{0.17em}{\sum }_j{d}_{jL}{g}_{ij}\right]\right]}^2}\\ \times \frac{{\sum }_i{v}_i\frac{{\left[{H^{\prime }}_{\tilde{m}}\hspace{0.17em}\left(H_{\tilde{m}}^{-1}\left(L\left({\alpha }_i\right)\right)\right)\right]}^2}{L\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}L\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{j\tilde{m}}^2{g}_{ij}\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{d}_{j\tilde{m}}{g}_{ij}\right)}^2\right]}{{\sum }_i{v}_i\frac{{\left[{H^{\prime }}_m\hspace{0.17em}\left(H_m^{-1}\hspace{0.17em}\left(L\left({\alpha }_i\right)\right)\right)\right]}^2}{L\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}L\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{jm}^2{g}_{ij}\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{d}_{jm}{g}_{ij}\right)}^2\right]}\end{array}$$ (4)

where the i subscript indicates stratum-level quantities, v_i = P(stratum i) and g_ij = P(j alleles | stratum i). If $H_{\tilde{m}}$ is the true population function L and $d_{j\tilde{m}}$ are the true gene doses d_jL, then this reduces to a form that is comparable to Tarone and Gart's result [4]: $=\hspace{0.17em}{\left[{\sum }_i{v}_i\frac{{H^{\prime }}_m\hspace{0.17em}\left(H_m^{-1}\hspace{0.17em}\left(H_{\tilde{m}}\left({\alpha }_i\right)\right)\right){H^{\prime }}_{\tilde{m}}\hspace{0.17em}\left({\alpha }_i\right)}{H_{\tilde{m}}\hspace{0.17em}\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}{H}_{\tilde{m}}\hspace{0.17em}\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{jm}{d}_{j\tilde{m}}{g}_{ij}\hspace{0.17em}-\hspace{0.17em}{\sum }_j{d}_{jm}{g}_{ij}\hspace{0.17em}{\sum }_j{d}_{j\tilde{m}}{g}_{ij}\right]\right]}^2\times {\left[{\sum }_i{v}_i\frac{{H^{\prime }}_{\tilde{m}}\hspace{0.17em}{\left({\alpha }_i\right)}^2}{H_{\tilde{m}}\hspace{0.17em}\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}{H}_{\tilde{m}}\hspace{0.17em}\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{j\tilde{m}}^2{g}_{ij}\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{d}_{j\tilde{m}}{g}_{ij}\right)}^2\right]{\sum }_i{v}_i\frac{{H^{\prime }}_m\hspace{0.17em}\left({H^{\prime }}_m\hspace{0.17em}{\left(H_m^{-1}\left(H_{\tilde{m}}\left({\alpha }_i\right)\right)\right)}^2\right)}{H_{\tilde{m}}\hspace{0.17em}\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}{H}_{\tilde{m}}\hspace{0.17em}\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{jm}^2{g}_{ij}\hspace{0.17em}-{\left({\sum }_j{d}_{jm}{g}_{ij}\right)}^2\right]\right]}^{-1}\cdot$

Stratified Test, Case-Control Data, Case-Control Sample Model

When we assume that the true conditional probability of disease in the case-control sample can be written as a simple function L of the gene dosage score, the ARE formula for case-control stratified data is the same as equation 4, except that α_i is replaced by δ_i, and g_ij is replaced by g^(cc)_ij = P(j alleles | stratum i, sampled). Thus the ARE depends on the assumed function for the conditional probability of disease in the case-control sample L, the true gene doses d_jL, the sampling ratio π, the population allele frequency g_ij, and the probability of subjects' being in each stratum v_i. Note that under H₀, the allele frequency in the case-control sample g^(cc)_ij is equal to the population allele frequency, so they can be used interchangeably in formula 4.

Stratified Test, Case-Control Data, Population Model

When we assume that the true conditional probability of disease in the case-control sample is a function J_π of the population parameters, then the modified ARE that is calculated under this population-level assumption, derived in online supplementary Section A, is:

ARE(m,$\tilde{m}$)

$$\begin{array}{c}=\frac{{\left[{\sum }_i{v}_i\frac{{H^{\prime }}_m\hspace{0.17em}\left(H_m^{-1}\hspace{0.17em}\left(J_{\pi }\left({\alpha }_i\right)\right)\right)L^{\prime }\hspace{0.17em}\left({\alpha }_i\right)}{L\hspace{0.17em}\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}L\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{jm}{d}_{jL}{g}_{ij}^{\left(cc\right)}\hspace{0.17em}-\hspace{0.17em}{\sum }_j{d}_{jm}{g}_{ij}^{\left(cc\right)}{\sum }_j{d}_{jL}{g}_{ij}^{\left(cc\right)}\right]\right]}^2}{{\left[{\sum }_i{v}_i\frac{{H^{\prime }}_{\tilde{m}}\hspace{0.17em}\left(H_{\tilde{m}}^{-1}\hspace{0.17em}\left(J_{\pi }\left({\alpha }_i\right)\right)\right)L^{\prime }\hspace{0.17em}\left({\alpha }_i\right)}{L\hspace{0.17em}\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}L\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{j\tilde{m}}{d}_{jL}{g}_{ij}^{\left(cc\right)}\hspace{0.17em}-\hspace{0.17em}{\sum }_j{d}_{j\tilde{m}}{g}_{ij}^{\left(cc\right)}\hspace{0.17em}{\sum }_j{d}_{jL}{g}_{ij}^{\left(cc\right)}\right]\right]}^2}\\ \times \frac{{\sum }_i{v}_i\frac{{\left[{H^{\prime }}_{\tilde{m}}\hspace{0.17em}\left(H_{\tilde{m}}^{-1}\left(J_{\pi }\left({\alpha }_i\right)\right)\right)\right]}^2}{J_{\pi }\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}{J}_{\pi }\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{j\tilde{m}}^2{g}_{ij}^{\left(cc\right)}\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{d}_{j\tilde{m}}{g}_{ij}^{\left(cc\right)}\right)}^2\right]}{{\sum }_i{v}_i\frac{{\left[{H^{\prime }}_m\hspace{0.17em}\left(H_m^{-1}\hspace{0.17em}\left(J_{\pi }\left({\alpha }_i\right)\right)\right)\right]}^2}{J_{\pi }\left({\alpha }_i\right)\left[1\hspace{0.17em}-\hspace{0.17em}{J}_{\pi }\left({\alpha }_i\right)\right]}\left[{\sum }_j{d}_{jm}^2{g}_{ij}^{\left(cc\right)}\hspace{0.17em}-\hspace{0.17em}{\left({\sum }_j{d}_{jm}{g}_{ij}^{\left(cc\right)}\right)}^2\right]}\cdot \end{array}$$ (5)

The ARE depends on the true function for the conditional probability of disease in the population L, the true gene doses d_jL, the sampling ratio π, the population allele frequency g_ij, and the probability of subjects' being in each stratum V_i. The function for the conditional probability of disease in the case-control sample J_π can be computed from these other quantities. Again the allele frequency in the case-control sample g^(cc)_ij is interchangeable with the population allele frequency g_ij under H₀.

Because equations 4 and 5 differ, assumptions about the truth should be carefully considered before deciding which of these expressions to use.

ARE Examples

Unstratified Tests

The unstratified ARE for either cohort or case-control data depends on the following parameters: the high-risk allele frequency g_j, the true gene doses d_jL, and the gene doses d_jm and $d_{j\tilde{m}}$ assumed by the statistics being compared. Figure 1 plots ARE versus allele frequency for high-risk allele frequencies ranging from 0 to 0.5. The corresponding relationships for high-risk allele frequencies above 0.5 can be inferred by noting that a dominant genetic dose effect with an allele frequency g_j above 0.5 can also be modeled by a recessive genetic dose effect with an allele frequency 1 – g_j. For each model pair comparison, the plotted value is the ARE associated with using the statistic derived under one of the models when, in fact, the data arise under the other model, i.e. assuming that d_jL = $d_{j\tilde{m}}$ or d_jL = d_jm. The ARE formula 3 that applies to this scenario is symmetric so either of the pair of models can be the one that generates the observed data.

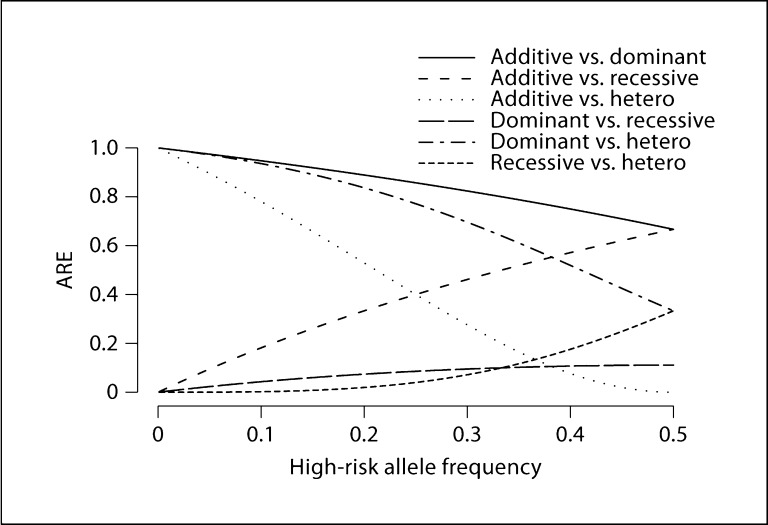
Fig. 1.

Asymptotic relative efficiency (ARE) for unstratified tests, comparing two different statistics, one of which reflects the true model underlying the data. Either one could be the true model because the ARE formula (equation 3) is symmetric. Note that ARE is equal to 1 when comparing any of additive, multiplicative, or logistic.

The ARE is equal to 1 when comparing models that use identical gene doses to calculate the statistic (scenario not shown in fig. 1. However, if the truth is dominant, recessive, or heterozygous, then the ARE varies depending on which statistic is compared to the truth [5]. The ARE clearly depends on the high-risk allele frequency (fig. 1). When the CA trend test based on the additive model is used, the ARE under dominant truth is highest when allele frequency is low; the ARE under recessive truth is highest when allele frequency is high; and the ARE under heterozygous truth is highest when allele frequency is near 0 or 1. On the other hand, if the statistic based on the recessive model is used but the true gene effect is dominant, or vice versa, then the ARE is low regardless of the allele frequency, but best at 0.5. Therefore, although additive tests are most commonly used, they may have low power to detect associations when the true genetic effect is dominant or recessive, especially if the high-risk allele frequency is extreme. This reinforces results reported previously [3, 5],

Stratified Tests

When stratified analyses are conducted, the ARE depends not only on the gene doses and the high-risk allele frequencies in the different strata, but also on the stratum-specific disease frequencies, the H functions that are used in different statistics, and the L or J_π functions that define the true underlying model. Figures 2, 3, 4 as well as online supplementary figures 1, 2, 3, 4, 5, 6 plot ARE values assuming 6 strata of equal size, in each of which both the disease frequency and the high-risk allele frequency can vary. Each plot represents fixed disease frequencies across a range of high-risk allele frequencies. The stratum-specific disease frequencies represent both rare and common diseases. Each line in a figure represents the ARE comparing the statistic using the additive model to one using the true model underlying the data. In all of these figures, when ARE is illustrated using case-control data, a population model, which induces a more complicated model for the way the probability of disease in the sample depends on genotype (see also ‘Model for Relationship between Disease and Genotype’ above), is assumed.

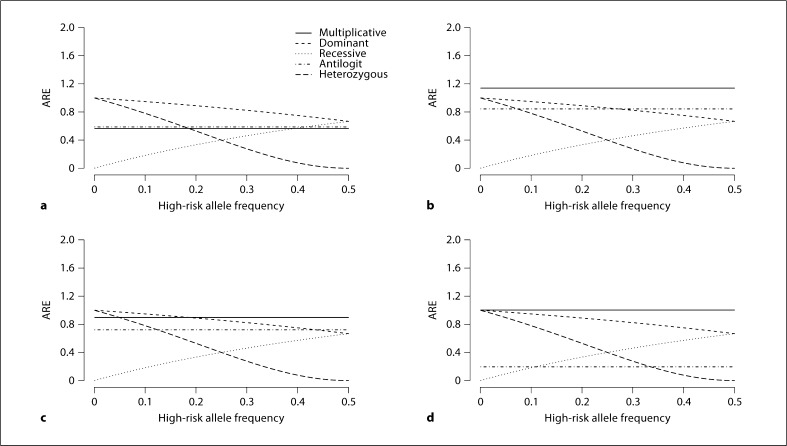
Fig. 2.

Asymptotic relative efficiency (ARE) for stratified tests, comparing the statistic using the additive model to one using the true model underlying the data. ARE is calculated using equation 4 for cohort data and equation 5 for case-control data. There are 6 strata with equal distribution of subjects across strata and constant high-risk allele frequencies across strata. Truth is assumed at the population level for both cohort and case-control data. For case-control data, the sampling ratio π is 100, meaning that cases are 100 times more likely to be sampled than controls, a, c Cohort data; b, d case-control data. In a, b, stratum-specific population disease frequencies of 0.01,0.025,0.0375,0.0625,0.075, and 0.1 are used; in c, d, stratum-specific population disease frequencies of 0.25, 0.375, 0.5, 0.75, 0.875, and 0.95 are used.

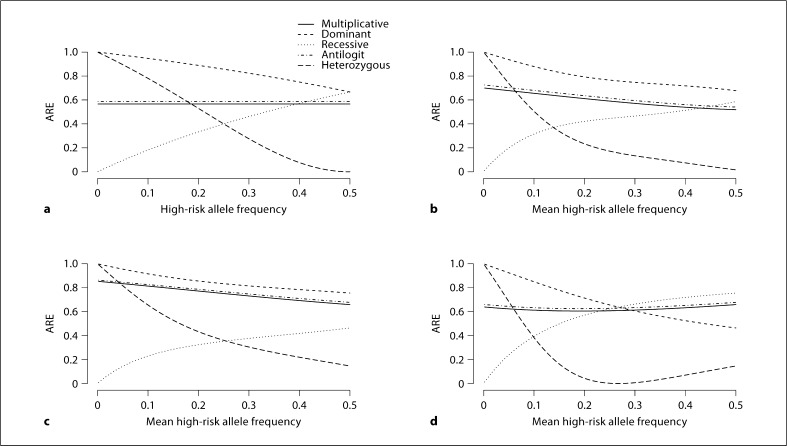
Fig. 3.

Asymptotic relative efficiency (ARE) for stratified tests using cohort data in the presence of confounding, comparing the statistic using the additive model to one using the true model underlying the data (low disease frequency, high allele frequency variance). ARE is calculated using equation 4. There are 6 strata with equal distribution of subjects across strata, stratum-specific population disease frequencies of 0.01, 0.025, 0.0375, 0.0625, 0.075, and 0.1, and stratum-specific high-risk allele frequencies as follows: in a, constant high-risk allele frequencies across strata are used, while b-d use stratum-specific high-risk allele frequencies with the mean value displayed on the X-axis and variance across strata of 2.1. High-risk allele frequencies have arbitrary association with disease frequencies (b), monotone positive association (c), and monotone negative association (d).

Fig. 4.

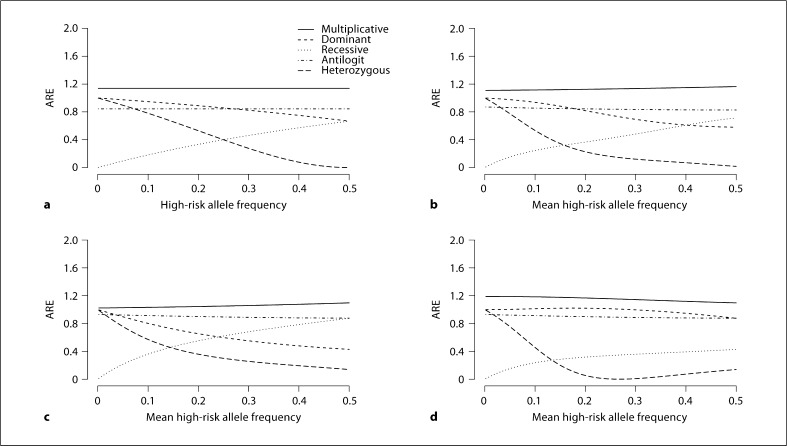
Asymptotic relative efficiency (ARE) for stratified tests using case-control data in the presence of confounding, comparing the statistic using the additive model to one using the true model underlying the data (low disease frequency, high allele frequency variance). ARE is calculated using equation 5. The sampling ratio π is 100, meaning that cases are 100 times more likely to be sampled than controls. There are 6 strata with equal distribution of subjects across strata, stratum-specific population disease frequencies of 0.01,0.025,0.0375,0.0625,0.075, and 0.1, and stratum-specific high-risk allele frequencies as follows: in a, constant high-risk allele frequencies across strata are used, while b-d use stratum-specific high-risk allele frequencies with the mean value displayed on the X-axis and variance across strata of 2.1. High-risk allele frequencies have arbitrary association with disease frequencies (b), monotone positive association (c), and monotone negative association (d).

In figure 2, high-risk allele frequencies are constant across strata. The top row (fig. 2a, b) represents a rare disease, and the bottom row (fig. 2c, d) represents a more common disease. The left column (fig. 2a, c) represents cohort data, and the right column (fig. 2b, d) represents case-control data. For case-control data, the sampling ratio π is 100, meaning that cases are 100 times more likely to be sampled than controls. Given the same underlying population disease frequency, e.g. figure 2b versus 2a, the disease frequency in the sample is higher in case-control data than in cohort data.

When the high-risk allele frequencies are constant across strata, and interest lies in models with the same gene doses, e.g. additive and multiplicative, the ARE is the same regardless of the high-risk allele frequency. However, for these models, ARE does vary with disease frequency and with type of data. Multiplicative and logistic models have efficiency more similar to each other than to the additive model for low sample disease frequencies. But as sample disease frequency increases, both their efficiencies become more similar to the additive model, until the logistic model diverges from both at very high sample disease frequencies.

Figure 2 also shows that when the statistic based on the additive model is compared to a statistic with different gene doses, e.g. dominant, recessive, or heterozygous, and one of the statistics being compared reflects the true model, then the ARE varies with high-risk allele frequency as it does for unstratified data. Only two parameters are needed to describe these true models, so the choice of gene dose d_j makes ARE vary with allele frequency, but this relationship does not change further with disease frequency.

Figures 3 and 4 reflect high-risk allele frequencies that vary across strata, as would occur in the presence of confounding. They display the average allele frequency across the strata in place of the allele frequency that was assumed to be constant in figure 2. We chose the stratum-specific allele frequencies to be additive on the logit scale. Sample high-risk allele frequencies are displayed in table 3.

Table 3.

Examples of stratum-specific high-risk allele frequencies with specified variance

Variance	Association with disease frequency	Stratum
		1	2	3	4	5	6
0.525	monotone positive	0.08	0.13	0.16	0.24	0.29	0.40
	monotone negative	0.40	0.29	0.24	0.16	0.13	0.08
	arbitrary	0.16	0.40	0.13	0.29	0.08	0.24
2.1	monotone positive	0.03	0.08	0.13	0.29	0.40	0.65
	monotone negative	0.65	0.40	0.29	0.13	0.08	0.03
	arbitrary	0.13	0.65	0.08	0.40	0.03	0.29

The values displayed are centered around logit(0.2), with subtraction of (1, 0.5, 0.25, −0.25, −0.5, −1) when the variance on the log it scale is 0.525 and subtraction of (2,1, 0.5, −0.5, −1, −2) when the variance on the logit scale is 2.1. For example, the first cell is anti-logit (logit (0.2) −1) = 0.08.

Figures 3 and 4 display the ARE for a disease that is rare in the population, in the presence of several different types of confounding for cohort data (fig. 3) and for case-control data (fig. 4). These figures assume highly variable high-risk allele frequencies. The top left plot in each (3a, 4a) is the one with constant high-risk allele frequency. The other panels (3b−d, 4b−d) allow stratum-specific high-risk allele frequencies to vary, as specified in table 3. Plots for positive and negative associations are reflections of each other, with the exception of dominant and recessive curves, each of which is the reflection of the other.

The ARE is more variable when there is greater variance in high-risk allele frequency across strata. Also the arbitrary associations between high-risk allele frequency and stratum-specific disease frequency have ARE that is similar to the ARE for constant high-risk allele frequency. The monotone associations have ARE that is less similar to the ARE for constant high-risk allele frequency.

For cohort data collected in a rare disease setting, as in figure 3, comparing a positive association to constant high-risk allele frequency, the efficiency of the additive statistic is generally closer to that of the fully efficient true statistic for dominant, multi-plicative, and logistic truths, while it is further for recessive truth. For case-control data collected in a rare disease setting, as in figure 4, assuming the underlying population follows the named model, the relationships among the individual panels are similar to those in cohort data. Online supplementary figures 1, 2, 3, 4, 5, 6 examine different parameter values, but yield similar conclusions to figures 3 and 4. Online supplementary figures 7 and 8 examine scenarios in which the true underlying model is neither the additive model nor the model used for the specified statistic.

Simulations: Performance of ARE Formulae in Finite Samples

Description of Scenarios

By definition, ARE is only guaranteed to apply to data collected on samples of infinite size. Therefore we conducted a series of simulations to investigate its performance in more realistic finite samples. For a range of see-narios we generated data assuming that various alternatives were true, simulating 1,000 samples and conducting a trend test on each sample. We conducted two sets of analyses, one using a significance cutoff of 5 × 10⁻⁸, which is typical of GWA studies, and one using a significance cutoff of 0.01 which is representative of candidate gene studies that focus on testing a limited number of genes or tag SNPs within a gene. We repeated this process for each test of interest, varying the sample size until the test rejected approximately 80% of the time. After recording the sample size with 80% power for each test, we then calculated relative efficiencies by taking the ratios of these sample sizes. We compared these simulated relative efficiencies to the relevant AREs developed in ‘ARE of the Trend Test’ above.

We performed these simulations for a wide range of scenarios (see online suppl. table 1), using both unstratified and stratified tests. We varied the true relationship between genotype and disease frequency to reflect additive, multiplicative, logistic, dominant, recessive, and heterozygous models with varying effect sizes. For case-control data, we used a sampling ratio π of 100, meaning that cases were 100 times more likely to be sampled than controls. We varied the disease frequency to reflect the cases considered in ‘ARE Examples.’ We also considered a range of high-risk allele frequencies. As for stratified analyses in ‘ARE Examples’, we considered both cases where only the disease frequency varied across strata and cases where both the disease frequency and the high-risk allele frequency varied across strata, with the latter reflecting scenarios with confounding. For each of these scenarios, we calculated efficiencies for each test relative to the test that reflected the true model. For example, when the truth was additive, we calculated efficiencies for each of multiplicative, logistic, dominant, recessive, and heterozygous tests relative to an additive test.

Relative Efficiency Results

Depending on the scenario under investigation, achieving 80% power required anywhere from thousands of subjects to millions of subjects. All else being equal, the smaller the true effect, the greater the sample size that was needed to detect it at 80% power. Because greater sample sizes are closer to the infinite sample size required for the validity of the ARE, the simulated relative efficiencies for smaller effect sizes reflect more closely the calculated AREs.

In unstratified scenarios, the finite sample relative efficiencies are shown only for cohort data because they also apply to case-control data. The unstratified relative efficiencies closely reflect the calculated AREs regardless of sample size and type of genetic study (see online suppl. tables 2, 6).

However, some differences between simulated relative efficiencies and calculated AREs appear in the stratified analyses, especially with the smaller sample sizes typical of candidate gene studies (online suppl. tables 3, 4, 5, 6). That said, the rank order of simulated relative efficiencies using various test statistics in a given scenario generally reflect the rank order of the calculated AREs. Online supplementary tables 7 and 8 give sample results for larger GWA studies using cohort data. Online supplementary table 9 gives results for larger GWA studies using case-control data, assuming the assumed model holds in the population.

Discussion

The relative efficiency of trend tests using different assumptions to evaluate associations between potential high-risk alleles and binary outcomes depends on whether design and/or analysis are stratified, the true underlying genetic model, the population-level high-risk allele frequency, and the population-level disease frequency. Additionally, in case-control data, relative efficiency depends on the proportion of the sample who are cases. Because several of these factors are not necessarily known, choosing the optimal test to use in a given scenario is not straightforward. However, by employing estimates of these factors based on previous data, concerns regarding loss of efficiency for a given trend test can be evaluated via the ARE formulae that we have developed.

Loss of efficiency can be substantial, given specific combinations of high-risk allele frequencies, disease frequencies, and assumed versus actual genetic models. Thus if there is prior evidence indicating that the underlying genetic model is something other than additive, then there is motivation to conduct trend tests assuming a non-additive model in order to avoid potentially large losses in power. Other approaches are also possible. Extending the maximin efficiency robust testing (MERT) procedure of Gastwirth for trend tests [11] to the stratified setting might yield a test that is more robust to the choice of plausible alternatives for the genetic model. Similarly, extending the max test [5, 12] to stratified data might yield procedures with near-optimal power under plausible models. In addition, it would be interesting to see if an extension of the inequality constrained penetrance test (ICPT) of Song and Nicolae [13] to stratified data would enjoy good power under all plausible monotone genetic models.

When case-control data are collected, and a stratified trend test is used, but the underlying model for the trend test applies at the population level rather than in the case-control sample, the statistic corresponding to the true population model (i.e. the one with H equal to L instead of J_π) is not necessarily the most efficient one. The tables of simulated data in online supplementary Section B show that the logistic and sometimes the dominant statistics are more efficient than the additive one for an additive population model, and the logistic statistic can be more efficient than the true statistic in any true population model except the heterozygous one. Therefore with case-control data, consideration should be given to using the logistic stratified statistic.

In general, when the true model is unknown, the choice of statistic influences power most when the high-risk allele frequency is near 0 or 1. This is consistent with previous findings [3], and supports the recommendation to use tests not based on the additive model when allele frequency is very high or very low. Alternate tests should also be considered when allele frequency is moderate and it is biologically plausible that the heterozygote has the highest risk.

The relative efficiencies that we have derived are only guaranteed to apply asymptotically. However, we have found that our ARE calculations generally reflect comparable relative efficiencies to those found in finite sample simulations. There is more divergence from the asymptotic results with the smaller sample sizes that are typically used for candidate gene studies, but the ARE approximations remain reasonable in most scenarios and the relative rankings of test power they give apply even more often.

Useful extensions of the concepts in this paper would include discussion of relative efficiency for continuously adjusted tests, as opposed to stratified tests, as well as extensions of alternative testing procedures such as the MERT test [11], the max test [12], or the ICPT [13] to stratified data.

Supplementary Material

Supplementary materials

supplementary table 1