PSEUDOMARKER: A Powerful Program for Joint Linkage and/or Linkage Disequilibrium Analysis on Mixtures of Singletons and Related Individuals

Abstract

A decade ago, there was widespread enthusiasm for the prospects of genome-wide association studies to identify common variants related to common chronic diseases using samples of unrelated individuals from populations. Although technological advancements allow us to query more than a million SNPs across the genome at low cost, a disappointingly small fraction of the genetic portion of common disease etiology has been uncovered. This has led to the hypothesis that less frequent variants might be involved, stimulating a renaissance of the traditional approach of seeking genes using multiplex families from less diverse populations. However, by using the modern genotyping and sequencing technology, we can now look not just at linkage, but jointly at linkage and linkage disequilibrium (LD) in such samples. Software methods that can look simultaneously at linkage and LD in a powerful and robust manner have been lacking. Most algorithms cannot jointly analyze datasets involving families of varying structures in a statistically or computationally efficient manner. We have implemented previously proposed statistical algorithms in a user-friendly software package, PSEUDOMARKER. This paper is an announcement of this software package. We describe the motivation behind the approach, the statistical methods, and software, and we briefly demonstrate PSEUDOMARKER's advantages over other packages by example.

Introduction

There has been an ongoing debate among gene mappers about the most efficient study design for identifying genetic variants that influence phenotypic variation related to complex traits in humans. The debate has been between those who favor the traditional approach of collecting large families from less genetically diverse populations, and those who suggest that although large families are more powerful on a per individual basis [1], it is easier to collect much larger datasets of unrelated individuals that share some trait [2], with the relative loss of power being compensated for by much larger potential sample sizes. The first substantial efforts to study the genetics of complex disease in the late 1980s took an intermediate approach of collecting nuclear families with at least two affected siblings, and using allele-sharing statistics to detect linkage, following similar arguments about power loss being compensated for by increased sample sizes. The shift from sibships to a case-control design started in the late 1990s, stimulated by the influential commentary of Risch and Merikangas [3]. As time went on, investigators ended up collecting data from a variety of relationship structures, sampling whatever was most easily available. However, statistical geneticists had often designed algorithms and software based on homogeneous relationship structures (case-control, trios, sib-pairs, etc.) because that allowed them to perform ‘model-free’ analyses with manageable degrees of freedom [4,5]. As a consequence, even leading biologists seeking to find genes often ended up analyzing only homogeneous subsets of their data (e.g. [6]), or letting the available analysis methods inform their study design a priori.

Realizing there was a problem, some statistical geneticists began trying to extend methods designed for simple, homogeneous relationship structures so that they could analyze data from more complex relationship structures, in order to make this square peg fit more easily into a round hole. Such methods include those implemented in the software packages FBAT [7,8], QTDT [9,10], TRANSMIT [11], UNPHASED [12], and PedGenie [13]. These approaches, however, were not designed to maximize the use of all the information from larger pedigrees. Power and statistical behavior proved suboptimal, as was the case when similar approaches were taken in ‘model-free’ linkage analysis to extend sib-pair analysis to larger sibships [4]. Other investigators began to address the ascertainment/analysis conundrum from the opposite direction, starting from general likelihood models for large pedigrees, parameterizing linkage disequilibrium (LD) in terms of haplotype frequencies between families, and linkage in terms of the recombination fraction within families, in a model-based manner. Such methods were used already early on in segregation analysis packages, such as PAP [14] (applied for example in [15]), and linkage analysis software, such as LINKAGE [16] (applied for example in [17,18]). Later programs that implemented similar likelihood-based linkage and LD pedigree analyses include LAMP [19,20] and MENDEL [21]. However, each of these has certain properties that can lead to inefficient statistical behavior and unnecessarily low power, as illustrated below. None of the most commonly used family-based association methods are fully satisfactory when it comes to: (1) using full information of multiplex pedigrees; (2) allowing for missing data; (3) combining singletons, sib-pairs, larger nuclear pedigrees and multiplex pedigrees in one analysis, and/or (4) the null hypothesis actually being tested (table 1).

Table 1.

Programs and test types

Program [reference]	Test type
	linkage	LD given linkage	linkage given LD	joint test of linkage andLD
FBAT [7, 8]		X	X
TRANSMIT [11]		X	X
GENEHUNTER TDT [52]			X
PLINK [53]			X
QTDT [9,10]		X	X
UNPHASED [12]		X	X
HHRR [29]		X
MENDEL [21]	X	X	X	X
LAMP [19,20]	X	X
PSEUDOMARKER	X	X	X	X

We have earlier proposed an algorithm based on combining aspects of both ‘model-based’ likelihood methods and ‘model-free’ methods that was shown to have better statistical properties in general, based on the use of ‘pseudomarkers’ [4]. Such methods were shown to lead to statistics with properties that were: (1) identical to the affected sib-pair linkage analysis mean test (ASP) on sib-pair structures; (2) identical to case-control association analysis (CC) when applied to singletons; (3) identical to TDT and HHRR statistics when applied to trios consisting of affected individuals and their parents, and (4) extensible to general pedigrees and heterogeneous relationship structures in a manner that left the type I error rates unaffected and allowed for joint analysis of all relationship structures in a single analysis using methods analogous to the likelihood methods described for parametric linkage analysis below. Despite our demonstration of relatively high power and robustness [4], the methods have not been widely used outside our group and our collaborators for several reasons: (1) these methods can be computationally intensive; (2) there was no user-friendly software, and (3) the proofs of the statistical equivalence of these test procedures relied on complex-valued recombination fractions [22,23], discouraging some potential users.

To address this problem of analyzing heterogeneous relationship structures (table 2), we have polished our set of programs, made them more user friendly, and incorporated an intelligent interface for two-stage SNP chip analysis that first looks for marginal evidence of linkage and/or association before choosing a subset of markers for the computationally intensive joint analyses. We also present some simulated data comparing the statistical properties of PSEUDOMARKER to the existing programs using relationship structures for which we have ongoing studies testing linkage and LD jointly, to make the case for the wider application of our approach to joint linkage and association analysis using PSEUDOMARKER.

Table 2.

Programs and relationship structures

Program [reference]	Relationship structure
	singletons	trios	sib-pairs	larger nuclear families	extended families
FBAT [7, 8]		X	X		decomposed into nuclear families and treated as independent
TRANSMIT [11]		X	X		decomposed into nuclear families and treated as independent
GENEHUNTER TDT [52]		X
PLINK [53]	X	X	X
QTDT [9,10]		X	X
UNPHASED [12]	X	X	X		decomposed into nuclear families and treated as independent
HHRR [29]	X	X
MENDEL [21]	X	X	X	X	X
LAMP [19, 20]	X	X	X	X	small pedigrees only∗
PSEUDOMARKER	X	X	X	X	X

^∗LAMP uses the Lander-Green-algorithm and it can only analyze small extended families in feasible time.

Materials and Methods

PSEUDOMARKER Analysis Method

Linkage Analysis

There is an equivalence between the affected sib-pair mean test [24,25,26] and traditional parametric lod score analysis on a sib-pair under a rare recessive parametric model with no phenocopies. In other words, the equivalence holds assuming that P(Affected ∣ D+) = P(Affected ∣ ++) = 0; and P(Affected ∣ DD) = ∊ > 0, and P(D) = ν > 0, where ∊ and ν are both very small. In practice, we typically set ∊ and ν to 0.00001, for reasons described in [4] (hereafter, this model is referred to as the ‘pseudomarker model’). Performing the linkage analysis using this likelihood-based parametric approach allows one to analyze all meioses jointly in larger nuclear pedigrees without the need to break them into multiple ‘quasi-independent’ sib-pairs. We further showed that, under all models we considered, the power was superior to such ‘pairs-based’ approaches and the type I error rates were better predicted by asymptotic theory (‘pairs-based’ approaches lead to inflated type I error rates and loss of power) [4]. In the PSEUDOMARKER program, we also treat the allele frequencies of the marker locus as a nuisance parameter for reasons described in Göring and Terwilliger [[4] and [27]], estimating them separately under the null hypothesis of no linkage (and no association) L(θ = 0.5, δ = 0), and the alternative of linkage (and no association) L(θ, δ = 0) (table 3).

Table 3.

Likelihoods

Hypothesis	Linkage	Linkage disequilibrium	Likelihood	What is estimated from the data
H0	no	no	L(θ = 0.5,δ=0)	Marker allele frequencies
H1	yes	no	maxL(θ, δ=0) θ	Marker allele frequencies and recombination fraction
H2	no	yes	max L(θ=O.5, δ) δ	Conditional marker allele frequencies (on disease)
H3	yes	yes	maxL(θ, δ) θ δ	Conditional marker allele frequencies (on disease) and recombination fraction

Linkage Disequilibrium (Case-Control Data)

We further demonstrated that there is an equivalence between testing for allele frequency differences between randomly sampled cases and controls from the population and an analysis of LD under the same parametric model described above [4]. Under that parametric model, all affected individuals would be inferred to have genotype DD at the trait locus, and all unaffected individuals would be inferred to have genotype ++ at the trait locus (because of the very small allele frequency assumed for the disease allele), so that contrasting allele frequencies in cases and controls would be equivalent to contrasting conditional allele frequencies on haplotypes with + or D alleles inferred. In PSEUDOMARKER, we parameterize LD in terms of marker allele frequencies conditional on the trait locus allele found on the same haplotype. The conditioning in this direction is critical because marker allele frequencies in the population are unconstrained nuisance parameters, while in model-based analysis, the disease allele frequencies are highly constrained. Thus, we are testing whether P(1 ∣ D) = P(1 ∣ +), and so on for the other marker locus alleles for markers with >2 alleles. The null hypothesis likelihood is then estimated by maximizing the likelihood of the entire dataset of the allele frequency L(θ, δ = 0), and the alternative hypothesis likelihood would be estimated by maximizing the likelihood over allele frequencies conditional on the trait allele on the same haplotype L(θ, δ). For singleton data, the θ term is included only to show the symmetry across relationship structures – though it is essential to be aware that the likelihood is not a function of θ in that case.

LD Analysis Conditional on Linkage (Trios – HHRR)

Under the same penetrance model, in a trio consisting of an affected child and two unaffected parents, the child would be inferred to be DD as in sib-pair analysis or case-control analysis above. The parents under this model would both be inferred to be D+. If we assume that there is complete linkage between marker and disease loci, then the transmitted alleles would be on the chromosomes in the parents containing the D alleles, and the non-transmitted alleles would be inferred to be on the chromosomes containing the + alleles. Thus, contrasting transmitted and non-transmitted alleles (as in the HHRR statistic [28,29]) is equivalent to the estimation of conditional allele frequencies conditional on the trait locus alleles under this extreme parametric model. Comparing the null hypothesis likelihood under which both linkage and the marker allele frequencies assuming no LD are estimated, L(θ = 0, δ = 0), with the alternative hypothesis likelihood under which both linkage and conditional allele frequencies are estimated, L(θ = 0, δ) provides a test equivalent mathematically to the HHRR for reasons described in Göring and Terwilliger [4]. Note that under the null hypothesis, if one has only trios (and singletons), the likelihood is not a function of θ.

Linkage Conditional on LD (Trios – TDT)

While not formally something one would often be interested in testing (why test for linkage once a genetic association has been established?), this is the null hypothesis of the transmission/disequilibrium test when applied to multiple individuals from a single pedigree as proposed by Spielman et al. [30]. As we previously pointed out [4], this same symmetry applies also to the TDT test if one has a sample of trios and computes the likelihood under the identical model maximized over conditional allele frequencies in both null and alternative hypotheses, but with no linkage under the null hypothesis as L(θ = 0.5, δ) and with linkage under the alternative as L(θ, δ). By computing such a test using a full likelihood model, one can analyze large pedigrees without confounding linkage and LD. For example, one can obtain statistically significant TDT results from the analysis of large multiplex pedigrees even when there is no association because the TDT is formally a test of linkage. Analyzing data in the PSEUDOMARKER framework allows one to see this formally and explicitly.

Joint Analysis of Heterogeneous Relationship Structures

In our exposition above, each pedigree structure was analyzed under the same model to compute test statistics equivalent to the commonly used ‘model-free’ statistics. We can combine all the pedigree structures together and do the same analyses using all the data jointly, to provide an easy way to analyze heterogeneous relationship structures together. Under the null hypothesis of no linkage and no association, L₀ = L(θ = 0.5, δ = 0), the likelihood is maximized solely over allele frequencies of the marker, assuming it is independent of the trait. Under the simplest alternative, of linkage and no association, the marker allele frequencies are estimated from all the data jointly, and only in families with multiple affected individuals does the recombination fraction parameter influence the likelihood, L₁ = L(θ, δ = 0). One could also compute the likelihood, L₂ = L(θ = 0.5, δ), though testing for association without linkage is not a particularly meaningful hypothesis. The most general likelihood is that of linkage in families where there are multiple affected individuals (i.e., the correlation in marker genotypes due to linkage among individuals who share a common ancestor within the pedigree), and LD (i.e., the allele frequencies in the unrelated individuals from our families and singletons conditional on the trait locus allele found on the same haplotype), L₃ = L(θ, δ). Based on these three likelihoods, we can test for linkage by the statistic

$$\Lambda \hspace{0.17em}=\hspace{0.17em}\mathrm{2l}\text{n}\hspace{0.17em}\frac{L_1}{L_0},$$

we can test for LD in the presence of linkage with the statistic

$$\Psi \hspace{0.17em}=\hspace{0.17em}\mathrm{2l}\text{n}\hspace{0.17em}\frac{L_3}{L_1},$$

and we can test jointly for LD and/or linkage with the statistic

$$\Xi \hspace{0.17em}=\hspace{0.17em}\mathrm{2l}\text{n}\hspace{0.17em}\frac{L_3}{L_0},$$

where Ξ = Λ + Ψ. The statistical distributions and properties of these test statistics have been analyzed from a theoretical perspective in Göring and Terwilliger [4]. It is important to note that unless there are at least some multiplex pedigrees in the sample, conditional testing of LD given linkage is not meaningful or appropriate because the null hypothesis likelihood would not be a function of the recombination fraction!

While use of this extreme parametric model may seem illogical to those used to working with parametric linkage analysis, we have demonstrated that, in general, this approach is more powerful than even linkage analysis under a ‘correct’ model [4,31], if one were to exist, so long as one allows for ‘complex-valued recombination fractions’ [23] in conceptually thinking about how to interpret the resulting recombination fraction parameters. PSEUDOMARKER also allows the user to perform these joint linkage and LD analyses under any user-specified model in addition to the ‘pseudomarker model’ we advocate as generally most powerful and robust.

PSEUDOMARKER Software

The likelihood method described above has been implemented in our PSEUDOMARKER program, which uses a specially modified version of the ILINK program derived from the FASTLINK 4.1P package [16,32,33,34,35] for likelihood calculation under various assumptions.

A key feature of the PSEUDOMARKER program is that it estimates marker allele frequencies, LD (i.e., marker allele frequencies conditional on disease-locus alleles), and recombination fractions jointly. PSEUDOMARKER uses the modified ILINK to model LD through ‘conditional allele frequencies’, meaning that rather than specifying haplotype frequencies as is conventionally implemented, this approach allows one to specify the marker allele frequencies conditional on the disease-locus alleles (as was done manually in a few studies such as [36]). For traversing the pedigrees, FASTLINK, like LINKAGE from which it was derived [16], uses a peeling method [37] that generalizes the Elston-Stewart algorithm [38]. Thus, the PSEUDOMARKER likelihood computation uses all family relationships correctly and could theoretically analyze any size pedigree, though one must constrain the number of loops, markers, and alleles per marker for computational efficiency.

The ILINK program finds the recombination fraction(s) that yield a local optimum for the likelihood function, while the more commonly used MLINK and LINKMAP programs compute the likelihood at a user-specified grid of points. ILINK can also optimize other parameters, including allele frequencies at either the trait locus or marker loci, and it is this feature that makes ILINK useful as a subroutine for PSEUDOMARKER. LINKAGE/ILINK uses the GEMINI optimization procedure [39] to compute the sequence of parameter values converging to a local optimum; GEMINI is retained in the standard version of FASTLINK/ILINK. The variant of ILINK in PSEUDOMARKER uses an implementation of ‘direct-search’ or ‘pattern search’ [40], which generally takes more iterations to converge than GEMINI but, in practice, is more likely to find a better local optimum, if not the global optimum (see below).

Any user-specified mode of inheritance model can be applied, while by default dominant and recessive models that mimic model-free analyses are applied (i.e., infinitesimal disease allele frequency and penetrance, with no phenocopies [4]). Additional cases and controls can be included in PSEUDOMARKER analysis by creating artificial trio pedigrees by setting singletons as parents of an imaginary child, which allows ILINK to treat them as unrelated founders – this is necessary as the FASTLINK 4.1P software package is not designed to analyze unrelated singletons.

PSEUDOMARKER Analysis Work Flow

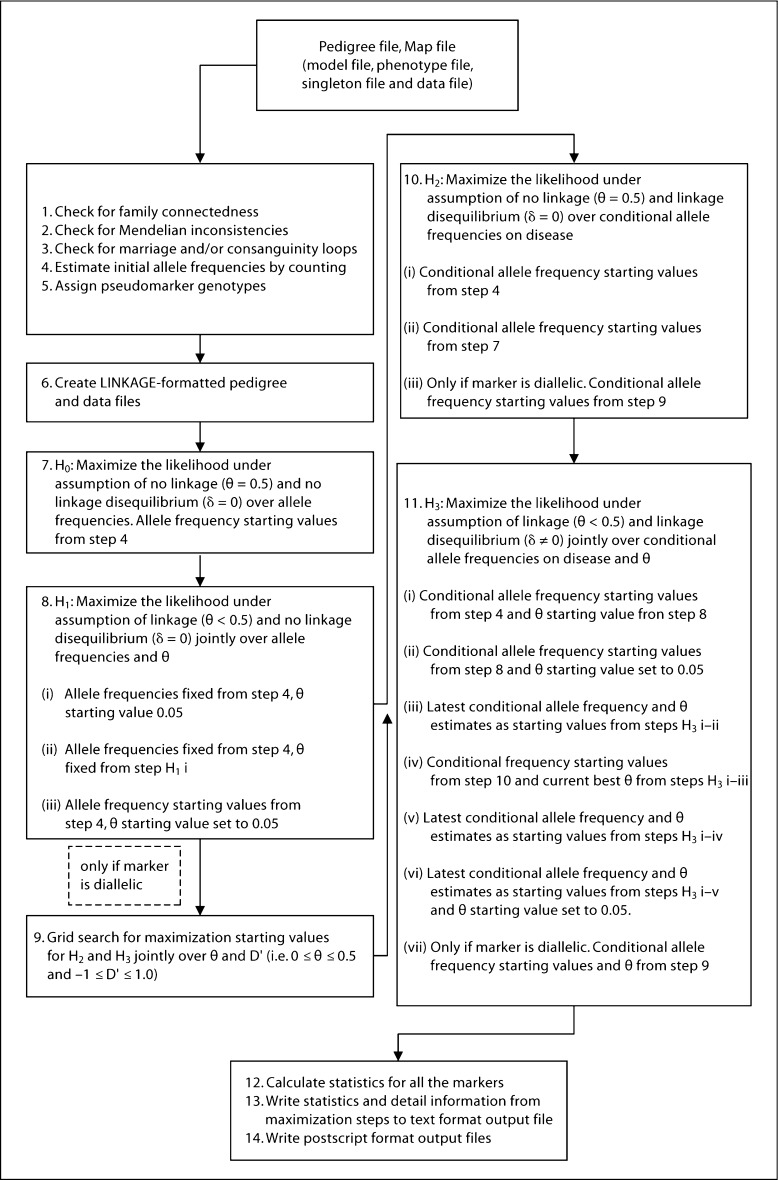
The PSEUDOMARKER program analysis work flow is described in figure 1, and the program requires standard input file formats: LINKAGE format ‘pedigree file’ [41] (defining the pedigree structure, affection status phenotype, if any, and marker locus genotypes) and MEGA2 [42] format ‘map file’ (chromosome number, marker positions in Haldane cM, and marker names). Additional optional input files include a model file (defining parametric disease locus models), a phenotype file (including additional phenotypes) and a singleton file (genotypes from cases and/or controls).

Fig. 1.

PSEUDOMARKER analysis work flow. Steps 6–11 are repeated for each marker locus.

After input files are read successfully, and dummy pedigrees are created from the singleton files, the next step is to check the integrity of the pedigree data. We have implemented the following algorithms: (a) check for family connectedness; (b) check for Mendelian inconsistencies and (c) processing of loops. Detection of loops in preprocessing is essential because ILINK requires breaking of the loops in the input pedigree file. Loop breaking could be done manually with the MAKEPED program [41], but it can be difficult in complex pedigrees, and this additional user intervention is unnecessary. If loops are detected, PSEUDOMARKER uses the UNKNOWN program (-l option) from the FASTLINK 4.1P package to automatically and optimally select loop breakers [43]. In some cases, this loop breaker selection can save considerable computation time.

If there are no errors in the pedigree data, the additionally required data columns are added to the pedigree file with the MAKEPED program, and allele frequencies are crudely estimated from the data for each marker by simple allele counting.

Modifications to the Optimization Procedure in FASTLINK's ILINK Program

The ILINK program used as a subroutine within PSEUDOMARKER has two major differences from the version distributed as part of FASTLINK 4.1P. The first difference is engineering support for conditional allele frequencies as a command line option. The second difference is the use of a more robust optimization procedure called ‘direct search’ to maximize the likelihood. This subsection concerns the direct search optimization procedure and how it differs from the default procedure GEMINI.

LINKAGE's ILINK has always used the GEMINI procedure. This procedure was originally coded in FORTRAN [39], then recoded in PASCAL for LINKAGE, and then translated to C automatically with p2c for FASTLINK. During the development of FASTLINK, a few bugs in the GEMINI implementation were fixed. GEMINI is a ‘quasi-Newton’ method that uses estimated gradient information to converge from a single starting point to a local optimum. The starting point is chosen by the user, typically via the LINKAGE auxiliary program LCP. Decades of experience have shown that GEMINI performs well when: (a) only recombination fractions, but not allele frequencies, are varied; (b) the LCP-default starting value of 0.1 is used for each recombination fraction, and (c) there is linkage, so that the globally optimal recombination fractions are far below 0.5. Under these conditions, there is often only a single local optimum, which GEMINI finds.

The problem of jointly estimating recombination fractions and allele frequencies is harder because of the higher dimensionality. When allele frequencies are estimated unconditional on disease status and the number of founders is large, then counting alleles in the founders can lead to a good initial estimate. However, problems can arise when there is a local, but not global, optimum that has one of the allele frequencies mistakenly close to 0. Once a GEMINI iterate sets this value too close to 0, it gets trapped for the rest of the search. Because the allele frequencies must sum to 1.0, GEMINI estimates m-1 frequencies at a marker with m alleles directly and estimates the frequency of the highest numbered allele indirectly using the sum constraint. This works especially poorly when the frequency of the highest numbered allele is close to 0 at a local optimum that differs substantially from the global optimum.

The optimization problems that ensue when using conditional allele frequencies are much harder for GEMINI because the number of frequency dimensions is doubled and it is hard to get good initial estimates. Therefore, we sought an alternative optimization method that is robust, easy to implement, and not as likely to get trapped at local optima. We chose to implement ‘direct search’ (sometimes called ‘pattern search’) as described by Dennis and Torczon [44]. Direct search methods were developed for situations in which the gradient was not available or too expensive to compute, which is appropriate for the ILINK setting in which the gradient can only be estimated.

The basic idea of direct search methods is to poll the objective function value at a set of points defined geometrically with respect to the current best point. Then, the new best point is chosen by moving to the vertex of the simplex that has the best function value. Dennis and Torczon showed that when the pattern of polled points forms a simplex around the current best point, then the iterates converge. In contrast to some previous, similar methods, the Dennis/Torczon method polls a point for each direction of the simplex in a single iteration, and this all-dimension polling is essential to proving that the method converges to a local optimum [40]. The dimension of the simplex equals the number of variables in the objective function (in our setting the variables are the recombination fractions and allele frequencies). Later research has suggested replacing the simplex with other geometric ‘patterns’ for the sampled points, leading to the alternative name ‘pattern search’. The simplex-based pattern search is encoded in ilink.c in the procedures direct_search, initialize_simplex, and evaluate_point. Using this information, experts in numerical optimization may substitute alternative direct search methods, without needing to understand the rest of the ILINK source code.

Experience with the problems in GEMINI and test cases for PSEUDOMARKER led us to add two heuristics to the direct search implementation in ILINK. First, we try a defined set of multiple starting points for the recombination fraction to reduce the risk of getting trapped in a local, not global optimum. Second, for the allele frequencies, we make the (dimension of) the initially largest allele frequency to be the one whose value is determined indirectly by the sum constraint. For conditional allele frequencies, the allele that has the highest allele frequency for + at the trait locus may differ from the allele that has the highest frequency for D.

Results

We examined the statistical properties of PSEUDOMARKER and compared its performance with that of all software packages mentioned above, using real-life mixtures of families and singletons. We chose two datasets taken from Finnish migraine [45,46] and schizophrenia [47] studies. The migraine dataset consisted of large multigenerational pedigrees, while the schizophrenia dataset was primarily nuclear pedigrees (see details in [48]). In addition, we simulated data for an entire population under complex oligogenic models using our phenogenetic evolutionary simulator, For Sim [49].

Type I Error Rate

Empirical type I error rates were compared to their theoretical predictions (i.e., they were compared to what the program claimed) for each of the programs and analysis options (except PedGenie [13], which requires a Java runtime library that was unavailable on our supercomputer). To examine properties of each test when there was neither linkage nor association, we simulated randomly segregating markers in each dataset, independent of the trait. Under these conditions, as seen in table 4, all the programs provided valid tests, with the exception of LAMP that gave a slightly elevated type I error rate when there was neither linkage nor association. Results are shown for p values of 0.05, based on 1,000 replicates. The picture remained the same at p value 0.01. Unfortunately, it was impossible to do enough replicates to evaluate more stringent p values because certain programs (LAMP in particular) are extremely computationally intensive and, thus, to analyze a sufficient number of replicates would have taken years.

Table 4.

Empirical estimates of the type-I error rate (a < 0.05) and power (a < 0.0001) using schizophrenia (1,000 replicates), migraine (1,000 replicates), and For Sim simulated data sets (500 replicates)

Program	Schizophrenia (recessive)			Migraine (dominant)			For Sim
	no linkage, no association (α ≤ 0.05)	complete linkage, no association (α ≤ 0.05)	complete linkage and association, RR = 5 (α ≤ 0.0001)	no linkage, no association (α ≤ 0.05)	complete linkage, no association (α ≤ 0.05)	complete linkage and association, RR = 1.8 (α ≤ 0.0001)	300 pedigrees (α ≤ 0.0001)
PSEUDOMARKER	0.06	0.04	1.00	0.05	0.05	0.98	0.99
FBAT	0.04	0.06	0.96	0.03	0.03	0.02	0.06
GENEHUNTER TDT	0.04	0.17	_∗	0.06	0.12	_∗	_∗
PLINK	0.05	0.17	_∗	0.05	0.13	_∗	_∗
MENDEL	0.00	0.01	0.54	0.03	0.03	0.91	0.85
HHRR	0.04	0.05	0.68	0.06	0.05	0.96	0.93
TRANSMIT	0.05	0.06	0.36	0.06	0.07	0.13	0.78
QTDT	0.06	0.05	0.25	0.04	0.04	0.01	0.05
LAMP	0.08	0.18	_∗	0.08	0.11	_∗	_∗
UNPHASED	0.04	0.06	0.25	0.06	0.07	0.35	0.01

Simulation parameters for no linkage and no association were P(D) = 0.00001 and P(l) = 0.1. For complete linkage and no association simulations, recessive (schizophrenia) and dominant (migraine) 'pseudomarker' models were used. In power simulations, with complete linkage and complete LD, disease prevalence for recessive schizophrenia was 1% and for dominant migraine 10%. In For Sim simulations, 5 genes on 5 different chromosomes were contributing to the disease phenotype in an additive manner. Each program's analysis option(s) selection was based on results from complete linkage and no association simulation, the option with the most accurate type I error rate (a < 0.05) from our simulations was used, or if the program allowed for a recessive or dominant analysis model. The statistics presented for the schizophrenia data are as follows: PSEUDOMARKER: recessive LD given Linkage; FBAT: recessive and robust variance estimator; PLINK: sib-TDT; MENDEL: recessive 'pseudomarker' model and association given linkage; HHRR: allele-based randomized; TRANSMIT: one affected per nuclear family; LAMP: recessive; GENEHUNTER TDT, QTDT and UNPHASED: no additional options. The statistics presented for the migraine data are as follows: PSEUDO-MARKER: dominant LD given linkage; FBAT: dominant and robust variance estimator; PLINK: sib-TDT; MENDEL: dominant 'pseudomarker' model association given linkage; HHRR: allele-based randomized; TRANSMIT: one nuclear family and robust estimator; LAMP: dominant; GENEHUNTER TDT, QTDT and UNPHASED: no additional options. For Sim data were analyzed with the same models and options as for the schizophrenia data.

^∗Power of GENEHUNTER TDT, PLINK, and LAMP is not reported because of excessive type-I error rates in complete linkage and no association analysis, though despite this, power remained lower than for the statistically valid tests in PSEUDO-MARKER (data not shown).

Since most of these programs purport to also be able to test for LD conditional on linkage, we also did a simulation in the same pedigree structures of a marker that was completely linked to the trait locus but which had no allelic association under the assumption of autosomal recessive and dominant traits with no phenocopies to examine the validity of these various statistics in the presence of linkage. These empirical null distributions were estimated from 1,000 replicates of the migraine (dominant) and schizophrenia (recessive) pedigree sets under each model. Replicates were simulated with the (Fast)SLINK program [50,51], which was especially modified for this simulation study to use a more sophisticated random number generator to allow for a more diverse collection of unique replicates. The empirical type I error rates were again estimated for the theoretical 0.05 significance level, with results shown in table 4. As shown, GENEHUNTER TDT, PLINK (Sib-TDT option), and LAMP had excessively elevated type I error rates, though GENEHUNTER TDT does not purport to control for linkage, so that is not surprising.

Power

The power was estimated for each combination of program and analysis options under the assumption of complete linkage between marker and trait locus, with LD and fixed-genotype relative risk. In each simulation, the disease allele frequency (diallelic disease locus) and the minor allele frequency at the diallelic marker locus were both 0.1 (i.e., p₁ = p_D = 0.1). Note that the power is estimated for a p value of 0.0001 in contrast to the type I error rates estimated above, though the same pattern applies over the entire range.

We first simulated data in the schizophrenia family set (mostly nuclear families) under a recessive model, assuming a prevalence of 0.01 in the population, complete linkage (θ = 0), complete LD (D’ = 1), and a recessive risk allele with frequency of 0.1 in the population conferring a relative risk of disease of 5 (for demonstration that the same pattern holds across models, see [48]). In this simulation, we compared the power of each method to detect a genotyped functional variant. As can be seen in table 4, PSEUDOMARKER was the most powerful approach, followed by FBAT, HHRR, and MENDEL. Interestingly, HHRR did quite well in the schizophrenia dataset, even though it only analyzes one randomly selected offspring per pedigree and therefore had significantly less power than PSEUDOMARKER.

Next, we examined the effects of the strength of LD on the relative power of each test, this time using the migraine families (largely multi-generational pedigrees with intergenerational transmission), assuming a prevalence of 0.1, completely linked disease and marker loci each with a minor allele frequency of 0.1, and a dominant risk allele conferring a relative risk of 1.8, and complete LD. In table 4, the results of this analysis are shown. PSEUDOMARKER again was the most powerful approach, followed by HHRR and MENDEL. Because LAMP was anticonservative throughout, we omitted that program from the power analyses presented, though the ‘reported’ p values from LAMP performed similarly with MENDEL and PSEUDOMARKER, although the ‘reported’ p values are anti-conservative. Note that the migraine families are multigenerational, and the software packages that break complex pedigrees into ‘quasi-independent’ nuclear families for analysis perform poorly on this dataset compared with schizophrenia families that are predominately nuclear.

Lastly, we used a For Sim [49] simulated population which contained full sequence data simulated over evolutionary time on a total of 10,000 pedigrees. From this pool of pedigrees, we randomly sampled w/o replacement 300 three-generation pedigrees with at least two affected individuals and additional controls with a SNP linked to and associated with the trait. Results were similar with those from the migraine dataset, except that the power of UNPHASED was reduced and that of TRANSMIT was higher. A more detailed analysis comparing power and type I error rates among the several programs is in progress [48].

Conclusions

We announce the availability of the software package PSEUDOMARKER for linkage and LD analysis of heterogeneous relationship structures. We and some collaborators have been using parts of PSEUDOMARKER for many years; now, the software engineering is robust enough for widespread usage. However, PSEUDOMARKER is a computationally intensive program, which maximizes the likelihood of large datasets over many parameters – allele frequencies, allele frequencies conditional on trait locus genotypes, recombination fractions and so on, and these likelihood surfaces are highly complex. For this reason, it would be computationally prohibitive to use this method as a first-pass analysis of one's genome-wide SNP data. In practice, we typically perform a standard linkage analysis and assess preliminary evidence for LD conditional on linkage using the HHRR program, which was shown in these simulations to have high power, even compared to methods purporting to test LD conditional on linkage using all the available data, to our surprise, as it samples one affected per pedigree only. As a rule of thumb, we would then follow up our most interesting findings with either linkage or association, or preferentially both linkage and association, with a full and robust analysis with PSEUDOMARKER. We tend to focus as well on the statistic that tests for LD conditional on linkage (meaning that linkage is treated as a nuisance parameter), so that we are sure that what we are detecting is due to allelic association and not merely due to linkage which extends over a much larger genomic region, so long as there are some multiplex families in the dataset from which to glean linkage information. Note that PSEUDOMARKER does not deal with population stratification, but assumes the user has cleaned the data and tested for such problems a priori. The main application of this method is to studies within a given population where the user has sampled pedigrees with care.

PSEUDOMARKER provides a powerful way to analyze linkage and LD jointly on a mixture of family and singleton samples, using the pedigree relationships as they actually exist without the need for approximations to correct for linkage based on rather contrived assumptions about the effects of linkage on the statistics. We have shown that it has higher power than other existing methods in standard usage, while retaining validity over a wide range of pathological assumptions regarding linkage and etiology.

Electronic-Database Information

PSEUDOMARKER software http://www.helsinki.fi/∼tsjun tun/pseudomarker/index.html.