Topologically correct reconstruction of tortuous contour forests

Abstract

Motivated by the need for correct and robust 3D models of neuronal processes, we present a method for reconstruction of spatially realistic and topologically correct models from planar cross sections of multiple objects. Previous work in 3D reconstruction from serial contours has focused on reconstructing one object at a time, potentially producing inter-object intersections between slices. We have developed a robust algorithm that removes these intersections using a geometric approach. Our method not only removes intersections but can guarantee a given minimum separation distance between objects. This paper describes the algorithm for geometric adjustment, proves correctness, and presents several results of our high-fidelity modeling.

1. Introduction

Much work on 3D reconstruction from planar cross-sectional data has been done in recent years to the benefit of many applications. These methods generate a 3D model of an object from given contours, and many of them are extremely efficient and accurate. These single-component reconstruction methods are not sufficient, however, when faced with reconstructing models involving multiple components. This type of reconstruction is necessary in many different fields, including neuronal modeling, surgical planning, and composite materials simulation. The problem is that reconstructing components one by one can yield intersections between components after compositing them into the same model, regardless of the guarantees made by the algorithm. The intersections occur frequently in data that is highly tortuous and densely packed, and is exacerbated further by highly anisotropic data, where the spacing of slices is large compared to the geometric behavior of the objects. The methods presented in this paper aim to fill the gap in generating topologically correct multi-component models while maintaining the accuracy of existing single-component methods.

Our ultimate goal is to better understand the brain through accurate modeling and simulation of neuronal processes (e.g. axons, dendrites, glial cells). Previously this modeling has been done using the simplified cases of treating the dendritic arbor as a series of cylinders. However, serial section transmission electron microscopy (ssTEM) reveals highly complex geometries among neuronal processes, including high tortuosity, varying caliber, spiny protrusions and extremely tight packing. Our work of simulating neuronal electrophysiological function at high resolution requires very accurate and topologically correct 3D reconstructions of neuronal processes. These reconstructions can be used in a variety of modeling experiments using high-fidelity versions of the traditional cable model approach [13] or, more recently, an approach based on meshless Weighted Extended B-spline-based finite element methods [11].

The source data for generating these neuronal reconstructions is generally ssTEM imagery. Neuronal contours are generated from these images by neurobiology experts who trace out the contours using a variety of tools [30]. Pixel spacing in the xy plane of neuronal ssTEM images is roughly 2–5 nm, while spacing between slices is closer to 45 nm. Extracellular spacing (spacing between neuronal processes) is on the order tens of nanometers [31, 23]. This close spacing, combined with the comparatively large distance between slices can cause inter-object intersections between slices when using single-component reconstruction techniques. This topological incorrectness prohibits any type of multi-component analysis based on finite element methods.

We have developed an intersection removal method that acts in concert with any surface reconstruction method, provided it conforms to several criteria. Our approach is to remove intersections by moving triangle vertices and induced points along the axis orthogonal to the slice plane. This approach can remove intersections efficiently and without causing additional intersections. Using an approach that moves vertices in the slice plane is possibly more intuitive, but yields considerably greater computational complexity [3].

We have also developed improvements to the single-component reconstruction approach, including dealing with several cases of numerical degeneracies and triangle shape improvement in some cases.

We first give a brief outline of work that has been done both in single component and multi-component surface reconstruction from cross-sectional contour data (Section 2). We then build up a set of rules and theorems to prove correctness and robustness of our algorithm (Section 3), followed by a discussion of the single-component reconstruction improvements and intersection removal algorithm (Section 4). We then present results of our implementation (Section 5) followed by conclusions and future work (Section 6).

2. Related work

A large amount of work has been done to solve the single-component reconstruction problem. Fuchs et al. [17] presented the problem and proposed a solution based on triangulations guided by a toroidal graph. Barequet and Sharir [6] introduced a method using linear interpolations between slices of medical images. Bajaj et al. [2] expanded on their work by using medial axes to tile regions with no legal slice-to-slice tiling. Oliva et al. [27] specifically targeted difficult objects (objects with multiple branches, holes, and other irregularities) and used Voronoi diagrams to construct topologically correct surfaces.

Somewhat more recent works interpolate contours using 2D skeletons in valid tile regions [5], Delaunay triangulation [33] and contour morphing [26]. Most works use some type of linear interpolation and thus require a smoothing post-processing step. One approach that performs non-linear smoothing during tiling is found in [7]. Other recent approaches reconstruct surfaces from non-parallel contours [25, 10, 8, 9]. The approach in [32] is notable because is uses implicit methods based on radial basis functions and naturally handles multiple components. This is elegant, but implicit approaches can be troublesome when it comes to generating a geometric surface, as determining at what resolution to discretize the level-set isn’t always straightforward. In addition, small components can be overwhelmed mid-slice by larger components and thus capped off at the slices rather than carried through the unknown inter-slice region. [25] uses a geometric approach but requires expensive calculation of both the arrangment of slices and the medial axis.

A different class of approaches that work directly from image data rather than contours exist, such as energy-minimizing 3D snakes [22] and a 3D extension to path cost-minimizing LiveWire [16]. These approaches require a level of user interactivity, however, and often don’t scale well to massive datasets with large numbers of components.

Surprisingly little work has dealt with the issue of intersections between multiple components. Bajaj and Gillette [3] produced a method for removing intersections by removing contour overlaps in intermediate planes. This algorithm uses an inflated medial axis surface to separate mid-slice contours, but there is no guaranteed bound on the number of mid-slice contours to be separated. In addition, branching of components (where a single contour in one slice correlates to multiple contours in an adjacent slice) is treated in a pre-processing step, where branch points are moved as needed to enable intersection removal. Our algorithm has provably finite computational bounds and it also handles branching of components without treating them as a special case.

Of course, there are algorithms that use erosion morphological operators together with general boolean set operations on surfaces to solve the intersection problem [19]. These approaches, however, are more computationally expensive and don’t preserve constraints imposed on the original initial single component reconstruction.

3. Rules

Our intersection removal algorithm is correct and robust and, in addition, it has bounded computational complexity and requires neither parameter optimization nor iterative mesh refinement. The only modifications made to the original surface are the addition of induced points and moving of points parallel to the axis orthogonal to the image plane, which we call the z axis. Restricting movement of offending points to the z axis we can provably remove intersections without causing additional intersections among other components. Allowing points to be moved in the x–y plane may yield better surfaces, but complicates intersection removal significantly. We discuss this in section 6. Our method can also guarantee a minimum separation distance of δ. This is an important guarantee for applications that are sensitive to inter-component spacings.

Preconditions

We state here criteria on which our method relies, as well as various theorems which prove correctness and completeness. We define the xy plane to be the plane of the original images (and slice contours), and the z axis to be perpendicular to the xy plane. For simplicity, we assume that each component has a unique color and each element belonging to that component (e.g. contour, boundary) inherits the same color. So if two contours have different colors, they belong to different components.

Criterion 1. The reconstructed surfaces are piecewise closed polyhedra.

Criterion 2. Any vertical (parallel to the z axis) line segment between two adjacent slices either intersects a single component exactly once or not at all. Any intersection occurs either at a point or along a line segment.

Criterion 3. Slicing the reconstructed surface on any of the original slices produces exactly the input contours.

Criterion 4. All contours on the same slice have a minimum separation distance of δ.

Criterion 5. A contour cannot be nested inside a different colored contour. (This applies only to intersection removal. See discussion below.)

Criteria 1–3 are borrowed from [2] and are required to ensure high quality and topologically correct surfaces. Criterion 1 ensures that each component surface given to our algorithm are topologically correct and water-tight. Note that this does not guarantee that intersections between components won’t exist. Criterion 2 also applies only to single components and helps to avoid topologies that are unlikely. Without it, a host of additional correspondences are possible, most of which are incorrect. In order to avoid additional complexity and a large number of false positive correspondences, this criterion is carried through into our work. It assumes, however, that the slice spacing is close enough to enable reasonable reconstructions even with the criterion in place. Criterion 3 ensures that interpolation is bounded by only that required to generate a likely topology and avoids adding information to the original contours.

We enforce criterion 4 by adding a pre-processing step to our algorithm – that of separating contours by δ. Of course, if the application prohibits this then either δ can be decreased or application-specific contour separation methods can be used.

Criterion 5 is currently required as intersection removal between nested contours of different colors is not currently supported. In other words, components are treated as solids without any nested components. While this is a requirement of our current algorithm, we expect this criterion to be removed in future versions. See section 6. Note that this does not preclude nested contours of the same color, which can occur when there are concavities in the surface.

Properties

Armed with these five preconditions we show that our algorithm has certain desirable properties that we mentioned earlier in the section and restate here for emphasis.

1. No more than two components can intersect in the same region (see lemma 5), so intersections can be resolved between components pair by pair.

2. Removing intersections in one region will not cause intersections in other regions (see theorem 2).

3. Pulling intersecting components apart at a finite number of appropriately chosen vertices will resolve all intersecting regions (see theorem 3).

We now argue these properties formally. In the following discussion, it is assumed that the data we are dealing with lies on and between a pair of adjacent slices. We also deal with only two components at a time, C^g and C^y, the green and yellow components, respectively. Lemma 5 shows that working with only two components at a time is justified. Proofs of the following lemmas and theorems can be found in the appendix.

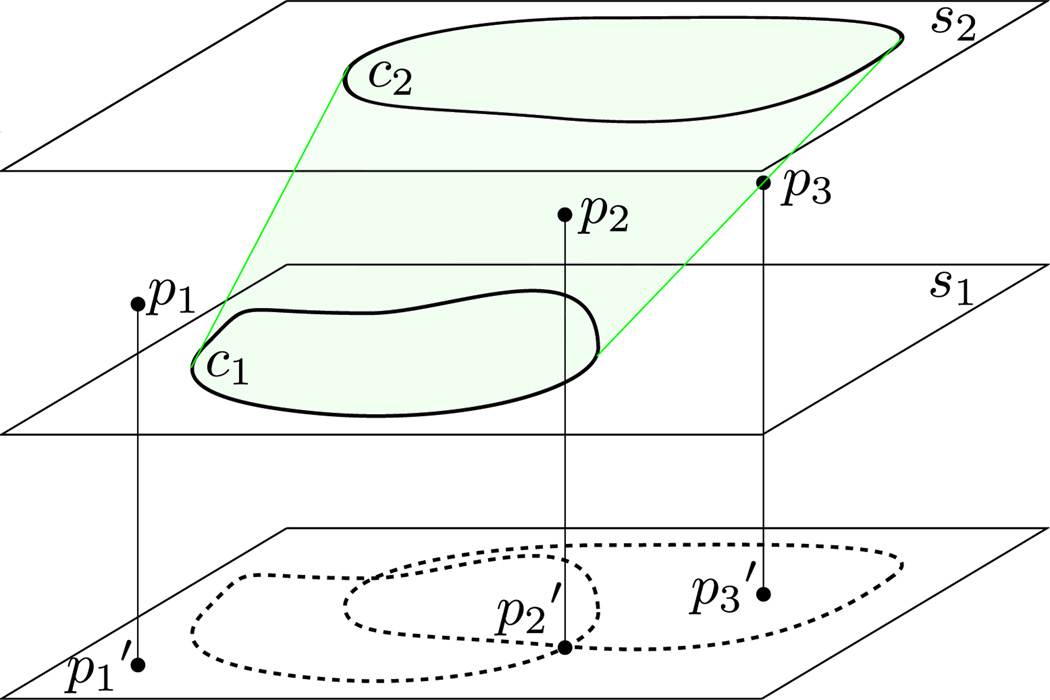
Definition 1. Suppose p′ is the projection of point p onto the xy plane. We say that contour c is a containing contour of p if p′ is inside or on the boundary of c′ (see figure 2). We define 𝒞(p) to be the set of all containing contours of point p and 𝒞^g(p) to be 𝒞(p) restricted to all green contours $\{c_i^g\},i.e.,{𝒞}^g(p)=𝒞(p)\mathrm{\cap }\{c_i^g\}$.

Figure 2.

s₁ and s₂ are two adjacent slices and the lower plane is an arbitrary xy plane showing containing contours of various points. p₂ and p₃ are on the green component, while p₁ cannot be according to lemma 1. 𝒞(p₁) = ∅, 𝒞(p₂) = {c₁, c₂}, 𝒞(p₃) = {c₂}.

Lemma 1. Suppose p^g is a point on the surface ∂C^g of component C^g. Then 1 ≤ |𝒞p^g)| ≤ 2.

This lemma states that any point on a surface must have at least one containing contour (of any color) but no more than two. In figure 2, p₁ has no containing contour and so cannot exist on the surface of the reconstructed component.

Lemma 2. If |𝒞(p^g)| = 2 then the two contours in 𝒞(p^g) lie on separate slices.

Definition 2. S^g is the set of all points p^g ∈ ∂C^g such that |𝒞 ^g(p^g)| = 2. These points lie “sandwiched” between two green contours. Similarly, U^g is the set of all points p^g ∈ ∂C^g such that |𝒞 ^g(p^g)| = 1. These points have no containing contour on one of the slices. For a point p^g ∈ U^g, we call its single containing green contour the penumbral contour 𝒫(p^g).

In figure 2, 𝒫(p₃) = c₂ and the penumbral contour for the other two points is undefined.

As it happens, points in S^g cannot lie on the inside of both contours, but must lie on the boundary of at least one, but this distinction is not necessary for our analysis here.

Definition 3. Suppose p^g ∈ U^g. Then 𝒵(p^g) is the z coordinate value for 𝒫(p^g). We call this the z-home value for p^g. 𝒵(q^g) is undefined for all q^g ∉ U^g.

Definition 4. Consider a sphere of radius δ centered at a point p. Consider also the cylinder of radius δ about the vertical line segment from p to p′ where p′ is the projection of p onto the slice at 𝒵 (p). The union of the open sphere and open cylinder is called the buffer region ℬ(p) of p.

Definition 5. Point p^g ∈ U^g is called a conflict point if there is some point p^y ∈ U^y such that p^y ∈ ℬ(p^g).

Conflict points are points at which two components are closer than δ or at which some point p^y is inside or on the surface of two components.

Lemma 3. No point p^g ∈ S^g can be a conflict point.

Lemma 4. Let p^g ∈ ∂C^g be a conflict point. Then there is no other point q^g ∈ ∂C^g such that p^g′ = q^g′.

Lemma 5. Let p^g ∈ ∂C^g be a point conflicting with at least one point on another component C^y. Then for all components Cⁱ such that i ≠ g and i ≠ y, Cⁱ∩ℬ(p^g) = ∅.

Lemma 5 shows that a point p can conflict with points of only one other component. This is important because it frees us to deal with only component pairs. That is, we are guaranteed that if component A and component B intersect, there is no other component C that intersects in the same region, even though C may intersect A and/or B elsewhere. In other words, there are no triple intersections. This naturally leads to the algorithm described in section 4, in which conflict points are found and dealt with between pairs of components.

Theorem 1. Two components C^g and C^y are within δ distance of each other if and only if there is at least one conflict point on the surface of either component.

Corollary 1. If two components C^g and C^y intersect then there is at least one conflict point on the surface of either component.

By this theorem and corollary we see that removing all conflict points between two components is necessary and sufficient to guarantee that the components are not intersecting and are separated at every point by at least δ.

Theorem 2 Moving any point p^g ∈ U^g in the direction of 𝒵(p^g) will not generate any additional conflict points among any pair of components.

This theorem is important to justify removing conflict points between pairs of components. If it wasn’t so then the algorithm would be computationally far more complex as we would have to continuously check previously resolved components for additional conflict points after any modification is made in the region.

Theorem 3. Conflict points exist on the triangulated surfaces of two components if and only if at least one conflict point exists either at a triangle vertex or along a triangle edge of either component.

4. Implementation

Our algorithm removes conflict points in a manner conforming to theorem 2, i.e., no additional conflict points are introduced at any step. And since removing all conflict points at locations defined in theorem 3 effectively removes all conflict points, our algorithm is bounded by the number of those locations.

The algorithm removes conflict points between pairs of components. We rely on theorem 2 to justify working with only two components at a time: resolving conflict points between two components will not increase the number of conflict points among any other pair of components.

In addition to working with only two components at a time, we also deal only with reconstructions between two given slices at a time. This is appropriate given that inter-slice interpolation is linear. There are no component intersections on the slices themselves (by criteria 3 and 4), and the algorithm does not modify any points on the slices. So the contours on the slices act as natural boundary points between intra-slice reconstructions, even after intersection removal.

The algorithm is as follows:

1. Separate contours in slices z_i and z_i+1

2. Run single component tiling on each component in slices

3. Determine conflict points

4. Trace cut from conflict point to its exit in a triangle

5. Triangulate (planar) polygons

6. Adjust z values

We now describe each step in detail.

Slice contour separation

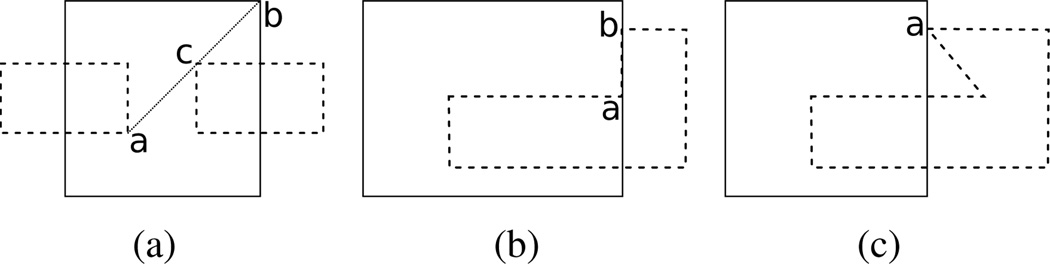
Our 2D contour intersection removal algorithm is a simple and efficient algorithm aimed at separating contours by a value δ (see figure 4). All contours in a given slice are first dilated by δ/2 after which proper intersections between contours (proper, in this case, meaning intersections such that a segment from one contour touches both the interior and exterior of another contour) are found using a sweep line and marked. We are guaranteed that there are an even number of intersections as only proper intersections are marked. Intersection points are paired up such that the mid-point of the line segment defined between two intersections is in the interior of two contours. For each of these pairs, the intersecting contours are clipped along this line segment. The contours are then eroded back to roughly their original shape minus the clipped areas.

Figure 4.

Contour intersection removal. (a) shows the original contours and (b) shows the contours after dilation by δ/2. In (c) the dilated contours have been clipped and (d) shows the final result after erosion.

This approach is simple and fast, but it does have its failings. For one, it doesn’t support intersections of more than two contours. This is, of course, possible, but generally doesn’t happen often in the data we have dealt with. Another side effect is a smoothing of the contours, which is dependent on δ. In our case this is actually desirable, as the contours we generally deal with are rather noisy, which is why we have to perform the intersection removal in the first place.

Single component reconstruction

The single component reconstruction algorithm we use is adapted from [2]. It takes planar contours in adjacent slices as input and outputs a series of triangles, or “tiles”, forming a surface between the contours. It supports branching and conforms to all of the criteria as they apply to single component reconstructions. The algorithm proceeds roughly as follows:

Given contours in adjacent slices,

1. find all contours with the same object labels

2. of these contours, find contours that correspond to (overlap with) each other

3. determine penumbral regions of corresponding contours

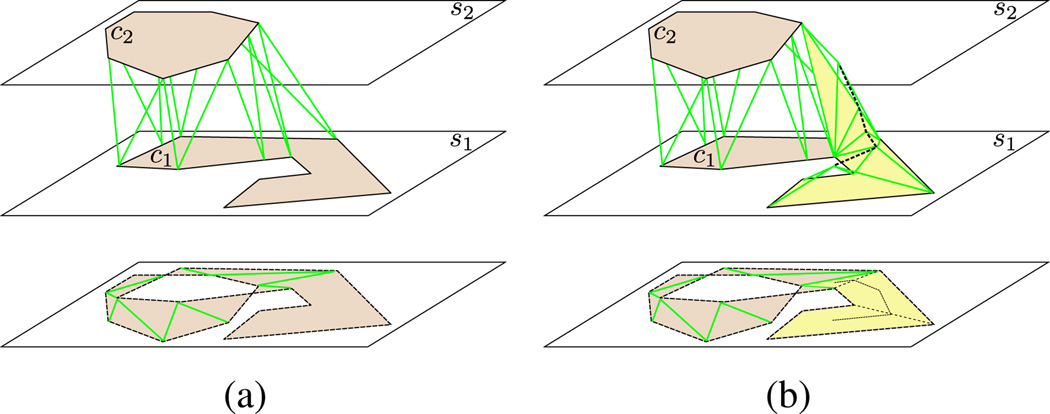
4. construct tiling between contours in penumbral regions (figure 5(a))

5. construct tiling in untiled regions (figure 5(b))

Figure 5.

Single-component tiling algorithm. (a) shows the tiling after stage one of the algorithm. As highlighted in yellow in (b), there remains an untiled region that is then tiled by connecting contour edge segments to the medial axis of the untiled region. Our algorithm interpolates points of the medial axis to the appropriate locations between slices to avoid undesired artifacts, as shown in figure 7.

We defer to [2] for in-depth description of the algorithm except for three degenerate cases of tiling and the final step, where untiled regions are resolved.

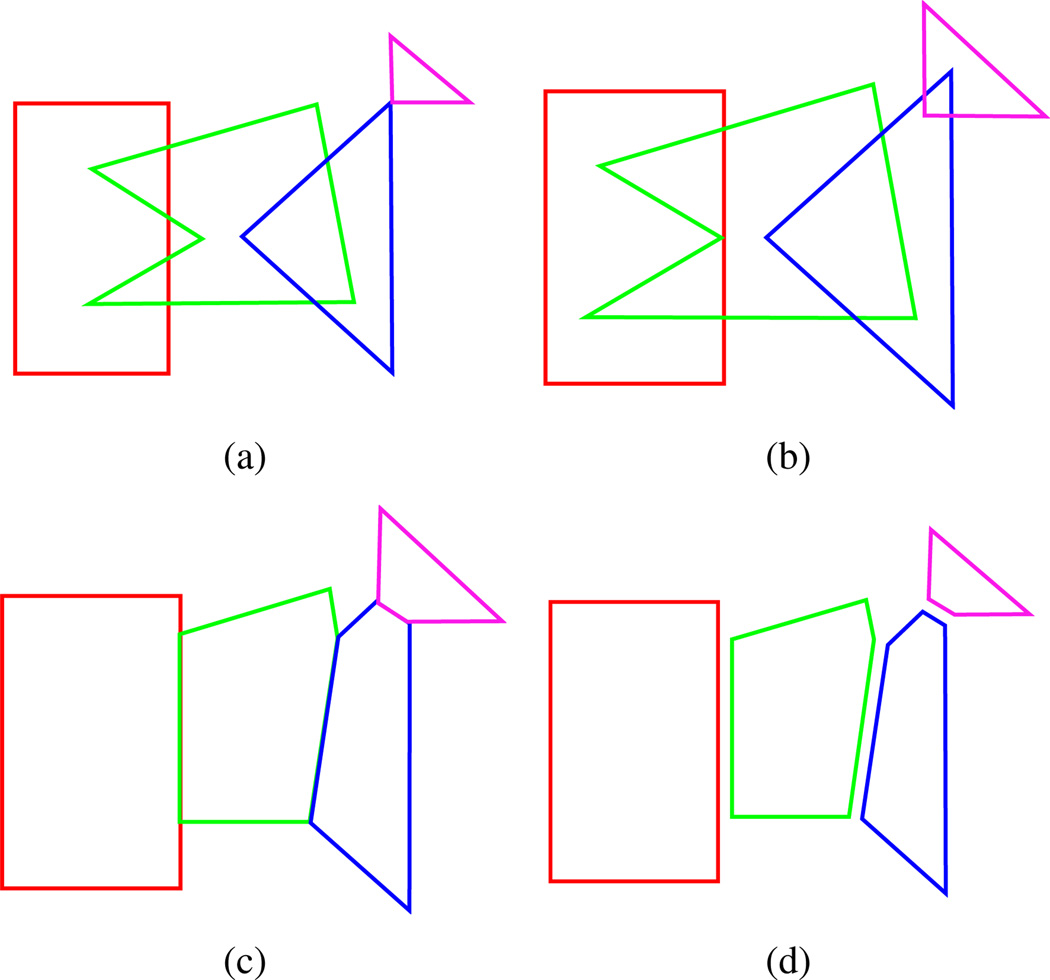
There are three tiling cases that we detect and handle in our algorithm that aren’t discussed in the original paper. These are degeneracies that we have found to occur in our data that we handle as special cases in order to make the tiling algorithm more robust with resorting to ε-perturbation. We discuss them informally and sketch our solutions. The first occurs when a chord is proposed as shown in figure 6(a). Here the projection of a chord (a, b) intersects with the projection of a vertex c in another contour. This chord is legal according to the original theorems, but can cause problematic tilings, e.g. if a chord (c, b) is proposed and accepted then criterion 2 will be violated. We detect this case and consider the chord (a, b) illegal.

Figure 6.

Three cases now detected and handled in augmented algorithm. The lower contour is solid while the upper contours are dashed. (a) The proposed chord (a, b) is now correctly labeled as illegal due to its intersection with vertex c. (b) No chords are legal between contours between a and b. (c) Vertex a is no longer tiled directly to the lower contour.

The second case occurs when edges from adjacent contours overlap along a segment. Consider directional arrows on each contour traveling counter-clockwise. In the overlapping case shown in figure 6(b) the arrows along the overlapping segment will be pointing different directions. The nature of this problem is such that it is difficult to solve in the context of the overall algorithm. As it happens rarely, our algorithm reports when it occurs and the regional tiling is corrected manually.

The third case occurs when a contour vertex a overlaps with an adjacent contour c, but both vertices adjacent to a are on the same side of the boundary of c, as in figure 6(c). We detect this case and treat a as if it were non-overlapping.

We use a novel algorithm to triangulate untiled regions. Untiled regions occur when no legal slice chord can be placed between a vertex of contour c_i and a vertex of contour c_j. The approach to tiling these regions is to first approximate the medial axis of the projection of the region. We do this by decomposing the region into convex polygons. Once we have the convex decomposition, we connect the centers of each sub-polygon with the midpoints of the corresponding cut lines. See the dashed lines in figure 5(b). We then place the approximate medial axis into space between the slices and tile using chords from the vertices of the untiled region to the approximate medial axis line.

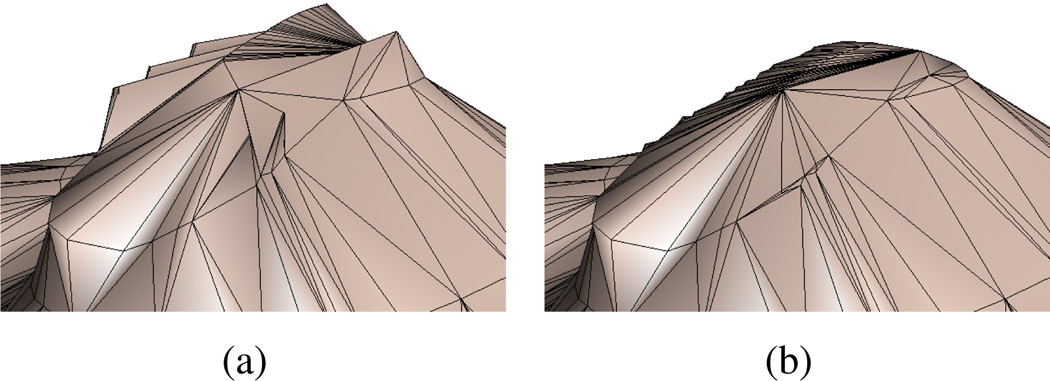
In the description thus far, our untiled region resolution algorithm matches that reported in [2]. But the previous approach uniformly placed the medial axis at z = (z_i + z_i+1)/2. This ensures that the criteria are met (specifically criterion 3), but can cause bad triangles (see figure 7(a)). Since the sub-polygons produced in the decomposition algorithm need meet only the criterion that they are convex, they can be arbitrarily bad, including sliver triangles and other undesirable shapes. When the centers of these sub-polygons are raised between the slices the tiling is jagged.

Figure 7.

Results of improvement to single contour reconstruction algorithm. 7(a) Shows jaggies resulting from the original algorithm placing medial axis vertices of untiled regions halfway between the two slices. 7(b) Our algorithm produces a more pleasing result by interpolating the medial axis points.

Ideally, medial axis vertex height should be interpolated using the vertices of the untiled regions. There are various interpolation approaches using barycentric coordinates for non-convex polygons [20, 21, 24]. In order to meet criterion 3 however, no point v ∈ Ω\∂Ω where Ω is the untiled region and ∂Ω is the region boundary, can lie on z_i or z_i+1. Thus any barycentric approach would require that, given v, there must be at least one vertex v_j on each slice z_j such that the barycentric coordinate λ_j(v) ≠ 0. A simple formulation of this requirement is λ_i(v) ≠ 0 for all i and all points v ∈ Ω \ ∂Ω.

We use a simple algorithm to ensure that each point on the medial axis lies strictly between the slices. Let 𝒮 be the union of the set of vertices of the polygon and the set of vertices of the medial axis. We compute Sibson’s natural neighbor coordinates [29] for each vertex of the medial axis, such that the z-value at a medial axis vertex v is

$$v_z={\displaystyle \sum _{p\in 𝒮}}{\lambda }_p(v)p_z$$ (1)

We then compute v_z for every vertex v of the medial axis. At this point, at least one medial axis vertex u will be strictly in-between the slices, but many vertices may remain on the slices. But since vertices of the medial axis are neighbors of each other, we can iteratively perform interpolation and the z-value of u will propagate down the medial axis. At most n iterations, where n is the number of medial axis vertices, are required to ensure that all vertices are strictly between slices. The results are shown in 7(b): the regions are smoothed out while still meeting criterion 3.

Determine conflict points

Once all components between two slices are found, we use a modified sweep line to find all tile edges of different colors that are closer than δ in the xy plane. In addition, all tile vertices that are inside of a tile of another component (still in the xy projection of the tiles) are considered. We call these potential conflict points “approach” points. They are marked and stored in a data structure that maps the approach point to the two tiles and every edge passing through the point. There will usually be exactly two edges unless the approach point is at a tile vertex, in which case the number of edges is greater since every tile vertex touches at least two tiles.

We consider conflict points at only these approach points. We determine whether a point is conflicting or not by examining the minimum distance between the different colored edges on which the approach points lie. Then, if the minimum distance is less than δ, we mark each approach point as conflicting.

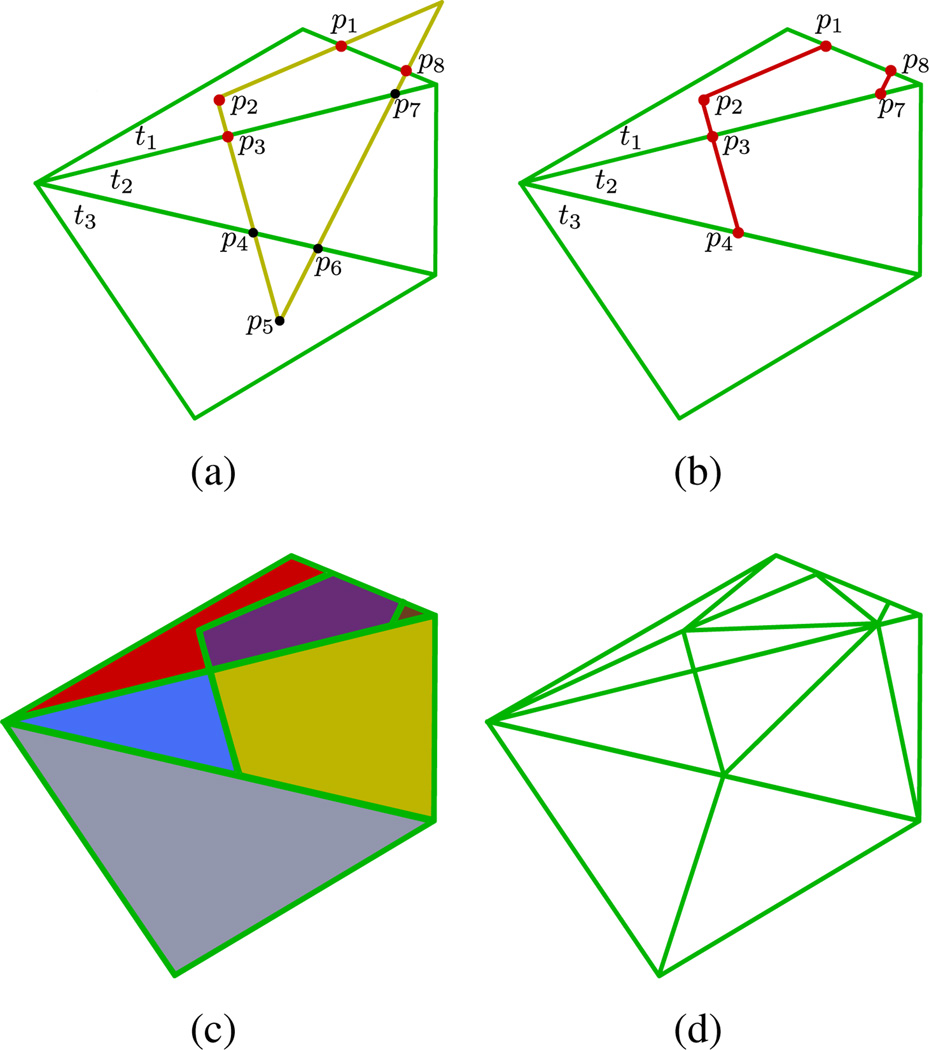
Figure 8(a) shows a yellow tile and three green tiles. The algorithm finds all approach points (black dots) and then determines which of these are conflict points (red dots).

Figure 8.

Steps of the intersection removal algorithm. Conflict points are red while non-conflict approach points are black. (a) Conflict points on the green tile are detected. (b) Cut paths are traced. Note that cut paths occur along the yellow tile’s edge and are only between two points of which at least one is a conflict point. Thus (p₃, p₄) is a cut path while (p₄, p₅) is not. (c) New polygons are induced by cut paths. The polygons are colored for clarity. (d) After triangulation of the polygons.

Trace tile cuts

The algorithm for tracing tile cuts is as follows:

Algorithm 1.

TRACE CUTS

1:	cuts := empty array of polylines for all points p in conflict points do   py := projection of p onto yellow component   ty := yellow tile containing py   tg := green tile containing pg   polyline := empty array of points   push p onto polyline   dir := direction to travel on ∂ty to go to interior of tg   boundary := ordered intersections on ∂ty   for all approach points qy in boundary do     if qy′ ∈ tg′ ⋃ ∂tg′ then       qg := projection of qy onto green component       q := qg′       push q onto polyline     end if   end for   push polyline onto cuts end for return cuts
2:
3:
4:
5:
6:
7:
8:
9:
10:
11:
12:
13:
14:
15:
16:
17:
18:
19:

For each conflict point, we must trace out cut polylines that we will use to induce new polygons that will then be triangulated. The way this is done is to start at a conflict point p and find its projection onto the yellow component to get p^y (line 3). p^y will be on a yellow tile’s boundary. Now follow the points on the boundary of the tile that have been marked as intersections from p^y to the exit point where the yellow tile exits the green tile (lines 8–10). Each point encountered in this trace are added to the polyline (line 14).

This can be seen visually in figure 8(a). Point p₁ is a conflict point. The algorithm builds an ordered array of points following the yellow tile from p₁ all the way to point p₈. Then it loops over each point in the array checking to see if the current point p is inside of the projection of the green tile t₁′. If it is, then the point is added to the cut. So the cut from point p₁ = [p₁, p₂, p₃]. All cuts can be shown in red in figure 8(b).

Cut polylines are specific to a tile. So cuts for the green component’s tiles are first found, and then cuts for the yellow component. These polylines are superimposed onto the tiles to generate a set of induced polygons (figure 8(c)). Even though the cuts are different for green tiles vs. yellow tiles, the projection of green tiles and cuts will be identical to that of the yellow.

Figure 8 shows an interesting case in that if the induced polygons are triangulated naively, an illegal triangulation can result. Consider point p₄ in the figure. There will be a triangle vertex at this point due to the triangulation of tile t₂. If, then, it is not a vertex in the triangulation of tile t₃, then the triangulation will not be legal. Because of this, the algorithm checks for any point on a tile edge that is involved in the triangulation of any adjacent tile, and induces that point onto all adjacent tiles. This ensures legal triangulations.

Triangulate polygons

At this point we have polygons that are ready to be triangulated into a new induced surface. An intuitive approach would be to simply run a constrained Delaunay 2D triangulation on the xy projection of all induced points on the tile. This has two problems: first, the tiles can be vertical and thus the projections of the triangles are degenerate and second, inducing points on edges of triangles causes a large number of collinear points.

The first problem can be addressed by checking to see if the tile is vertical before triangulation. If it is, then rotate by 90 degrees and then triangulate. Happily, the tiles are still coplanar and so we can safely rotate the tile with induced points without worry of causing additional degeneracies.

The second problem is more troublesome. The combined problem of collinear points coupled with numerical error causing possible triangle edges outside of the original tile requires something more than a naive approach. Our solution is to maintain a data structure mapping points to the edges of the original tile from which they were induced. Now a numerically error-prone check for collinearity is perfectly safe by simply doing a hash lookup for each point and comparing the original edges. If all three edges are the same then the points are collinear. If not, then they are not collinear, provided the original tiling algorithm returns non-degenerate tiles (which it does in our case).

We used a simple ear-cutting algorithm [28] using this data structure to ensure legal triangulations. Even with the check, an additional modification is required to ensure numerical stability. That is to first generate triangles involving at least one unused collinear point. Without this, the result often includes very long thin triangles if at least one induced point is very close to an existing vertex.

Adjust z values

The result of triangulating induced polygons is an induced triangulated surface, which still has conflict points between components. At this point we can adjust z values of all conflict points in the new triangulation to separate component surfaces. Each conflict point p is checked and its two associated component points p^g and p^y are given new z values as follows:

$$p_z^g=\frac{p_z^g+p_z^y}{2}+s^g\epsilon$$ (2)

where

$$s^g=\{\begin{array}{cc}\hfill -1\hfill & \hfill z^g>z^y\hfill \\ \hfill 1\hfill & \hfill z^g<z^y\hfill \end{array}$$ (3)

$p_z^y$ is calculated similarly.

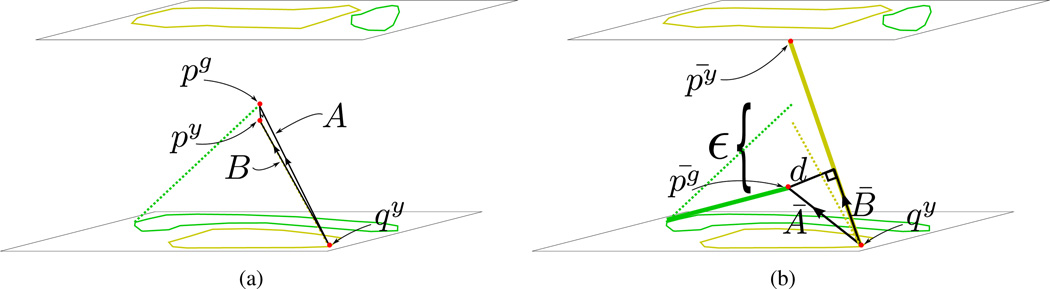
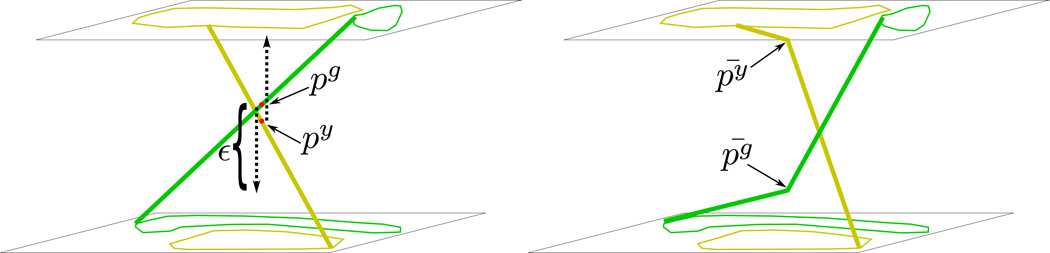
ε and δ are related but distinct. δ is the input parameter of minimum separation distance between components. ε is the distance along the z axis to move conflict points such that the new surfaces will be separated by δ. Determining ε to achieve the desired minimum distance δ between components is done as follows. A conflict point p^y is either an induced point on an edge or a vertex. Let B be the vector p^y − q^y where q^y is either an induced point or vertex such that $p_z^y$ is between $q_z^y$ and 𝒵(p^y). See figure 10. Further, let A be the vector p^y − q^y. Now let ${\overline{p}}^y=\{p_x^y,p_y^y,p_z^y+s^y\epsilon \}\text{ and }{\overline{p}}^g=\{p_x^g,p_y^g,p_z^g+s^g\epsilon \}$. And lastly, B̄ = p̄ ^y − q^y and Ā = p̄^g − q^y. Distance d is

$$d=\frac{|\overline{\mathbf{A}}\times \overline{\mathbf{B}}|}{|\overline{\mathbf{B}}|}$$ (4)

Figure 10.

Calculation of ε. A and B are vectors from q^y to the original conflict points. Ā and B̄ are vectors from q^y to the resolved conflict points. ε is calculated using these vectors and input minimum separation distance parameter δ.

Substituting for Ā and B̄ and assuming that s^g = 1 we get

$$d^2=({(A_y(B_z-\epsilon )-(A_z+\epsilon )B_y)}^2+{((A_z+\epsilon )B_x-A_x(B_z-\epsilon ))}^2+{(A_x{B}_y-A_y{B}_x)}^2)/(B_x^2+B_y^2+{(B_z+\epsilon )}^2)$$ (5)

Factoring ε yields a quadratic:

$$0={\epsilon }^2({(A_y+B_y)}^2+{(A_x+B_x)}^2-d^2)+\epsilon (2)((A_x+B_x)(A_z{B}_x-A_x{B}_z)-(A_y+B_y)(A_y{B}_z-A_z{B}_y)-d^2{B}_z)+{(A_y{B}_z-A_z{B}_y)}^2+{(A_z{B}_x-A_x{B}_z)}^2+{(A_x{B}_y-A_y{B}_x)}^2-d^2(B_x^2+B_y^2+B_z^2)$$ (6)

We then substitute δ in for d and find the two roots for ε. It is possible that both roots yield shifts in the direction of 𝒵(p^g). This occurs when the surface intersections are gross enough to cause conflict points that are more than δ apart. So we choose the solution for ε with the greatest value and then multiply by s^g (since we assumed that s^g = 1).

There is a denominator on the right hand side of (6) which we have omitted for brevity. But it should be clear from (5) that the denominator is zero only when B̄ is degenerate which cannot happen since p^y is moved in the direction of 𝒵(p^y) for ε > 0.

Theorem 4. ε < |p^g − 𝒵(p^g)| and ε < |p^y − 𝒵(p^y)|.

This theorem bounds ε by the distance from the conflict points to the slices. In other words, no value of ε can cause a point shift in z such that the point crosses a slice boundary. This is important because any such shift would cause the reconstruction to violate criterion 3, not to mention all the criterion’s dependent guarantees.

Computational complexity

The computational complexity of our algorithm is bounded by the number of conflict points. The maximum number of conflict points between the boundaries of two triangles is 12: 6 for the xy-plane intersections and 6 for the vertices. For m components, each with n_i triangles, the maximum number of conflict points is 12n_in_j where n_i and n_j are the two largest numbers of triangles in a single component. Thus, the computational complexity is O(n²) where n is the largest number of triangles in a single component.

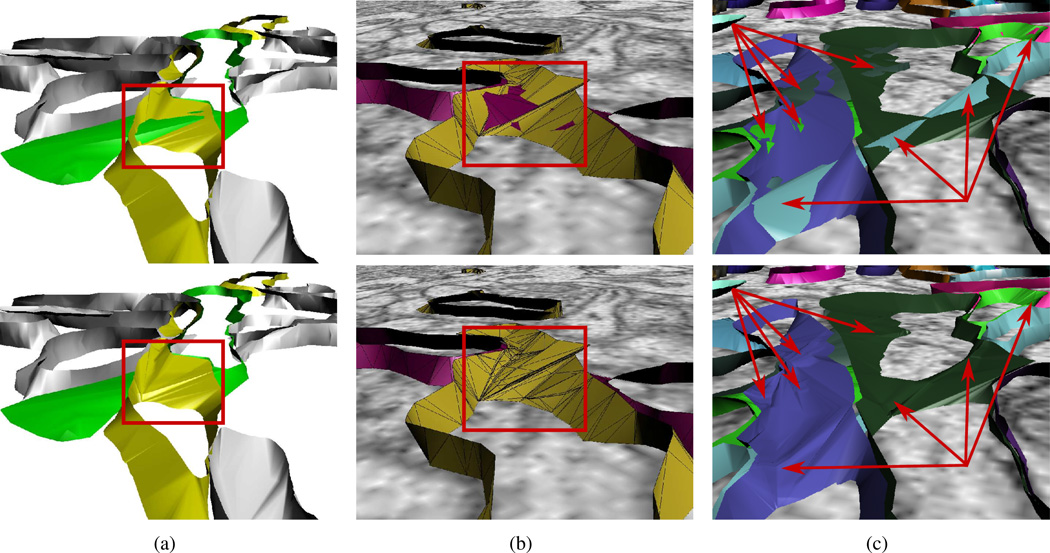
In practice we have found that there are far fewer conflict points, even in highly tortuous datasets. Statistics of the reconstruction of which a small part is shown in figure 13(c) is reported on line 1 of table 1. Between two of the slices there were 21330 total triangles before intersection removal. Among these triangles there were 7691 detected conflict points. Our testing of our most tightly-packed data showed similar ratios of number of triangles to number of conflict points.

Figure 13.

Results of running intersection removal on various portions of neuronal contour data. (a) Before and after intersection removal at branch point. (b) Result of intersection removal is shown on top of the original ssTEM data. (c) Shows prevalence of intersections. This small portion of the data alone has at least eight component intersections.

Smoothing

One additional step in our pipeline is that of smoothing the surfaces. Initial surface reconstruction can introduce numerically-troublesome thin triangles, and the intersection removal adds O(n²) triangles. So at completion of intersection removal we run the surfaces through our quality improvement pipeline, which includes edge contraction using the QSlim software package [18] after which we decimate [34] and improve triangles [4]. These tasks are done using a library version of our Level Set Boundary Interior and Exterior Mesher [14] which is also embedded in our Volume Rover software package [15].

5. Results

We have implemented both the single component contour tiler and intersection removal algorithm.

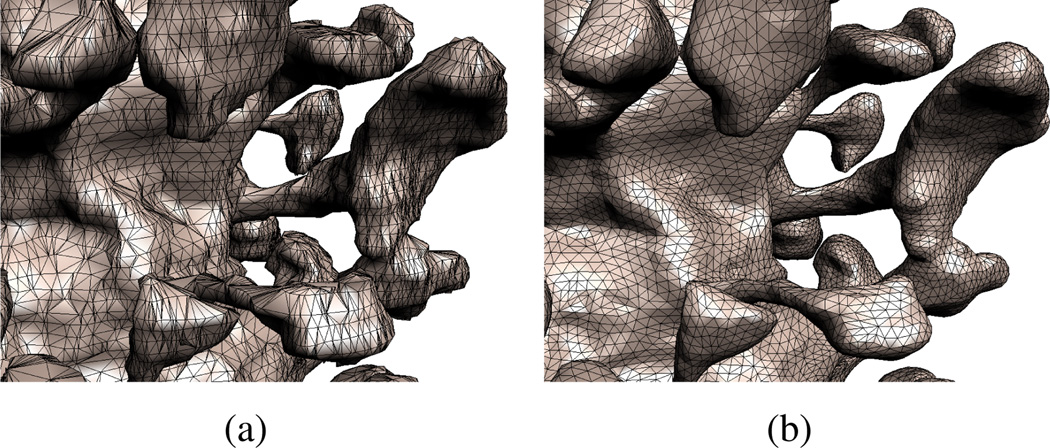
Figure 11 zooms in on a dendrite to show the effect of our smoothing algorithm, and figure 12 shows the effects of varying the separation distance δ parameter.

Figure 11.

(a) An apical dendrite before smoothing. (b) After smoothing. The number of triangles composing the final, smoothed surface is a parameter. In this example the number of triangles was cut to roughly half the original number.

Figure 12.

Shows the effects of varying the separation distance δ parameter when reconstructing two axons that come very close in one region. (a) Separation δ = 0. (b) δ = 40 nm. Note that the surfaces are changed only in the region of close approach.

Figure 9 shows some interesting cases of intersection between tiles (though it is by no means exhaustive). Figure 9(a) shows intersection of a vertical tile. This requires the tile to be rotated by 90 degrees before being re-triangulated after new points are induced. 9(b) shows conflict points at only tile vertices and not xy-plane intersections. As can be seen this case is handled since conflict points are checked at tile vertices in addition to xy-plane intersections.

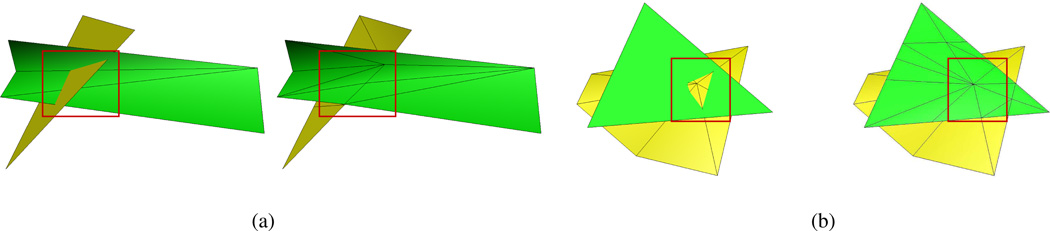
Figure 9.

Examples showing two interesting cases of intersection. The left figure of (a) shows a classic intersection between yellow and green tiles. The right figure shows the resolution of the intersection. The left figure of (b) shows a slightly more complicated case containing conflict points both at tile edges and at vertices. On the right is shown the resolution.

Figure 13 shows results of intersection removal from reconstructions of the hippocampal region of the brain. The contours used were hand-traced from 4K × 4K pixel resolution ssTEM images. Image pixels are approximately 2 nm square and inter-slice spacing is 45 nm. We show results from various regions of the dataset at different slices and using different components. The intersection removal algorithm is run immediately after all components between two slices are reconstructed. Only one pass over conflict points is made and, as can be seen, no additional conflict points are generated. These results show a number of interesting things: 1) Every intersection except for one in figure 13(c) occur where one or both components is branching. This highlights the power of handling branching cases smoothly. 2) Figure 13(b) shows the mesh triangles and it is clear that new triangles are only induced from original triangles. It also shows that are large number of triangles are generated in intersection removal. 3) Figure 13(c) is striking in that it shows just how prevalent these intersections can be when using a linear interpolation reconstruction approach on tightly-packed anisotropic data. In that small region of the data (three slices and approximately 5 μ²) there are more than eight distinct intersecting regions, some of them grevious. We emphasize that any interpolatory single-component reconstruction method will run into this problem. Our algorithm detects and removes every intersection while maintaining original tiling criteria.

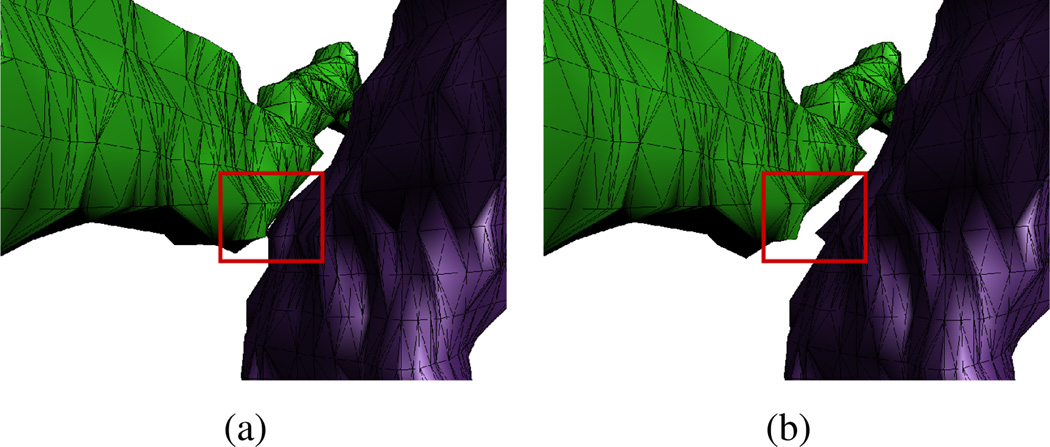
Figure 14 shows reconstructed data in the large. Two axons come in close proximity with each other, causing an intersection as can be seen in 14(b) after cutting away part of the red axon. The intersection is repaired in 14(c) and 14(d) shows the results of smoothing after intersection removal.

Figure 14.

Results of running intersection removal on two axons that intersect. (a) Two axons whose reconstructions intersect between slices. (b) Zoomed in with part of the top axon cut away to reveal the intersection. (c) Result of intersection removal. (d) After smoothing.

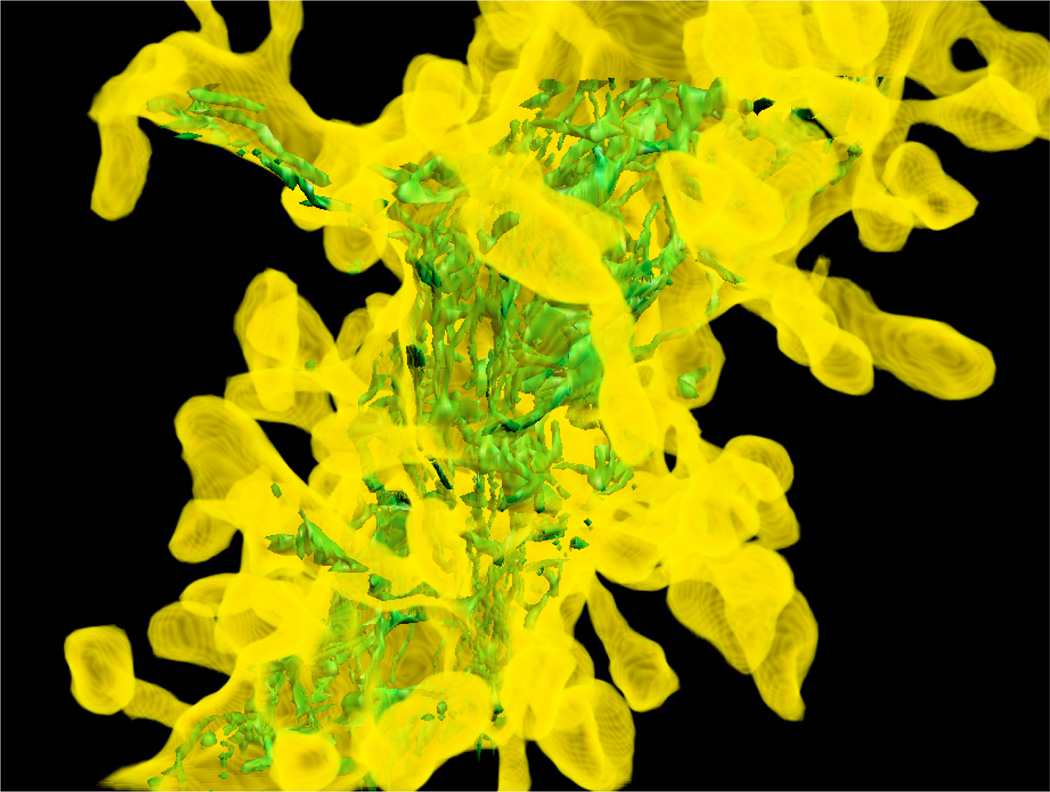
Figure 15 shows a complex dendritic structure with nested endoplasmic reticulum (ER). While both structures are neuronal, their geometries are vastly different, with the ER looking far more fractured than the bulbous branching of the dendrite. Our algorithm is oblivious to such varied geometries and handles each correctly.

Figure 15.

A zoomed-in view of the apical dendrite shown with transparency to reveal interior endoplasmic reticulum.

Table 1 shows various statistics of our tests on neuronal data. In our most tightly-packed data (CA1), intersection removal took up roughly half the time and increased the number of total triangles to about double the original number. As noted earlier, the number of intersections was generally far less than the n² theoretical maximum.

An eventual goal is to reconstruct a global brain model, or even, somewhat more modestly, a reasonably large region of the brain. It turns out that both of these goals are ambitious, as the physical slicing and EM imaging process yields only very small data footprints [12]. But we are well-positioned to tackle the reconstruction challenge once the data becomes available as our algorithm will handle any arbitrary topologies and complicated geometries present in different brain regions. Also, as discussed in section 6, the algorithm will scale to support full brain reconstructions.

6. Discussion and future work

Without correct topologies, multiple component modeling is severely limited, and this work provides a solution to this important problem. This problem has not received significant attention due to the nature of data used in reconstructions in the past – automatic removal of intersections could be done manually because there were generally very few such intersections. But with the advent of reconstructions of tortuous, densely packed and anisotropic data, the importance of an automatic and robust method has increased. This paper presented just such a method. Using single component reconstructions that adhere to certain guidelines, the method presented in this paper can remove intersections between components correctly and robustly, preserving the guarantees of the single-component reconstruction method: the output surface is water-tight, and any cross-section through an original slice yields precisely the input contours. It also guarantees a minimum separation distance between all components. This is important when dealing with e.g. neuronal data, as a rough idea of the average distance between components is generally well known.

The algorithm is efficient, performing the intersection removal in roughly the same amount of time as the original reconstruction by using efficient 2D geometric calculations. The algorithm is also scalable in the number of slices, since it reconstructs and resolves intersections slice-by-slice. Scalability in the number and complexity of components is slightly less straightforward, as the current implementation stores in memory all components between two slices. While this has not caused any problems in practice, it is possible that a very large number of components would not fit in computer memory. In this case, a simple heuristic could partition components into overlapping regions and work with them region-by-region.

Moving intersection points only in the z-axis enables proofs of correctness and solves the intersection problem, but it also restricts the algorithm. Enabling movement in the x–y plane may make it possible to produce smoother surfaces and better-behaved triangles from the intersection removal process. We are interested in determining whether the same correctness guarantees can be made while allowing conflict point movement in any direction. Of course, our smoothing process greatly improves any poor triangulations, but our current smoothing algorithm, which uses geometric flow, does not respect inter-component spacing restrictions. A constrained smoothing algorithm would be beneficial.

Our algorithm does produce a large number of triangles in the process of removing intersections, and some of these triangles are poorly shaped. However, we have shown that our smoothing software is highly effective at transforming the surfaces into triangulations suitable for visualization and analysis. One question that needs to be addressed is how much does smoothing affect the minimum separation distance guaranteed by the intersection removal algorithm. We are interested in finding a quantitative measure and whether the error introduced is acceptable.

Another improvement that needs to be made is the removal of criterion 5, that a contour cannot be nested inside a different colored contour. This criterion prohibits intersection removal between nested components. In the case of neuronal modeling, so-called intracellular components such as endoplasmic reticulum and mitochondria are treated separately. But to get a truly accurate model, these will need to be included.

A fundamental issue still exists with criterion 2, which states that a vertical line cannot pass through more than one of a component’s boundaries between any two given slices. This means that with very high anisotropy, an oblique component may be disconnected because its contours that in reality correspond may not be labeled as corresponding in the algorithm. As this criterion is a basis for many of our theorems and guarantees, an approach to resolving it may be to add a special case.

There are a number of interesting generalizations that may be possible in the framework of these methods. One is support of incomplete contours, which could generate either open polyhedra in the unknown regions, or closed polyhedra, thereby closing the original contour.

Another generalization is support for non-parallel slices. This would require re-visiting the fundamental theoretical guarantees of the single-component algorithm. The follow-up question would be whether the intersection removal algorithm could enjoy versions of the same guarantees our current parallel-slice version does, e.g., no more than two components can intersect in the same region, all intersection points can be resolved by resolving a finite number of intersections, etc.

The contribution described in this paper is part of a larger effort to build “analysis-ready” surface reconstructions, that is, geometric models that are water-tight and topologically correct and that have low aspect ratio triangles and bounded error, among other properties. As shown, reconstructions using the method described here satisfy the first three of the properties. The last, that of quantifying and bounding the surface error, is a challenging but important next step.

highlights.

• *Geometric reconstruction from contours can cause intersections
• *Our algorithm generates topologically correct reconstructions
• *Our algorithm generates geometrically accurate reconstructions

Figure 1.

Overview of our automated neuronal reconstruction process. We begin with EM (TEM and SEM) images of the brain. We contour neuronal processes in 2D then generate each process individually. Finally we put everything together for a complete 3D reconstruction. See also figure 13(a).

Figure 3.

Conflict points are detected and removed by moving the points along the z axis. p^g and p^y are corresponding conflict points. The conflict is removed by moving p^g and p^y in the z direction by s^gε and s^yε, respectively (equation 3) to produce new points p̄^g and p̄^y.

Table 1.

Table of tiling timing and triangle statistics. Tiling time includes 2D contour curation and single contouring. Tests were performed on a Linux Kubuntu workstation with an Intel Xeon quad core CPU at 3.20 GHz with 4 GB memory. The CA1 dataset (figure 1) was taken from the hippocampal region of the brain and has 452 axons and about 50 dendrites. The CA3 dataset is unreleased.

dataset	slices	tiling time	num triangles	num intersections	intersection removal	final num triangles	smoothing time
CA1 (axons)	115–116	79.2s (46%)	21330	7691	85.1s (49%)	48778	7.8s (4%)
CA1 (all)	61–62	503.3s (40%)	37849	26965	759.7s (59%)	105434	9.2s (1%)
CA3	150–151	90.9s (86%)	9812	52	13.5s (13%)	10078	1.4s (1%)

Appendix A. Proofs of theorems

Our proofs rely on an additional theorem from [2], which we restate here in a slightly weaker formulation, but sufficient for our purposes:

Theorem 5. ([2], Theorem 2) For every point p^g on the surface ∂C^g of the green component, 1 ≤ |𝒞 ^g(p^g)| ≤ 2.

Proof of lemma 1. Since |𝒞(p^g)| ⊃ |𝒞^g (p^g)|, then 1 ≤ |𝒞 ^g(p^g)| by theorem 5. We prove that |𝒞 ^g(p^g)| ≤ 2 by contradiction. Suppose |𝒞 ^g(p^g)| > 2. Then by the pigeonhole principle, at least 2 contours must exist on some adjacent slice. These contours share the projection $p_s^g$ onto the slice of point $p_s^g$. This violates criterion 4.

Proof of lemma 2. If the 2 containing contours exist on the same slice, then they share the projection $p_s^g$ onto the slice of point $p_s^g$. This violates criterion 4.

Proof of lemma 3. This is a proof by contradiction. Consider a point p^g ∈ S^g. Suppose that p^g is a conflict point. Then there exists some point p^y such that p^y ∈ ℬ(p^g) (for the moment, set aside the fact that 𝒵(p^g) is undefined). By lemma 1 we know that the projection of point p^g can have no more than 2 containing contours. By virtue of being in S^g, p^g indeed has 2 containing contours, both of which belong to the green component by definition. Since p^y ∈ ℬ(p^g), the projections of p^y onto each adjacent slice are within δ of the projections of p^g. Then the projection of p^y onto 𝒞(p^y) (by theorem 5 there must be at least one) is within δ of a green contour 𝒞(p^g) which contradicts criterion 4. Thus no point p^y exists and p^g is not a conflict point.

Proof of lemma 4. By lemma 3, p^g ∈ U^g and thus cannot be on a vertical tile edge. Then, by criterion 2, a vertical line passing through p^g passes through no other point.

Proof of lemma 5. By definition of a conflict point, there exists some p^y such that p^g′ = p^y′. By lemma 4, p^g and p^y are the only points lying on the vertical line passing through them. In addition, these two points are unique, as the addition of a third point on the vertical line would violate theorem 5 and lemma 1.

Proof of theorem 1. We first prove that if a conflict point p^g ∈ ∂C^g exists, then the two components are, at some point, within δ of each other. Let p^g ∈ ∂C^g be a conflict point. Let Γ be the vertical path from p^g to the slice at 𝒵(p^g). By definition of a conflict point, Γ will pass within δ of some point p^y ∈ ∂C^y before reaching the slice. By criterion 2, Γ intersects ∂C^g exactly once, at p^g, and since every point inside the planar contour 𝒞(p^g) is inside the green component, every point on Γ between p^g and the projection of p^g onto 𝒵(p^g) is inside the green component. Therefore, some point q^g ∈ (Γ ∪ C^g) is within δ of ∂C^y.

If two components are within δ of each other, then by definition there exists a conflict point.

Proof of corollary 1. If p^g is the intersection point between two components it is by definition a conflict point.

Proof of theorem 2. Let p^g ∈ U^g and let p̄^g be p^g shifted by ε in the direction of 𝒵(p^g). ℬ(p̄^g) ⊂ ℬ(p^g) and therefore {p^y|p^y ∈ ℬ(p̄^g)} ⊂ {q^y|q^y ∈ ℬ(p^g)}. Therefore the number of conflict points will only decrease.

Proof of theorem 3. We prove this by contradiction. Suppose there exists a single pair of conflict points p^g ∈ ∂C^g and p^y ∈ ∂C^y on the interiors of triangles t^g ∈ ∂C^g and t^y ∈ ∂C^y, respectively. Further, suppose that every point p ∈ (∂C^g ∪ ∂C^y) is not a conflict point. Then |p^g − p^y| < δ while the minimum separation distance between ∂C^g and ∂C^y is at least δ. This violates planarity of the triangles, and therefore there must be some conflict point p ∈ (∂C^g ∪ ∂C^y).

Proof of theorem 4. By definition, the projection p^g′ of p^g onto the slice at z = 𝒵(p^g) lies inside or on the boundary of a green contour. It can lie on a boundary only if p^g ∈ S^g, so by lemma 3 we know that p^g′ lies on the interior of a green contour. Since the contours are separated by δ, and q^y lies on a yellow contour, then |p^g′ −q^y| > δ. Thus there is some point p̄^g on the vertical line between p^g and p^g′ such that $\frac{|\overline{\mathbf{A}}\times \overline{\mathbf{B}}|}{|\overline{\mathbf{B}}|}=\delta$ proving the first statement. The second follows with a similar argument.