Mechanism of Conduction Block in Amphibian Myelinated Axon Induced by Biphasic Electrical Current at Ultra-High Frequency

Abstract

The mechanism of axonal conduction block induced by ultra-high frequency (≥20 kHz) biphasic electrical current was investigated using a lumped circuit model of the amphibian myelinated axon based on Frankenhaeuser-Huxley (FH) equations. The ultra-high frequency stimulation produces constant activation of both sodium and potassium channels at the axonal node under the block electrode causing the axonal conduction block. This blocking mechanism is different from the mechanism when the stimulation frequency is between 4 kHz and 10 kHz, where only the potassium channel is constantly activated. The minimal stimulation intensity required to induce a conduction block increases as the stimulation frequency increases. The results from this simulation study are useful to guide future animal experiments to reveal the different mechanisms underlying nerve conduction block induced by high-frequency biphasic electrical current.

1. INTRODUCTION

It has been known for more than 70 years that high frequency (≥4 kHz) biphasic electrical current can block axonal conduction (Reboul and Rosenblueth, 1939; Rosenblueth and Reboul, 1939). Since the conduction block is quickly reversible after termination of the stimulation and the biphasic electrical current causes less tissue damage than uniphasic current due to electrochemical reactions (Agnew and McCreery, 1990), this nerve blocking method has many potential clinical applications, for example, alleviating chronic pain (Nashold et al., 1982), stopping unwanted muscle movements (muscle spasms and spasticity) (Bhadra and Kilgore, 2005), or improving voiding efficiency (Gaunt and Prochazka, 2009; Tai et al., 2004). Although many studies (Bhadra and Kilgore, 2005; Tai et al., 2004, 2005c, 2008; Williamson and Andrews, 2005) have recently focused on this type of nerve conduction block, the underlying mechanisms are still not fully understood.

Due to electrical artifacts generated by the high-frequency blocking stimulation, it is very difficult to investigate the blocking mechanisms at the ion channel level in animal experiments using traditional electrophysiological methods. Therefore, recent studies (Bhadra et al., 2007; Liu et al., 2009; Tai et al., 2005a,b; Williamson and Andrews, 2005; Zhang et al., 2006a,b) have focused on computer simulation using axonal models. Our previous studies (Liu et al., 2009; Tai et al., 2005a,b; Zhang et al., 2006a,b) using both unmyelinated and myelinated (amphibian or mammalian) axon models indicated that both fast and slow potassium currents might play a role in axonal conduction block induced by high frequency biphasic electrical current at a frequency range of 4–10 kHz. At this frequency range the potassium channels are tonically activated at the axonal node under the stimulation electrode causing a conduction block. Since the sodium channel has much faster kinetics than the potassium channel, it can still close or open during the oscillation of the membrane potential (Liu et al., 2009; Tai et al., 2005a,b; Zhang et al., 2006a,b). However, ultra-high frequency (≥20 kHz) stimulation has also been used to induce axonal conduction block in both unmyelinated (Joseph and Butera, 2009) and myelinated (Bhadra and Kilgore, 2005; Reboul and Rosenblueth, 1939; Rosenblueth and Reboul, 1939; Tanner, 1962) axons. In myelinated axons the blocking threshold intensity increases monotonically as stimulation frequency increases (Bhadra and Kilgore, 2005; Graunt and Prochazka, 2009). However, in unmyelinated axons the blocking threshold is maximal at a frequency about 12 kHz (Joseph and Butera, 2009), and then starts to decline gradually as the frequency is increased into the ultra-high frequency range (≥20 kHz), indicating a possible different blocking mechanism. It is possible that the sodium channel is not able to follow the rapid change of the membrane potential induced by the ultra-high frequency stimulation, thereby causing an axonal conduction block. However, how the sodium channel reacts to the ultra-high frequency biphasic stimulation is un-known. Whether sodium channels are tonically closed or opened by the ultra-high frequency needs to be determined.

Several axonal models that are based on intracellular recordings from either amphibian (Hodgkin and Huxley, 1952; Frankenhaeuser and Huxley, 1964) or mammalian (Schwarz and Eikhof, 1987; Schwarz et al., 1995) axons are available to investigate the sodium channel response to ultra-high frequency stimulation. A thorough investigation using different axonal models will certainly provide a better understanding of sodium channel responses in different types of axons. However, in this study we focused on the amphibian myelinated axonal model (FH model) to determine: 1. How does the blocking threshold change as the stimulation frequency increases into ultra-high frequency range? 2. How does the sodium channel respond to ultra-high frequency stimulation? The results from this simulation study will further improve our understanding of the biophysics underlying the axonal conduction block induced by high frequency biphasic electrical current, that will in turn guide future experiments on animals and provide better designs of the stimulation waveforms to satisfy the different requirements in many clinical applications (Gaunt and Prochazka, 2009; Gerges et al., 2010; Nashold et al., 1982; Tai et al., 2004).

2. METHODS

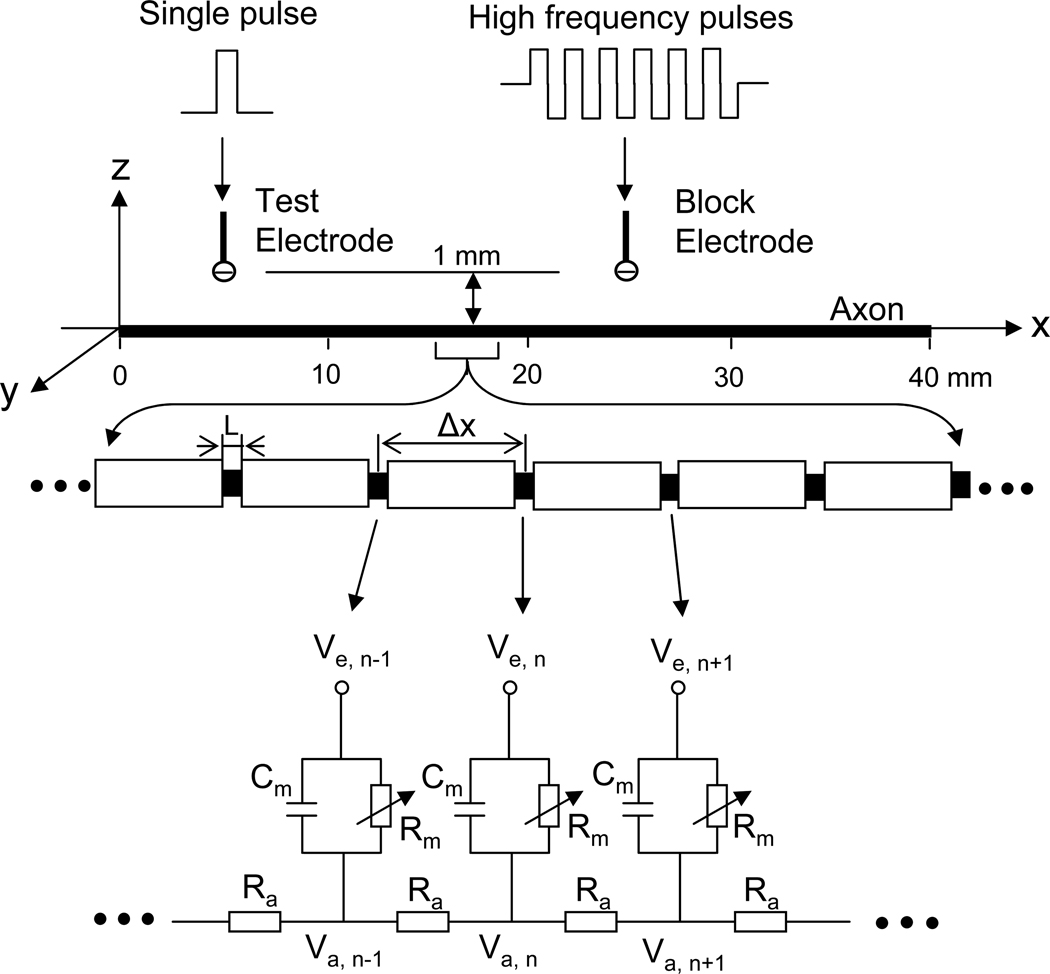
The axonal model used in this study is shown in Fig.1. A 40 mm long, myelinated axon is modeled with the inter-node length Δx = 100d (where d is the axon diameter). Each node (nodal length: L = 2.5 µm) is modeled by a membrane capacitance (C_m) and a variable membrane resistance (R_m). The ionic currents passing through the variable membrane resistance are described by FH equations (Frankenhaeuser and Huxley, 1964; Rattay and Aberham, 1993). Two monopolar point electrodes (with the indifferent electrode at infinity) are placed at 1 mm distance from the axon (Fig.1). One is the block electrode at the 25 mm location along the axon, where the high frequency biphasic current is delivered. The other is the test stimulating electrode at the 5 mm location, which delivers a uniphasic single pulse (pulse width 0.1 ms and intensity 1 mA) to evoke an action potential and test whether this action potential can propagate through the site of the block electrode. The test electrode is always the cathode (negative pulse), and the block electrode delivers biphasic pulses with the cathodal phase first.

Fig.1.

Myelinated axonal model used to simulate conduction block induced by high-frequency biphasic electrical current. The inter-node length Δx = 100d; d is the axon diameter. L is the nodal length. Each node is modeled by a resistance-capacitance circuit based on the FH model. Ra: inter-nodal axoplasmic resistance; Rm: nodal membrane resistance; Cm: nodal membrane capacitance; Vi,j: intracellular potential at the jth node; Ve,j: extracellular potential at the jth node.

We assume that the axon is in an infinite homogeneous medium (resistivity ρ_e= 300 Ωcm). After neglecting the small influence induced by the presence of the axon in the homogeneous medium, the extracellular potential V_e,j at the j^th node along the axon can be calculated by:

$$V_{e,j}(t)=\frac{{\rho }_e}{4\pi }\left[\frac{I_{\mathit{\text{block}}}(t)}{\sqrt{{(j\mathrm{\Delta }x-x_0)}^2+z_0^2}}+\frac{I_{\mathit{\text{test}}}(t)}{\sqrt{{(j\mathrm{\Delta }x-x_1)}^2+z_1^2}}\right]$$

where I_block(t) is the high frequency biphasic rectangular pulse current delivered to the block electrode (at location x₀ = 25 mm, z₀ = 1 mm); I_test(t) is the single test pulse delivered to the test electrode (at location x₁ = 5 mm, z₁ = 1 mm).

The change of the membrane potential V_j at the j^th node is described by:

$$\frac{{\mathit{\text{dV}}}_j}{\mathit{\text{dt}}}=\left[\frac{d\mathrm{\Delta }x}{4{\rho }_{i}L}\left(\frac{V_{j-1}-2V_j+V_{j+1}}{\mathrm{\Delta }{x}^2}+\frac{V_{e,j-1}-2V_{e,j}+V_{e,j+1}}{\mathrm{\Delta }{x}^2}\right)-I_{i,j}\right]/c_m$$

where V_j = V_i,j −V_e,j−V_rest; V_i,j is the intracellular potential at the j^th node; V_e,j is the extracellular potential at the j^th node; V_rest is the resting membrane potential; ρ_i is the resistivity of axoplasm (100 Ωcm); c_m is the capacity of the membrane (2 µF/cm²); I_i,j is the ionic current at the j^th node described by FH equations (Frankenhaeuser and Huxley, 1964; Rattay and Aberham, 1993). See “Appendix” for more detail about the FH equations.

The axonal model was solved by Runge-Kutta method (Boyce and Diprima, 1997) with a time step of 0.001 ms. The simulation always started at the initial condition V_j = 0. The potentials (both trans-membrane potential V_j and extracellular potential V_e,j) at the two end nodes of the modeled axon were always equal to the potentials of their closest neighbors, which implemented the sealed boundary conditions (no longitudinal currents) at the two ends of the modeled axon. The simulations were performed for axons of different diameters (10, 12, and 20 µm) with the temperature parameter set at 37 °C.

3. RESULTS

3.1. Conduction Block Induced by Ultra-High Frequency Biphasic Electrical Current

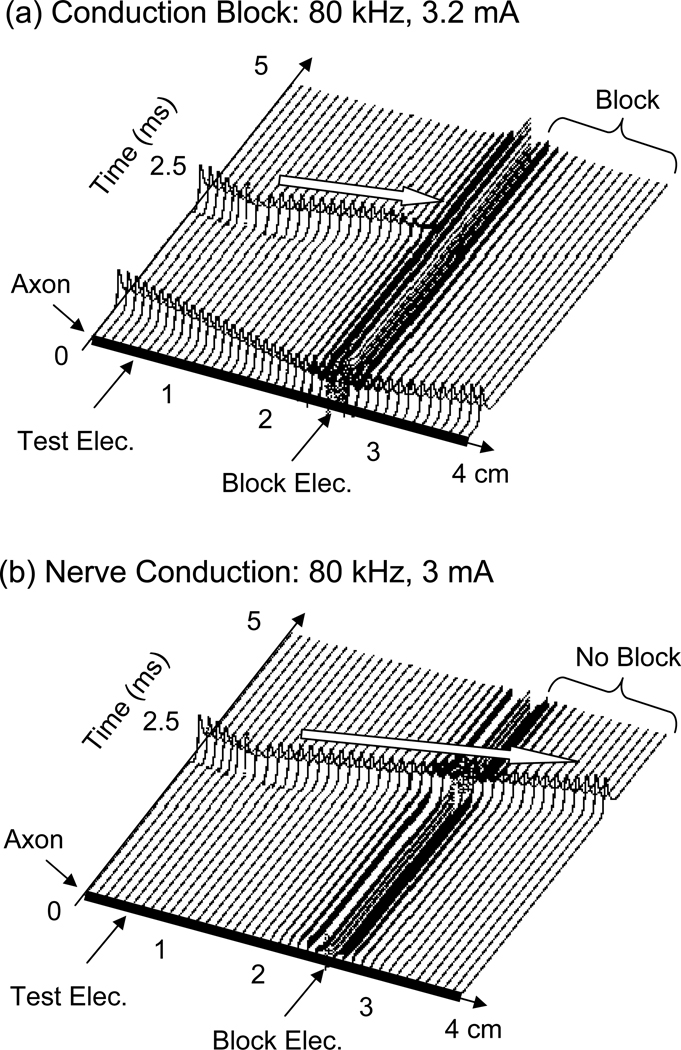
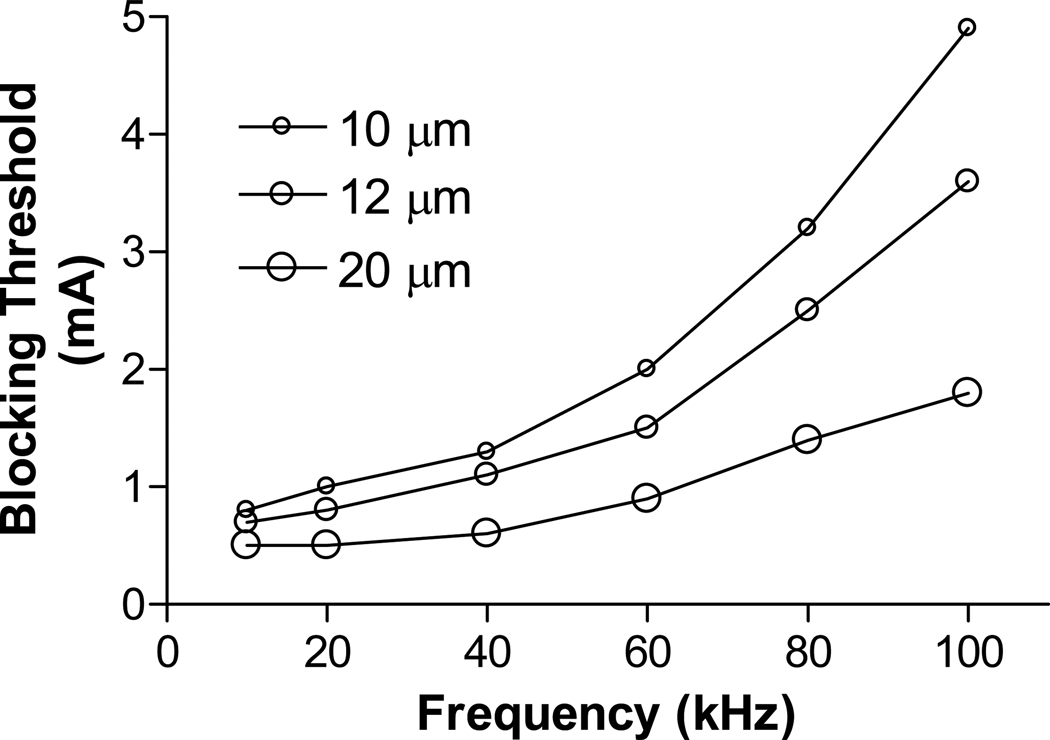
Fig.2 shows that the FH model can simulate the conduction block in myelinated axons induced by ultra-high frequency (80 kHz) biphasic electrical current. In Fig.2 (a) the ultra-high frequency blocking stimulation (3.2 mA) at the block electrode generates an initial action potential that propagates in two directions. Then the ultra-high frequency stimulation alternately depolarizes and hyperpolarizes the axon membrane without generating action potentials. At 2.5 ms after the start of blocking stimulation, the test electrode delivers a single pulse that generates another action potential propagating toward the block electrode [see the white arrow in Fig.2 (a)]. This action potential fails to propagate through the block electrode due to the presence of the ultra-high frequency biphasic electrical stimulation. However, at a lower stimulation intensity [3.0 mA in Fig.2 (b)] the ultra-high frequency stimulation fails to block nerve conduction and the action potential propagates through the site of the block electrode. Fig.3 shows the effective stimulation intensity ranges for inducing conduction block at different frequencies (10–100 kHz). The minimal stimulation intensity required for conduction block increases as the stimulation frequency increases, or as the axon diameter decreases (Fig.3).

Fig.2.

Conduction block induced by ultra-high frequency (80 kHz) biphasic electrical current. The white arrow indicates the propagation of an action potential that is induced by the test electrode at 0.5 cm location along the axon after 2.5 ms of 80 kHz stimulation that is applied by the block electrode at the 2.5 cm location. (a). 80 kHz stimulation blocks the nerve conduction at intensity of 3.2 mA. (b). Conduction block does not occur at 3 mA. Axon diameter: 10 µm.

Fig.3.

Threshold intensity for conduction block changing with stimulation frequency for different diameter axons.

3.2. Mechanism of Conduction Block

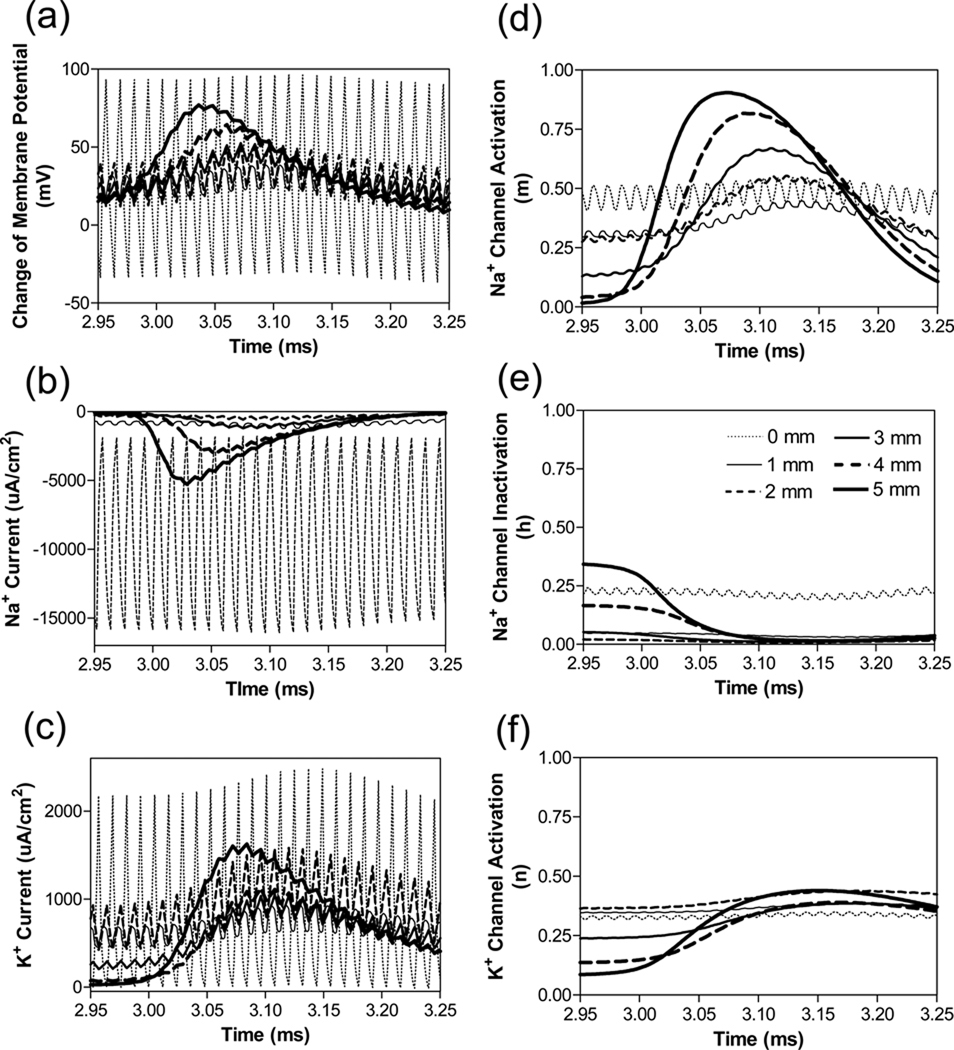
In order to evaluate the possible mechanisms of conduction block at ultra-high frequencies, we further investigated the time course and propagation of membrane potentials, ionic currents, and activation/inactivation of the ion channels near the block electrode when nerve conduction block occurs as shown in Fig.2 (a). Fig.4 shows the same simulation as in Fig.2 (a), including more detailed information about action potentials, sodium currents, and potassium currents at six consecutive nodes at distances of 0–5 mm from the block electrode [node at 0 mm is under the block electrode].

Fig.4.

Propagation of membrane potentials, ionic currents, and activation/inactivation of the ion channels near the block electrode when nerve conduction block occurs as shown in Fig.2 (a) (80 kHz, 3.2 mA). The legends in (e) indicate the distances of each node to the block electrode (node at 0 mm is under the block electrode). Axon diameter: 10 µm.

At nodes approaching the block electrode, the amplitude of these measurements gradually declined [Fig.4 (a)–(c)]. Action potential propagation is completely abolished at the node (0 mm) under the block electrode, where the axon membrane is alternately depolarized and hyperpolarized [Fig.4 (a)] with large sodium and potassium currents [Fig.4 (b) and (c)]. The behavior of the action potential and ionic currents can be explained by the activation/inactivation of the sodium and potassium channels as shown in Fig. 4 (d)–(f). As the action potential propagates toward the block electrode, the activation (m) of sodium channels progressively declines at each node and eventually becomes constant near 0.5 at the node under the block electrode [Fig.4 (d)]. Meanwhile, inactivation (h) of sodium channels is maximal (0.01–0.06) at nodes 1–3 mm from the block electrode [Fig.4 (e)]. Under the block electrode, inactivation (h) of sodium channels is almost constant near 0.25 [Fig.4 (e)]. The combination of activation (m) and inactivation (h) of sodium channels [Fig.4 (d) and (e)] predicts that the amplitude of sodium current gradually attenuates at nodes close to the block electrode and eventually becomes a pulsed inward current at the node (0 mm) under the block electrode [Fig.4 (b)]. The pulsed inward sodium current is synchronized with the change of membrane potential at the node (0 mm) under the block electrode [Fig.4 (a) and (b)], because at this node the sodium channels are constantly open [Fig.4 (d) and (e)] and behave like a resistor.

Meanwhile, the changes in potassium activation (n) induced by the action potentials also gradually disappear at the nodes close to the block electrode [Fig.4 (f)] because the potassium channels are constantly activated at those nodes. The level of potassium channel activation is maximal at nodes within 2 mm of the block electrode, which results in a large pulsed outward potassium current at the node (0 mm) under the block electrode [Fig4 (c)]. This large outward potassium current is also synchronized with the change of membrane potential. Therefore, at ultra-high frequency both sodium and potassium channels are constantly open causing them to behave like resistors rather than gated ionic channels. The persistent open state of both sodium and potassium channels causes the node (0 mm) under the block electrode to become un-excitable leading to block of action potential propagation. The same blocking mechanism is observed for different diameter axons (10, 12, and 20 µm).

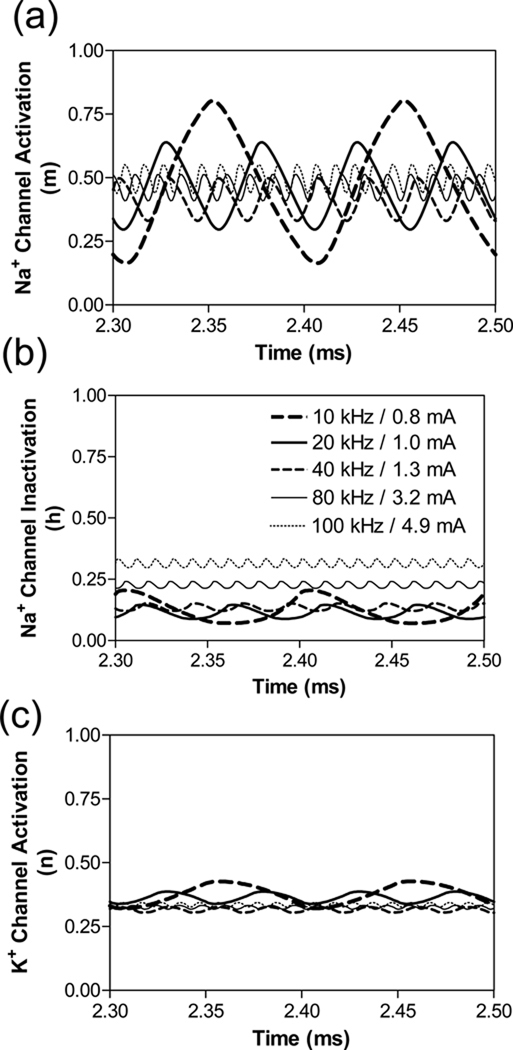
The effect of different frequencies of blocking stimulation on activation and inactivation of sodium and potassium channels is shown in Fig.5. At the 10 kHz frequency the sodium channel activation (m) and inactivation (h) at the node under the block electrode are largely oscillatory between open (m = 1) and closed (m = 0) states during the blocking stimulation [Fig.5 (a) and (b)]. This allows sodium current to be regulated during blocking stimulation. However, as the stimulation frequency increases to the ultra-frequency range (≥20 kHz) both sodium activation (m) and inactivation (h) are almost constant [Fig.5 (a) and (b)] eliminating the ability for the sodium channels to regulate the sodium current during the ultra-high frequency stimulation and resulting in axonal conduction block. In addition, potassium channels are constantly open as the frequency increases to the ultra-high range [Fig.5 (c)].

Fig.5.

The state of ion channels at blocking threshold intensity changes with stimulation frequency. (a). Na⁺ channel activation, (b). Na⁺ channel inactivation, (c). K⁺ channel activation. Legend in (b) indicates the blocking threshold intensity for each frequency. Axon diameter: 10 µm.

4. DISCUSSION

In this study we investigated the possible mechanisms underlying axonal conduction block induced by ultra-high (≥20 kHz) frequency biphasic electrical current in an amphibian myelinated axon using FH model. It reveals that the constant activation of both sodium and potassium channels at the node under the block electrode causes axonal conduction block (Fig.4 and Fig.5). The minimal stimulation intensity required to induce a conduction block increases as the stimulation frequency increases (Fig.3).

The main difference between the mechanisms of conduction block induced by high frequency biphasic electrical current at different frequency ranges (4–10 kHz or ≥20 kHz) lies in the different states of the sodium channels. Our previous studies (Liu et al., 2009; Tai et al., 2005a,b; Zhang et al., 2006a,b) have shown that at a frequency between 4 kHz and 10 kHz the sodium channels are still able to open or close [Fig.5 (a) and (b)] resulting in a large inward sodium current during membrane depolarization. However, due to a constant activation of the potassium channels [Fig.5 (c)] a large outward potassium current is also generated during membrane depolarization, which opposes the large inward sodium current resulting in axonal conduction block (Liu et al., 2009; Tai et al., 2005a,b; Zhang et al., 2006a,b). At a frequency of ≥20 kHz the sodium channels are almost constantly open [Fig.5 (a) and (b)] losing the ability to regulate the sodium current. Therefore, the membrane depolarization does not generate a large inward sodium current [Fig.4 (b)]. Instead, the sodium current is mainly driven by the potential difference across the membrane and becomes synchronized with the change of membrane potential [Fig.4 (b)] causing axonal conduction block. The large outward potassium current during membrane depolarization, although still present at the ultra-high frequency [Fig.4 (c)], is not an essential contributor to the conduction block because the large inward sodium current is absent during depolarization.

A previous computer simulation study (Bhadra et al., 2007) also suggested a different blocking mechanism indicating that a dynamic steady-state depolarization along the axon induced by the high frequency stimulation caused the conduction block. In order to illustrate the dynamic steady-state depolarization existing along the axon, the value of each variable at each axonal node was averaged over two stimulation cycles (Bhadra et al., 2007). The averaging process eliminated the dynamic changes of the membrane potential, ion currents, and ion channel activation/inactivation induced by the high frequency stimulation. Their method was unable to analyze how the sodium and potassium currents were regulated by the ion channel gating parameters during the alternating depolarization and hyperpolarization induced by the biphasic high frequency stimulation. Therefore, the different blocking mechanisms at different frequency ranges of 4–10 kHz and ≥20 kHz could not be distinguished by the dynamic steady-state depolarization theory.

This theory was also used in an early study (Bromm, 1975) to correlate the spike frequency of the nodal membrane to the mean depolarization generated by 4–20 kHz alternating current. However, this theory has a flaw when it is used to analyze axonal conduction block. It can not explain why dynamic steady-state depolarization does not generate repetitive action potentials. The proposed dynamic steady-state depolarization along the axon is different from the depolarization induced by a cathodal DC electrode (Bhadra et al., 2007) because it does not have the large hyperpolarized regions on each side of the depolarized region. Action potentials will be generated if such a depolarization truly exists along the axon (rather than by averaging). Furthermore, the dynamic steady-state theory can not explain why a minimal frequency of 4–5 kHz is required to induce a conduction block since the averaging process eliminates the difference of axonal responses to different stimulation frequencies. On the other hand the dynamic changes of the ion channel gating parameters can be used to successfully explain why the high frequency stimulation ceases generating action potential when conduction block occurs and why a minimal blocking frequency of 4–5 kHz is required (Liu et al., 2009; Tai et al., 2005a,b; Zhang et al., 2006a,b).

High frequency biphasic stimulation can block nerve conduction in both myelinated (Bhadra and Kilgore, 2005; Graunt and Prochazka, 2009; Reboul and Rosenblueth, 1939; Rosenblueth and Reboul, 1939; Tai et al., 2004; 2005c, 2008; Tanner, 1962) and unmyelinated (Joseph and Butera, 2009) axons. In myelinated axons the blocking threshold increases monotonically with the stimulation frequency at the experimentally tested frequency range of 10–30 kHz (Bhadra and Kilgore, 2005), which agrees with our simulation result (Fig.3) in the amphibian myelinated axon model (FH model). We chose the FH model in this study because it successfully simulated spike frequency of the axonal membrane generated by 4–20 kHz alternating current, indicating the model’s ability to accurately predict axonal responses to very high frequency stimulation. Our previous study using another axon model derived from rabbit myelinated nerves (CRRSS model) (Chiu et al., 1979), which ignores the contribution of potassium currents to membrane dynamics, revealed that a minimal blocking frequency of 15 kHz is required to induce inactivation of the sodium channels. Although the 15 kHz is in agreement with this study using FH model in terms of the minimal ultra-high frequency (10–20 kHz), the underlying sodium channel mechanisms are very different. The CRRSS model predicted an inactivation of sodium channels during block, but FH model indicated a constant activation of sodium channels (Figs. 4–5). Whether other mammalian (rat/human) myelinated axon models (SE/SRB models) (Schwarz and Eikhof, 1987; Schwarz et al., 1995) can demonstrate a similar blocking mechanism at minimal ultra-high frequencies (10–20 kHz) or different blocking mechanisms needs to be further investigated. In unmyelinated axons of Aplysia the blocking threshold is maximal at a frequency about 12 kHz, but starts to decrease as the frequency is increased into the ultra-high frequency range (≥20 kHz) (Joseph and Butera, 2009). Whether the unmyelinated axon model (HH model) (Hodgkin and Huxley, 1952) can simulate the change of blocking threshold and reveal a different blocking mechanim at ultra-high frequencies also needs to be investigated.

The results from our computer simulation studies will ultimately need to be confirmed by electrophysiological experiments. Because the electrical artifact generated by the high frequency blocking stimulation makes it very difficult to perform electrophysiological recording of ion channel activity in a single axon, the blocking mechanisms revealed by simulation studies (Liu et al., 2009; Tai et al., 2005a,b; Zhang et al., 2006a,b) have not been verified by direct nerve recordings. However, previous studies (Bikson et al., 2001; Jensen and Durand, 2007; Lian et al., 2003) in rat hippocampal slices showed that the neuronal epileptiform activity and axonal conduction could be blocked by 50–500 Hz sinusoidal electrical field stimulation. The block was always coincident with a stimulus-induced rise in the extracellular potassium concentration, suggesting the opening of the potassium channels and increased potassium outflow from the neurons/axons during the stimulation. The stimulation frequency necessary to block hippocampal neurons/axons is relatively low (<500 Hz) compared to the minimal stimulation frequency (4–5 kHz) required to block conduction in peripheral nerves (Reboul and Rosenblueth, 1939; Rosenblueth and Reboul, 1939). However, this frequency discrepancy might be caused by the slow membrane dynamics of the hippocampal neurons/axons (Bikson et al., 2001; Jensen and Durand, 2007; Lian et al., 2003).

Many results from computer simulation studies also agree very well with animal experiments. For example, our previous simulation studies (Liu et al., 2009; Tai et al., 2005a,b; Zhang et al., 2006a,b) indicate that the minimal axonal blocking frequency is about 4–5 kHz which is similar to the blocking frequency reported in animal studies (Bowman and McNeal, 1986; Reboul and Rosenblueth, 1939; Rosenblueth and Reboul, 1939). Other results predicted by simulation studies and confirmed by animal experiments include: 1) the relationship between minimal blocking frequency and temperature (Tai et al., 2008; Wang et al., 2008); 2) the relationship between minimal blocking intensity and stimulation frequency for myelinated axons (Fig.3) (Graunt and Prochazka, 2009; Bhadra and Kilgore, 2005; Liu et al., 2009; Zhang et al., 2006a,b) and for unmyelinated axons at 4–10 kHz (Joseph and Butera, 2009; Tai et al., 2005a,b); 3) the relationship between blocking intensity and axon diameter (Liu et al., 2009; Tai et al., 2005a,b; Tanner, 1962; Zhang et al., 2006a,b). More animal experiments are warranted to further investigate and confirm the results predicted by computer simulation studies.

Understanding the different blocking mechanisms might help to optimize the blocking stimulation waveforms for different clinical applications. One of the clinical requirements in applying the high frequency nerve block to suppress the chronic pain of peripheral origin is to minimize the initial nerve firing induced by the blocking stimulation. A recent study (Gerges et al., 2010) has shown that the initial firing can be significantly reduced by first applying a 30 kHz stimulation and then shifting the stimulation to a lower frequency (10 kHz). However, why this transition was effective was not discussed. Our current study indicates that different nerve blocking mechanisms might be involved during 10 kHz or 30 kHz stimulation, suggesting that a higher initial frequency (40 or 80 kHz) might further reduce the un-wanted initial nerve firing.

The nerve conduction block induced by high frequency biphasic electrical stimulation can find many applications in both clinical medicine and basic neuroscience (Bhadra and Kilgore, 2005; Graunt and Prochazka, 2009; Tai et al., 2004, 2005c, 2008). Understanding the biophysics underlying this nerve block could improve the design of new stimulation waveforms (Roth, 1994) and further promote their clinical application in neuroprosthetic devices for people with disabilities (Loeb, 1989). Simulation analysis using computer models provides a tool to reveal possible blocking mechanisms and may help to design new animal experiments to further improve the nerve blocking method.

APPENDIX

The ionic current I_i,j at j^th node is described as:

$$\begin{array}{c}{I}_{i,j}=i_{\mathit{\text{Na}}}+i_K+i_P+i_L\hfill \\ i_{\mathit{\text{Na}}}=P_{\mathit{\text{Na}}}{m}^{2}h\frac{{\mathit{\text{EF}}}^2}{\mathit{\text{RT}}}\frac{{[\mathit{\text{Na}}]}_0-{[\mathit{\text{Na}}]}_i{e}^{\mathit{\text{EF}}/\mathit{\text{RT}}}}{1-e^{\mathit{\text{EF}}/\mathit{\text{RT}}}}\hfill \\ i_K=P_K{n}^2\frac{{\mathit{\text{EF}}}^2}{\mathit{\text{RT}}}\frac{{[K]}_0-{[K]}_i{e}^{\mathit{\text{EF}}/\mathit{\text{RT}}}}{1-e^{\mathit{\text{EF}}/\mathit{\text{RT}}}}\hfill \\ i_P=P_P{p}^2\frac{{\mathit{\text{EF}}}^2}{\mathit{\text{RT}}}\frac{{[\mathit{\text{Na}}]}_0-{[\mathit{\text{Na}}]}_i{e}^{\mathit{\text{EF}}/\mathit{\text{RT}}}}{1-e^{\mathit{\text{EF}}/\mathit{\text{RT}}}}\hfill \\ i_L=g_L\left(V_j-V_L\right)\hfill \\ E=V_j+V_{\mathit{\text{rest}}}\hfill \end{array}$$

where P_Na (0.008 cm/s), P_K (0.0012 cm/s) and P_P (0.00054 cm/s) are the ionic permeabilities for sodium, potassium and nonspecific currents respectively; g_L (30.3 kΩ⁻¹ cm⁻²) is the maximum conductance for leakage current. V_L (0.026 mV) is reduced equilibrium membrane potential for leakage ions, in which the resting membrane potential V_rest (−70 mV) has been subtracted. [Na]_i (13.7 mmole/l) and [Na]_o (114.5 mmole/l) are sodium concentrations inside and outside the axon membrane. [K]_i (120 mmole/l) and [K]_o (2.5 mmole/l) are potassium concentrations inside and outside the axon membrane. F (96485 c/mole) is Faraday constant. R (8314.4 mJ/K/mole) is gas constant. m, h, n and p are dimensionless variables, whose values always change between 0 and 1. m and h represent activation and inactivation of sodium channels, whereas n represents activation of potassium channels. p represents activation of non-specific ion channels. The evolution equations for m, h, n and p are the following:

$$\begin{array}{c}\mathit{\text{dm}}/\mathit{\text{dt}}=[{\alpha }_m(1-m)-{\beta }_{m}m]k_m\hfill \\ \mathit{\text{dh}}/\mathit{\text{dt}}=[{\alpha }_h(1-h)-{\beta }_{h}h]k\hfill \\ \mathit{\text{dn}}/\mathit{\text{dt}}=[{\alpha }_n(1-n)-{\beta }_{n}n]k\hfill \\ \mathit{\text{dp}}/\mathit{\text{dt}}=[{\alpha }_p(1-p)-{\beta }_{p}p]k\hfill \end{array}$$

and

$$\begin{array}{c}{\alpha }_m=\frac{0.36(V_j-22)}{1-\text{exp}(\frac{22-V_j}{3})}\hfill \\ {\beta }_m=\frac{0.4(13-V_j)}{1-\text{exp}(\frac{V_j-13}{20})}\hfill \\ {\alpha }_h=\frac{0.1(V_j+10)}{1-\text{exp}(\frac{V_j+10}{6})}\hfill \\ {\beta }_h=\frac{4.5}{1+\text{exp}(\frac{45-V_j}{10})}\hfill \\ {\alpha }_n=\frac{0.02(V_j-35)}{1-\text{exp}(\frac{35-V_j}{10})}\hfill \\ {\beta }_n=\frac{0.05(10-V_j)}{1-\text{exp}(\frac{V_j-10}{10})}\hfill \\ {\alpha }_p=\frac{0.006(V_j-40)}{1-\text{exp}(\frac{40-V_j}{10})}\hfill \\ {\beta }_p=\frac{0.09(V_j+25)}{1-\text{exp}(\frac{V_j+25}{20})}\hfill \\ k_m={1.8}^{(T-293)/10}\hfill \\ k=3^{(T-293)/10}\hfill \end{array}$$

where T is the temperature in °Kelvin. The initial values for m, h, n and p (when V_j = 0 mV) are 0.0005, 0.0268, 0.8249 and 0.0049 respectively.