Multi-scale Modeling in Biology: How to Bridge the Gaps between Scales?

Abstract

Human physiological functions are regulated across many orders of magnitude in space and time. Integrating the information and dynamics from one scale to another is critical for the understanding of human physiology and the treatment of diseases. Multi-scale modeling, as a computational approach, has been widely adopted by researchers in computational and systems biology. A key unsolved issue is how to represent appropriately the dynamical behaviors of a high-dimensional model of a lower scale by a low-dimensional model of a higher scale, so that it can be used to investigate complex dynamical behaviors at even higher scales of integration. In the article, we first review the widely-used different modeling methodologies and their applications at different scales. We then discuss the gaps between different modeling methodologies and between scales, and discuss potential methods for bridging the gaps between scales.

1. Introduction

1.1. Multi-scale regulation of biological systems

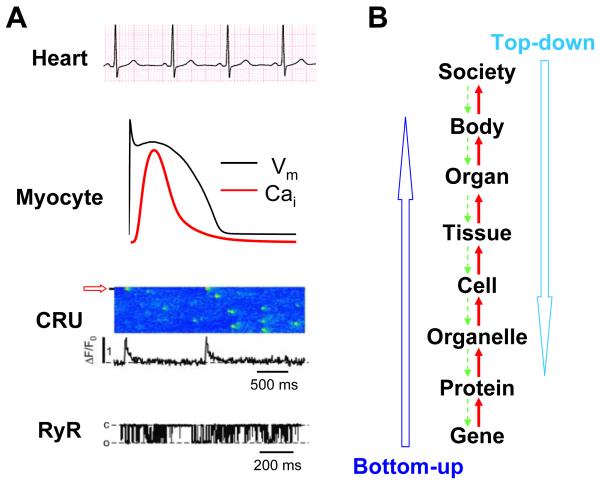
Biological systems are regulated at scales of many orders of magnitude in space and time, with space spanning from the molecular scale (10⁻¹⁰ m) to the living organism scale (1 m), and time from nanoseconds (10⁻⁹ s) to years (10⁸ s). At the molecular scale, the dynamics is dominated by random and short time scale fluctuations, while at the organ or organism scale, the dynamics is more deterministic with longer time scale variations. As a typical example, Fig.1A illustrates the scale and dynamical changes of cardiac excitation (Cheng and Lederer, 2008; Weiss et al., 2011; Zima et al., 2008). A single ion channel, e.g., a ryanodine receptor (RyR), opens and closes randomly, at sub-millisecond or millisecond time scales. A group of RyRs (20 to 100) that form a calcium (Ca) release unit (CRU) opens and closes collectively to give rise to a Ca flux pulse (Ca spark) of 20-50 milliseconds duration with a firing interval at the second scale, which still occurs randomly with large variations in duration and timing. At the whole-cell scale, an electrical stimulation gives rise to an action potential which elicits a whole-cell Ca transient. Since the action potential is the result of thousands of ion channels and the Ca transient the summation of thousands of Ca sparks, the randomness is substantially reduced at the cellular level. In the whole heart, the electrical impulses originating from the sino-atrial node propagate from the atrium to the ventricles, causing synchronous contractions of the ventricles at a period of 1 sec or so, as shown by the electrocardiogram. Since a heart contains millions of cells, the randomness is further reduced. In general, biological systems exhibit a hierarchical structure (Fig.1B): genes encode proteins; proteins are building blocks of organelles and cells; and cells form tissue and organ, etc. However, the higher levels also affect the lower ones, such as proteins modulating gene expression, forming feedback loops between scales. Therefore, in a biological system, interactions can occur at the same scale (such as interactions between different genes) as well as between scales, forming a complex system with multiple spatial and temporal scales and feedback loops, which becomes not only extremely difficult for interpreting experimental results, but also is nontrivial for mathematical modeling.

Figure 1. Multi-scale regulation in biology.

A. An example of multi-scale regulation in cardiac excitation. RyR: A recording of a single RyR opening and closing (Zima et al., 2008). CRU: Ca sparks in a cardiac myocyte shown as a line-scan (time-space plot) (Zima et al., 2008). Red arrow indicates the location where the Ca transient (below) was recorded. Myocyte: An action potential (black) and the companion whole-cell Ca transient (red). Heart: A normal ECG. B. A schematic plot of different scales and their interactions in biology.

1.2. Bottom-up and top-down approaches

Biological systems are usually modeled in two ways: bottom-up or top-down (Fig.1B). The bottom-up approach models a system by directly simulating the individual elements and their interactions to investigate the system’s behaviors. For example, one can use Newton’s second law of motion to describe the motions of the molecules composed of a protein or an ion channel (the so-called molecular dynamics simulation), to study protein folding dynamics or ion channel opening and closing, or one can use the cells as the basic elements and study tissue-level properties as results of the interactions of the cells. This type of model has the advantage that it is adaptive and robust, and it is suitable for studying the emergent properties of systems consisting of a large number of interacting elements. The disadvantage is that it is computationally intensive, often prohibitively so, and the model itself can become too complicated to be grasped. Instead of looking into the details of the individual elements, the top-down approach considers the system as a whole and uses the macroscopic behaviors of the system as variables to model the system dynamics at the macroscopic scale, largely based on experimental observations. For example, when modeling the action potential of a cell, one can ignore the detailed properties of the individual ion channels, and directly model the whole-cell currents and their voltage dependence based on whole-cell experimental recordings. This approach was used by Hodgkin and Huxley for the action potential model of the giant axon (Hodgkin and Huxley, 1952). The advantage of the top-down approach is that it is relatively simple and more easily grasped. The disadvantage is that the model is less adaptive and robust. In addition, the variables and parameters in these models are largely phenomenological without direct connection with detailed physiological parameters, so that information on how to experimentally alter the system behavior is usually not clear (e.g., the link between a genetic defect of an ion channel and cellular electrophysiology may not be clear in the Hodgkin and Huxley formulation but may be more explicit in the Markovian formulation (Clancy and Rudy, 1999)). Sometimes, where there are multiple mechanisms for the same behavior or a single mechanism resulting in multiple phenomena, the top-down approach may not correctly reveal the actual responsible mechanism.

1.3. Multi-scale modeling

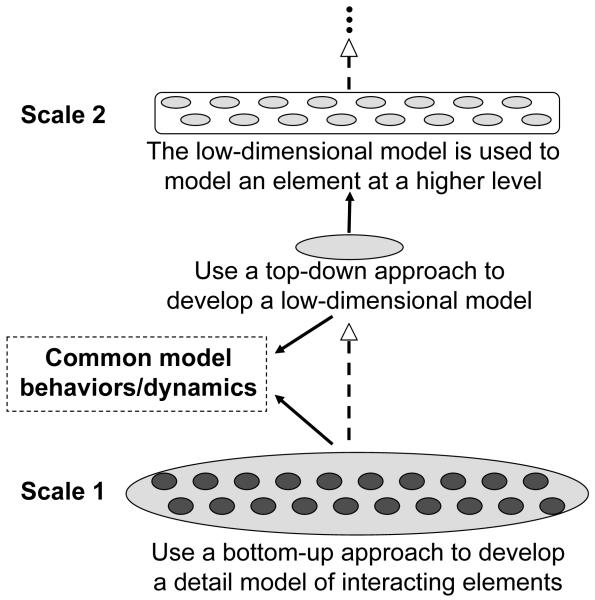
To link a gene or a protein to a biological function of an organ or a disease, we need to understand how the genes or proteins interact with each other to result in the function. In theory, one can construct a model of a biological system (such as a cardiac cell or the heart) consisting of the genes and proteins, or even the atoms. In practice, however, existing computational tools are radically insufficient for this task. On the other hand, biological experiments are conducted at many scales, ranging from single proteins to whole organs, and therefore, the experimental information exists at many different scales. Based on the experimental information, a model can be developed either using the top-down approach or the bottom-up approach. For example, the whole-cell ionic currents can be modeled using the Hodgkin and Huxley formulation of differential equations based on the experimental measurements of the whole-cell ion channel conductance and kinetics; it can also be modeled by summing up the single channel currents which are simulated from stochastic Markovian models based on single channel recordings. In modeling cardiac conduction in tissue or heart, one usually take the differential equation description of the cell model and couples cells together to study the excitation dynamics. But if one wants to link the single channel behaviors to conduction dynamics in tissue, one needs to represent the cell by stochastic single channels and couple the cells to form tissue and heart. Since a cell is composed of thousands of ion channels and a heart contains millions of cells, this is an almost impossible task using current computational technology. A compromise approach is that one first models the cell by simulating the single channel with Markovian transitions to study single cell behaviors. Combining the simulated behaviors with the experimental results of whole-cell recordings, one then develops a low-dimensional single cell model and couples many of them to form a tissue or whole-heart model. We refer to this type of modeling approach as multi-scale modeling. Multi-scale modeling has been drawn a great deal of attention in biological modeling and is discussed in many recent review articles (Bassingthwaighte et al., 2005; Coveney and Fowler, 2005; Engler et al., 2009; Grima, 2008; Hunter and Nielsen, 2005; Meier-Schellersheim et al., 2009; Murtola et al., 2009; Schnell et al., 2007; Southern et al., 2008; Bradley et al., 2011; Joshi et al., 2011). Although a common definition of multi-scale modeling is still lacking, the goal of multi-scale modeling is not simply to model a system at multiple scales, but rather to conserve the information from a lower scale (modeled by high-dimensional models) to a higher scale (modeled by low-dimensional models), so that the information from the very bottom scale can be carried to the top scale correctly. Figure 2 illustrates the basic idea of multi-scale modeling. One first uses a bottom-up approach to develop a model at one scale composed of the interacting elements, such as the atoms forming a protein or the ion channels in a cell, and then studies by simulation the behaviors of the system. Based on the simulated properties (and also the known experimental observations), one can then use a top-down approach to develop a low-dimensional model to describe those same properties of the system. The model can be either totally phenomenological or derived using statistical methods, or from a mixed approach. A key requirement is that the two types of models should exhibit the same behaviors or dynamics (and also be validated experimentally) so that the low-dimensional model is an accurate (or appropriate) representation of the system. Then one can use the low-dimensional model to represent the elements in a higher scale. The same treatment can be repeated for higher scales. In the multi-scale approach, it requires different mathematical means of description at different scales and different computational technologies. For example, one uses Markovian transitions to simulate stochastic opening and closing of a single ion channel, ordinary differential equations (ODEs) to model the action potential and the whole-cell Ca transient of a cell, and partial differential equations (PDEs) to model electrical wave conduction in tissue and heart. However, despite the attractiveness of this method, it faces many challenges, such as the gaps between models of different scales and inconsistencies between different methodologies.

Figure 2. Multi-scale modeling.

See text for detailed description.

In this review, we first summarize the methodologies used in modeling biological systems and the gaps and inconsistencies between methodologies and between models at different scales. We then discuss what existing methods and theories may be used to bridge these gaps.

2. Modeling methodologies and their applications at different scales

Many computational and mathematical methods have been used in modeling biological systems, including deterministic, stochastic, and discrete and rule-based approaches. Here we summarize the different methodologies and their applications to modeling in biology.

2.1. Differential equations

Deterministic systems are usually modeled by differential equations, which have been widely used in biological modeling. The most fundamental one is in molecular dynamics simulations (Karplus and Petsko, 1990) in which the atoms or molecules are modeled using the Newton’s second law of motion, i.e.,

$$m_{i}d{v}_i∕dt=F_i$$ (1)

where m_i is the mass of a molecule in the system, v_i is its velocity, and F_i is total force acting on the molecule, via van der Waals interactions (Karplus and Petsko, 1990). Therefore, as long as F_i is defined, the motion of the molecules can be simulated. Although this method is widely used for many biological problems (Chu et al., 2007; Dodson et al., 2008; Kamerlin et al., 2010; Karplus and Kuriyan, 2005; Murtola et al., 2009), it is computationally very difficult, and one can rarely simulate a system beyond the microsecond time span, even with the most powerful available computational tools (Klepeis et al., 2009), although a recent simulation study with a special purpose computer was able to simulate protein dynamics over a remarkable 1 millisecond (Shaw et al., 2010).

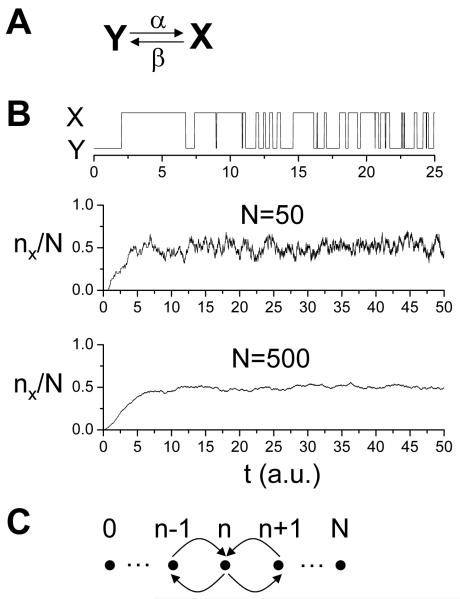
Biological oscillations occur at many time scales [e.g., from one-second heart beat intervals to 24-hour periods of cell cycle and circadian rhythm (Tsai et al., 2008)], that are much longer than a microsecond. To simulate such systems, modeling molecular dynamics at the atomistic level is impossible. Traditionally, ODEs describing the macroscopic properties are widely used to model these systems (Keener and Sneyd, 1998; Murray, 1993). One typical example is biochemical reactions (such as gene regulation, protein-protein interactions, and metabolic reactions, etc.) which are modeled with ODEs following the law of mass action (Michaelis and Menten, 1913) under the assumption that the number of molecules of the reactants is large and the system is well stirred. For example, for a simple reaction in which protein Y changes to protein X and vice versa (Fig.3A) (such as the protein phosphorylation-dephosphorylation cycle or the conformational change of an ion channel protein resulting in random openings and closings), the ODE for the concentration of molecule X (or the probability of the open state of the ion channel) is derived as follows: the production rate of X is α[Y]=α(1-[X]) and the decay rate is β[X], and thus the total rate change of [X] is:

$$d\left[X\right]∕dt=\alpha (1-\left[X\right])-\beta \left[X\right]$$ (2)

where [X]+[Y]=1. ODEs derived following the law of mass action have been widely applied in modeling biological oscillations and signal transduction (Goldbeter, 1995; Kholodenko, 2000; Qu et al., 2003; Tyson et al., 2003). Other typical examples of ODE modeling are action potential models of excitable cells (Hodgkin and Huxley, 1952), whole-cell Ca transient in Ca signaling (De Young and Keizer, 1992; Greenstein and Winslow, 2011), and membrane potential of mitochondria (Cortassa et al., 2003; Magnus and Keizer, 1997; Wu et al., 2007), etc.

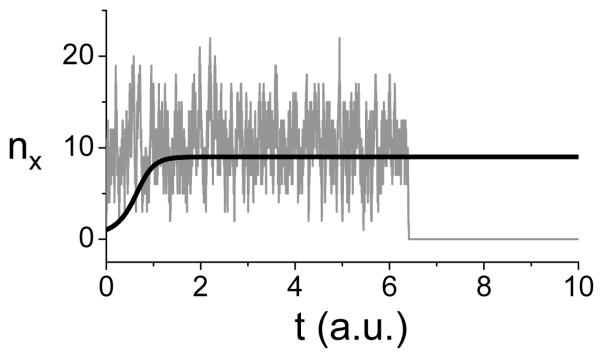
Figure 3. Stochastic simulation.

A. A simple reaction scheme in which Y changes to X with a reaction rate constant α and changes back with rate β. B. Upper trace: A stochastic simulation of the model in A using the Gillespie algorithm, showing random switching between Y and X. α=β=1 was used in the simulation. Middle trace: The ratio between the number (n_x) of the X molecule and the total molecules (N) versus time when N=50. Bottom trace: n_x/N versus time when N=500. For this simple model, as N increases, n_x/N approaches the steady state of the deterministic equation (Eq.2): α/(α+β)=0.5, with smaller and smaller fluctuations. C. A schematic plot of the transitions from different states of the X molecule in an N-molecule system.

If the ions or molecules also diffuse in space, diffusion terms are added to the ODEs to form PDEs, the reaction-diffusion equations, to model spatiotemporal properties. For example, if X diffuses in space, then the reaction-diffusion equation is:

$$\partial \left[X\right]∕\partial t=\alpha (1-\left[X\right])-\beta \left[X\right]+D{\partial }^2\left[X\right]∕\partial x^2$$ (3)

where D is the diffusion constant. Reaction-diffusion equations have been used for pattern formation (Garfinkel et al., 2004; Kondo and Miura, 2010; Meinhardt and Gierer, 2000), that was first studied by Turing (Turing, 1952). Reaction-diffusion equations are also used to model electrical wave conduction in cardiac systems and in neurons (Keener and Sneyd, 1998). Other types of PDEs are used in modeling mechanics and fluid dynamics in many biological systems, such as cardiovascular systems (Hunter et al., 2003; Nordsletten et al., 2011).

2.2. Stochastic methods

Deterministic ODEs, PDEs or coupled ODEs have been the dominant methods used in biological modeling in the past. However, the proteins that accumulate in biological systems are subject to thermodynamic fluctuations, and therefore, stochastic properties may play important roles in cellular and tissue scale functions, which is a major topic in current modeling of biological systems. Since the noise strength of a system with N molecules is proportional to $1∕\sqrt{N}$, deterministic modeling, except of course for molecular dynamics simulation, requires that the number of molecules is large or the concentration is high (therefore $1∕\sqrt{N}\to 0$. In real systems, the protein concentrations may not be high enough and are usually distributed in space, thus deterministic modeling may not be accurate or even appropriate, and stochastic methods are needed to take into account the random fluctuations that occur in these systems.

Gillespie (Gillespie, 1977; Gillespie, 2007) developed an exact stochastic simulation algorithm (SSA) to simulate chemical reactions by representing the individual reactions as Markov transitions. This method is widely known as the Gillespie algorithm. For example, for the reaction in Fig.3A, once the molecule has changed from state X to state Y, the chance that it remains in state Y decays with time as e^−t/α with an average dwell time 1/α. To simulate the stochastic transition from Y to X, a random number r, uniformly distributed between 0 and 1, is generated from the computer and the equation r = e^−τ/α is used to determine the actual dwell time τ of molecule Y. Therefore, at time point τ, the reaction from Y to X occurs. Once the molecule has changed from Y to X, another random number r is generated and the equation r = e^−τ/β is used to determine the dwell time τ of molecule X. By iterating this process, one obtains the stochastic reaction sequence of a single molecule or many molecules (Fig.3B). The reaction in Fig.3A is the simplest reaction, but the method is applicable to any chemical reaction scheme (Gillespie, 1977; Gillespie, 2007). However, as the copy number of the molecules becomes larger, the SSA is computationally more and more expensive. The method has been improved to speed up computation (e.g., the tau-leaping method by Cao et al (Cao et al., 2005)). SSA has been widely used in recent years for biochemical reactions (Bishop and Qian, 2010; Miller and Beard, 2008; Samoilov et al., 2005), and the same method or similar ones are also widely used in simulating stochastic opening and closing of ion channels (Clancy and Rudy, 1999; Clay and DeFelice, 1983; Rovetti et al., 2010).

Another exact representation of a stochastic chemical reaction system is called the chemical master equation (CME) (Liang and Qian, 2010; Nicolis and Prigogine, 1977). For example, for a total of N molecules in the reaction shown in Fig.3A, the possible states of the system are 0, 1, 2, …, N X molecules and correspondingly N, N-1, N-2, …, 0 Y molecules. Assuming that the probability of n X molecules at time t is p_x(n,t), then the rate change of this probability is composed of four transitions (Fig.3C), which give rise to a set of (N+1) ODEs:

$$d{p}_x(n,t)∕dt=\alpha (N-n+1)p_x(n-1,t)+\beta (n+1)p_x(n+1,t)-\beta n{p}_x(n,t)-\alpha (N-n)p_x(n,t),n=0,\dots ,\mathrm{N}$$ (4)

Starting from an initial distribution p_x(n,0) (n=0,1,…,N), the ODEs can be solved to obtain p_x(n,t). However, as the copy number N becomes very large, the CME becomes computationally difficult.

When the copy number of the molecules is large, the CME can be reduced to a Langevin equation, which is a stochastic differential equation. The Langevin equation was originally proposed to describe the motion of a Brownian particle according to Newton’s law of motion subjected to a frictional force and a stochastic force (Coffey et al., 2004). The general form of the Langevin equation is as follows:

$$dx∕dt=f(x,t)+g(x,t)\xi \left(t\right)$$ (5)

where ξ(t) represents the noise. If g(x,t) is a constant, the noise is called additive noise. If g(x,t) is not a constant, then the noise is called multiplicative noise or intrinsic noise. The advantage of the Langevin equation is that it is computationally trivial compared to solving the CME or a stochastic simulation using the SSA, and it is much easier for mathematical analysis. However, it can be derived from the CME only when N is very large.

The probability distribution of a stochastic system can be described by a PDE, the Fokker-Plank equation (Risken, 1989). The corresponding Fokker-Plank equation for Eq.5 is (Stratonovich’s definition):

$$\frac{\partial p(x,t)}{\partial t}=-\frac{\partial }{\partial x}[f(x,t)+g^{\prime }(x,t)g(x,t)]p(x,t)+\frac{{\partial }^2}{\partial x^2}{g}^2(x,t)p(x,t)$$ (6)

Although the Langevin equation is much simpler than the CME, it is still computationally intensive to obtain a probability distribution. The Fokker-Plank equation is more convenient for analytical treatment of the time evolution of the probability distribution and for the calculation of the steady state probability distribution (Horsthemke and Lefever, 1984; Hu et al., 1990; Qu et al., 1993; Risken, 1989; Smythe et al., 1983).

2.3. Discrete and rule-based methods

Temporally and spatially discrete methods are widely used in modeling biological systems. In some of the methods, the elements in the system are not described by well-defined functions as in the continuous methods, but instead rules are assigned to the participating elements to study the properties that emerge due to the interactions of the elements, generally known as rule-based or agent-based modeling. These methods include difference equation, cellular automata, Boolean networks, multi-agents, and Ising models, etc. In general, these models are used to describe large systems with many elements, and are computationally much cheaper than the corresponding continuous models.

Difference equations (or iterated maps) are used to describe the functional relation of the state of a system at the present time to the state in a previous time point. For example, the well known Logistic Equation (May, 1976):

$$x_{n+1}=a{x}_n(1-x_n)$$ (7)

is used to describe the relationship of the population of a system at the present generation (x_n+1) to the previous generation (x_n). In nonlinear dynamics, this type of equation is generally called a Poincare map or a return map (Hilborn, 1994). Iterated maps have been used in many biological problems, such as cardiac excitation and excitation-contraction coupling (Cui et al., 2009; Guevara et al., 1981; Lewis and Guevara, 1990; Qu et al., 2007; Qu et al., 2010) and neural excitation (Achuthan and Canavier, 2009), etc. Iterated maps are also coupled to study spatiotemporal dynamics of complex systems (Kaneko, 1992; Qu and Hu, 1994), such as cardiac conduction (Wang et al., 2007).

Cellular automata are widely used to study complex behaviors of coupled simple elements, including many biological systems (Gerhardt et al., 1990; Schnell et al., 2007; Torquato, 2011; Wolfram, 1983). They are discrete models consisting of a regular grid of elements (or cells), in which each element can exhibit several discrete states. The states of the elements are updated at discrete time points following certain rules in which the current state of an element is determined by the state of that element and its neighboring elements at the previous time point. For example, the rule can be that the element itself changes from state “0” to state “1” with a certain probability, but if the majority of the neighbors are already in state “1”, the probability for the transition from state “0” to state “1” then increases to a higher value, and otherwise the probability discreases.

Boolean networks were first proposed by Kauffman (Kauffman, 1969) to study gene expression dynamics in gene networks. These are random network models in which the states of an element (gene) are discrete, being either 0 (inactive) or 1 (active). Differing from typical cellular automaton models, each element has several random inputs and state of the element is determined by a Boolean function. Time is also discrete, and the state of an element at the present time is determined using a Boolean function associating with the element to the state of its input elements at the previous time point. Besides its wide use in modeling gene networks, it has also been used to study other biological functions, such as cell cycle control (Bornholdt, 2008; Li et al., 2004; Singhania et al., 2011).

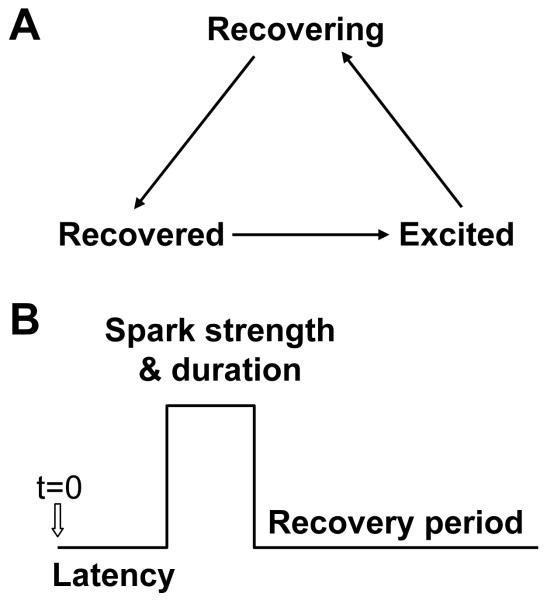
Agent-based modeling is a modeling methodology that stems from cellular automata, but where the elements (agents) are assigned more complex rules and the rules can differ among agents. An agent can be a company, a group, a person, a species, a cell, an organelle, or a protein. Agent-based modeling is used for social networks (Bankes, 2002) and biological systems (Cui et al., 2009; Emonet et al., 2005; Levin et al., 1998; Maltsev et al., 2011; Nadell et al., 2010; Sneddon et al., 2011; Sutterlin et al., 2009). For example, in a cardiac myocyte, a Ca spark is a discrete random event (Bridge et al., 1999; Cheng and Lederer, 2008), which is a collective behavior of many RyRs in a CRU. One can directly model a Ca spark by using the RyRs described by stochastic Markovian transitions as shown in many studies (Rovetti et al., 2010; Sobie et al., 2002). One can also represent a CRU as an agent, and assign certain experimentally observed characteristic behaviors to it (Cui et al., 2009; Maltsev et al., 2011). Figure 4 shows such a model of a Ca spark, in which a CRU is described by a 3-state agent undergoing the following cycle: recovered→excited→recovering→recovered. The transition from the recovered state to the excited state is random which models the latency of spark firing observed in experiments (Inoue and Bridge, 2005). The duration of the spark can be either fixed or random, and the strength of the spark can also be varied based on experimental observations. After the spark, the CRU undergoes a recovery period which may also be random, due to random ion channel opening and closing. By coupling many such agents together, one can study the collective behaviors of the system of many CRUs, which has been used in recent studies (Cui et al., 2009; Maltsev et al., 2011) to study the whole-cell Ca dynamics. Besides the obvious advantage of being computationally much simpler, the agent-based model is also suitable for sorting out the effects of the individual properties of the elements (such as spark duration, recovery period, etc.) on the whole-cell dynamics, since the properties of the agents can be varied independently in this type of modeling.

Figure 4. An agent-based model of a Ca spark.

A. A 3-state model of a CRU. Recovered—the CRU is recovered available to spark; Excited—the CRU fires; Recovering—the CRU is in the recovery period. The transitions between these states are random. B. Schematic plot of Ca spark showing the latency period after a stimulus applied at t=0, the spark duration and strength, and the recovery period.

The Ising model or its general form, the Potts model, is also used in modeling in biology (Scianna et al., 2011; Torquato, 2011). The Ising model is a model of ferromagnetism in statistical physics, which was used to study phase transitions in physical systems. The model consists of a regular lattice with the elements (the magnets) having two states: +1 and −1. Each element only interacts with its nearest neighbors. A phase transition can occur depending on the temperature of the system. In the Potts model, the elements can have more states.

Except for iterated maps, the elements in the other discrete methods are not governed by well defined mathematical functions but follow certain given rules. In general, this methodology is also called rule-based modeling. The common idea behind these models is that the individual elements follow simple rules, but their interactions can give rise to wholly new behaviors at the whole-system level. Thus, they can be used to investigate emergent behaviors in complex systems. The advantage is that these types of models can be used for systems in which the elements cannot be well defined by a mathematical function but can be defined with rules. Most importantly, they are computationally much simpler than the corresponding continuous models. The disadvantage is that it is not accurate for quantitative modeling. In many cases, these discrete models are used in combination with continuous models to form hybrid models to study certain problems (Cui et al., 2009; Maltsev et al., 2011; Singhania et al., 2011; Wylie et al., 2006).

3. Gaps between methodologies and between scales

3.1. Keizer’s paradox

Keizer’s paradox is an example illustrating that one may draw very different conclusions from a stochastic model and a deterministic model (Vellela and Qian, 2007). Consider the set of reactions: A + X ↔ 2X , X → C , where we assume that the number of molecule A is constant and allow the number of molecule X to vary. The deterministic model for these reactions using the law of mass action is an ODE: d[X]/dt = α[X] − β[X ]², which has two fixed points, an unstable fixed point at [X]=0 and a stable fixed point at [X]=α/β. Thus, starting with any nonzero amount of [X], the system will tend toward the nonzero fixed point (black line in Fig.5).

Figure 5. Keizer’s paradox.

Black line: the concentration of the X molecule versus time obtained by solving the differential equation. Gray line: the number (n_x) of the X molecule from a stochastic simulation of the model using the Gillespie algorithm.

The stochastic model can be written in terms of the CME (Vellela and Qian, 2007). For all sets of parameter values, as time tends toward infinity, the probability density function becomes a delta function over n_x=0, where n_x is the number of molecule X. In other words, the CME only has one stable steady state corresponding to n_x=0. This is different from the prediction of the deterministic model in which [X]=0 is an unstable steady state and [X]=α/β is the stable steady state. Therefore, the conclusion from the deterministic model is that the system will always approach the nonzero steady state while the conclusion from the CME is that the system will always undergo extinction. In direct stochastic simulation of the CME with finite number of molecule X, the system fluctuates around the deterministic solution but it eventually undergoes extinction (gray line in Fig.5), and the time to extinction grows exponentially with the total number of molecules in the system (Vellela and Qian, 2007).

3.2. Noise-induced phase transitions

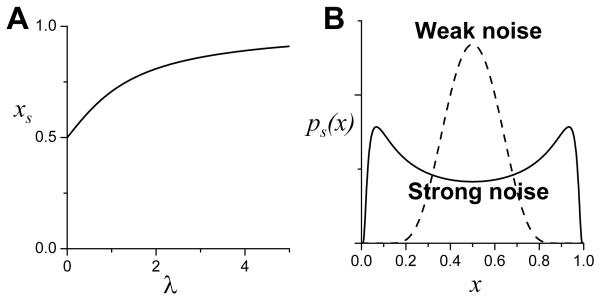
A system with noise may exhibit qualitatively different behaviors than a system without noise. In other words, a phase transition can be induced by noise. This has been widely studied in nonlinear dynamics both theoretically and experimentally (Horsthemke and Lefever, 1984; Hu and He, 1992; Kawai et al., 2004; Lett et al., 1987; Smythe et al., 1983). A typical such example is noise-induced bistability. Consider the following deterministic model (Horsthemke and Lefever, 1984; Smythe et al., 1983):

$$\stackrel{.}{x}=0.5-x+\lambda x(1-x)$$ (8)

which only has one steady state between 0 and 1 (Fig.6A). Assuming that noise is present in parameter λ, then substituting λ with λ+σξ(t) in Eq.8, one obtains a Langevin equation:

$$\stackrel{.}{x}=0.5-x+\lambda x(1-x)+\sigma \xi \left(t\right)x(1-x)$$ (9)

where σ is the strength of noise and ξ(t) is the random white noise satisfying: < ξ(t) >= 0 and < ξ(t)ξ(t’) > = δ(t − t’). One can use the corresponding Fokker-Plank equation to obtain the steady state distribution of the probability p_s(x). When the noise is weak (small σ), p_s(x) has a single peak located at the steady state of Eq.8, but when the noise is strong, p_s(x) can exhibit two peaks (Fig.6B). Therefore, in a deterministic system that cannot exhibit bistability, bistability could be induced by noise under certain conditions. Noise-induced bistability has been shown recently in biochemical reactions using direct stochastic simulations (Bishop and Qian, 2010; Miller and Beard, 2008; Samoilov et al., 2005). In addition, oscillatory behaviors in stochastic representation are also qualitatively different from those in the deterministic representation (Qian et al., 2002; Vellela and Qian, 2009). Therefore, the presence of noise plays a very nontrivial role by inducing qualitatively new properties to the system under certain conditions, raising the issue of how to choose a proper method to model a system.

Figure 6. Noise-induced phase transition.

A. Steady state of the deterministic model (Eq.8). B. Steady state of probability distributions of the stochastic model (Eq.9) when λ=0 with weak noise (dashed) and strong noise (solid).

3.3. Gaps between a three-dimensional cell and a zero-dimensional cell model

A cell is traditionally treated as a basic unit of a biological system, and therefore, many models have treated the cell as a point, also called a 0-dimensional (0D) system. Treating a cell as a point is a simplification for tissue scale modeling, such as modeling the excitation and contraction of the heart, since a cell is in reality a three-dimensional system with complex heterogeneous sub-cellular compartments. Therefore whether a cell can be treated as a 0D system is an open question. A typical example is Ca signaling. In many cells, spatiotemporal Ca dynamics occurs as Ca sparks, short lived Ca waves, full Ca waves, and spiral waves (Cheng et al., 1996; Girard et al., 1992; Lechleiter et al., 1991; Lipp and Niggli, 1993; Marchant and Parker, 2001; Wier et al., 1997). At the whole-cell level, these sub-cellular Ca dynamics give rise to whole-cell Ca oscillations. However, the whole-cell Ca transient depends strongly on the form of the sub-cellular Ca waves. As illustrated in Fig.7, a Ca wave can originate from one end of the cell, from the center of the cell, or multiple waves can occur at different locations and time, or even spiral waves can develop. These waves result in different whole-cell Ca transients. For example, in the first two cases, the Ca waves are the same, but the one originating from one end of the cell takes twice as long to conduct through the cell as the one originating from the center. Therefore, the corresponding Ca transient is wider and smaller in the former case, but narrower and larger in later. In cardiac myocytes, this also results in different properties of contraction. How to consistently reconcile the two situations in a low-dimensional model of Ca signaling is not clear at all. Although in many models of Ca signaling, both low-dimensional models (top-down models) and high-dimensional models (bottom-up models) have been developed, the question of how to bridge the gaps between the two types of models has never been addressed. Similar to Ca signaling, proteins also exhibit spatiotemporal dynamics, such as in cell cycle control (Clute and Pines, 1999; Pines, 1999; Yang et al., 2006), protein kinase signaling (Kholodenko, 2003; Neves et al., 2008), and metabolic dynamics (Aon et al., 2004; Brady et al., 2004; Yang et al., 2010). The sub-cellular dynamics occur in a three-dimensional space, and how to represent the spatiotemporal dynamics accurately in a 0D cell model so that the sub-cellular information is carried to the tissue scale is unclear.

Figure 7. Illustrative plots of sub-cellular waves.

A. A wave occurring at one end of a cell propagates to the other end. B. A wave occurring at the center of a cell propagating to both ends. C. Multiple waves occurring at different locations and time. D. A spiral wave.

4. Closing up the gaps—methods and challenges

Modeling a biological system at multiple scales unavoidably leave gaps between scales due to the different methodologies and reduction in dimensions of freedom, as discussed in the examples above. Multi-scale modeling, besides modeling the system, needs to address the issue of how to bridge the gaps between different methodologies and between models at different scales. There is no straightforward way to go from one scale to another, but there are useful methods that may be used to bridge the gaps.

4.1. Mean field theory

Mean field theory is widely known in statistical physics as a method for reducing a many-body problem to a one-body problem with macroscopic/phenomenological variables (Kadanoff, 2000), it is also widely used in biological modeling (Baker and Simpson, 2010; Cui et al., 2009; Grima, 2008; Loew et al., 2009; Naundorf et al., 2006; Rovetti et al., 2010). Mean field theory treats a system by assuming that the elements are controlled by a single mean field, which is created by all the elements themselves. Mean field theory is accurate when the elements are globally coupled or when the system is well mixed. Using this theory, one can reduce a very high-dimensional problem into a very low-dimensional problem so that it is convenient for mathematical analysis and mechanistic understanding. However, when the temporal and spatial fluctuations are large (e.g., when the protein copy number is low or the coupling is strong), the mean field representation becomes inaccurate and even incorrect. For example, the mean field approach may not be appropriate for the case illustrated in Fig.7, since at each moment, the Ca concentration is very different in different locations, and thus the assumption of all the elements (the CRUs) experiencing the same mean field (e.g., averaged Ca concentration) is invalid. Nevertheless, mean field theory is a good approximation under many conditions and can provide mechanistic insights. In particular, one may be able to develop a useful low-dimensional representation of a high-dimensional system, which is key for multi-scale modeling.

4.2. Coarse graining

Coarse graining is also a general concept first developed in statistical physics which represents an ensemble with a sort of averaged behavior. For example, reducing a 1024 × 1024-pixel picture to a 512 × 512-pixel picture by using the average color of the original four pixels for the corresponding new pixel in the new picture is a simple coarse graining process. One can continue this process for several steps, while still maintaining the necessary information of the picture. However, since real systems are not static and change dynamically, coarse graining in this setting is much more complicated. Mean field theory, rule-based modeling, or describing the properties of an ideal gas with pressure, volume, and temperature are also coarse graining techniques, as is the multi-scale modeling illustrated in Fig.2. Coarse graining techniques have been developed recently for molecular dynamics simulations of protein dynamics (Chu et al., 2007; Kamerlin et al., 2010; Murtola et al., 2009) and for protein-protein interactions (Sneddon et al., 2011; Stein et al., 2007). In fact, coarse graining is commonly used in biology by treating a cell as the smallest unit. In many cases, numerical discretization itself is a type of coarse graining. For example, in whole-heart modeling (Ten Tusscher et al., 2007; Xie et al., 2004), the volume of a voxel (representing tens to hundreds of myocytes) is much larger than that of a myocyte, which is a way of coarse graining under the assumption that the activation of the myocytes in a voxel is simultaneous.

4.3. Nonlinear dynamics, statistical physics, and self-organization theories

New properties emerge at different scales due to interactions between the elements, which are usually described by nonlinear dynamics, statistical physics, and self-organization theories (Hilborn, 1994; Nicolis and Prigogine, 1977; Prigogine, 1978; Turing, 1952). The theories of nonlinear dynamics and self-organization have been successfully applied to cell biology (Karsenti, 2008), pattern formation in tissue (Kondo and Miura, 2010; Meinhardt and Gierer, 2000), and many other biological functions (Aon et al., 2004; Camazine et al., 2001; Gardner et al., 2000; Qu et al., 2003; Sha et al., 2003; Xiong and Ferrell, 2003; Yang et al., 2010), which play important roles not only in mechanistic understanding of the system but also in scaling a system from one level to another in multi-scale modeling. In other words, using insights from nonlinear dynamics, one may be able to develop low-dimensional representations of a high-dimensional system.

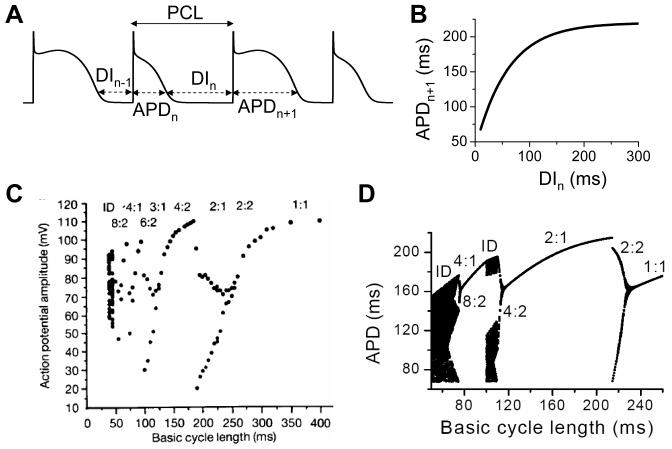
One well-known method of representing a high-dimensional system by a low-dimensional model in nonlinear dynamics is the so-called Poincare map or iterated map (Hilborn, 1994), as the Logistic map shown in Eq.7. For example, cardiac excitation is governed by a high-dimensional system, but a low-dimensional map can well capture the excitation-recovery dynamics as first elucidated by Nolasco and Dahlen (Nolasco and Dahlen, 1968) more than 40 years ago. In a cardiac cell, the action potential duration (APD) changes with its previous diastolic interval (DI), which is called APD restitution. It can be mathematically denoted by the following equation (Figs.8A and B):

$${\mathrm{APD}}_{\mathrm{n}+1}=f\left({\mathrm{DI}}_{\mathrm{n}}\right),$$ (10)

Under periodic pacing, the pacing cycle length (PCL) is the summation of the APD and DI at any beat number n (see Fig.8A), i.e.,

$$\mathrm{PCL}={\mathrm{APD}}_{\mathrm{n}}+{\mathrm{DI}}_{\mathrm{n}}.$$ (11)

Using Eqs.10 and 11 and the function in Fig.8B, APD alternans and other complex dynamics can occur (Qu et al., 2010), showing bifurcations from the stable equilibrium state (1:1) to alternans (2:2), from 2:2 alternans to 2:1 block, and more complex action potential dynamics at faster pacing rates (Fig.8C). In experimental recordings from a sheep Purkinje fiber by Chialvo et al (Chialvo et al., 1990), the same bifurcation sequence was observed (Fig.8D) indicating that the low-dimensional map may indeed be a good representation of the high-dimensional cardiac excitation system. Similar low-dimensional representations have also been widely used for Ca cycling dynamics in cardiac myocytes (Qu et al., 2007; Rovetti et al., 2010; Shiferaw et al., 2003) and conduction dynamics in cardiac tissue (Courtemanche et al., 1993; Echebarria and Karma, 2007; Wang et al., 2007).

Figure 8. APD alternans and complex dynamics due to APD restitution.

A. A voltage trace showing the relationship between DI, APD, and PCL. B. An APD restitution curve (APD_n+1 versus DI_n). C. A bifurcation diagram by plotting APD versus PCL obtained by iterating Eqs.10 and 11 with the APD restitution curve shown in B. For each PCL, the first 100 APDs were dropped and the next 100 APDs were plotted. When the equilibrium point is stable for a PCL, the 100 APDs are the same so that only one point on the plot for that PCL. When alternans (or chaos) occurs, two (or many) APD points show up for that PCL. The bifurcation sequence is: 1:1 → 2:2 → 2:1 → 4:2 → ID → 4:1 → 8:2 → ID. ID stands for irregular dynamics. D. Bifurcation diagram from an experiment of a sheep cardiac Purkinje fiber (Chialvo et al., 1990). The bifurcation sequence is: 1:1 → 2:2 → 2:1 → 4:2 → 3:1 → 6:2 → 4:1 → 8:2 → ID. The notion m:n indicates that every m stimuli result in n different action potentials, e.g., 4:2 indicates that every 4 stimuli give rise to 2 different action potentials, which is APD alternans. Basic cycle length is the same as PCL.

Other methods have also been developed to reduce a system to a lower-dimensional one based on nonlinear dynamics, such as manifold reduction (Keener, 2009; Oppo and Politi, 1989) or the slaving principle (Haken, 1983). However, a typical biological system (such as a cell) is composed of a large number of genes, proteins, and metabolites, which is a nonequilibrium system far from thermodynamic equilibrium. Unlike equilibrium systems where the macroscopic behaviors can be derived from the microscopic behaviors, for nonequilibrium systems, how to derive the macroscopic behaviors from the microscopic behaviors is still an open question of nonlinear dynamics and statistical physics. Nevertheless, theories developed in nonlinear dynamics and complex systems still play key roles in biological modeling, since when one understands the complex behaviors of the system at the lower scale, it is more likely to develop a correct low-dimensional mathematical representation that can be used in a higher scale system.

4.4. Systems biology and integrative approaches

The goal of systems biology is to consider a biological system from a holistic perspective, and use both experiments and modeling and the interactions between experiments and modeling to reveal how the system behaves (Kitano, 2002; Kohl et al., 2010). In mathematical modeling of biology, close model-experiment interactions are crucial for developing valid models. The experiments first provide the necessary information for model development, and then one uses the developed model to make predictions and test them in experiments. If the predictions do not agree with experimental observations, one may ask: what is missing in the model? Has there been enough information for model development? Is the methodology appropriate? and so on. By addressing these questions, one then develops an improved model, makes new predictions, and tests them in experiments again. By the feedbacks between experiments and modeling, one may finally develop a model that is valid for the system. Interactions between experiments and modeling in biology have had a long history, however, the recent progress in imaging (Tsien, 2009; Xie et al., 2006) and high throughput technologies (Deane et al., 2002; Uetz et al., 2000) can provide important experimental information on the interactions between different genes proteins, and metabolites, which is crucial for multi-scale modeling as well as for closing up the gaps between modeling methodologies and between scales.

5. Conclusions and Perspectives

Due to the multi-scale nature of biological systems, we must develop models at different scales to understand the system’s properties. However, the goal of multi-scale modeling is not just about developing models at different scales: the models need to be linked in a consistent manner so that the information from a lower scale can be carried into the simplified model of a higher scale. This is nontrivial and challenging. In addition, there are scales that cannot be coarse grained, such as the coarse graining of sub-cellular spatiotemporal dynamics into whole-cell low-dimensional models, as the case discussed in Fig.7. For some problems, there may be just a right scale that is important (Stoneham and Harding, 2003). Therefore, how to choose appropriate modeling scales is also an important issue in multi-scale modeling.

A mathematical model is a simpler representation of a real system. The major goal of modeling is to bring a complex system into an abstractive level of understanding that can be grasped by the human brain. Even though at some time point in the future we may have the computational technology to simulate a biological system, such as a heart or a brain, using an accurate Newtonian description of the atoms or molecules, simpler representations are still necessary to understand the underlying mechanisms (Garfinkel, 1981). For example, knowing the motion of each gas molecule in a box of ideal gas by simulating the corresponding Newtonian equations cannot bring us to the level of understanding that we get from ideal gas theory, developed through statistical mechanics and thermodynamics. Higher order mathematical modeling and theory development are necessary no matter how fast our computers are, and the multi-scale modeling approach will be a very powerful means facilitating our understanding of complex biological systems.

Finally, a good mathematical model should not just fit a set of experimental data, but should explain the underlying mechanisms and make predictions or generate experimentally testable hypotheses. A good model should also be simple enough to facilitate mechanistic understanding for the human brain. The seminal models and theories developed by Michaelis and Menten (Michaelis and Menten, 1913), by Hodgkin and Huxley (Hodgkin and Huxley, 1952), by Turing (Turing, 1952), and by Goodwin (Goodwin, 1966) are beautiful in their simplicity but revolutionary in biology. One may keep Einstein’s words in mind for mathematical modeling: “Make everything as simple as possible, but not simpler.” This is the real challenge in biological modeling.