BM-Map: Bayesian Mapping of Multireads for Next-Generation Sequencing Data

Summary

Next-generation sequencing (NGS) technology generates millions of short reads, which provide valuable information for various aspects of cellular activities and biological functions. A key step in NGS applications (e.g., RNA-Seq) is to map short reads to correct genomic locations within the source genome. While most reads are mapped to a unique location, a significant proportion of reads align to multiple genomic locations with equal or similar numbers of mismatches; these are called multireads. The ambiguity in mapping the multireads may lead to bias in downstream analyses. Currently, most practitioners discard the multireads in their analysis, resulting in a loss of valuable information, especially for the genes with similar sequences. To refine the read mapping, we develop a Bayesian model that computes the posterior probability of mapping a multiread to each competing location. The probabilities are used for downstream analyses, such as the quantification of gene expression. We show through simulation studies and RNA-Seq analysis of real life data that the Bayesian method yields better mapping than the current leading methods. We provide a C++ program for downloading that is being packaged into a user-friendly software.

1. Introduction

Next-generation sequencing (NGS) technology produces a vast amount of sequence data at low cost and provides enormous opportunities for the life sciences. RNA-Seq is an NGS application that generates millions of short RNA reads. By mapping and counting individual short sequence reads to specific genomic locations on the source genome, gene expression can be quantified as the number of mapped reads, which is considered the “digital” expression as opposed to the “analog” expression of relative transcript abundance in microarrays. Due to its low cost and high precision, RNA-Seq has become the primary tool for sequencing all the RNAs in species ranging from yeast to human (Nagalaskshmi et al., 2008; Lister et al., 2008; Cloonan et al., 2008; Mortazavi et al., 2008; Marioni et al., 2008; Morin et al., 2008; Trapnell et al., 2010).

Many statistical challenges lie ahead in various steps of the RNA-Seq, preventing the technology from reaching its full potential. A key step in the RNA-Seq is read mapping, which infers the origin of short reads on a reference genome. Below we provide a quick review of the main issues in this step.

1.1 Read mapping and related sources of variations

We consider short RNA reads generated from major NGS platforms such as the Genome Analyzer (Solexa) from Illumina (San Diego, CA, USA), and SOLiD from Applied Biosystems (Foster City, CA, USA). Regardless the platform, a key step in processing the RNA-Seq data is to align each short read to a reference genome based on sequence similarities.

Two sources of variations in read alignment complicate the accuracy of this step.

1. The first source is sequencing errors (Bravo and Irizarry, 2009; Ji et al., 2010; Kao et al., 2008; Rougemont et al., 2008) from upstream analysis, which occasionally occur during the process of generating short reads. In particular, there could be machine and systemic errors in sequencing the bases of a read. The error rates can be represented by the quality score underlying each base (see Figure 3 in the Web Appendix 1). These sequencing errors will cause mismatches between the short reads and the genome, which should not be counted.

2. The second source is called hidden nucleotide variations, such as a mutation or SNP. The main cause for this type of variations is that the short reads are typically mapped to a public reference genome rather than the sample genome from which the reads are generated. Hence, variations between the two genome versions (i.e., SNPs) may cause mismatches between the reads and the reference genome.

Several published methods have been developed for aligning the short reads to the reference genome. For example, Li, Ruan and Durbin (2008) considered mapping short DNA sequences based on the quality scores and developed software called MAQ. Another popular program is Bowtie (Langmead et al. 2009), an ultrafast, memory-efficient alignment program that aligns short reads to large genomes. Additional representative works include the SOAP by Li et al. (2009), the RMAP by Smith, Xuan, and Zhang (2008), and the SHRiMP by Rumble et al. (2009). Despite the aforementioned sources of variations in read mapping, most mappable short reads (> 75%) based on available methods (e.g., Bowtie) align to a single genomic location with relatively high precision. These reads are called unique reads. However, a significant number of reads are mapped to more than one genomic location with similar fidelity, and these reads are called multireads. Importantly, multireads disproportionally come from the genes with similar sequences (e.g., duplicated genes) and essentially determine their expression levels. The alignment of multireads is highly susceptible to the two sources of variations above, making it difficult to map them to appropriate locations.

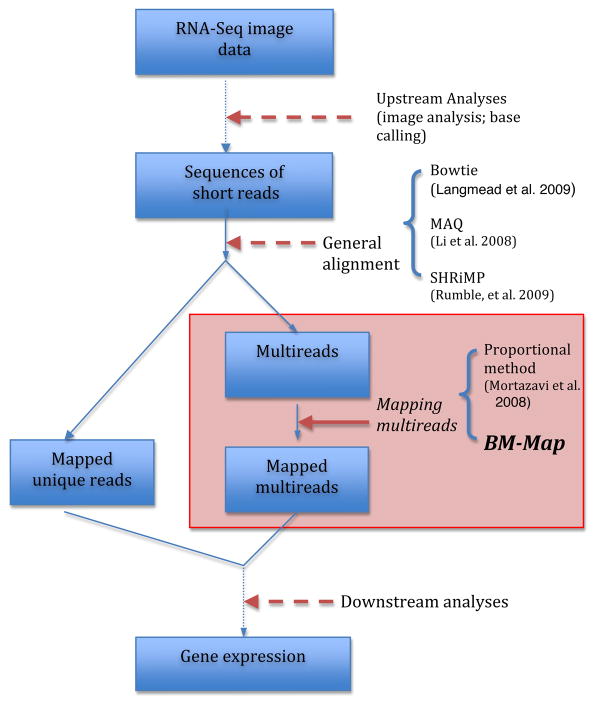
We aim to improve the mapping of the multireads, as a refinement step after the general reads alignment is completed. Figure 1 demonstrates where our proposed method stands in the entire process of the NGS data analyses.

Figure 1.

(Colored) A flow chart of the main steps in the RNA-Seq approach. Our proposed method, BM-MAP, considers mapping the multireads after the general read alignment is finished. The available tools for each step are listed on the right side of the chart. Currently, there is only one method, the proportional method, that deals with the mapping of the multireads. The drawbacks of the proportional method are discussed in Section 1.1.

Currently, most practitioners would discard the multireads in subsequent analyses such as gene expression quantification. This practice generates a large bias in estimating the expression levels of duplicated genes. As an initial attempt, Mortazavi et al. (2008) proposed a proportional alignment method in which unique reads are first mapped, and then multireads are aligned to equally similar loci in proportion to the number of corresponding mapped unique reads. The key idea of the proportional method is that the individual numbers of unique reads are used to infer the probabilities of mapping the multireads. While the proportional method provides a simple and valuable solution to the mapping of the multireads, it fails to account for the mismatch profiles between the unique reads and the genomic locations. For example, using the proportional method a multiread will be mapped to a genomic location with a high probability as long as that location possesses a large number of unique reads, even when the unique reads are relatively poorly matched to the location. In other words, the proportional method ignores the matching quality between the unique reads and the reference genome, hence it is unable to account for the source of variation (ii) listed above.

Subsequent research development in the literature has also attempted to address the problem of mapping multireads, see Li et al. (2010), and Taub, Lipson, and Speed (2010). These authors correctly pointed out that the aforementioned sources of variations need to be accounted for in mapping the multireads. To this end, we propose a Bayesian mapping of multireads (BM-Map) approach that computes a posterior probability of mapping each multiread to a genomic location as well. Unlike the proportional method which only considers the equally best aligned genomic locations, the BM-Map evaluates genomic locations with unequal numbers of mismatches to a multiread. More importantly, the BM-Map utilizes three sources of information when mapping the multireads: the sequencing error profiles, the likelihood of hidden nucleotide variations, and the expression levels of competing genomic locations (see Figure 1 in the Web Appendix 1). In contrast, the proportional method only uses the last source of information.

1.2 RNA-Seq data

We will analyze a yeast RNA-Seq data set from Nagalaskshmi et al. (2008) and a human RNA-Seq data set from Pickrell et al. (2010). The read length for the yeast data K = 35 while for the human data K = 46. We will use the yeast data analysis to illustrate our methodology. In particular, the yeast data set contains a total of 22.4 million reads, and are generated using the Solexa Genome Analyzer. We apply Bowtie (version 10.0.1; Langmead et al., 2009) to process the initial read alignment, allowing a read to be mapped to multiple locations. To include as much information as possible, we consider the multireads that are mapped to a genomic location with up to three mismatches (the default is up to two mismatches). Consequently, we refer to a genomic location as a hit if a read is mapped to that location with no more than three mismatches. A top hit is a genomic location to which a read is mapped with the fewest number of mismatches. The following is assumed in preprocessing the data: (1) a read is considered mappable if it has a top hit with no more than two mismatches; (2) given the top hit of a mappable read, other hits with no more than two extra mismatches and no more than three total mismatches are defined as additional competing genomic locations (we did not include any hits with more than three total mismatches because Bowtie only outputs hits with up to three mismatches); (3) reads with more than five competing locations are excluded because these reads likely originate from repetitive elements in the genome. With these criteria, we obtain 6,912,733 mappable reads, and among them, 5,256,339 are unique reads (those with only one hit) and 1,656,394 are multireads (with more than one hit).

2. Methodology

2.1 Probability model

To avoid confusion, we use term “location” to represent a segment of the genome to which each read is mapped. We use term “position” to represent a single base of a read or a genomic location. We proceed by introducing our model for a single multiread. The same model will be applied independently and repeatedly to other multireads in the read mapping. We will index multireads by m but will drop the index when needed for simplicity. This strategy allows us to analyze the ~1.6 million multireads in parallel, achieving reasonable computational speed. For a given multiread, suppose that it is mappable to T genomic locations, indexed by t = 1, …, T. Each genomic location corresponds to a segment of the genome with the same length as the multiread. That is, the multiread and each genomic location aligns perfectly from the first position to the last. For the yeast data, the length K = 35. Therefore, each genomic location consists of K = 35 positions.

We assume that a set of unique reads overlap with genomic location t, t = 1, …, T. Here overlap means partial alignment, i.e., a unique read can overlap with a subset of the positions on the location, rather than the entire location as the multiread. For example, if the location t spans from genomic position 101 to 135, the starting position of the multiread aligns to position 101 and the ending position of the multiread aligns to position 135. In contrast, any overlapping unique read only needs to have a starting position or ending position in [101, 135] (see Figure 2 in the Web Appendix 1). Among the set of unique reads, we assume that n_kt reads at least overlap with the k-th position of genomic location t, and we index these unique reads by l, l = 1, …, n_kt.

[Mismatch profiles] Given the multiread, the observed data consist of the position-level mismatch profiles between the genomic location t and the multiread, and between the genomic location t and all the overlapping unique reads. Below we introduce the labels for these mismatch profiles. We will use a generic notation r = [r₁, r₂] to denote a row vector of two scalars r₁ and r₂. Two row vectors r₁ and r₂ concatenated in the form [r₁, r₂] forms a new row vector.

• For the multiread and location t, a mismatch could occur at each of the K positions. Let e_kt = 1 or e_kt = 0 denote the event that there is a mismatch or perfect match between the multiread and location t at the k-th position, respectively. Then the observed data at location t for the multiread are given by a K-dimensional mismatch vector e_t = [e_1t, …, e_Kt].

• We need an additional label l to index the n_kt unique reads that overlap with the k-th position of location t. Let g_l,kt = 1 or g_l,kt = 0, l = 1, …, n_kt, denote the event that there is a mismatch or perfect match between the unique read l and location t at the k-th position, respectively. We denote the row vector g_kt = [g_1,kt, …, g_nkt,kt] the mismatch indicators at the k-th position for all the corresponding overlapping unique reads. Lastly, define g_t = [g_1t, …, g_Kt] as the vector of mismatch indicators for all the overlapping unique reads with location t, which is the observed data at location t for its overlapping unique reads.

In summary, the full data are the vector [e_t, g_t, t = 1, …, T].

[Parameters] We want to estimate the probability of mismatch between the k-th position of the genomic location t and the corresponding position of a read, unique or multiple. We denote p_kt ≡ Pr(e_kt = 1) the probability of a mismatch between the k-th position of location t and the k-th position of the multiread. Similarly, denote q_l,kt ≡ Pr(g_l,kt = 1) the probability of mismatch between the k-th position of location t and the corresponding position of unique read l. Again, due to partial alignment, the corresponding position of the unique read may not be the k-position of the read. Let α_kt be the probability of sequencing error at the k-th position of the multiread mapped to location t. Let β_kt be the probability of hidden nucleotide variations at the k-th position of location t. We assume that

$$p_{kt}={\alpha }_{kt}+{\beta }_{kt}(1-{\alpha }_{kt}).$$ (1)

Similarly, let α_l,kt be the probability of sequencing error at the position of unique read l that corresponds to the k-th position of location t. We assume that for unique read l

$$q_{l,kt}={\alpha }_{l,kt}+{\beta }_{kt}(1-{\alpha }_{l,kt})$$ (2)

Models (1) and (2) essentially follow the probability law of two independent joint events. To see this, consider p_kt and use A to label the event that {there is a sequencing error} and B to label the event that {there is a hidden nucleotide variation}. Then using our notation, we have that the probability of mismatch p = Pr(A ∪ B), the probability of sequencing error α = Pr(A), and the probability of hidden nucleotide variation β = Pr(B). Model (1) says that p = α + β − αβ, which is the probability law of two independent events Pr(A ∪ B) = Pr(A) + Pr(B) − Pr(A)Pr(B).

In our subsequent analysis of the RNA-Seq data, we compute simple estimates (sample proportions) for α_kt and α_l,kt based on the position specific or quality score specific mismatch profiles from all the unique reads. The main idea is to use the millions of unique reads from the RNA-Seq data to reliably estimate the α values and plug in the estimates in our proposed model. Due to the large sample size, rather than imposing a prior distribution on the α’s, we decide to fix them at their estimated sample means. Figure 3 in the Web Appendix 1 shows these values and how they are computed. We estimate β_kt based on posterior inference, which is described below.

[Likelihood, prior, and posterior] We write the likelihood contribution from the unique reads and the multiread separately. First, the contribution to the likelihood from the unique reads at location t is given by

$$L({\mathit{g}}_t)=\prod _{k=1}^K\prod _{l=1}^{n_{kt}}{q}_{l,kt}^{g_{l,kt}}{(1-q_{l,kt})}^{1-g_{l,kt}}.$$ (3)

Recall that n_kt is the number of unique reads that at least overlap with the k-th position of the genomic location t. Second, let Z^M be the true unknown genomic location for the multiread and define Z^M = t as the event that the multiread is generated from genomic location t. Then the contribution to the likelihood from the multiread at location t is

$$L({\mathit{e}}_t)\equiv Pr({\mathit{e}}_t\mid Z^M=t)=\prod _{k=1}^K{p}_{kt}^{e_{kt}}{(1-p_{kt})}^{-1e_{kt}}·I(Z^M=t),$$ (4)

where I() is the indicator function. The full likelihood is

$$\prod _{t=1}^{T}L({\mathit{g}}_t)L({\mathit{e}}_t),$$

in which β_kt is an unknown parameter (the values of α’s are fixed), and the probability of the event Z^M = t is to be estimated.

We assume that the prior for β_kt is given by

$${\beta }_{kt}\sim B(a,b),$$ (5)

where B(a, b) represents a beta distribution with the density function proportional to x^a−1(1−x)^b−1, a > 0, b > 0. In our analysis for the yeast RNA-Seq data, a = b = 1. In addition, we assume that the prior Pr(Z^M = t) is proportional to the number of unique reads mapped to location t. Note that this construction of Pr(Z^M = t) follows the main idea in Mortazavi et al. (2008).

We want to estimate the posterior probability of mapping the multiread to location t, given by

$$p^M(t)\equiv Pr(Z^M=t\mid {\mathit{e}}_t,{\mathit{g}}_t).$$

We can easily express p^M(t) in terms of the likelihood (4) and the posterior distribution of β_kt given g_t. Denoting β_t = {β_1t, …, β_Kt}, the vector of probabilities of mismatches at all K positions of genomic location t, we have

$$\begin{array}{l}{p}^M(t)\equiv Pr(Z^M=t\mid {\mathit{e}}_t,{\mathit{g}}_t)\\ =\int \underset{\mathit{part}1}{\underbrace{Pr(Z^M=t\mid {\mathit{e}}_t,{\mathit{\beta }}_t)}}\underset{\mathit{part}2}{\underbrace{f({\mathit{\beta }}_t\mid {\mathit{g}}_t)}}d{\mathit{\beta }}_t,\end{array}$$

The above equation says that the posterior probability p^M(t) equals the integral of part 1 with respect to the posterior of β_t, where part 2 is the posterior distribution of β_t given the observed mismatch profiles for all the unique reads. We will numerically evaluate this integral by drawing random samples from the posterior of β_t via Markov chain Monte Carlo (MCMC) simulations, described in Section 2.2. Suppose an MCMC sample is denoted as [β_t ^(s), s = 1, …, S] for t = 1, …, T. We apply Bayes’ theorem to part 1 and obtain

$$\mathit{part}1{\mid }_{{\mathit{\beta }}_t={\mathit{\beta }}_t^{(s)}}=\frac{Pr({\mathit{e}}_t\mid Z^M=t,{\mathit{\beta }}_t^{(s)})}{{\sum }_{t^{\prime }=1}^{T}Pr({\mathit{e}}_{t^{\prime }}\mid Z^M=t^{\prime },{\mathit{\beta }}_t^{(s)})},$$

which can be easily evaluated based on (4). Finally we obtain an MCMC estimate p̂^M(t) given by

$${\widehat{p}}^M(t)=\frac{1}{S}\sum _{s=1}^S\mathit{part}1{\mid }_{{\mathit{\beta }}_t={\mathit{\beta }}_t^{(s)}}=\frac{1}{S}\sum _{s=1}^S\frac{Pr({\mathit{e}}_t\mid Z^M=t,{\mathit{\beta }}_t^{(s)})}{{\sum }_{t^{\prime }=1}^{T}Pr({\mathit{e}}_{t^{\prime }}\mid Z^M=t^{\prime },{\mathit{\beta }}_t^{(s)})}.$$ (6)

2.2 Markov chain Monte Carlo simulations

We augment the parameter space (Tanner and Wong, 1987) and employ a simple Gibbs sampler to simulate random numbers from the marginal posterior distributions of the unknown parameters [β_kt]. The basic idea is to introduce a latent Bernoulli variable for unique read l with a conditional distribution defined by

$$u_{l,kt}\mid {\beta }_{kt}\sim \mathit{Bern}\left\{\frac{(1-{\alpha }_{l,kt}){\beta }_{kt}}{{\alpha }_{l,kt}+(1-{\alpha }_{l,kt}){\beta }_{kt}}\right\}.$$

Then denote the set W_kt = {l: g_l,kt = 1} the indices of the unique reads with a mismatch to the k-th position of location t. Denoting u_kt = Σ_l∈Wktu_l,kt, with the augmented Bernoulli distribution we can easily show that [β_kt | u_kt] follows a beta distribution

$$B(u_{kt}+a,n_{kt}-\sum _{l=1}^{n_{kt}}{g}_{l,kt}+b).$$

Alternating the random sampling of [u_l,kt | β_kt] and [β_kt | u_kt] in a Gibbs sampler, we obtain imputed values of [ $u_{kt}^{(s)},{\beta }_{kt}^{(s)}$] in the s-th iteration of the Gibbs sampler. We use the MCMC samples [ ${\beta }_{kt}^{(1)},\dots ,{\beta }_{kt}^{(S)}$] to calculate (6) and evaluate the posterior probability p̂^M(t).

The proposed Gibbs sampler is as follows.

• Step 1: Let ${\beta }_{kt}^{(1)}=\epsilon$, where ε is an arbitrary small probability close to zero.

• Step 2: In the s-th iteration, sample $u_{l,kt}^{(s)}$ from

  $$\mathit{Bern}\left\{\frac{(1-{\alpha }_{l,kt}){\beta }_{kt}^{(s-1)}}{{\alpha }_{l,kt}+(1-{\alpha }_{l,kt}){\beta }_{kt}^{(s-1)}}\right\},l\in W_{kt}.$$

  Compute $u_{kt}^{(s)}={\sum }_{l\in W_{kt}}{u}_{l,kt}^{(s)}$.

• Step 3: Sample ${\beta }_{kt}^{(s)}$ from $B(u_{kt}^{(s)}+a,n_{kt}-{\sum }_{l=1}^{n_{kt}}{g}_{l,kt}+b)$.

• Step 4: Iterate steps 2 to 3 S number of times, for a large integer S.

For the special case in which n_kt = 0, set $u_{kt}^{(s)}=0$ and ${\beta }_{kt}^{(s)}={\beta }_{kt}^{(s-1)}$.

In our analysis, the number of iterations S was set to 1,000 with the first 200 iterations as burn-in. The Markov chain converged fast and mixed well.

3. Simulation studies

We conducted simulation studies to evaluate the performance of the proposed BM-Map method in comparison with two other approaches.

3.1 Simulation setup

As an illustration, we considered multireads potentially mapped to T = 2 genomic locations. We designed seven scenarios with different combinations of three factors that would affect read mapping: 1) Diff = (Yes; No), defined as whether there was a true sequence difference between the two genomic locations in the reference genome; 2) Mut = (Yes, No), defined as whether there was a hidden nucleotide variation (e.g., mutation) at a position belonging to one of the two genomic locations; 3) Exp = (Yes, No), defined as whether the expression levels, measured as the numbers of mapped unique reads, between the two genomic locations were the same. Enumeration of the three factors would give us eight scenarios. However, the scenario in which all three factors were false was of no interest and did not provide any information about to where the multireads should be mapped. Hence, that scenario was not considered in this simulation. When Diff was Yes, we assumed that there was a sequence difference at position 18 between the two genomic locations. When Mut was Yes, we assumed that the mutation rate at position 16 of genomic location 1 was β_16,1 = 0.9; when Mut was No, the rate was 0. When Exp was Yes, i.e., the expression levels were the same for the two locations, we assumed that the same number of unique reads originated from both genomic locations, and the number could have been 4, 10, or 100. When Exp was No, we assumed different numbers of unique reads from locations 1 and 2: (4, 3), (10, 5), or (100, 10). Therefore, combining the three sets of sample sizes for all seven scenarios, we obtained a total of 21 possible simulation cases, see Table 1 in the Web Appendix 1. For each of the cases, we generated 200 multireads with a mismatch probability at the k-th position equal to p_kt, m = 1, …, 200, and t = 1, 2, where p_kt = α_k + (1 − α_k)β_kt. Finally, the values of α_k’s were fixed at the sample means of the mismatch rates of position k using all the unique reads in the yeast data. The probability β_kt was 0 unless when Mut was true, in which case β_16,1 = 0.9. The first 200 × N₁/(N₁ + N₂) (round to an integer) multireads were assumed to originate from genomic location 1, where N₁ and N₂ were the numbers of the unique reads originated from locations 1 and 2, respectively.

3.2 Simulation results

We compared three methods for each of the 21 cases in the simulation studies.

• BM-Map – the proposed Bayesian method.

• Prop – the proportional method (Mortazavi et al., 2008) in which reads are mapped to the location with the fewest number of mismatches. When there are ties, the multireads are mapped to each tied location with a probability proportional to the number of unique reads mapped to that location.

• Rand – a reference method that assigns the multireads to each of the genome locations with a uniform probability.

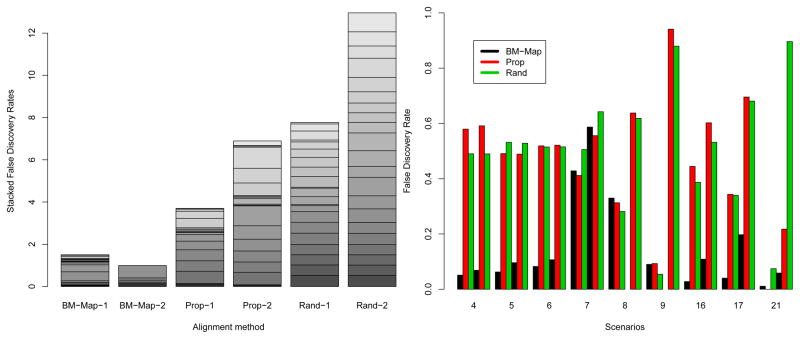
Figure 2 summarizes the false discovery rates (FDRs) for the three methods after they were applied to the 200 simulated multireads originated from two genomic locations. Here the FDR is defined as the percentage of multireads being falsely mapped to a genomic location among all the multireads mapped to that location. The left panel presents the stacked 21 FDRs for mapping the multireads to genomic locations 1 and 2 under each of the three methods. The lower the bar, the better the overall performance. The BM-Map method has much lower bars than both the Prop and Rand. The right panel shows the FDRs of a list of representative cases (4,5,6,7,8,9,16,17,21). In other cases, the BM-Map and Prop methods performed equally well. For each presented case in the right panel, the six vertical bars represent the FDRs of the three methods, with the first three bars for location 1 and the next three for location 2. Almost in all the cases, the BM-Map has much smaller FDRs than the other two methods. Highlighted is case 21, in which all three factors are true with the numbers of unique reads being 100 and 10 for the two genomic locations. While the BM-Map has an FDR (0.01) at genomic location 1 comparable to that of the Prop (0.00), it has a much smaller FDR at genomic location 2 (0.06 vs. 0.32). Further examination shows that the Prop method mapped many multireads to location 2 that belonged to location 1. This is due to the fact that when there is a mismatch between a read and the location 1 at the 16th position, the Prop method could not tell whether the mismatch was due to mutation or sequence difference. Because there was a high mutation rate 0.9 (β_16,1 = 0.9), most mismatches between the multireads and the location 1 at this position were due to the mutation. The BM-Map was able to learn and borrow the information based on the mismatch profiles of the unique reads, and thus correctly map most of the multireads.

Figure 2.

(Colored) Results summarizing the false discovery rates (FDRs) of the three methods in the simulation studies. Left panel: stacked FDRs over the 21 simulated cases in Section 3.1. A method name followed by “−1” and “−2” respectively represents the stacked 21 FDRs for mapping multireads to locations 1 and 2. Right panel: FDRs for selected simulation cases in which there are large differences in the FDRs among the three methods.

In Figure 4 of the Web Appendix 1, we present additional results comparing the ROC curves and the areas under the curves, which further confirm the superiority of the BM-Map method.

4. RNA-Seq data analysis

We present results for the analysis of the yeast and human RNA-Seq data described in Section 1.2. We will again focus on the yeast data for illustrative purposes. Results from human data analysis will be reported whenever needed as a complement.

4.1 Read mapping

In mapping the multireads to the yeast or human genome, we first identified the genomic locations with the fewest number of mismatches as the top hits. We required that the number of mismatches between the best hits and the short read be no larger than two. Additional hits are included according to the three criteria listed in Section 1.2. For the yeast data, there are a total of 5,256,339 unique reads. The numbers of multireads with 2 to 5 hits are respectively (1,494,678, 147,142, 12,079, 2,495). For the human data, there are a total of 4,237,908 unique reads, and the numbers of multireads with 2 to 5 hits are (652,577, 355,109, 197,189, 144,601).

We applied the BM-Map method to map the multireads. For each multiread, we first identified the set of unique reads for each of its candidate genomic locations. Matching the sequences of the multiread to its candidate genomic locations, we obtained the mismatch profiles [e₁, …, e_T]. Matching the sequences of the unique reads and their corresponding genomic locations, we obtained the mismatch profiles [g₁, …, g_T]. With these profiles, for each multiread indexed by m, we applied the Gibbs sampler outlined in Section 2 and computed the posterior probabilities that the multiread m is mapped to location t, p̂_m(t) (this was p̂^M(t) before without the index m). These probabilities are used to compute gene expression in downstream analyses.

For comparison, we applied the proportional method (Mortazavi et al., 2008) to map the multireads as well. Let n. loci {2, 3, 4, 5} be the number of hits for a multiread. Let r̂_m(t) denote the probability of mapping multiread m to location t using the proportional method. For each multiread m with n. loci candidates, we compute the difference in the probabilities of read mapping between the BM-Map method and the proportional method as

$$D_m(p,r)\equiv \sum _{t=1}^{n.\mathit{loci}-1}\mid {\widehat{p}}_m(t)-{\widehat{r}}_m(t)\mid .$$

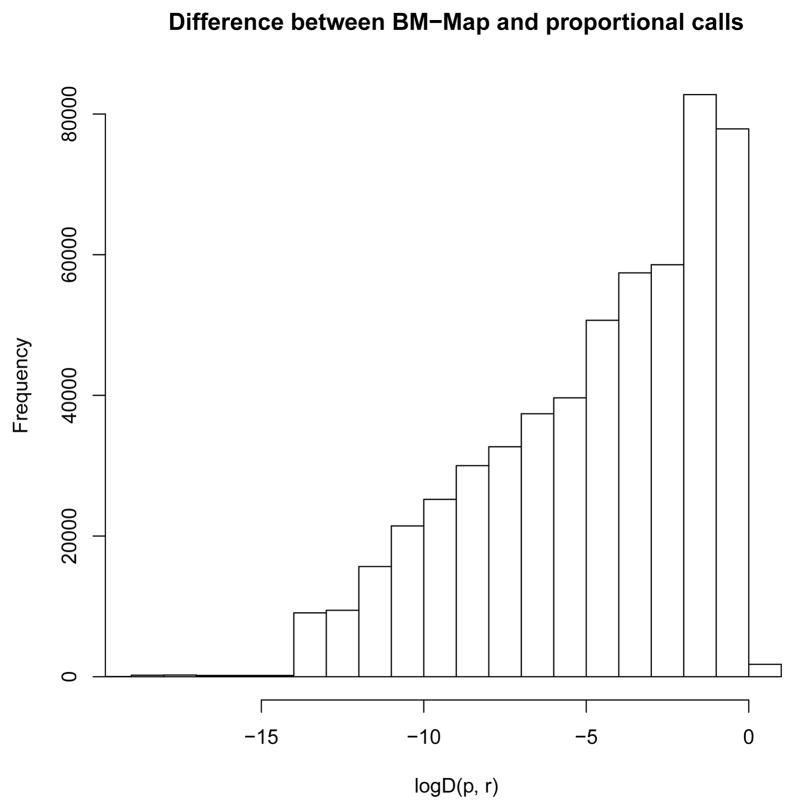
For example, for a multiread with n. loci = 2 hits, the proportional method might yield r̂_m(1) = 0.6 and r̂_m(2) = 0.4 while the BM-Map method might yield p̂^M(1) = 0.3 and p̂^M(2) = 0.7; we would have D_m(p, r) = |0.6 − 0.3| = 0.3. Figure 3 presents the histogram of the log D_m(p, r) for those multireads in the yeast data with at least one unique read mapped to each hit, when n. loci = 2. Figure 4 demonstrates three representative examples of mapping multireads, again from the yeast data. The left two columns demonstrate cases in which the BM-Map and proportional methods gave contrasting results, mapping the multireads to opposing genomic locations. The right column is an example in which the two methods agree. In each plot, we present the posterior mean of β_kt, the probability of a hidden nucleotide variation for the k-th position at genomic location t, as a function of k. A large posterior mean of β_kt implies that a large number of unique reads have mismatches at the k-th position of location t, which are due to hidden nucleotide variations. We present these important phenomena in Figure 4.

Figure 3.

Histogram of the differences in mapping the multireads of the yeast RNA-Seq data between the BM-Map method and the Prop method.

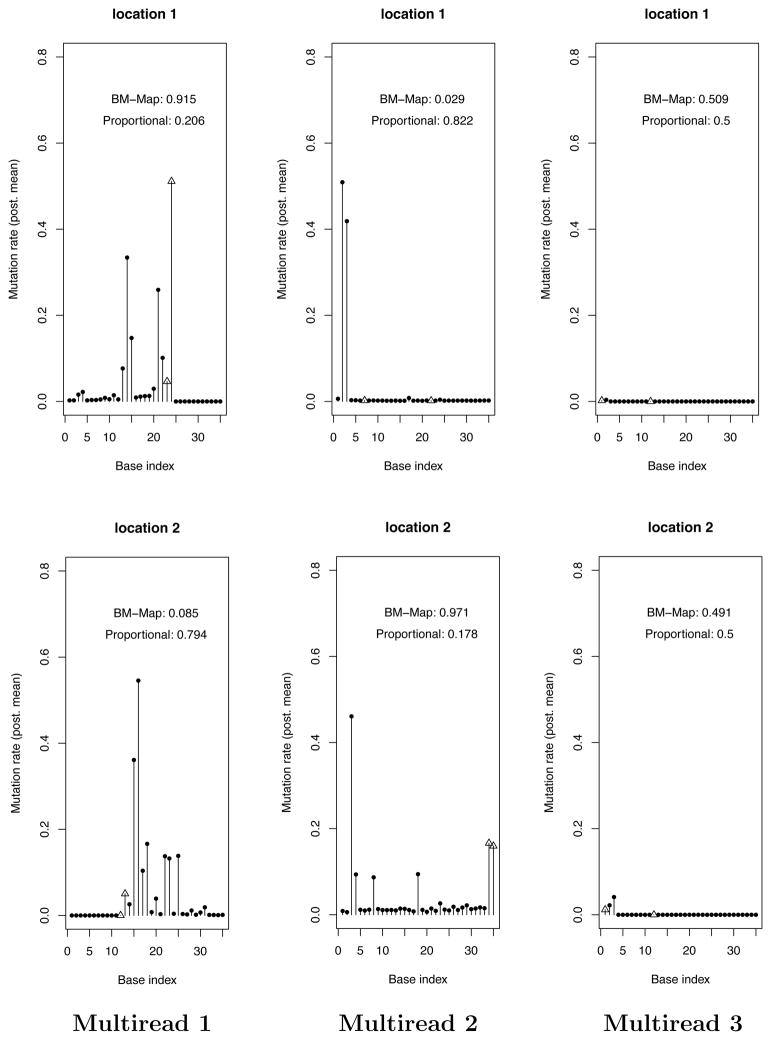
Figure 4.

Three examples of multireads mapped to two hits based on the probabilities of the BM-Map and Prop methods. In each column, the two plots (rows) correspond to two competing genomic locations for a multiread. Plotted are the posterior means of β_kt, the probability of hidden nucleotide variation. These are estimated based on the error mismatch profiles between the unique reads and the genomic locations. The verticle lines ended with empty triangles indicate where the multireads have mismatches. Left panel: the multiread has mismatches at positions (23, 24) to location 1 and (12, 13) to location 2. Middle panel: the multiread has mismatches at positions (7, 22) to location 1 and (34, 35) to location 2. Right panel: the multiread has mismatches at positions (1, 12) to both locations. The probabilities of mapping based on the BM-Map and proportional methods are presented in each plot.

• [Left panel] If a hit has a high probability of a hidden nucleotide variation at a position where the multiread has a mismatch, the mismatch will be down-weighted because it could be caused by a mutation. Consequently, the probability of mapping the multiread to that hit will increase due to improved matching. This is the case for the left plot in the top panel (high β_24,1).

• [Middle panel] In contrast, if a hit has a high probability of a hidden nucleotide variation at a position where the multiread has a perfect match, the perfect match will be down-weighted and the probability of mapping the multiread to that hit will decrease. This is the case for the right plot in the top panel (high β_15,1 and β_16,1) and the left plot in the middle panel (high β_2,1 and β_3,1).

• [Right panel] The bottom panel in Figure 4 presents a “null” case in which the BM-Map method and the proportional method give the same mapping probabilities. In both plots, the probabilities of hidden nucleotide variations are negligible at all positions of both genomic locations. Therefore the probability of mapping the multiread is based on the numbers of mismatches between the multiread and the locations, and the number of unique reads on each location.

In summary, the first two examples above highlight the importance of borrowing the matching information between the unique reads and the genomic locations in refining the mapping of the multireads. This is a key advantage of the BM-Map method comparing over the proportional method.

4.2 Gene expression quantification

The final goal in processing the RNA-Seq data is to quantify gene expression. A fast and easy quantification is simply to count the number of reads that are mapped to the gene. In the yeast data there are 5,862 genes and we obtained 5,862 counts for each of the three methods. We compare three read mapping approaches: the BM-Map method, the proportional method, and the naive method that simply discards all the multireads in computing the counts. For fair comparison, we present the normalized counts for the three methods in Figure 5. For the proportional and the BM-Map methods, the normalized count for each gene is defined as the count of reads mapped to the gene divided by the total number of reads (per million). For the naive method, since it only uses the unique reads, the total number of reads is the total number of unique reads. The definition of the normalized read count remains the same. For simplicity, we call the normalized counts the counts.

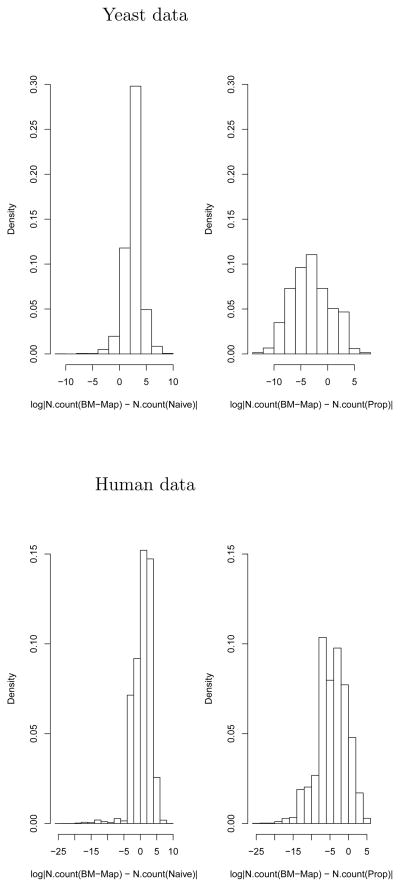
Figure 5.

Results comparing the normalized counts from three methods. Shown are the log absolute differences in the normalized counts between the BM-Map and the Naive method (left panel) and between the BM-Map and the proportional method (right panel) for the yeast data (top) and the human data (bottom).

In Figure 5 top left panel, the counts of over 40% of the genes from the BM-Map method are different from those from the naive method, because the naive method ignores the multireads when quantifying the read counts. The proportional method and the BM-Map method yield identical counts for 5,049 genes out of the 5,813 yeast genes with non-zero counts from both methods. This is because for most of the 5,049 yeast genes, there are no multireads. However, when there are multireads mapped to the genes, the two methods can be very different (top right panel). In the analysis for the human data, ~ 10% of the genes have different read counts between the proportional method and the BM-Map approach(Figure 5 bottom panel). We also summarized gene quantification as the number of reads that map per kilobase of exon model per million mapped reads (RPKM). See Web Appendix 1 on the Biometrics website for more results.

In our BM-Map method, β_kt is designed to quantify the uncertainty due to the variations between the sample and reference genomes (e.g., SNP). Since the human data set is known to come from one Yoruba HapMap sample (Pickrell et al. 2010), we obtained the common SNP data of the Yoruba population from the 1,000 Genome project and investigated the relation between β_kt and the annotated SNP frequency. Indeed, we found a convincing trend of SNP enrichment towards positions with higher β_kt. For example, for positions with β_kt > 0.2, the SNP frequency is ~70 fold higher than the transcriptome-wide average.

As a further evaluation of the impact of the BM-Map method on gene expression quantification, we present in Table 1 the normalized differences between the read counts from the BM-Map method and the proportional method, defined as

Table 1.

A representative list of yeast and human genes whose expression levels show significant variation between the BM-Map method and the proportional method. All the ten genes listed below are duplicate genes, hence possessing sequences similar to other genes. They all play important biological functions.

Yeast genes
ORF name	Gene name	Protein product description	Expression diff %
YLR134W	PDC5	Pyruvate deCarboxylase	37.5%
YPL036W	PMA2	Plasma membrane ATPase	24.6%
YMR121C	RPL15B	Ribosomal protein of the large subunit	21.2%
YJL052W	TDH1	Triose-phosphate deHydrogenase	20.9%
YPL081W	RPS9A	Ribosomal protein of the small subunit	11.1%

Human genes
Gene name	Protein product description	Expression diff %
RPL13	Ribosomal L13	83.7%
HAUS1	HAUS augmin-like complex, subunit 1	54.8%
H3F3C	H3 histone, family 3C	41.1%
NDUFAF2	NADH dehydrogenase 1 alpha subcomplex, assembly factor 2	41.1%
HIGD1A	HIG1 hypoxia inducible domain family, member 1A	34.9%

$$\frac{\mid {\text{Count}}_{\text{prop}}-{\text{Count}}_{\text{BM}-\text{Map}}\mid }{{\text{Count}}_{\text{BM}-\text{MAp}}}.$$

Table 1 shows that the counts of some genes based on the BM-Map method differ with that from the proportional method by more than 50%.

5. Discussion

We have proposed a read mapping method that utilizes the full information contained in NGS data. Specifically, the proposed BM-Map method maps the multireads by taking into account the sequencing error profiles and the information related to the mapping of unique reads. The Bayesian paradigm works very well and yields desirable results in our simulation studies and the analysis of yeast and human RNA-Seq data.

Computation is a challenging for analyzing NGS data with millions of short reads. We have achieved a remarkably fast speed in computation, thanks to efficient C++ programing. The C++ source code and a package is available for download at http://odin.mdacc.tmc.edu/~ylji We are in the process of releasing user-friendly software, to facilitate the use of the C++ package above. For the 6.9 million of mapped short reads (with ~ 1.6 million multireads) from the yeast genome, it took the package about 5.5 hours to complete the computation on a PC (Intel Core i7 2.9 GHz), requiring < 2 GB of memory.

Although not many genes in the examples were found to have different counts between the BM-Map and proportion methods through our RNA-Seq analysis, we show in Table 1 that the ones that did exhibit differences play crucial biological functions. In addition, through careful examination of our analysis results we found that our method shows significant improvements when hidden nucleotide variations are present in the competing mapping loci. Therefore, the proposed methodology is expected to have a larger effect in the species with high polymorphism frequencies or in cross-reference situations where RNA-Seq reads from one species without available genome sequence are mapped to the genome of a closely related species as a surrogate reference. In addition, as pointed out in Degner et al. (2009), our approach would help better quantify allele-specific gene expression, especially when SNP alleles are present.

Finally, we would like to point out that although our study is primarily based on RNA-Seq data, the proposed Bayesian framework can be easily extend to other NGS applications such as DNA-resequencing and Chip-Seq.