Absolute backscatter coefficient estimates of tissue-mimicking phantoms in the 5–50 MHz frequency range

Abstract

Absolute backscatter coefficients in tissue-mimicking phantoms were experimentally determined in the 5–50 MHz frequency range using a broadband technique. A focused broadband transducer from a commercial research system, the VisualSonics Vevo 770, was used with two tissue-mimicking phantoms. The phantoms differed regarding the thin layers covering their surfaces to prevent desiccation and regarding glass bead concentrations and diameter distributions. Ultrasound scanning of these phantoms was performed through the thin layer. To avoid signal saturation, the power spectra obtained from the backscattered radio frequency signals were calibrated by using the signal from a liquid planar reflector, a water-brominated hydrocarbon interface with acoustic impedance close to that of water. Experimental values of absolute backscatter coefficients were compared with those predicted by the Faran scattering model over the frequency range 5–50 MHz. The mean percent difference and standard deviation was 54% ± 45% for the phantom with a mean glass bead diameter of 5.40 μm and was 47% ± 28% for the phantom with 5.16 μm mean diameter beads.

INTRODUCTION

Estimation of the fundamental acoustic properties of tissue-mimicking (TM) materials in the clinical frequency range, 2 to 15 MHz, has been extensively studied.1, 2 Accurate determinations of the amplitude attenuation coefficients, speed of sound, and backscatter coefficients are important. Phantoms intended for quality assurance and performance assessment of imaging systems must have acoustic properties similar to those exhibited by soft tissue.3 Additionally, well-characterized reference TM materials are needed to validate algorithms that attempt to generate quantitative ultrasound feature images based on these properties.4, 5 Some of these algorithms also require reference echo-signals from well-characterized TM materials.6

High frequency ultrasound, greater than 15 MHz, has found increased utility in intravascular, small animal, ophthalmologic, and dermatologic applications, and there is an equivalent need for well-characterized TM materials at these frequencies. Relatively little work has been performed in this area. Brewin et al. reported on amplitude attenuation coefficient, speed of sound, and backscattered power spectral density of an agar-based phantom material from 17 to 23 MHz; however, they did not address the absolute backscatter coefficient.7

Challenges emerge at high ultrasound frequencies. Because the attenuation coefficient increases with frequency in soft tissue-like materials, test sample thicknesses for measurement of attenuation coefficients at higher-end frequencies must be small enough to achieve adequate signal-to-noise ratios (SNRs). In a similar manner, the attenuation coefficient of water decreases SNRs and requires limiting the net water-path length in a water displacement measurement. Thus for higher-end frequencies, experimental apparatus must be constructed in a compact manner to limit the transmission path. Higher amplitude signals can be generated to boost signal amplitude; however, care must be taken to avoid non-linear propagation effects.

Estimation of the absolute acoustic backscatter coefficient can be particularly difficult relative to estimation of speed of sound and attenuation coefficients.1, 2 In a 2005 comparison between laboratories examining the same TM materials, disagreements of up to two orders of magnitude resulted for the backscatter coefficient (BSC). Although there is better agreement in the general frequency dependent characteristics; the trends (first and second derivatives) on a log-BSC versus frequency plot generally possess similar values.2

Employing the same data reduction method as that used in the present work, excellent agreement between a Faran8 scattering model and a broadband technique was obtained for 1-6 MHz by Madsen et al.9 and 1.5-4 MHz by Chen et al.10 In this paper, experimentally determined values are reported for sound speed, attenuation coefficients, and absolute backscatter coefficients from 5 to 50 MHz on agarose-based TM materials designed for use at high frequencies.11 These known BSCs then can be used to estimate backscatter coefficients for in vivo tissues using a clinical pulse-echo system.6 BSC results are presented for two phantoms with different glass bead concentrations and diameter distributions, and BSC results are compared to a Faran model for spherical glass bead scatterers.8

MATERIALS AND METHODS

TM phantoms

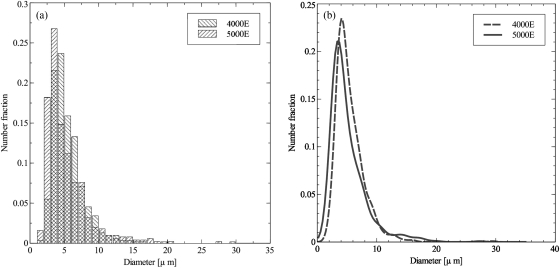
The TM phantoms examined in this paper were produced as reference phantoms for use at high frequencies.11 Each phantom was macroscopically uniform. The base material of the phantoms consists of a mixture of agarose, propylene glycol, Germall Plus (preservative), and ultra-filtered whole bovine milk. Scattering was due to glass beads with a spatially random distribution. Two phantoms were examined with different glass bead concentrations (mass per unit volume) and different diameter distributions (catalog numbers 4000E and 5000E, Potter Industries, Valley Forge, PA). The two phantoms will henceforth be referenced as the “4000E phantom” and “5000E phantom,” respectively. The diameter distributions of the two glass bead categories that were utilized in these phantoms are shown in Fig. 1. The diameter distributions for the 4000E and 5000E beads were measured by placing beads in an agarose suspension and viewing with a calibrated optical microscope. Approximately 500 diameter measurements were made for each bead type. A histogram of the diameter distribution is shown in Fig. 1a. A smoothed distribution was also found using the kernel density estimation (KDE) technique12, 13 resulting in the fraction per micrometer shown in Fig. 1b. A Gaussian kernel was used with bandwidth automatically calculated using the method of Silverman.14 Mean scatterer diameters of the 4000E and 5000E phantoms were 5.40 and 5.16 μm, respectively. The concentration of the 4000E beads was 6.00 g∕l, and that of the 5000E beads was 15.60 g∕l.

Figure 1.

(Color online) Size distribution of the TM phantom glass bead scatterers. (a) 4000E and 5000E distribution determined with a histogram divided by the total frequency. (b) 4000E and 5000E distribution determined with the KDE method.

For making attenuation and speed measurements, two test cylinders consisting of a 5-mm-thick acrylic cylindrical ring with parallel 12-μm-thick Saran Wrap^® transmission windows filled with the same materials used in the backscatter measurements; one cylinder was filled with the 4000E material and the other with the 5000E material. The density of the TM material is 1.045 g∕ml for the 4000E phantom and 1.062 g∕ml for the 5000E phantom.

Sound speed and attenuation

Sound speed and attenuation of the TM phantom material were estimated with narrowband substitution, using a through transmission technique that has been described previously.1, 15 This method involves measuring the ultrasound signal in a water tank with a transmitting and receiving transducer, then repeating the signal acquisition after introducing a sample of known thickness into the water between the receiver and transmitter. The shift in arrival time was used to calculate the speed of sound, and the amplitude ratio was used to calculate the material’s attenuation.1, 15

The equipment and setup used has been described previously11 and included a Wavetek model 81 function generator set to tone burst mode, generating a sinusoid of 30 wavelengths at the target frequency of 20, 30, 40, or 50 MHz. The input signal was amplified by a model 75A250A radio frequency (RF) amplifier (Amplifier Research, Souderton, PA). The signal was transmitted and received by a V358 50 MHz center frequency unfocused transducer pair (Olympus Panametrics-NDT, Waltham, MA). These transducers, serial numbers 630 314 and 630 315, were well matched in their spectral response with a −6 dB bandwidth of 80%. These 50 MHz broadband transducers were used because they are most sensitive at the higher values of frequency addressed where SNRs must be optimized for the speed and attenuation determinations. The transducers were aligned by peaking the received signal with a micrometer controlled translation unit (Ardel Kinematic, Stratford, CT) and gimbal mount (Newport Oriel, Stratford, CT). The compressional wave was transmitted through deionized water maintained at 22 °C by a Haake DC10 heater (Thermo Fisher Scientific, Newington, NH). However, the circulating heater was temporarily turned off during signal acquisition to reduce vibrations that would impact time delays and cause jitter while averaging sweeps with the WaveRunner LT342 oscilloscope (LeCroy, Chestnut Ridge, NY). The transducers were separated by a 42 μs delay (62.5 mm signal propagation path). The received signal was collected at 500 MS∕s, and 10 independent sets of 100 averaged tone bursts were transferred to a computer for further offline analysis.

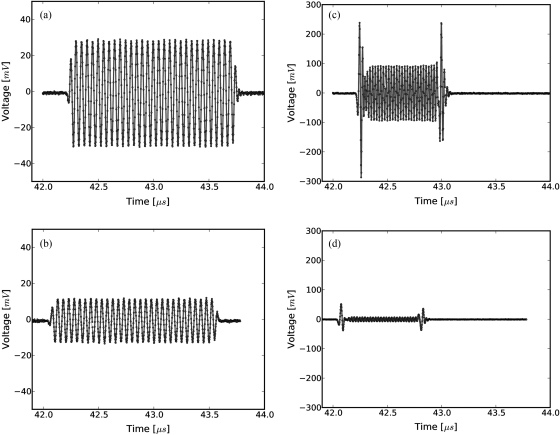
To determine the phase speed, it is necessary to find the shift in the central part of the narrowband pulse. Considerable changes in the shape of the tone burst occur because of frequency dependent attenuation (see Fig. 2). These changes were restricted to the leading and trailing edges of the tone burst. First, the approximate shift was obtained by monitoring the shift of a point on the leading part of the pulse. Because the leading part involves lower frequencies than the pulse center frequency, the shift was approximate. Next, the shift, Δt, in a zero-crossing near the center of the pulse was determined by assuming it was approximated by the leading edge shift; this assumption was justified because propagation speeds are not very dependent on frequency.11 Using the lag of the cross correlation peak was also investigated, but it did not always yield the monotonic increase in sound speed expected by the Kramers–Krönig relations.

Figure 2.

(Color online) Averaged, received signals obtained using the narrowband substitution method. (a) Water-only signal at 20 MHz, (b) 5 mm sample inserted with the center frequency at 20 MHz, (c) water-only signal at 40 MHz, and (d) sample inserted with the center frequency at 40 MHz. Time is relative to excitation at the source transducer, and the plotted time axes limits are kept consistent to demonstrate time shifts. Amplitudes are kept consistent at each frequency, but the excitation amplitude is adjusted with frequency so sufficient signal-to-noise ratio is obtained without saturation and non-linear propagation. The dramatic effects of frequency-dependent attenuation on the signal shape can be seen in (d).

The speed of sound was then obtained by inserting the zero-crossing time shift, Δt, and sample thickness, d, into the following equation16

$$c=\frac{c_w}{1+c_w\Delta t∕d}$$ (1)

where the speed of sound in pure water, c_w, at 22 °C is 1 488.3 m∕s (Ref. 17).

The attenuation coefficient, α, in decibels per unit length, was calculated using the signal amplitude in the absence of the sample, A_w, the signal amplitude with the sample in place, A_s, the transmission coefficient of the thin layer material holding the sample in place, T_total, and the thickness of the sample, d.

$$\alpha \left(f\right)=\frac{20}{d}{\mathit{log}}_{10}\left(\frac{A_w{T}_{\mathrm{total}}}{A_s}\right)+{\alpha }_{\mathrm{w}}\left(f\right).$$ (2)

Attenuation of water, α_w, which is negligible at lower frequencies, must be accounted for at high frequencies. The transmission coefficient of the Saran Wrap^® layer, a function of frequency, was calculated using Eq. 3 from Wear et al.2 where the speed of sound in Saran Wrap^® was found to be 2 400 m∕s, density 1.69 g∕ml, thickness 12.2 μm, and the amplitude attenuation coefficient

$$\alpha \left(f\right)={\alpha }_0{f}^n$$ (3)

where α₀ = 2.26 Np m⁻¹ MHz⁻ⁿ and n = 1.285 for the 4000E TM phantom α₀ = 5.0 Np m⁻¹ MHz⁻ⁿ and n = 1.50 in the 5000E case.

Only the amplitude in the central portion of the tone burst was used for calculating the attenuation at the central frequency. As shown in Figs. 2c, 2d, the 40 MHz tone burst signal’s leading and trailing edges, which have lower local frequency content, experience less attenuation. In the case of Fig. 2c, the differential attenuation results from attenuation in water and in Fig. 2d results from attenuation due to both water and sample.

Absolute backscatter coefficient

Calculation of the BSC, the differential scattering cross section per unit volume at a scattering angle of 180°, followed the method described by Chen et al.9, 10 Using a single element ultrasound transducer, pulses were propagated through water and into the material of interest, and the spectrum of the received backscattered signal voltage was used to calculate the BSC after correcting for characteristics of the transducer, instrumentation properties, and ultrasonic properties of intervening materials. The data reduction equation is

$$\mathit{BSC}\left(f\right)\approx \frac{〈V_g\left(f\right)V_g^{*}\left(f\right)〉}{C^2\parallel T\left(f\right)B_0\left(f\right){\parallel }^2\int \int {\int }_{\Omega }\parallel A(\mathbf{r},f){\parallel }^{4}d\mathbf{r}}$$ (4)

where the volume, Ω, is extensive enough that all significant values of ∥A(r,f)∥⁴ are accounted for.

The backscattered signal spectrum, V_g, was averaged using statistically independent signals from many locations in the phantom to obtain the mean power spectrum. The term C was a constant that accounts for windowing of the signal; C = 0.63 for the Hamming Window. A(r,f) was the complex superposition coefficient determined by the geometric properties of the transducer. Attenuation in the phantom is accounted in the calculation of A(r,f), via the imaginary component of the complex wave number. The amount of attenuation is determined by the power-law fit. A planar reflector was used to determine T(f) B₀(f), where T(f) represents the complex transfer function of the transducer, and B₀(f) was the complex superposition coefficient for the uniform monopole radiator assumed to exist on the transducer surface.9

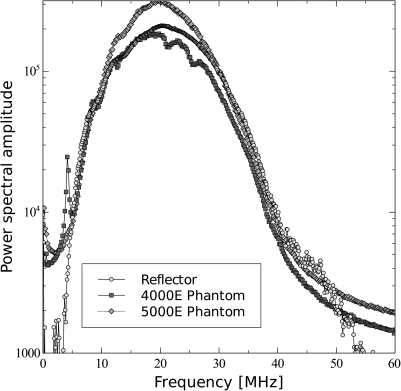
The transducer used for backscatter analysis was the 710B on a Vevo 770 scanning system (VisualSonics, Toronto, Canada). This transducer has a center frequency of about 25 MHz, and a broad bandwidth, 82% fractional bandwidth at −6 dB, as illustrated in Fig. 3. The transducer active element was a spherical cap with a projected aperture of 3.5 mm and 15.0 mm radius of curvature. The received signal was digitized at 420 MS∕s with 12 bit precision.

Figure 3.

(Color online) Power spectrum derived from radio frequency data acquired using the Vevo710B for the planar reflector and TM phantoms.

The Vevo 770, designed for high frequency imaging of small animals, is easily saturated when presented with signal from a high-amplitude acrylic or stainless steel planar reflector that experiences the relatively weak attenuation of a water path. To prevent saturation, a liquid–liquid planar interface, where the two liquids have closely matched acoustic impedances, was used.18 The interface reported by Hall et al.18 was recreated; it consists of a brominated hydrocarbon mixture covered by water. The hydrocarbon consists of 39.018% by weight 1-bromoheptane (99% purity, Acros Organics, Sommerville, NJ) and 60.982% by weight 1,6-dibromohexane (97% purity, Aldrich Chemical, Milwaukee, WI). The normal incidence amplitude reflection coefficient is 0.0138.18 A reduction of the gain by 5 dB for the planar reflector case—relative to the TM phantom signal gain—was still required to avoid saturation, but measurements of the phantom echo signals at different gains with corresponding corrections verified that the amplifier is linear and accurate within 2% over the frequency range analyzed. The reflector was carefully aligned to a normal orientation with respect to the transducer. Alignment was achieved with a gimbal mount by obtaining the highest possible amplitude for the backscattered signal. To prevent non-linear effects, the planar reflector and TM phantom signals were collected at a 10% transmit power. At 10% power, a reasonable trade-off was achieved that reduces non-linear propagation effects in the planar reflector signal while leaving sufficient SNR in the backscattered signals acquired from the TM phantom over the 5-50 MHz range.

The single element transducer was moved laterally and elevationally, and 1 200 independent power spectra of the scattering instances were averaged to obtain the backscattered power spectrum, shown in Fig. 3. The 5000E phantom was covered with a thin Saran Wrap^® layer as previously described in the substitution experiment, and the 4000E phantom is covered with a 128 μm-thick TPX^® (polymethyl-pentene) layer. A TPX^® layer was advantageous relative to a Saran Wrap layer because of its low reflection coefficient, which minimizes reverberation effects at higher frequencies. The gated window for spectral analysis in the phantoms was placed at the focus and in an area free from any reverberation artifacts and had a duration of 4.6 μs.

It is important that the phantom signal be devoid of reverberations between the transducer-water interface and the water-phantom interface. Reverberations can sometimes be observed in the A-mode signal, but during acquisition, use of the system’s real-time B-Mode display is also a convenient method to ensure that reverberations are avoided. The B-Mode display shows possible reverberations as locations with high intensity signal that extend laterally across the length of the phantom. The planar reflector spectrum is shown in Fig. 3 along with the two spectra for the TM phantoms averaged over 1 200 scan lines.

Experimentally determined BSCs were compared to those predicted by the theoretical model of Faran8 with the latter employing the following values. The medium density was 1.045 g∕ml and 1.062 g∕ml for the 4000E and 5000E phantoms, respectively, and the glass bead longitudinal speed of sound was 5 572 m∕s, with a density of 2.380 g∕ml and shear wave speed of 3376 m∕s. The bead mass per volume was 6.0 kg∕m³ and 15.6 kg∕m³ for the 4000E and 5000E phantoms, respectively. Summation of the BSC corresponding to each bin in the histograms of Fig. 1 yielded the predicted total BSC.

The contribution to the BSC of each diameter increment bin was determined by N_v(D_i), the number of beads of the bin per unit volume, which can be computed using the total mass of beads per unit volume, M_V, the number fraction of beads in the bins, g(D_i), and the glass bead mass density, ρ_m.

If N_v is the total number of beads per unit volume, then

$$M_v={\rho }_m\frac{\pi }{6}\sum _{i=1}^N{D}_i^3{N}_{v}g\left(D_i\right)$$ (5)

or

$$N_v=\frac{M_v}{{\rho }_m\frac{\pi }{6}\sum _{i=1}^N{D}_i^{3}g\left(D_i\right)}.$$ (6)

The number of beads per unit volume in the diameter, D_i, bin is then,

$$N_v\left(D_i\right)\equiv N_{v}g\left(D_i\right).$$ (7)

Equations 6, 7 give

$$N_v\left(D_i\right)=\frac{M_{v}g\left(D_i\right)}{{\rho }_m\frac{\pi }{6}\sum _{i=1}^N{D}_i^{3}g\left(D_i\right)}.$$ (8)

The BSC then equals the sum of the contributions from each bin, viz.,

$$\mathrm{BSC}\left(f\right)=\sum _{i=1}^N\mathit{DSC}(f,D_i)N_v\left(D_i\right)$$ (9)

where BSC(f,D_i) is the differential scattering cross section at 180° for one scatterer of diameter D_i at frequency f.

RESULTS

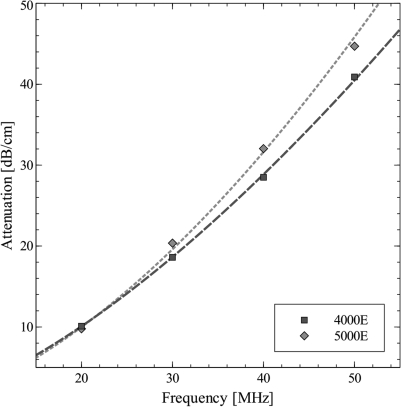
Attenuation coefficient values are shown in Fig. 4 along with the power law fits using the relation attenuation coefficient α=α₀fⁿ where f is the frequency and α₀ and n are constants given in Table TABLE I.. The medium sound speeds were found to be 1 541 m∕s for the both 4000E and 5000E TM phantoms. These results along with the other defining characteristics of the two phantoms are summarized in Table TABLE I..

Figure 4.

(Color online) Attenuation coefficients and power law fits for the 4000E and 5000E phantom.

Table 1.

Summary of properties of the 4000E and 5000E TM phantoms.

Quantity	4000E TM phantom	5000E TM phantom
Bead concentration (g∕l)	6.00	15.60
Mean bead diameter (µm)	5.40	5.16
Thin layer covering	TPX	Saran wrap
Density (g∕ml)	1.045	1.062
Speed of sound (m∕s)	1541	1541
Atten. α0 (dB∕cm)	0.107	0.069
Atten. n	1.52	1.66
BSC at 30 MHz (sr−1cm−1)	0.040	0.130

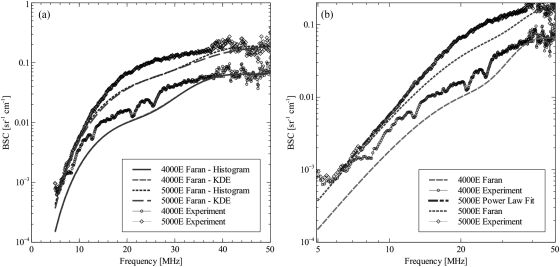
Experimentally determined and computed BSCs (Faran) versus frequency for both phantoms are displayed in Fig. 5. Because the spectral plots in Fig. 3 suggested there may be sufficient SNR between 5 and 50 MHz, analysis was displayed over that range. There were significant differences between the two phantoms’ BSCs, which are amplified at higher frequencies. This relationship was observed in both the Faran calculation and experimentally determined results. Differences in the predicted BSC of the Faran calculation results were much greater in the 15–30 MHz range than the 5–15 MHz range. Power law regression to the 5000E experimental data between 6 and 15 MHz [Fig. 5b] resulted in a slope of 3.76 and a coefficient of determination, R², of 0.997; thus, Rayleigh scattering was approximated. Rayleigh scattering was expected more for the 5000E phantom than the 4000E distribution because of the smaller bead diameter distribution evident in Fig. 1.

Figure 5.

(Color online) Absolute backscatter coefficient for the two TM phantoms examined. A curve derived from the phantom composition and Faran scattering theory for spherical scatterers is displayed along with results phantom and planar reflector RF data. Dashed lines are the Faran predicted BSC for the acoustic properties assumed for the component materials. Curves with markers represent the experimental results. In (a), Faran curves for both the histogram approximation of size distribution and the KDE approximation of the size distribution are presented. The same data are present in (b) but with logarithmic scaling on both axes. Only the KDE Faran curves are plotted, but results from power law fit of the 5000E experimentally determined data in the 6-15 MHz range are also shown.

The lower BSCs of the 4000E phantom may explain the noisier appearance of the curve compared with that of the 5000E phantom. The general trend of the 4000E experimentally determined BSC appears to be correct, although there are some variations not found in the Faran calculation curve. The experimentally determined BSC values are higher in the 5–35 MHz frequency range before converging to the Faran calculation. The mean and standard deviation of the percent difference of the 4000E experimentally determined values from the Faran calculation values from 5 to 50 MHz are 54% ± 45%. Agreement between the Faran calculation and experimentally determined results for the 5000E is very close in the 5–15 MHz frequency range. The experimentally determined BSC values are higher from 15 to 35 MHz before also converging again. The mean and standard deviation of the percent difference of the 5000E experimentally determined values from the Faran calculation values from 5 to 50 MHz are 47% ± 28%. The overall agreement between the experimental results with the Faran calculations within approximately a factor of two is very good considering the many possible sources of error in both calculations and outcomes experienced by other research groups.1, 2

DISCUSSION

In this paper, methods were presented that can be used to estimate the absolute BSC at high frequencies. Accurate estimation of this quantity has proven difficult for low frequencies,2 and additional challenges caused by alignment and attenuation make it significantly more difficult at high frequencies. There were a number of input parameters and assumptions in the broadband BSC data reduction that can be sources for error.

The accuracy of the estimation method used in this work depends on the uncertainties in the radius of curvature and the effective projected diameter of the transducer’s active element; determination of values for these parameters depended upon mapping of the radiation field at a set of frequencies spanning the frequency range of interest. The mapping’s purpose is to find the focal plane where the directivity function is defined for each frequency. The center of curvature will be at the peak of the directivity function’s central maximum. The diameter of the active element’s projected area is calculable from the width of the central maximum of the directivity function.9 Unfortunately, to our knowledge, a calibrated hydrophone at higher frequencies with a sufficiently small receiving diameter is not currently available. Thus estimates of values for the transducer’s center of curvature and active diameter supplied by the manufacturer had to be relied upon.

Calculation of the BSC also relies on determinations of the sample speed of sound and attenuation coefficients over the 5 to 50 MHz range. These quantities were again used in the acoustic radiation field calculation. High sampling frequencies were required for precise estimation of the speed of sound, and linear interpolation of the zero-crossing can increase the precision of delay measurement. Care had to be taken to prevent offsets in the delay from occurring due to building vibration, inadvertent load on the apparatus by the experimenter, or vibrations of the transducer from water flow due to the tank heater. Distortion of the signal at the tone burst edges, as shown in Fig. 2, made determination of the phase velocity challenging for frequencies of 30 MHz or higher. Attenuation estimation relied on proper alignment and sufficient signal amplitude. The transducers must be placed close together to prevent excessive signal loss in the water path. This required precise alignment of the transducers. The TM specimen used for substitution needs to have a small thickness to prevent signal loss, but this also makes precise and accurate thickness measurement more important. High excitation voltages were required to obtain adequate signal at high frequencies, but these same high voltages cannot also be used at lower frequencies because non-linear propagation would occur in water.

Non-linear propagation was also a concern when performing BSC estimates. Additionally, the small distances between the transducer and the phantom interface required to retain signal amplitude introduced issues due to reverberations between these interfaces. Special care relative to lower frequency BSC methods must be taken to guard against interference from the reverberations.

There are three significant differences between the two phantoms examined: the thin layer material covering the phantom and the glass bead size distributions and concentrations. Incorrect assumptions of the thin layer properties would affect the estimated BSC, and uncertainties in the bead diameter distribution would result in uncertainties in the Faran calculation.

Kernel density estimation was investigated as a method to improve estimation of the bead diameter distribution, but this is found to have negligible effects on the BSC curves. Diameters of 500–600 beads of each type were measured. A small fraction of larger diameter beads were found in both the 4000E and 5000E cases. Due to their large sizes relative to the average, their contribution to backscatter was much greater than average. Thus the uncertainty regarding the number density of the larger beads contributed considerably to the uncertainty of the Faran theoretical result itself. In practice, it is easier to obtain agreement between experimental and theoretical results when the bead diameter distribution is much smaller than the wavelength (Rayleigh scattering), and the distribution lacks rare outliers.

An advantage of the Vevo 770 transducer was its broadband spectrum and high SNR. In this experiment, values were obtained over a wide frequency range, 5–50 MHz, and a BSC that spanned two orders of magnitude. Note that transmit power needed to be reduced to 10% excitation power to prevent harmonics due to non-linear propagation. This again illustrates the challenges non-linear propagation poses at these high frequencies.

SUMMARY AND CONCLUSIONS

Using a high frequency transducer with 82% fractional bandwidth at −6 dB, agreement between Faran predictions and experimentally determined broadband estimates was 54% ± 45% for the 4000E phantom with a 5.40 μm mean particle diameter and 47% ± 28% for the 5000E phantom with mean particle diameter of 5.16 μm over the range from 5 to 50 MHz. BSCs spanned two orders of magnitude. Reasonable agreement between Faran predictions and the experimentally determined BSC results are observed consistently for two TM phantoms that differed in terms of the thin layer covering material, glass bead size distribution, and glass bead concentration. Use of a VisualSonics Vevo 770 scanning system coupled with a precisely aligned liquid planar reflector is a promising system for making high frequency, broadband BSC estimates.