Abstract
This study tests how peripheral auditory processing and spectral dominance impact lateralization of precedence effect (PE) stimuli consisting of a pair of leading and lagging clicks. Predictions from a model whose parameters were set from established physiological results were tested with specific behavioral experiments. To generate predictions, an auditory nerve model drove a binaural, cross correlation computation whose outputs were summed across frequency using weightings derived from past physiological studies. The model predicted that lateralization (1) depends on stimulus center frequency and the inter-stimulus delay (ISD) between leading and lagging clicks for narrowband clicks and (2) changes differently with lead click level for different ISDs. Behaviorally, subjects lateralized narrowband and wideband click pairs whose stimulus parameters were chosen based on modeling results to test how peripheral processing and frequency dominance contribute to lateralization of PE stimuli. Behavioral results (including unique measures with the lead attenuated relative to the lag) suggest that peripheral interactions between leading and lagging clicks on the basilar membrane and strong weighting of cues around 750 Hz influence lateralization of paired clicks with short ISDs. When combined with auditory nerve adaptation, which emphasizes onset information, lateralization of PE click pairs with a short ISD can be well predicted.
INTRODUCTION
The term the “precedence effect” (PE) (Wallach et al., 1949) describes the phenomenon whereby a pair of temporally close sounds from different directions are heard as a single “fused” image whose perceived direction is near the location of the first-arriving sound. Physiologically, the binaural information conveyed by a lagging click is suppressed when paired clicks are presented with inter-stimulus delays (ISDs) as long as 10–20 ms (Yin, 1994; Fitzpatrick et al., 1995). This suppression is often described as the physiological basis of the perceptual dominance of the spatial information in the leading click. The PE has received a great deal of attention from psychophysicists, physiologists, and modelers. Some studies performed behavioral experiments to test predictions of computational models of the PE directly (Lindemann 1986; Tollin and Henning, 1999; Braasch and Blauert, 2003; Zurek and Saberi, 2003). The current study builds on these past efforts using a physiologically based model whose parameter values were set from previous physiological results. The model was used to make explicit predictions of how various stimulus parameters influence perception. We then measured lateralization of novel PE stimuli to test model predictions, concentrating on cases in which specific mechanisms in the model were expected to affect results.
The dominance of a leading stimulus on sound localization has often been explained by assuming that inhibition triggered by the leading sound reduces the importance of spatial information in the lagging stimulus. Inhibitory connections are generally invoked in models of the PE (e.g., Lindemann, 1986; Braasch and Blauert, 2003; Xia et al., 2010). However, other mechanisms contribute to lateralization judgments of typical PE stimuli. Peripheral interference between lead and lag clicks arises because of the band-pass filtering of the cochlea, which causes “ringing” of the basilar membrane (BM). When the temporal delay between the lead and lag clicks is very short, the BM response to the lead may still be present when the lag occurs. For some ISDs, the lag response may be out of phase with the lead, causing cancellation of the BM response. Alternatively, at different ISDs, lead and lag responses will be in phase, producing a larger total response. In addition to changing the amplitude of the BM response, such interactions also change the monaural phase of the total responses of the left and right basilar membranes. As a result, the effective, internal interaural time difference (ITD) generated by the lead and lag click BM responses (i.e., the ITDs that are measured at the output of the auditory-nerve fibers, and are processed by the binaural system) can differ from those imposed on the external, physical stimuli.
Two previous models explored how lateralization judgments of PE stimuli are influenced by non-inhibitory interactions between leading and lagging responses. Hartung and Trahiotis (2001) demonstrated that a model of the auditory periphery, consisting of a gammatone-filter bank and a hair-cell model (Meddis, 1986), can predict PE lateralization results for lead-lag click pairs separated by short ISDs (< 5 ms). They assumed that listeners perceive the click pair as coming from the location corresponding to the peak in the cross correlation of left and right peripheral outputs. In their model, adaptation in the auditory nerve response emphasizes onset information, while peripheral interactions produce internal ITDs that differ from the lead and lag ITDs. Together, these effects can account for judgments of source laterality for some PE stimuli with short ISDs.
A similar approach explored the importance of including a spectral dominance region that places greater perceptual weight on interaural differences around 750 Hz, compared to other frequencies (Tollin, 1998). Results from a number of PE experiments were explained by focusing on the spectral dominance region around 750 Hz (Tollin and Henning, 1999): monaural interactions between the lead and lag produce interaural differences in the energy-density spectrum whose sign and size depends on both frequency and the delays between the clicks in each ear. In addition, the interaural differences in energy density that result can account for some anomalous lateralization that occurs when ISDs are shorter than 2 ms (Wallach et al., 1949; Blauert and Cobben, 1978; Zurek, 1980; Gaskell, 1983; Tollin and Henning, 1996). Due to these internal interaural differences, in some conditions the perceived source location can be on the side of the head opposite the side expected from the external ITD of the stimulus. They argued that both lead and lags clicks that arrive within short ISDs have especially strong effects on localization through their contribution to the spectral characteristics near 750 Hz, which predominantly determine a listener’s localization performance.
The primary aim of the current study was to use both modeling and behavioral results to explore how three mechanisms (the peripheral interaction between the lead and lag responses on the basilar membrane, response adaption in the auditory periphery, and frequency dominance) influence lateralization of PE stimuli with short ISDs. A physiologically based auditory nerve model (Carney, 1993) was used to simulate effects in the auditory periphery, including band-pass filtering on the basilar membrane and firing-rate adaptation generated at the synapse between the inner hair cell and auditory nerve. Perceived laterality was predicted by computing the centroid of the weighted interaural cross correlation (IACC) functions of left and right peripheral outputs. The IACC functions were weighted according to a physiologically plausible distribution of best ITDs and best frequencies (Hancock and Delgutte, 2004) in order to test integration of localization information across frequency. Specifically, in the model, greater perceptual weight is given to localization information from the frequency region around 750 Hz. We selected a set of key stimulus conditions that lead to qualitatively different model predictions to test them behaviorally. We found that for narrowband clicks, the effective, internal ITDs produced in the cochlea affect perceived laterality of paired clicks with different ISDs. For wideband clicks, decreasing the level of the lead relative to the lag decreased the leading dominance; importantly, the size of this change with lead level depended on the ISD, consistent with model predictions. Finally, we analyzed the model components to isolate the contributions of peripheral basilar membrane interactions, adaptation, and spectral dominance to the full model predictions.
METHODS
Modeling
The auditory nerve model
To model neural processing of ITD, left and right ear signals were presented to an auditory nerve (AN) model based on the Carney (1993) model. This model generates neural responses of low-frequency AN fibers in response to acoustic stimuli, simulating the principle processing stages in the cochlea. Each modeled location along the basilar membrane responds to a band-passed version of the acoustic input. In the Carney (1993) model, the filter’s bandwidth varies continually over time with fluctuations in stimulus amplitude, capturing the characteristics of the compressive nonlinearity in BM mechanisms. Such nonlinear properties of the BM were simulated in the Carney (1993) model by a feed-forward control path that specified a level-dependent, time-varying time constant of the cochlear filter. In the current study, a fourth-order gammatone filter with a fixed time constant (Patterson et al., 1995) was used to simulate the band-pass filtering of the BM. We used a linear-phase gammatone filter, rather than a filter with a level-dependent, time-varying bandwidth like that used by Carney (1993), so that we could compute the interaural cross correlation (IACC) function of the gammatone filter outputs analytically. This approach allowed us to isolate the effect of the BM filtering from effects of adaptation occurring in the latter stages of peripheral processing (see Sec. 4A of the Discussion).1 The impulse response of the gammatone filter used here is given by
| (1) |
where γ is the order of the filter, fCF is the center frequency (CF), and τ is the time constant, which was calculated based on the time-invariant equivalent-rectangular bandwidth (ERB) (Glasberg and Moore, 1990). Fourteen filters were used, spaced from 244 Hz to 1670 Hz CF in steps of one ERB.
The output of the filter was then passed through models of the IHC and the IHC-AN synapse. The inner hair cells (IHCs) at a given location transduce the mechanical responses of the corresponding portion of BM to electrical potentials that result in the release of neurotransmitters at the IHC-AN synapse, generating action potentials of the AN fibers. Here, the IHC was modeled as a nonlinear compressive function followed by two low-pass filters (as in Carney, 1993) so that (1) the ac and dc components of the IHC responses saturate at high stimulus intensities and (2) the ratio of ac to dc components, which affects the synchrony coefficient of AN-fiber responses to tones at CF, decreases with increasing stimulus frequency.
Adaptation of the IHC-AN synapse is a strongly nonlinear process that affects the discharge rates of AN fibers. The time decay of the firing rate following the response peak at stimulus onset was simulated by a three-compartment diffusion model (Westerman and Smith, 1988). Detailed descriptions of the supporting equations and parameter values of the IHC and the IHC-AN synapse model can be found in Carney (1993). Compared to the Meddis (1986) hair-cell model, the amount of adaptation generated by the Carney (1993) model has a strong dependence on stimulus level and frequency, which plays an important role in predicting the behavioral lateralization of PE stimuli, especially for wideband clicks. The AN model output in the current study is the instantaneous, time-varying probability of observing a neural spike in an AN fiber of a specified CF, which drives a non-homogeneous Poisson process in the Carney (1993) model, generating the timing of neural spikes.
Interaural time difference processing
The medial superior olive (MSO) is thought to be the initial site of significant ITD processing in the mammalian auditory pathway. MSO neurons are “tuned” (i.e., respond preferentially) both to a particular input frequency (best frequency) and a particular ITD (best ITD). Many binaural models approximate the output of the MSO cells by computing the IACC of narrowband, frequency-matched left and right inputs. The magnitude of this function at a particular interaural delay predicts the expected firing rate of a neuron with the corresponding best ITD and best frequency.
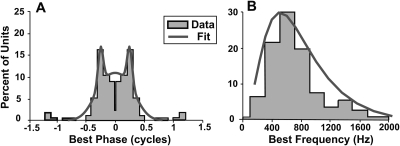
The IACC function was computed by taking 40-ms lengths of the output of the CF-specific AN model, for interaural delays spanning the range from −1500 to +1500 μs in 50-μs steps. The predicted activity of each MSO neuron was then weighted by an across-best-phase weighting function [Fig. 1A] to account for the physiological distribution of best phases of inferior colliculus (IC) neurons (Hancock and Delgutte, 2004). These distributions were assumed to be constructed from identically distributed left and right MSO neurons whose best ITD favors contralateral locations. The distribution of best ITDs on each side of the brain was parameterized by a weighted sum of two Gaussians (taken from Hancock and Delgutte, 2004), which emphasizes the activity at best interaural phases equal to ± 1∕4 cycle (see also McAlpine et al., 2001).
Figure 1.
(A) Best-phase distribution for ITD-sensitive inferior colliculus units. The distribution is based on the data from one side of the brain (Hancock and Delgutte, 2004, shown as gray-filled histogram) by assuming left∕right symmetry. Reprinted with permission. The model used a best sum-of-Gaussians fit, shown by the solid gray line. (B) Best-frequency distribution taken from the same study (Hancock and Delgutte, 2004, shown as gray-filled histogram). The model used a best lognormal fit, shown by the solid gray line.
To predict the perceived location of narrowband stimuli, the IACC function was generated from the outputs of left and right AN models corresponding to the center frequency of the stimulus. For wideband stimuli, the magnitudes of the IACC functions in each frequency channel were first weighted at each interaural delay by the above sum-of-Gaussians weighting function. Then, the resulting IACC functions were weighted in frequency by a lognormal function [Hancock and Delgutte, 2004; see Fig. 1B], capturing the physiological distribution of CFs of IC neurons, which favors middle to low frequencies. This across-frequency weighting function realizes a spectral dominance region for lateralization near 750 Hz, which is consistent with the spectral dominance region that has been observed behaviorally in previous studies (Bilsen and Raatgever, 1973; Tollin and Henning, 1999). Finally, the weighted IACC functions were added together for each interaural delay across 14 frequency channels (c.f., Shackleton et al., 1992). This integration favors perceived locations whose ITDs are consistent across frequency, an operation that is functionally similar to the “straightness weighting” employed in previous interaural-cross correlation models that integrate information across frequency (e.g., see Trahiotis et al., 2001).
The ITD of the perceived image, αITD, was estimated by the interaural delay corresponding to the centroid of these computed IACC functions. By using the centroid rather than the peak activity to estimate αITD, double-peaked IACC patterns yielded robust, stable results (in most other respects, predictions based on the peak, as were computed in Hartung and Trahiotis, 2001, yield results similar to our predictions). Given the bimodal distribution of best ITDs we used, this physiologically based population rate code is also similar to the hemisphere opponent model of Hancock (2007), which pools the activity of neurons across best phase and best frequency to form ITD channels on each side of the brain and then estimates the lateral position by comparing the relative activity of the left- and right-hemisphere channels.
Behavioral experiments
The model described above makes quantitative predictions of how lateralization judgments vary for paired clicks with different ISDs, different relative lead-lag levels, and different frequencies. Behavioral experiments were designed to test specific model predictions for critical stimulus parameter values in order to explore the effects of peripheral interactions on the basilar membrane, adaptation, and frequency dominance on sound lateralization. The stimulus parameters that we tested were chosen to be similar to those used in past modeling and behavioral work of the PE with short ISDs to enable comparison (e.g., Blauert, 1997, p. 204; Hartung and Trahiotis, 2001).
Two lateralization experiments were conducted, using identical methods but slightly different stimuli. The main experiment was designed to explore how differences in stimulus bandwidth affected perception at two key ISDs for which narrowband results were expected to differ from wideband results. These differences were predicted in the model because, for a given frequency, peripheral effects change with ISD, causing narrowband predictions to vary significantly with ISD. Because the peripheral interactions differ with frequency for a given ISD, less extreme predictions arise when information is combined across frequency; as a result, wideband stimuli change more smoothly with ISD than do predictions for narrowband stimuli. The follow-up experiment was conducted to better delineate how lateralization of wideband stimuli varied with ISD at a few additional ISDs not tested in the main experiment. These follow-up data specifically address whether the model’s weighting of information across frequencies predicts behavioral results. Both experiments included stimuli in which the lead sound was attenuated relative to the lag in order to explore the importance of adaptation in peripheral auditory responses. While there have been many studies of the precedence effect, we know of no previous studies of “localization dominance” (e.g., see Litovsky et al., 1999) in which the lateralization of otherwise identical leading and lagging clicks was measured with the lead click level attenuated relative to the lag. Previous studies have measured other aspects of perception of PE stimuli when varying the lead level (e.g., experiments that measured trading of spatial cues in lead and lag that produced a central image, Leakey and Cherry, 1957; or used lead and lag stimuli that differed in frequency content, Shinn-Cunningham et al., 1995); however, none are directly comparable to the current experiment.
Stimuli
Either wideband or narrowband pairs of binaural clicks were used as test stimuli. The test stimuli were presented for a three-second-long duration at a rate of two per second. Wideband clicks were generated using frozen white noise bursts of 1-ms duration (sufficiently brief that we henceforth refer to them as “clicks”), constructed with a rectangular time window. In order to reveal cochlear interactions between lead and lag clicks within one frequency channel, narrowband clicks centered at 500 Hz were generated by filtering the wideband clicks by the same gammatone filter used in the modeling sections. The peak sound pressure level (SPL) was 87 dB for the wideband clicks and 79 dB for the narrowband clicks.
These wideband or narrowband clicks were used to generate both leading and lagging binaural clicks. For each ear, the ISD was defined from the onset of the leading click to the onset of the lagging click. ISDs of 1 and 2 ms were tested in the main experiment; ISDs of 0.65 and 1.3 ms were tested in the follow-up experiment. ITDs τ1 and τ2 were imposed on the leading and lagging binaural clicks, respectively, by advancing the timing of the click in one ear and delaying it in the other ear by half of the specified ITD. For negative ITDs, the click in the left ear was advanced while the click in the right ear was delayed. In the current study, the position of the lead and lag were always symmetric about midline (τ2 = –τ1), and τ1 could be +200 or −200 μs. In control trials, a single binaural click (ITD = τ1) was presented. For trials presented with the lead-lag composite stimuli, the level of the leading click was attenuated by 0, 5, 9, 12, or 15 dB relative to that of the lagging click.
The pointer stimulus was a three-second-long ongoing noise with a spectral composition similar to that of the test stimulus. Specifically, the test stimuli were generated by selecting very brief duration “clicks” from noise like that used to construct the pointer. To generate the narrowband test and pointer stimuli, the same filter was used. The pointer was normalized to have a power equal to that of the test stimuli, and was presented at 67 dB SPL for both bandwidths. The interaural level difference (ILD; applied by increasing and decreasing the levels in opposite ears each by half the total ILD) αILD of the pointer stimuli was controlled by the subject. At the start of each trial, the initial ILD of the pointer stimulus was randomly chosen from the range of −20 to +20 dB (with a step of 0.5 dB). Subjects could adjust the ILD in 2-dB steps in either direction, as described below. The pointer’s ILD was always limited to the range of ± 20 dB. Digital stimuli were generated at a sampling rate of 25 kHz and sent to Tucker-Davis Technologies (TDT) System II hardware for D∕A conversion. All the stimuli were presented with circumaural headphones (Sennheiser HD580) to subjects seated in an IAC sound attenuating booth.
Task
On each trial, subjects were asked to adjust the lateral position of the pointer stimulus to match the intracranial position of the test stimulus. During the presentation of the pointer stimulus, subjects adjusted in real time the position of the pointer by pressing one button to increase its ILD and a different button to decrease its ILD. Three-second-long test and pointer stimuli were alternated repeatedly until subjects were satisfied that the perceived position of the test stimulus matched that of the pointer stimulus, at which time they pressed a third button to terminate the trial. This alternation ensured that the local context of the test and pointer stimuli was always comparable across trials as a way to control any effects of PE “buildup” and to keep the perceived location of the test stimulus perceptually constant (Freyman et al., 1991).2 On each trial, the final ILD of the pointer stimulus, αILD, was used as a measure of the perceived lateral position of the test stimuli.
Procedures
In both the main experiment and the follow-up experiment, subjects performed two experimental sessions in which the trials were statistically identical. Within each session of the main experiment, two blocks of trials were presented, one with wideband clicks and the other with narrowband clicks; block order was counterbalanced for each subject and random from subject to subject. Two ISDs (1 and 2 ms) were tested within each block of the main experiment (see below). In each session of the follow-up experiment, subjects performed one wideband block with ISDs equal to 0.65 or 1.3 ms. Other than these differences in the stimuli used and the number of blocks per session, procedures were identical in the main and follow-up experiments.
Within each block, both composite and single runs were presented. A composite run was made up by two composite trials, in which paired clicks with +200- and −200-μs lead ITD (and therefore −200-μs and +200-μs lag ITD) were presented, respectively. Within each composite run, the ISD and inter-stimulus level difference were held constant. A single run was made up by two single trials, in which single binaural clicks with +200-μs and −200-μs ITD were presented, respectively. In the composite runs, five inter-stimulus level differences (0, 5, 9, 12, and 15 dB) and two ISDs (1 and 2 ms in the main experiment; 0.65 and 1.3 ms in the follow-up experiment) were tested. Thus, there were 10 types of composite runs (5 levels × 2 ISDs) in addition to one type of single run. Each of the 11 run types, consisting of two trials (with +200- and −200-μs lead ITD, respectively), was repeated twice, resulting in 44 trials in total in each block. Finally, the order of the 44 trials in each block was randomized separately for each subject and block. Thus, across both experimental blocks, eight pointing measurements were made in total by each subject for each of the 11 conditions.
Subjects
Five subjects (two female, three male) with audiologically normal hearing and no reported histories of hearing loss completed both the main and follow-up experiments. All were students at Boston University with ages between 21 and 33 yr. All subjects gave written informed consent in accordance with procedures approved by the Charles River Institutional Review Board.
Data analysis
The strength of the PE was quantified by finding the relative influence of the lead and lag on lateralization judgments (as in Shinn-Cunningham et al., 1993). Specifically, the perceived ITD corresponding to the location of the PE stimuli (αITD) was assumed to be a weighted average of the leading (τ1) and lagging (τ2) ITDs:
| (2) |
A weight of c = 1 indicates that precedence is complete and that the lead dominates lateralization entirely. A weight of c = 0.5 indicates that the perceived location of the PE stimulus falls midway between the location of the lead alone and the lag alone. A weight of c = 0 indicates that lag dominates lateralization completely. The c estimates were used here to quantitatively compare the model predictions with the behavioral results. Values of c can be estimated from the model results by inverting Eq. 2 to
| (3) |
where αITD is the estimated ITD of the PE stimuli from the model and τ1 = −200 μs and τ2 = +200 μs. The model is symmetric, so that the τ1 = +200 μs and τ2 = −200 μs condition will result in the same model c value as τ1 = −200 μs and τ2 = +200 μs.
In the behavioral experiment, we used ILDs to measure the perceived lateral location of PE stimuli as well as of single-click stimuli. Assuming that there is a one-to-one correspondence between perceived laterality as measured by ITDs and as measured by ILDs, the c value can be calculated from results of the acoustic pointing task as
| (4) |
where αILD is the perceived lateral position of a PE stimulus as measured by the matched ILD of the pointer and ψ1 and ψ2 are the matched ILDs of a single stimulus presented in isolation at the leading location and lagging location, respectively. Note that values of c larger than 1.0 can occur when the perceived location of a PE stimulus is to the same side as but more lateral than the location of the leading source, and negative c values can occur when the perceived location is to the same side as but more lateral than the lagging source.
RESULTS
Model predictions
The peripheral processing of the auditory nerve was simulated by the AN model using one frequency channel (CF = 500 Hz) for the narrowband stimuli and 14 channels for the wideband stimuli. Behavioral results were predicted by computing the long-term IACC functions of the left- and right-ear AN outputs and then integrating across frequency as appropriate (for the wideband stimuli).
Narrowband predictions
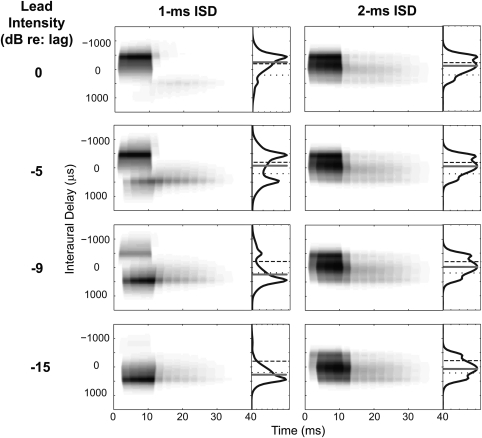
Figure 2 illustrates the IACC as a function of time in response to a stimulus with a lead click containing an ITD of –200 μs and a lag with an ITD of +200 μs, computed for the 500-Hz AN outputs after weighting the raw IACC by the across-best-phase weighting function. This weighted IACC was used to predict results from the behavioral experiment conducted in the narrowband block. The running IACC was computed over a rectangular time window (length equal to four cycles of the CF, or 8 ms, with a step of one sample). The resulting time-varying IACC at a given best ITD gives an estimate of the instantaneous firing rate of an MSO neuron tuned to that ITD. The plots to the right of each running IACC show the IACC functions integrated over time. The gray bars in these panels indicate the centroid of the corresponding weighted long-term IACC function, which estimates the perceptually equivalent ITD of the corresponding narrowband PE stimulus. The dashed and dotted lines indicate the ITDs used to construct the leading and lagging clicks of the input stimulus, respectively.
Figure 2.
Time-varying IACC functions computed from left- and right-ear AN model outputs for fibers with best frequency equal to 500 Hz. The short-term correlation at each interaural delay (y axis) is shown as a function of time (x axis), after being weighted by the across-best-phase distribution. Higher activity is indicated by darker gray scale. The plot to the right of each panel shows the IACC functions integrated across time. The interaural delays corresponding to the centroid of the weighted, long-term IACCs are indicated by the gray bars. The dashed and dotted lines indicate the ITDs used to construct the leading and lagging clicks of the input stimulus, respectively.
The top row of Fig. 2 shows the IACC when the lead and lag clicks were presented at the same level. For the 1-ms ISD (left panel), at the onset of the response, the maximal activity of the instantaneous IACC occurred at negative interaural delays (around –500 μs), toward the side of the leading click. Later in the output, positive instantaneous values of ITDs also occurred (around +500 μs), toward the lagging side. The centroid of the long-term IACC, integrated over time, fell near, but remained farther to the side than the lead ITD of –200 μs. For the 2-ms ISD (right panel), the maximal activity of the instantaneous IACC moved from negative interaural delays (around –250 μs) to interaural delays around zero as time progressed. The overall centroid fell at an ITD more central than the leading ITD (the gray bar was closer to 0 than the dashed line in the top right panel of Fig. 2). For both ISDs, due to the high level of initial activity, the centroid of the IACC functions, averaged over time, was dominated by the instantaneous ITDs at the onset of the response, which favored the leading ITD. However, the instantaneous ITDs changed over time, and often took on values that did not equal the ITD of either the lead or the lag.
When the lead level was 5 dB lower than that of the lag (second row), the estimated positions of the PE stimuli with both 1- and 2-ms ISDs were close to the midline. It is noteworthy that although estimated ITDs were similar for the 1- and 2-ms ISDs, these predictions came about from very different long-term IACC functions (bimodal for the 1-ms ISD and single-peak for the 2-ms ISD). When the lead level was 9 dB lower than that of the lag (third row), the estimated positions of the PE stimuli with the 1-ms ISD were more lateral to the lagging side (around +300-μs ITD) than with the 2-ms ISD (near 0-μs ITD). Finally, when the lead level was attenuated by 15 dB (bottom row), the estimated ITD approached the ITD of the lagging click for both ISDs (+200 μs, shown by the dotted line), indicating the diminished influence of the leading click.
Wideband predictions
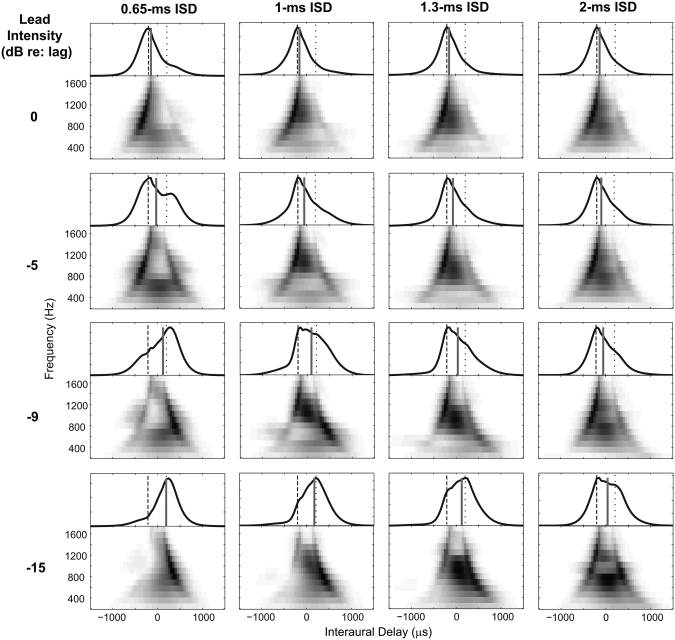
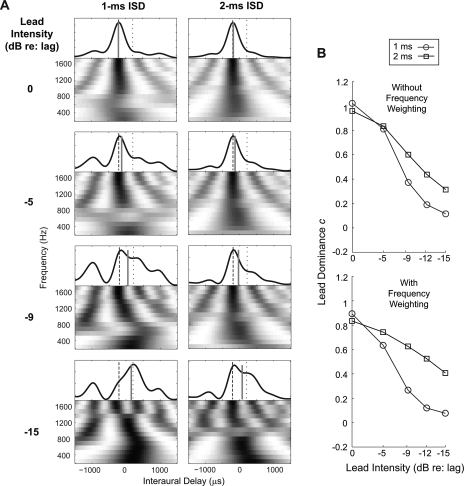
Figure 3 shows the long-term IACC functions for all frequency channels, weighted to account for the physiological distribution of best ITDs for all the wideband conditions. Each row shows results for one lead level; each column contains the prediction for one ISD. These best-ITD-weighted IACC functions were used to generate a weighted summary IACC by weighting frequency channels by the lognormal weighting function [Fig. 1B], emphasizing the impact of mid frequencies on localization judgments. The overall activity shown on top of the IACC functions in each panel was obtained by summing the responses across frequency for each interaural delay with this weighting. The centroid of these weighted long-term IACC functions integrated across frequency gives the estimated ITD of the wideband PE stimuli, which is shown by the vertical gray bars.
Figure 3.
Long-term IACC functions based on the outputs of left- and right-ear AN model outputs. Within each panel, the abscissa shows the interaural delay of the IACC function; the ordinate shows the CF of model neurons making up the population. The IACC functions were weighted by the across-best-phase distribution and the across-frequency distribution. The weighted IACCs integrated across frequency are shown on the top of each panel as a function of ITD, with gray bars indicating the centroid ITD. The dashed and dotted lines indicate the ITDs used to construct the leading and lagging clicks of the input stimulus, respectively.
When the lead and lag had the same intensity (first row), the IACC functions for CFs above 1000 Hz were similar for all the ISDs: the greatest activity (shown in black) occurred around the ITD of the leading click (–200 μs) in these high frequency responses. Different patterns of activity arose for different ISDs in the low-frequency responses. As already demonstrated in Fig. 2, the peak activity around 500 Hz was located father to the side than the lead for the 1-ms ISD (the second column), but toward a central position for the 2-ms ISD (the rightmost column). However, after integrating across frequency, the overall peak occurred near the leading ITD for all ISDs, as indicated at the top portion of each panel.
As the lead level decreased, the peak in the IACC corresponding to the lead ITD gradually disappeared from the high-frequency regions. The centroid of the weighted long-term IACC functions, integrated across frequency, moved from the leading side (negative ITDs) to the lagging side (positive ITDs). Moreover, for each lead-attenuation level, the centroid was located closer to the ITD of the lagging click (+200 μs) in the left panels than in the right panels, which shows that as lead level is attenuated, the predicted location of paired clicks moves to the location of the lagging click more rapidly with short ISDs than with long ISDs.
Prediction of lead dominance
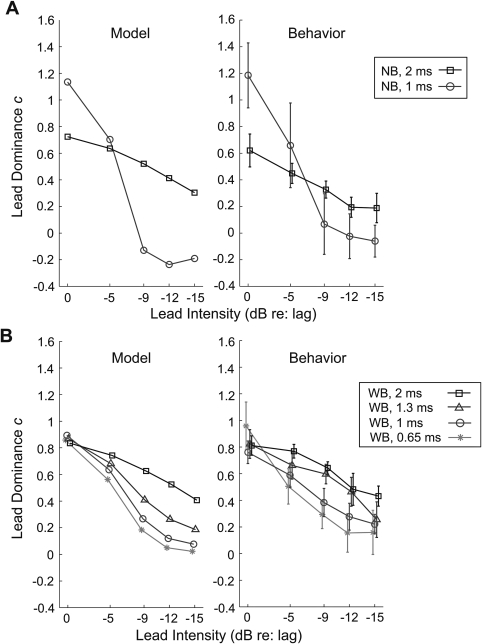
The lead dominance c values were calculated from the model by comparing the predicted ITD of the paired clicks (αITD) to the ITDs of the leading and lagging click (–200 and +200 μs, respectively) using Eq. 3. In order to compare the model results with behavioral data, we plotted the c values predicted by the model [left panels in Figs. 4A, 4B] alongside the corresponding c values obtained in the behavioral experiment [right panels in Figs. 4A, 4B, which are described below].
Figure 4.
The lead dominance value, c, as a function of the intensity of the leading click. The left panels show c values predicted by the model. The right panels show the corresponding c values estimated from the behavioral results. Error bars indicate the 90% confidence intervals. (A) c values for narrowband clicks (NB). (B) c values for wideband clicks (WB). The ISDs of the paired clicks are specified in the legend.
In the model, the values of c decreased as the level of the leading click decreased. For the narrowband stimuli [Fig. 4A], c values spanned a larger range as a function of lead level for the 1-ms ISD than the 2-ms ISD. For the wideband stimuli [Fig. 4B], c values were around 0.8–0.9 for all ISDs when the lead and lag were at the same level. With attenuation of the lead level, c values decreased more rapidly for paired clicks with short ISDs than long ISDs.
Behavioral performance
Perceived locations of paired clicks
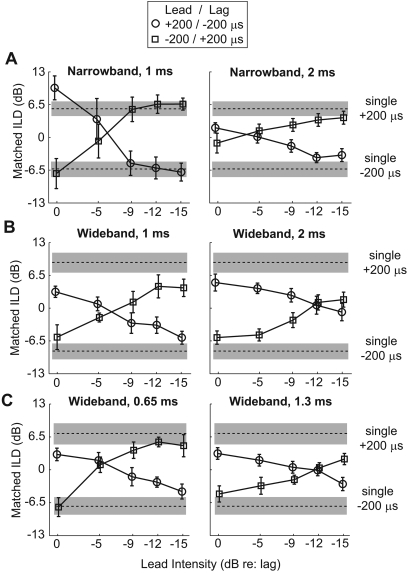
Consistent with previous psychophysical studies of the PE (Wallach et al., 1949; Zurek, 1987; Blauert, 1997, p. 204), here, for ISDs between 0.65 and 2 ms, subjects generally perceived a single, fused sound image and were able to localize it at a stable position. Figure 5 displays the matched ILD of the fused auditory image as a function of the level of the leading click, averaged across five subjects (note that all subjects showed similar patterns in their responses, so individual results are not shown). For comparison, the gray regions repeated in each panel show the match values obtained for single clicks with +200-μs ITD (top) and −200-μs ITD (bottom).
Figure 5.
Lateralization judgments, averaged across subjects, as a function of the level of the leading click. Error bars show the 90% confidence intervals around the means. The lagging click was always symmetrically opposite the lead, which had an ITD of either +200-μs (circles) or −200-μs (squares). The dashed lines show the perceived location of a single binaural click presented at the ± 200-μs ITDs, with the gray region surrounding these values displaying the 90% confidence intervals around these means. (A), (B) Lateralization in the main experiment for narrowband and wideband clicks, respectively. (C) Lateralization for wideband clicks in the follow-up experiment.
For all of the experimental conditions, the perceived location gradually moved from the side of the leading click to the side of the lagging click as the level of the lead click decreased. Figure 5 shows the lateralization results for narrowband and wideband stimuli from the main experiment [Figs. 5A, 5B, respectively] and wideband stimuli from the follow-up experiment [Fig. 5C]. The lines in each panel start at the left side either above zero (for the +200∕−200-μs condition) or below zero (for the −200∕+200-μs condition), then shift to the other side of zero as the lead attenuation increases. The results were left∕right symmetric, as confirmed by one-way repeated analysis of variance (ANOVA), which found no significant effect of the side of the leading click [F(1, 8) = 0.31; p = 0.8].
For narrowband clicks, we found that the perceived laterality of the PE stimulus depended on the ISD when the lead and lag clicks had equal intensity [Fig. 5A, leftmost points in each panel]. For the 1-ms ISD, the perceived location was to the side of the leading stimulus, but tended to be even farther to that side than the perceived laterality of a single click from the lead location [the leftmost points in the left panel of Fig. 5A fall outside the ranges of the single-click stimuli]. For the 2-ms ISD, the narrowband, equal-level clicks were heard close to the midline [in the right panel of Fig. 5A, the leftmost points fall near zero].
Figures 5B, 5C show results using typical PE stimuli consisting of a wideband pair of lead and lag clicks; however, unlike in most past studies, we also varied the relative level of the lead click relative to the lag. With short ISDs, past results show that subjects generally perceive the PE composite stimuli with equal-level lead and lag clicks near the location at which they would perceive the lead if it were presented alone. We found similar results here. When the lead and lag were presented with equal level [Figs. 5B, 5C, leftmost points in each panel], the perceived location of the PE stimulus with +200∕−200-μs lead∕lag ITD (circles) was close to the location of a single click with +200-μs ITD (shaded area above zero). Symmetrically, the perceived location of the PE stimulus with −200∕+200-μs lead∕lag ITD (squares) was close to the location of a single click with −200-μs ITD (shaded area below zero).3
As noted above, the perceived location of wideband PE stimuli for short ISDs started at a position close to the single lead and moved to the side of the lag as the lead level decreased. This is consistent with past PE studies in which the relative influence of each stimulus can be decreased by decreasing the relative intensity of that stimulus (Aoki and Houtgast, 1992; Shinn-Cunningham et al., 1995). However, the rate at which the location changed with changes in lead level depended on the ISD. In both wideband conditions, as the lead was attenuated, the perceived location approached the lagging side more rapidly for the shorter ISD than for the longer ISD, an effect that can be seen in that the two lines in Figs. 5B, 5C cross at a higher lead intensity in the left panels than in the right panels. For long ISDs (1.3 or 2 ms), the leading dominance was strong enough that the lateralized image fell close to the center even when the lead was attenuated by 15 dB.
Estimates of lead dominance
The lead dominance value c was computed for each subject individually using Eq. 4. Given that results were left-right symmetric, the c values were taken as an average of the two values computed in the conditions with ± 200-μs lead ITDs. These results are shown in the right panels of Figs. 4A, 4B.
Consistent with what is shown in Fig. 5, the behaviorally derived c values displayed in the right sides of Figs. 4A, 4B gradually decreased with decreasing intensity of the leading click for both narrowband and wideband clicks, indicating that the lead influence on lateralization of the PE stimuli decreased as the lead level decreased. For narrowband stimuli [right panel of Fig. 4A], c took on a larger value for equal-level lead and lag clicks when the ISD was 1 ms than when the ISD was 2 ms. The c value was near 1.2 for the 1-ms ISD, indicating that the PE image was perceived at a position more lateral than the perceived position of the leading click presented in isolation. In contrast, the c value was near 0.6 for the 2-ms ISD, indicating that the fused image was perceived relatively close to the midline, but slightly toward the side of the lead. Over the range of lead levels tested, c values spanned a greater range for the 1-ms ISD than the 2-ms ISD [in the right panel of Fig. 4A, the circles span a larger range than the squares], just as in the model prediction [left panel of Fig. 4A]. A two-way repeated measures ANOVA confirmed that the main effect of ISD was not significant [F(1, 40) = 0.02; p = 0.9]; however, the interaction of ISD and lead level was [F(4, 40) = 6.27; p < 0.01], indicating that c decreased at different rates with lead attenuation for ISDs of 1 and 2 ms, even though the overall strength of leading dominance averaged across all tested lead levels was similar for these two ISDs.
For the equal-level wideband clicks [far left data points in the right panel of Fig. 4B], c was similar (around 0.8) for all tested ISDs. As the lead attenuation increased, the lead dominance decreased more rapidly for shorter ISDs. Both the effect of ISD [F(3, 40) = 16.88, p < 0.001] and the interaction of ISD and lead level [F(4, 40) = 53.64, p < 0.001] were significant. This result shows that in the ISD range tested here (0.65 to 2 ms), the dominance of the lead on lateralization is stronger at longer ISDs, situations in which the lead-ITD in the stimulus onset is not affected by the lag for a longer time. Again, these results closely match the predictions made by the model [compare left and right panels in Fig. 4B]. Quantitatively, the model predictions account for 82% of the variance in the data for the narrowband stimuli and 85% of the variance in the data for the wideband stimuli.4
DISCUSSION
As can be seen in Fig. 4, model predictions achieved a good fit to the behavioral data. The fit is especially good considering that we did not manipulate the model parameters in order to fit the behavioral results, but simply used parameter values taken from past studies. Specifically, we used an established auditory nerve fiber model (Carney, 1993), and generated distributions of best ITDs and best frequencies based on previous physiological results.
Below, we analyze how various aspects of the model contribute to the behavioral predictions. First, using analytic expressions for the IACC of band-passed stimuli, we look in more detail into how the ISD affects interactions between the lead and lag responses on the basilar membrane, causing internal ITDs that differ from those present in lead or lag clicks (Sec. 4A; see also Hartung and Trahiotis, 2001). This analysis does not include the effects of adaptation in the auditory nerve model; we show that without such adaptation, there is little dominance of the lead on lateralization (i.e., no precedence effect), even though the effects of ISD are apparent. We then review how adaptation of the auditory nerve response contributes to the dominance of the lead-click response for PE stimuli, reducing the relative strength of the later-arriving spatial information from the lag click (Sec. 4A; see also Hartung and Trahiotis, 2001). We extend these ideas by explaining how reducing the lead click intensity can counterbalance adaptation effects to reveal the peripheral interactions of lead and lag responses on the basilar membrane for narrowband stimuli. In the next section (Sec. 4A), we consider how the strength of adaptation differs in different frequency channels, and how this affects lateralization predictions for wideband stimuli. We also explore how the model predictions of the lateralization of wideband clicks depend upon across-frequency weighting of ITDs. Finally, we discuss how our model relates to previous PE modeling studies (Sec. 4A).
The effect of peripheral interaction
As discussed in the Introduction, peripheral interactions between the lead and lag responses on the basilar membrane alter the internal ITD computed from auditory nerve responses. Here, we examine how such interactions influence predictions in the absence of any adaptation of the auditory nerve.
Figure 6 plots the running IACC computed from the outputs of linear, gammatone filters centered on 500 Hz (i.e., without IHC-AN adaptation) in response to equal-level lead and lag clicks with −200 and +200-μs ITDs, respectively, for an ISD of 1 (left panel) and 2 ms (right panel). For the 1-ms ISD, the running IACC had two peaks, each of which was far off midline (near −1000 and +1000 μs). For the 2-ms ISD, in contrast, there was a single peak occurring near zero. These differences in the IACC from a linear model help explain why the peak value of IACC calculated from AN model outputs is located far to the side for the 1-ms ISD, but toward a central position for the 2-ms ISD (compare results of Fig. 6 to results in the first row in Fig. 2). Results from Fig. 6 make clear that a model without adaptation would not produce good predictions of PE stimulus lateralization; for instance, for an ISD of 1 ms, the linear model would predict lateralization results near midline, not far to the side of the leading click, as is observed behaviorally.
Figure 6.
Time-varying IACC functions (bottom) based on the outputs of the left- and right-ear gammatone filters with CF of 500 Hz in response to a pair of equal-level clicks (i.e., without including adaptation from an inner-hair cell model). Results are shown for an ISD of 1 ms (left panel) and 2 ms (right panel). Above each panel is a plot of the left-ear (black) and right-ear (gray) narrowband outputs. The narrowband IACC functions, summed across time, are plotted to the right of each panel.
This linear-system gammatone model without adaptation allows us to write analytic expressions for the long-term IACC function rxx(λ), making it easy to analyze the ways in which lead and lag interact. As shown in the Appendix, rxx(λ) is a function of the lead and lag ITD, the ISD, as well as the autocorrelation of the impulse response of the gammatone filter rg(λ), which depends on its CF:
| (5) |
where τ1 and τ2 are the ITD of the leading and lagging click, respectively, and D is the ISD.
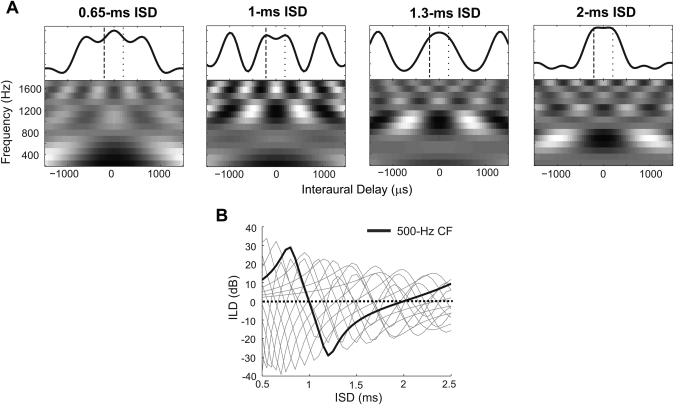
The gray-scale plots in Fig. 7A display the long-term IACCs, rxx(λ), in response to equal-level lead and lag clicks with −200 and +200-μs ITDs, calculated using Eq. 5, for all tested ISDs. In the high-frequency channels (CF > 1000 Hz), quasi-periodic IACC functions arise, with multiple peaks at separations of 1∕CF. In the low-frequency channels (CF < 1000 Hz), the peak values of IACC occur at different internal delays for different ISDs, due to the lead and lag monaural phase interactions. Different low-frequency patterns of IACCs of the full AN model outputs (shown in the first row of Fig. 3 for the model we used) are thus a direct consequence of linear interactions between the lead and lag responses on the basilar membrane.
Figure 7.
Interaural time and level differences in gammatone filter outputs. (A) Long-term IACC of the gammatone filter outputs as a function of interaural delay (x axis), as well as the center frequency of the gammatone filter (y axis) for different ISDs. The wideband summary IACC functions are shown above each grayscale plot. (B) The long-term values of ILD of the gammatone filter outputs as a function of ISD. The ILD for each individual frequency channel is illustrated by dashed lines. The ILD from the channel centered on 500 Hz is plotted as a solid line. ILD of 0 is indicated by a dotted line.
Auditory filters differing slightly in CF produce IACC peaks with very different values in Fig. 7A. As a result of these frequency-channel-specific interactions, the grand activity summed across frequency shows a central peak for all tested ISDs. This explains why wideband results were not very sensitive to the ISD, while narrowband results for equal-level paired clicks varied with ISDs in both model predictions and behavioral data. While the phase interactions in any narrowband can yield idiosyncratic internal ITDs, these internal ITD values differ in each frequency band; “extreme” behavior of narrowband predictions is reduced for predictions that sum activity across frequency. However, similar to the narrowband case described above, the −200-μs value of ITD conveyed by the leading click was not well represented by the internal ITDs in the outputs of a bank of linear gammatone filters [see Fig. 7A], summed across frequency.
Within-filter interactions can also result in non-zero ILDs of the outputs of the gammatone filter, despite the fact that the ILD in the lead and lag inputs was 0 dB. An analytic function for the ILD in the linear gammatone filter response, derived in the Appendix, is given by
| (6) |
Just as for the long-term IACC, the long-term ILD Ixx also depends on the leading and lagging ITD of the stimulus (τ1 and τ2), the ISD (D), and the autocorrelation of the filter impulse response rg(λ). Figure 7B displays the long-term ILDs, calculated using Eq. 6, for the 14 filters used in the current model. As shown by the solid line for the 500-Hz channel, the 1- and 2- ms ISDs were carefully chosen as stimuli for our behavioral experiments not only because they produce very different phase interactions at 500 Hz, but because the ILD is very small for narrowband stimuli filtered by a gammatone filter with CF of 500 Hz. Therefore, lateralization for a narrowband 500 Hz stimulus should be primarily based on ITD cues, and relatively unaffected by ILDs. Note also that the effective internal ILDs are very likely to influence lateralization of narrowband PE stimuli for bands other than 500 Hz and∕or ISDs other than 1 and 2 ms; such effects are worthy of further consideration in future experiments.
Similar to the ITD processing described above, the ILD will be near zero if energy is integrated across all frequencies. However, the PE can fail when the bandwidth of the signals is narrower than 100 Hz (Braasch and Blauert, 2003; Dizon and Colburn, 2006); this may occur because listeners’ lateralization judgments are influenced by not only the effective ITDs, but also the effective ILDs in the stimuli. In previous studies of the PE, diffuse and ambiguous images are often reported, and individual differences tend to be substantial. Given that our five subjects behaved similarly, it may be that inter-subject variability is reduced when effective ILDs are near zero and all subjects base their responses on ITDs, rather than a combination of nonzero ITDs and ILDs, which may be weighted differently by different people.
The effect of adaptation
As described above, linear gammatone filtering cannot account for the dominance of the binaural cues in the leading click on perceived stimulus laterality. As noted by Hartung and Trahiotis (2001), adaptation in auditory nerve responses undoubtedly contributes to lead dominance in perception.
The effect of adaptation on model predictions can be seen by comparing the first row of Fig. 2 with Fig. 6 for the narrowband, equal-level paired stimuli. The lateralization estimate from the full model (Fig. 2) was more central for the narrowband PE stimuli with the 2-ms ISD than the 1-ms ISD, reflecting differences in the early portion of the linear-model IACC responses for ISDs of 1 and 2 ms (Fig. 6). However, the IHC-AN synapses cause the AN model responses to be very large at the stimulus onset and then to rapidly decline toward a smaller steady-state value. Adaptation increases the relative weighting given to the initial responses (the lead), shifting the centroid of the IACC functions toward the leading ITD (around -200 μs), regardless of the ISD of the stimuli. Adaptation therefore causes the lead to dominate so that lateralization is always near the lead.
While adaptation was a key component of the PE model of Hartung and Trahiotis (2001), we realized that if we counteracted adaptation by attenuating the lead intensity, the model predictions would vary more strongly with ISDs, revealing in greater detail the interactions of lead and lag responses on the BM. This manipulation results in more equal-level lead and lag responses on the BM, allowing the monaural phase interactions to emerge fully. This realization is what motivated our behavioral experiment, in which we tested lateralization when lead-lag level was manipulated.
In Fig. 2, the IACC patterns changed as the intensity of the leading click decreased. For the 1-ms ISD when the lead was attenuated by 5 and 9 dB, the long-term IACC function of the full model had two peaks, each far from midline (one to the leading side; the other to the lagging side), reflecting a strong influence of within-filter, monaural phase interactions. Compared to results when lead and lag are at the same level, these results are more similar to the results predicted by the linear model, which included no adaptation (compare the second and third rows of Fig. 2 to the results in Fig. 6). These effects of basilar membrane interactions are less evident when the lead was equal in intensity to the lag, as adaptation strongly favored the lead ITD, which then dominated the overall long-term IACC of the AN model outputs.
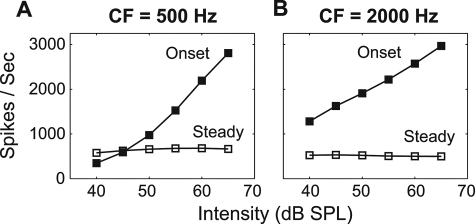
The adaptation of the IHC-AN synapse model can be visualized by plotting the average discharge rate of the AN model in response to pure-tone stimuli at CF as a function of stimulus level (Fig. 8). The onset response (calculated from the initial 10 ms of the response; filled squares) grew quickly with intensity and exhibited a greater range than the steady-state response (from 10–40 ms; open squares), suggesting that rapid adaptation in the AN response was relatively more influential at high intensities than at low intensities. These observations suggest that as overall sound intensity increases, the predicted strength of the precedence effect should increase, something that could be tested in future experiments.5 Importantly, the onset response of high-frequency fibers was generally larger than that of low-frequency fibers when they were driven by stimuli with the same intensity, suggesting that rapid adaptation in the AN response influenced model predictions more at high frequencies than at low frequencies.
Figure 8.
The rate-level function of the AN model response to 50-ms-long pure tones at CFs of (A) 500 Hz and (B) 2000 Hz. The steady-state rate was calculated over a time window from 10 to 40 ms; the onset rate was computed as the maximum discharge rate during the first 10 ms, which captures the rapidly adapting component of the AN response (Westerman and Smith, 1988).
Consistent with the responses to pure tones, the onset adaptation was strong in high frequency responses of the AN model when the lead and lag clicks had the same intensity (first row of Fig. 3). Compared to the output of a bank of linear gammatone filters, shown in Fig. 7A, the leading ITD strongly dominated the IACC functions in frequencies above 1000 Hz, which then dominated the overall results integrated across frequency. The peaks of activity (shown in black) for those frequencies were around −200 μs. The effect of peripheral interactions was greater in low-frequency responses [corresponding to different low-frequency IACC patterns in Fig. 7A] both because onset adaptation was weaker and because the click response on the BM has a longer duration at low frequencies compared to high frequencies, so that the lead response had a stronger interaction with the lag response in low-frequency channels.
Importantly, the relative phases of lead and lag had even greater impact on model predictions when the lead level was reduced. Specifically, for equal-level lead and lag, the lag response had little effect and model predictions for wideband clicks were near the lead for all the tested ISDs. However, at large lead attenuations, low-frequency lead and lag responses added and cancelled more dramatically; in these cases, the result depended more strongly on the ISD, revealing ISD influences on predictions. Thus, it is the nonlinear interaction between adaption and monaural lead-lag interactions that produces different changes in predicted lateralization of wideband clicks as a function of lead-lag level for different ISDs [see left panel of Fig. 4B]. This strong interaction was observed behaviorally [see right panel of Fig. 4B], lending strong support to the model.
The effect of spectral dominance
The above two sections confirm the theory that peripheral processing, including lead-lag interaction and firing-rate adaption (Hartung and Trahiotis, 2001), contributes to lateralization of narrowband and wideband paired clicks separated by brief ISDs. Past results also show that the spatial information in the mid-frequency region near 750 Hz is weighted heavily (Bilsen and Raatgever, 1973; Tollin and Henning, 1999).
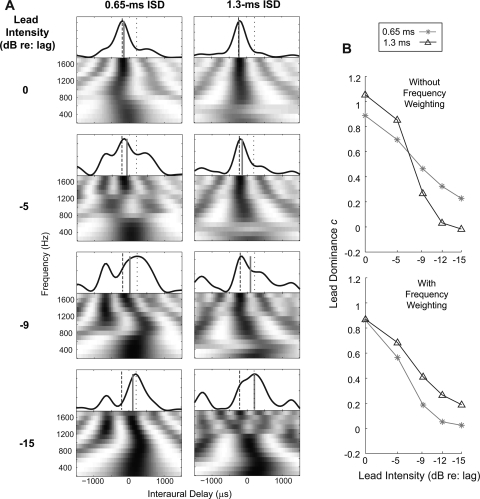
In order to illustrate the effect of spectral dominance, we compared model predictions for wideband clicks with those generated by a model that included only peripheral processing, without any differential weighting of different interaural delays and different best frequencies. The perceived ITD of the PE stimuli was estimated by the centroid the IACC functions of the left and right-ear AN model outputs summed across time and frequency, assuming a uniform distribution of best phases. Because our estimates are based on the centroid of IACCs rather than the peak, predictions are less sensitive to the choice of distribution of best phases than other approaches (such as selecting the peak), at least for left-right symmetric distribution like we used [Fig. 1A]. Therefore, the spectral weighting we adopted is likely to be the dominant factor causing any differences between the full model predictions and those shown in Figs. 910, which plot the lateralization predictions when equal weight is given to all frequencies for the wideband stimuli used in the main experiment and in the follow-up experiment, respectively. Figures 9A, 10A are laid out like Fig. 3, while Figs. 9B, 10B compare the full-model lateralization predictions to those using the model with ITD and frequency weighting.
Figure 9.
(A) Long-term IACC functions of the outputs of AN model across frequencies without any weighting of best ITDs and frequency. The ISDs are 1 and 2 ms in the left and right columns, respectively. (B) Lead dominance values are similar whether predicted by the activities shown in (A) (top) or by the full model, which includes physiologically motivated across-frequency weighting (bottom).
Figure 10.
(A) Long-term IACC functions of the outputs of AN model across frequencies without any weighting of best ITDs and frequency. The ISDs are 0.65 and 1.3 ms in the left and right columns, respectively. (B) The resulting lead dominance values (top) show very different patterns than those predicted from the model with frequency weighting (bottom).
For 1- and 2-ms ISDs, the predicted lateralization without any weighting [top panel in Fig. 9B] yielded results fairly similar to those with frequency weighting [bottom panel in Fig. 9B], which suggests that peripheral interactions of lead and lag and adaptation observed at the level of AN can account for many aspects of the behavioral data. The perceived location of equal-level clicks was close to the leading click location for both ISDs due to strong onset adaptation in high-frequency regions. With a reduction in lead level, the perceived location moved to the lagging side more rapidly with 1-ms ISD than 2-ms ISD. This occurred because, when the lead was attenuated by more than 9 dB, the maximum activity in low-frequency regions tended to be more lateral to the side of the lagging click for the 1-ms ISD than the 2-ms ISD [two bottom rows in Fig. 9A], resulting in a greater shift of the composite cross-frequency IACC for the 1-ms ISD than the 2-ms ISD.
Predicted lateralization results with and without frequency weighting were very different for paired clicks with 0.65- and 1.3 ms ISDs (Fig. 10); this observation in the model predictions is what inspired the follow-up behavioral experiment using wideband clicks with these ISDs. When the lead was attenuated by more than 9 dB, the predicted strength of the lead dominance without any weighting was weaker for clicks with a 1.3-ms ISD than with a 0.65-ms ISD. In the model predictions with frequency weighting, the lead dominance remains stronger for stimuli with a 1.3-ms ISD than with a 0.65-ms ISD for all lead levels. With across-frequency weighting, greater weight was assigned to frequency channels around 750 Hz, where the peak activity of IACC functions for stimuli with the lead level attenuated by 9 or 15 dB was further to the lag side with the 0.65-ms ISD than the 1.3-ms ISD [two bottom rows in Fig. 10A, around 750 Hz]. The behavioral results for 0.65- and 1.3-ms ISDs [right panel in Fig. 4B] support the full-model predictions that as the lead level decreases, the leading dominance remains stronger at longer ISDs.
Across-frequency weighting has been implemented in several models before (e.g., see Stern et al., 1988; Tollin, 1998). Tollin and Henning (1999) assumed that the auditory system estimates the position of the auditory event exclusively from the information in the dominance region. Although the effects of within-filter interaction and firing-rate adaptation play very important roles in the model predictions in the current study, a frequency weighting that enhances the activity around 750 Hz is also necessary to predict how wideband clicks are lateralized in our study. In the current model, the 750 Hz dominance emerges due to the assumed distribution of best frequencies of ITD-sensitive cells, which was selected to fit physiological observations (Hancock and Delgutte, 2004), not from behavioral results. Our analysis shows that the good agreement between the full-model predictions and the behavioral results for broadband stimuli depends on this frequency weighting.
Comparisons with other models
The current model explains lateralization experiments in which a single auditory image is perceived for click pairs with short ISDs (< 2 ms). The stimuli of the experiments were designed specifically to test various mechanisms that affect model predictions. The effects of basilar-membrane interaction and auditory-nerve adaptation are consistent with analysis reported by Hartung and Trahiotis (2001). However, by using a more physiologically realistic, IHC-AN-synapse model (Westerman and Smith, 1988), the current model generates adaptation that varies with frequency and the relative levels of lead and lag clicks. In contrast, Hartung and Trahiotis (2001) used a Meddis (1986) hair-cell model, which does not capture these effects as well. In our model, changes in the strength of adaptation with center frequency were important for predicting the observed behavioral results for paired clicks when the lead level was decreased (see Figs. 910). Although the current model builds on past work, it extends previous models by including more realistic frequency-dependent effects. In the current study, we set all model parameters from published physiological results and then conducted new experiments to explicitly test model predictions; the new behavioral results used specific PE stimuli selected to quantitatively challenge model predictions. Thus, our work provides a strong test and validation of the general approach introduced by Hartung and Trahiotis (2001). We accomplished this by attenuating the lead level, so that lead and lag interactions played a stronger role on perception than when adaptation causes strong lead dominance.
The current results show that spatial information around 750 Hz has a very strong effect on lateralization. This finding of a spectral dominance region is consistent with past behavioral results in which a lagging click that arrives within about 1–3 ms of the lead has a substantial effect on the resultant spectral characteristics (Tollin and Henning, 1999). This past work looked at the ITD and ILD cues separately and found that the ITD-based lateralization performance was predicted by considering only spatial information in the 750 Hz frequency region. In contrast, the current model focuses only on ITD information, and, by design, tests lateralization of stimuli for which ILD cues were not expected to contribute significantly. By weighting ITD cues based on the reported distribution of best frequencies of IC neurons that are ITD sensitive (Hancock and Delgutte, 2004) and including frequency-specific adaptation, our model also emphasizes lateralization cues in the 750-Hz frequency region. Thus, despite the very different experimental designs, our results support the finding from Tollin and Henning (1999) that lateralization cues in this mid-frequency range play a disproportionately strong role in spatial hearing.
Just as in the above referenced studies, the current study also focuses on PE stimuli consisting of lead and lag clicks separated by brief ISDs. Different phenomena occur with ISDs longer than 2 ms, especially when two source images are perceived. For such stimuli, other mechanisms beyond those discussed in the current study are necessary to explain lateralization data. For example, psychophysical evidence suggests that the PE is slightly weaker when sources are farther apart in space than when they are close (Litovsky and Shinn-Cunningham, 2001), an effect that cannot be explained by the model described here. Similarly, the PE persists for ISDs that are too long to cause interactions on the basilar membrane, and for which adaptation is likely to cause relatively less emphasis on the lead click. ITD-dependent synaptic inhibition observed in the IC can help to account for the PE in such cases (e.g., Xia et al., 2010).
When long-duration stimuli, rather than clicks, are used, models that do not include explicit inhibitory elements fail (Braasch and Blauert, 2003). However, such results can be explained by previous models that include contralateral inhibition in the basic interaural cross correlation function (e.g., Lindemann, 1986). Such an approach assumes that a primary cross correlation peak corresponding to the lead initiates inhibition that suppresses secondary peaks within a definite time interval. Such effects are not included in the current study.
The current model is therefore not complete; it is not able to account for the PE when there are long ISDs or when there are ongoing noise bursts. In such cases, explicit inhibition triggered by onsets or by transients in ongoing signals is necessary to account for perceptual results. Nonetheless, the current experiments and model reveal the importance of peripheral interactions, adaptation, and across-frequency integration in lateralization perception; for the short ISDs studied here, many aspects of the behavioral response can be explained without including additional effects, such as explicit inhibition.
SUMMARY
A previous AN model (Carney, 1993) together with a binaural model based on cross correlation was used to predict behavioral data and to explore the effects of peripheral interactions in the auditory nerve and spectral dominance of localization cues in the mid-frequency region in response to precedence-effect stimuli. Interactions caused by cochlear filtering accounted for differences in how the ISD influenced lateralization of narrowband lead-lag clicks. Adaptation in AN responses enhanced lead dominance, leading to a strong PE, especially for wideband clicks. Importantly, adaptation had a strong influence on predictions of how lateralization changed as lead level was attenuated for different ISDs. Spectral weighting based on the best-frequency distributions in physiological studies increased the influence of the ITDs in the region around 750 Hz. This frequency weighting was important for predicting lateralization of wideband clicks.
Psychophysical experiments were performed to test model predictions. Narrowband stimuli centered on 500 Hz produced lateralization judgments that depend on the ISD, in line with lead-lag peripheral interactions in the model. Specifically, as lead level was attenuated, the differences in the lateralization were larger for stimuli with a 1-ms ISD than a 2-ms ISD. Typical precedence effect (i.e., leading dominance) was observed for equal-level wideband clicks with ISDs from 0.65 to 2 ms, a consequence of the firing-rate adaptation of the auditory nerve. When the lead level was attenuated, the lead dominance remained stronger for wideband clicks with longer ISDs, reflecting ITDs computed from auditory nerve responses from frequency channels around 750 Hz, consistent with a spectral dominance of lateralization cues at these frequencies.
ACKNOWLEDGMENTS
This work was supported by a grant from the National Institutes of Health (Grant No. R01 DC009477).
APPENDIX: INTERAURAL DIFFERENCE DERIVATIONS
Interaural differences were computed as in Dizon and Colburn (2001). The left and right ear signals are given by the convolution of the wideband click w(t) with left and right acoustic impulse responses hL(t) and hR(t), respectively:
| (A1) |
| (A2) |
These impulse responses are given by
| (A3) |
| (A4) |
where D equals the ISD, τ1 is the lead ITD, τ2 is the lag ITD, and δ(t) is the Dirac δ function. After filtering by a gammatone filter, the signals become
| (A5) |
| (A6) |
Interaural timing information is commonly characterized by the interaural cross correlation (IACC). In this case, we focus on the long-term IACC function rxx(λ), i.e., the cross correlation of the full length of the time signals xL(t) and xR(t). This can be computed by convolving the left signal with the time reversal of the right signal:
| (A7) |
where rhh(λ) is the cross correlation of hL(t) and hR(t), rg(λ) is the autocorrelation of the impulse response of the gammatone filter, and λ is the lag of the cross correlation operation. Using Eqs. (1) and (2), rhh(λ) can be shown to be
| (A8) |
rxx(λ) is then given by
| (A9) |
The Fourier transform of click w(t) has magnitude and phase given by
| (A10) |
As
| (A11) |
and
| (A12) |
We have
| (A13) |
The Fourier transforms of xL(t) and xR(t) are then given by
| (A14) |
| (A15) |
where G(ω)is the frequency response of the gammatone filter.
Thus, the left and right energies EL and ER are
| (A16) |
| (A17) |
The Wiener–Khinchin theorem (see Bracewell, 2000) states that the autocorrelation is the inverse Fourier transform of the corresponding power spectrum:
| (A18) |
Since |X(ω)|2is even, we have
| (A19) |
| (A20) |
The resulting interaural intensity difference Ixx is given by
| (A21) |
Footnotes
It is noteworthy that predictions of lateralization for paired clicks are similar using the current AN model, which has no level-dependent compression, and using the Carney (1993) model. This similarity arises because the interactions between the lead and lag responses being discussed are dominated by energy in the center frequency of the cochlear filters, where level effects are modest. As long as they are identical in both ears, the filters’ bandwidth and the spectral shape have little effect on predictions.
Notably, none of our subjects reported any changes in lateralization perception over time, and none reporting hearing multiple images. Thus, we do not think that PE buildup influenced the reported results.
The single-click lateralization matches in the follow-up experiment were independent of the single-click matches from the main experiment. While single-click results are not identical in the main experiment and the follow-up experiment [compare gray regions in Figures 5B, 5C], a paired t-test showed that the difference was not statistically significant (p = 0.085).
The overall percentage of the variance accounted for by the model was found by averaging over data points indexed by i, computing , where xi and pi represent the observed and predicted values of the lead dominance, respectively, for data point i, and represents the mean of the observed values over i.
The only study of which we know that looked at effects of level on PE judgments can be found in Shinn-Cunningham et al. (1993). Moreover, in this work, the effect of level was both weak and in the wrong direction: the precedence effect was slightly weaker for click pairs with a peak intensity of 110 dB SPL than stimuli with a peak intensity of 80 dB SPL. These intensities are relatively high, outside the range of values explored in the current study.
References
- Aoki, S., and Houtgast, T. (1992). “A precedence effect in the perception of inter-aural cross correlation.” Hear. Res. 59, 25–30. 10.1016/0378-5955(92)90098-8 [DOI] [PubMed] [Google Scholar]
- Bilsen, F. A., and Raatgever, J. (1973). “Spectral dominance in binaural lateralization,” Acustica 28, 131–132. [Google Scholar]
- Blauert, J. (1997). Spatial Hearing (MIT Press, Cambridge, MA: ), pp. 201–287. [Google Scholar]
- Blauert, J., and Cobben, W. (1978). “Some considerations of binaural cross correlation analysis,” Acustica 39, 96–104. [Google Scholar]
- Braasch, J., and Blauert, J. (2003). “The precedence effect for noise bursts of different bandwidths. II. Comparison of model algorithms,” Acoust. Sci. Technol. 24, 293–303. 10.1250/ast.24.293 [DOI] [Google Scholar]
- Bracewell, R. N. (2000). The Fourier Transform and Its Applications, 3rd ed. (McGraw-Hill, Boston: ). [Google Scholar]
- Carney, L. H. (1993). “A model for the responses of low-frequency auditory-nerve fibers in cat,” J. Acoust. Soc. Am. 93, 401–417. 10.1121/1.405620 [DOI] [PubMed] [Google Scholar]
- Dizon, R. M., and Colburn, H. S. (2006). “The influence of spectral, temporal, and interaural stimulus variations on the precedence effect,” J Acoust Soc Am 119, 2947–2964. 10.1121/1.2189451 [DOI] [PubMed] [Google Scholar]
- Fitzpatrick, D. C., Kuwada, S., Batra, R., and Trahiotis, C. (1995). “Neural responses to simple simulated echoes in the auditory brain stem of the unanesthetized rabbit,” J. Neurophysiol. 74, 2469–2486. [DOI] [PubMed] [Google Scholar]
- Freyman, R. L., Clifton, R. K., and Litovsky, R. Y. (1991). “Dynamic processes in the precedence effect,” J. Acoust. Soc. Am. 90, 874–884. 10.1121/1.401955 [DOI] [PubMed] [Google Scholar]
- Gaskell, H. (1983). “The precedence effect,” Hearing Res. 11, 277–303. 10.1016/0378-5955(83)90002-3 [DOI] [PubMed] [Google Scholar]
- Glasberg, B. R., and Moore, B. C., (1990) “Derivation of auditory filter shapes from notched-noise data,” Hear Res. 47, 103–138. 10.1016/0378-5955(90)90170-T [DOI] [PubMed] [Google Scholar]
- Hancock, K. E. (2007). “A physiologically-based rate code for interaural time differences predicts bandwidth-dependent lateralization,” in Hearing—From Basic Research to Applications, edited by Kollmeier B., Klump G., Hohmann V., Langemann U., Mauermann M., Upperkamp S., and Verhey J. (Springer, New York), pp. 389–398. [Google Scholar]
- Hancock, K. E., and Delgutte, B. (2004). “A physiologically based model of interaural time difference discrimination,” J. Neurosci. 24, 7110–7117. 10.1523/JNEUROSCI.0762-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartung, K., and Trahiotis, C. (2001). “Peripheral auditory processing and investigations of the ‘precedence effect’ which utilizes successive transient stimuli,” J Acoust Soc Am 110, 1505–1513. 10.1121/1.1390339 [DOI] [PubMed] [Google Scholar]
- Leakey, D. M., and Cherry, E. C. (1957). “Influence of noise upon the equivalence of intensity differences and small time delays in two loudspeaker systems,” J. Acoust. Soc. Am. 29, 284–286. 10.1121/1.1908858 [DOI] [Google Scholar]
- Litovsky, R. Y., Colburn H. S., Yost W. A., and Guzman. S. J. (1999). “The precedence effect,” J. Acoust. Soc. Am. 106, 1633–1654. 10.1121/1.427914 [DOI] [PubMed] [Google Scholar]
- Litovsky, R. Y., and Shinn-Cunningham, B. G. (2001). “Investigation of the relationship among three common measures of precedence: fusion, localization dominance, and discrimination suppression,” J. Acoust. Soc. Am. 109, 346–358 10.1121/1.1328792 [DOI] [PubMed] [Google Scholar]
- Lindemann, W. (1986). “Extension of a binaural cross-correlation model by contralateral inhibition. II. The law of the first wave front,” J. Acoust. Soc. Am. 80, 1623–1630. 10.1121/1.394326 [DOI] [PubMed] [Google Scholar]
- McAlpine, D., Jiang, D., and Palmer, A. R. “A neural code for low-frequency sound localization in mammals,” (2001). Nat. Neurosci. 4, 396–401. 10.1038/86049 [DOI] [PubMed] [Google Scholar]
- Meddis, R. (1986). “Simulation of mechanical to neural transduction in the auditory receptor,” J. Acoust. Soc. Am. 79, 702–711. 10.1121/1.393460 [DOI] [PubMed] [Google Scholar]
- Patterson, R. D., Allerhand, M. H., and Giguere, C. (1995). “Time-domain modeling of peripheral auditory processing: A modular architecture and a software platform,” J. Acoust. Soc. Am. 98, 1890–1894. 10.1121/1.414456 [DOI] [PubMed] [Google Scholar]
- Shackleton, T. M., Meddis, R., and Hewitt, M. J. (1992). “Across frequency integration in a model of lateralization,” J. Acoust. Soc. Am. 91, 2276–2279. 10.1121/1.403663 [DOI] [Google Scholar]
- Shinn-Cunningham, B. G., Zurek, P. M., and Durlach, N. I. (1993). “Adjustment and discrimination measurements of the precedence effect,” J. Acoust. Soc. Am. 93, 2923–2932. 10.1121/1.405812 [DOI] [PubMed] [Google Scholar]
- Shinn-Cunningham, B. G., Zurek, P. M., Durlach, N. I., and Clifton, R. K. (1995). “Cross-frequency interactions in the precedence effect,” J. Acoust. Soc. Am. 98, 164–171. 10.1121/1.413752 [DOI] [PubMed] [Google Scholar]
- Stern, R. M., Zeiberg, A. S., and Trahiotis, C. (1988). “Lateralization of complex binaural stimuli: A weighted image model,” J. Acoust. Soc. Am. 84, 156–165. 10.1121/1.396982 [DOI] [PubMed] [Google Scholar]
- Tollin, D. J. (1998). “Computational model of the lateralization of clicks and their echoes,” in Proceedings of the NATO Advanced Study Institute on Computational Hearing, edited by Greenberg S. and Slaney M., pp. 77–82.
- Tollin, D. J., and Henning, G. B. (1996). “Anomalous lateralization in the precedence effect with novel two echo stimuli,” J. Acoust. Soc. Am. 100, 2593A. 10.1121/1.417579 [DOI] [Google Scholar]
- Tollin, D. J., and Henning, G. B. (1999). “Some aspects of the lateralization of echoed sound in man. II. The role of stimulus spectrum,” J. Acoust. Soc. Am. 105, 838–849. 10.1121/1.426273 [DOI] [PubMed] [Google Scholar]
- Trahiotis, C., Bernstein, L. R., and Akeroyd, M. A. (2001). “Manipulating the ‘straightness’ and ‘curvature’ of patterns of interaural cross correlation affects listener’s sensitivity to changes in the interaural delay,” J. Acoust. Soc. Am. 109, 321–330. 10.1121/1.1327579 [DOI] [PubMed] [Google Scholar]
- Wallach, H., Newman, E. B., and Rosenzweig, M. R. (1949). “The precedence effect in sound localization,” Am J Psychol 52, 315–336. 10.2307/1418275 [DOI] [PubMed] [Google Scholar]
- Westerman, L. A., and Smith, R. L. (1988). “A diffusion model of the transient response of the cochlear inner hair cell synapse,” J. Acoust. Soc. Am. 83, 2266–2276. 10.1121/1.396357 [DOI] [PubMed] [Google Scholar]
- Xia, J., Brughera, A., Colburn, H. S., and Shinn-Cunningham, B. G. (2010). “Physiological and psychophysical modeling of the precedence effect,” J. Assoc. Res. Otolaryngol. 11, 495–513. 10.1007/s10162-010-0212-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin, T.C.T. (1994). “Physiological correlates of the precedence effect and summing localization in the inferior colliculus of the cat,” J. Neurosci. 14, 5170–5186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zurek, P. M. (1980). “The precedence effect and its possible role in the avoidance of interaural ambiguities,” J. Acoust. Soc. Am. 67, 953–964. 10.1121/1.383974 [DOI] [PubMed] [Google Scholar]
- Zurek, P. M. (1987). “The precedence effect,” in Directional Hearing, edited by Yost W. A. and Gourevitch G. (Springer-Verlag, New York), pp. 85–106. [Google Scholar]
- Zurek, P. M., and Saberi, K. (2003). “Lateralization of two-transient stimuli,” Percept. Psychophys. 65, 95–106. 10.3758/BF03194786 [DOI] [PubMed] [Google Scholar]