Mechanisms of Slower Nitric Oxide Uptake by Red Blood Cells and Other Hemoglobin-containing Vesicles

Abstract

Nitric oxide (NO) acts as a smooth muscle relaxation factor and plays a crucial role in maintaining vascular homeostasis. NO is scavenged rapidly by hemoglobin (Hb). However, under normal physiological conditions, the encapsulation of Hb inside red blood cells (RBCs) significantly retards NO scavenging, permitting NO to reach the smooth muscle. The rate-limiting factors (diffusion of NO to the RBC surface, through the RBC membrane or inside of the RBC) responsible for this retardation have been the subject of much debate. Knowing the relative contribution of each of these factors is important for several reasons including optimization of the development of blood substitutes where Hb is contained within phospholipid vesicles. We have thus performed experiments of NO uptake by erythrocytes and microparticles derived from erythrocytes and conducted simulations of these data as well as that of others. We have included extracellular diffusion (that is, diffusion of the NO to the membrane) and membrane permeability, in addition to intracellular diffusion of NO, in our computational models. We find that all these mechanisms may modulate NO uptake by membrane-encapsulated Hb and that extracellular diffusion is the main rate-limiting factor for phospholipid vesicles and erythrocytes. In the case of red cell microparticles, we find a major role for membrane permeability. These results are consistent with prior studies indicating that extracellular diffusion of several gas ligands is also rate-limiting for erythrocytes, with some contribution of a low membrane permeability.

Introduction

Hemoglobin (Hb)² encapsulated within red blood cells scavenges NO at a significantly slower rate than hemoglobin that is freely dissolved within blood plasma (cell-free Hb) (1–4). A similar effect is observed for the uptake of oxygen (5–7). This reduction in the scavenging rate allows NO that is produced in the endothelial cells within the walls of blood vessels to diffuse to the smooth muscle in sufficient concentrations to activate soluble guanylate cyclase (8–12), which would not be possible otherwise (13). NO thus effectively functions as a smooth muscle relaxant under normal physiological conditions. The reasons for the reduction of the rate of NO scavenging by red cell-encapsulated versus cell-free Hb have been extensively investigated and yet this remains a debated subject. The difference in the scavenging rates has been attributed to four possible factors: 1) a red blood cell (RBC)-free zone adjacent to the endothelium due to the velocity gradient in laminar flow (2–4), 2) NO uptake being rate-limited by diffusion of NO to the RBC, which contributes to the phenomenon of an unstirred layer around the RBC (1, 6, 14–16), 3) an intrinsic, physical RBC membrane barrier to NO diffusion (14, 17–20), and 4) NO uptake being rate-limited by diffusion of NO within the RBC (intracellular diffusion) (17, 21). Although there is no disagreement about the effect of the RBC-free zone along the endothelium on reducing NO reaction rates with red cell hemoglobin, the influence of the unstirred layer versus membrane permeability versus intracellular diffusion of NO is still disputed (21–24). There is, however, increasing evidence that the membrane of the RBC does provide some resistance to the passage of NO (14, 19, 20, 22).

Disease states highlight the importance of the reduced rate of NO scavenging by red blood cells. The mechanisms of retardation of NO scavenging by red cell-encapsulated Hb are disrupted in hemolytic anemias due to intravascular hemolysis (25–33). This also occurs during administration of some hemoglobin-based oxygen carriers (34–48). Transfusion of banked blood of more than 2 weeks of age may show similar effects in vivo due to release of hemoglobin as the red cells degrade (49, 50).

It is desirable to design blood substitutes that would not have the detrimental effects of cell-free hemoglobin. A potential candidate is hemoglobin encapsulated within phospholipid vesicles that are a few hundreds of nanometers in diameter (51–55). The vesicles are large enough to avoid extravasation into the endothelium and could potentially be affected by the radial pressure gradient within blood vessels so that NO consumption would be limited. Investigating the reaction kinetics of these vesicles with NO is therefore important to validate their functionality in place of red blood cells. Phospholipid vesicles of differing sizes and concentrations of intracellular hemoglobin may be made (21). Measuring the dependence of their uptake rates of NO on size and hemoglobin concentration may also provide insight into the relative importance of factors intrinsic to the erythrocyte that influence its scavenging rate of NO.

To elucidate the relative importance of factors that are intrinsic to red blood cells and phospholipid vesicles in their reactions with NO, another group of investigators (Sakai et al. (21)) performed stopped-flow experiments of the reaction of NO with vesicles of various sizes and with a number of different hemoglobin concentrations under anaerobic conditions. One great advantage of the elegant system developed by these authors is that it allows for modeling of well characterized systems. The authors performed computer simulations of their experiments and also simulated reactions with smaller and larger vesicle diameters, from 50 nm up to that of a red cell (8000 nm). In their simulations the authors did not include either extracellular diffusion of NO (i.e. extravesicular, or diffusion to a vesicle through the bulk fluid up to (but not through) the membrane) or membrane permeability to NO (21). Only the diffusion of NO inside of a vesicle was simulated. The results obtained both experimentally and computationally showed that the bimolecular binding rate constant of NO decreases as intracellular hemoglobin concentration and vesicle diameter increase. The authors attributed these results to increasing viscosities of hemoglobin solutions and to increased diffusional distances of NO inside vesicles of larger diameters. This led them to conclude that the diffusion of NO inside a phospholipid vesicle is the rate-limiting factor in the reaction and that this may also be the case for NO scavenging by red blood cells.

In contrast, we hypothesize that rapid mixing of NO and phospholipid vesicles does not eliminate rate limitations due to extracellular diffusion. Performing our own computer simulations of the stopped-flow experiments with vesicles and NO, we show that the effective diffusion distance of NO through this extracellular space is not reduced sufficiently by the rapid mixing in stopped-flow. In fact, it is the rate-limiting factor in the reaction.

In support of our simulations, we conducted stopped-flow absorption measurements of NO uptake by red blood cells under oxygenated and deoxygenated conditions. To explore the role of external diffusion, we employed a viscous and nonviscous buffer. We found that the viscosity of the buffer had a substantial effect on external diffusion, supporting our computational simulations and previous reports that demonstrate the importance of external diffusion in limiting oxygen uptake by red blood cells (6, 7).

In addition, we have simulated our own kinetics measurements of NO uptake by microparticles derived from aged red blood cells under aerobic conditions (50). Unlike phospholipid vesicles, these microparticles still have lipid raft proteins and other components characteristic of red cells in their membrane (56). Our simulations show that, in our fast time-resolved kinetic measurements of NO scavenging by red cell microparticles under aerobic conditions, membrane permeability mostly likely limits the reaction rate.

We also performed competition experiments that support the notion that in the case of these red cell microparticles, membrane permeability plays a substantial role in limiting NO uptake. These results support our previous data, showing that NO uptake by oxygenated red blood cells is mostly limited by extracellular diffusion, with a smaller contribution of reduced membrane permeability under aerobic conditions (14, 20).

EXPERIMENTAL PROCEDURES

Computational Model Development

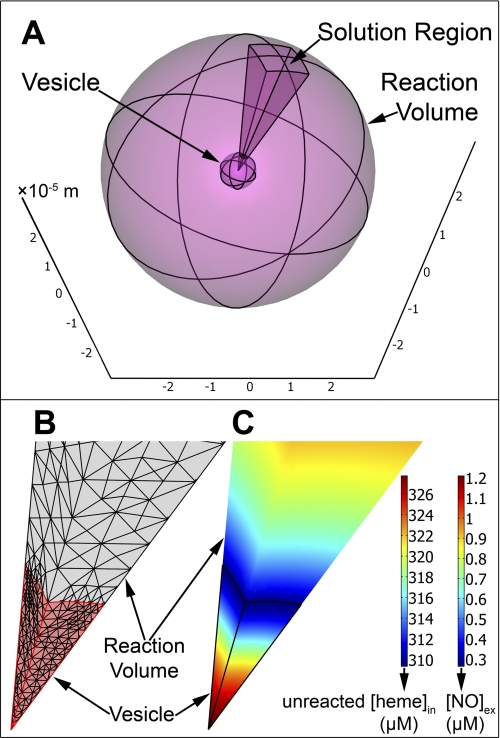
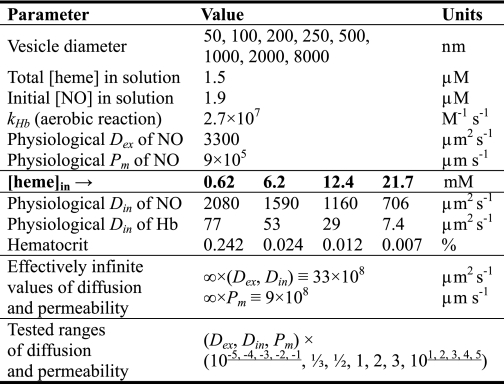
We have constructed a three-dimensional model to simulate stopped-flow experiments of the anaerobic reaction between phospholipid vesicle-encapsulated hemoglobin and NO within the software package COMSOL Multiphysics (Comsol Inc., Burlington, MA, version 3.5), a partial differential equation-based finite element modeling environment. In these experiments deoxygenated hemoglobin within vesicles binds NO to form a ferrous heme-NO complex (Fe^II-NO). We have assumed that vesicles are distributed homogeneously within the reaction volume. The reaction may then be simulated with a spherically symmetric model consisting of two spheres. The inner sphere represents a vesicle and the outer sphere represents the reaction volume, such that the difference between its radius and the radius of the vesicle is an average half-distance between any two vesicles in a real experiment (Fig. 1A). To sufficiently resolve both the reaction volume and vesicles with enough finite elements we exploited the spherical symmetry of our model. The reaction was simulated solely over a 20 × 20 degree square cone cut out of the two-sphere system (Fig. 1A). This reduced the number of degrees of freedom that had to be solved to between 20,000 and 30,000, allowing a sufficient number of finite elements (Fig. 1B).

FIGURE 1.

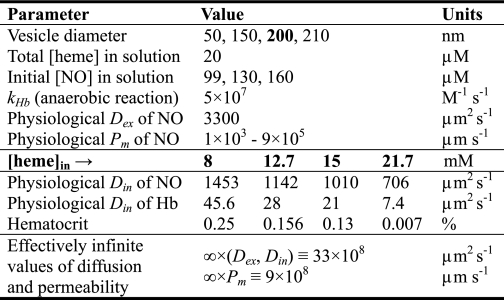
Three-dimensional model of NO uptake by phospholipid vesicles. A, the two-sphere model of a stopped-flow experiment between NO and 0.62 mm deoxygenated hemoglobin encapsulated within a phospholipid vesicle with a diameter of 8000 nm. The radius of the large outer sphere represents the half-distance between the centers of any two vesicles in a real experiment. The axes are marked in units of 10⁻⁵ meters. On this scale the vesicle diameter is 0.8 × 10⁻⁵ m and the outer sphere diameter is 6 × 10⁻⁵ m. The 20 × 20 degree square cone is the region over which we have solved our system of equations. B, a zoom-in to the finite element mesh of the cone solution region shown in A. The vesicle domain is the bottom section colored in pink and part of the extracellular volume domain is the gray section above. The border between the vesicle domain and the extracellular volume domain is the membrane of the vesicle. Each straight edge of the vesicle domain is the 4000-nm vesicle radius. C, the simulated concentrations in micromolar of unreacted hemoglobin inside the vesicle and NO in the extracellular space (Reaction Volume) at the half-life of the reaction. The domains are displayed with the same zoom as in panel B and the vesicle domain is outlined in black. The same color code is applied to both domains, but maps the concentration of unreacted hemoglobin inside the vesicle ([heme]_in) and NO outside of the vesicle ([NO]_ex).

Model Governing Equations

The general mass-transport equation governing the reaction was as follows.

Here C represents the concentration of NO or hemoglobin. The extra terms S and R refer to the rate of reactant production and consumption, respectively. In our case neither reactant was being produced so S was zero, and inside a vesicle,

where [NO] and [Hb] are time-dependent concentrations and k_Hb is the known bimolecular rate constant for the reaction of cell-free deoxygenated hemoglobin with NO (20, 57, 58). We used the value given in the recent work on phospholipid vesicles (21) (2.7 × 10⁷ m⁻¹ s⁻¹, Table 1). D is the diffusion rate constant of the particular diffusing species described by the equation (NO outside or inside or hemoglobin inside of a vesicle, Table 1). The boundary condition employed on the surface of the outer sphere was,

and at the surface of the vesicle, the inward flux of NO was defined as,

Here C_ex and C_in represent the concentrations of NO on the outside (extracellular region) and inside (intracellular region) of the vesicle, respectively, n is the unit vector normal to the sphere surface pointing in the radial direction and P_m is the lipid membrane permeability coefficient of NO (Table 1).

TABLE 1.

Simulation parameters for phospholipid vesicles

The bimolecular rate constant for the NO reaction with free deoxygenated hemoglobin is represented by k_Hb. D_ex is the diffusion rate constant of NO in saline (in the extracellular space) and D_in refers to the diffusion rate constants of both NO and hemoglobin inside a vesicle (in the intracellular space). P_m is the phospholipid membrane permeability of NO. The bottom row shows factors by which physiological parameter values were multiplied to test how this affects reaction kinetics. Bold indicates that heme concentrations given correspond to values below for D and hematocrit.

Simulation Parameters for NO Uptake by Phospholipid Vesicles

Each reaction was simulated until half of the intracellular hemoglobin had reacted with NO and this time was taken as the half-life (t_½) of the reaction. Fig. 1C shows an example of simulated concentration profiles of unreacted hemoglobin inside a vesicle and NO outside of the vesicle at the half-life of the reaction. The apparent bimolecular reaction rate constant was calculated at 5 ms of reaction time, as in the recent publication on vesicles, from the following formula,

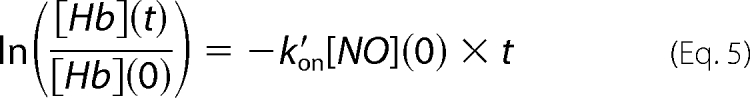which assumes pseudo first-order initial kinetics with a constant concentration of NO equal to the initial concentration. The model parameters we used in our simulations are summarized in Table 1. To properly simulate the stopped-flow experiment we included physiological values for the diffusion of NO in the extracellular region (D_ex, 3300 μm² s⁻¹) and the lipid membrane permeability of NO (P_m, 9 × 10⁵ μm s⁻¹), which we have previously used (20, 59). In the intracellular region we have used the diffusion constants for both NO and hemoglobin cited in the work on phospholipid vesicles (21), which increase with decreasing concentration of hemoglobin inside a vesicle. The total hemoglobin (in heme) used in our simulations was 1.5 μm and the initial concentration of NO in the whole reaction volume was 1.9 μm, as in the publication on vesicles (21). To assess whether extra- or intracellular diffusion of NO or the membrane permeability of NO is rate-limiting we have performed simulations where each of these parameters was varied over a range of 15 different values by multiplying the physiological value of a parameter by 15 different factors (from as small as 10⁻⁵ to as large as 10⁵, Table 1, bottom row) while maintaining the other parameter constants at either physiological values (data not shown) or at very high values. The very high values were selected to make the corresponding parameters effectively infinite so that they would not contribute to the reaction rate (Table 1, bottom row). These simulations were performed for intracellular hemoglobin concentrations of 0.62, 12.4, and 21.7 mm and for vesicle radii of 50, 500, and 8000 nm (Table 1). For simulations where intracellular diffusion was varied while extracellular diffusion and membrane permeability were constant the NO and hemoglobin diffusion coefficients were both multiplied by the same factor. Because these two parameters were always varied synchronously together they are both referred to by the same symbol, D_in (intracellular or intravesicular diffusion). To fit all of the experimental and computational data presented in the recent work on phospholipid vesicles (21), we have also performed some simulations with vesicle diameters of 100, 200, 250, 1000, and 2000 nm. The experimental and simulated data in the recent work on phospholipid vesicles by Sakai et al. (21) have been obtained by precisely estimating the values from the graphs of their publication to compare it to our own. Some values explicitly given in the publication were also estimated from the graphs and these deviated by a maximum of 1.4% from the exact values.

Computational Model Validation for Simulations of NO Uptake by Phospholipid Vesicles

Several approaches were taken to confirm the validity of our computational approach. Normally the mesh of our three-dimensional model had been created with a fine setting and further refined twice in the extracellular domain and five times in the intracellular (vesicle) domain (Fig. 1B). Comparing these to simulations performed with a coarser mesh, we have identified that models with the largest vesicle diameter and the highest concentration of intracellular hemoglobin need the most number of mesh refinements to be properly resolved. To make sure that our chosen number of mesh refinements provided a sufficient number of finite elements the simulations requiring the most number of refinements were also performed with three and six refinements for the intra- and extracellular domains, respectively. The average percent difference from simulations with lower, normally used, number of mesh refinements at physiological parameter values (Table 1) was 0.16 ± 0.19% for the apparent rate constants and 18 ± 4% for the reaction half-lives (n = 2). When parameter values one-tenth of physiological values and higher were included the percent difference was 1.65 ± 4.45% for initial rates and 12 ± 8% for half-lives (n = 26). All of the simulations performed in three dimensions have also been performed in one dimension in spherical coordinates with only a radial dependence (data not shown). It was determined that to appropriately simulate apparent bimolecular rate constants for the smallest values of extra and intracellular diffusion used (10⁻⁵ × D_ex and 10⁻⁵ × D_in, Table 1) the number of mesh refinements in one dimension had to be increased to 10 for the extracellular space and 12 for the intracellular space, so that our three-dimensional model was not resolved enough at low diffusion rates (below one-tenth of physiological values presented in Table 1). However, the simulated half-lives had little dependence on the mesh size and gave qualitatively the same results for both one- and three-dimensional simulations. Importantly, the mesh size in three dimensions resolved the model sufficiently for accurate simulations of both initial rates and half-lives at physiological parameter values. We are confident that our conclusions about mechanistic issues surrounding NO uptake by Hb containing vesicles could not be due to any deficiencies in the grid size or other model parameter.

Computational Model Settings and Data Analysis

Normally, simulations were performed with three application modes: two for diffusion of NO in the extra- and intracellular regions and one for the diffusion of hemoglobin in the intracellular region. In some cases formation and diffusion of the product of the reaction, iron-nitrosyl hemoglobin (Fe^II-NO), was simulated with a fourth application mode and the results were found to be insignificantly different from that of a system of NO and hemoglobin only. Some simulations were also performed to completion, until all of the intracellular hemoglobin had reacted. Mass conservation of reactants and products was observed in all cases. The direct, UMFPACK, linear system solver was used by COMSOL Multiphysics during the simulations and the time stepping was performed by the default, Backward Differentiation Formula method. To perform a large number of simulations in series, a Matlab code was used to control COMSOL Multiphysics. This included setting up the geometry of each model, creating and refining the mesh, collecting simulation data, and calculating the apparent reaction rate constant of each simulation.

Measurements of NO Reactions with Red Blood Cells

Stopped-flow time-resolved absorption measurements were conducted using a Molecular Kinetics three-syringe mixer (Indianapolis, IN) coupled to an Olis RSM spectrometer (Bogart, GA) using similar methods as described previously (14, 50). Red blood cells were suspended in either Dulbecco's phosphate-buffered saline (DPBS) (14) or a viscous buffer. The viscous buffer was made by first dissolving 50 g of dextran in 34 ml of water, 200 ml of DPBS, and 10 ml of Opti-Prep (Sigma) and then mixing this solution with the nonviscous buffer (DPBS) in a ratio of 3:1 under aerobic or anaerobic conditions. Anaerobic conditions were maintained using sodium dithionite at a maximum concentration of 5 mm. The NO donor PROLINONOate (Cayman Chemicals) was prepared in 0.01 m NaOH at a concentration of 35 mm. These two solutions were loaded in two of the syringes and the third contained either the viscous or nonviscous buffer. The viscosity of the viscous buffer used in our experiments (after dilutions) was measured to be 7.7 centistokes. In the first mixture, the NO donor was diluted into the one containing buffer and then this mixture was aged for 20 s so that the NO would be released. Afterward, the NO buffer was rapidly mixed with the red cells. This two-step mixing procedure was performed to avoid degradation of the NO either from reactions with air or dithionite, as the donor is quite stable in 0.01 m NaOH. Time-resolved absorption spectra were collected and analyzed using Specfit software (Boston, MA) through singular value decomposition and global analysis as previously described (14, 50).

Measurements of NO Uptake by Red Blood Cell Microparticles

We also simulated our own photolysis experiments measuring the very fast uptake of NO by red blood cell microparticle-encapsulated hemoglobin under aerobic conditions (50). In these experiments oxygenated hemoglobin inside microparticles reacts with NO to form methemoglobin (MetHb, Fe^III). Microparticles were obtained from outdated packed red blood cell units with acid citrate dextrose anticoagulant purchased from the Interstate Blood Bank, Inc. (Memphis, TN). The microparticles were prepared as previously described (50, 60). The preparation was confirmed to contain only microparticle-encapsulated hemoglobin via microscopy and absorbance measurements (50). We used dynamic light scattering to estimate the size of our microparticles. Samples were measured in a Zetasizer series instrument by Malvern Instruments Ltd. and analyzed with Malvern software to obtain a size average by number. We found the diameter to be 200 ± 10 nm (from 4 separate microparticle preparations). The internal hemoglobin concentration was determined by measuring the total hemoglobin concentration in a resuspended microparticle pellet.

Hemoglobin was purified as described previously (61). All chemicals were purchased from Sigma unless stated otherwise. Measurements of NO dioxygenation by microparticles via the time-resolved photolysis method were performed similarly to those described previously (50, 62). NO was photolyzed off the donor compound potassium pentachloronitrosyl-ruthenate (II) in the presence of microparticle-encapsulated or cell-free Hb and absorbance of the reaction mixture was simultaneously recorded by a CCD camera. A quantum yield of NO in each experiment was calculated from each observed reaction rate between cell-free Hb and NO and a 5 × 10⁷ m⁻¹ s⁻¹ bimolecular rate constant for the same reaction, a lower bound which we have previously established (20). Each obtained value for the yield of NO was used to calculate a corresponding bimolecular rate constant for every observed reaction rate between microparticle-encapsulated hemoglobin and NO. Microparticles were confirmed to have remained intact during an experiment by measuring the absorbance in the Soret and visible ranges of the supernatant (after sedimention at 30,000 × g for 90 min) after photolysis, which showed no detectable amount of freely dissolved hemoglobin. The age of blood used for preparation of microparticles for photolysis experiments was 28 or 33 days old.

Competition Experiments

Competition experiments were performed similarly to those described previously (14, 17). Cell-free Hb at a concentration of 50 or 800 μm was mixed with red cell microparticles (prepared as described above) at similar concentrations in heme (50 or 800 μm) in PBS. The NO donor DEANONOate was added to a final concentration of 12.5 μm for the low heme concentration experiments and 200 μm for the high heme concentration experiments. After 150 min the mixtures were centrifuged at 37,000 × g for 60 min to sediment the microparticles. The amount of reacted NO in each fraction was determined by absorption and electron paramagnetic resonance spectroscopy as previously described (14, 17). Experiments were performed under aerobic conditions. Control experiments were performed as described previously to account for any autoxidation or MetHb reductase activity (14).

The ratio of the bimolecular rate constants for NO uptake by cell-free Hb compared with that encapsulated by red cell microparticles, k_f/k_mp is given by,

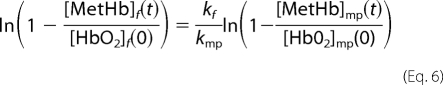where the subscript f refers to cell-free Hb and mp to red cell microparticles Hb. The natural log terms on both sides of the equation derive from the fact that the total amount of oxygenated hemoglobin in the free and microparticle fractions may decrease with time from its initial amount (18).

Simulations of NO Uptake by Red Blood Cell Microparticles

Photolysis experiments were simulated with the same computational model that we used to simulate the experiments with phospholipid vesicles. The different parameter values for these simulations are summarized in Table 2. For simulations of each experiment the measured average NO yield was used as the initial concentration of NO (Table 2). The total amount of oxygenated hemoglobin in each experiment was 19.8 μm. Our simulations focused on our own measured values of vesicle diameter and internal Hb concentration, but also included the full range of microparticle diameters that have been reported by Kriebardis et al. (56) based on measurements of microparticle preparations similar to ours. Based on our measurements of the volume of a pellet of microparticles after sedimentation and on absorbance of the same microparticles suspended in buffer, we have estimated the average hemoglobin concentration inside microparticles to be ∼12.7 mm. The diffusion rate constants of NO and hemoglobin inside solutions of various concentrations of internal Hb (Table 2) were obtained by extrapolating the diffusion coefficients provided in a recent publication on phospholipid vesicles (21) (Table 1) with a third degree polynomial. For each initial concentration of NO, total hemoglobin and microparticle diameter, the experiment was simulated with 25 to 28 different microparticle membrane permeability values of NO, from 1 × 10³ to 9 × 10⁵ μm s⁻¹. Some simulations were also performed when only one parameter (diffusion of NO outside, diffusion of NO and hemoglobin inside, or membrane permeability to NO) had a physiological value, whereas the other two were assigned effectively infinite values (Table 2), as in the simulations of vesicles. The time of each simulation at which Equation 5 was used to compute a bimolecular rate constant was changed from 5 to 0.05 ms, because under the given conditions the reaction proceeds much faster and is complete within ∼1 ms. The reported bimolecular rate constants are an average of three identical simulations but with different initial concentrations of NO (Table 2).

TABLE 2.

Simulation parameters for red blood cell microparticles

The bimolecular rate constant for the NO reaction with free oxygenated hemoglobin is represented by k_Hb. D_ex is the diffusion rate constant of NO in saline (in the extracellular space) and D_in refers to the diffusion rate constants of both NO and hemoglobin inside a microparticle (in the intracellular space). P_m is the microparticle membrane permeability of NO. Bold indicates that heme concentrations given correspond to values below for D and hematocrit.

RESULTS

Extracellular Diffusion Limits the Uptake Rate of NO by Phospholipid Vesicles More than Intracellular Diffusion

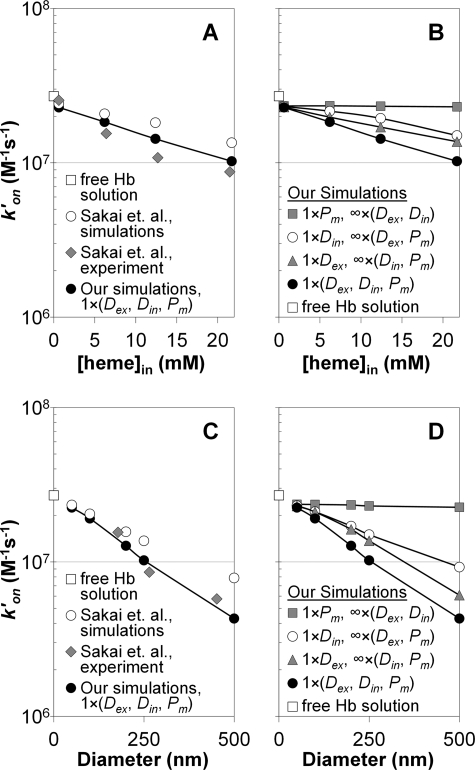
The effect of different parameters (extracellular versus intracellular diffusion versus membrane permeability) on the apparent bimolecular reaction rate constant is compared with values obtained experimentally and with simulated data from the recent work on phospholipid vesicles (21) in Fig. 2. The bimolecular rate constant for a solution of cell-free Hb is shown on the y axes (white squares). Fig. 2, A and B, display apparent reaction rate constants versus intracellular hemoglobin concentrations at a vesicle diameter of 250 nm. In Fig. 2A the experimental results of Sakai et al. (21) are plotted along with their simulations that only include internal diffusion of NO as a rate-limiting factor. Our simulations, where we include extra- and intracellular diffusion and membrane permeability of NO set to physiological values (Table 1) are also plotted. It is evident that the rate constants obtained from our simulations where we have included physiological values of all parameters fit the experimental data of Sakai et al. (21) more closely than their simulations that only include internal diffusion as a rate-limiting factor.

FIGURE 2.

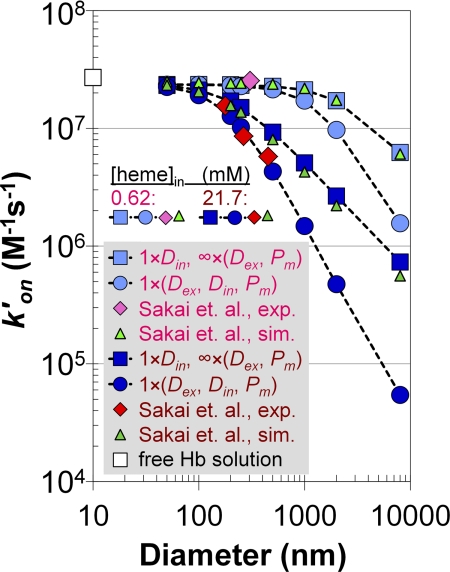
Apparent bimolecular binding rate constants for NO uptake by phospholipid vesicles under anaerobic conditions. A, the apparent bimolecular rate constant (y axis, logarithmic scale) plotted versus intracellular Hb concentration for a vesicle with a diameter of 250 nm. Our simulations, which included physiological values of NO diffusion outside (D_ex), diffusion of NO and Hb inside (D_in), and membrane permeability of NO (P_m) are shown as black circles. The multiplication factor of 1 used in the legend indicates that these parameters retained physiological values presented in Table 1. The simulated rate constants of Sakai et al. (21) are displayed as white circles and their experimentally measured rate constants are shown as gray diamonds. The rate constant for NO binding by a solution of free deoxygenated Hb is shown with the white square on the y axis. B, our simulated rate constants plotted versus intracellular Hb concentration for a vesicle of 250 nm in diameter when all parameters had physiological values (black circles, the same data as in panel A), when only the diffusion rate of NO outside a vesicle had a physiological value, whereas the other parameters were effectively infinite (gray triangles), when only the diffusion rate inside (of both NO and Hb) had a physiological value (white circles) and when only membrane permeability of NO had a physiological value (gray squares). For each set of simulations, the parameter that was assigned its physiological value presented in Table 1 is indicated with a multiplication factor of 1 in the legend. The parameters that were assigned effectively infinite values (Table 1) are indicated with a multiplication factor of infinity in the legend. For example, 1 × P_m refers to the physiological phospholipid membrane permeability of 9 × 10⁵ μm s⁻¹ and ∞ × (D_ex, D_in) indicates the very high diffusion rate constants of 33 × 10⁸ μm² s⁻¹ for both diffusion of NO outside (D_ex) and diffusion of NO and Hb inside (D_in). C, rate constants analogous to those of panel A, but plotted versus vesicle diameter at an intracellular Hb concentration of 21.7 mm. D, rate constants analogous to those of panel B, but plotted versus vesicle diameter at an intracellular Hb concentration of 21.7 mm.

Fig. 2B shows the effect of each individual rate-limiting mechanism in our simulations on the apparent reaction rate constant. We also include results from the simulation where all three parameters (intracellular diffusion constant, extracellular diffusion constant, and membrane permeability) are kept at their physiological values (as also plotted in Fig. 2A). We display results from when only extracellular diffusion was set to its physiological value and the intracellular diffusion (of both NO and Hb) and membrane permeability of NO were effectively infinite. In addition the panel displays results from simulations where we have set diffusion parameters only inside a vesicle (both of NO and Hb) to physiological values while letting extracellular diffusion and membrane permeability be effectively infinite. Finally, the case where only membrane permeability of NO had a physiological value (for a phospholipid vesicle) while diffusion rate constants inside and outside of a vesicle were effectively infinite is also shown, and the effect of this single factor alone is minimal. The fact that including only extracellular diffusion as a rate limitation reduces the rate constants more than including only intracellular diffusion as a rate limitation, demonstrates that diffusion of NO through the extracellular space limits the reaction rate more than diffusion inside of the vesicle. In addition, although extracellular diffusion by itself is not sufficient to explain the observed rate, it gives a better approximation to experimental data than when only intracellular diffusion is included in our simulations.

The data displayed in Fig. 2, C and D, are analogous to those of Fig. 2, A and B, but here the apparent bimolecular rate constant is plotted versus vesicle diameter at the highest concentration of intracellular hemoglobin of 21.7 mm. In Fig. 2C, again, we overlay our simulated rates when physiological values of all parameters were included with the experimental and simulated data from recent work with phospholipid vesicles (21). As before, our simulations using all three physiological parameters agree best with the experimental data. Fig. 2D shows a similar pattern to Fig. 2B where diffusion of NO to a vesicle through the extracellular space limits the reaction rate more than diffusion inside of a vesicle. Membrane permeability has little additional effect. Importantly, our simulations in which physiological values of intracellular diffusion only were included (Fig. 2, B and D, white circles) agree well with the similar simulations presented in recent work with vesicles (21) (Fig. 2, A and C, white circles). These and other data are overlaid for better comparison in Fig. 4.

FIGURE 4.

Simulated apparent bimolecular rate constants for NO uptake by deoxygenated phospholipid vesicles compared with the experimentally measured constants. The bimolecular rate constant (y axis, logarithmic scale) is plotted versus vesicle diameter (x axis, logarithmic scale) for two different concentrations of intracellular Hb (0.62 mm, pink legend items and 21.7 mm, dark red legend items). Experimentally obtained rate constants (21) are shown as red diamonds (21.7 mm [heme]_in) and pink diamonds (0.62 mm [heme]_in). The simulated rate constants of Sakai et al. (21) are represented by light green triangles (0.62 mm [heme]_in) and dark green triangles (21.7 mm [heme]_in). Our simulations mimicking the simulations of the other authors, when NO (and Hb) diffuses only inside of a vesicle, are shown in light blue (0.62 mm [heme]_in) and dark blue squares (21.7 mm [heme]_in). That the physiological rate constant presented in Table 1 was used for intracellular diffusion of NO (D_in) is indicated by multiplying this parameter with a factor of 1 in the legend. The diffusion rate outside (D_ex) and the membrane permeability of NO (P_m) were assigned effectively infinite values (Table 1, second-to-bottom row), this is indicated by multiplying these parameters with a factor of infinity in the legend. Finally, our simulations with physiological values of extra (D_ex) and intracellular (D_in, both NO and Hb) diffusion and membrane permeability (P_m) of NO are displayed as light blue circles (0.62 mm [heme]_in) and dark blue circles (21.7 mm [heme]_in). These parameters are multiplied with a factor of 1 in the legend to indicate that they have the same physiological values as presented in Table 1. The rate constant for the reaction of NO with free deoxygenated Hb is plotted as a white square on the y axis.

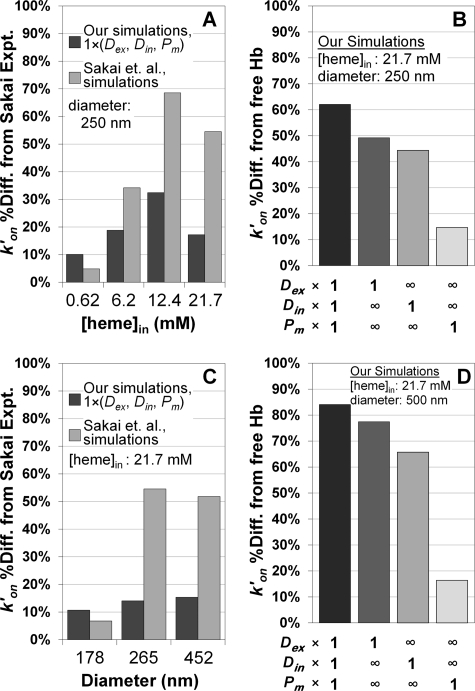
In Fig. 3, A and C, the percent difference between the data and the theoretical simulations are shown. The comparisons support the notion that simulations that include all three potential rate-limiting factors set at their physiological levels fit the data substantially better than when only intracellular diffusion is included. In addition, as shown in Fig. 3, B and D, when any single one of the three potential rate-limiting factors is included, external diffusion has the largest effect. The data shown in Figs. 2 and 3 compare rate constants for the reactions under certain conditions and simulation parameters, as expected, similar results are obtained when comparing half-lives of the reactions (supplemental Fig. S1).

FIGURE 3.

Comparisons of bimolecular rate constants for NO uptake by phospholipid vesicles. A, the percent difference between experimentally obtained rate constants by Sakai et al. (21) and simulated rate constants plotted versus intracellular Hb concentration from the data in Fig. 2A (250 nm vesicle diameter). A multiplication factor of 1 in the legend for extracellular diffusion of NO (D_ex), intracellular diffusion of NO and Hb (D_in), and membrane permeability of NO (P_m) indicates that the physiological values of these parameters were used in our simulations (Table 1). B, the percent difference between the cell-free Hb uptake rate constant of NO and our simulated rate constants for a vesicle of 250 nm in diameter and with 21.7 mm intracellular hemoglobin from Fig. 2B. Employed parameter values for extra (D_ex) and intracellular diffusion (D_in) and membrane permeability (P_m) are indicated below the x axis. A multiplication factor of 1 refers to the physiological value presented in Table 1 and the infinity symbol signifies the effectively infinite parameter value from Table 1. C, percent difference between simulated rate constants and the experimentally measured rate constants of Sakai et al. (21) from the data of Fig. 2C (intracellular hemoglobin concentration of 21.7 mm) plotted versus vesicle diameter. Our simulated data and that of the other authors were extrapolated with a third degree polynomial to the average vesicle diameters (x axis) in the experiments of the other authors. D, percent difference between the NO uptake rate of cell-free Hb and our simulated NO uptake rate constants for a vesicle of 500 nm in diameter and with 21.7 mm intracellular Hb plotted, analogous to data in panel B, from the data in Fig. 2D. Parameter values in each simulation are indicated below the x axis.

Effect of Extracellular Diffusion on NO Uptake by Phospholipid Vesicles Increases with Vesicle Size and Concentration of Encapsulated Hemoglobin

We summarize the differences between the simulations presented in recent work with phospholipid vesicles (21) and our simulations that best approximate the experimental data of the same authors in Fig. 4. This figure displays the bimolecular reaction rate constant calculated by Equation 5 versus vesicle diameter at the lowest (0.62 mm, light colors) and highest (21.7 mm, dark colors) concentrations of hemoglobin inside a vesicle. The bimolecular rate constant for a reaction of cell-free Hb with NO (2.7 × 10⁷ m⁻¹ s⁻¹) is shown on the y axis as a white square. We have already pointed out that our simulations where only the intracellular diffusion is rate-limiting (light blue and blue squares) appropriately agree with the simulations of Sakai et al. (21) (light green and green triangles). Our simulations where physiological values of all parameters (extracellular diffusion of NO and intracellular diffusion of NO and Hb, as well as membrane permeability to NO, Table 1) were used are plotted as light blue circles (0.62 mm intracellular Hb) and blue circles (21.7 mm intracellular Hb). With 0.62 mm intracellular hemoglobin, only one experimentally measured bimolecular rate constant for a vesicle diameter of 305 nm (pink diamond) was provided (21). At this diameter and hemoglobin concentration all of the data converge to the bimolecular rate constant of the cell-free Hb reaction. However, experimental data of the other authors at 21.7 mm intracellular hemoglobin (red diamond) agrees best with our simulations where both diffusion inside and outside and membrane permeability were included. The results of these simulations indicate that, at high concentrations of intracellular hemoglobin and large vesicle diameters, the reaction is limited by diffusion of NO through the extracellular space and suggest that intracellular diffusion alone is not sufficient to explain the decrease in the reaction rate compared with cell-free Hb. This conclusion and the relationships between vesicle diameter and the extent of rate limitations shown in Fig. 4 were previously demonstrated for the case of oxygen uptake by red cells of various sizes and artificial vesicles (7).

Experimental Support of Contribution by External Diffusion for Large Vesicles

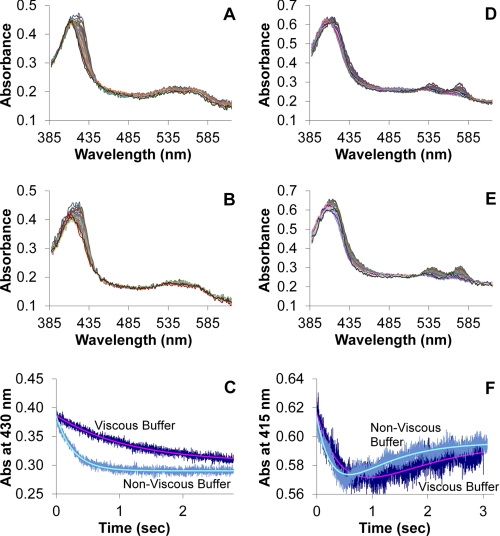
To provide experimental support for our conclusion that extracellular diffusion is a major contributor to rate limitations in NO reactivity with large vesicles with high hemoglobin concentrations, we performed stopped-flow absorption experiments with red blood cells (Fig. 5). In these experiments we varied the viscosity of the buffers similar to experiments published previously examining the reaction of red blood cells and oxygen (6). If external diffusion is not a major factor in limiting NO reactivity, we would expect the viscosity of the buffer not to have any effect on the kinetics of the reaction. Fig. 5A shows typical spectra for the reaction of NO and red blood cells under anaerobic conditions in nonviscous buffer and that in Fig. 5B shows analogous data for when viscous buffer is used. These data represent the binding of NO to deoxygenated Hb to form the nitrosyl (NO bound) species. Fig. 5C shows kinetic traces and their fits for the reaction of NO and red cells for the viscous and nonviscous buffers. The average rate constant was 4.2 ± 1.0 × 10³ m⁻¹ s⁻¹ for viscous buffer and 20.9 ± 8.1 × 10³ m⁻¹ s⁻¹ for nonviscous buffer (from greater than 25 mixes from three separate sample preparations on different days). Analogous data for the reaction of NO with red blood cells under aerobic conditions are shown in Fig. 5, D and E. Here, NO reacts with oxygenated Hb to form MetHb and then can bind to the ferric heme to form a NO bound MetHb species. Thus, the data were fit to a biexponential process to properly represent these two reactions. Fig. 5F shows kinetic traces and their fits for the reaction of NO and red cells for the viscous and nonviscous buffers under aerobic conditions (from greater than 25 mixes from three separate sample preparations on different days). The average rate constant for MetHb formation in viscous buffer was 8.5 ± 1.3 × 10³ m⁻¹ s⁻¹ and 29.8 ± 10.4 × 10³ m⁻¹ s⁻¹ for nonviscous buffer. The large deviations in the data for nonviscous buffer are due to the reaction being very fast for the instrumentation employed. However, the data under both aerobic and anaerobic conditions clearly demonstrate that the reaction is retarded when a viscous buffer is employed (p < 10⁻⁶), supporting a major role for external diffusion in limiting NO uptake by red blood cells as similarly observed in the case of oxygen uptake (6, 7).

FIGURE 5.

Stopped-flow absorption of red blood cells in viscous and nonviscous buffer. Red blood cells were diluted into NO-containing buffer and absorption spectra were collected as a function of time. A, a subset of absorption spectra collected every millisecond is shown after a mixture in nonviscous buffer under anaerobic conditions. The final mixture contained Hb at 50 μm and NO at 200 μm. The data show NO binding to deoxygenated Hb and analysis yielded an observed rate constant of 3.7 1/s. B, a subset of absorption spectra collected every millisecond is shown after a mixture in viscous buffer under anerobic conditions. The final mixture contained Hb at 50 μm and NO at 200 μm. The data show NO binding to deoxygenated Hb and analysis yielded an observed rate constant of 0.86 1/s. C, the kinetics of the absorption at 430 nm are shown for both viscous and nonviscous buffers for data collected under anaerobic conditions. Both the raw data (noisy) and the fits from singular value decomposition and global analysis are shown. D, a subset of absorption spectra collected every millisecond is shown after a mixture in nonviscous buffer under aerobic conditions. The final mixture contained Hb at 59 μm and NO at 180 μm. The data show NO reacting with oxygenated Hb to form MetHb with subsequent NO binding to the MetHb and analysis yielded an observed rate constant of 3.1 1/s for the initial reaction. E, a subset of absorption spectra collected every millisecond are shown after a mixture in viscous buffer under aerobic conditions. The final mixture contained Hb at 64 μm and NO at 190 μm. The data show NO reacting with oxygenated Hb to form MetHb with subsequent NO binding to the MetHb and analysis yielded an observed rate constant of 1.5 1/s for the initial reaction. F, the kinetics of the absorption at 415 nm are shown for both viscous and nonviscous buffers for data collected under aerobic conditions. Both the raw data (noisy) and fit from singular value decomposition and global analysis are shown.

Bimolecular Reaction Rate Constants in Simulations of NO Uptake by Red Blood Cell Microparticles

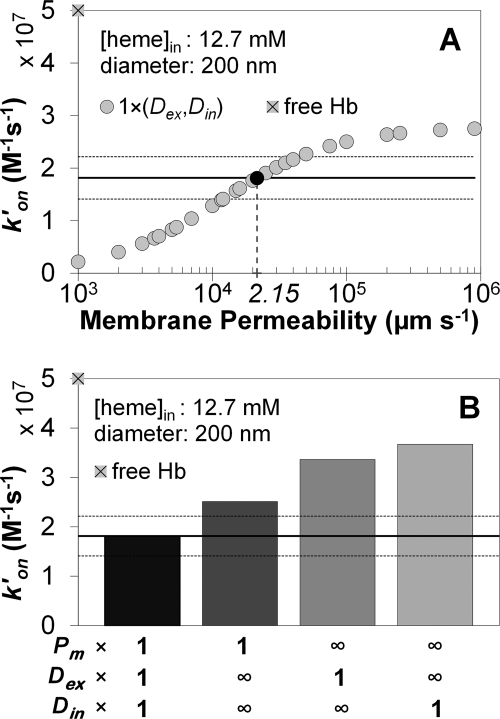
The bimolecular reaction rate constants obtained in simulations of our photolysis experiments under aerobic conditions are presented in Fig. 6. The experimentally measured bimolecular rate constant for NO dioxygenation by microparticle-encapsulated hemoglobin was 1.81 ± 0.40 × 10⁷ m⁻¹ s⁻¹ (n = 301, 3 separate experiments) (50). This number is shown as a continuous black line in the panels of Fig. 6 and the standard deviation is displayed as the two dotted horizontal lines. The bimolecular rate constant for the cell-free Hb reaction is represented by the gray square with a black cross on the y axis of the panels in Fig. 6 (5 × 10⁷ m⁻¹ s⁻¹). Fig. 6A shows simulated bimolecular rate constants (y axes) for microparticles with the average intracellular Hb concentration of 12.7 mm and a diameter of 200 nm, as determined experimentally. In these simulations 26 different values of membrane permeability (x axes, logarithmic scale) were used, whereas extra- and intracellular diffusion were assigned physiological values (Table 2). The simulated rate constant that is most similar to the experimentally observed bimolecular rate constant for NO uptake by microparticles is marked as a black circle. This gives an estimate of the microparticle membrane permeability to NO (marked on the x axis). The extent to which this permeability value limits the reaction rate is compared with the effects of extra- and intracellular diffusion of NO in Fig. 6B. The physiological membrane permeability value is that obtained from Fig. 6A. The results from simulations where all three mechanistic parameters are included are compared with simulations where only one of the parameters has its physiological value, whereas others are effectively infinite. We find that for these red cell microparticles, including membrane permeability alone, yields a theoretical bimolecular rate constant that is closer to the experimental value than when either external or internal diffusions are included by themselves. The contribution of internal diffusion is the smallest. These data suggest that in the case of red blood cell microparticles, membrane permeability plays the largest role in limiting NO uptake.

FIGURE 6.

Computer simulations of the apparent bimolecular rate constants for NO uptake by oxygenated red blood cell microparticles. A, our simulated bimolecular rate constant is plotted for 26 different values of membrane permeability to NO (x axis). As indicated in the legend with a multiplication factor of 1, extracellular diffusion of NO (D_ex) as well as intracellular diffusion of NO and Hb (D_in) were set to the physiological values from Table 2. The rate constant for NO uptake by a solution of freely dissolved oxygenated Hb is shown on the y axis as a gray square with a black cross. The experimentally measured bimolecular rate constant (1.81 ± 0.40 × 10⁷ m⁻¹ s⁻¹) appears as a horizontal black line (in all panels) and its standard deviation as two dotted horizontal black lines. The simulated rate constant that is the same as that obtained experimentally is shown as a black circle, the corresponding membrane permeability is indicated on the x axis below. B, effect of membrane permeability determined in panel A (2.15 × 10⁴ μm s⁻¹) compared with diffusion effects in limiting the NO uptake rate. Four simulated rate constants are shown as bars. The left-most represents the same simulation as the black circle in panel A, where extra (D_ex) and intracellular (D_in) diffusion were set to the physiological values given in Table 2 and membrane permeability was set to the value determined in panel A, as indicated with a multiplication factor of 1 for all of these parameters below the x axis. In each of the remaining three simulations the parameter with a multiplication factor of 1 (as indicated below the x axis) was set to its physiological value, whereas the other two were effectively infinite (indicated by the infinity symbols).

In Fig. 6 we have used the values for red cell microparticle diameter and internal Hb concentration that we determined experimentally. However, both of these values could be a source of error in our simulations, particularly that of the internal Hb concentration as our sedimentation technique assumes that there is no empty volume in the red cell microparticle pellet. Thus, we have also conducted simulations over a range of diameters and internal Hb concentrations (Table 2 and supplemental Fig. S2). In all these simulations, we find that membrane permeability plays a substantial, in fact the largest, role in limiting NO uptake by red cell microparticles except for conditions where the highest internal Hb concentration (21 mm) and highest diameter (210 nm) are used.

Experimental Support for Membrane Limitation of NO Uptake by Red Cell Microparticles

To provide experimental support for our conclusions based on theoretical modeling of photolysis-based measurements of NO uptake by red cell microparticles, we conducted competition experiments involving the red cell microparticles and cell-free Hb similar to those described previously (14, 17). In these experiments red cell microparticles are mixed with cell-free Hb in the presence of the NO donor DEANONOate at two different concentrations of Hb. When the Hb concentration of the red cell microparticles is increased, this effectively increases the “hematocrit,” decreases the average distance between microparticles, and hence should lead to a decrease in the average time for external diffusion of NO to the microparticle. Thus, at the higher concentration, external diffusion should have a diminished effect on limiting the rate of NO uptake. At a hematocrit of 100% there is no external diffusion and thus no limitation due to this process on the kinetics of NO uptake. In previous experiments using this approach, we demonstrated the importance of external diffusion on the rate of NO uptake by oxygenated red blood cells (14).

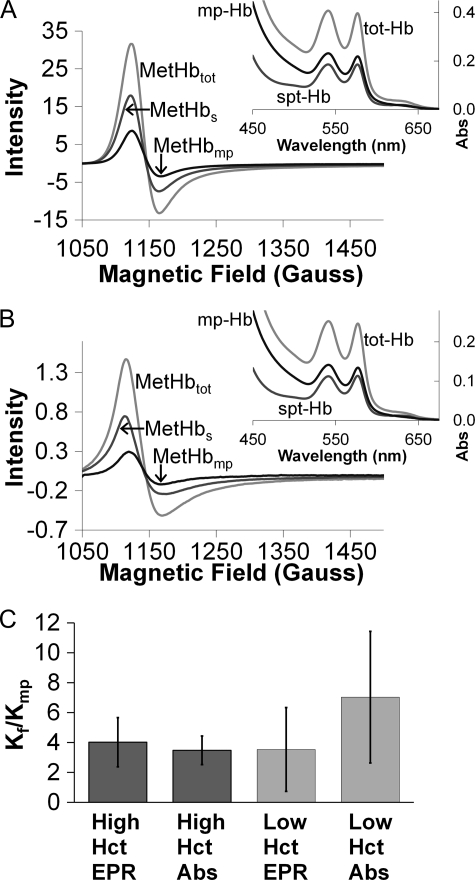
Typical spectra from electron paramagnetic resonance (EPR) and visible absorption (insets) are shown in Fig. 7. Spectra are shown for the supernatants (cell-free Hb) and re-suspended pellets (red cell microparticles) after sedimentation for experiments at high (800 μm, Fig. 7A) and low (50 μm, Fig. 7B) Hb concentrations. There is no obvious effect of Hb concentration. The average and standard deviation of the ratio of the bimolecular rate constants for NO uptake by cell-free Hb (k_f) compared with that by red cell microparticles (k_mp) are plotted in Fig. 7C for the case when the hemoglobin concentrations in each fraction are high and low. Note that for each experiment, the concentration of cell-free Hb and that contained in microparticles are equal. For each experiment, the amount of NO reacted with each fraction was determined by separating the cell-free Hb from the microparticles by sedimentation and then determining reacted Hb (MetHb) using absorption and electron paramagnetic resonance spectroscopy. Overall, the EPR data are more reliable because in the case of absorption we are looking for a small signal from the reacted Hb (MetHb) in the background of absorption that is due to unreacted Hb (oxygenated Hb), whereas in EPR spectra, oxygenated Hb is silent and the entire signal is due to MetHb. In addition, the absorption spectra include scattering from microparticles that could lead to some error in fitting the data. We find that the red cell microparticles scavenge NO only about 3 to 5 times slower than cell-free Hb, consistent with our previously reported measurements based on time-resolved absorption experiments (50). Unlike what was previously observed for red cells under aerobic conditions (14), we do not observe a significant effect of hematocrit on k_f/k_mp.

FIGURE 7.

Competition experiments between red cell microparticles and cell-free Hb for reaction with NO. A, typical EPR and absorbance (inset) spectra collected after the competition of low concentrations (50 μm, ∼0.3% microparticle Hct) of microparticle-encapsulated and cell-free Hb for NO. The main panel shows the EPR signal from the product of the reaction, methemoglobin, in the microparticle fraction (MetHb_mp) (after spinning, supernatant removal, and re-suspension), in the supernatant after spinning out the microparticles (MetHb_s) and in the whole mixture (MetHb_tot) plotted versus magnetic field. In the inset, absorbance in the visible wavelength range of the microparticle-encapsulated Hb (mp-Hb), the Hb in the supernatant (spt-Hb), and hemoglobin in the whole mixture (tot-Hb) is presented. A shoulder due to the formation of methemoglobin (seen with EPR) is visible around 630 nm in each of the spectra. B, data analogous to those in panel A, but from a competition experiment of high concentrations (800 μm, ∼6.3% microparticle Hct) of microparticle-encapsulated and cell-free Hb for NO. C, the ratio of the bimolecular rate constant for NO uptake by cell-free Hb to that for NO uptake by microparticle-encapsulated Hb calculated using Equation 6 with data obtained from the competition experiments. The ratios obtained by analysis of the EPR and absorbance data are shown for the high and low microparticle-encapsulated and cell-free Hb amounts. By EPR, the amounts of MetHb formed during competition were obtained by fitting to a standard MetHb EPR spectrum, double integrating, and comparing to a standard curve. The absorbance data were analyzed for MetHb by fitting to standard oxygenated Hb and MetHb spectra.

DISCUSSION

We have simulated the uptake of NO by deoxygenated hemoglobin encapsulated in phospholipid vesicles (as in the recent experiments carried out by another group of researchers (21)) and by oxygenated hemoglobin encapsulated in red blood cell microparticles, and conducted experiments on NO uptake by red blood cells and red cell microparticles. Generally, we find that all of the factors considered, diffusion to the vesicle, inside the vesicle, and permeability through the vesicle can (in principle) affect the NO uptake rates. We found that in the experiments of Sakai et al. (21) and in our experiments with red cells, extracellular diffusion of NO to the encapsulated Hb is the major rate-limiting factor, whereas, in our experiments with red cell microparticles, membrane permeability of NO appears to be rate-limiting.

The best fit to the experimental data with phospholipid vesicles was obtained when physiological values of NO diffusion rate outside and inside of a vesicle and of membrane permeability to NO have been used (Table 1), as shown in Figs. 2, A and C. From our simulations we may safely conclude that, in the stopped-flow experiments performed by Sakai et al. (21), both diffusion of NO to a vesicle and inside of a vesicle contributed to the rate of the reaction, but that diffusion of NO through the extracellular space was the major rate-limiting factor.

To confirm that external diffusion plays the major role in limiting NO uptake by red blood cells, we conducted stopped-flow absorption experiments where we modulated the viscosity of the external buffer. We found that increasing the buffer viscosity decreased the rate of NO uptake under both aerobic and anaerobic conditions. These data support our simulations that show that as particle diameter and internal heme concentration increase, NO uptake rates decrease and this is dominated by the effect of external diffusion. These results are analogous to those reported previously in the case of oxygen uptake (7).

We have previously estimated (20) that the red blood cell membrane under aerobic conditions may be at least 12.5 times less permeable to NO (4.4–5.1 × 10³ μm s⁻¹) than under anaerobic conditions (64–900 × 10³ μm s⁻¹). The effect of oxygen was hypothesized to be linked to binding of deoxygenated Hb to Band 3 tetramers in the cytoskeleton thereby displacing ankyrin (14, 20), similar to a previously proposed mechanism involving intracellular HbNO modulation of RBCs (24). However, it is also possible that the perceived change in membrane permeability is actually due to reactions of NO that occur specifically or preferentially in the membrane, such as the accelerated reaction of NO with oxygen due to the high solubility of these molecules in the lipid phase (63). In such a case, it would not be a real effect of membrane permeability in limiting the rate of NO diffusion from the exterior to the interior of the red cell, but rather competing NO reactions in the membrane that lead to an apparent effect of membrane permeability.

The results from simulations of our photolysis experiments indicate that membrane permeability may contribute substantially to slower NO uptake by microparticles derived from red blood cells under aerobic conditions. The membrane of these microparticles is known to contain many of the same components as the membrane of red blood cells, including lipid raft proteins (56). In our fast time-resolved photolysis experiments of NO uptake by red cell microparticles, we have measured that they scavenge NO ∼3 times slower (1.81 × 10⁷ m⁻¹ s⁻¹) than cell-free Hb (5 × 10⁷ m⁻¹ s⁻¹). These experiments, unlike those with phospholipid vesicles, were performed with higher excess amounts of NO of 5 to 8 times as much as total hemoglobin concentration, and at slightly higher hematocrits. Using our best estimate for the average concentration of hemoglobin inside a microparticle of 12.7 mm and our measured diameter of 200 nm, our simulations suggest a larger role for membrane permeability than other factors in limiting NO uptake by these red cell microparticles.

Generally, it is seen that whereas particle size and internal Hb concentration greatly affect the degree of rate limitation by diffusion mechanisms, membrane permeability is independent of particle size and internal Hb concentration in its ability to limit the rate. Thus, if membrane permeability is to have an effect, we might expect it to be most noticeable with small particles. It is worth noting that the overall decrease in the rate of NO uptake by red cell microparticles compared with that by intact red cells is very small (a factor of about 3 versus cell-free Hb compared with a factor of up to 1000 versus cell-free Hb). In the case of red blood cells, the effect of membrane permeability is washed out by the effect of external diffusion. However, in the case of the much smaller red cell microparticles, one would expect the relative role of membrane permeability in limiting the rate of NO uptake to be greater than in the case of red cells, due to the fact that the effect of external and internal diffusion decrease as particle size decreases.

One would not expect a simple phospholipid membrane to limit NO uptake as NO is more soluble in the membrane than in aqueous solution. The difference between red cell microparticles and the phospholipid vesicles is that the former are likely to contain membrane proteins previously hypothesized to decrease membrane permeability (17, 18), whereas the latter do not.

Our results from competition experiments between red cell microparticles and cell-free Hb did not show a significant effect of hematocrit. Although there was a trend in data collected by absorption spectroscopy that support a role of external diffusion in limiting NO uptake by the red cell microparticles, this was not shown in EPR data and did not reach significance. Thus, these data suggest major roles of other rate-limiting factors such as membrane permeability or internal diffusion. Our results, as well as previous analogous experiments on oxygen uptake (7), show that as the diameter of the Hb containing particles decreases, limitations on NO uptake decrease. As shown in Fig. 2, the effect of diameter is seen in diffusion, but not in membrane permeability. Thus, to the extent that membrane permeability does play a role, it should be expected to do so in the smallest vesicles. Overall, these data suggest that, for the case of red cell microparticles that likely maintain membrane proteins and other structures that may partially obstruct NO, the small decrease in NO uptake compared with cell-free Hb could be due to decreased membrane permeability. However, several caveats should be considered. First, the difference in NO uptake between these red cell microparticles and cell-free Hb is much smaller than that between red blood cells and cell-free Hb, so the cause of the rate limitation is harder to draw firm conclusions on. In addition, the physical and chemical makeup of red cell microparticles could be complex and involve a wider size and shape distribution as well as free hemin or degradation products that our computational modeling did not account for. Finally, our simulations for a range of microparticle sizes (supplemental Fig. S2) show a smaller effect of membrane permeability for dense, larger particles.

In vivo we would expect NO diffusion to a phospholipid vesicle to contribute even more to the slow uptake rate of NO than in stopped-flow experiments due to the cell-free (or vesicle-free) zone. There should still be a plasma layer of some thickness next to the wall of a blood vessel that is mostly free of vesicles due to the radial pressure gradient in laminar flow, similar to the red blood cell-free zone. Under physiological conditions the fraction of NO that reacts with Hb is very small, so NO would never have to diffuse very far into a vesicle before reacting. Thus, NO would only have to diffuse through the membrane of a vesicle before being scavenged by hemoglobin. Therefore, even if there is no vesicle-free zone as with red blood cells, the NO diffusion distance inside a phospholipid vesicle might be negligible. The same argument can be applied to NO uptake by red blood cells in vivo. So, intracellular diffusion of NO is not likely to limit the rate at which it is scavenged by red blood cells or by phospholipid vesicles in vivo. Our work also suggests that, in addition to the main rate-limiting factor of extracellular diffusion, erythrocyte membrane permeability could be low enough to partially modulate its uptake of NO under aerobic conditions as also suggested by others (14, 18–20, 22). Our results have important implications regarding the mechanism of increased NO scavenging by cell-free hemoglobin or red cell microparticles that form in pathological conditions or in older stored blood (27, 49, 50). The results of our work on NO reactivity with red blood cells and other membrane-encapsulated Hb could also potentially have implications in other biological situations where a signaling molecule or drug must diffuse through a reactive medium such as oxygen, HNO, or hydrogen sulfide.

In summary, we have found that data obtained by Sakai et al. (21) on NO reactions with phospholipid vesicles can be explained by several mechanisms. Thus, agreement with a model where only intracellular diffusion is included does not prove that this is the only rate-limiting factor. In fact we found that extracellular diffusion is likely to play a larger role in limiting NO uptake by phospholipid vesicles used in those experiments, and that inclusion of this as well as some permeability barrier of the membrane best fits the data. Overall, our data support the concept that extracellular diffusion is the main rate-limiting factor for NO reactions with red cells or phospholipid vesicles in vivo. Similar conclusions have been drawn based on experiments examining oxygen uptake by red cells from different species and artificial vesicles (6, 7). We have also demonstrated that membrane permeability to NO may play a major role in limiting NO uptake by microparticles derived from red blood cells under aerobic conditions. Thus, which mechanism is the main factor in limiting NO uptake by membrane-encapsulated Hb depends on many factors including particle size, intracellular Hb concentration, and hematocrit.