Abstract
Nonlinear microscopy can be used to probe the intrinsic optical properties of biological tissues. Using femtosecond pulses, third-harmonic generation (THG) and four-wave mixing (FWM) signals can be efficiently produced and detected simultaneously. Both signals probe a similar parameter, i.e. the real part of the third-order nonlinear susceptibility χ(3). However THG and FWM images result from different phase matching conditions and provide complementary information. We analyze this complementarity using calculations, z-scan measurements on water and oils, and THG-FWM imaging of cell divisions in live zebrafish embryos. The two signals exhibit different sensitivity to sample size and clustering in the half-wavelength regime. Far from resonance, THG images reveal spatial variations |Δχ(3)(−3ω;ω,ω,ω)| with remarkable sensitivity while FWM directly reflects the distribution of χ(3)(−2ω1 + ω2;ω1, –ω2, ω1). We show that FWM images provide χ(3) maps useful for proper interpretation of cellular THG signals, and that combined imaging carries additional structural information. Finally we present simultaneous imaging of intrinsic THG, FWM, second-harmonic (SHG) and two-photon-excited fluorescence (2PEF) signals in live Caenorhabditis elegans worms illustrating the information provided by multimodal nonlinear imaging of unstained tissue.
OCIS codes: (180.4315) Nonlinear microscopy; (170.3880) Medical and biological imaging; (190.4160) Multiharmonic generation; (190.4380) Nonlinear optics, four-wave mixing
1. Introduction
Nonlinear (or multiphoton) microscopy is an effective method for obtaining 3D-resolved images of biological tissues, and two-photon-excited fluorescence (2PEF) microscopy has found a broad range of applications in the life sciences [1]. In addition to 2PEF imaging of exogenous labels and fluorescent proteins, multiphoton microscopy can be used to probe the intrinsic nonlinear optical properties of tissues. A growing literature shows that physiologically and/or structurally relevant information is obtained through the detection of coherent signals such as second-harmonic generation (SHG) [2], third-harmonic generation (THG) [3, 4, 5], or four-wave mixing (FWM) processes [6] such as coherent Raman scattering (CARS, etc) [7, 8] or stimulated parametric emission (SPE) [9]. In particular, THG imaging detects spatial variations of the electronic part of the third-order nonlinear susceptibility χ(3)(–3ω;ω,ω,ω) [10, 11], such as lipid inclusions in an aqueous environment [12], and has proven useful for embryo and tissue imaging applications [3, 4, 5, 13, 14]. When experimentally available, the combination of different nonlinear contrasts usually provides complementary information. Using pulsed excitation provided by a femtosecond Ti:sapphire oscillator and a synchronously pumped optical parametric oscillator (OPO), THG and four-wave mixing (FWM) signals can in principle be efficiently produced and detected simultaneously. In isotropic media exhibiting no electronic nor vibrational resonance, THG and FWM can be viewed as both probing a similar parameter, i.e. the real part of χ(3). However THG and FWM signal levels result from different phase matching conditions. In contrast with FWM, TH coherent signal buildup in the forward direction is frustrated by the Gouy phase shift of the focused excitation beam, resulting in no THG from a homogeneous medium having normal dispersion [10, 15]. Non-resonant FWM has received relatively little attention for nonlinear microscopy applications, apart for being considered as an unwanted “non-resonant background” in CARS microscopy. However, given their different dependence on sample size, combined THG and FWM imaging of the same objects should provide more structural information than either modality alone. In this study we first discuss the contrast mechanisms of THG and FWM imaging as a function of sample size and geometry and we then present imaging examples from model liquids and live tissues. We discuss the properties of the images and some implications for THG and CARS microscopy. THG and FWM are shown to provide complementary information on χ(3) variations, compatible with other femtosecond laser-based imaging modalities.
2. THG and FWM contrast mechanisms
In this part we first summarize a model for describing coherent nonlinear microscopy used in previous studies [16, 17], and we briefly discuss THG and FWM χ(3). We use numerical simulations relying on the Debye-Wolf description of focused fields [18] and on the Green’s function formalism [19] to review the contrast mechanisms of THG and FWM microscopies, and to highlight their different sensitivities to sample structure and size in the half-wavelength regime.
2.1. Excitation fields near focus
Throughout this paper, we assume that the excitation beams entering the objective are Gaussian with linear polarization along the x axis. In this case the vectorial nature of the focused fields can be neglected for parametric processes in isotropic media [16, 25, 17]. The x component of the field near focus can be expressed as [19]:
| (1) |
where n(ω) (resp. kω) is the index of refraction (resp. wave vector) at the fundamental wavelength, θmax = arcsin(NA/n(ω)), with NA being the numerical aperture of the objective, and f0 is the filling factor of the objective (ratio between the beam waist and the diameter of the back aperture).
2.2. THG-FWM third-order polarization and nonlinear susceptibility
The third-order polarizations induced by the focused fields are described by:
| (2) |
| (3) |
where 1 and 2 denote the two excitation fields in the case of FWM.
For isotropic media the THG and FWM nonlinear susceptiblities can be written as [7, 8, 15]:
| (4) |
| (5) |
If we consider isotropic media with isotropic resonances and beams linearly polarized along the x axis, the THG and FWM third-order polarizations read:
| (6) |
| (7) |
The THG and FWM nonlinear susceptiblity tensors then only have one independent element and can be developed as follows:
| (8) |
| (9) |
where nr and r denote the nonresonant and resonant parts of the tensors. χ(THG)r describes resonant THG and is related to one-, two- or three-photon absorption, see [20]. χ(FWM)r denotes resonant FWM and can be related to vibrational (e.g. CARS) or electronic (e.g. stimulated parametric emission) resonance, see [6, 7, 8, 9, 21].
Several semiempirical models have been proposed for relating the nonresonant component of χ(3) to linear indices [15, 22]. A generalized version of Miller’s rule valid for some materials [15] proposes that χ(3)(ω4,ω3,ω2,ω1) ≈ n(ω4)n(ω3)n(ω2)n(ω1), so that χ(THG) ≈ n(3ω)n(ω)3 and χ(FWM) ≈ n(ω)4. Far from resonance, THG and FWM can therefore be expected to probe a similar parameter χ(3)nr. However it is in practice uncommon to find materials that are transparent (i.e. non-resonant) for the frequency range involved in the processes considered here, i.e. encompassing ω and 3ω.
2.3. Propagation of the harmonic fields and signal creation
Once the polarization distribution near focus has been calculated, fields scattered from all positions r in the focal region are propagated to a position R in the collection optics aperture:
| (10) |
where V spans the excitation volume and GFF is the far-field Green’s function
| (11) |
where R = |R| and I is the third-order identity tensor. Finally the total THG/FWM intensity scattered in the forward direction is estimated by integrating |EFF (R)|2 over the front aperture of a transmission-collecting objective.
2.4. Phase-matching and structure sensitivity of THG and FWM
We used the previous analysis to compare the THG and FWM signals obtained from model geometries. We first considered the “classical” geometry where the focal point is z-scanned through a xy interface between two homogeneous media having different nonlinear susceptibilities: and . We then analyzed the situation of a two-media sample exhibiting heterogeneity in the sub-wavelength range while having a constant average χ(3) over the focal region. Specifically, we considered a 3-dimensional checkerboard-like sample with variable grid size, one grid corner being centered at the focus.
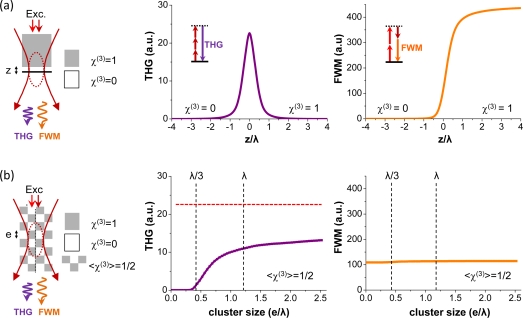
The interface case illustrates the effect of the different phase-matching conditions for the two processes. As pointed out in previous studies, under tight focusing conditions there is no significant phase mismatch between the excitation and forward-scattered beams in FWM (or CARS), so that the coherent construction length (or effective coherence length ) is comparable to the axial extent of the interaction volume [25]; in contrast the coherent construction length for forward-THG is smaller because phase matching is frustrated by the (tripled) Gouy phase shift of the excitation beam, so that [16]. This results in THG being observed only near heterogeneities or interfaces, whereas FWM increases with the excited volume. Since coherent signals scale as the square of the coherence volume, THG signals are expected to be significantly smaller than FWM signals for comparable pulse energy and duration. On the other hand, THG selectively highlights spatial < χ(3) > interfaces and heterogeneities over a dark background (Fig. 1).
Fig. 1.
Effect of phase matching and geometry on THG-FWM contrast. (a) Calculation of the THG and FWM intensity obtained when scanning a focused Gaussian beam across a transverse interface between vacuum and an isotropic nonlinear medium. The THG intensity is highest when the interface is in focus (z = 0). (b) Calculation of the THG and FWM intensity obtained from a three-dimensional checkerboard-like medium as a function of granularity. This geometry corresponds to a constant average value of < χ(3) > inside the excitation volume, with variable sub-wavelength spatial distribution. In this configuration, THG and FWM exhibit different sensitivities to sample granularity in the half-wavelength regime. The dashed red line on the THG graph indicates the signal level for a transverse interface geometry with similar < χ(3) >, shown for comparison. Simulation conditions: NA = 1.2, Excitation with λ1 = 1.2μm and λ2 = 0.8μm
The case of a structured sample is more intriguing. In the geometry considered here, the average value of χ3 inside the excitation volume is constant and the sample characteristic size varies from λ/20 to 2.5λ. It is seen that FWM does not depend on sample granularity, whereas THG intensity exhibits significant variation for structure sizes in the range λ/3 – λ, and almost no change outside this range. This can be interpreted as follows. For granularity the medium may be seen as homogeneous for the THG process, and therefore THG → 0 and FWM ∝ < χ(3) >2. In contrast for cube sizes in the range λ/3 – λ the medium is not homogeneous at the scale of the THG coherence length, and THG is observed due to partly non-destructive interferences, whereas < χ(3) > and FWM are unchanged. Finally for e >> λ the sample geometry resembles a corner interface with the same average < χ(3) >, and constant THG and FWM signals are predicted. Although the signals can also depend on sample position, these simulations indicate that the association of THG and FWM microscopy may provide more information on the sub-wavelength χ(3) spatial distribution than either modality alone, and motivates this combination.
3. Experimental results
3.1. Experimental setup
THG and FWM are third-order electronic processes, and can be efficiently produced and detected simultaneously using femtosecond pulses. The experimental setup is depicted in Fig. 2. Excitation pulses were provided by a titanium:sapphire (TiS) oscillator (80MHz, Chameleon, Coherent) and by a KTP-based synchronously pumped optical parametric oscillator (OPO) (APE). TiS and OPO pulses were overlapped using a dichroic mirror (Chroma 1000dcxr) and synchronized in the sample using a delay line. Imaging was performed on a lab-built microscope incorporating galvanometer mirrors (GSI Lumonics), photomultiplier tubes (PMT, SensTech), counting electronics, and water immersion objectives (Olympus). TiS and OPO beam polarizations in the microscope were linear and co-aligned. The objectives used for excitation were a 60× 1.2NA coverslip-corrected and a 20× 0.95NA with its pupil underfilled (approximately 0.75 effective excitation NA). For the experiments presented in this study, TiS and OPO pulse durations at the sample were approximately 250fs. Coherent scattering (THG, FWM, and optionally SHG) was detected in the forward direction and selected with dichroics and filters (Semrock).
Fig. 2.
Experimental setup. TiS: femtosecond titanium:sapphire laser. OPO: optical parametric oscillator. X-Y: beam scanning system. In this study coherent signals (FWM, THG, SHG) are detected in the transmitted direction and 2PEF signals are epidetected.
3.2. Nonlinear susceptibility measurement of isotropic media with THG and FWM
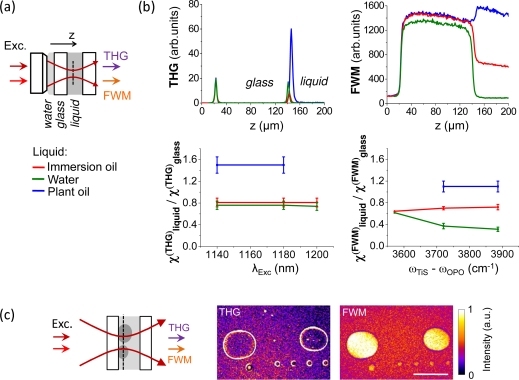
We performed z-scan measurements to evaluate χ(THG) and χ(FWM) for several isotropic media. We analyzed three types of liquids: water, chlorotrifluoroethylene (Voltalef® immersion oil) and triolein (plant oil). For the measurements, the liquid was sealed between two microscope coverslips (see Fig. 3). THG and FWM radiations were separated using a dichroic mirror and detected simultaneously on two detectors. Shortpass filters (Semrock) were used to isolate the signals from scattered laser noise.
Fig. 3.
Effect of χ(3) on THG-FWM contrast. (a) z-scan geometry used for estimating χ(THG) and χ(FWM) of various liquids relative to glass. The focus of a coverslip-corrected objective is scanned through a water-glass and a glass-liquid interface. (b) Top, THG (left) and FWM (right) z-scan profiles for different liquids (immersion oil, water, plant oil). The displayed profiles are normalized to their values at the first interface. Bottom, estimated values of χ(THG) (left) and χ(FWM) (right) relative to glass (see text), for different OPO wavelengths and TiS-OPO frequency differences. Deviation of the water χ(FWM) curve near 3600cm−1 is due to the presence of CARS at this frequency shift. It can be seen that in all the conditions explored here. (c) Simultaneously recorded images of immersion oil droplets in water for λOPO = 1140nm and ωTiS – ωOPO = 3890cm−1. Water/immersion oil interfaces are visible in the THG images, and immersion oil produces a stronger FWM signal than water. Scale bar: 50μm.
In the absence of resonance, the value of χ(FWM) of a pure liquid relative to glass can be estimated from a z-scan profile such as the ones displayed in Fig. 3 using the relation:
| (12) |
where Iliq (resp. Iglass) is the FWM intensity measured in liquid (resp. glass) just after (resp. before) the glass-liquid interface, and Inoise is noise principally due to imperfectly rejected TiS light, measured in air and corrected by the transmission of the setup. Measuring Iliq and Iglass close to the interface minimizes aberration variations between different experiments and the subsequent measurement errors [23].
The THG χ(3) of a liquid relative to glass can be estimated from two z-scan experiments: (i) a water-glass-liquid scan as shown in Fig. 3, and (ii) a water-glass-air reference scan (not shown). Following [20, 24], the χ(3) relative to glass can be estimated as:
| (13) |
where b is the confocal parameter: ,
J is the phase matching integral: ,
Δk = 3kω – k3ω is the phase mismatch, and C is a normalization factor that takes into account power fluctuation and transmission changes between the first and second z-scan. Iglass/liq and Iglass/air are the THG signals measured at the glass/liquid and glass/air interface in the first and second z-scan. Under moderate numerical aperture excitation, the above equation can simplified as follows:
| (14) |
As seen from this expression an ambiguity remains in the determination of χ(THG) due to the two possible signs. This ambiguity was resolved using additional relative measurements at the interfaces between the different liquids. [12, 20]
We estimated χ(FWM) as a function of the frequency difference between the Ti:S and the OPO for frequency shifts ranging from 3550cm−1 to 3890cm−1, and χ(THG) as a function of the OPO wavelength between 1140nm and 1200nm. The measured values relative to glass are displayed in Fig. 3.
Consistent with previous studies [12], these data show that , which explains why water/lipid interfaces are visible in THG microscopy [14]. The measurements also indicate that χ(FWM) values for water, immersion and plant oil are significantly different at 3890cm−1 where there are no vibrational resonances for the three liquids (Fig. 3b). Therefore nonresonant FWM microscopy is expected to distinguish oil droplets from water with a good contrast, as illustrated in Fig. 3c.
These experiments indicate that χ(THG) and χ(FWM) have comparable values, and that their relative values for the materials considered here have similar relative order, i.e. holds true for both processes.
Quantitative differences are observed in the case of plant oil and water for which the ratio is found to be higher than . This may be related to resonant enhancement of the χ(THG), since both liquids exhibit absorption in the 1100nm–1200nm range. Another difference between THG and FWM is observed in the spectral dependence of χ(FWM) for water (Fig. 3b). This is attributed to the presence of resonant CARS from water, since OH bonds exhibits vibrational resonance between 3300cm−1 and 3600cm−1, whereas immersion and plant oils have no vibrational resonance in the frequency range studied here. Consistently, the estimated value for χ(FWM) of water decreases with the frequency shift, while the estimated χ(FWM) of immersion oil is constant. We conclude that, despite the possible presence of electronic or vibrational resonances, the FWM signal can generally be considered as a qualitative χ(3) map for analyzing THG images.
3.3. THG-FWM microscopy of a zebrafish embryo during early divisions
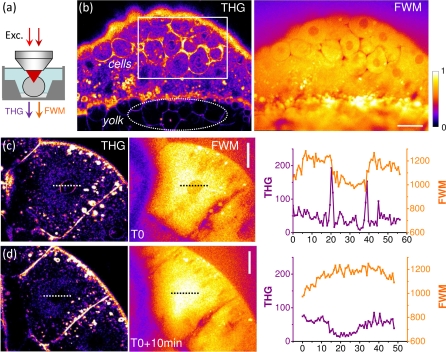
THG microscopy has proven effective for studying cell divisions in the early zebrafish embryo [5]. In particular, THG images highlight the boundaries of cells, nuclei, and yolk platelets with remarkable contrast [4, 5]. However the interpretation of these images is not immediate, since a strong THG signal can originate from different sample geometries (interfaces or inclusions), and from either a local increase or a local decrease in χ(3). To gain insight into the origin of these THG signals, we recorded time-lapse THG-FWM images of zebrafish embryos during early cell divisions. The embryos were mechanically dechorionated, and maintained in the observation chamber using low-density agarose as described in [4, 5]. Representative images are shown in Fig. 4.
Fig. 4.
THG-FWM microscopy of a zebrafish embryo during early divisions. (a) Imaging geometry. (b) Simultaneous THG and FWM images showing the different contrasts. THG highlights the spatial variations Δχ(3). FWM reveals χ(3) distribution, which is not homogeneous. THG contrast from cells, nuclei contours, vesicles, and yolk structures can be understood from the FWM image. (c,d, and Media 1 (8.5MB, AVI) ) Dividing cells before (c) and after (d) disruption of the nuclear envelope. THG and FWM images provide different information about the structural reorganisation of the cytoplasm and the nucleus (see text). Pixel accumulation time: 5μs. Scale bars: 30μm.
A first straightforward observation is that non-resonant FWM signals are not homogeneous in space, and therefore provide an image of the sample. As expected from χ(3) measurements in water and lipids, different media produce different signal levels. For example, the lipid-rich interface between the cells and the yolk is particularly visible in the FWM images. This has implications for CARS imaging since the FWM signal is what is usually termed “non-resonant background” in the context of CARS microscopy, where it interferes coherently with resonant vibrational CARS signals and signal scales as ICARS ∝ |χ(3)r|2 +|χ(3)nr|2 + 2χ(3)nr.ℜ(χ(3)r) [7, 8]. As illustrated in Fig. 4, this electronic (non-resonant) contribution is not homogeneous and, in short, generally hinders the detection of non-lipid-related signals in CARS microscopy.
Another observation is that THG and FWM images are significantly different. As discussed above, THG images highlight the spatial variations Δχ(3), and FWM can be qualitatively used as a χ(3) map to interpret THG images. In the zebrafish embryo during early divisions, THG signals produce contrasted images of cell contours. Such a contrast could result either from a χ(3) difference between adjacent cells, or from the presence of a large inter-cellular space at this stage of development. The latter interpretation was proposed in [5] and is here confirmed by combined THG-FWM imaging: a local FWM signal decrease is consistently detected around cells (figure 4b). This indicates that the cytoplasm has higher χ(3) than the extracellular medium, and that it is the inter-cellular spacing rather than optical differences between cells or a local lipid accumulation near membranes which is responsible from the high THG signal around cells. //
Signals in the yolk region are also remarkable. In the early zebrafish embryo, the vitelline stores form a foam-like arrangement of packed yolk globules (or platelets) separated by canaliculi filled with ooplasm (see e.g. [26]). The yolk generally produces a strong FWM signal, and the contours of the yolk globules are readily visible in THG microscopy images. From the ratio between xy and xz oriented yolk interfaces in THG images [5], the spacing (ooplasm) between globules can be estimated to be less than 500nm wide, in agreement with morphological observations [26]. Since signal in coherent nonlinear microscopy scales as the squared volume of the probed structure, this small size explains why these contours do not clearly emerge against the strong coherent signal from the yolk globules in the FWM images (figure 4b). This observation again illustrates the complementarity of the two images. THG exhibits superior sensitivity to χ(3) spatial variations, but images must be interpreted with care (different geometries and different Δχ(3) signs give the same signal), while FWM signal level provide clearer information about the geometry and media being observed. //
More intriguing is the time dependence of THG-FWM signals from nuclei during cell divisions. As previously reported, THG highlights the contours of the cell nuclei. FWM images indicate that the nuclei exhibit reduced χ(3) compared to the cytoplasm, which consistently explains why nuclear contours are visible in THG images (Figure 4c). Before cell division, the THG signal from the nucleus disappears [5], most likely when the nuclear envelope is disrupted. THG-FWM imaging shows that this THG signal coincides with an increase in nuclear FWM signal, which then becomes comparable to cytoplasmic FWM signal (Figure 4d). This may reflect a redistribution of material between the nucleus and the cytoplasm, and/or a reorganization of the nucleus. This latter hypothesis is strengthened by the observation that, after the disruption of the nuclear envelope, FWM is constant across the cytoplasm and nucleus whereas THG is lower in the nucleus (Figure 4d). This difference between the evolution of the two signals may be related to a sub-wavelength material reorganization, as illustrated by the simulations shown in Figure 1. Although more experiments are obviously needed to fully decipher these images, they illustrate that combining χ(3) signals with different phase matching conditions provides information about intracellular structures at the sub-μm scale.
3.4. Label-free multimodal THG-FWM-SHG-2PEF imaging of live Caenorhabditis elegans worms
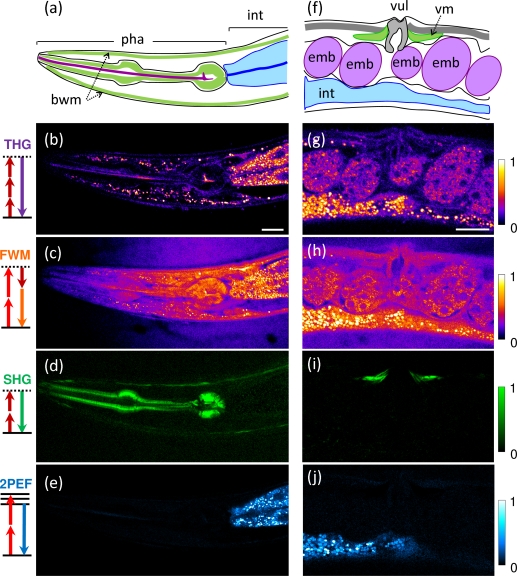
In addition to THG and FWM, other nonlinear signals can be produced with femtosecond pulses in biological tissues. We recorded simultaneous THG-FWM-SHG-2PEF images of live unlabeled C. elegans worms, shown in Fig. 5. Young adult worms from the wild type strain N2 were transferred to a microscope slide coated with a thin layer of agarose gel and were immobilized using sodium azide and levamisole. Coherent THG, FWM, and SHG signals were detected in the forward direction and separated with two dichroics, while 2PEF was epidetected. Signals were detected using standard pixel accumulation times, i.e. 5–10μs. We note that coherent nonlinear signals (THG, SHG, FWM) are emitted over spectrally separated narrow bandwidths (a few nanometers), so that independent detection of multiple coherent signals is relatively simpler than multicolor fluorescence detection.
Fig. 5.
Simultaneous THG-FWM-SHG-2PEF imaging of live unstained C. elegans worms. The four signals were detected simultaneously from the pharynx (a–e) and the midbody (f–j) of young adults. THG/FWM provide complementary morphological information from the pharynx, intestinal cells, embryos, and lipid stores. Additionally, SHG reveals pharynx, vulva, and crawling muscles, and 2PEF reveals fluorescent gut vesicles. pha: pharynx; int: intestine; bwm: body wall muscles; emb: embryo; vul: vulva; vm: vulva muscles. Scale bars: 20μm. See also Media 2 (3MB, AVI) .
Strongest signals in both THG and FWM images were obtained from vesicles in the intestinal cells and in the epithelium. These compartments are mostly lipidic and have been imaged previously using coherent Raman microscopies in various physiological contexts [27, 28, 29]. Apart from these lipid-related signals, THG and FWM signals provided complementary information, as in the zebrafish embryo. THG revealed optical variations (Δχ(3))2 such as interfaces over a dark background, while FWM revealed the distribution of (χ(3))2 levels within the sample. For example contrasted THG signals delineated interfaces in the pharynx and vulva, corresponding to signal level variations in the FWM image. Epithelial lipids not easily accessible to staining [28] are visible in FWM images and produce contrasted THG signals.
2PEF from fluorescent vesicles was simultaneously produced by the Ti:S beam and detected on a fourth channel. This signal identifies a particular subset of lysosome-related gut vesicles [30, 28], and is not observed from e.g. the epithelial lipid vesicles visible in the THG/FWM images. Finally, SHG was also simultaneously obtained from the pharynx, body wall, and vulva muscles with remarkable specificity [2]. A small amount of 2PEF was detected in the SHG channel due to imperfect filtering, and was removed by linear combination of the raw images.
4. Discussion
Far from resonance, THG and FWM probe a similar parameter (the real part of the third-order nonlinear susceptibility, even if χ(THG) and χ(FWM) are generally different). However the two signals result from different phase-matching conditions and therefore provide different information. Practical implementation of THG imaging is much simpler because it requires a single excitation beam and no spatio-temporal synchronization. As such, it is easily combined with e.g. SHG imaging. Moreover, THG highlights heterogeneities and produce contrasted, background-free images amenable to algorithmic analysis [5]. However THG image interpretation is complex, so that when working on a new application, THG contrast often needs to be characterized. FWM images provide χ(3) maps and are therefore useful for THG image interpretation. Moreover, we have shown that combined THG-FWM imaging has the potential to provide additional size information in the sub-wavelength range.
We note that with the experimental conditions used here (250 fs pulses), FWM signals were significantly higher than THG signals. This is related to the fact that the coherence length is shorter for THG than for FWM with focused beams, and that coherent signals scale as the square of the effectively probed volume. However balancing between the signals could be achieved by adjusting the relative power or temporal characteristics of the OPO and TiS pulses.
We also point out that wave-mixing processes such as FWM are sensitive to chromatic aberration induced by the microscope and the sample. Any mismatch between the foci results in efficiency drop and dark artefacts in the images - a difficulty common to imaging techniques combining two laser beams.
Our experiments show that, despite these technical difficulties, efficient multimodal imaging combining simultaneous 2PEF, THG, FWM and SHG signals is possible in live organisms, and illustrate the complementary information provided by these modalities.
Acknowledgments
We thank M. Zimmerley, M. Joffre, M.-C. Schanne-Klein, W. Supatto and J.-L. Martin for discussions and comments. This work was supported by Fondation Louis D de l’Institut de France, by Agence Nationale de la Recherche (ANR-RIB) and by ERC COST Action MP0603.
References and links
- 1.Zipfel W. R., Williams R. M., Webb W. W., “Nonlinear magic: multiphoton microscopy in the biosciences,” Nat. Biotechnol. 21, 1369–1377 (2003). 10.1038/nbt899 [DOI] [PubMed] [Google Scholar]
- 2.Mohler W., Millard A. C., Campagnola P. J., “Second harmonic imaging of endogenous structural proteins,” Methods 29, 97–109 (2003) 10.1016/S1046-2023(02)00292-X [DOI] [PubMed] [Google Scholar]
- 3.Oron D., Yelin D., Tal E., Raz S., Fachima R., Silberberg Y., “Depth-resolved structural imaging by third-harmonic generation microscopy,” J. Struct. Biol. 147, 3–11 (2004). 10.1016/S1047-8477(03)00125-4 [DOI] [PubMed] [Google Scholar]
- 4.Sun C. K., Chu S.-W., Chen S.-Y., Tsai T.-H., Liu T.-M., Lin C.-Y., Tsai H.-J., “Higher harmonic generation microscopy for developmental biology,” J. Struct. Biol. 147, 19–30 (2004). 10.1016/j.jsb.2003.10.017 [DOI] [PubMed] [Google Scholar]
- 5.Olivier N., Luengo-Oroz M., Duloquin L., Faure E., Savy T., Veilleux I., Solinas X., Débarre D., Bourgine P., Santos A., Peyriéras N., Beaurepaire E., “Cell lineage reconstruction of early zebrafish embryos using label-free nonlinear microscopy,” Science 339, 967–71 (2010). 10.1126/science.1189428 [DOI] [PubMed] [Google Scholar]
- 6.Wang Y., Lin C.-Y., Nikolaenko A., Raghunathan V., Potma E. O., “Four-wave mixing microscopy of nanostructures,” Advances in optics and photonics 3, 1–52 (2011). 10.1364/AOP.3.000001 [DOI] [Google Scholar]
- 7.Cheng J.-X., Xie X. S., “Coherent anti-Stokes Raman scattering microscopy: instrumentation, theory, and applications,” J. Phys. Chem. B 108, 827–840 (2004). 10.1021/jp035693v [DOI] [Google Scholar]
- 8.Volkmer A., “Vibrational imaging and microspectroscopies based on coherent anti-Stokes Raman scattering microscopy,” J. Phys. D: Appl. Phys. 38, R59–R81 (2005). 10.1088/0022-3727/38/5/R01 [DOI] [Google Scholar]
- 9.Isobe K., Kataoka S., Murase R., Watanabe W., Higashi T., Kawakami S., Matsunaga S., Fukui K., Itoh K., “Stimulated parametric emission microscopy,” Opt. Express 14, 786–793 (2006). 10.1364/OPEX.14.000786 [DOI] [PubMed] [Google Scholar]
- 10.Barad Y., Eisenberg H., Horowitz M., Silberberg Y., “Nonlinear scanning laser microscopy by third harmonic generation,” Appl. Phys. Lett. 70, 922–924 (1997). 10.1063/1.118442 [DOI] [Google Scholar]
- 11.Müller M., Squier J., Wilson K. R., Brakenhoff G. J., “3D-microscopy of transparent objects using third-harmonic generation,” J. Microsc. 191, 266–274 (1998). 10.1046/j.1365-2818.1998.00399.x [DOI] [PubMed] [Google Scholar]
- 12.Débarre D., Beaurepaire E., “Quantitative characterization of biological liquids for third-harmonic generation microscopy,” Biophys. J. 92, 603–612 (2007). 10.1529/biophysj.106.094946 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Débarre D., Supatto W., Farge E., Moulia B., Schanne-Klein M. -C., Beaurepaire E., “Velocimetric third-harmonic generation microscopy: micrometer-scale quantification of morphogenetic movements in unstained embryos,” Opt. Lett. 29, 2881 (2004). 10.1364/OL.29.002881 [DOI] [PubMed] [Google Scholar]
- 14.Débarre D., Supatto W., Pena A.-M., Fabre A., Tordjmann T., Combettes L., Schanne-Klein M.-C., Beaurepaire E., “Imaging lipid bodies in cells and tissues using third-harmonic generation microscopy,” Nat. Methods 3, 47–53 (2006). 10.1038/nmeth813 [DOI] [PubMed] [Google Scholar]
- 15.Boyd R. W., Nonlinear Optics, 2nd ed. (Academic, 2003). [Google Scholar]
- 16.Cheng J.-X., Xie X. S., “Green’s function formulation for third harmonic generation microscopy,” J. Opt. Soc. Am. B 19, 1604–1610 (2002). 10.1364/JOSAB.19.001604 [DOI] [Google Scholar]
- 17.Olivier N., Beaurepaire E., “Third-harmonic generation microscopy with focus-engineered beams: a numerical study,” Opt. Express, 16(19), 14703–14715 (2008). 10.1364/OE.16.014703 [DOI] [PubMed] [Google Scholar]
- 18.Richards B., Wolf E., “Electromagnetic diffraction in optical systems II. Structure of the image field in an aplanetic system.,” Proc. Royal Soc. A 253, 358–379 (1959). 10.1098/rspa.1959.0200 [DOI] [Google Scholar]
- 19.Novotny L., Hecht B., Principles of nano-optics (Cambridge Univ Press, 2006). [Google Scholar]
- 20.Clay G., Millard A., Schaffer C., Aus-der-Au J., Tsai P., Squier J., Kleinfeld D., “Spectroscopy of third-harmonic generation: evidence for resonances in model compounds and ligated hemoglobin,” J. Opt. Soc. Am. B 23, 932–950 (2006). 10.1364/JOSAB.23.000932 [DOI] [Google Scholar]
- 21.Liu X., Rudolph W., Thomas J. L., “Characterization and application of femtosecond infrared stimulated parametric emission microscopy,” J. Opt. Soc. Am. B 27, 787–795 (2010). 10.1364/JOSAB.27.000787 [DOI] [Google Scholar]
- 22.Wang C., “Empirical relation between the linear and the thord-order nonlinar optical susceptibilities,” Physssss; Rev. B 2, 2045–2048 (1970). 10.1103/PhysRevB.2.2045 [DOI] [Google Scholar]
- 23.Pillai R. S., Brakenhoff G. J., Müller M., “Analysis of the influence of spherical aberration from focusing through a dielectric slab in quantitative nonlinear optical susceptibility measurements using third-harmonic generation,” Opt. Express 14, 260–269 (2006). 10.1364/OPEX.14.000260 [DOI] [PubMed] [Google Scholar]
- 24.Barille R., Canioni L., Sarger L., Rivoire G., “Nonlinearity measurements of thin films by third-harmonic generation microscopy,” Phys. Rev. E 66, 067602 (2002). 10.1103/PhysRevE.66.067602 [DOI] [PubMed] [Google Scholar]
- 25.Cheng J.-X., Volkmer A., Xie X. S., “Theoretical and experimental characterization of coherent anti-Stokes Raman scattering microscopy,” J. Opt. Soc. Am. B 19, 1663–1675 (2002). 10.1364/JOSAB.19.001363 [DOI] [Google Scholar]
- 26.Fuentes R., Fernández J., “Ooplasmic segregation in the zebrafish zygote and early embryo: pattern of ooplasmic movements and transport pathways,” Dev. Dyn. 2392172–2189 (2010). 10.1002/dvdy.22349 [DOI] [PubMed] [Google Scholar]
- 27.Hellerer T., Axäng C., Brackmann C., Hillertz P., Pilon M., Enejder A., “Monitoring of lipid storage in Caenorhabditis elegans using coherent anti-Stokes Raman scattering (CARS) microscopy,” Proc. Nat. Acad. Sci. USA 37, 14658–14663 (2007). 10.1073/pnas.0703594104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Le T. T., Duren H. M., Slipchenko M. N., Hu C.-D., Cheng J.-X., “Label-free quantitative analysis of lipid metabolism in living Caenorhabditis elegans,” J. Lipid Res. 51, 672–677 (2010). 10.1194/jlr.D000638 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang M. C., Min W., Freudiger C. W., Ruvkun G., Xie X. S. , “RNAi screening for fat regulatory genes with SRS microscopy,” Nat. Methods 8, 135–138 (2011). 10.1038/nmeth.1556 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Clokey G. V., Jacobson L. A., “The autofluorescent lipofuscin granules in the intestinal cells of Caenorhabditis elegans are secondary lysosomes,” Mech. Ageing Dev. 35, 79–94 (1986). 10.1016/0047-6374(86)90068-0 [DOI] [PubMed] [Google Scholar]