Ca²⁺-induced delayed afterdepolarizations are triggered by dyadic subspace Ca²⁺ affirming that increasing SERCA reduces aftercontractions

Abstract

Ca²⁺-induced delayed afterdepolarizations (DADs) are depolarizations that occur after full repolarization. They have been observed across multiple species and cell types. Experimental results have indicated that the main cause of DADs is Ca²⁺ overload. The main hypothesis as to their initiation has been Ca²⁺ overflow from the overloaded sarcoplasmic reticulum (SR). Our results using 37 previously published mathematical models provide evidence that Ca²⁺-induced DADs are initiated by the same mechanism as Ca²⁺-induced Ca²⁺ release, i.e., the modulation of the opening of ryanodine receptors (RyR) by Ca²⁺ in the dyadic subspace; an SR overflow mechanism was not necessary for the induction of DADs in any of the models. The SR Ca²⁺ level is better viewed as a modulator of the appearance of DADs and the magnitude of Ca²⁺ release. The threshold for the total Ca²⁺ level within the cell (not only the SR) at which Ca²⁺ oscillations arise in the models is close to their baseline level (∼1- to 3-fold). It is most sensitive to changes in the maximum sarco(endo)plasmic reticulum Ca²⁺-ATPase (SERCA) pump rate (directly proportional), the opening probability of RyRs, and the Ca²⁺ diffusion rate from the dyadic subspace into the cytosol (both indirectly proportional), indicating that the appearance of DADs is multifactorial. This shift in emphasis away from SR overload as the trigger for DADs toward a multifactorial analysis could explain why SERCA overexpression has been shown to suppress DADs (while increasing contractility) and why DADs appear during heart failure (at low SR Ca²⁺ levels).

delayed afterdepolarizations (DADs) have been related to the initiation of arrhythmias (74). They occur when repolarization is complete and are thought to be caused by intracellular Ca²⁺ oscillations (46) due to Ca²⁺ release from the sarcoplasmic reticulum (SR) (56). Afterdepolarizations occur in pathological states including heart failure, diabetes, and ischemic heart disease (67, 79, 94) as well as under healthy conditions during increased sympathetic tone, exercise, hypokalemia, and rapid heart rate (9, 59, 87). In most experimental setups, Ca²⁺ overload of the cell was used to induce DADs [see, e.g., Orchard et al. (70) and Wier et al. (100)] (Table 1), although there have been instances when DADs were found when applying stretch (89), perhaps involving a stretch-induced increase in ryanodine receptor (RyR) open probability and leak in SR Ca²⁺ (Ca_SR) (31, 33).

Table 1.

Experimental results showing that DADs use either Ca²⁺ overload or increased RyR open probability

Type	Species/CellType	Reference
A	Mouse heart	Killeen et al. (41)
A	Rat papillary and guinea pig ventricle	Aomine et al. (2), Fedida et al. (20), Miura et al. (59)
B	Rat and guinea pig ventricle	Beresewicz and Horackova (4)
B	Guinea pig atrial cells	Song et al. (84)
B	Rabbit ventricle	Wu and Corr (104), Wongcharoen et al. (103)
B	Rabbit pulmonary vein	Wongcharoen et al. (102)
B	Canine ventricle	deGroot et al. (14)
B	Calf Purkinje cells	Lederer and Tsien (46), Kass and Tsien (40)
B	Sheep Purkinje cells	Neiman and Eisner (62)
C	Rat ventricle	Ruocco et al. (78), Xie et al. (105)
C	Rat atrial cells	Tavi et al. (89)
C	Guinea pig ventricle	Song and Belardinelli (83), Tweedie et al. (93), Song et al. (85)
C	Guinea pig heart (in vivo)	Xu and Pelleg (107)
C	Ferret ventricle	Marban et al. (56)
C	Canine ventricle	Priori and Corr (76), Laurita and Katra (44)
C	Canine ventricle wedge	Nam et al. (61)
C	Canine ventricle and Purkinje cells	Burashnikov and Antzelevitch (7)
C	Canine atrial and Purkinje cells	Burashnikov and Antzelevitch (8)
C	Canine atrial cells	Tseng and Wit (92)
C	Sheep Purkinje cells and ventricle	Verkerk et al. (95)
C	Human ventricle	Verkerk et al. (94, 96)
C	Human heart (in vivo)	Chen at al. (9)
D	Rat ventricle	Nordin et al. (67)
D	Guinea pig ventricle	Aomine et al. (1)
E	Guinea pig ventricle	Spencer and Sham (86)
F	Canine atrial cells	Stambler et al. (87)
G	Canine Purkinje cells	Levy and Wiseman (47)
H	Mouse cells	Wehrens (99), Liu et al. (49), Rizzi et al. (77)
H	RyR2 mutant in human embryonic kidney-293 cells	Jiang (38, 39)
I	Rabbit ventricle	Schlotthauer and Bers (80)

Four publications used hypokalemia (type A), nine publications used induced Na⁺ overload (type B), eighteen publications used increased L-type Ca²⁺ current (I_CaL; mainly via the β-adrenergic pathway; type C), two publications increased extracellular Ca²⁺ (type D), one publication used hyponatremia and uncaging of Ca²⁺ (type E), one publication used rapid pacing (type F), and one publication used a combination of these ways (type G) to increase intracellular Ca²⁺, which then lead to the observation of delay afterdepolarizations (DADs). Five more wet experimental studies used mutations of ryanodine receptors (RyRs; type H) to increase the incidence of DADs. One study used surrogates for DADs (type I) to investigate the relation between Ca²⁺ load of the sarcoplasmic reticulum (SR) and the ability to induce DADs that trigger full action potentials.

The term “spontaneous release” of Ca²⁺ from the SR used by many authors suggests that there is no extrinsic influence involved in triggering the release other than a more or less unpredictable incident. Experimental results (as mentioned above) have indicated that Ca²⁺ levels in the cell as well as stretch have an influence on the appearance of DADs and that DADs are reproducible; therefore, we refrain from using this term.

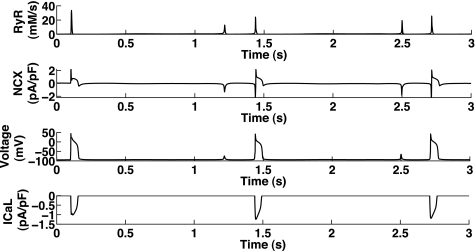
Noble and Varghese (64) have described the induction of DADs as follows: the release of Ca²⁺ from the SR activates the Na⁺/Ca²⁺ exchanger (NCX) or a Ca²⁺-activated Cl⁻ or nonspecific ion current, thus leading to depolarization of the membrane, a DAD, which could then trigger the initiation of an action potential (AP) by activating the fast Na⁺ current. Figure 1 shows an example of Na⁺ and Ca²⁺ overload triggering DADs in a mathematical model.

Fig. 1.

Development of delayed afterdepolarizations (DADs) in a mathematical model (Noble98). Top to bottom: Ca²⁺current through ryanodine receptors (RyRs; A), current through the Na⁺/Ca²⁺ exchanger (NCX; B), cell membrane potential (voltage; C), and L-type Ca²⁺ current (I_CaL; D). Shown is the Noble98 model under Na⁺ overload, which was found to produce Ca²⁺ oscillations and DADs (see text). The first action potential (AP; at 0.1 s) was produced as a result of stimulus current (after 1-Hz pacing), whereas the following depolarizations occurred as a result of Ca²⁺ release, where RyRs were activated by the increased Ca²⁺ within the cell. Note that the first and third DADs were not accompanied by enough membrane depolarization to activate fast Na⁺ current and I_CaL, whereas the second and fourth DADs did (see differences in NCX), thereby producing full APs.

Miura et al. (59) have shown that the mechanisms for early afterdepolarizations (EADs), i.e., depolarizations during phase 2 or 3 of an AP (i.e., before complete repolarization), and DADs differed in general, since EADs were accompanied by a concerted whole cell Ca²⁺-response, whereas DADs were related to local Ca²⁺ changes and intracellular Ca²⁺ waves. However, additional release from the SR could also occur during an AP either due to uncoupling of the Ca²⁺ oscillations or during very long APs such that the afterdepolarizations were then classified as EADs (98).

The actual mechanism initiating the Ca²⁺-release event in DADs has proved difficult to determine. Many reports have put a strong emphasis on the role of Ca_SR levels. It has been described that “the SR cannot maintain its increased store” (37) and “the mechanism of this release in Ca²⁺ overloaded SR is not yet determined. It could result from ‘breakdown’ of the membrane, backward transport through the Ca²⁺ pump, or opening of the SR Ca²⁺ channels” (37). Desantiago et al. (15) concluded with “β-[adrenergic receptor] stimulation is arrhythmogenic in [heart failure], mediated by SR Ca overload-induced SR Ca release and aftercontractions.” However, some experimental work indicated that “a more loaded SR is not the only prerequisite for the generation of [aftercontractions] since they can be present or absent when the SR Ca²⁺ content is similar” (93). Györke et al. (26) showed results in lipid bilayers indicating that there was a modulation of RyR open probability by Ca_SR via calsequestrin, but did not provide information on the relative importance of dyadic versus SR Ca²⁺. Also, the latest reports providing insights into stretch-induced Ca²⁺ release have indicated that SR content is not the sole determinant of the appearance of DADs.

In general, the experimental literature suggests that the main common feature of experimental models showing DADs was Ca²⁺ overload of the cell. (Table 1 provides a list of experimental publications and their methods of initiating DADs.) Most of the experimental procedures induced Ca²⁺ overload by changes in extracellular and intracellular ion concentrations (hypokalemia, block of the Na⁺-K⁺ pump, hyponatremia, or even laserflash photolysis of caged Ca²⁺) by increasing L-type Ca²⁺ current (I_CaL) via the β-adrenergic pathway or by rapid pacing. Five of the publications shown in Table 1 investigated the effects of changed open probability by mutation of RyRs.

The ambiguity in the literature regarding the actual mechanism of DADs could be a reason why they have rarely been investigated and were thought difficult to reproduce in computational models. Luo and Rudy (52) investigated a model for SR overload using a programmed logic switch to force Ca²⁺ release under defined conditions. This approach reproduced DADs due to Ca²⁺ overload and was also used in later publications, but due to its lack of physiological mechanism it was not considered further in this report. Noble and Varghese (64) studied the ability of the Earm and Noble (17) atrial cell model to produce DADs under simulated conditions of Na⁺ and thus Ca²⁺ overload (Na⁺-K⁺ pump block increased intracellular Na⁺) and were able to find DADs, but only within a narrow parameter space. A few other modeling studies addressed the appearance of DADs, but always using only one specific model (24, 34, 81). These approaches did not reflect the fact that DADs are a general phenomenon of atrial, Purkinje, and ventricular cells across species, as shown by the respective findings in the mouse, rat, guinea pig, ferret, rabbit, feline, canine, calf, sheep, and human (40, 56, 69, 77, 84, 87, 94–96, 103, 105). Ca²⁺ oscillations have also been found in sinoatrial node cells, pancreatic β-cells, astrocytes, and others (5, 29, 45, 46, 55, 64, 72) (see also Table 1).

In this work, we focused on investigating the properties and underlying mechanisms of DADs in 37 different mathematical cell models of Purkinje, atrial, and ventricular cells from the human, dog, guinea pig, rabbit, rat, and mouse (see Tables 2 and 3). This broad range helped to ensure that the results were not model dependent (in regard to species or model formulation) while they reflected the summarized knowledge from many different experimental results. We selected a subset of models as representatives used in the main part of this report (Table 2).

Table 2.

Overview of grouping of the investigated mathematical cell models according to their origin and Ca²⁺ subsystem structure

Base model	Derived models	RyR Model Type
DiFrancesco85 (16)		Other
Hilgemann87 (27)	Earm90 (17), Lindblad96 (48)	M + voltage dependence
Noble91 (63)	Noble98 (65)*, Espinosa98 (18), Noble01 (66)	M
Jafri98 (36)	Winslow99 (101), Pandit01 (71)*, Iyer04 (35)	M
Nygren98 (68)	Maleckar09 (54)*	M
Matsuoka03 (57)*	Iribe06 (32)*	M + ICaL additive + CaSR modulation
Hinch04 (28)*		M + ICaL additive + CaSR modulation
Shannon04 (82)*	Grandi10 (25)	M + CaSR modulation
tenTusscher06 (91)	Fink08 (21)*, Stewart09 (88)	HH + CaSR modulation
Iyer07 (34)*		M + CaSR modulation
Pasek08 (73)*		M + tubular Ca2+
Luo-Rudy91 (51)	Luo-Rudy94 (52), Priebe98 (75), Viswanathan99 (97), Faber00 (19)	Not physiological
Courtemanche98 (11)	Fox02 (22), Hund04 (30), tenTusscher04 (90), Livshitz07 (50), Mahajan08 (53), Aslanidi09 (3), Decker09 (13)	HH + ICaL multiplied
Bondarenko04 (6)		M + ICaL multiplied

^*Models were used in this article as representative of their group. M, Markov model type; Ca_SR, Ca²⁺ in the SR; HH, Hodgkin-Huxley type model.

Table 3.

Overview of model properties related to their ability to reproduce DADs

Model	Species (Cell Type)	DAD/CaOSS	Needs NCX for CaOSS	RyR Model Type	RyR Modulation by
Iyer07 (34)	Human (ventricle)	Yes	Yes	M	CaDyad and CaSR
Fink08 (21)	Human (ventricle)	Yes	Yes	HH	CaDyad and CaSR
Maleckar09 (54)	Human (atrium)	Yes	No	M	CaDyad and CaCyt
Shannon04 (82)	Rabbit (ventricle)	Yes	No	M	CaDyad and CaSR
Iribe06 (32)*	Guinea pig (ventricle)	Yes	Yes	M	CaCyt, CaSR, CaMK, and ICaL (additive)
Matsuoka03 (57)	Guinea pig (ventricle)	Yes	Yes	M	CaCyt, CaSR, and ICaL (additive)
Noble98 (65)†	Guinea-pig (ventricle)	Yes	Yes	M	CaDyad and CaCyt
Hinch04 (28)	Rat (ventricle)	Yes	Yes	M	CaDyad
Pandit01 (71)	Rat (ventricle)	Yes	No	M	CaDyad
Pasek08 (73)	Rat (ventricle)	Yes	No	M	CaDyad
Courtemanche98 (11)	Human (atrium)	No		HH	SR Ca2+-release current, voltage, Na+/Ca2+ exchange current (multiplicative), and ICaL (multiplicative)
Luo-Rudy91 (51)	Guinea pig (ventricle)	No		Other	Not physiological
Bondarenko04 (6)	Mouse (ventricle)	No		M	CaDyad and ICaL (multiplicative)

Twenty-three of thirty-seven models can physiologically replicate DADs [five models show Ca²⁺ oscillations in the subsystem (CaOSS) even with Na⁺/Ca²⁺ exchanger (NCX) = 0 with their default parameters]. Models that have a RyR formulation that couples RyR opening with the opening of I_CaL multiplicatively (RyRs can only open if I_CaL is open) cannot reproduce either DADs in the full model or Ca²⁺ oscillations in the reduced models (CaOSS); otherwise, the possibility to simulate DADs seems to be parameter dependent, but not dependent on the model structure. Ca_Dyad, Ca²⁺ in the dyadic space; Ca_Cyt, cytosolic Ca²⁺.

^*This model requires a change in the RyR parameter value “gain_K1.”

^†This model requires a change in the parameter value “NCX dNaCa” or “SERCA alphaUp.”

Initially, we showed that some models could reproduce experimental results that initiate DADs and that a simple criterion determined if a model could simulate DADs at all. All the other results provide evidence that unravel the relative contributions of different parts of the Ca²⁺ subsystem for the initiation of DADs.

METHODS

Models and Simulations

Mathematical models of Purkinje, atrial, and ventricular cells of different species were investigated for their ability to produce DADs (in the whole model) and Ca²⁺ oscillations in reduced versions of the models (as described below). The models covered a large proportion of the models published over the last 10 years, going back to the basic models developed in the laboratories of Denis Noble and Yoram Rudy (see Table 2 for the list of models used as examples for this report and the complete list of investigated models).

If there was no separate dyadic subspace for Ca²⁺ (Ca_Dyad) defined in a model, then cytosolic Ca²⁺ was used instead. Note that simulations with the Noble98 model were done using the sarco(endo)plasmic reticulum Ca²⁺-ATPase (SERCA) parameter “alphaUp” = 4 mM/s and with the Iribe06 model using RyR parameter “gain_K1” = 3 unless stated otherwise.

All models were converted into CellML code either from the published equations in the original reference and/or from working code obtained directly from the model authors. All models are available on the CellML website repository (http://www.cellml.org). Simulations were run using Cellular Open Resource (COR) [see Garny et al. (23) and http://cor.physiol.ox.ac.uk/] and Matlab (The Mathworks, Natick, MA).

Ca²⁺ Subsystem: Reduced Models

DADs in a full model are a transient phenomenon and subject to modulation by the full system of membrane currents, etc., making analysis of the necessary requirements and mechanisms to produce DADs more complex. However, models reduced down to their Ca²⁺ subsystem are potentially able to show sustained Ca²⁺ oscillations, and the required conditions for those oscillations in that subsystem are easily identified. These conditions can then be applied to the full system to investigate the occurrence and mechanism of DADs.

To determine at which levels of total intracellular Ca²⁺ each model was able to produce sustained Ca²⁺ oscillations, the models were reduced down to their “Ca²⁺ subsystems”:

• Transmembrane potential and intracellular Na⁺ and K⁺ concentrations, as well as all extracellular and t-tubular concentrations, were set constant using their end-diastolic values after 3,000 s of 1-Hz pacing.

• All transmembrane currents apart from NCX were set to zero.

  These changes still allowed intracellular Ca²⁺, Ca_SR stores, and any intracellular Ca²⁺ currents to vary.

By increasing the value of intracellular Na⁺ to simulate Na⁺ overload, the level of total Ca²⁺ could easily be varied to investigate the effect of Ca²⁺ overload in the reduced models. The CellML files of the models of the Ca²⁺ subsystem can be found in the Supplemental Material.¹

Bifurcation Analysis

Investigations of the oscillatory behavior of the reduced models were conducted using bifurcation analysis. For this, we exported the reduced models from COR to Matlab format and used matcont (43) to find the intervals of total intracellular Ca²⁺ (Ca_Tot) where Ca²⁺ oscillations occur within the cell (i.e., we used continuation of equilibria and Hopf bifurcations). The respective files can be found in the Supplemental Material. Due to the stiffness of the model equations, the sensitivities derived should be considered as approximations; the actual thresholds were determined by simulation using COR.

Note that, as mentioned above, the appearance of DADs (and EADs) in whole cells is a transient phenomenon and can therefore not be investigated using this mathematical approach.

Detailed Protocols for the Initiation of DADs

Introduction (Fig. 1).

NOBLE98 MODEL.

The model was run to “steady state” for 1,000 s paced at 1 Hz. The alphaUp value was then set to 3 mM/s, and intracellular Na⁺ was set to 12.5 mM. A simulation of 10 s was run, and DADs appeared ∼7.5 s into the run. The model was then rerun using its variable values at the end of the previous run, with the alphaUp value again at 3 mM/s and intracellular Na⁺ reset to 12.5 mM. The first depolarization was stimulated with a current pulse, while all later depolarizations were DADs.

Why are some models unable to show DADs?

For the set of models that were unable to show DADs, we found a mathematical reason (i.e., the link of RyR opening to I_CaL opening). To ensure that all other models were able to reproduce DADs (Ca²⁺ release from the SR at the membrane potential without activation of I_CaL), the intracellular Na⁺ concentration was manually set to varying levels to induce Ca²⁺ overload. The bifurcation analysis done on the Ca²⁺ subsystem provided information on the expected level of Na⁺ required to observe DADs.

Mathematical models replicate the initiation of DADs using experimental protocols (Fig. 2).

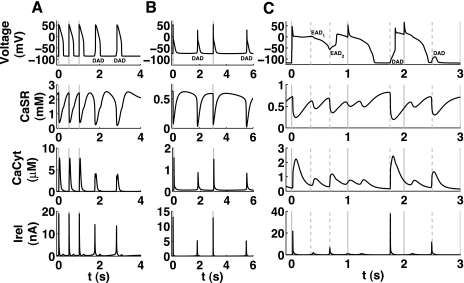
Fig. 2.

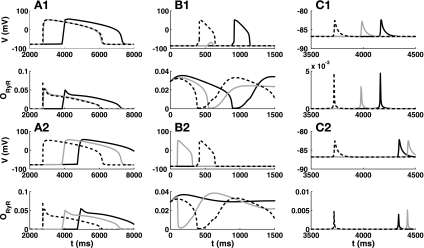
Models replicate different experimental methods for initiating DADs. The rows show changes in membrane voltage (V), sarcoplasmic reticulum (SR) Ca²⁺ (Ca_SR) content, cytosolic Ca²⁺ levels (Ca_Cyt), and RyR release current (I_rel), respectively. Stimulations of the cell are shown by solid gray vertical lines. A: example for the initiation of two DADs due to an increase in I_CaL in the Matsuoka03 model. B: result of increasing the opening rate of RyRs in the Maleckar08 model while increasing the basic cycle length (BCL) from 1 to 3 s. C: Ca²⁺ loaded [due to previous early afterdepolarizations (EADs)] in the Shannon04 model producing an EAD due to reopening of I_CaL (EAD₁) and an EAD (EAD₂) and two DADs due to Ca²⁺ release from the SR (see text for details). t, Time.

The protocols used in this section have been described in the section itself.

Necessary model properties for the simulation of DADs (Fig. 3).

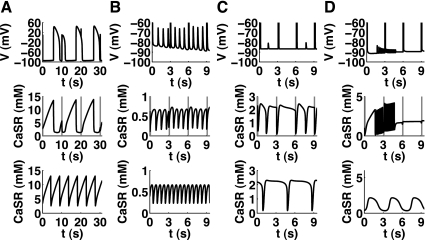
Fig. 3.

Elucidating the necessary underlying mechanism for DADs in different mathematical models. The top and middle rows show the output of the full model (Shannon04), whereas the bottom row denotes the Ca²⁺ content of the SR in the reduced model. Na⁺ and thus Ca²⁺ overload was established by setting the initial intracellular Na⁺ to 35 mM. A: original model. B: model without the modulation of sarco(endo)plasmic reticulum Ca²⁺-ATPase (SERCA) by SR content. C: model without modulation of RyRs by SR content. D: model without modulation of RyRs by the dyadic subspace. It was apparent that only the modulation of RyR by dyadic subspace Ca²⁺ (Ca_Dyad) is essential for DADs and Ca²⁺ oscillations, as its removal led to diminishing oscillations. In C, the x-axis is shifted as it took a longer time until the DADs appearred after the switch to the slower pacing frequency.

The initial condition for the intracellular Na⁺ concentration was set to 40 mM. Subsequent pacing at intervals of 3,000 ms led to the appearance of DADs after the fourth stimulated AP.

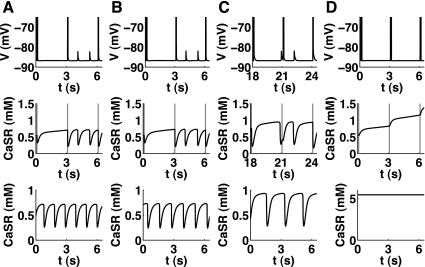
Relating DADs to oscillations in the underlying Ca²⁺ subsystem (Fig. 4).

Fig. 4.

Correlation between the appearance of DADs and oscillations in reduced models during Na⁺ overload. The top and middle top rows show the output of the full models, whereas the bottom row shows Ca²⁺ content of the SR in the reduced models. The initial value for intracellular Na⁺ was set to 80 mM for the Fink08 model (A), 15 mM for the Maleckar08 (B) and Matsuoka03 (C) models, and 35 mM for Pasek08 model (D), while the BCL was changed from 1 to 3 s (10 s for the Fink08 model). Due to the high level of intracellular Na⁺ necessary in the Fink08 model to produce oscillations, the Ca²⁺ cycling in the full model was almost independent of the AP stimulus (gray vertical lines).

As above, the fastest and most robust way to initiate DADs in the mathematical models was used, i.e., setting the initial value for intracellular Na⁺ to a high level. This was 80 mM for the Fink08 model (Fig. 4A), 15 mM for the Maleckar08 (Fig. 4B) and Matsuoka03 (Fig. 4C) models, and 35 mM for the Pasek08 model (Fig. 4D). To be able to observe the DADs, the basic cycle length was changed from 1 to 3 s (10 s for the Fink08 model).

Relative influence of dyadic and SR Ca²⁺ on the appearance of DADs in the full models (Fig. 7).

Fig. 7.

Appearance of DADs diminished or delayed with reduced sensitivity to Ca_SR and Ca_Dyad. The top and middle top rows (1) show membrane voltage and RyR open probability (ORyR; original results as dashed lines) for the scenarios where the sensitivity of gating dynamics to Ca_SR (gray solid lines) and Ca_Dyad (black solid lines) was reduced for three different models showing DADs. The middle bottom and bottom rows (2) additionally include the sensitivity to the driving force (Ca_SR-Ca_Dyad) of the RyR current. A–C: results for the Fink08 (A), Matsuoka03 (B), and Shannon04 (C) models. When only gating dynamics are considered, the appearance of DADs was more sensitive to Ca_Dyad in these models. When the driving force for RyR was included, the results were more similar for both Ca²⁺ compartments and overall inconclusive.

The respective CellML files can be found in the Supplemental Material (in “CellML-DADs”). For the derivation of the sensitivities, the respective concentrations in the RyR gating equations were multiplied by 0.7, 0.85, and 0.95, respectively. Note that this section was only concerned with models that included the modulation of RyR gating by Ca_SR.

IYER07 MODEL (NOT SHOWN).

The conductance of I_CaL was doubled, and the pacing rate was increased to 2 Hz. After 30 s, the pacing was stopped, and two DADs appeared after the last stimulated AP.

MATSUOKA03 MODEL.

Again the conductance of I_CaL was changed, this time to fourfold. Pacing at 2 Hz was stopped after 30 s, and the last AP was followed by two DADs: the first eliciting a full AP and the second only a small membrane depolarization.

SHANNON04 MODEL.

Due to difficulties in eliciting DADs using similar protocols to the ones mentioned above, the necessary raise in intracellular Ca²⁺ was achieved by setting the initial conditions such that intracellular Na⁺ reached a level of 35 mM. Subsequently, the Ca²⁺ level within the cell increased until a DAD appeared (not eliciting an AP).

FINK08 MODEL.

The Na⁺-K⁺ pump was blocked to increase intracellular Na⁺ and thus Ca²⁺.

When intracellular Na⁺ reached 26.3 mM, SR Ca²⁺-release events started to occur (during the AP, so not fully considered to be DADs). Our previous analysis on Ca²⁺ oscillations in the subsystem (CaOSS) indicated that real DADs would occur above an intracellular Na⁺ level of ∼50 mM. When pacing was stopped at around this concentration, DADs appeared, eliciting full APs.

RESULTS

Why Are Some Models Unable to Show DADs?

The occurrence of DADs has been investigated rarely in mathematical models. Some models, as we show in the following section, were able to replicate the initiation of DADs, inducing full APs under similar circumstances as in experimental settings. For others, it appeared that they only showed small membrane potential depolarizations (which also account for DADs), but more drastic changes were required to obtain APs (e.g., additional block of repolarizing currents). As this was not only dependent on the Ca²⁺ subsystem but all the membrane currents, a full discussion of these interactions would exceed the scope of this article.

There were also models from which we were unable to elicit DADs or Ca²⁺ release under any circumstances (see Table 2). We found that these were models where the open probability of the RyR was directly dependent on the opening of I_CaL [as in models based on the Courtemanche98 (11) and Bondarenko04 (6) models]. As DADs, by definition, start from a repolarized membrane, the I_CaL gates have to be closed at the initiation of the Ca²⁺ release from the SR, i.e., RyRs have to be able to open even when I_CaL is zero. This was the case for nine of the mathematical cell models investigated, thereby preventing them mathematically from showing DADs under any circumstances.

In contrast, the Matsuoka03 and Iribe06 models included a modulation of the open probability of RyRs by I_CaL as well, but this was additive to the influence of dyadic/cytosolic Ca²⁺ such that the RyRs could open even when I_CaL was closed.

We found that we could elicit Ca²⁺ release due to Ca²⁺ overload (and thus DADs) in all 23 models in which the RyRs could open when I_CaL was closed, and only for the Noble and Iribe06 models did we have to adjust the default parameter values slightly (see methods).

Note that the structure of the Ca²⁺ subsystem model, the RyR model type (Hodgkin-Huxley or Markov-Model), dependence of RyR opening on dyadic or cytosolic Ca²⁺, and inclusion of modulation of RyR state on Ca_SR were all not relevant for the model being able to replicate DADs. We selected representative examples based on model structure and history (see Table 2) to present further investigations on the appearance of DADs in these models (Table 3).

Mathematical Models Replicate the Initiation of DADs Using Experimental Protocols

To confirm the ability of models to replicate a variety of experiments, we chose to test two protocols in some of the “DAD-capable” models: 1) increase in I_CaL and 2) increase in the open probability of RyRs, and only in the Shannon04 model we simulated 3) hypokalemia and increase in late Na⁺ current (see Fig. 2 for an example of a model reproducing DADs for each case).

Models that could replicate the appearance of DADs under these experimental conditions without drastic parameter changes (e.g., Noble98, Matsuoka03, Shannon04, and Maleckar09 models) had a default total intracellular Ca²⁺ level close to the threshold for Ca²⁺ oscillations at 2-Hz pacing (see Ca²⁺ oscillations occur above a threshold and Table 4). For some of the other models, finding the parameters that would give DADs from our two selected protocols proved to be more difficult, and this may be due to the default and threshold values of total Ca²⁺ being more disparate in these models.

Table 4.

Values and sensitivities of the threshold for CaOSS to the main conductances of the reduced model

	CaTot			CaTot Sensitivities
Model	Original, fmol	Threshold, fmol	Ratio of threshold to original	kRyR	kSERCA	kSSdiff
Iyer07*	1.34	2.76	2.06	−0.185‡	0.024	0.162
Fink08*	13.23	30.85	2.33	−1.314	15.470‡	1.047
Maleckar09	1.07	1.01	0.94	−0.101‡	0.067	N/A
Shannon04*	8.08	8.68	1.07	−0.204	0.016	0.210‡
Iribe06*	0.84	2.66	3.17	0.028	0.130‡	N/A
Matsuoka03*	2.56	2.73	1.07	−0.406	1.615‡	N/A
Noble98	1.67	0.94	0.57	−0.144	0.210‡	N/A
Hinch04†	3.17	6.47	2.04	−1.592	2.451‡	N/A
Pandit01	33.32	57.87	1.74	−0.001	0.062	0.073‡
Pasek08	3.40	6.52	1.92	−1.923	3.037‡	1.239

^*RyR open probability is also modulated by Ca²⁺ in the SR.

^†Model uses rapid equilibrium approximation for the dyadic subspace. The total Ca²⁺ (Ca_Tot) in the cell varied from 0.84 to 33.32 fmol in the presented original models. The threshold for obtaining CaOSS in the reduced models varied from 57% to 317% of the baseline Ca_Tot level. An increase in RyRs (transfer rate or open probability) decreased the level of Ca_Tot necessary for inducing DADs, whereas an increase in sarco(endo)plasmic Ca²⁺-ATPase (SERCA) activity or diffusion from the dyadic subspace to the cytosol was found to increase the threshold.

^‡Most sensitive change for each model. Besides the need of an threefold increase in Ca_Tot for DADs, the Iribe06 model also has high sensitivities for cytosolic buffer capacities and k_NaCa, in contrast to all other models, and it showed an increase of threshold with an increase in k_RyR (this could be due to numerical accuracy). In general, changes in buffer capacities, the transfer rate from the network SR to the junctional SR, and k_NaCa did not change the threshold significantly (not shown), and sensitivities to RyR open probability were similar to the ones of RyR conductances (k_RyR; not shown). N/A, not applicable.

We present detailed results for only one model per protocol.

First, we increased I_CaL conductance to approximately fourfold in the Matsuoka03 model and paced the cell at 2 Hz, which changed the intracellular diastolic Ca²⁺ levels from 16.9 to 29 μM in the cytosol and 2.6 to 2.5 mM in the SR (note that there was a decrease in diastolic Ca_SR). Figure 2A shows that when the pacing was stopped, two DADs appeared.

Second, as all the mutations in RyR discussed in the published reports shown in Table 1 lead to an increase in open probability of the channels, we increased the activation rate of RyR by 50% in the Maleckar08 model and obtained DADs when increasing the basic cycle length from 1 to 3 s (see Fig. 2B). Some authors denoted this as an increase in SR leak current (10), which one would not associate with the fact that it represented a change in the general open probability of RyR channels (according to this terminology, every channel would have/be a leak current). We show below that for all mathematical models an increase in RyR open probability or maximum release rate would decrease the threshold for getting DADs and therefore increase the likelihood of obtaining DADs at normal Ca²⁺ levels.

However, if the “leak” from the SR became too high, it would diminish any Ca²⁺ oscillations; e.g., when substituting the Noble98 formulation for RyR for that of the Priebe98 model, a substantial leak current in the Priebe98 model prevented the appearance of DADs; only when the leak was reduced was the expected behavior observed. The leak current in the Priebe98 model was definitely too large, as it accounted for more Ca²⁺ efflux from the SR than through the regular RyR during one beat.

Finally, a number of experimental protocols included either blockade of repolarizing currents or enhancement of depolarizing currents. We used the Shannon04 model to induce EADs by removal of complete inactivation of the fast Na⁺ current and induction of hypokalemia [as in Milberg et al. (58)]. The appearance of EADs led to further loading of the cell with Na⁺ and Ca²⁺ and finally to the appearance of DADs (see Fig. 2C). The increase in intracellular Na⁺ was ∼1 mM, reaching ∼10 mM. The intracellular diastolic Ca²⁺ rose from 87 to 170 μM in the cytosol and 0.55 to 0.82 mM in the SR. Interestingly, the overall higher cytosolic Ca²⁺ level in the cell increased the speed and level of RyR inactivation as well as their reopening (a section discussing the relative contribution of Ca_SR and Ca_Dyad can be found below). This led to a lower trough immediately preceding the DADs for the SR Ca²⁺-release current and cytosolic Ca²⁺ than in the previous APs.

Necessary Model Properties for the Simulation of DADs

To investigate the contribution of Ca_SR versus dyadic/cytosolic Ca²⁺, we tested the dependencies of RyR gating dynamics and SERCA dynamics on these two compartments. The results shown in Fig. 3 for the Shannon04 model have been replicated with all models that included the modulation of RyR opening by Ca_SR. We eliminated one of the dependencies by clamping the concentration in the term for that modulation in the respective equations. This means we substituted the respective state variable by the precalculated end-diastolic concentration.

For example, for RyR in the Masuoka03 model:

$$\begin{array}{l}{i}_{\text{RyR}}=P_{\text{RyR}}\times \left({\text{Ca}}_{\text{rel}}-{\text{Ca}}_{\text{i}}\right)\times p_{\text{open}\_\text{RyR}}\hfill \\ \frac{\text{d}{p}_{\text{open}\_\text{RyR}}}{\text{d}t}=p_{\text{close}\_\text{RyR}}\times k_1-p_{\text{open}\_\text{RyR}}\times {\text{k}}_2\hfill \end{array}$$

$$\frac{\text{d}{p}_{\text{open}\_\text{RyR}}}{\text{d}t}=k_3\times \left[1-\left(p_{\text{open}\_\text{RyR}}+p_{\text{close}\_\text{RyR}}\right)\right]-\left(k_1+k_4\right)\times p_{\text{close}\_\text{RyR}}$$

$$\begin{array}{l}{k}_1=280,000\times {\text{Ca}}_{\text{i}}^2+{\text{Dyadic}}_{\text{Factor}}\times {\text{Ca}}_{\text{Dyad}}\hfill \\ k_2=0.08/\left(1+0.36/{\text{Ca}}_{\text{rel}}\right)\hfill \\ k_3=0.000377\times {\text{Ca}}_{\text{rel}}^{\text{2}}\hfill \end{array}$$

where i_RyR is RyR current, P_RyR is the conductance of the RyR, Ca_rel is Ca²⁺ release, Ca_i is intracellular Ca²⁺, p_{open_RyR} and p_{close_RyR} are the probabilities of RyR to be open or closed, respectively. When testing the cystolic Ca²⁺ dependence, a constant value (Ca_i_const) was put in the place of Ca_i in the following equation for k₁:

$$k_1=280,000\times {\text{Ca}}_{\text{i\_const}}^2+{\text{Dyadic}}_{\text{Factor}}\times {\text{Ca}}_{\text{Dyad}}$$

When testing the Ca_SR dependence, a constant value (Ca_rel_const) was put in the place of Ca_rel in the following equations for k₂ and k₃:

$$\begin{array}{l}{k}_2=0.08/\left(1+0.36/{\text{Ca}}_{\text{rel\_const}}\right)\hfill \\ k_3=0.000377\times {\text{Ca}}_{\text{rel\_rel\_const}}^{\text{2}}\hfill \end{array}$$

In a number of models, the influence of dyadic and SR Ca²⁺ content were multiplicatively acting on RyR opening or closing. This could be viewed as having the SR content altering the sensitivity on the dyadic/cytosolic side, but also vice versa. If one of the mechanisms acted only by altering the other one, then this would show up using this approach and would lead to the conclusion that this mechanism could be influential but not essential for eliciting DADs in general. This would be important from a structural point of view but would not be indicative of the relative importance under (patho)physiological conditions.

In Relative influence of dyadic and SR Ca²⁺ on RyR open probability we discussed the sensitivity of the RyR opening probability on the two Ca²⁺ pools (in the reduced models), Relative influence of dyadic and SR Ca²⁺ on the appearance of DADs in the full models shows examples of DADs and the influence of changing the modulation by dyadic and SR Ca²⁺ (in the full models).

Removing modulation of RyR by SR.

To investigate the importance of the modulation of the RyR open probability by luminal (SR) Ca²⁺ in producing DADs, we performed in silico experiments in which the modulation of RyR by Ca_SR was removed in the models in which it was included (see Table 3). The frequency and amplitude of the oscillations in the intracellular Ca²⁺ subsystem (see methods and the following section) were changed, and the appearance of DADs was altered, but they were not abolished. For example, in the Shannon04 model, the frequency of CaOSS was almost halved, and their amplitude increased; the appearance of DADs appeared somewhat delayed (compare Fig. 3, A with C), but the oscillations were still present.

Removing modulation of SERCA by the SR.

Similar to the modulation of RyR by the SR content, setting Ca_SR in the modulation term in the SERCA formulation to a constant also altered the frequency and amplitude of the oscillations but did not abolish them (compare Fig. 3, A with B). The change was much less dramatic than for the modulation of RyR by SR content.

Removing the modulation of RyR by Ca_Dyad.

As the modulation of RyR and SERCA by the Ca_SR level was not necessary in the models for DADs, we tested whether the dependency of the open probability of the RyR on dyadic (or cytosolic) Ca²⁺ would prove to be essential for DADs. When the modulation of RyR by Ca_Dyad was set to constant, Ca²⁺ oscillations were completely abolished in all models that previously showed DADs (see, e.g., Fig. 3D for the Shannon04 model), indicating that this is an essential property for the induction of DADs.

The top and middle rows of Fig. 3 show the effect of the respective interventions on a sample DAD protocol in the full model (in this case, increase in intracellular Na⁺ inducing a raise in intracellular Ca²⁺ via NCX). These results could not be considered as fully conclusive as different results could have been possible when using a different protocol for the initiation of DADs. Therefore, we also included the results on intracellular oscillations in the Ca²⁺ subsystem. As these were based on a change in total Ca²⁺ within the cell to induce Ca²⁺ overload, their results did hold for all possible protocols that increased Ca²⁺ within the cell.

To insure that the lack of CaOSS/DADs was not due to this choice of parameter value, we also tested other (higher) values, with similar results: no oscillations occurred with increasing Ca_Tot levels. When the RyR sensor for dyadic Ca²⁺ levels was set to larger values, the opening of the RyR increased and Ca_SR levels decreased, but no oscillations could be found with any parameter value tested. This indicated that there was no intrinsic “second mechanism” built into the models to induce DADs when the sensitivity of RyRs to dyadic Ca²⁺ was removed, independently of the parameter choices.

Relating DADs to Oscillations in the Underlying Ca²⁺ Subsystem

The physiological rationale for investigating the subsystem was that the initial trigger of DADs was coming from within the cell, i.e., from within the Ca²⁺ subsystem, when the membrane potential was at the resting potential (thus constant). The only influence of membrane currents was through regulation of the total intracellular Ca²⁺ content. This influence was subsumed under NCX (which existed in all models investigated).

Additionally, DADs in a full model are a transient phenomenon and subject to modulation by the full system of membrane currents (etc.), making analysis of the necessary requirements and mechanisms to produce DADs more complex. However, models reduced down to their Ca²⁺ subsystem were able to show sustained Ca²⁺ oscillations, and the required conditions for those oscillations in that subsystem could be more easily investigated in a systematic way. The subsystem could thereby be investigated more thoroughly, and the results obtained could be fed back into the whole cell models.

We applied the model reduction algorithm described in methods section to all models and found that all cell models that showed DADs also showed oscillations in the Ca²⁺ subsystem and vice versa (see Table 3). No incidences were found where a model produced DADs but did not show Ca²⁺ oscillations and vice versa. Therefore, the appearance of Ca²⁺ oscillations in the subsystem was concurrent with the appearance of DADs. Figure 4 shows the results of four models as examples, giving membrane potential and SR Ca²⁺ content for the full models showing DADs and SR Ca²⁺ content for the reduced models showing CaOSS. Note that DADs, as found in experiments, are in general a transient phenomenon, and their shape and the occurrence of DAD-triggered APs are dependent on the specific cell (model) and its physiological state.

Ca²⁺ Oscillations Occur Above a Threshold

To investigate the behavior of the cell models with increasing intracellular Ca²⁺ levels (Ca_Tot) we used the mathematical approach of “continuation of equilibria” used in bifurcation analysis (43). This approach enables tracking of the steady states of, e.g., Ca_SR concentrations in their dependence on changes in a parameter like Ca_Tot, without having to run the model to the steady state for each CaTot value; furthermore, more than one solution can exist for a specific parameter (see Fig. 5, D and E), which one would not pick up easily by just simulating from the model. We used the intracellular Na⁺ concentration to increase Ca_Tot via NCX. Note that this approach was only feasible using the reduced models as they showed sustained oscillations, whereas DADs in the full models were transient and did not occur via a bifurcation.

Fig. 5.

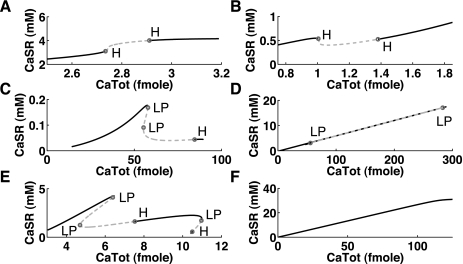
Occurrence of Ca²⁺ oscillations is dependent on total Ca²⁺ (Ca_Tot) in various mathematical models. Increasing Ca_Tot within the cell changes the Ca²⁺ level within the SR. Above a certain threshold of Ca_Tot, intracellular Ca²⁺ oscillations occur (regions indicated by dashed lines). Most often this is accompanied with a decrease in Ca_SR, but not always (e.g., in A). Note that this is not the cause but the result of the Ca²⁺ oscillations (see Fig. 3). There appear to be qualitative differences between the models (similar cases have been collated): the Matsuoka03 model showed a continuous increase in Ca_SR with increasing Ca_Tot (A); the Maleckar08 model (as well as the Shannon04 and Noble98 models) showed a slight decrease with the oscillations appearing in the notch (B); the Pandit01 model (as well athe s Iyer07 and Iribe06 models) showed a substantial decrease in Ca_SR and two limit points (LP), indicating that there was a range of Ca_Tot values with three solutions (C); the Fink08 model also showed two LPs and its Ca_SR content changed almost linearly with Ca_Tot (D); the Pasek08 model showed several LPs and also two phases of oscillations with a stable region between (E); and the default Noble models (without parameter changes) did not show oscillations even for the high levels of Ca²⁺ load (F). H, Hopf bifurcation.

The change from a stable equilibrium point to oscillations (where the equilibrium becomes unstable) occurred via supercritical Hopf bifurcations in all models. This means that when the systems switched from stable to unstable, the resulting oscillations had a finite frequency and an amplitude larger than zero.

Differences between models could be found based on the shapes of the resulting bifurcation diagrams, as shown in Fig. 5. In the Matsuoka03 model, the level within the SR was continuously increasing (Fig. 5A), whereas in all other models showing oscillations there was at least a slight decrease before the oscillations occurred. This decrease could be substantial (compare the Maleckar08 model in Fig. 5B with the Pandit01 model in Fig. 5C). The Fink08 model showed similarities to the Pandit01 model, but its Ca_SR level showed an almost linear dependence on Ca_Tot (compare Fig. 5, C with D). Note that the decrease in Ca_SR and the position or threshold for the instability was dependent on the parameter choices within the model (see sensitivities of the threshold below) and could therefore change due to different physiological or pathophysiological states of the cell.

For the Pandit01 and Fink08 models, Ca_Tot had to be rather high (>30 fmol) before CaOSS could be observed, but for the original Noble98 model (without parameter changes), no changes in stability were found up to 300 mM of intracellular Na⁺, i.e., Ca_Tot = 130 fmol (Fig. 5F). Note that a change in parameters (NCX denominator factor dNaCa = 5e⁻³ or SERCA uptake pump rate alphaUp = 4 mM/s) created a notch at around Ca_Tot = 1.7 fmol, associated with the appearance of oscillations (similar to Fig. 5B).

The basic Ca_Tot level in the 23 models was rather variable and ranged from 0.33 to 33.32 fmol (see Table 4). Additionally, in the Pandit01 model, the high cytosolic buffering capacity chelated 99% of Ca_Tot, whereas in the Shannon04 model, only 74% of Ca_Tot was buffered. This indicated that the absolute values in the models might not be very reliable for predicting the occurrence of CaOSS and DADs. Further analysis showed that similar considerations would also hold for the total free Ca²⁺ within the cell as given by the mathematical models.

Much better suited were the ratios between Ca_Tot threshold for observing CaOSS and the Ca_Tot (default) base level. These ranged from 0.57- to 3.14-fold, as shown in Table 4. The ratios were able to explain why it was easier to obtain DADs with only minor parameter changes in the models showing the lowest ratios (0.57–1.07). For the Noble98 and Maleckar09 models (ratio < 1.0), simply a change in pacing rate was sufficient to obtain DADs. We compare this with experimental results in the discussion. (The Noble98 model needed a change in parameters to actually initiate DADs.)

Sensitivities of the Threshold for Ca²⁺ Oscillations

The value for the threshold at which the oscillations started was very dependent on the specific parameter choices in the model and was expected to change due to the (patho)physiological situations investigated (e.g., β-adrenergic stimulus or congestive heart failure). To highlight the most important features/parameters of the Ca²⁺ subsystem with respect to the initiation of CaOSS (and thus DADs), we investigated the sensitivities of the threshold for oscillations (the first Hopf bifurcation point) with respect to conductances and maximum pump rates of the main components of the Ca²⁺ subsystem (see Table 4).

The threshold was most sensitive to changes in RyRs, SERCA, and the diffusion coefficient for Ca²⁺ between the dyadic subspace and the cytosol, with an overall prevalence toward SERCA in most models; there was no significant difference (<1%) regarding the sensitivities between changes in the conductance of RyR or its open probability in all models (not shown). All models indicated that an increase in SERCA or the diffusion rate would lead to an increase in threshold, and most models showed that an increase in RyRs would decrease the threshold, making the system more likely to show CaOSS and DADs [exceptions were the ten Tusscher06 (not shown) and Iribe06 models, but this might have been due to computational accuracies].

Most models showed no substantial changes in the threshold with respect to the Ca²⁺ buffer capacities (except for the Iribe06 model, where the threshold was most sensitive to the intracellular Ca²⁺ buffer) as well as to the exchange rate of NCX and Ca²⁺ transfer rate within the SR (not shown).

The overall range of sensitivities varied substantially: an increase in the SERCA pump rate by 1% in the Fink08 model would increase the (already very high) threshold by 15%, whereas the same change in the Pandit01 model would increase the threshold by only 0.062%. Considering this variability and the numerical stiffness of the problem, these numbers should be considered mainly qualitatively.

Relative Influence of Dyadic and SR Ca²⁺ on RyR Open Probability

We have shown before in the full and reduced models that the dependence of RyR gating on the dyadic subspace was necessary to initiate DADs, whereas the influence of Ca²⁺ in the SR acted as a modifier only in the mathematical models. However, this result did not reveal the relative influence of the two concentrations on the opening of the RyRs when both were present.

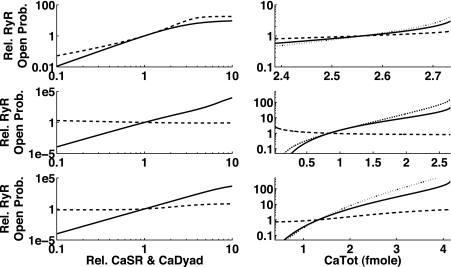
We used the steady-state RyR open probability as the metric for the models that included influences of both Ca²⁺ concentrations. A 10-fold increase or decrease in the default diastolic Ca²⁺ levels led to a 100- or 1,000-fold change in the steady-state open probability of the RyRs (see Fig. 6, left). Six of the seven models showed a higher sensitivity to changes in Ca_Dyad than in Ca_SR (except for the Matsuoka03 model for increasing concentrations). The Iribe06 model counterintuitively showed a decrease in open probability with an increase in Ca_SR.

Fig. 6.

Dependence of relative RyR open probability on relative changes of Ca_SR and Ca_Dyad as well as Ca_Tot. Left: changes in the Ca²⁺ contents of SR (dashed line) and dyadic subspace (solid line) change the open probability of RyRs (here shown as steady-state open probability). Right: model-predicted changes of open probability when Ca_Tot is changed (dotted line) and due to the respective underlying changes of Ca_SR (dashed) and Ca_Dyad (solid line). Top to bottom: Matsuoka03, Iribe06, and Iyer07 models (results for the Shannon04 and Fink08 models were similar to the Iyer07 model). Note that in the Matsuoka03 model the RyR open probability was more sensitive to increasing SR content than to dyadic subspace, whereas the Iribe06 model showed a decrease in RyR open probability with increasing Ca_SR content. The sensitivity in the Matsuoka03 model to the SR content was more than compensated by the more drastic change in Ca_Dyad concentration (top right), leading to an overall higher sensitivity to Ca_Dyad.

Furthermore, we used the information on Ca²⁺ concentration changes gained from the bifurcation analysis in the reduced models. A change in Ca_Tot in all models led to more substantial (relative) changes in Ca_Dyad than in Ca_SR, and thus the opening of RyRs was in all cases influenced more by Ca_Dyad than by Ca_SR (see Fig. 6, right).

Relative Influence of Dyadic and SR Ca²⁺ on the Appearance of DADs in the Full Models

To supplement the systematic findings on the Ca²⁺ subsystem with simulations on whole cells, different ways for inducing DADs were tested in the models that included dyadic and SR modulation of RyR opening. Several instances of Ca²⁺ release from the SR were found under various conditions, from which three representative examples were selected. When the influence of dyadic or SR Ca²⁺ content on the gating of the RyR was reduced, the effect on the appearance of DADs was more dramatic for changes in the sensitivity to dyadic Ca²⁺, confirming our previous results on the Ca²⁺ subsystem (see top and middle top rows in Fig. 7). When including the driving force for RyR-release current due to the concentration gradient (Ca_SR-Ca_Dyad) into consideration, the results were model dependent but more balanced (see middle bottom and bottom rows in Fig. 7).

Ca²⁺ Oscillations and Reduction of NCX

Block of NCX has been shown to be antiarrhythmic (58, 84), as it appears to be the main transducer of intracellular Ca²⁺ oscillations and release from the SR to membrane potential. To see if block of NCX would also inhibit Ca²⁺ oscillations per se in the reduced models, we ran simulations in COR as well as two-dimensional bifurcation analysis (continuation of Hopf points), changing the maximum exchange rate of NCX and Ca_Tot (by changing intracellular Na⁺).

There were only a few models that showed oscillations with NCX = 0 (see Table 3). For all other models, NCX was necessary to obtain CaOSS. Note that the necessity of NCX was also dependent on the model parameter values, e.g., Noble98 (with 10 × SERCA) and Matsuoka03 (with 5 × SERCA) models also showed oscillations without NCX.

Thus, NCX block removed or limited translation of Ca²⁺ oscillations to the membrane potential but did not necessarily diminish intracellular Ca²⁺ oscillations.

DISCUSSION

Ca²⁺ oscillations have been found in many different cell types, such as Purkinje cells, sinoatrial node cells, atrial cells, ventricular cells, pancreatic β-cells, astrocytes, and others (see references in the Introduction). The general mechanism (besides stretch) has been assumed to be based on an intracellular Ca²⁺ storage (endoplasmic reticulum) rapidly unloading its content into the cytosolic space, while reuptake has shown a much longer time constant, making the system prone to self-sustained intracellular Ca²⁺ oscillations.

Despite the large number of experimental results, and the range of mathematical models available, only a limited number of modeling studies have been conducted to reproduce DADs based on biophysical mechanisms (24, 34, 64, 81). Using 37 mathematical models of atrial, Purkinje, and ventricular cells of various species, we found that 23 of them could be used to reproduce DADs (see Table 3). Only direct/multiplicative coupling of RyR opening with the opening of I_CaL prevented some models from being able to simulate DADs. This was reasonable as Ca²⁺ release gets initiated at the resting potential when I_CaL is closed. If this was prevented (in the model), no DADs could occur.

Ca_SR Modulates the Appearance and Determines the Amplitude of DADs; the Mechanism for DADs Is Closely Related to Ca²⁺-Induced Ca²⁺ Release

The main hypothesis for the underlying mechanism of DADs to date has been that due to “Ca²⁺ overload of the SR” (above a specific threshold) a release event would occur (74). Mathematical models (Shannon04 and Iyer07) have been used in the past to confirm the principal plausibility of this hypothesis (34, 81), but alternative mechanisms were not quantitatively assessed. Our results show that both of these models can be used to reproduce DADs in the absence of a dependence of the RyR open probability on Ca_SR levels (see Table 3 and Fig. 3), indicating that this mechanism would not be essential for the initiation of DADs from a theoretical, structural point of view. However, the sensitivity results (and also the literature) point out that Ca_SR levels have a substantial influence on the actual appearance of DADs. The same was seen using all the other models that included the modulation of RyR by Ca_SR.

Note that all models stopped producing DADs when the dependence of RyR opening on the Ca²⁺ concentration in the dyadic subspace was removed (cf. Fig. 3D). This suggests that all mathematical models of Ca²⁺-induced DADs share a common triggering pathway that involves Ca²⁺-induced Ca²⁺ release (CICR), i.e., the modulation of RyR open probability by Ca²⁺ in the dyadic subspace. The loading of the SR plays a role more in determining the magnitude of Ca²⁺ release and hence the amplitude of the DAD and whether it can trigger an AP.

The Appearance of DADs Is Most Sensitive to SERCA, RyRs, and Ca²⁺ Diffusion: Possible Pharmaceutical Targets

The main influence on the threshold for intracellular Ca²⁺ at which DADs appear was given by the sensitivities shown in Table 4. As main components, we identified SERCA, RyRs, and the diffusion of Ca²⁺ from the dyadic subspace to the cytosol. The latter indicated the importance of obtaining good estimates for the diffusion coefficient as the Ca²⁺ subsystem was very sensitive to this parameter. As expected, an increase in RyRs in general made the system more likely to produce DADs (c.f. Table 4). That an increase in SERCA would be beneficial was counterintuitive when thinking only of Ca²⁺ overload of the SR as the trigger for DADs, but based on our modeling results, it would be a good measure to reduce the amount of Ca²⁺ in the dyadic subspace. (We will discuss the experimental evidence for this hypothesis later in this section.)

Even though the proposed scheme for the underlying mechanisms of DADs included only components of the Ca²⁺ subsystem (see Fig. 8), obviously every interaction and thus change in the cell had an effect on the appearance of DADs due to the feedback loops via membrane potential, Ca²⁺, and ion currents (cf. Fig. 2C). That these interactions could have clinical consequences had been shown in a patient with Andersen syndrome, where reduction of the K⁺ current Kir2.1 contributed to the development of DADs (60).

Fig. 8.

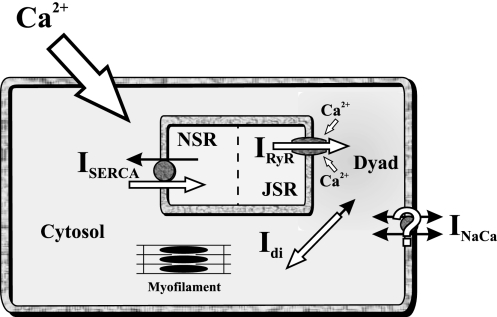
Schematic of the underlying mechanism of DADs. An increase in Ca_Tot within the cell increases the level of Ca²⁺ within each compartment. The increase in the dyadic subspace leads to a higher open probability of RyRs, increasing the spark rate, which, at some point, initiates a concerted opening of RyRs throughout the cell (a release). (As shown in Fig. 3, the modulation by Ca_SR content is influential but not essential.) The intracellular (Ca²⁺ subsystem) oscillations are maintained by the fast and slow time constants of diffusion, uptake, and release; in some models, NCX is necessary for the oscillations, but parameter changes in the model can make it redundant. The intracellular Ca²⁺ oscillations are then translated either via NCX, the Ca²⁺-activated Cl⁻ channel, or nonspecific Ca²⁺-activated current to changes in voltage, which can eventually trigger a complete AP (see Fig. 1). I_SERCA, SERCA current; NSR and JSR, network and junctional SR; I_di, diffusion current; I_NaCa, Na⁺/Ca²⁺ exchange current.

Changes in RyR Opening Probability and Appearance of DADs Are More Influenced by Changes in Ca²⁺ Levels of the Dyadic Subspace Than the SR

We investigated the relative influence of Ca²⁺ concentrations in the dyadic subspace and the SR on the steady-state open probability of the RyR in the mathematical models that included both concentrations as modulators of RyR gating. Only the Matsuoka03 model showed a higher sensitivity to Ca_SR, which could be due to the lack of a dyadic compartment in the model, such that cytosolic Ca²⁺ is used to determine RyR gating (see Fig. 6).

When the actual change of Ca²⁺ levels during Ca²⁺ overload was included into consideration, all models showed a more drastic change in RyR open probability due to changes in Ca_Dyad than due to Ca_SR (Fig. 6), indicating that the main trigger mechanism underlying the appearance of DADs is the same as for CICR, i.e., modulation of the opening of RyRs by Ca²⁺ in the dyadic subspace. Note that a change in Ca_Tot in the cell led to a larger relative change in Ca_Dyad than in Ca_SR.

In five examples of DADs in whole cells, we also investigated the sensitivity of DAD appearance to the two Ca²⁺ pools and found that when only the sensitivity of the gating was changed that the results were equivalent to the results above, indicating that also in whole cell simulations the trigger mechanism is similar to Ca²⁺-induced Ca²⁺ release (Fig. 7). When including the driving force, the results were inconclusive, as different models conveyed different messages; in these simulations, there was no precedence for dyadic or SR Ca²⁺ (Fig. 7).

Underlying Mechanism of DADs

From the in silico experiments performed (Figs. 3, 6, and 7 and Table 4), we concluded that RyRs, SERCA, and Ca²⁺ diffusion within the cell are the main determinants of the triggering of DADs. The trigger mechanism appears to be similar to CICR. The levels of Ca_SR modulate the appearance and determine the amount of release and amplitude of the DAD. Our results also indicate that stretch-induced changes leading to an increased open probability of RyRs could readily initiate DADs as well.

The results instigated the following schematic for the underlying mechanism of Ca²⁺-induced DADs (see Fig. 8):

• Increased (free and total) Ca²⁺ load of the cell leads to

• An increased Ca²⁺ level in the dyadic subspace close to RyRs (and all other Ca²⁺ pools)

• Which increases the open probability of RyRs.

• Thereby, RyRs are more sensitive to stochastic release events from neighboring Ca²⁺-release units (this can be amplified by increased SR load or stretch)

• Which finally leads to Ca²⁺ release accompanied by an intracellular Ca²⁺ wave.

• The amplitude of the release depends on Ca_SR.

  The current cell models do not include enough of the three-dimensional structure of the cell to replicate the Ca²⁺ wave, but they replicate the cellular scale results very well. Even more detailed/mechanistic Ca²⁺ models, such as Hinch et al. (2004) and Williams et al. (2007), would not be able to reproduce this phenomenon in more detail, as they lack the three-dimensional interactions between neighboring Ca²⁺-release units.

Relation of Our Findings to Previous Experimental Results on DAD Induction

The models that reproduce DADs (Table 4) have done so under the various experimental protocols used to elicit DADs. All experimental protocols found in the literature (see Table 1) either increased the Ca²⁺ load of the cell or increased the open probability of RyRs via drug interactions with RyRs. We showed examples for Na⁺ overload (Fig. 1), increased I_CaL (Fig. 2A), increased RyR open probability (Fig. 2B), and hypokalemia with Na⁺ channel inactivation block (Fig. 2C). The last example also agreed with previous experimental findings (98) showing afterdepolarizations during an AP that are caused by release from the SR. (This highlights the fact that the notion of EADs and DADs is only related to the timing and not the underlying mechanism of afterdepolarizations.)

Furthermore, the results on the mechanism of DADs are supported by experimental findings that showed that “a more loaded SR is not the only prerequisite for the generation of [aftercontractions] since they can be present or absent when the SR Ca²⁺ content is similar” (93). Davia et al. (12) have shown that SERCA overexpression reduced the incidence of aftercontractions, which was concurrent with the model results and our hypothesis. Pogwidz and Bers (74) also suggested that a combined increase in SERCA and the inward rectifying K⁺ current in congestive heart failure would reduce DADs but maintain or enhance contractility (which would be counterintuitive if Ca_SR overload is the main determinant of the appearance of DADs).

Laurita and Katra (44) also showed that cells in the endocardium have higher diastolic Ca²⁺ levels under Ca²⁺ overload, which correlates with the frequently observed onset of DADs from the endocardium.

The models suggest that the level of Ca_Tot necessary for the induction of DADs is close to the normal Ca²⁺ content of the cells (1- to 3-fold). In some models, a train of fast pacing that gets interrupted is sufficient to induce DADs. Experimental results have suggested that this might be possible in isolated Purkinje fibers (46), but to our knowledge thus far ventricular cells have only been shown to show DADs with rapid pacing under conditions in which, for example, BayK 8644 and isoproterenol help increase Ca²⁺ (106).

Changes in Total Intracellular Ca²⁺ Levels Are Necessary to Induce DADs

Even though the absolute values of total intracellular Ca²⁺ showed high variability, the necessary relative changes to baseline were in the range of 0.6- to 3.6-fold.

We found that for models with a ratio smaller than unity only slight interferences (like changes in pacing frequency) were necessary to obtain DADs (e.g., Noble98 and Maleckar09 models). The Ca²⁺ level in these cell models was already high enough under the default physiological conditions to be able to induce DADs, even though during normal pacing no Ca²⁺ release from the SR or DADs were observable. For models with a ratio slightly higher than unity, minor changes, e.g., increasing I_CaL conductance, were sufficient to induce DADs (e.g., Shannon04, Matsuoka03, and Noble98 models).

Transduction of the Ca²⁺ Signal to the Membrane Potential: Role of NCX

The transduction of intracellular Ca²⁺ cycling (or a release event of Ca²⁺ from the SR) to the membrane voltage might be beneficial [as suggested for the sinoatrial node by, e.g., Kim et al. (42)] or arrhythmogenic, as in the case of DADs in Purkinje and ventricular cells (74). Experimental results have shown that at least two membrane proteins could provide a transient inward current that depolarizes the membrane potential due to released Ca²⁺: NCX and Ca²⁺-activated Cl⁻ current. The relative contribution of these two proteins seems to be species dependent, as Ca²⁺-activated Cl⁻ current has been found in rabbits and dogs but not humans (94). However, Schlotthauer and Bers (80) found only a negligible effect when Ca²⁺-activated Cl⁻ current was blocked in the rabbit. We therefore investigated whether partial block of NCX would abolish intracellular Ca²⁺ cycling. The modeling results shown in Table 3 demonstrate that 5 of the 23 models that showed intracellular Ca²⁺ oscillations did so even without the presence of NCX in the reduced model. We also found suitable parameter changes for some of the other models so that they showed oscillations with NCX = 0 as well (not shown). This indicated that the ability of NCX block to stop intracellular oscillations was very much dependent on the (patho)physiological state of the cell and that the main effect would be the block of signal transduction to the membrane potential.

Conclusions

Our modeling study supports a new hypothesis about the initiation of DADs. Even though the influence of SR content is an important regulator of the Ca²⁺ subsystem (and thus influences DADs), it is not essential for the induction of DADs except in the sense that, if the SR Ca²⁺ level is too low, no release can occur. Our results show that both dyadic and SR Ca²⁺ influence the appearance of DADs (with often higher sensitivity to dyadic Ca²⁺) in addition to changes in Ca²⁺ diffusion within the cell and Ca²⁺ uptake into the SR via the SERCA pump. The relative contribution to the appearance of DADs is different in different mathematical models (the sensitivity to the SERCA pump rate was higher than to changes in RyR opening probability for a number of models) and is dependent on species and pathological state of the heart.

Two properties of the RyR models were found that could not be removed without losing the ability of the model to simulate DADs: 1) RyRs had to be able to open when I_CaL was closed and 2) influence of Ca_Dyad on RyR opening dynamics.

Our modeling results suggest that the underlying mechanism of DADs is that the elevated Ca²⁺ levels in the dyadic subspace and cytosol increase the open probabilities of RyRs, leading to Ca²⁺ release from the SR and thus to DADs. In other words, the DAD mechanism is similar to that for normal excitation-contraction coupling. That mechanism is usually expressed by saying that Ca_Dyad is the trigger while the amount of Ca²⁺ stored in the SR determines the amplitude of the response. In both cases, the mechanism is multifactorial, so that referring to a single cause is misleading. It would be better to think in terms of a multidimensional space within which there are areas that satisfy all the conditions for release to occur. This new hypothesis conforms with and can explain experimental results on SERCA overexpression and the occurrence of DADs in heart failure with a decreased Ca_SR content.

GRANTS

The work in Oxford, UK, was supported by British Health Foundation Grant PG/08/019, European Union FP7 preDiCT Grant ICT-2007-2-224381, and euHeart Grant ICT-2007-224495.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).