Free energy considerations for nucleic acids with dangling ends near a surface: a coarse grained approach

Abstract

A coarse grain model for the thermodynamics of nucleic acid hybridization near surfaces has been extended and parameterized to consider unpaired dangling end contributions. The parameters of the model differ when representing a double stranded DNA section, or a single stranded DNA section. The thermodynamic effects of the possibility of different dangling end combinations were considered in the presence of different types of surfaces. Configurational sampling was achieved by Metropolis Monte Carlo. To have a more complete picture of the free energy changes, an estimation of the conformational entropy was included. We find a strong thermodynamic effect for dangling mismatches due to sequence requirements when they are nearer the surface as opposed to being held away from the surface.

1. Introduction

Concomitant with the tremendous improvements in DNA detection seen in recent years, a wide variety of technologies have been developed. Many of these technologies involve nucleic acids near a surface or support, either tethered or adsorbed. Experimentally DNA’s thermodynamic behavior in this condition is increasingly well characterized [1, 2, 3, 4] but our theoretical understanding is more limited.[5] Recent computational works [6, 7] have modeled DNA as a self avoiding walk in a cubic lattice with specific interactions for hybridizing base pairs, or with a DNA-hard surface interaction but few other energy considerations are made. Some all-atom simulations have been performed [8, 9, 10, 11, 12], but the computational cost is still quite high to run them for every different possible set of conditions (sequence, salt concentration, type of surface, temperature, etc.) required for design. However, simulations contain a wealth of detail and specific cases show significantly different behaviors.

Phenomenological thermodynamic models have proven accurate when predicting the hybridization free energy of two single stranded DNA(ssDNA) molecules coming together to form a double stranded DNA (dsDNA) complex in bulk solution [13]. However, it is well known that hybridization thermodynamics is modified when it happens near a surface [10, 5]. The model presented in this paper improves quantitative corrections to the thermodynamics of DNA pairing near surfaces to yield more accurate free energy predictions when the system is not perfectly paired in length and/or sequence.

In an effort to capture the physics of nucleic acids near a surface, we recently developed an coarse grain model for perfectly matched DNA systems of arbitrary length [14] as an extension to our earlier studies [15, 16, 17]. However, in typical applications the solution targets and surface mounted probe molecules are rarely, if ever, of equal size and in perfect base pairing match. In this paper we expand the scope of this class of models by considering cases that might have sections of dsDNA, as well as ssDNA simultaneously, resulting from less than perfect matches in length and sequence. This allows us to study the effect that possible dangling or overhanging ends (ssDNA sections tethered to an dsDNA main body) might have on the thermodynamic and structural behavior of the molecule and the subsequent detection. We note such overhangs could happen on either strand, tethered probe or target, either proximal to or away from the surface. We also expanded the scope of our thermodynamic modeling by calculating the entropy of the strands to complete a picture of the free energy.

2. Model

We start with a recently introduced a coarse grained model[14] for the thermodynamics of arbitrary lengths of isolated single strand DNA or perfectly paired DNA immersed in an ionic aqueous solution and tethered to a surface. The model successfully reproduced some experimental data under certain conditions [1, 2, 3, 4] and theoretical simulation trends [8, 9, 10, 11, 12], such as the end to end distance and the tilt angle. The magnitude of the surface effects vary widely depending on the ionic strength of the liquid, the surface concentration of DNA molecules tethered to the surface, the surface conditions (dielectric, conductor, charged, etc.) and the temperature. [15, 16, 17]

The model consists of a discrete worm-like chain of spheres including mean field electrostatic potentials and surface polarization fields. The spheres have different properties to represent ssDNA, dsDNA and, for an idealized linker, polyethylene (table 1). The radius of each sphere was fixed according to the polymer’s radius, fixing also for DNA the number of base pairs, the charge, and the mass. The persistence length for a linearly elastic model was taken from empirical models developed experimentally [18, 19, 20, 21, 22, 23].

Table 1.

	dsDNA	ssDNA	Polyethylene
Charge	12 e−	6 e−	0
Mass	4048 g/mol	506 g/mol	50 g/mol
Radius	1 nm	0.5 nm	0.134 nm
Presistence Length	$50+\frac{0.03797}{I}nm$	$1.481+\frac{0.0324}{I}nm$	0.76 nm

In this paper, we expand the scope of the original model by considering polymers with ssDNA and dsDNA sections. The DNA system may branch from a dsDNA section to one or two ssDNA sections when length mismatches occur or base pairing would be disallowed by sequence. This allows us to study dangling ends in all forms and combinations. To take into account the possible range of flexibility we calculate the conformational entropy changes as well.

Since the main goal of this paper is to understand the effects of different dangling ends, we isolated each molecule from any other possible neighboring molecule, only considering the intramolecular energy (bending and dangling ends) and the interaction with the surface and solution. Given typical experimental surface densities in the range of 10¹²probes/cm² this is a reasonable idealization although it does not allow for surface density fluctuations. The effective free energy conformational function without polymer entropy considerations is given by:

$$E_{\mathit{Total}}=E_{\mathit{Bending}}+E_{\mathit{Surface}}+E_{\mathit{DanglingEnds}}$$ (1)

The energy required to bend a segment of length L through an angle θ is given by [20, 24]:

$$E_{\mathit{Bending}}=\frac{k_{B}TP}{2L}{\theta }^2$$ (2)

Where k_B is the Boltzmann constant, T is the absolute temperature and P is the persistence length given in table 1 as a function of I, the ionic strength of the liquid [18]. When the biopolymer branches, each branch contributes independently to the bending energy.

The electrostatics of the model here is governed by the Poisson-Boltzmann equation [25, 26]. If we consider the spheres over the surface to be ion-penetrable, an analytic solution exists for our geometry [27, 28, 15]. The surface imposes an electrostatic boundary condition that can be taken into account simply by using the well known method of images [15, 14]. The free energy contribution including the solvation enthalpy and entropy changes will be different depending on the type of surface, conductor (C) or dielectric (D). Each strand contribution is given by:

$$E_{\mathit{Surface}}^C=-\sum _j\frac{{\alpha }_j}{\epsilon {\epsilon }_{0}k}\left[\frac{V\epsilon {\epsilon }_{0}k}{2}{e}^{-k{z}_j}+\sum _i\frac{k{\alpha }_i}{8\pi l_{i,j}}{e}^{-k{l}_{i,j}}\right]$$ (3)

$$E_{\mathit{Surface}}^D=-\sum _j\frac{{\alpha }_j}{\epsilon {\epsilon }_{0}k}\left[\sigma e^{-k{z}_j}-\sum _i\frac{k{\alpha }_i}{8\pi l_{i,j}}{e}^{-k{l}_{i,j}}\right]$$ (4)

Where j runs over all spheres, z_j is the distance between the center of the j^th sphere and the surface, l_i is the distance between the center of the j^th sphere and the i^th image sphere (i runs over all image spheres), ε is the relative permittivity of the solvent (water at 25 C in this case), ε₀ is the electric permittivity of the free space. V and σ are the electric potential and the surface charge density that the plane may have. k⁻¹ is the Debye-Hückel screening length given by:

$$k^2=\frac{2I{q}^2}{\epsilon {\epsilon }_0{k}_{B}T}$$

where q is the basic charge. I, the ionic strength, is simply the ion (salt) concentration C for monovalent ions such as the widely used NaCl or KCl. The constant α depends on the charge of the sphere Q, and is given by:

$$\alpha =\frac{\mathit{Qsinh}\left(k{r}_0\right)}{k{r}_0}$$

The dangling end contribution is the electrostatic interaction between dangling end segments on the same molecule. That interaction with surface is accounted for above. This effect is calculated using the same mean field PB electrostatics.

$$E_{\mathit{DanglingEnds}}=\frac{{\alpha }^2}{8\pi \epsilon {\epsilon }_0}\sum _{i,j\ne i}\frac{e^{-k{l}_{i,j}}}{l_{i,j}}$$

where the indices run over all spheres in the dangling ends. We do not consider electrostatic interactions within the same dangling end, because they are already considered in the contribution to the bending energy.

The main goal of this paper is to understand the dependence of the surface induced thermodynamics given the configurations of overhanging parts of the sequence. We have constructed the possible permutations and labeled the different structures with capital letters from A to O. For the purpose of examining the extent of the effects we consider an 18 base pair dsDNA section as the central “helical” structure. A dangling end on the attached probe strand between the surface and the dsDNA segment is often just aspacer but may be sequence relevant by pairings with certain target strands. Structures A, G, M, N and O are the central structure, plus a spacer of 0, 3, 6, 9 or 12 base pairs respectively. Structures A to F are all the possible combinations of 3 base pair overhangs on either end having no spacer, and G to L the same for a 3 base pair spacer. All probe strands are tethered to the surface by 0:536nm (2 spheres) of polyethylene. Figure 1 illustrates the structures considered and the correspondence to an example atomic representation.

Figure 1.

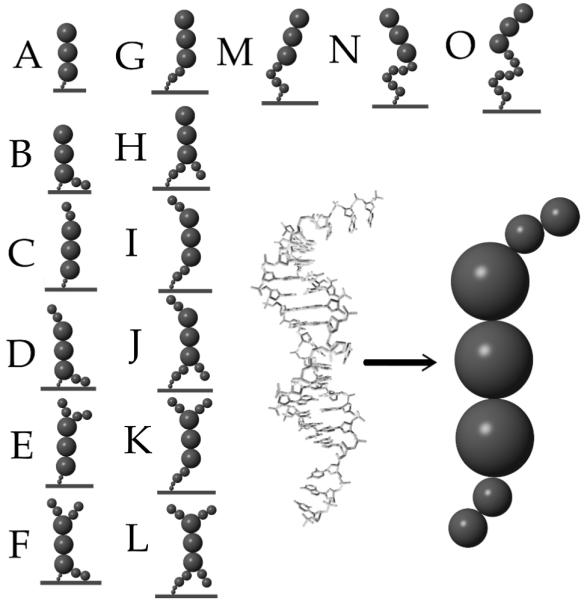
Different permutations of nucleic acids structures with ssDNA overhangs near a surface. The correspondence between a detailed model and our coarse grained representation is shown at the right for one case.

3. Method

For each simulation, we ran 10 million steps Metropolis Monte Carlo to sample the configurations. A step often called a pass is counted when on average, every sphere has had the option to move; the moves are done by the well-known “kink jump” [29] algorithm. We accumulated measurements every 25 steps.

To complete the thermodynamic picture of the system, it is necessary to measure the entropy; to do so we have tested two different methods: the quasi-harmonic approximation (QH) [30, 31, 32, 33, 34, 35, 36, 37, 38, 39] and hypothetical scan (HS) Monte Carlo [40, 41, 42, 43, 44, 45, 46, 47, 48, 49].

3.1. Quasi-Harmonic Approximation

An effective harmonic potential is assumed for each degree of freedom. The appropriate probability distribution is a normalized multivariate Gaussian [31],

$$P\left(\mathrm{q}\right)=\frac{1}{{\left(2\pi \right)}^{n∕2}{\sigma }^{1∕2}}\mathit{exp}\left[-\frac{1}{2}(\mathrm{q}-\langle \mathrm{q}\rangle )•{\sigma }^{-1}•(\mathrm{q}-\langle \mathrm{q}\rangle )\right]$$

q is a 3N long vector that contains all the mass weight Cartesian coordinates of all N particles. The covariance is given by:

$${\sigma }_{ij}=\langle (q_i-\langle q_i\rangle )(q_j-\langle q_j\rangle )\rangle$$

The conformational entropy can now be calculated by simply diagonalizing σ, and using the analytical solution for a harmonic oscillator.

$$S=\frac{1}{2}n{k}_B+\frac{1}{2}{k}_{B}ln\left[{\left(2\pi \right)}^n\sigma \right]$$

Where n is the number of degrees of freedom. To calculate the covariance, a reference structure is chosen (usually the minimum energy). Every structure used as a measurement has to be rigidly moved to have the same center of mass and then least squares rotated [50, 51, 52].

3.2. Hypothetical Scan Monte Carlo

The hypothetical scan method [41, 42, 43, 44, 45, 46, 47, 48] is based on the concepts proposed by Rosenbluth and Rosenbluth [40]. They calculated average extensions of random walks in a two dimensional square lattice by so called construction probabilities subsequently using them as sampling probabilities. For the hypothetical scan (HS), a subset of structures is taken from the Monte Carlo sampling and each one is hypothetically reconstructed to calculate its construction probability. The probabilities are normalized and the definition for entropy is then used.

$$S^B=-k_B\frac{1}{n}\sum _{i=1}^{n}ln{P}_i$$

where n is the total number of samples considered. S^B can be proved to be a lower limit for the entropy. We can also use importance sampling [49] to get an upper limit S^A [42, 43].

$$S^A=-k_B\sum _{i=1}^n{P}_{i}ln{P}_i$$

In our case, the construction probabilities are generated by starting with one of the spheres and adding new spheres one by one. Every time we add a new sphere k we calculate the transition probability for it. The construction probability is simply the product of the transition probabilities in the structure.

$$P_i=\prod _{k=2}^{N}pk$$

The transition probabilities are basically the probability of choosing a new sphere location from the set of possibilities. In a lattice you have a finite number of options for the new bead, but in a continuous model like ours, a discretization is required. The number of options O is chosen, and a probability assigned to each of them according to their Boltzmann weight.

$$p_k=\frac{\mathit{exp}(-E_{\nu =1}∕k_{B}T)}{\sum _{\nu }\mathit{exp}(-E_{\nu }∕k_{B}T)}$$

Where ν is the direction of the next sphere, and runs over all O. We are arbitrarily taking ν = 1 as the direction of the next sphere in the actual structure. The accuracy of the method can be improved by hypothetically constructing b spheres, instead of just one.

$$\begin{array}{cc}\hfill p_k& =\frac{M_k^{\nu =1}\left(b\right)}{\sum _{\nu }{M}_k^{\nu }\left(b\right)}\hfill \\ \hfill M_k^{\nu }\left(b\right)& =\sum _{l\left(\nu \right)}\mathit{exp}\left(\frac{-E_{l\left(\nu \right)}}{k_{B}T}\right)\hfill \end{array}$$

Now the total number of options Ω = O^b, and l(ν) is the subset of Ω whose hypothetical first sphere has the direction ν. A fine tuning of b and O is required for the success of the method. If Ω is too small, the energy landscape will not be correctly captured, and if Ω is too large, the method becomes computationally intractable. Another parameter that has an impact in the balance between accuracy and computational economy of the method is the number of molecules reconstructed, n.

3.3. Comparing QH and HS

We compared both methods to calculate the conformational entropy of two structures, A and C. We know that if the evolving structure changes its conformation drastically, the QH approximation can fail to capture the landscape without care to consider multiple basins[34]. We also note that the dsDNA section is quite rigid and this prevents extreme cases. However, the persistence length for the single stranded sections is significantly less although not quite in the freely jointed chain limit. We note that the HS easily obtains the freely jointed chain limit and clearly the QH method trivially obtains the stiff spring constant limit.

For the HS method, we tuned Ω and n to have S^A and S^B converge. The number of optional directions O in a solid angle was 800 and the number of spheres considered in each transition b = 2; hence Ω = 640000. n was set at 2,000.

Figure 2 shows a comparison between both methods where we use the inverse Debye length to vary the effective spring constants. Although there is not a significant difference in the accuracy of them (never differing by more than 0.5%), the computational time required for the HS method is two orders of magnitude larger than for the QH analysis. The error bars on the HS data points are significant. We find that we are far enough away from the freely jointed chain limit to avoid the computations inherent to the HS method. Thus, in the rest of the paper we only report the entropy calculated by the QH approximation.

Figure 2.

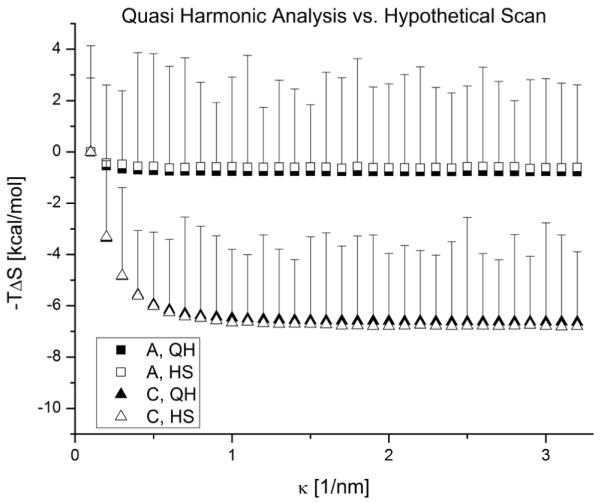
Comparing the quasi harmonic and hypothetical scan Monte Carlo methods to calculate the conformational entropy for structures A and C. Error bars are the statistical error in the HS method.

4. Results and Discussion

We ran the described simulations for each structure (A to O) both in bulk solution and tethered to a surface either conductor or dielectric. The salt concentration varies according to $k\propto \sqrt{C}$, from κ = 0.1 (0.001 M) to kappa = 3.2 (0.945 M). We used steps of 0.1nm⁻¹.

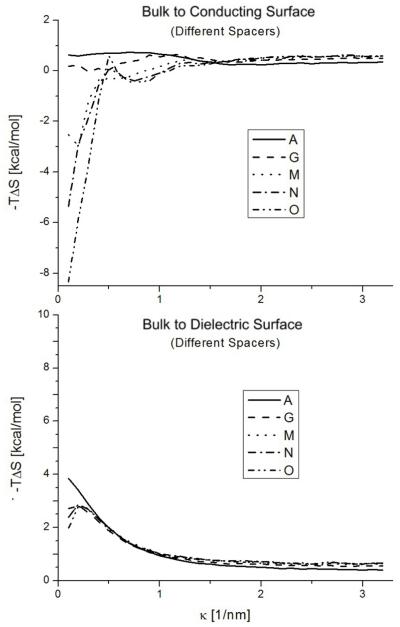
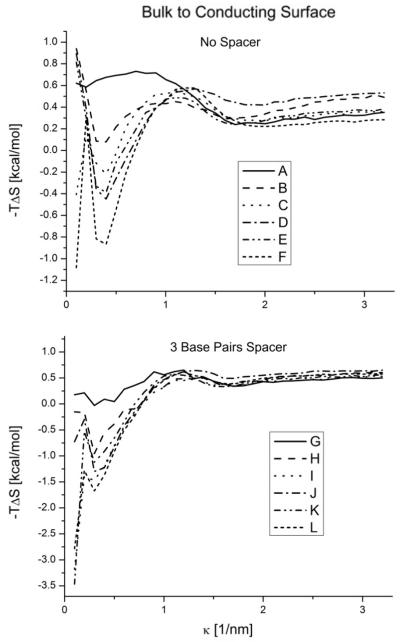
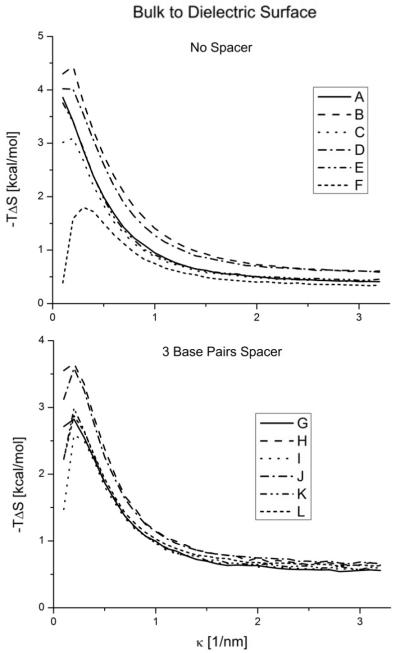
In figure 3 we show the conformational entropic part of the free energy change (−T△S) for the basic structure (18 base pairs of dsDNA) with different spacers, tethered to a conducting and a dielectric surface. Recall that the solvation entropic contributions are already approximately included in the PB treatment. In figures 4 and 5 we show all possible dangling end combinations with either no spacer or a 3 bp spacer for the same two types of surface. All dangling ends are also 3 bp long.

Figure 3.

Conformational entropy free energy contribution of the molecules in the bulk versus the molecules tethered to a conductor or a dielectric surface as a function of κ. Structures with different base pair spacers: A (0), G (3 bp), M (6 bp), N (9 bp) and O (12 bp).

Figure 4.

Conformational entropy free energy contribution of the molecules in the bulk versus the molecules tethered to a conductor surface as a function of κ. Different structures with no spacer on the top and with a three base pair spacer on the bottom. Notice different scales on the plots.

Figure 5.

Conformational entropy free energy contribution of the molecules in the bulk versus the molecules tethered to a dielectric surface as a function of κ. Different structures with no spacer on the top and with a three base pair spacer on the bottom.

For large κ the entropic changes decrease and plateau. This phenomena is expected because the electrostatic interactions are screened. However, the entropic changes never go to zero because of the surface volume exclusion. This effect ranges from ~ 0.5 to ~ 1kcal/mol depending on the structure.

For low k the electrostatic interactions are stronger. In this regime, we clearly see the effects of the two opposing phenomena that can happen. The surface interactions can constrain the movement of the DNA molecule, reducing its configurational space, and ultimately its entropy. On the other hand, the surface interactions can just disturb the configurational space (possibilities) without any external influence and increase its fluctuations to increase the entropy. In figure 3 we can see how in general, the conducting surface tends to increase the configurational entropy of the system, diminishing the free energy, and the dielectric surface tends to increase the free energy. However, both phenomena are present in both surface cases. They are responsible for the non-monotonic behavior observed. This non-monotonic salt behavior is more drastic when the spacer is shorter. Different dangling end configurations also show notably different behaviors (figs 4 and 5).

The competition between both surface phenomena is also responsible for the different effects a longer spacer has depending on the surface. As we can see in fig. 3, for a conducting surface, the entropic energy changes are considerably stronger as the spacer is longer. However, for the dielectric case, the surface effect is slightly reduced for longer spacers. Nonetheless, in both cases the configurational entropic part of the free energy decreases for larger spacers.

A central result of our simulation was the change in free energy and its components (configurational entropy and the rest) for the DNA molecule near a surface versus in the bulk electrolyte. We report the total intramolecular effetive (free) energy instead of bending and dangling ends energy separately because the dangling end contribution is never larger than 1% of the bending energy.

$$E_{\mathit{Intra}}=E_{\mathit{Bending}}+E_{\mathit{DanglingEnds}}$$

Figure 6 shows energy differences for all structures, using a conducting surface. The plot on the left has a salt concentration of 0.156 M (close to physiological), and the one on the right of 0.945 M (high end for C). Figure 7 is equivalent to figure 6, but for a dielectric surface.

Figure 6.

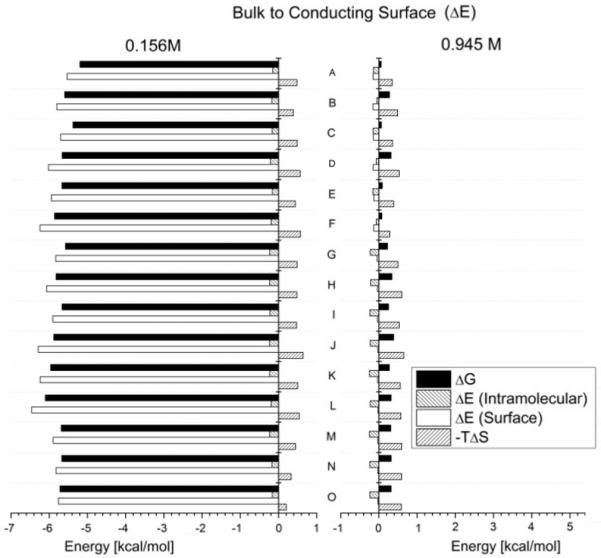
Free energy differences of the molecules in the bulk solution with the molecules tethered to a conducting surface. Structures A to O. C = 0.156 M on the left and C = 0.945 M on the right.

Figure 7.

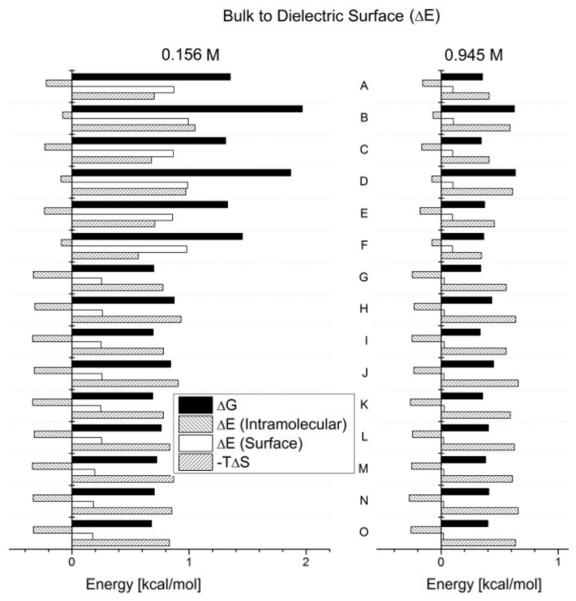
Free Energy differences of the molecules in the bulk solution with the molecules tethered to a dielectric surface. Structures A to O. C = 0.156 M on the left and C = 0.945 M on the right.

In both figures we see how different structures (A to O) show a distinct behavior. In the left plot of figure 6, we see the surface effects are particularly strong and almost completely dominated by the electrostatic interactions, as expected for a conducting surface, and a weakly screening electrolyte. When comparing both plots of figure 6, we notice that for a higher salt concentration, the electrostatic contributions have drastically diminished and the systems are now dominated by the configurational entropic contributions. The same can be said for a dielectric surface (figure 7). Nonetheless, for this type of surface the interaction is repulsive, pushing the molecule away from it, diminishing the electrostatic contribution. So, although electrostatic interactions are stronger for low salt concentrations, contrary to what happens near a conducting surface, the configurational entropic contributions are never negligible for DNA of sufficient length near a dielectric surface. In addition, the double layer causedby counterion condensation, even at low concentrations, is significant in contributing to the thermodynamics and of course duplex stability for the system.

Another result worth noting is that structures B,D,F,H,J and L show a rather strong change in free energy when compared to structures otherwise similar to them. These are the structures which have a dangling forced to be in proximity to the surface. The effect this has on the free energy is especially notable for a dielectric surface such as glass. We will explore this phenomena more deeply in our subsequent work which will consider trends in large micro array data sets.

5. Conclusions

In this paper a recently derived coarse grain model for nucleic acid surface hybridization was extended to consider the thermodynamic effects of unpaired dangling end contributions both proximal and away from the surface. The parameters of the model differ were tuned to represent both a double stranded and single stranded DNA sections. The free energetic effects of different dangling end combinations were considered in the presence of different types of surfaces both conducting and insulating. Configurational sampling was achieved by Metropolis Monte Carlo to calculate the conformational entropy. We found a strong effect for dangling mismatches when they occur near the surface due to sequence as opposed to being held away from the surface.

These changes are caused by both a direct electrostatic interaction between the surface and the molecule, and an entropy reduction induced by the electrostatic interactions and the physical boundary that the surface represents. As the salt concentration increases, the electric fields become more screened and the system is dominated by entropic changes due to the surface excluded volume. The entropy as a function of the inverse Debye length, which is proportional to the square root of the salt concentration, shows some non-monotonic behavior, especially when the surface is conducting. This can be understood as a result of two different surface effects (attraction or repulsion): trapping the molecule, confining it to a smaller phase space, versus increasing the size of its thermal fluctuations.

The results of our method can be used to understand DNA hybridization experiments where the solution targets are not of the same length as the surface probes. Except for rather contrived control experiments this is the usual experimental case encountered. Using the model described and allowing for various surface coverage effects will allow further comparisons with experiment and design.