Abstract
Glutamate spillover in the mossy fiber to granule cell cerebellar glomeruli has been hypothesized to increase neurotransmission reliability. In this study, we evaluate this hypothesis using an experimentally-based quantitative model of glutamate spillover on the N-methyl-d-aspartate receptors (NMDA-Rs) at the cerebellar glomerulus. The transient and steady-state responses of NMDA-Rs were examined over a physiological range of firing rates. Examined cases included direct glutamate release activation, glutamate spillover activation, and a combination of direct and spillover activation. Our results illustrate that the effects of spillover alone are equivalent to direct release and, notably, combined spillover and direct release effects on NMDA-Rs are not additive. Our results show that spillover does in fact provide a high degree of reliability given that the synaptic vesicle release rate must fall to approximately 15–25% of what is considered the normal baseline level in order to substantially alter neurotransmission across the examined range of frequencies. We suggest that the high reliability provided by activation due to glutamate spillover could be used to conserve energy by reducing the required overall glutamate load at higher frequencies.
Keywords: quantitative model, NMDA receptor, granule cell, mossy fiber, glutamate diffusion, neurotransmitter spillover, synaptic vesicle release failure, glutamate uptake
Introduction
Neurotransmitter spillover has been a topic of special interest over the last decade, with several theoretical and experimental papers identifying its presence at multiple synapse types, including stellate cells (Carter and Regehr 2000), climbing fibers (Szapiro and Barbour 2007), purkinje (Huang and Bordey 2004), and granule cells (Rossi, Sola et al. 2002; Cathala, Brickley et al. 2003; Xu-Friedman and Regehr 2003; Sargent, Saviane et al. 2005; Mitchell, Feng et al. 2007). In particular, the role of glutamate spillover on the activation of N-methyl-d-aspartate receptors (NMDA-Rs) has been debated. In some cases, spillover activation is thought to be pathological, such as the spillover activation of NMDA-Rs in the spinal dorsal horn, which is associated with neuropathic pain (Nie and Weng) and especially in the case of excitotoxicity due to neural injury (Mitchell and Lee 2008). However, in most cases, spillover is thought to be a physiological phenomenon, including the activation of extrasynaptic NMDA-Rs (Asztely, Erdemli et al. 1997; Kullmann and Asztely 1998; Harney, Jane et al. 2008), the activation of climbing fiber interneurons, where spillover is thought to be the sole means of synaptic communication (Szapiro and Barbour 2007) and especially activation of NMDA and AMPA receptors at the cerebellar glomeruli (D’Angelo, De Filippi et al. 1995; DiGregorio, Nusser et al. 2002; Cathala, Brickley et al. 2003; Sargent, Saviane et al. 2005).
Each cerebellar glomerulus contains a single mossy fiber rosette at its center with up to twenty granule cell dendritic claw contacts followed by a sheath of glial cells surrounding the entire assemblage (Llinas, Walton et al. 2004). Given that spillover at the glomeruli has been identified in multiple theoretical (Saftenku 2005; Mitchell, Feng et al. 2007) and experimental studies (D’Angelo, De Filippi et al. 1995; DiGregorio, Nusser et al. 2002; Cathala, Brickley et al. 2003; Sargent, Saviane et al. 2005), the question has moved from “Does spillover physiologically occur?” to “How does spillover impact synaptic transmission?” Based on experimental and theoretical evidence, glutamate spillover at mossy fiber to granule cell synapse has been hypothesized to increase transmission reliability (Otis 2002; Saftenku 2005; Sargent, Saviane et al. 2005), reduce variability (Otis 2002), synchronize granule cell firing (DiGregorio, Nusser et al. 2002), and assist in long term potentiation and depression (Nieus, Sola et al. 2006), to name just a few possibilities.
The role of NMDAR-s at the glomerulus has been a particular topic of recent interest (Mapelli, Gandolfi et al. 2010; Solinas, Nieus et al. 2010). The role of the NMDA-R at the glomerulus has been difficult to elucidate with different experimental studies showing differing locations of NMDA-Rs (i.e. synaptic versus extrasynaptic) (Yamada 2001; Petralia, Wang et al. 2002; Xu-Friedman and Regehr 2003), as well as different properties of the glomerulus at different cell ages (D’Angelo, Rossi et al. 1994; Brickley, Cull-Candy et al. 1996; Cathala, Brickley et al. 2003). The goal of the current theoretical study was to examine the potential role of synaptic NMDA-Rs at the cerebellar glomerulus in both direct and spillover transmission. We examine the impact of glutamate spillover on NMDA activation at a variety of physiological firing rates over a time course of 10 seconds using an experimentally-based quantitative model (Mitchell, Feng et al. 2007; Mitchell and Lee 2007). Our results indicate that spillover activation alone can be nearly equivalent to direct activation at most frequencies, lending credence to the increased reliability hypothesis. However, our results may suggest that spillover could also be used as a means to conserve energy by reducing the overall glutamate load without sacrificing overall synaptic efficacy.
Methods
We utilize our previously published quantitative model of glutamate spillover (Mitchell, Feng et al. 2007; Mitchell and Lee 2007) to determine the temporal glutamate concentration and NMDA-R open probability profiles at a neighbor synapse in the glomerulus. Glutamate diffusion and uptake in the glomerulus is simulated using the Saftenku diffusion model (Saftenku 2005), and NMDA-R open probabilities are simulated using the Banke and Traynelis NMDA-R model. The methods that are most pertinent to the current study are described below. For additional information on model detail, namely model equations and experimental validation, we refer the reader to Saftenku (Saftenku 2005) and Banke and Traynelis (Banke and Traynelis 2003) as well as our previous studies where sensitivity analyses and derivation of parameters, model application, comparison and limitations have been exhaustively covered (Mitchell, Feng et al. 2007; Mitchell and Lee 2007). To briefly summarize, the spillover model closely matches experimental data examining the EPSC at the glomerulus, and varying parameters within their experimentally determined range, as shown in Table 1, does not substantially alter the model results.
Table I.
Diffusion model parameter definitions, values and references.
| Parameter Description | Name | Base Value | Physiological Range | Reference(s) | |
|---|---|---|---|---|---|
| Mossy fiber radius (μm) | RMF | 1.5 | 1.5–2 | Hamori, 1997; Xu-Friedman, 2003 | |
| Distance from center of mossy fiber to glial sheath (μm) | rabs | 3.0 | RMF+1.5 | Xu-Friedman, 2003 | |
| Distance from mossy fiber to glial sheath (μm) | Rdd | 1.5 | 1–1.5 | Saftenku, 2005 | |
|
|
rMD | 0.46 | 0.3–0.46 | Saftenku, 2005 (equation). See vs references (values). | |
| Initial glutamate concentration (mM) | C0 | 8.77 | 4.39–17.54 | Xu-Friedman, 2003 | |
| Effective diffusion constant (μm2/ms) | Deff | 0.41 | 0.41–0.76 | Barbour, 2001; Nicholson, 1998; Nielsen, 2004; Saftenku, 2005 | |
| Average release site density (μm−2) | vs | 1.5 | 1.5–3.5 | Rusakov, 1999; Sorra, 1998; Xu-Friedman, 2003 | |
| Average radius of post-synaptic density (μm) | a | 0.11 | 0.11 | Xu-Friedman, 2003 |
Diffusion Model
The Saftenku cerebellar glomerulus diffusion model (Saftenku 2005) utilizes a cylindrical geometry to represent glutamate diffusion from a point source that includes neighbor synapse contributions and a simple residence time based method for glutamate uptake to represent the transient glutamate concentration at a neighbor synapse. This model utilizes parameters that have been experimentally determined. Table 1 lists the diffusion model parameter base values, physiological ranges, and references. The most pertinent parameters, which are specific to the cerebellar glomerulus, were determined using experimental electromicrographs from Xu-Friedman and Regeher (Xu-Friedman and Regehr 2003) taken from rats age 17–21 days.
The geometry of the glomerulus used by the diffusion model is as follows: The glomerulus contains a mossy fiber at its center that is 3–4μm in diameter (RMF) and 6.5–10μm in length. The mossy fiber is encapsulated in a glial sheath located approximately 1–1.5μm from the mossy fiber terminal (Hamori, Jakab et al. 1997; Xu-Friedman and Regehr 2003). Assuming that the release sites form a uniform pattern in the circle, rMD is the radius of a circle, which on average contains one release site. This radius is equal to 1/√ vs Π, where vs is the release site density, 1.5–2.3 μm2 as determined by electromicrographs from Xu-Friedman and Regeher (Xu-Friedman and Regehr 2003) and others (Sorra and Harris 1998; Rusakov, Kullmann et al. 1999) (see Table 1). The concentration of glutamate in the synaptic cleft created by spillover of glutamate from neighboring release sites is calculated by integrating glutamate concentration arising from a single release event at different locations of neighboring release sites scattered from rMD to RMF (Saftenku 2005). Using the base parameter values, there are approximately 5 neighbors.
Glutamate uptake is handled by an absorbing boundary utilizing the experimentally determined residence time of glutamate in the extracellular space (Trommershauser, Marienhagen et al. 1999), which includes the combined effects of transporters located at the glial sheath as well as synaptic uptake (Figure 1). This technique allows inclusion of transporter effects without requiring the detailed mechanics and kinetics of GLAST (thought to be the main transporter at the glomerulus—see (Overstreet, Kinney et al. 1999), which are yet to be determined. The absorbing boundary in the radial direction, rabs, is 2.5–3.5μm measured from the center of the mossy fiber. The normal or z-direction absorbing boundary (Rdd) is equal to the difference between rabs and RMF, which is equivalent to at least the thickness of a single dendritic digit. When glutamate molecules reach rabs in a radial direction or Rdd in the normal direction, they are absorbed by the glial sheath, which is known to contain the majority of transporters (Overstreet, Kinney et al. 1999; Trommershauser, Marienhagen et al. 1999).
Figure 1. Saftenku cerebellar glomerulus diffusion model (Saftenku 2005).
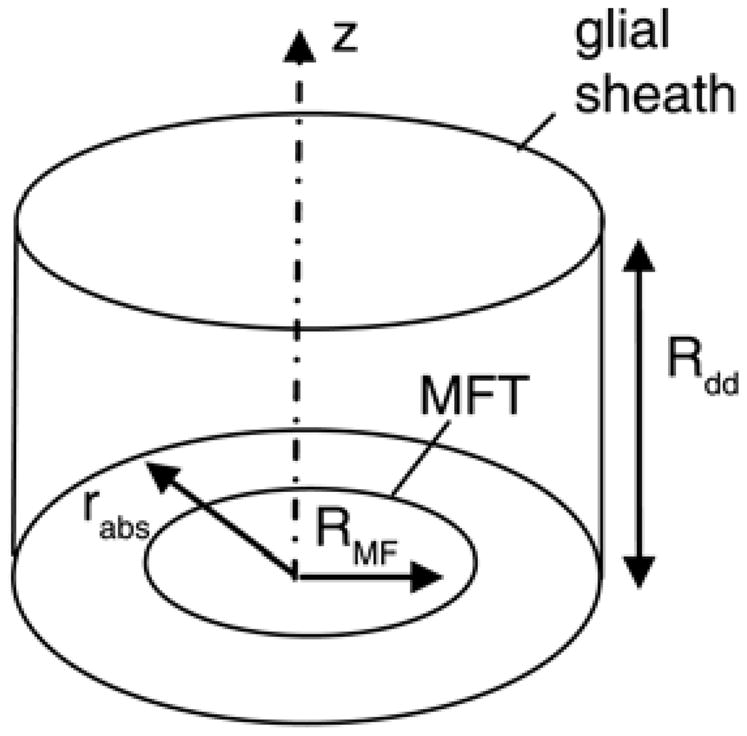
Mossy fiber terminal (MFT) is surrounded by a glial sheath. Rabs is the radius of the absorbing boundary representing glutamate uptake by the sheath, and Rdd is the thickness of a single dendritic digit.
The diffusion model assumes instantaneous release of glutamate at the center of the synaptic cleft. While this is utilized as a mathematical simplification (Saftenku 2005), sensitivity results examining diffusion revealed that it is a valid assumption, and does not result in quantitatively distinguishable results (Mitchell, Feng et al. 2007). We utilize an initial concentration, c0, of 8.77mM, equivalent to one vesicle containing 4,000 molecules of glutamate corresponding to a vesicle concentration of 100mM. However, other initial concentrations were investigated (not shown), including 4.385, 8.77, and 17.54mM to represent 0.5, 1, and 2 vesicles, respectively. There are many citations for possible diffusion coefficient values (Nicholson and Sykova 1998; Nielsen, DiGregorio et al. 2004; Saftenku 2005). Accounting for the effects of macromolecule obstacles and overcrowding, the glutamate diffusion coefficient is 0.2μm2/ms (Saftenku 2005). The highest diffusion coefficient, describing diffusion within the synaptic cleft, is thought to be 0.76 μm2/ms (Barbour, 2001). The value of 0.41μm2/ms represents the aqueous glutamate diffusion coefficient corrected for temperature and a brain tortuosity of 1.6 as calculated and previously published (Nicholson and Sykova 1998). We investigated the effect of varying Deff within the synaptic cleft and determined that its effect was minimal (<0.01%), likely due to the small span of the cleft compared to the distance to the glial sheath. Thus, we ultimately chose to use a Deff = 0.41 μm2/ms for both the direct and spillover activation cases in order to obtain a more conservative estimate of the effects of spillover on NMDA-R activation. For more information or to view illustrations on the impact of diffusion model parameters on the glutamate concentration profile, please see Mitchell et al., 2007 (Mitchell, Feng et al. 2007).
NMDA-R kinetic model
NMDA-Rs are on the post-synapse(s), which are located at the synaptic release sites determined by rMD and vs. Based on our prior examination of NMDA-R models (Mitchell and Lee 2007), the Banke and Traynelis NMDA-R model (Banke and Traynelis 2003) is used as the NMDA-R model of choice because it produces spillover relationships that best match those seen experimentally. The Banke and Traynelis model of the NR1/NR2B NMDA receptors incorporates two desensitized receptor states and two transition states representing a fast and a slow conformation change. The 2-glutamate bound state, the two transition states and the activated receptor state comprise a loop (Figure 2), which allows for two conformational changes to proceed before receptor activation. Rate constants were experimentally determined for the Banke and Traynelis NMDA-R model (see Banke and Traynelis 2003 for details) and are as previously published (Mitchell and Lee 2007).
Figure 2. Banke and Traynelis NMDA-R binding model (Banke and Traynelis 2003).
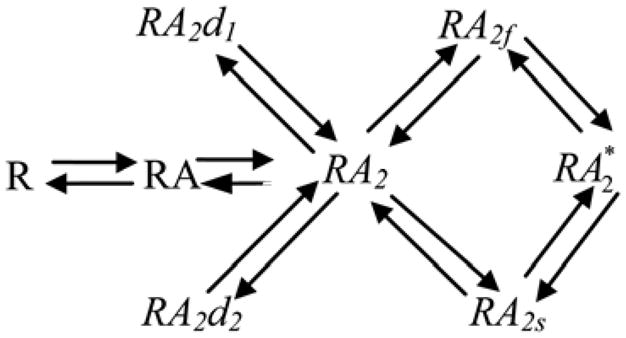
This model examines the binding of the two NR2 subunits, though co-agonist binding is necessary to open the ion channel. Glycine concentration is assumed to be high enough such that NR1 subunits are saturated. The binding of the first and second glutamate molecules is represented by RA and RA2, respectively. The desensitized states are labeled RA2d1 and RA2d2. The fast and slow transition states are labeled RA2f and RA2s, respectively. The activated state is RA2*. Adapted from (Banke and Traynelis 2003; Mitchell, Feng et al. 2007; Mitchell and Lee 2007).
Firing rates
Based on experimental data for average firing rates of the glomerulus (van Kan, Gibson et al. 1993; D’Angelo, De Filippi et al. 1995), we simulate a frequency range of 1–40 Hz. Higher firing rates have been induced experimentally (100–300 Hz) at the glomerulus. However, we chose to focus on the average range where the implications of spillover can be more easily examined and visualized with clarity. Simulations of higher firing rates (not shown) did not change the presented results. We examined NMDA-R open probabilities when both the direct and neighboring synapse(s) were firing separately and together. A sensitivity analysis was performed to determine the effect of frequency.
Simulation of direct, spillover, and combined activation
The same NMDA-R kinetic model was utilized for all three types of activation. Only input into this model (i.e. the glutamate concentration profile) changed for each type of activation. The glutamate concentration profiles for direct release and spillover activation were simulated using equations published by Saftenku (Saftenku 2005). Simple diffusion theory predicts that the glutamate concentration reached at a particular location is the linear sum of the concentrations arising from each source (Otis, Wu et al. 1996). The shape of the mean transmitter waveform at a particular location will be independent of reductions in release probability if they occur uniformly across release sites (DiGregorio, Nusser et al. 2002). Therefore, the only substantive change needed is the amplitude waveform. Thus, glutamate concentration profiles for combined activation were derived by linearly adding the direct release and spillover glutamate concentration profiles (i.e. the glutamate concentration arising from each type of activation, direct and spillover, was summed at each fixed time point) prior to being fed into the NMDA-R kinetic model.
Implementation
The entire model and all of the protocols are implemented in MATLAB R2009a. Each protocol was run for 10 s using a fixed time step of 10 μs. Use of smaller time steps and longer runs had no impact on the results. Further, a sensitivity analysis varying the glutamate diffusion model parameters within the experimental range shown in Table 1 had no substantial impact on the conclusions of this study.
Results
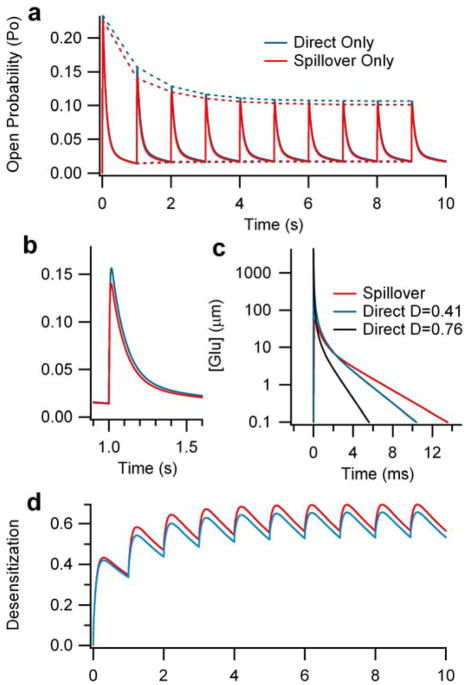
We divide our analysis of NMDA-R activation at the cerebellar glomerulus into three main cases: 1) direct activation, which represents traditional independent synaptic activation without spillover contributions; 2) spillover activation, which represents activation due to the diffusion of glutamate out of neighboring, directly activated synapses into a quiescent synapse; and 3) combined activation, which represents activation due to glutamate derived from both direct release and spillover. Furthermore, we examined each of these cases over a physiological range of frequencies (1–32 Hz). The output of the model is in the form of glutamate concentration profiles and NMDA-R open probability profiles. Differential effects are best illustrated at 1 Hz, including the transient and steady-state profile (Figure 3a), as well as single-spike properties for open probability (Figure 3b) and glutamate concentration (Figure 3c), and NMDA-R desensitization probability (Figure 3d).
Figure 3. Glutamate concentration and NMDA-R open probability profiles for direct release versus spillover activation at the cerebellar glomerulus.
The figure illustrates a detailed example of model output at a firing rate of 1 Hz, where differences between direct release and spillover activation can best be detected. A.) Transient and steady-state open probability of NMDA-Rs over 10 seconds, due to either direct-release (blue) or spillover (red) activation. B.) Close-up illustration of the glutamate concentration of an individual spike (same units as A). C.) Close-up illustration of the open probability of NMDA-Rs of a steady-state spike. D.) Desensitization probability profile (probability of NMDA-Rs being in one of the two desensitized states shown in Figure 1) for direct release or spillover activation.
Direct release versus spillover activation
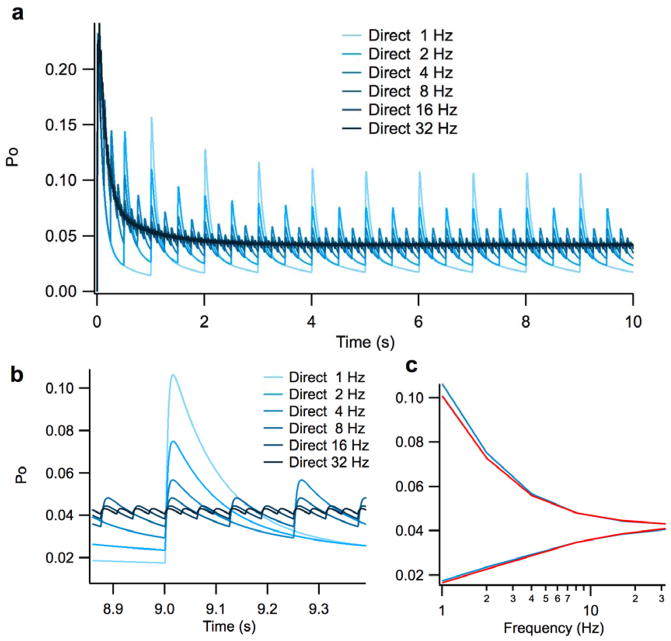
The differences between direct and spillover activation are not substantial. Thus, at a firing rate of 1 Hz, the difference between the steady-state maximum and minimum open probabilities for direct versus spillover activation is only 5.3% and 5.9%, respectively (Figure 3a, b – measured at 2 sec). This approximate 10% difference between the steady-state spikes of the direct and spillover response is approximately half the percent difference that is seen between the first spikes of the direct versus spillover response. Because the responses are so similar, only the direct profiles are plotted to illustrate the effects of frequency (Figure 4), as the addition of spillover traces would be indistinguishable due to the scaling. Thus, our simulations predict that direct and spillover activation are equivalent from the perspective of NMDA-R response, at what are considered the most physiologically relevant frequencies (8–34 Hz) (van Kan, Gibson et al. 1993; D’Angelo, De Filippi et al. 1995).
Figure 4. Effect of firing rate on NMDA-R open probability at the cerebellar glomerulus.
The figure illustrates the impact of firing rate over a range of 1–32 Hz. A.) Transient and steady-state open probability of NMDA-Rs over 10 seconds. Given that the direct release and spillover profiles are essentially the same and thus indistinguishable, only the direct release profiles are shown. B.) Close up illustration of the open probability of NMDA-Rs of a steady-state spike at each simulated firing rate. C.) Plot of the maximum and minimum NMDA-R open probabilities across the entire range of firing rates.
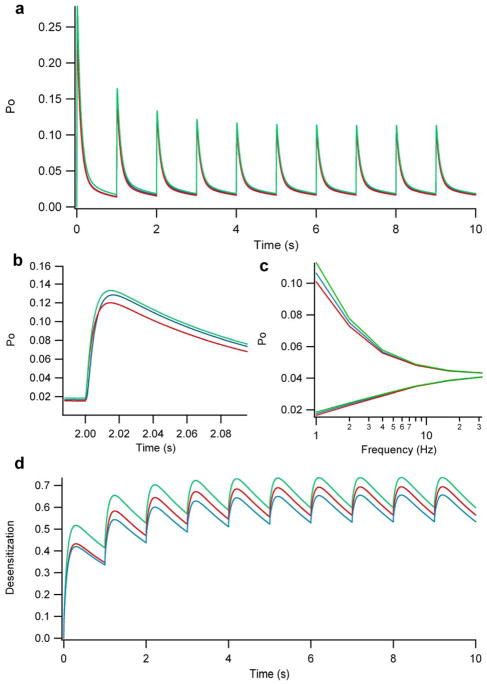
Combined activation
Simultaneous exposure to glutamate derived from both direct release and spillover does not substantially add to the NMDA-R response (Figure 5a,b). In particular, the effect on the minimum open probability is negligible (Figure 5c – lower traces). Even the differences between maximum open probabilities are small except at the lowest frequencies (Figure 5c – upper traces). The largest differences at steady state among the activation types occur at 1 Hz, where combined activation, direct release, and spillover activation result in peak open probabilities of 0.113, 0.106, and 0.101, respectively (measured at 8 seconds – Figure 5a,c). We simulated combined activation across multiple frequencies, and found that the effects of combined activation on NMDA-Rs remained highly non-additive. In fact, at the most physiological frequencies, the NMDA-R responses were nearly indistinguishable to that of either direct release or spillover activation. Also, similar to direct or spillover activation, the maximum and minimum open probabilities of combined activation converge as frequencies increase (Figure 5c) with the result that NMDA-R open probability behaves increasingly like a constant background level rather than responding to individual spikes. This behavior is similar to what has been seen experimentally in another study examining the effects of NMDA currents in EPSC trains at the mossy fiber to granule cell synapse (Nieus, Sola et al. 2006).
Figure 5. Effect of combined activation on the NMDA-R open probability at the cerebellar glomerulus.
A.) Transient and steady-state open probability of NMDA-Rs over 10 seconds. Notice that the combined activation (green) is essentially equivalent to direct release (blue) or spillover (red); that is, combined activation is does not result in additive effects on NMDA-R response. B.) Close-up illustration of the open probability of NMDA-Rs of an individual spike, highlighting the very small quantitative differences between combined, direct release, and spillover activation. C.) Plot of the maximum and minimum NMDA-R open probabilities for combined, direct release, and spillover activation across a range of firing rates. Notice that the different activation types become indistinguishable at higher frequencies. D.) Desensitization probability profile (probability of NMDA-Rs being in one of the two desensitized states shown in Figure 3) for direct release, spillover and combined activation.
Effects of spillover on NMDA-R desensitization
NMDA-Rs are known to exhibit desensitization with prolonged exposure to glutamate (Banke and Traynelis 2003). Therefore, we examined the impact of direct, spillover and combined activation on NMDA-R desensitization (Figure 3d, 5d). Combined activation via direct release and spillover increases desensitization by about 20% (Pd = 0.51) compared to direct release or spillover activation (Pd =0.41) alone after the first spike. At most frequencies, the NMDA-R reaches a steady-state level of desensitization after as few as 5 spikes, resulting in desensitization probabilities of 0.656, 0.694, and 0.737 for direct, spillover and combined activation, respectively, at a firing rate of 1 Hz. Consequently, the maximum and minimum open probabilities for this steady state level of desensitization decrease substantially with firing frequency, with the largest differences between the minimum and maximum open probabilities occurring at the lower frequencies (Figure 4b, 5c). The steady-state maximum and minimum open probabilities converge as firing rate increases (Figure 5c). For example, the maximum and minimum open probability is 0.106 and 0.0175 at 1 Hz compared to 0.0432 and 0.0407 at 32 Hz. This trend for NMDA-R open probability is qualitatively similar to what has been seen in an experimental study examining the frequency response of the glomerulus (Saviane and Silver 2006).
Transmission reliability
The most commonly proposed benefit of the presence of spillover is that it could potentially increase transmission reliability e.g. (DiGregorio, Nusser et al. 2002; Otis 2002; Saftenku 2005; Sargent, Saviane et al. 2005). Spillover has been found to experimentally reduce the variability of AMPA-Rs in the cerebellar glomerulus (DiGregorio, Nusser et al. 2002), but it’s impact on the reliability of NMDA-Rs remains in question. To fully assess NMDA-R reliability at the glomerulus, we simulated the impact of complete synaptic transmission failure (i.e. a single event wherein no synaptic vesicles are released during activation) and the impact of constrained vesicle release on NMDA-R open probability over a time course 10s and at a variety of firing rates (1 – 32 Hz).
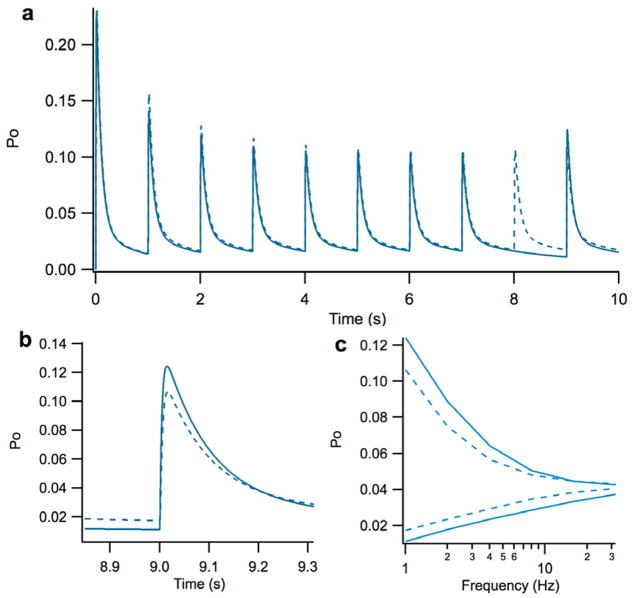
Synaptic transmission failure was simulated to examine the worse case scenario of missed releases on the reliability of NMDA-R activation during direct, spillover, and combined activation (Figure 6). We found that while such missed releases could substantially impact the next spike in all cases, the impact was negligible in later spikes. Essentially, the first spike after the miss would have a minimum and maximum open probability that corresponded to the steady-state values associated with the longer interspike interval. For example the peak open probability of the first spike after a missed released at 8 Hz has essentially the same peak open probability as a steady-state spike at 4 Hz, but subsequent spikes return to having the same properties as other steady-state 8 Hz spikes. Thus, even during the worst case scenario of synaptic transmission failure, the overall impact on the open probability of NMDA-Rs is minimal.
Figure 6. Effect of missed glutamate vesicle release(s) on transmission reliability.
A.) Transient and steady-state open probability of NMDA-Rs over 10 seconds at a firing rate of 1 Hz for steady-state (dotted) and missed spike (solid) cases. There is a missed release at 8 s, which results in a dropped spike. Notice that the next spike at 9 s (last spike in the trace) has increase in the maximum open probability. B.) Close-up illustration of the open probability of NMDA-Rs of for spike following missed release. C.) Plot of the maximum and minimum open probabilities for steady-state and missed spike properties across a range of firing rates.
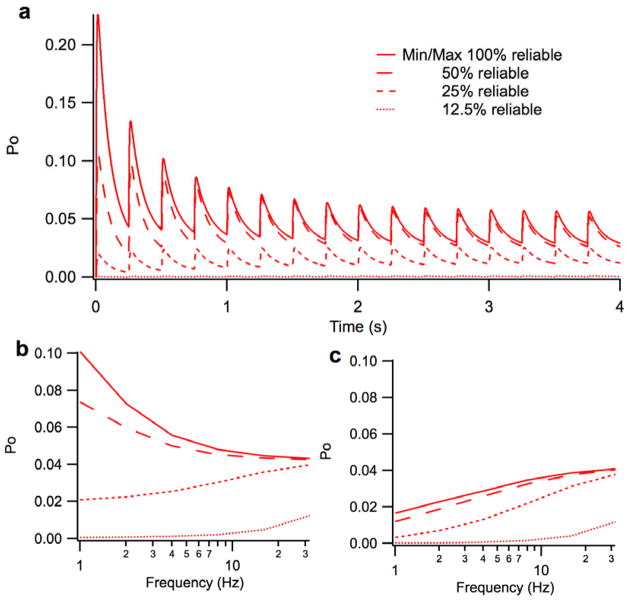
It has been suggested that at low firing frequencies spillover would boost the quantal content of EPSPs such that threshold could be attained with fewer mossy fiber inputs, and thus, glomerulus firing would continue to be reliable even with fewer releases (DiGregorio, Nusser et al. 2002). To examine this hypothesis, we investigated the impact of missed synaptic vesicle releases on the open probability of NMDA-Rs. We found that the glomerulus could have an extremely high percentage of missed release events with little effect on NMDA-R open probability (Figure 7). In fact, a 50% drop in the synaptic vesicle release results in only a minor effect on NMDA open probability, mostly at frequencies <4 Hz (Figure 7b). However, a 75% drop in the synaptic vesicle release (i.e. 25% reliability) becomes quite notable at lower frequencies as illustrated by the large difference in the steady-state maximum open probabilities at firing rates less <15–20 Hz. However, even the effects of 25% reliability may not be substantial in terms of glomerulus function at higher frequencies, given that the maximum open probability is still qualitatively similar to baseline at firing rates >20 Hz (Figure 7b; See Discussion). Thus, given that mossy fibers often fire at such rates, 25% reliability or less is still viably functional. Not until the release rate drops to near 85% (i.e. ~15% reliability) is neurotransmission consistently impaired at all examined frequencies, low through high. Based on these results, we propose that vesicle release could be rate-limited to about 8–10 Hz, with little to no significant impact on NMDA-R response. Thus, it is quite possible that spillover does allow for fewer mossy fiber inputs to retain transmission reliability.
Figure 7. Effect of constrained release of glutamate vesicles.
The figure illustrates the effects of constrained vesicle release as a function of percent reliability (e.g. where 25% reliability equates to a 75% drop in vesicle release). A.) Transient and steady-state open probability of NMDA-Rs over 10 seconds at a firing rate of 4 Hz for 100%, 50%, 25% and 12.5% reliability. B.) Maximum steady-state open probability of NMDA-Rs at 100%, 50%, 25% and 12.5% reliability. C.) Minimum steady-state open probability of NMDA-Rs at 100%, 50%, 25% and 12.5% reliability.
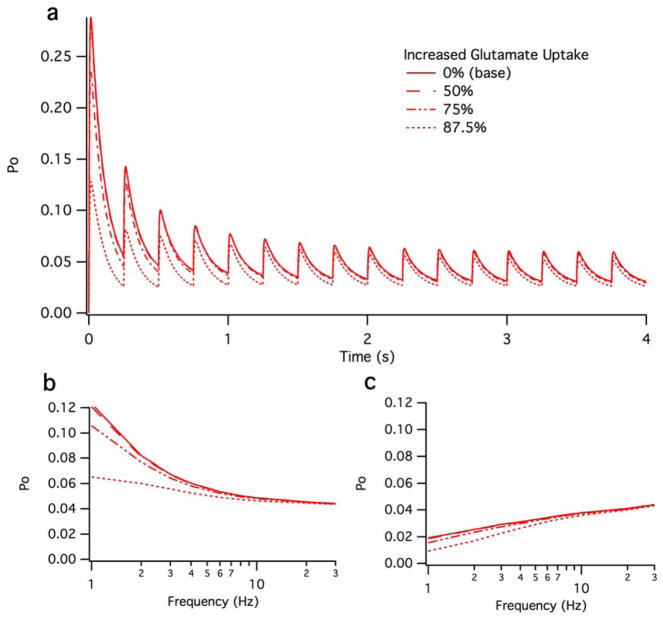
We examined the possibility that increased glutamate uptake could compensate for the effects seen by spillover. We simulated 50%, 75%, and 87.5% increases in glutamate over the full range of frequencies (Figure 8). Only after a 75% increase in uptake can any substantive change be detected, and those changes only occur at frequencies less than 4Hz. Differences are larger among the steady-state maximum open probabilities (Figure 8a) then they are among the minimum steady-state open probabilities (Figure 8b). At frequencies greater than 4Hz, no substantive change can be detected over the examined range of increased uptake. The ratio of differences between direct, indirect, and combined activation with increased uptake remained similar; that is, all three types of activation remained qualitatively indistinguishable (~0.2% difference between spillover and direct, not shown). Thus, we conclude that increased glutamate uptake, at least over the examined ranges, does not alter the findings of this study.
Figure 8.
Effect of enhanced glutamate uptake. A.) Transient and steady-sate open probability of NMDA-Rs over 4 seconds at a firing rate of 4 Hz. B.) B.) Maximum steady-state open probability of NMDA-Rs at 100%, 50%, 75% and 87.5.5% increased uptake. C.) Minimum steady-state open probability of NMDA-Rs at 100%, 50%, 75% and 87.5.5% increased uptake.
Discussion
While previous studies have shown the impact of spillover as the result of a single direct firing event, here we are able to illustrate its effects during longer-term repetitive firing over a time period of 10 s and over a broad range of physiological firing rates. Our finding that spillover activation is nearly equivalent to direct activation over longer time courses, particularly over the range of 8–34 Hz, is supportive of the contention that spillover could indeed be a normal, physiological phenomenon that occurs in the cerebellar glomeruli. Only at the lowest end of the physiological range and during the transient period, prior to reaching steady-state, can the difference between direct and spillover activation be seen in the open probability profiles of the NMDA-Rs. Furthermore, even combined activation via the simultaneous direct and spillover events, is unable to produce substantial changes to the steady-state NMDA-R open probability profile, indicating that spillover can naturally occur without interfering with neurotransmission. In fact, our simulations of missed synaptic vesicle releases provide convincing quantitative support for the contention that spillover greatly increases the reliability of neurotransmission at the glomerulus.
We suggest that the glomerulus may utilize the extremely high reliability provided by spillover as means to conserve energy. That is, at higher frequencies, the glomerulus could dramatically cut back on the number of glutamate vesicle releases without significantly altering the NMDA-R response. Cutting back the number of vesicle releases would lessen the overall glutamate load, including the required number of synaptic vesicles as well as the required amount glutamate uptake and transporters. By reducing the glutamate load, the glomerulus could, in essence, operate at higher frequency range while expending the equivalent amount of energy of that to low to middle firing rates. Given that neurotransmitter uptake and transport makes up significant percentage of the energy expenditure of a neuron (Hertz and Fillenz 1999; Magistretti, Pellerin et al. 1999) synaptic vesicle conservation via spillover activation could be a key feature leveraged not only by glomeruli but potentially other types of neurons.
An additional factor to consider in this analysis is the role the NMDA ion channels have in the post-synaptic response. At sufficient densities, NMDA channels are known to support plateau potentials (Baldino, Wolfson et al. 1986). Thus, if their role in the glomeruli is to generate a background plateau then the rate-limiting of vesicle release would make sense as there would be little purpose in driving the NMDA conductances further once a plateau has been turned on. Alternatively, it is also possible that rate-limiting and desensitization serve to keep NMDA channel activation below plateau activation so as to better maintain its potential for amplification of the AMPA channel inputs (Cook and Johnston 1999).
Comparison to experimental work
The large degree of NMDA-R desensitization well aligns with desensitization seen in the hippocampus. A study by Arnth-Jensen and colleagues reported 50–60% desensitization in organotypic culture with incomplete glutamate uptake (Arnth-Jensen, Jabaudon et al. 2002). A recent theoretical study of spillover also reported high desensitization (Boucher, Kroger et al.). However, quantified spillover at the CA1 pyramidal synapse in the Arnth-Jensen study (Arnth-Jensen, Jabaudon et al. 2002) was not equivalent to direct release unlike the current study where spillover at the cerebellar glomerulus was nearly equivalent to direct release. This could in part be due to the closed geometry of the glomerulus (Xu-Friedman and Regehr 2003; Saftenku 2005). The qualitative trends of the role of frequency in the NMDA response are similar to those that have been reported experimentally for the cerebellar glomerulus (Saviane and Silver 2006).
Limitations and Future Directions
The goal of this paper was to look at synaptic glutamate spillover on to NMDA receptors of the cerebellar glomerulus. Thus, we did not include extrasynaptic NMDA receptors. Extrasynaptic receptors could play a different, yet important, role in the spillover response (Asztely, Erdemli et al. 1997; Kullmann and Asztely 1998; Harney, Jane et al. 2008).
Additionally, future experimental and theoretical work should address differences between immature and mature cerebellar cells as previous studies have shown differences between NMDA-R location (Yamada 2001; Petralia, Wang et al. 2002; Xu-Friedman and Regehr 2003) as well as neurophysiological properties such as cell input conductance, capacitance (D’Angelo, Rossi et al. 1994; Brickley, Cull-Candy et al. 1996; Cathala, Brickley et al. 2003). The model of this study is based on electromicrographs of cells in rats between the ages of 17–19 days. Previous work has shown that the EPSCs due to NMDA-Rs of younger (day 8) rats are much higher and prominent than that of older (day 39) rats, see study by Cathala and colleagues (2003). We have previously examined changes in cell radius (which would change the capacitance) in the current model see (Mitchell, Feng et al. 2007). While radius does have an impact on the results, it does not substantially change the results and conclusions presented in this study (result not shown).
Finally, the Banke and Traynelis NMDA-R model is based on the activation of NR1/NR2B receptor subtypes. The kinetic scheme utilized was chosen based on our previous theoretical findings showing that it best matches experimental relationships identified at this synapse (Mitchell and Lee 2007). However, recent model predictions examining different NMDA-R subtypes reveal varying quantitative properties (Singh, Hockenberry et al.); such properties could potentially impact neurotransmission at the glomerulus as well.
Conclusion
Our overall conclusion is that activation of NMDA-Rs due to combined glutamate spillover and direct release is nearly equivalent to activation due to either spillover or direct release. This results in an extremely high reliability such that NMDA-Rs are largely insensitive to even dramatic reductions in vesicle release. Such a high reliability via spillover may in turn be leveraged to conserve energy and resources by reducing the required glutamate load at higher frequencies.
Spillover activation of glomerulus NMDA-Rs is nearly equivalent to direct release
Vesicle release rates must fall 15–25% to substantially alter neurotransmission
Spillover could be used to conserve energy by reducing glutamate load
Acknowledgments
This work was supported by the National Institute of Health (NS069616 and NS062200) and the National Science Foundation (DGE-0333411).
Footnotes
Conflict of Interest
The authors have no conflict of interest with regard to this manuscript.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Arnth-Jensen N, Jabaudon D, et al. Cooperation between independent hippocampal synapses is controlled by glutamate uptake. Nat Neurosci. 2002;5(4):325–331. doi: 10.1038/nn825. [DOI] [PubMed] [Google Scholar]
- Asztely F, Erdemli G, et al. Extrasynaptic glutamate spillover in the hippocampus: dependence on temperature and the role of active glutamate uptake. Neuron. 1997;18(2):281–293. doi: 10.1016/s0896-6273(00)80268-8. [DOI] [PubMed] [Google Scholar]
- Baldino F, Jr, Wolfson B, et al. An N-methyl-D-aspartate (NMDA) receptor antagonist reduces bicuculline-induced depolarization shifts in neocortical explant cultures. Neurosci Lett. 1986;70(1):101–105. doi: 10.1016/0304-3940(86)90445-3. [DOI] [PubMed] [Google Scholar]
- Banke TG, Traynelis SF. Activation of NR1/NR2B NMDA receptors. Nat Neurosci. 2003;6(2):144–152. doi: 10.1038/nn1000. [DOI] [PubMed] [Google Scholar]
- Boucher J, Kroger H, et al. Realistic modelling of receptor activation in hippocampal excitatory synapses: analysis of multivesicular release, release location, temperature and synaptic cross-talk. Brain Struct Funct. 215(1):49–65. doi: 10.1007/s00429-010-0273-x. [DOI] [PubMed] [Google Scholar]
- Brickley SG, Cull-Candy SG, et al. Development of a tonic form of synaptic inhibition in rat cerebellar granule cells resulting from persistent activation of GABAA receptors. J Physiol. 1996;497(Pt 3):753–759. doi: 10.1113/jphysiol.1996.sp021806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter AG, Regehr WG. Prolonged synaptic currents and glutamate spillover at the parallel fiber to stellate cell synapse. J Neurosci. 2000;20(12):4423–4434. doi: 10.1523/JNEUROSCI.20-12-04423.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cathala L, Brickley S, et al. Maturation of EPSCs and intrinsic membrane properties enhances precision at a cerebellar synapse. J Neurosci. 2003;23(14):6074–6085. doi: 10.1523/JNEUROSCI.23-14-06074.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook EP, Johnston D. Voltage-dependent properties of dendrites that eliminate location-dependent variability of synaptic input. J Neurophysiol. 1999;81(2):535–543. doi: 10.1152/jn.1999.81.2.535. [DOI] [PubMed] [Google Scholar]
- D’Angelo E, De Filippi G, et al. Synaptic excitation of individual rat cerebellar granule cells in situ: evidence for the role of NMDA receptors. J Physiol. 1995;484(Pt 2):397–413. doi: 10.1113/jphysiol.1995.sp020673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Angelo E, Rossi P, et al. The relationship between synaptogenesis and expression of voltage-dependent currents in cerebellar granule cells in situ. J Physiol Paris. 1994;88(3):197–207. doi: 10.1016/0928-4257(94)90006-x. [DOI] [PubMed] [Google Scholar]
- DiGregorio DA, Nusser Z, et al. Spillover of glutamate onto synaptic AMPA receptors enhances fast transmission at a cerebellar synapse. Neuron. 2002;35(3):521–533. doi: 10.1016/s0896-6273(02)00787-0. [DOI] [PubMed] [Google Scholar]
- Hamori J, Jakab RL, et al. Morphogenetic plasticity of neuronal elements in cerebellar glomeruli during deafferentation-induced synaptic reorganization. J Neural Transplant Plast. 1997;6(1):11–20. doi: 10.1155/NP.1997.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harney SC, Jane DE, et al. Extrasynaptic NR2D-containing NMDARs are recruited to the synapse during LTP of NMDAR-EPSCs. J Neurosci. 2008;28(45):11685–11694. doi: 10.1523/JNEUROSCI.3035-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertz L, Fillenz M. Does the ‘mystery of the extra glucose’ during CNS activation reflect glutamate synthesis? Neurochem Int. 1999;34(1):71–75. doi: 10.1016/s0197-0186(98)00071-0. [DOI] [PubMed] [Google Scholar]
- Huang H, Bordey A. Glial glutamate transporters limit spillover activation of presynaptic NMDA receptors and influence synaptic inhibition of Purkinje neurons. J Neurosci. 2004;24(25):5659–5669. doi: 10.1523/JNEUROSCI.1338-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kullmann DM, Asztely F. Extrasynaptic glutamate spillover in the hippocampus: evidence and implications. Trends Neurosci. 1998;21(1):8–14. doi: 10.1016/s0166-2236(97)01150-8. [DOI] [PubMed] [Google Scholar]
- Llinas R, Walton K, et al. Cerebellum. In: Shepherd G, editor. The Synaptic Organization of the Brain. Ch 7. New York: Oxford University Press; 2004. [Google Scholar]
- Magistretti PJ, Pellerin L, et al. Energy on demand. Science. 1999;283(5401):496–497. doi: 10.1126/science.283.5401.496. [DOI] [PubMed] [Google Scholar]
- Mapelli J, Gandolfi D, et al. High-Pass Filtering and Dynamic Gain Regulation Enhance Vertical Bursts Transmission along the Mossy Fiber Pathway of Cerebellum. Front Cell Neurosci. 2010;4:14. doi: 10.3389/fncel.2010.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell CS, Feng SS, et al. An analysis of glutamate spillover on the N-methyl-D-aspartate receptors at the cerebellar glomerulus. J Neural Eng. 2007;4(3):276–282. doi: 10.1088/1741-2560/4/3/013. [DOI] [PubMed] [Google Scholar]
- Mitchell CS, Lee RH. Output-based comparison of alternative kinetic schemes for the NMDA receptor within a glutamate spillover model. J Neural Eng. 2007;4(4):380–389. doi: 10.1088/1741-2560/4/4/004. [DOI] [PubMed] [Google Scholar]
- Mitchell CS, Lee RH. Pathology dynamics predict spinal cord injury therapeutic success. J Neurotrauma. 2008;25(12):1483–1497. doi: 10.1089/neu.2008.0658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholson C, Sykova E. Extracellular space structure revealed by diffusion analysis. Trends Neurosci. 1998;21(5):207–215. doi: 10.1016/s0166-2236(98)01261-2. [DOI] [PubMed] [Google Scholar]
- Nie H, Weng HR. Impaired Glial Glutamate Uptake Induces Extrasynaptic Glutamate Spillover in the Spinal Sensory Synapses of Neuropathic Rats. J Neurophysiol. doi: 10.1152/jn.00013.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen TA, DiGregorio DA, et al. Modulation of glutamate mobility reveals the mechanism underlying slow-rising AMPAR EPSCs and the diffusion coefficient in the synaptic cleft. Neuron. 2004;42(5):757–771. doi: 10.1016/j.neuron.2004.04.003. [DOI] [PubMed] [Google Scholar]
- Nieus T, Sola E, et al. LTP regulates burst initiation and frequency at mossy fiber-granule cell synapses of rat cerebellum: experimental observations and theoretical predictions. J Neurophysiol. 2006;95(2):686–699. doi: 10.1152/jn.00696.2005. [DOI] [PubMed] [Google Scholar]
- Otis T. Helping thy neighbors: spillover at the mossy fiber glomerulus. Neuron. 2002;35(3):412–414. doi: 10.1016/s0896-6273(02)00796-1. [DOI] [PubMed] [Google Scholar]
- Otis TS, Wu YC, et al. Delayed clearance of transmitter and the role of glutamate transporters at synapses with multiple release sites. J Neurosci. 1996;16(5):1634–1644. doi: 10.1523/JNEUROSCI.16-05-01634.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overstreet LS, Kinney GA, et al. Glutamate transporters contribute to the time course of synaptic transmission in cerebellar granule cells. J Neurosci. 1999;19(21):9663–9673. doi: 10.1523/JNEUROSCI.19-21-09663.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petralia RS, Wang YX, et al. NMDA receptors and PSD-95 are found in attachment plaques in cerebellar granular layer glomeruli. Eur J Neurosci. 2002;15(3):583–587. doi: 10.1046/j.1460-9568.2002.01896.x. [DOI] [PubMed] [Google Scholar]
- Rossi P, Sola E, et al. NMDA receptor 2 (NR2) C-terminal control of NR open probability regulates synaptic transmission and plasticity at a cerebellar synapse. J Neurosci. 2002;22(22):9687–9697. doi: 10.1523/JNEUROSCI.22-22-09687.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rusakov DA, Kullmann DM, et al. Hippocampal synapses: do they talk to their neighbours? Trends Neurosci. 1999;22(9):382–388. doi: 10.1016/s0166-2236(99)01425-3. [DOI] [PubMed] [Google Scholar]
- Saftenku EE. Modeling of slow glutamate diffusion and AMPA receptor activation in the cerebellar glomerulus. J Theor Biol. 2005;234(3):363–382. doi: 10.1016/j.jtbi.2004.11.036. [DOI] [PubMed] [Google Scholar]
- Sargent PB, Saviane C, et al. Rapid vesicular release, quantal variability, and spillover contribute to the precision and reliability of transmission at a glomerular synapse. J Neurosci. 2005;25(36):8173–8187. doi: 10.1523/JNEUROSCI.2051-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saviane C, Silver RA. Fast vesicle reloading and a large pool sustain high bandwidth transmission at a central synapse. Nature. 2006;439(7079):983–987. doi: 10.1038/nature04509. [DOI] [PubMed] [Google Scholar]
- Singh P, Hockenberry AJ, et al. Computational Investigation of the Changing Patterns of Subtype Specific NMDA Receptor Activation during Physiological Glutamatergic Neurotransmission. PLoS Comput Biol. 7(6):e1002106. doi: 10.1371/journal.pcbi.1002106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solinas S, Nieus T, et al. A realistic large-scale model of the cerebellum granular layer predicts circuit spatio-temporal filtering properties. Front Cell Neurosci. 2010;4:12. doi: 10.3389/fncel.2010.00012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorra KE, Harris KM. Stability in synapse number and size at 2 hr after long-term potentiation in hippocampal area CA1. J Neurosci. 1998;18(2):658–671. doi: 10.1523/JNEUROSCI.18-02-00658.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szapiro G, Barbour B. Multiple climbing fibers signal to molecular layer interneurons exclusively via glutamate spillover. Nat Neurosci. 2007;10(6):735–742. doi: 10.1038/nn1907. [DOI] [PubMed] [Google Scholar]
- Trommershauser J, Marienhagen J, et al. Stochastic model of central synapses: slow diffusion of transmitter interacting with spatially distributed receptors and transporters. J Theor Biol. 1999;198(1):101–120. doi: 10.1006/jtbi.1999.0905. [DOI] [PubMed] [Google Scholar]
- van Kan PL, Gibson AR, et al. Movement-related inputs to intermediate cerebellum of the monkey. J Neurophysiol. 1993;69(1):74–94. doi: 10.1152/jn.1993.69.1.74. [DOI] [PubMed] [Google Scholar]
- Xu-Friedman MA, Regehr WG. Ultrastructural contributions to desensitization at cerebellar mossy fiber to granule cell synapses. J Neurosci. 2003;23(6):2182–2192. doi: 10.1523/JNEUROSCI.23-06-02182.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada K. Immunohistochemical distributions of NMDA receptor channel subunits in the synaptic glomeruli of adult mouse cerebellum. Hokkaido Igaku Zasshi. 2001;76(6):385–394. [PubMed] [Google Scholar]