A model for Vibrio cholerae colonization of the human intestine

Abstract

Vibrio cholerae is a strict human pathogen that causes the disease cholera. It is an old-world pathogen that has re-emerged as a new threat since the early 1990s. V. cholerae colonizes the upper, small intestine where it produces a toxin that leads to watery diarrhea, characterizing the disease [36]. The dynamics of colonization by the bacteria of the intestines are largely unknown. Although a large initial infectious dose is required for infection, data suggests that only a smaller sub-population colonizes a portion of the small bowel leading to disease. There are many barriers to colonization in the intestines including peristalsis, fluid wash-out, viscosity of the mucus layer, and pH. We are interested in identifying the mechanisms that allow this sub-population of bacteria to survive and colonize the intestines when faced with these barriers. To elaborate the dynamics of V. cholerae infection, we have developed a mathematical model based on a convection-diffusion-reaction-swimming equation capturing bacterial dynamics coupled with Stokes equations governing fluid velocity where we developed a novel non-local boundary condition. Our results indicate that both host and bacterial factors contribute to bacterial density in the gut. Host factors include intestinal diffusion and convection rates while bacterial factors include adherence, motility and growth rates. This model can ultimately be used to test therapeutic strategies against V. cholerae.

1 Introduction

Diarrheal disease is a leading cause of morbidity and mortality in the world today. Vibrio cholerae, the caustive agent of cholera, is a key pathogen inducing diarrhea throughout the world. It is ingested through infected water or food products and once it establishes infection, it induces a severe watery diarrhea that persists for days to weeks. This can lead to dehydration and death if not treated. Cholera is most prevalent in the developing world, particularly in warm climates, and V. cholerae has been shown to be seasonally correlated [47].

Upon ingestion, the majority of bacteria are killed by the acidic pH in the stomach. Those that survive enter the lumen of the small intestine and begin colonization. Data suggest that human inoculum size is likely large, since there is approximately a 4–6 log reduction of V. cholerae by due to the low pH in the stomach [11]. A certain percentage of bacteria swim towards the epithelial cells, defying the influence of the convective current (derived from water or digested food), also withstanding propulsive gut mobility [28].

While near the epithelium, V. cholerae make a potent enterotoxin, cholera toxin, which modifies a key regulatory protein in intestinal cells. The ultimate effect of cholera toxin is constitutive cyclic AMP production in intoxicated cells that results in the opening of normally gated channels in the membrane. This leads to loss of chloride and other ions from the cells, followed by water. The result for the infected individual is massive fluid and ion loss in the form of a watery diarrhea that is the hallmark of cholera infection. The diarrhea in cholera can reach volumes of 20 liters per day and leads to shock and death if not treated by oral rehydration therapy [18]. As fluid is introduced into the intestine the bacterial population is subject to the influence of convective flow [26], [37], [38].

The prevailing assumption regarding dynamics of V. cholerae within the intestinal tract is that bacteria close to the epithelium cease to swim and begin to adhere as a necessary step towards colonizing the host. Experiments performed on mice and rabbits reveal that bacteria are found concentrated within the crypts [49] [28], the structure of which may allow for protection against removal by natural intestinal flows. Adherence of bacteria through elaboration of extracellular organelles such as the toxin-coregulated pilus (TCP) is likely to be a key feature of V. cholerae pathogenicity [18]. However, the contribution of the adherent population within the context of the larger overall microbial population in an infected intestine is more difficult to assess using experimental models, although recent advances have allowed this adherent population to be more carefully studied [41]. A series of mathematical models representing bacteria colonization of the human stomach by Helicobacter pylori showed that adherence was an integral factor of colonization [7],[8], [34]. These models were two-compartmental ordinary differential equations systems representing the relevant spatial aspects of the stomach (lumen, mucous layer, epithelium). The intestines are more complex in space and length, and also have a strong fluid flow present, so different mathematical models are necessary to capture the dynamics of V. cholerae in the gut.

While animal models and bacterial genetics have begun to unravel the natural history and pathogenesis for this centuries old pathogen, many aspects of the interaction between V. cholerae and its human host remain unknown. For example, while the primary determinants of V. cholerae colonization include adhesion, mobility and toxin production, [18] less is known about the dynamics of the interactions of these processes with the human host. Similarly, host factors such as pre-existing immunity and both physical and physiological responses in the gut likely play key roles and may directly or indirectly affect bacterial factors. Animal models allow for some analysis of the host-pathogen interaction in humans. However the ability to study and manipulate groups of variables individually or collectively in these models is currently experimentally limited.

To this end, we have developed a novel mathematical model describing the dynamics of V. cholerae in the human intestine. Our overall objective is to gain an understanding of the mechanisms that control the interaction between V. cholerae and the human host. Elaboration of processes that allow the microbe to sense and respond to its host environment will allow us to apply the model to explore antimicrobial therapies. These therapies could be aimed, for example, at blocking bacterial mechanisms as well as physical forces acting on the microbe as it establishes itself in the host.

2 Methods

In the course of V. cholerae colonization, several processes co-exist: bacterial growth, motility, and diffusion of bacteria and convective fluid flow in the gut from the digestive process and from water excreted from walls of the intestines. The latter process, (diarrhea), is triggered by toxic stimulation caused by V. cholerae, and is therefore absent during initial colonization events. The life cycle of bacteria evolves from the interaction of these processes, and the goal of this work is to study the dynamics of its evolution. As a first approach, we derive a mathematical model for density of bacteria and velocity of fluid that flows through the intestinal cross-section.

Developing a model to study V. cholerae dynamics in the human intestines requires us to consider factors related to both bacteria and host. Bacterial factors constitute sub-populations of invading bacteria and their different functional characteristics, while host factors include structural and physiological environmental factors that impact V. cholerae. We describe these in detail together with the derivation of the mathematical model representing this system.

2.1 Modeling The Bacteria

As noted in animal experiments, most notably in the infant rabbit model, which most closely replicates human pathogenesis, bacteria are found adherent throughout the epithelial surface including within crypt-like structures [46]. Data from sensitive measures of gene expression during infection of mice show that only a small fraction of the initial inoculum reaches the appropriate micro-environment of the intestine that allows for colonization [41], suggesting that this sub-population is critical for establishing infection. In other words, the majority of the inoculum, which do not express factors for adherence, likely do not contribute to the infection. This is a similar observation to that shown in models of H. pylori where the adherent population serves as an epidemic ‘core’ population driving infection dynamics [7], [8], [34].

Based on these considerations, we define three mutually exclusive sub-populations of bacteria, namely luminal, mucosal, and epithelium (adherent) populations. As a first assumption, the luminal and mucosal are the motile populations; the environments they reside in directly affect their motility, respectively. For example, the luminal population does not have to contend with the viscosity of the mucus layer. We assume that the adherent population is not motile. Our model also allows for variations in bacterial diffusion [17] in different subpopulations as well as different growth rates in each sub-population [15]. It is reasonable to neglect a term representing bacterial death since it is more likely that bacteria are removed by other mechanisms, such as epithelial cell sloughing in the time period of interest (as in [7],[8], [34]).

The exact percentage of bacteria that swim in vivo is unknown, but is included in the list of model parameters. A strength of modeling is that we can vary the parameters in the model in order to study the dynamics more carefully. For example, we can compare simulated outcomes under different sets of parameter values. This approach could be useful in predicting and understanding V. cholerae infection dynamics in humans.

2.2 Modeling The Environment

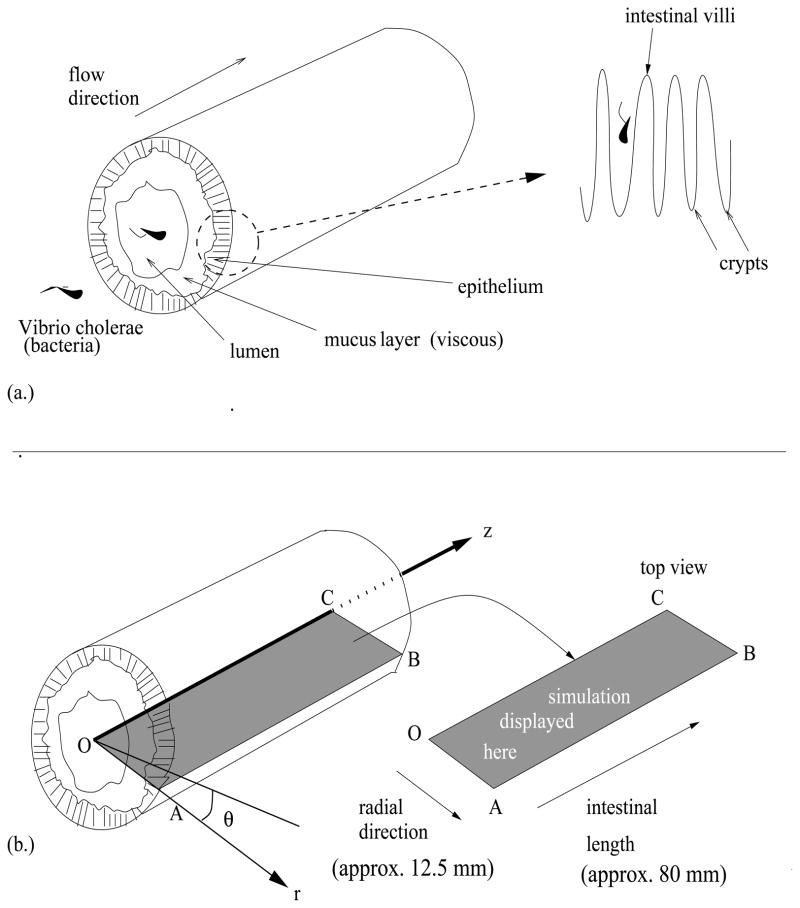
The geometry and composition of a typical cross-section of human intestine is shown in Figure 1a for readers who aren’t familiar with villi and crypts. The lumen, mucus layer, and epithelium constitute the basic structure of the intestine. The lumen is the inner cavity, and it allows for the passage of digested food. The mucus layer lies over the epithelium and consists of a gel-like substance that protects the body from bacterial penetration. The epithelium, the surface of the intestinal wall, is composed of epithelial cells which are organized into villi and crypts.

Figure 1.

(a.) Small intestinal section. A 3-dimensional cross-section of the intestine including the detailed structure of the epithelium, which is composed of villi and crypts. (b.) Mathematical framework. The mathematical description of the intestinal cross-section in terms of the coordinates r, z, and θ,. The left is the three-dimensional illustration of an intestinal cross section. The rectangular slice OABC is the display platform for our simulations (see Figure 2). The line segment OC represents the line through the center of the lumen, and AB represents the outer edge of the intestinal wall. The three-dimensional result is visualized using radial symmetry of the intestinal section. See [54].

In order to model the dynamics of interest, we define a three-dimensional coordinate system. The standard Cartesian coordinate system consists of three mutually perpendicular directions, namely x₁, x₂, and x₃. However, since the intestinal cross-section is cylindrical, we transform the coordinate system into one involving cylindrical coordinates for convenience. See Figure 1b for an illustration of the radial, angular, and intestinal length directions, namely r, θ, and z, respectively. Figure 2 shows a two-dimensional simulation platform for the reduced mathematical model. In a straightforward manner, we use the following conversion formulas [1]

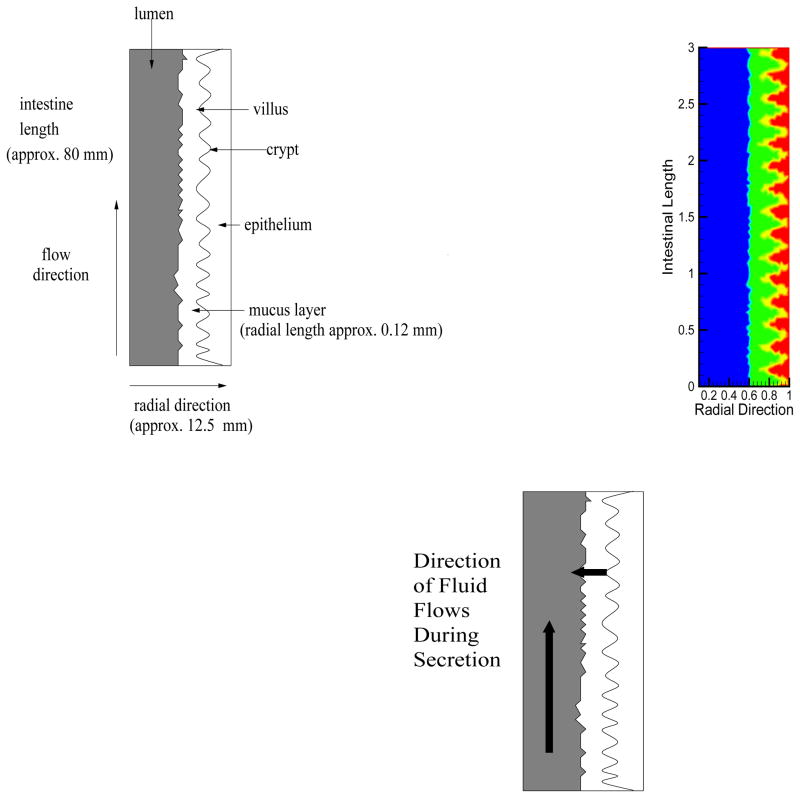
Figure 2.

(a.) Simulation display platform (not to scale). A cross-section of the small intestine in two-dimensions. This illustration corresponds to the simulation display platform as indicated in Figure 1b [54],[55] (b.) Simulation display with color. The two-dimensional figure shows the computational region used in the simulations. The lumen is the region shown in blue, the mucus is the region shown in yellow, and the epithelium (as a layer) is the region shown in red. The boundary curve separating the mucus from the epithelium is given by 0.9 + 0.1 sin(10πz). (c.)Fluid flow directions are shown during fluid secretion times. Fluid flows (downstream) the small intestine due to digestion and fluid flows out of the intestinal wall due to fluid secretion.

$$x_1=rcos\theta ,x_2=rsin\theta ,x_3=z,$$

and the orthogonal curvilinear basis {e_r, e_θ, e_z} via the relation

$$e_r=(cos\theta )e_1+(sin\theta )e_2$$ (1)

$$e_{\theta }=-(sin\theta )e_1+(cos\theta )e_2$$ (2)

$$e_z=e_3,$$ (3)

where {x_k; k = 1, 2, 3} is the Cartesian coordinates and {e_k; k = 1, 2, 3} is the standard orthonormal basis in R³ respectively.

Let v denote the the velocity of the water in the intestines. By equations (1)–(3), the cylindrical components of the velocity are given by

$$v_r=v·e_r,v_{\theta }=v·e_{\theta },v_z=v·e_z,$$ (4)

where v_r, v_θ, and v_z denote the components along the radial, angular, and tubular directions, respectively. The primary assumptions we make in deriving the mathematical model are stated as follows:

• A1The density of bacteria and the velocity of the water are independent of the angular direction θ.
• A2The angular component of the water velocity, v_θ, is equal to zero.

The assumptions are based on reasonable approximations of the physical quantities with respect to the angle θ, because the flow velocity in the tubular, z, and radial, r, directions are dominant, and the diffusion along different angular directions is similar.

The geometry of the intestinal cross-section (Figure 1b) is now reduced to a rectangular planar geometry in terms of the cylindrical coordinate directions r and z (Figure 2). We point out that the topology of the true intestinal region is not changed by our assumptions.

2.3 The Fluid Flow Model

The simulations presented in this work are performed under an assumed velocity profile. However, to keep the model general for future considerations, we derive the equations that govern the water flow through the intestines using standard three-dimensional incompressible non-steady Stokes equations [23] for the velocity, since we are assuming a low Reynolds number system [29]. Recall that v_r, v_θ, and v_z are the radial, angular, and tubular velocity components, respectively. Then, the cylindrical setting as we described above allows us to arrive at the following modified and simplified version of the Stokes equations in the two-dimensional setting:

$$\frac{\partial v_r}{\partial t}=-\frac{1}{\rho }\frac{\partial p}{\partial r}+\mu (\mathrm{\Delta }{v}_r-\frac{v_r}{r^2})+F_1,$$ (5)

$$\frac{\partial v_z}{\partial t}=-\frac{1}{\rho }\frac{\partial p}{\partial z}+\mu \mathrm{\Delta }{v}_z+F_2,$$ (6)

$$\frac{1}{r}\frac{\partial }{\partial r}({rv}_r)+\frac{\partial v_z}{\partial z}=0,$$ (7)

where t is time, μ and ρ are the viscosity and the density of the water, respectively, F₁ and F₂ are external forces, Δ is the θ–independent cylindrical coordinate version of the Laplacian given by

$$\mathrm{\Delta }=\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial }{\partial r})+\frac{{\partial }^2}{\partial z^2},$$ (8)

and in what follows v · ∇ is understood to be in terms of cylindrical coordinates via

$$v·\nabla =v_r\frac{\partial }{\partial r}+\frac{v_{\theta }}{r}\frac{\partial }{\partial \theta }+v_z\frac{\partial }{\partial z}.$$ (9)

2.4 Derivation of a Model for Bacterial Density

We remark that equations (5)–(9) are the basic equations that describe the flow in the intestinal cross-section, to be coupled with a mass-balance equation for bacteria that we now describe.

Let u = u(r, θ, z) denote the density of the bacteria in the intestine. Let V be a fixed representative sample volume inside the intestine (Figure 1b). Denote the boundary of V by ∂V. Then, conservation of mass yields that the rate of change in mass over V is given by

$$\underset{\mathit{Total}\mathit{Rate}of\mathit{Change}}{\underbrace{{\int }_V\frac{\partial u}{\partial t}dx}}=\underset{\mathit{Amount}\mathit{Crossing}\mathit{Boundary}}{\underbrace{-{\int }_{\partial V}q·\mathit{ndS}}}+\underset{\mathit{Multiplication}\mathit{Change}}{\underbrace{{\int }_V\mathit{cudx}}}+\underset{\mathit{External}\mathit{Influences}}{\underbrace{{\int }_V\mathit{Sdx}}},$$ (10)

where q is the flux, c is the coefficient of the reaction term: the birth rate of the bacteria when c > 0 and the mortality rate when c < 0; and the last integral in (10) allows for changes in bacterial density due to external sources/sinks S, such as ingestion of bacteria or introduction of antibiotics.

One of the most challenging and important aspects of the mathematical problem involves designing a way to incorporate the necessary components of the flux into the model. We decompose the flux into its diffusion, convection, and motility terms as follows:

$$\text{Flux}=\underset{\mathit{Amount}\mathit{Crossing}\mathit{Boundary}}{\underbrace{{\int }_{\partial V}q·\mathit{ndS}}}=-\underset{\mathit{Diffusion}}{\underbrace{{\int }_{\partial V}a\nabla u·\mathit{ndS}}}+\underset{\mathit{Convection}}{\underbrace{{\int }_{\partial V}uv·\mathit{ndS}}}+\underset{\mathit{Motility}}{\underbrace{k{\int }_{\partial V}\alpha {ue}_r·\mathit{ndS}}},$$ (11)

where the symmetric diffusion tensor a assumes different values in the lumen, mucus, and epithelium. For this study, it is reasonable to assume that a is a scalar function of radial and length directions only, such that a = a(r, z), since there are no fixed obstructions in the intestine that could define a preferred diffusion direction. The values of a(r, z) have significant jumps across neighboring layers of the intestinal cross-section, reflecting distinctly different compositions within the intestine. Indeed, the mucus layer is composed of a very viscous gel-like substance which serves as the only barrier against bacterial penetration into the epithelium. Thus the value of a(r, z) is smallest in the mucus layer. However, once bacteria break through the mucus layer they are free to access the epithelium, where they adhere. Thus, the value of a(r, z) is also small in the epithelium. The second integral on the right-hand side of (11) is the standard convection term by which the equation is coupled to the water-flow equations (5)–(9). The motility phenomenon of the bacteria is given by the last integral in (11). This term is absent from the constitutive relations commonly seen in general reaction-diffusion processes ([21], [22], [20]).

Since experimental data reveal that a percentage k of bacteria swim against the current (likely via chemotaxis) toward the epithelial cells, (located in the direction e_r), the motility term resembles a bacterial-initiated convection along a preferred direction (vs. the media-initiated convection). In the motility term, α represents the known swimming velocity of the bacteria in each layer. We turn our attention to the parameter k, an important part of the motility effect. First, k ∈ [0, 1] since not all bacteria swim toward the epithelium. Secondly, its value is set to zero in the epithelium layer reflecting that the bacteria adhere to the epithelium. Physical factors such as peristalsis, epithelial cell sloughing, and diarrhea are the only ways in which they can be removed by the body.

Pointwise versions of equations (10) and (11) are obtained by applications of the divergence theorem, followed by letting |V | → 0. After combining the resulting equations with an appropriate rearrangement of terms, we arrive at an equation in Cartesian coordinates that describes the combined diffusion-convection-motility-reaction process of bacterial density:

$$\frac{\partial u}{\partial t}-\text{div}\{a\nabla u\}+\text{div}\{uv\}+k\alpha \text{div}\{{ue}_r\}-cu=S.$$ (12)

Let ∂Ω_L be the boundary between the epithelium and the mucus and let J = [0, T ] be the time interval of interest. We assume that α = 0, on ∂Ω_L × J, since the bacteria do not swim once they reach ∂Ω_L. Since the bacteria adhere to the epithelium, we impose the following boundary conditions on ∂Ω_L:

$$\begin{array}{r}\nabla u·n=0,\text{on}\partial {\mathrm{\Omega }}_L\times J,\\ v·n=-\gamma (u),\text{on}\partial {\mathrm{\Omega }}_L\times J,\end{array}$$

where γ(u) is, in general, a non-decreasing function of the bacterial density. For the purposes of this work, we shall make the following assumption: once the bacterial density reaches a given value of u* at time t* on the epithelium, then the body secretes fluids (water and electrolytes, etc.) at a rate of v_sec for a duration of T* days (where T* = 3). That is,

$$\gamma (u)=\{\begin{array}{ll}0,\hfill & \text{if}0\le u\le u^{\ast },\hfill \\ v_{\mathit{sec}}\hfill & \text{if}{u}^{\ast }<u\text{for}t\in [t^{\ast },t^{\ast }+T^{\ast }].\hfill \end{array}$$

See Figure 2c for an illustration of fluid flow directions during secretion of fluids.

For example, if we assume the average size of the bacteria is 1μm long with a radius of 0.25μm, the maximum possible concentration is $u^{\ast }=\frac{16\times {10}^9}{{\pi }^2}\text{bacteria}/{\text{mm}}^3$. The value of v_sec that we will take is 6 L/day over the entire epithelial surface in the duodenum.

Let L =∫_∂ΩL v·n dS be the total velocity of the water that leaves ∂Ω_L times the surface area of ∂Ω_L. We also impose the following radial symmetry conditions: $\frac{\partial }{\partial r}{v}_r(0,z)=0$ and $\frac{\partial }{\partial r}u(0,z)=0$.

In addition, we impose no diffusion on the lateral surfaces:

$$\nabla u·n=0,\text{on}\partial {\mathrm{\Omega }}_{in}\cup \partial {\mathrm{\Omega }}_{\mathit{out}}\times J,$$ (13)

and we assume a known initial concentration of inoculum, namely

$$u(x,y,z,0)=u_{\mathit{init}},\text{in}\mathrm{\Omega }.$$

We begin by taking a given (parabolic profile) velocity field. With m denoting a given metabolic rate, we define

$$f(r)=\frac{2m}{\pi R^4}(R^2-r^2),$$ (14)

and write v = (0, f(r)). Note that ∇ · v = 0. In addition, we impose the following boundary conditions on ∂Ω_in and on ∂Ω_out:

$$v·\mathbf{n}=-f(r),v_r=0,\text{on}\partial {\mathrm{\Omega }}_{in}\times J,$$ (15)

$$v·\mathbf{n}=f(r)-\frac{L}{\pi R^2},v_r=0,\text{on}\partial {\mathrm{\Omega }}_{\mathit{out}}\times J.$$ (16)

Next, we transform (12) into cylindrical coordinates using the notation shown at the beginning of this section, and we arrive at the θ–independent cylindrical-coordinate version of conservation of mass in Ω, where Ω is the intestinal cross- section under study:

$$\frac{\partial u}{\partial t}-\left(\frac{1}{r}\frac{\partial }{\partial r}\left(ra(r,z)\frac{\partial u}{\partial r}\right)+\frac{\partial }{\partial z}\left(a(r,z)\frac{\partial u}{\partial z}\right)\right)+{\nabla }_{r,z}u·v+k\alpha \left(\frac{\partial u}{\partial r}+\frac{1}{r}u\right)-cu=S.$$ (17)

This is the desired governing equation for bacterial density. See Appendix A for the derivation of the weak formulation of the model used in the continuous finite element numerical scheme and for the proof of a conservation relation.

2.5 Numerical Assumptions and Domain Specifications

For the simulations presented here, a piecewise linear continuous finite element method was implemented to compute the solution to the bacterial density equation (17). To make the computations straightforward, we assume that the epithelium is a region, rather than a boundary, better reflecting the biology. The model system together with parameter values given in Table 1 were coded in gfortran [25] and were solved on a computer running Cent OS with a 64-bit Intel Xeon Westmere processor and 6 gigabytes of memory.

Table 1.

Baseline Parameters.

Symbol	Parameters	Simulation Value	Reference
α	V. cholerae Motile Velocity	75 microns/s	[3]
k	Fraction of Motile Bacteria	1	see text
c	Growth Rate (doubling time) in lumen and mucus	71 min	[52]
v	Convection Coefficient (m) for 0 ≤ r ≤ 0.8	0.167 mm/s	[31], equation (14)
AL	Scaled Diffusion Coefficient in lumen region	E0.001 mm2/s	see text
AM	Scaled Diffusion Coefficient in mucus region	E0.0001 mm2/s	see text
AE	Diffusion Coefficient in epithelium region	0 mm2/s	see text

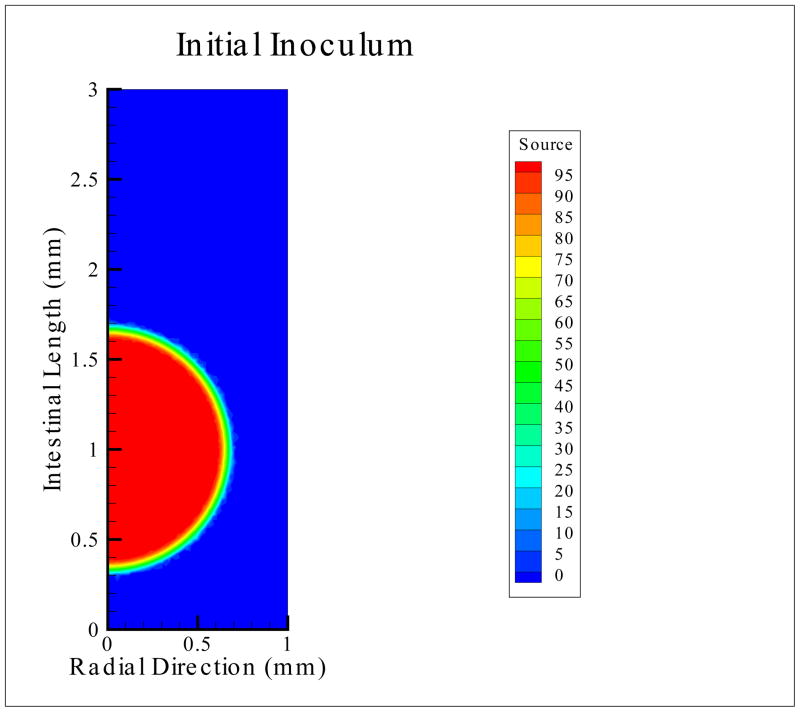
Our computational domain consists of the region of intestine shown in Figure 2b. Our finite element mesh was created using the open-source mesh generator, triangle [50], which was used to create Delaunay triangles with a maximum area of 0.00025 mm². We also used a time step of 0.00025 seconds. In all simulations, we introduce bacteria in a spherical bolus located in the lumen of the small intestine ( See Figure 3 and the Host and Initial Conditions Subsection for the exact form of the source term S).

Figure 3.

Bacterial Inoculum Distribution, measured in the units of number of bacteria per mm³ per second. In the simulations to follow, it is distributed over a time period of 10 seconds, after which the value is set to zero.

As shown in Figure 1, the small intestinal section is almost one order of magnitude larger, in each of the radial and length directions, than the sizes we are using for our simulations (see Figure 2b). This is due to the limitations we experienced with computer power and we explore this scaling issue further in the Discussion Section. Because the simulation region is so small, we can capture the dominant colonization dynamics in approximately 15 seconds for the bacteria in that region. These alterations in the domain specifications are not unreasonable for studying dynamics near the mucus and epithelium. In current work, we are developing a simulation method based on a locally conservative discontinuous Galerkin Method [14],[13],[2],[33] to capture more biologically realistic space and time scales.

2.6 Parameter Estimation

Here we indicate how we estimated values for the majority of the parameters in the model to use for our baseline (standard) case study. Others are studied through numerical simulations of the system in order to calibrate the model and also test for effects. A summary of the parameters and their values is given in Table 1 with references when available.

Based on experiments in which human volunteers were given doses of V. cholerae with and without bicarbonate to buffer the stomach acid, then followed for cholera symptoms, there is approximately a 4–6 log reduction of V. cholerae due to the low low pH environment in the stomach [11]. Therefore, the number of V. cholerae ingested is likely orders of magnitude larger than the number that eventually enters the small intestine. We chose to study colonization dynamics under the assumption that approximately 1000 bacteria enter the lumen of the small intestine (see Figure 3). Our model is flexible to variations in this number.

Peristalsis rates in the intestine are given in [31]. Specifically, the movement of chyme in the small intestine is at a rate of approximately 1 cm/minute. Therefore, we use the value m = 0.167 mm/s and R = 0.8 mm in equation (14) for 0 ≤ r ≤ 0.8 for the convection rate v = (0, f(r)) throughout our simulation domain shown in Figure 2b. Also, since V. cholerae swims at rates reaching 75 microns per second in media of medium viscosity [51], we use this value for the swimming rate in the lumen and in the mucus (up to a distance of 0.05 mm away from the epithelium layer where it is set to 0 for numerical convenience) in our baseline simulations.

Next, studies have shown that increasing viscosity ten-fold reduces maximum swimming rates of a similar bacterium V. alginolyticus by about two-fold (to approximately 30 microns/second) [3]. In our simulations, we represent this by assuming the diffusion coefficient, A_L, in the lumen is ten times larger than the diffusion coefficient, A_M, in the mucus. Since there is currently no data on the diffusion values in the lumen and mucus of the small intestine, we chose the following numerically convenient values: A_L = 0.001 mm²/s, A_M = 0.0001 mm²/s, and A_E = 0 mm²/s in the epithelial layer, because bacteria do not cross the epithelial cell layer.

Since the fraction of bacteria that can swim is not known, in our baseline simulations we chose k = 1.0, assuming all bacteria swim at the same rate. This will be studied in more details in future work.

A kinetic analysis using a rabbit model of V. cholerae colonization, [52], demonstrated a doubling time of 71 minutes for V. cholerae in vivo for the first six hours of infection. Therefore, we set c = 0.00016 per second in equation (17).

2.7 Host and Bacterial Initial Conditions

The initial conditions for the model reflect a healthy host system with the introduction of a single bolus inoculum of bacteria equal to 100 bacteria per mm³ per second for 10 seconds. This leads to approximately 1000 bacteria entering the spherical region. While the bacteria are typically ingested and enter the intestines in a non-homogeneous fashion, here we assume that the bacteria enter at the site as a sphere in the 3-D lumen of the intestine (Figure 1). This is visualized as a semicircular shape in the 2-D representation and is shown in Figure 3, where the source term is prescribed as

$$S(r,z,t)={\chi }_{0\le t\le 10}\left(100{\chi }_{0\le r\le 0.6}+100cos(2(d_0-0.6)\pi /0.2){\chi }_{0.6\le r\le 0.7}\right),$$

where $d_0=\sqrt{r^2+{(z-1)}^2}$, and r and z are measured in millimeters and seconds, respectively. The model is flexible and can test a range of initial inoculum shapes and sizes.

2.8 Simulating Infection Dynamics of V. cholerae

To begin to study the dynamics of V. cholerae infection, we simulated the bacterial density mathematical model (see Section 2.4). The geometry of the region under study is shown in Figure 1. For clarity of visualization, we demonstrate our simulation results in a two-dimensional platform. Figure 2b depicts how the figures that show the simulation results should be interpreted. Our outcome variable of interest is bacterial density. In future work we can also explore other outcome variables.

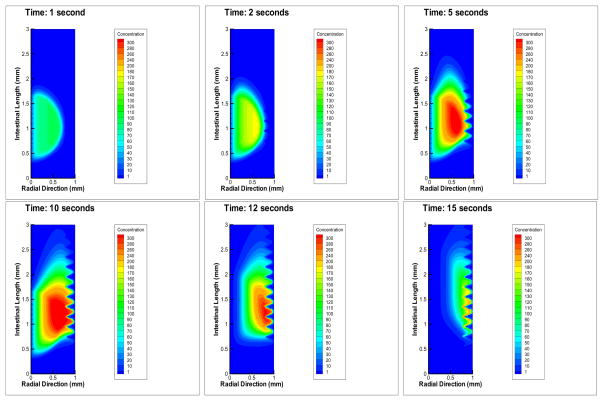
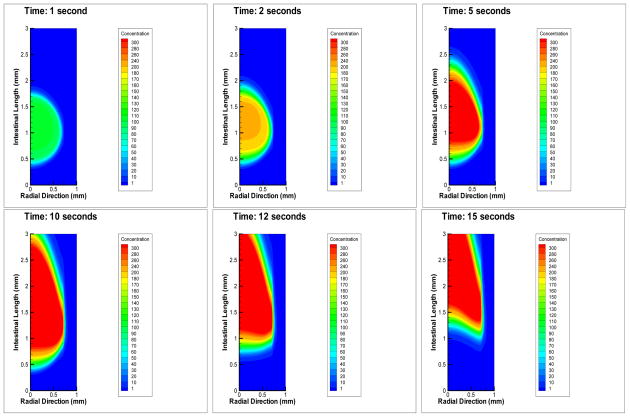
In the absence of bacteria, the negative control simulations show the system has fluid flow representing a healthy intestine. When bacteria are input into the model, as described in Section 2.7, and it is simulated with parameter values from Table 1, the results of a typical simulation of colonization inside the intestinal region are shown in Figure 4. We refer to this as our baseline case, at six time points. Tecplot was used to create all simulation pictures. As the system evolves in time, bacteria move from the lumen toward the epithelial cells and then colonize.

Figure 4.

This is a typical infection scenario we refer to as the virtual wild-type. Shown are changes over time, with time points: 1 s, 2 s, 5 s, 10 s, 12 s, 15 s. Note that the bacteria have difficulty maintaining their position in the mucus layer due to its gel-like composition, but once they pass through it, they colonize the epithelium. Bacteria travel downstream (due to convection).

Note that due to convection, the bacteria cannot migrate directly to the epithelial cells, but they are forced downstream while they attempt to reach the epithelial cells. Bacterial adherence to epithelial cells is evidenced by the high density of bacteria near the epithelial cells. Bacteria have difficulty sustaining a position in the mucus layer due to its gel-like composition (parameterized by a small diffusion coefficient), but once they pass through it, they can colonize at the epithelial cell surface. In the lumen they are washing out as indicated by the lower density values there.

To study the dynamics of our system, we can now alter bacterial factors such as motility and host factors such as convection rates to observe the effects on bacterial colonization.

2.8.1 Cryptotaxis: A Key Mechanism of Colonization

Although it has not been explicitly shown experimentally, the behavior of V. cholerae is assumed to have the following dynamics: most of the bacteria are motile, a small population migrate through the mucus gel toward the epithelial layer, liking sensing nutrient rich cells. It is here where they are in the close vicinity of intestinal crypts and thus they begin multiplying and producing toxins. Because of the strong convective forces and difficulty penetrating the mucus gel, likely only a small percentage arrive at the epithelial layer. Bacteria then change phenotype from motile to non-motile, adherent. Our model development to this point has assumed this same dynamic.

We define this bacterial-sensored migration along with the self-controlled habitation as cryptotaxis. In an experimental setting it is difficult to quantify cryptotaxis. To test whether V. cholerae can colonize in the absence of directed motility, we can compare model simulations where we virtually ‘knock-out’ the bacteria’s ability to swim.

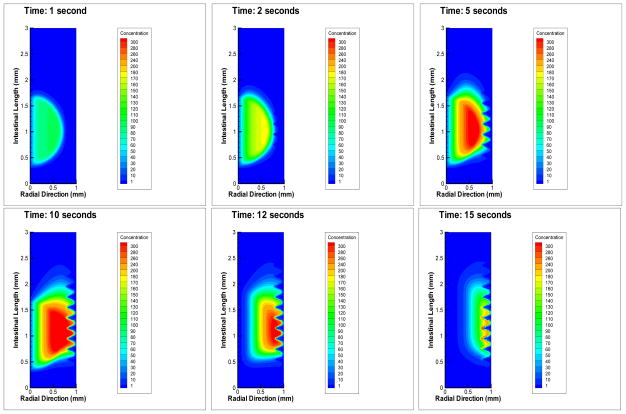
Figure 5 shows the time-series bacterial dynamics for the simulated directed motile knockout. Comparing that with Figure 4, it is clear that cryptotaxis is a key mechanism for V. cholerae to achieve a colonization.

Figure 5.

Virtual knockout of Motility. To achieve a virtual simulated motility knockout, the motility parameter is set to zero, while all other parameters are set to the wild-type values (Table 1). The result is dramatically different from wild-type (compare with Figure 4). Bacterial density pattern is influenced by downstream convection. The washout effect begins to emerge as dominant in comparison to wild-type as the maximum bacterial density decreased one order of magnitude in the knockout simulation. Time points: 1 s, 2 s, 5 s, 10 s, 12 s, 15 s. The bacteria cannot penetrate the mucus layer to colonize before being washed out.

2.8.2 Motility in altered Convective Environment

It is interesting to study how the environment of the intestines also affects colonization dynamics. In the final simulation, we study the scenario where all parameters are set to their baseline values (Table 1), except that the convection rate of chyme or fluid moving through the intestine, m, is decreased by 50%. This could help us understand how the fluid flow itself affects colonization. Figure 6 shows the simulation results. One noticeable difference in this case when compared to the wild-type simulation is that bacteria colonize almost directly across (in the radial direction) from the source of the initial inoculation, rather than pushed away from the strong covective force.

Figure 6.

Low convection significantly enhances colonization. In the current simulation, we decreased the convection rate m by 50% and left all other parameters at their baseline values. Notice that the bacteria colonize closer to the initial inoculation as compared to the baseline case. Also, notice the larger bacterial concentration in the epithelium as compared to the baseline case over the same time points: 1 s, 2 s, 5 s, 10 s, 12 s, 15 s. The low convection allows bacterial motility to dominate so that the bacteria can colonize the epithelium sooner.

3 Discussion

In this work we present the first model capturing the dynamics of V. cholerae in the human small intestine. Our goal was to determine which host and bacterial factors contribute to colonization leading to infection versus clearance. Although we did not perform a complete sensitivity analysis of the parameter space in this initial work, we were able to predict some key factors that we will explore in future work.

First, our model suggests that motility, directed by taxis to the crypts, is a key component of colonization of the epithelial layer because the mucus layer presents a challenge to diffusion-based epithelial colonization. From experiments in animal models, the role of chemotaxis and bacterial motility in the pathogenesis of infection by V. cholerae has been the subject of investigation, although there remain questions that might be settled with future mathematical modeling. A strain lacking the major flagellin subunit FlaA was severely attenuated for colonization in competitive assays with wild type bacteria in an infant mouse model [40]. Chemotaxis directed movement towards or away from attractants or repellants is evidently critical for establishing wild type levels of colonization [40],[24]. V. cholerae that are rendered genetically unable to respond to stimuli by alternating between smooth swimming and tumbling required for chemotactic behavior, heavily out-compete wild type bacteria in an infant mouse model. However, the colonization behavior is altered and they do not exhibit the same spatial distribution of wild type bacteria within the intestines and their ability to properly regulate virulence gene expression is altered as well [10].

Notwithstanding the apparent role for chemotactic-directed motility in the mouse model suggested by the observations noted above, a recent study using an infant rabbit model demonstrated crypt colonization by V. cholerae non-motile mutants lacking the major flagellar subunits [48]. Strains used in this study lack the cholera toxin genes and therefore do not induce the physiological responses of wild type strains in these animals, such as elevated mucin production and secretory diarrhea. The lack of such responses may enable non-motile mutants to colonize crypts more readily than they would in the presence of the secretory response caused by toxins. Another possibility is that chemotactic motility through a flagellar-independent mechanism may direct crypt colonization, a hypothesis supported by the fact that, unlike other motile bacteria, V. cholerae encodes multiple sets of chemosensory systems related to motility [9].

In addition to host factors, we also explored a host environmental factor and its role in modulating colonization. Imposing strong convection forces in the model resulted in a significant reduction of the bacteria from the intestine (not shown). Although we are not modeling the population level dynamics, release of V. cholerae from an infected host back into the environment as a consequence of diarrhea is an obvious assumption about how the disease is transmitted. Experimental evidence supports this assumption: in the infant rabbit, which models both colonization of V. cholerae and diarrhea, intestinal bacterial counts increase steadily until the time secretory diarrhea is observed, when their numbers begin to plataeu, suggesting that the diarrhea is causing shedding of intestinal bacteria [46].

While our preliminary work reveals many important aspects of the V. cholerae colonization process, many additional elements of the dynamics need to be explored. Among these are the interaction with diarrhea and the need to go from a ‘local’ simulation in one small region of the intestine to a larger scale simulation to see if ‘global’ behavior remains consistent over a much larger physiological scale. Finally, the ability to perform sensitivity analysis on the parameter space in the model is essential, and we are currently exploring that using methods developed in our group [43]. To this end, we are developing a new numerical method in order to better study colonization dynamics. This new method will allow us to run simulations with more accurate results, since it will be a locally conservative method that handles jump discontinuities, such as those in the diffusion coefficient from the lumen to the mucus layer, accurately.

More specifically, we are interested in simulating the model with the same parameters as the baseline case, but with the following assumption on the growth rate: the bacteria in the lumen and mucus do not divide, but the bacteria that are adherent to the epithelium do divide. As it is now, the diffusion coefficients are too large for us to see a noticeable difference when we perform that simulation.

Our model is not limited to the study of V. cholerae colonization. It can be modified to study the dynamics of host-pathogen interactions with other microbes [6], [42]. Significant efforts have been made in simulating bacterial motility in a viscous fluid [12], [26], [27], [30], [35],[19], [32], [56], [16], [53] as well as in simulating pattern formation and spatio-temporal complexity [44] as well as in swimming cells [37], [38], [45]. More recent work on the bacterial motility in a fluid can be found in [4], [5], [19], [35] and references therein. Our study is unique as the impact of the host environments on bacterial colonization are key the observed dynamics.

Summary Point Highlights.

• First model describing dynamics of human intestine cells and fluid flow in them

• First model to consider infection with Vibrio cholerae in the intestines

• Predict that cryptotaxis is a key component of V. chlorae colonization

• Predict that the intestinal environment is also a key player in colonization dynamics

Appendix A: Weak Formulation of the Bacterial Density Model

Let us multiply (12) by a smooth function w and integrate over Ω to obtain the following weak form [57] of the pde:

$${\int }_{\mathrm{\Omega }}\frac{\partial u}{\partial t}wdx-{\int }_{\mathrm{\Omega }}w\text{div}\{a\nabla u\}dx+{\int }_{\mathrm{\Omega }}\text{div}\{uv\}wdx+{\int }_{\mathrm{\Omega }}k\alpha \text{div}\{{ue}_r\}wdx-{\int }_{\mathrm{\Omega }}\mathit{cuw}dx={\int }_{\mathrm{\Omega }}Swdx.$$

which, after simplifying and applying the Divergence Theorem, becomes

$${\int }_{\mathrm{\Omega }}\frac{\partial u}{\partial t}wdx+{\int }_{\partial \mathrm{\Omega }}(-a\nabla u+uv+k\alpha {ue}_r)w·\mathbf{n}dS-{\int }_{\mathrm{\Omega }}(-a\nabla u+uv+k\alpha {ue}_r)·\nabla wdx-{\int }_{\mathrm{\Omega }}\mathit{cuw}dx={\int }_{\mathrm{\Omega }}Swdx,$$

or,

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}\frac{\partial u}{\partial t}wdx+{\int }_{\partial {\mathrm{\Omega }}_{in}\cup \partial {\mathrm{\Omega }}_{\mathit{out}}}(-a\nabla u+uv+k\alpha {ue}_r)w·\mathbf{n}dS\\ +{\int }_{\partial {\mathrm{\Omega }}_L}(-a\nabla u+uv+k\alpha {ue}_r)w·\mathbf{n}dS-{\int }_{\mathrm{\Omega }}(-a\nabla u+uv+k\alpha {ue}_r)·\nabla wdx\\ -{\int }_{\mathrm{\Omega }}\mathit{cuw}dx={\int }_{\mathrm{\Omega }}Swdx.\end{array}$$

Since e_r · n = 0 on ∂Ω_in and on ∂Ω_out, it is clear that the above weak form becomes

$${\int }_{\mathrm{\Omega }}\frac{\partial u}{\partial t}wdx+{\int }_{\partial {\mathrm{\Omega }}_{in}\cup \partial {\mathrm{\Omega }}_{\mathit{out}}}(-a\nabla u+uv)w·\mathbf{n}dS++{\int }_{\partial {\mathrm{\Omega }}_L}(-a\nabla u+uv+k\alpha {ue}_r)w·\mathbf{n}dS-{\int }_{\mathrm{\Omega }}(-a\nabla u+uv+k\alpha {ue}_r)·\nabla wdx-{\int }_{\mathrm{\Omega }}\mathit{cuw}dx={\int }_{\mathrm{\Omega }}Swdx.$$

Imposing the boundary conditions on ∂Ω_in ∪ ∂Ω_out, the integral equation reduces to

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}\frac{\partial u}{\partial t}wdx+{\int }_{\partial {\mathrm{\Omega }}_{in}}w(-a\nabla u·\mathbf{n}-uf(r))dS+{\int }_{\partial {\mathrm{\Omega }}_L}(-a\nabla u+uv+k\alpha {ue}_r)w·\mathbf{n}dS\\ +{\int }_{\partial {\mathrm{\Omega }}_{\mathit{out}}}w(-a\nabla u·\mathbf{n}+u(-f(r)+\frac{L}{\pi R^2}))dS-{\int }_{\mathrm{\Omega }}(-a\nabla u+uv+k\alpha {ue}_r)·\nabla wdx\\ -{\int }_{\mathrm{\Omega }}\mathit{cuw}dx={\int }_{\mathrm{\Omega }}Swdx.\end{array}$$

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}\frac{\partial u}{\partial t}wdx-{\int }_{\partial {\mathrm{\Omega }}_{in}}\mathit{wuf}(r)dS+{\int }_{\partial {\mathrm{\Omega }}_L}(-a\nabla u+uv+k\alpha {ue}_r)w·\mathbf{n}dS\\ +{\int }_{\partial {\mathrm{\Omega }}_{\mathit{out}}}wu(-f(r)+\frac{L}{\pi R^2})dS-{\int }_{\mathrm{\Omega }}(-a\nabla u+uv+k\alpha {ue}_r)·\nabla wdx\\ -{\int }_{\mathrm{\Omega }}\mathit{cuw}dx={\int }_{\mathrm{\Omega }}Swdx.\end{array}$$

We impose the boundary conditions on ∂Ω_L to simplify the above equations to

$${\int }_{\mathrm{\Omega }}\frac{\partial u}{\partial t}wdx-{\int }_{\partial {\mathrm{\Omega }}_{in}}\mathit{wuf}(r)dS+{\int }_{\partial {\mathrm{\Omega }}_L}u\gamma (u)w·\mathbf{n}dS+{\int }_{\partial {\mathrm{\Omega }}_{\mathit{out}}}wu(-f(r)+\frac{L}{\pi R^2})dS-{\int }_{\mathrm{\Omega }}(-a\nabla u+uv+k\alpha {ue}_r)·\nabla wdx-{\int }_{\mathrm{\Omega }}\mathit{cuw}dx={\int }_{\mathrm{\Omega }}Swdx.$$

Following Ladyzhenskaya [39], let J(Ω) be the set of sufficiently smooth solenoidal vectors of compact support in Ω. Consider the following scalar product:

$$[v,\mathrm{\Phi }]={\int }_{\mathrm{\Omega }}{v}_{x_k}·{\mathrm{\Phi }}_{x_k}dx,$$

and the norm

$$\left|\right|v\left|\right|=\sqrt{[v,v]}$$

Now, let H(Ω) be the complete Hilbert space defined as the completion of J(Ω) in the metric corresponding to this scalar product.

Define V (Ω) to be the closure in (H¹(Ω))ⁿ of all smooth solenoidal vector fields. Then, the weak formulation of the problem is to

Find all axially symmetric solutions u ∈ H¹(Ω × J) and v ∈ (L²(Ω, H¹(J)))ⁿ ∩ L²(J, V (Ω)) such that

$${\int }_{\mathrm{\Omega }\times J}\frac{\partial v}{\partial t}·\mathrm{\Phi }\mathit{dxdt}-\mu {\int }_{\mathrm{\Omega }\times J}\nabla v:\nabla \mathrm{\Phi }\mathit{dxdt}={\int }_{\mathrm{\Omega }\times J}F·\mathrm{\Phi }\mathit{dxdt},\forall \mathrm{\Phi }\in L^2(J;H(\mathrm{\Omega }))$$

and

$$\begin{array}{l}{\int }_{\mathrm{\Omega }\times J}\frac{\partial u}{\partial t}wdxdt-{\int }_{\partial {\mathrm{\Omega }}_{in}\times J}\mathit{wuf}(r)dSdt+{\int }_{\partial {\mathrm{\Omega }}_L\times J}u\gamma (u)w·\mathbf{n}dSdt\\ +{\int }_{\partial {\mathrm{\Omega }}_{\mathit{out}}\times J}wu(-f(r)+\frac{L}{\pi R^2})dSdt-{\int }_{\mathrm{\Omega }\times J}(-a\nabla u+uv+k\alpha {ue}_r)·\nabla wdxdt\\ -{\int }_{\mathrm{\Omega }\times J}\mathit{cuw}dx={\int }_{\mathrm{\Omega }\times J}Swdxdt,\\ \text{for}\text{all}w\in C^{\infty }(\overline{\mathrm{\Omega }}\times J)\end{array}$$

Note that the volumetric flow rate is conserved throughout Ω as can be seen by the following calculation:

$$\begin{array}{ll}0& ={\int }_{\mathrm{\Omega }}\nabla ·\mathit{vdx}={\int }_{\partial \mathrm{\Omega }}v·\mathit{ndS}\\ & ={\int }_{\partial {\mathrm{\Omega }}_{in}}-f(r)dS+{\int }_{\partial {\mathrm{\Omega }}_{\mathit{out}}}(f(r)-\frac{L}{\pi R^2})dS\\ & +{\int }_{\partial {\mathrm{\Omega }}_L}v·\mathit{ndS}.\end{array}$$

If we now write Ω = {(r, θ, z): 0 ≤ z ≤ Z, 0 ≤ θ ≤ 2π, 0 ≤ r ≤ f(z)}, in cylindrical coordinates, and let Ω̃ = {(r, z): 0 ≤ z ≤ Z, 0 ≤ r ≤ f(z)}, where f(z) represents the epithelium boundary, then, converting to cylindrical coordinates and using the assumption of angular independence, the equations can be reduced to

$$\begin{array}{l}2\pi {\int }_{\stackrel{\sim }{\mathrm{\Omega }}}\frac{\partial u}{\partial t}wrdrdz-2\pi {\int }_{\partial {\stackrel{\sim }{\mathrm{\Omega }}}_{in}}\mathit{wuf}(r)rdS+2\pi {\int }_{\partial {\stackrel{\sim }{\mathrm{\Omega }}}_L}u\gamma (u)w·\mathbf{n}\mathit{rdS}\\ +2\pi {\int }_{\partial {\stackrel{\sim }{\mathrm{\Omega }}}_{\mathit{out}}}wu(-f(r)+\frac{L}{\pi R^2})\mathit{rdS}\\ -2\pi {\int }_{\stackrel{\sim }{\mathrm{\Omega }}}(-a\nabla u+uv+k\alpha {ue}_r)·\nabla wrdrdz\\ -2\pi {\int }_{\stackrel{\sim }{\mathrm{\Omega }}}\mathit{cuw}rdrdz=2\pi {\int }_{\stackrel{\sim }{\mathrm{\Omega }}}Swrdrdz.\end{array}$$