Effects of temporal association on recognition memory

Abstract

The influence of temporal association on the representation and recognition of objects was investigated. Observers were shown sequences of novel faces in which the identity of the face changed as the head rotated. As a result, observers showed a tendency to treat the views as if they were of the same person. Additional experiments revealed that this was only true if the training sequences depicted head rotations rather than jumbled views; in other words, the sequence had to be spatially as well as temporally smooth. Results suggest that we are continuously associating views of objects to support later recognition, and that we do so not only on the basis of the physical similarity, but also the correlated appearance in time of the objects.

As viewing distance, viewing angle, or lighting conditions change, so too does the image of an object that we see. Despite the seemingly endless variety of images that objects can project, the human visual system remains able to rapidly and reliably identify them across huge changes in appearance. It has been argued that recognition of an object undergoing small changes in appearance can be achieved on the basis of physical similarity to a stored view, and that a collection of such views would be sufficient to recognize an object under any transformation (1, 2). What remains unclear is how these multiple views can be linked to the representation of a single object because, particularly in the case of viewing direction changes, the object's appearance will change considerably (3). Theorists have proposed the solution that views of an object are associated on the basis not only of their physical similarity but also of their temporal correlation. Temporal correlation provides information about object identity because different views of an object are often seen in rapid succession (4–7). This paper presents results of four recognition experiments that support this proposal, although the evidence presented here suggests that spatiotemporal, rather than merely temporal, correlation is required. The work reveals that observers erroneously perceive views of two different people's faces as being views of a single person, if these views have been previously seen in a spatiotemporally smooth sequence.

Experiment I

If, as theorists have suggested (4–7), object appearance is learned by associating views on the basis of their appearance in time, then exposure to any sequence of images should cause the images to be represented as views of a single object. Hence, by exposing observers to sequences comprising two different faces, one would expect them to be worse at discriminating these two faces than pairs of faces not associated in this way.

In the following experiment, this theory is put to the test by associating pairs of faces through short sequences. To enhance the possible effects of learning, we chose the relatively difficult task of matching frontal to profile views of faces (8–10). Our aim was to associate a frontal view of one face with the profile view of another by showing the two views in a pretest training sequence. Because such large changes of view are not usually experienced in the real world, we elected to include a 45° view between presentation of the other two views. Because this view is not only halfway between the frontal and profile views in terms of viewing direction, but also in terms of the identity of the person being shown, we elected to present a 45° rendering of a full three-dimensional head morph between the two veridical heads. Despite the relatively few views, the inclusion of a 45° view gave a compelling impression of head rotation.

Methods.

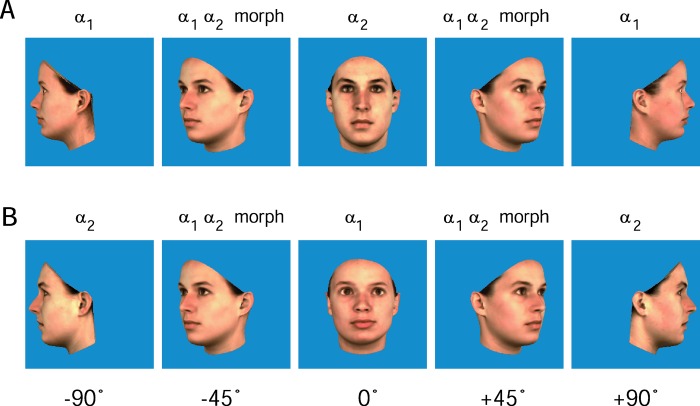
As part of the preparation for this and later experiments, the heads of 12 female volunteers were scanned to produce a set of 12 three-dimensional models. The heads were scanned by using a Cyberware 3D laser scanner (Cyberwave, Monterey, CA), which samples texture and shape information on a regular cylindrical grid with a resolution of 0.8 degrees horizontally and 0.615 mm vertically. The 12 heads were then divided equally into 3 groups: α, β, and γ (Fig. 1). Within each group, six morph heads were generated by taking the mean shape coordinates of every possible pairing, colored with the pair's mean facial pigment (11). For each face pair, a sequence of five views was generated. Each sequence contained veridical views of, for instance, face α₁ in left profile, the facial morph between α₁ and α₂ in the −45° view, then face α₂ viewed frontally, the morph at +45°, and finally back to face α₁ in right profile. For each pairing of faces, two sequences were generated, such that both faces appeared once in profile and once in frontal view, resulting in a total of 12 sequences per group (Fig. 2).

Figure 1.

(A) Twelve three-dimensional head models were generated by scanning the heads of 12 female volunteers. These scans, which contained both textural and shape information, were then cropped to remove extraneous cues such as hair. (B) The heads were split into three groups (α, β, and γ), each containing four individuals (1, 2, 3, and 4). The figure shows the grouping used for one of the 10 observers.

Figure 2.

(A) The heads were used to render two-dimensional (2D) facial images in the frontal (0°) and both profile views (±90°). A new set of head models was then generated by morphing both the shape and textural information of pairs of heads selected from a single training group. These new heads were then rendered to 2D facial images in left and right ±45° views. The images were then organized into sequences of five views. (B) The complementary sequence was also prepared in which the second head was seen in profile and the first head from the front, resulting in a total of 12 such sequences per training group.

To test the view-association hypothesis, we aimed to associate views of pairs of heads from within the same training group by showing the prepared morph sequences to our observers. Our prediction was that after association, discrimination performance for pairs of faces from within a group (WG) would be worse than for pairs of faces chosen from between groups (BG), because only faces within a group had been temporally associated.

Ten naive observers took part in the experiment, which was divided into four blocks split evenly over 2 days. Each block contained a training followed by a testing phase. During training, observers were shown all 36 of the prepared sequences twice. The precise grouping of the 12 heads was randomized for each observer to mitigate the effect of similarities between particular heads. Images in each sequence appeared for 300 ms before being replaced immediately by the next view, giving the impression of a head moving from left to right profile. By also presenting the same sequence of views in reverse order, the head was made to rotate back and forth two times.

Testing took the form of a standard same/different task, in which observers were required to indicate whether a pair of images were of the same person (match) or not (nonmatch). The first view (probe) was followed by an image mask, a second view (target), and then the mask again, each for a duration of 150 ms. The testing phase consisted of 384 test trials, in which the total number of match and nonmatch trials was the same. The number of between-group and within-group nonmatches was also balanced with 96 of each. Test images always depicted a face either directly from the front or in profile; i.e., no morphed images were tested (Fig. 3).

Figure 3.

(A) During training, subjects were exposed to the morph sequences such that for each sequence, a single head appeared to rotate twice from left profile to right and back. Examples of the training sequences can be viewed at the following web sites: http://www.kyb.tuebingen.mpg.de/bu/people/guy/morph.html and http://www.kyb.tuebingen.mpg.de/bu/people/guy/webexpt/index.html. (B) After training, individual faces were tested in a delayed match-to-sample task, in which observers were asked to indicate whether the two faces were different views of the same head. Test images always depicted a face either directly from the front or in profile, i.e., no morphed images were tested.

Subjects were made aware of the layout of the experiment and, more specifically, that they would be performing a speeded discrimination task after the training. To help motivate them to attend to the images during training, they were told that their performance in the discrimination task would be affected by what they learned in the training phase. They were, however, not told that learning might actually lead to worse performance!

Results.

Overall performance was good: on average, 74.7% of the face pairs were correctly categorized as being the same or different. In a study with the same face database, subjects with no prior exposure to the faces managed only 65.4% correct (10). This figure is lower than the worst performance of 72.6% recorded in the first block of the experiment, confirming that exposure to the morph sequences had not impaired overall performance in the task.

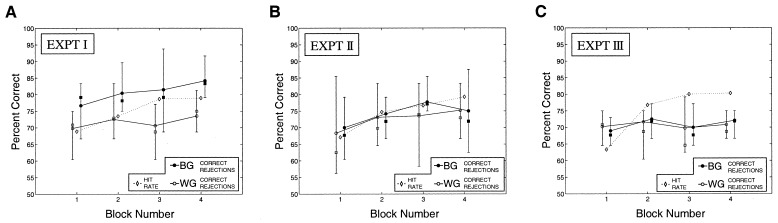
To analyze the effects of the training, signal detection techniques were used. The value of d′ was calculated for each subject and a within-subject ANOVA constructed with the block number and group membership of each pair (WG or BG) as factors. Analysis revealed a significant effect of block F(3,27) = 4.327, MS_e = 0.2605, P = 0.013, indicating a differentiation in overall performance across blocks. A Page's L analysis (12) of the ranked average d′ values revealed a strong trend L(10,4) = 274, P < 0.01, indicating that overall discrimination performance rose as a function of block.§

ANOVA also revealed a significant effect of group membership. Discrimination performance on pairs of faces chosen from WG was significantly worse than for faces chosen from BG, F(1,9) = 8.854, MS_e = 0.2782, P = 0.016. A Page's L analysis on the ranked d′ values for the WG condition revealed a small but significant trend across blocks: L(10,4) = 269.5, P < 0.05. The BG condition revealed a similar but stronger trend: L(10,4) = 276.5, P < 0.01. As can be seen from the graph (Fig. 4A), although performance rose under both conditions, performance on BG faces appears to increase more rapidly than on WG faces. A best-fit straight line revealed an increase in d′ of 0.14 per block for WG versus 0.21 for BG face pairs. However, despite this apparent difference in what is effectively learning rate, the group × block interaction fell well short of significance F(3,27) = 0.867, MS_e = 0.0563, P = 0.470.

Figure 4.

The variation in d′ for the first three experiments, in which the effect of viewing sequences of morphed face pairs on later discrimination performance was measured. (A) Discrimination performance in experiment I separated into stimuli chosen from WG that had been morphed and those from BG that had not. Note the more rapid rise in d′ for BG trials. (B) The same analysis for experiment II. Note BG and WG performance levels are indistinguishable. (C) The same analysis for experiment III. Note BG and WG performance levels are once again indistinguishable.

Although signal-detection analysis gives the best overall impression of performance changes, it is worth pointing out that the temporal association hypothesis actually predicts three quite specific effects rather than just one. First, the observers' ability to distinguish faces on nonmatch trials for WG stimuli should become worse, because the views have been erroneously associated during training. Second, their ability to recognize faces as the same during match trials should also become worse, because each face has been seen with views of other faces from within its group, but never in its veridical form. Third, performance on nonmatch trials for BG stimuli should improve, because BG views have never been seen together, whereas other associations have been forged.

As a primary indicator of different levels of performance in the various categories, it is interesting to note that the average hit rate across all trials was around 5% more than the overall WG correct rejection rate and around 5% less than the overall BG correct rejection rate, suggesting that training had differentially affected the three types of trial in the manner described in the preceding paragraph. Concentrating on the most straightforwardly comparable nonmatch trials, a new ANOVA was constructed, once again with training type and block as conditions, but now based on the Fisher Z-transformed BG and WG correct rejection rates. Here, we expect a significantly higher correct rejection rate on BG than on WG trials, which is indeed what the ANOVA revealed: F(1,9) = 6.492, MS_e = 0.3243, P = 0.031.

Overall, predictions of the temporal association hypothesis appear to have been borne out in these experiments. There are, however, various issues that must be addressed and that form the basis for the following two experiments.

Experiment II

One question raised by the first experiment is whether the use of morph faces affected recognition, in other words, whether seeing intermediate views of the faces was decisive in confusing the identity of the WG faces, rather than their being seen in smooth temporal order. To test this theory, we devised a second experiment in which the same morph sequences were presented, but now simultaneously, rather than in temporal order. If seeing the morph images was in and of itself sufficient to produce the erroneous association of views reported in experiment I, one would predict a similar effect of training under these new conditions.

Methods.

Ten observers took part in the experiments. The overall design was the same as for the previous experiment, with the exception that the five views of each training sequence were presented simultaneously. The images were presented along the circumference of a circle centered at the point of fixation. Presentation time was equal in length to the total viewing time of the sequences used in the first experiment (6,000 ms).

Results.

The results of the experiment were analyzed by using the same within-subject design of experiment I. Analysis revealed a significant effect of block F(3,27) = 5.857, MS_e = 0.2485, P = 0.003, but no effect of having seen morphed versions of the faces or not, F(1,9) = 0.133, MS_e = 0.0619, P = 0.724, (Fig. 4B). Unlike in the previous experiment, average performance hit rates differed by less than 2% from both WG and BG correct rejection rates, suggesting that simply seeing the morphs was not sufficient to affect performance on specific trial types (Fig. 5B).

Figure 5.

Percent correct performance for the three experiments. Squares represent the median and circles the mean for correct rejections; diamonds indicate the mean hit rate. Error bars represent upper and lower quartiles. (A) Results from experiment I. Note that BG correct rejection rate is consistently higher than both the hit rate and WG correct rejection rate. (B) Results from experiment II. Note that with training, the hit rate rises above the two correct rejection rates, which are themselves indistinguishable. (C) Results from experiment III. Note that, once again, the hit rate rises above the two correct rejection rates, and that they are indistinguishable.

The validity of this result was tested further for the nonmatch trials by using the Fischer Z-transformed correct rejection rates. Whereas the difference was significant in the previous experiment, no such difference was evident in this case F(1,9) = 0.002, MS_e = 0.0523, P = 0.969, suggesting that WG and BG performance levels were comparable.

From these results, it is possible to conclude that neither the viewing of morphs nor the simultaneous appearance of the five views was sufficient to associate views of the WG faces. The latter conclusion is particularly interesting in that it indicates that scanning across different views is not equivalent to seeing them located in one location, suggesting that the mechanism for learning invariance may be spatiotemporally, rather than simply temporally, triggered. However, an alternative explanation is that the mechanism is disrupted by fixational eye movements, which would seem reasonable because a change of fixation often indicates the fixation of a new object. Hence, associating across fixations would tend to lead to the erroneous association of different objects.

Experiment III

The previous experiment raises the question of whether the effects seen in the first experiment were truly caused by temporal association alone, or whether the spatiotemporal smoothness of the stimuli was a necessary component of the learning. Although we can conclude that the training of experiment II was insufficient to cause association of the magnitude seen in experiment I, it is unclear whether the absence of an effect was because of the spatial dislocation of the stimuli or the absence of the smooth spatiotemporal correlation present in experiment I. In the last of this set of experiments, we address this issue further by focusing on the need for spatiotemporal smoothness.

Methods.

The methods used were identical to those described in experiment I, with the exception that the order in which the images within a training sequence were presented was randomized. This procedure had the effect of maintaining temporal coherence between the views of the morphed heads as well as spatial location, while largely removing local spatialtemporal correlation.

Results.

Observers once again showed an increase in overall discrimination performance from one block to the next, F(3,27) = 11.841, MS_e = 0.1310, P < 0.001, but as in the previous experiment, revealed no effect of training type, F(1,9) = 0.008, MS_e = 0.1320, P = 0.930, (Fig. 4C). Overall hit rate differed from WG and BG correct rejection rates by less than 1% (Fig. 5C). Analysis of the two correct rejection rates revealed no difference in performance for the WG and BG conditions, F(1,9) = 0.044, MS_e = 0.0728, P = 0.839, showing that WG and BG performance levels were, once again, indistinguishable. Thus, presentation of the morph sequences in a continuous but spatiotemporally disrupted manner rendered training ineffectual when compared to that achieved in experiment I. Hence, on the basis of this experiment, it is not possible to say that temporal association alone is sufficient to cause association of object views. However, if it is, it is a much weaker effect than that generated by spatiotemporal association.

Experiment IV

Previous experiments have demonstrated that spatiotemporal sequences can lead to the association of image views. However, what remains unclear is whether learning truly affected the observers' representations of the faces or merely forged links between still-intact representations of individuals. That match trial performance dropped below that on BG nonmatch trials in experiment I supports the argument that the representations were indeed affected, but this experiment aims to tackle the point more directly.

The assumption of this experiment was that if one sees the frontal view of face A turn to the profile view of face B, there will be an associated subjective impression of a change in identity or facial expression. Conversely, if no such change is detected, then the profile and frontal views must appear to belong to the same unchanging face.

Methods.

Twenty observers took part in the experiment. The first 10 were shown 10 sequences of faces rotating from left to right profile, as in the training phase of experiment I. Five of the heads shown were the veridical views of a single person's head. The other five, however, were actually morph sequences of the type shown in Fig. 2. Each of these morph sequences was constructed from one of the five heads seen in the veridical sequences morphed with the head of one of five other individuals.

The observers were told that they would see heads rotating, and that some might appear to change in some way as they rotated. The observer's task was to indicate whether the heads appeared to change during rotation. The second group of 10 observers were tested on the same set of heads. The critical difference in this case, however, was that prior to testing, they saw all five morph sequences twice. During this training phase, they were once again told that they would see rotating heads, and that some might appear to distort. They were simply told to study the heads carefully, as they would be tested on a discrimination task later. The testing phase then proceeded exactly as for the untrained observers.

Results.

Untrained observers were able to distinguish most of the morph sequences from the veridical ones. Overall, they achieved a d′ of 1.011 (Table 1, Untrained). In contrast, observers who were tested after seeing the morph sequences showed the completely opposite tendency (Table 1, Trained). Their value of d′ = −1.400 was actually large and negative, demonstrating a strong tendency to choose the morph sequences as veridical. Note also that the magnitude of d′ was larger in the trained than the untrained case, although the difference was not significant, F(1,18) = 0.612, MS_e = 0.9917, P = 0.444. This difference may well be because the trained subjects had prior exposure to the stimuli, whereas the untrained subjects did not. Training with the veridical faces would presumably result in selectivity as high, if not higher, than for subjects trained on the morph sequences.

Table 1.

Stimulus-response matrices for subjects told to discriminate rotating heads containing views from more than one person (deforming), from real heads containing views from just one person (nondeforming)

Stimulus	Untrained		Trained
	Response		Response
	Deforming	Nondeforming	Deforming	Nondeforming
Deforming	0.687	0.313	0.315	0.685
Nondeforming	0.300	0.700	0.821	0.179

(Untrained) naive subjects were able to select the real heads in preference to the deforming ones (d′ = 1.011). (Trained) Prior exposure to the deforming heads, however, caused subjects to see these heads as nondeforming in preference to the veridical ones (d′ = −1.400). 

In summary, we can conclude that naive subjects were able to predict the true profile appearance of the faces without having seen them before. However, observers previously exposed to the morph sequences preferred to choose these sequences as veridical, to the exclusion of the true frontal to profile view pairings.

Discussion

The question of how humans represent objects and the mechanisms behind recognition remains under debate. We have argued that objects are represented as collections of associated two-dimensional views (6, 13, 14), consistent with the findings reported in this paper. Other explanations including either object-centered models (15–17) or structural descriptions that contain explicitly associated parts (18, 19) may well have to be modified to take into account spatiotemporal association as a key to invariance learning.

Apart from psychophysical evidence, any theory of object recognition must also attune itself to recent neurophysiology findings. Many neurophysiologists now believe that multiple views of objects are represented by collections of neurons, each selective to a combination of features within each view (20–23). Neurophysiologists have proposed that the visual system builds up tolerance to changes in object appearance over several processing stages. By the time processing has reached the temporal lobe, single cells are tuned to respond invariantly over any one of the many natural transformations (22, 24). There is good reason to think that this invariance is achieved via a final layer of processing in which the output of view-dependent neurons feeds forward to build view-invariant neurons (24). Further recording work in the same cortical areas has led to the proposal that these associations are rapidly modifiable via experience (25).

A common misconception of the multiple-view approach to object representation and recognition is that each view is equivalent to an inflexible template, selective for only one particular view at a particular scale. Such templates would not support recognition of objects from novel viewpoints (26). There is also concern that whole-object views are encoded at the level of single neurons in the style of earlier theories of object representation, since criticized for their inefficiency and susceptibility to cell damage (27–29). Both of these problems are countered by the use of a distributed feature-based recognition system (6, 30). At the neural level, many hundreds or thousands of neurons, each selective for its specific feature, would act together to represent an object. New combinations of these features could then be recruited to uniquely represent a completely new object. The upshot of this type of encoding is that although a face may be new, experience with a similar nose or configuration of mouth and eyes, for example, would provide some level of generalization for a novel face across view change. Indeed, the numerous beneficial emergent properties of a distributed representation have long been realized by neural network theorists (1, 30).

The task of reconciling theories of object recognition that have grown out of the traditional fields of human psychophysics, neuropsychology, neural networks, artificial intelligence, and neurophysiology is currently underway. The picture that is emerging is perhaps surprisingly encouraging. Certainly the concept of a distributed multiple-view-based representation of objects encapsulates much of the accumulated evidence. The results reported here are consistent with this form of representation as well as with other recent reports about the effects of temporal order on our ability to recognize objects (31–33). More importantly, the results are also consistent with neurophysiological results, which demonstrate that over long periods of exposure, single neurons become selective to images on the basis of temporal contiguity alone (7, 34). Of course, the picture is not always so clear-cut, as contrary psychophysical results have revealed (35), and many questions remain. Not the least of these is the inability of temporal association to produce a measurable effect in experiment III. Although the results of experiment III suggest that temporal association alone is less effective than smooth spatiotemporal association, they do not rule out the presence of a purely temporal mechanism of the sort Miyashita describes (7).

Conclusions

The idea that temporal information can be used in setting up spatial representations is not new and was recognized by some of the earliest researchers studying learning in cortical circuits (36). The aim of our work has been to test the temporal association hypothesis in humans and, in so doing, to provide concrete evidence for a behavioral level equivalent to the theoretical predictions and neurophysiological data cited. Our results indicate that a temporal association mechanism may indeed exist, but we were able to measure its effect only when using small more continuous changes in appearance. This, of course, makes ecological sense in that it is the type of view change experienced in everyday life, one to which we may well be best attuned.

Although the evidence presented here relates directly to face recognition, we would argue that the mechanism extends beyond face recognition to all types of object representation and recognition, consistent with recent evidence that it also affects the perception of object rigidity (31). The inescapable consequence of these findings is that the system underlying object recognition is molded by the temporal as well as physical appearance of our world.

Abbreviations

WG

within group

BG

between group