Enhanced video indirect ophthalmoscopy (VIO) via robust mosaicing

Abstract

Indirect ophthalmoscopy (IO) is the standard of care for evaluation of the neonatal retina. When recorded on video from a head-mounted camera, IO images have low quality and narrow Field of View (FOV). We present an image fusion methodology for converting a video IO recording into a single, high quality, wide-FOV mosaic that seamlessly blends the best frames in the video. To this end, we have developed fast and robust algorithms for automatic evaluation of video quality, artifact detection and removal, vessel mapping, registration, and multi-frame image fusion. Our experiments show the effectiveness of the proposed methods.

1. Introduction

Hardware improvements yield quickly diminishing returns when gathering useful information from medical images, because the optical components necessary to capture very high-quality scans become prohibitively expensive for many practical applications. The image processing community has developed several multi-frame image fusion algorithms [1, 2] that generate high-quality imagery from lower-quality imaging detectors. In this paper, we develop fast and robust multi-frame image fusion algorithms to produce wide Field of View (FOV) and artifact-free images from a large collection of narrow FOV images of varying quality.

While the proposed algorithms are general and can be adapted to a variety of image enhancement and analysis applications, this paper targets a very challenging medical imaging scenario. We address the problem of generating high-quality images from non-sedated premature infants’ eyes captured during routine clinical evaluations of the severity of Retinopathy of Prematurity (ROP). ROP is disorder of the retinal blood vessels which is a major cause of vision loss in premature neonates, in spite of being preventable with timely treatment [3]. Important features of the disease include increased diameter (dilation) as well as increased tortuosity (wiggliness) of the retinal blood vessels in the portion of the retina centered on the optic nerve (the posterior pole). Studies have shown that when the blood vessels in the posterior pole show increased dilation and tortuosity (called pre-plus in intermediate, and plus in severe circumstances), this correlates well with the severity of the ROP [4].

Thus, an important prognostic sign of severe ROP is the presence of plus disease, consisting of dilation and tortuosity of retinal vessels. Plus disease is the primary factor in determining whether an infant with ROP requires laser treatment. Unfortunately, human assessment of plus disease is subjective and error-prone. A previous study showed that ophthalmologists disagree on the presence or absence of plus disease in 40% of retinal images [4].

Semi-automated image analysis tools such as ROPtool [4] and RISA [5] show similar or even superior sensitivity and specificity compared to individual pediatric ophthalmologists when high-quality retinal photographs are obtained with the RetCam imaging system (Clarity Medical Systems, Inc., Pleasanton, CA). The full details of the procedure for using ROPTool have been previously published [6]. In summary, ROPTool displays the image to be analyzed and the operator identifies the key anatomical parts of the retina, such as the optic nerve and the vessels in each quadrant, by clicking on the image. However, RetCam is expensive and inconvenient for imaging pediatric patients, and is not commonly used during routine examinations. Instead, examination with the Indirect Ophthalmoscope (IO) is the standard of care for ROP evaluation of neonate eyes. A Video Indirect Ophthalmoscope (VIO) is a relatively inexpensive imaging system (about 6 times cheaper than RetCam) and much more convenient for capturing retinal images during IO examinations. In VIO, the physician wears a head-mounted video camera during routine IO evaluations. Unfortunately, many individual VIO frames have poor quality, and a previous study reports that only 24% of these videos can be utilized for ROP evaluation with ROPtool [7].

Several types of artifacts make the raw recorded VIO images difficult to analyze automatically, including interlacing artifacts, brightness saturation, white or black spots, and distorted colors. Frames often contain non-retinal objects, as shown in Fig. 4 (a), and have a narrow FOV. Some of these problems are highlighted in Fig. 1. Furthermore, a raw VIO video indiscriminately records every part of an IO examination, and therefore contains numerous spurious and low quality frames that need to be removed prior to any form of automated analysis.

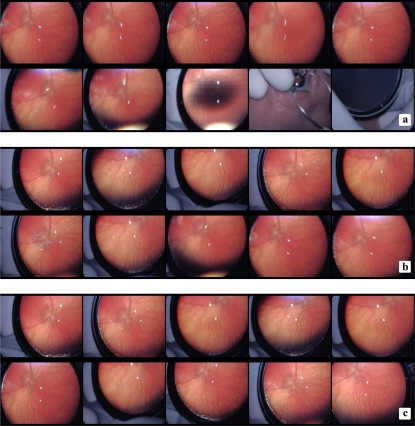
Fig. 4.

Frames classified by quality scores: Frames from a 2500-frame video ranked based on the (a) HSV and (b) spatial frequency scores. Scores decrease from left to right and top to bottom. The frames in (c) are ranked by the convex combination (7) of the two scores, with υ = 0.3. The convex combination score balances crispness with coverage. Each collage shows frames with ranks 1 through 10. Images are best viewed on screen.

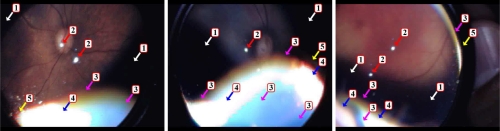
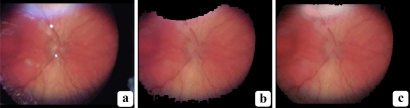
Fig. 1.

VIO frame artifacts: Three sample VIO frames, from three different videos, display a number of common artifacts. Each arrow’s number and color indicate the type of artifact: (1) (white) black regions; (2) (red) white spots; (3) (magenta) artificial colors; (4) (blue) saturation near the lens’ rim; (5) (yellow) interlacing artifacts. All but the interlacing artifacts are produced by the optics of the hand-held condensing lens.

In this paper, we develop a framework for obtaining the relevant retinal data from a VIO video in the form of a single, high quality image, suitable for analysis manually or with semiautomated tools such as ROPTool. While multi-fundus image registration methods exist, such as [8, 9], the VIO frames’ low quality and large number of artifacts and spurious objects adversely affects the performance of these methods. Our proposed video processing pipeline (Fig. 2) involves novel algorithms for: (1) rapid detection of the most relevant and highest-quality VIO images, (2) detection and removal of VIO imaging artifacts, (3) extraction and enhancement of retinal vessels, (4) registration of images with large non-translational displacement under possibly varying illumination, and (5) seamless image fusion. We validated the diagnostic usability of our technique for semi-automated analysis of plus disease by testing how well the semi-automated diagnosis obtained using our mosaics matched an expert physician’s diagnosis.

Fig. 2.

Retinal mosaicing pipeline: Our proposed pipeline generates a single, high quality mosaic from a raw VIO recording. We select frames based on a hue-saturation-value (HSV) quality score, a spatial frequency measure, and a combination of the two measures. We then remove artifacts present in the selected frames and compute a high contrast vessel map from each of them. We register the selected frames based on these maps and fuse the registered frames into a single mosaic, suitable for human and semi-automated analysis.

The rest of this paper is organized as follows: We select frames in Section 2. We then enhance the image by removing artifacts in Section 3, and map vessels in Section 4. In Section 5, we fuse the enhanced images through frame registration, color mapping, and pixel selection. We present our experimental results in Section 6 and discuss future research and clinical applications in Section 7.

2. Frame selection

Only a small fraction of the frames in raw VIO data is suitable for analysis: patient preparation and switching from eye to eye result in numerous frames that do not feature the retina. In addition, as Fig. 1 illustrates, a significant portion of retinal frames are poorly focused and are marred by artifacts that arise from the condensing lens, sensor noise, and video compression. Manually searching for the best frames in a VIO sequence is impractical. In our approach, we find retinal frames by the percentage of pixels with retina-like colors, and we estimate the degree of image focus by the ratio of the signal contents at intermediate and high bandpass frequencies. We explain these two criteria in the following subsections.

In our framework, we view each frame as an X × Y × 3 matrix I. The indexed set of N frames is denoted as I = I₁, I₂,..., I_N. A pixel position in I is given by a two-dimensional vector of integers, p = [x,y]^T. The set of valid pixel positions, such that x ∈ [1,X] and y ∈ [1,Y], is denoted by P. The value at each pixel position for a given frame is given by a 3-dimensional vector v:

$$I\left(\mathbf{p}\right)=\mathbf{v}.$$ (1)

Unless otherwise specified, v represents an RGB value with entries normalized between 0 and 1.

2.1. HSV classification

We classify pixels in the Hue-Saturation-Value (HSV) color space [10] to assign a retinal or non-retinal label to every pixel. Classification in HSV space is more robust to highlights, shadows, and texture variations than in other color spaces [11]. We use color for pixel classification because we empirically determined that retinal pixels for a given patient exhibit a narrow and consistent color distribution. Furthermore, the color distribution of any frame can be determined reliably and efficiently.

In HSV classification, we specify a closed decision boundary S in HSV space. Vectors within S are classified as retinal pixels, while those outside S are labeled non-retinal. We specify S as the Cartesian product of three intervals, S_H, S_S, and S_V. We eschew more complex boundaries for computational efficiency. We construct the set P_R of retinal pixels as those whose HSV values lie within S. A frame’s HSV score is given by the proportion of retinal pixels in the image:

$$h\left(I\right)=\frac{\left|P_R\right|}{\left|P\right|}.$$ (2)

where the bars denote set cardinality. Fig. 3 shows a sample color distribution, and Fig. 4 (a) displays a series of frames from a single video ranked by their HSV score, from highest to lowest. For further processing, we retain only a fixed number of top-score frames.

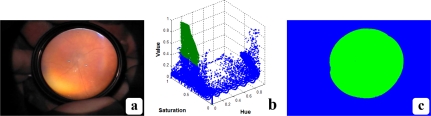
Fig. 3.

Frame HSV color distribution: (a) A sample VIO frame. (b) The scatter plot of the HSV color values of the sample frame. Retinal pixels (green), exhibit a narrow color distribution in HSV space relative to the rest of the image (blue). While the retinal pixels constitute 30% of the image, they are more tightly clustered than the non-retinal pixels. (c) Color-coded frame: retinal pixels are shown in green and non-retinal pixels in blue.

2.2. Spatial frequency estimation

Only a fraction of VIO frames are properly focused. Camera and patient motion lead to blurry frames and frames with interlacing artifacts, such as those in Fig. 1, both of which need to be discarded prior to image fusion. HSV classification accurately identifies frames with high retinal content, but does not account for these types of image degradation. We further refine the selected frame sequence I′ by determining a spatial frequency score for each frame.

A number of approaches have tackled image focus [12, 13, 14, 15, 16]. Most focusing methods measure the quantity of high frequencies in an image using image gradients [13] or high-pass filtering [12].

For our application, however, the presence of high frequency interlacing artifacts [17, 18] precludes the direct use of these techniques. When the scene motion is fast relative to the frame capture rate in interlaced video, a combing effect arises [19]. This interlacing artifact occurs across adjacent rows of a single frame, so it has very high frequency.

To account for the simultaneous presence of interlacing and blurring, we observe that relevant anatomical information in the frames is present at intermediate spatial frequencies. Very high frequencies correspond to interlacing artifacts, while blurry images only contain low frequency values. We employ differences of Gaussians [20] in the frequency domain to obtain two bandpass filters at high and intermediate frequencies. We then estimate a ratio of the norms of the intermediate and high band-pass frequencies. A high ratio reveals sharp frames with little interlacing. The use of a ratio between higher and lower pass bands was shown by Kautsky et al. [12] to be both robust and monotonic with respect to the degree of defocus. Unlike their original ratio, however, we account for high frequency interlacing by using a band-pass, rather than a low-pass image.

To obtain the band-pass filters, we first construct two low-pass Gaussian filters 𝒩_σm and 𝒩_σl:

$${𝒩}_{{\sigma }_m}=\frac{1}{\sqrt{2\pi {\sigma }_m^2}}{e}^{-\left[{\left(u-{\mu }_u\right)}^2/2{\sigma }_m^2+{\left(v-{\mu }_v\right)}^2/{\sigma }_m^2\right]},\hspace{0.17em}{𝒩}_{{\sigma }_l}=\frac{1}{\sqrt{2\pi {\sigma }_l^2}}{e}^{-\left[{\left(u-{\mu }_u\right)}^2/2{\sigma }_l^2+{\left(v-{\mu }_v\right)}^2/2{\sigma }_l^2\right]}.$$ (3)

The parameter σ controls the amount of smoothing, and we set σ_m = 2σ_l. Note that 𝒩_σm is anisotropic, while 𝒩_σl is isotropic. This is to account for the fact that interlacing only occurs between image rows, not columns. We then compute the Fast Fourier Transform (FFT) of each frame, F_h = ℱ{I}, and window it with 𝒩_σm:

$${\mathbf{F}}_m\left(u,v\right)={\mathbf{F}}_h\left(u,v\right){𝒩}_{{\sigma }_m}\left(u,v\right).$$ (4)

𝒩_σm (u,v) attenuates the very high frequencies of F_m and more so in the y direction. We then window F_m with the second Gaussian filter 𝒩_σl:

$${\mathbf{F}}_l\left(u,v\right)={\mathbf{F}}_m\left(u,v\right){𝒩}_{{\sigma }_l}\left(u,v\right).$$ (5)

Our spatial frequency measure is given by the ratio of the differences of the two operations:

$$b\left(I\right)=\frac{{\Vert {\mathbf{F}}_m-{\mathbf{F}}_l\Vert }_1}{{\Vert {\mathbf{F}}_h-{\mathbf{F}}_m\Vert }_1}.$$ (6)

The above measure is a ratio of intermediate to high band-pass frequency norms, and accounts for both interlacing artifacts and blurring: b(I) will only have a high value when the frame contains significant intermediate frequencies (vessels) and few very high frequencies (interlacing artifacts). As Fig. 4 (b) shows, our spatial frequency measure gives the highest score to frames with high vessel content and minimal interlacing distortion. The successive smoothing scheme described above is similar to a Laplacian pyramid [21], but we apply the Gaussian filters in the frequency domain with no downsampling.

The cascade of selection steps based on color and spatial frequency criteria still leaves a large number of frames for mosaicing. We reduce this number further by retaining only those frames with a high value for the convex combination of the normalized HSV and spatial frequency scores for each frame:

$$q\left(I\right)=\upsilon h\left(I\right)+\left(1-\upsilon \right)b\left(I\right),\hspace{0.17em}\forall I\in {\mathbf{I}}^{\prime }.$$ (7)

This combined score balances retinal coverage with vessel crispness, as Fig. 4 (c) illustrates.

3. Artifact removal

Lens and compression artifacts are present in most, if not all, raw VIO frames, as noted in Section 1 and as Fig. 1 illustrates. Furthermore, when frames are fused, each frame’s artifacts accumulate in the resulting mosaic. Figure 5 shows how the existence of even a few white spots per frame can overwhelm a naive fusion of several frames.

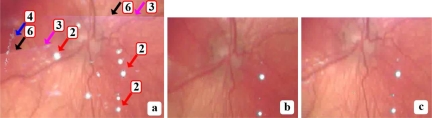
Fig. 5.

Accumulating artifacts can overwhelm naive frame fusion: (a) A close-up of the naive fusion of five frames with no artifact removal. White spots, speckles, distorted colors and other artifacts from various frames accumulate in the mosaic. Following the labeling scheme of Fig. 1, the colored arrows indicate the different types of artifacts: (2) (red) white spots; (3) (magenta) distorted colors; (4) (blue) saturation caused by the lens’ rim; (6) (black) spurious inter-frame borders. In (b) and (c), two of the originating frames are shown, which exhibit fewer artifacts in the same region.

We address these problems by directly removing artifacts and non-retinal regions from the source frames prior to further processing. To this end, we use directional local contrast filtering to remove high-saliency lens artifacts. We then fully mask non-retinal regions using HSV color classification.

Lens artifacts saturate the video’s luminance, resulting in regions of high contrast with respect to the local background. We make use of this visual saliency to detect and remove these artifacts. We model saliency based on Weber’s measure of contrast [22]:

$$c_o=\frac{m_o-m_b}{m_b},$$ (8)

where m_o is the median intensity of the object and m_b is the median intensity of the background. We use the median value, as opposed to the mean, due to its greater robustness to outliers. The Weber contrast measure is defined for grayscale images. We apply it to RGB images by considering only the green channel, as is standard practice for retinal images [23, 24] because of its stronger vessel contrast. We define a local Weber contrast measure for each individual pixel p by determining m_b from a small, rectangular neighborhood around p:

$$c_{\mathbf{p}}=\frac{{\mathbf{v}}^g-m_b^g\left(\mathbf{p}\right)}{m_b^g\left(\mathbf{p}\right)},$$ (9)

where the g superscript indicates the green channel. The exact value of $m_b^g\left(\mathbf{p}\right)$ depends on the size of the neighborhood window. In our experiments, results were robust to variations in window size, as long as the window is larger than the targeted artifacts.

The sign of c_p is different for bright (c_p > 0) and dark (c_p < 0) contrast. Regions of dark contrast include the vessels. Therefore, we do not modify these pixels. The only anatomical region in VIO frames with bright contrast is the optic nerve head, which is not diagnostically relevant for ROP. We therefore identify pixels with bright contrast that exceed a threshold value t_c and replace them with the corresponding median value:

$$c_{\mathbf{p}}>t_c\Rightarrow I\left(\mathbf{p}\right)\leftarrow m_b\left(\mathbf{p}\right).$$ (10)

Figure 6 illustrates the effects of these operations. The threshold value t_c was determined empirically in our experiments. In multi-frame fusion, bright contrast pixels can also be replaced with the corresponding pixel values from overlapping frames instead of the local median value.

Fig. 6.

The steps of directional local contrast filtering: (a) The original frame. (b) The local median for a 50 × 50 pixel filtering window V_p. (c) Pixels that far exceed the local median brightness are marked as invalid (black in the image). (d) Invalid pixels are replaced with the local median values. This removes white spots and speckles.

3.1. Distorted color adjustment

The condensing lens of the ophthalmoscope often produces saturation near its rim, clearly visible in all three samples in Fig. 1. Pixels around the edges of these regions (see magenta arrows in Fig. 1) have their hue values distorted, particularly towards magenta, because of the nearby saturation. Directly incorporating these regions into the mosaic creates novel artifacts, as Fig. 5 shows.

We minimize the hue distortion around saturated regions by replacing the hue of these pixels with the nearest hue value that lies inside the color classification surface S, effectively enlarging the frame’s retinal area. We identify the affected pixels by expanding the hue interval into S′_H = [S_Hmin – t_p, S_Hmax + t_p], where 2t_p is the extent of expansion. With S′_H, we construct a new closed boundary S′ in HSV space. We then determine the set of distorted color pixels by taking the difference of the sets:

$$S^d=S^{\prime }\backslash S.$$ (11)

We adjust the pixels that belong to S^d by shifting their hue values so that they lie within S:

$${\mathbf{v}}_{\text{HSV}}\in S^d\Rightarrow v_{\text{HSV}}^h\leftarrow v_{\text{HSV}}^h\pm t_p.$$ (12)

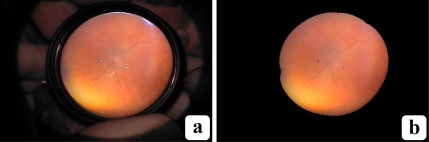
Figure 7 illustrates this adjustment. After artifact removal, we mask any pixels which fall outside the HSV boundary S to remove the remaining spurious objects such as the physician’s hands, the condensing lens’ disk, and other surrounding objects, as shown in Fig. 8.

Fig. 7.

Distorted color adjustment: (a) Frame affected by distorted colors arising from the lens’s optics. (b) HSV masking without distorted color adjustment (c) HSV masking with distorted color adjustment. Note that the retinal area is significantly larger in (c) than in (b).

Fig. 8.

HSV masking: Pixels in (a) that fall outside the HSV boundary S are flagged and discarded from further processing. Non-retinal pixels are shown as black in (b).

4. Vessel mapping

In VIO frames, the vessels are often too faint to be detected reliably. In this section, we propose a two-step algorithm to maximize the contrast between vascular and non-vascular pixels. General contrast enhancement methods [25, 26] are insufficient to address this issue because we wish to selectively enhance only the vessels in the image and not other parts of the retina. We enhance the detectability of retinal vessels through a multi-scale approach using Laplacian-of-Gaussian (LoG) filters and Gabor wavelets [27]. Filtering kernels are widely used to enhance retinal vessels [28, 24, 29, 30, 31] due to the vessels’ marked elongation and their narrow intensity distribution relative to the surrounding tissue.

4.1. LoG filter bank

The LoG filter convolves the image with a LoG operator, which is the result of convolving a low-pass Gaussian filter with a contrast-sensitive Laplace operator:

$$L_{\sigma }\left(\mathbf{p};\sigma \right)=\left({\nabla }^2𝒩\left(\mathbf{p};\sigma \right)\right)*I_g\left(\mathbf{p}\right),$$ (13)

where I_g is a grayscale version of I, “*” is the convolution operator, and 𝒩 (p;σ) is an isotropic, zero-mean Gaussian kernel with variance σ². To enhance vessels at different scales, we convolve the original image with filters that vary in the value of their scale parameter σ and retain the maximum response at every pixel:

$$L\left(\mathbf{p}\right)=\underset{\sigma }{\text{max}}{L}_{\sigma }\left(\mathbf{p};\sigma \right).$$ (14)

4.2. Gabor wavelet bank

To enhance vessel connectivity, we make use of Gabor wavelets, defined by multiplying a complex sinusoid by an Gaussian kernel [27]:

$$B\left(\mathbf{p};\lambda ,\Sigma ,\theta \right)=s\left(\mathbf{p};\lambda \right){𝒩}^{\prime }\left(\mathbf{p};\Sigma ,\theta \right),$$ (15)

where s(·) is the sinusoidal component and 𝒩 ′(·) is an anisotropic, scaled, and rotated Gaussian function. We convolve the LoG filtered image with filters of varying wavelength (λ), scale (Σ), and orientation (θ), and keep the maximum response at each pixel:

$$G\left(\mathbf{p}\right)=\underset{\lambda ,\Sigma ,\theta }{\text{max}}\left(L\left(\mathbf{p}\right)*B\left(\mathbf{p};\lambda ,\Sigma ,\theta \right)\right).$$ (16)

5. Image mosaicing

Image mosaicing refers to the process of fusing two or more partially overlapping images into a composite whole with a larger FOV [32]. Mosaicing consists of three distinct steps: (1) spatial registration, (2) color mapping, and (3) pixel selection or blending. We address each subproblem in the following subsections in turn.

5.1. Frame registration

Standard registration techniques [1, 33, 34, 35, 36, 37] produce significant alignment errors when applied to VIO frames directly: dense methods fare poorly due to low contrast and large inter-frame motion, and feature-based methods can be biased by more visually salient but anatomically irrelevant parts of the raw images, such as the lens’ rim and the various speckles.

To address these problems, we developed a three stage registration method that takes advantage of the high contrast and lack of artifacts in the Gabor vessel maps. As discussed in detail in the following paragraphs, in the first stage a global L₂-norm fit computes an approximate rigid transformation between source and target Gabor images. The second stage refines this initial estimate by matching pixels locally in high-contrast, anatomically relevant regions of the Gabor image using local rigid transformations. Finally, from the set of matched point pairs, we estimate a full affine transformation using robust L₁-norm minimization. Unlike ICP-based approaches [38, 39], our method requires only a single execution of the three stages, without any iteration. The three stages are described next.

5.1.1. Global fit

In this stage, two Gabor filtered images G_t and G_s are aligned through a rigid transformation

$${\mathbf{d}}_b,{\theta }_b=\underset{\mathbf{d},\theta }{\text{argmin}}\underset{\mathbf{d},\theta }{\text{SSD}},$$ (17)

where the sum-of-squared differences (SSD) for a translation d and rotation θ is given by:

$$\underset{\mathbf{d},\theta }{\text{SSD}}=\sum _{\mathbf{p}\in P}{\left(G_t\left(\mathbf{p}\right)-G_s\left(R\mathbf{p}+\mathbf{d}\right)\right)}^2,\hspace{0.17em}R=\left[\begin{array}{cc}\text{cos}\theta & -\text{sin}\theta \\ \text{sin}\theta & \text{cos}\theta \end{array}\right].$$ (18)

We efficiently minimize the SSD in the frequency domain [40, 41]. Specifically, we expand Eq. (18) into three components:

$$\underset{\mathbf{d},\theta }{\text{SSD}}=\sum _{\mathbf{p}\in P}{\left(G_t\left(\mathbf{p}\right)\right)}^2+\sum _{\mathbf{p}\in P}{\left(G_s\left(R\mathbf{p}+\mathbf{d}\right)\right)}^2-2\sum _{\mathbf{p}\in P}{G}_t\left(\mathbf{p}\right)G_s\left(R\mathbf{p}+\mathbf{d}\right).$$ (19)

The first term does not depend on either d or θ, so we ignore it. The last term is a cross-correlation, and the second is the sum of squares of the pixels in the warped G_s that overlap G_t. For a fixed θ, we determine the last two terms for every possible translation using phase correlation:

$$\underset{\theta }{\text{PSSD}}={ℱ}^{-1}\left\{ℱ\left\{{\left(G_s\left(R\mathbf{p}\right)\right)}^2\right\}ℱ\left\{U\left(\mathbf{p}\right)\right\}\right\}-2{ℱ}^{-1}\left\{ℱ\left\{G_t\left(\mathbf{p}\right)\right\}ℱ\left\{G_s\left(R\mathbf{p}\right)\right\}\right\},$$ (20)

where ℱ is the Fourier transform and U is an uniform weighing function over G_t. Due to frame heterogeneity, using polar or log-polar coordinates to estimate the rotation between frames [42, 43] does not yield good results in VIO. Instead, we minimize the above equation for a set of possible rotations Θ = {θ₁,θ₂,...,θ_Q}:

$${\theta }_b=\underset{{\theta }_i}{\text{argmin}}\underset{{\theta }_i}{\text{PSSD}},\hspace{0.17em}i\in \left[1,Q\right],$$ (21)

from which we obtain d_b = argmin_d PSSD_θb.

5.1.2. Local fit

The optimal SSD rigid-body warping removes large differences between the two frames. However, other deformations between the two vascular networks remain due to the condensing lens’s optics and eye motion. We use a feature-based approach to refine the rigid-body warping into a full affine transformation. This refinement consists of two steps: correspondence point matching and transform estimation. Inferring a rigid transformation requires at least two matched pixel pairs [1]; we determine between 20 and 30 pairs for both accuracy and robustness. Our initial rigid-body estimate provides a good starting value that reduces the likelihood of converging to a local optimum.

To estimate the set of matching pixel pairs, we use the Gabor responses to determine a set of K small pixel windows ${\mathbf{W}}^s=\left\{W_1^s,W_2^s,\dots ,W_K^s\right\}$ in the source image. We then find a matching window $W_k^t$ in the target image for each $W_k^s$ in the source image. These windows act as corresponding features between the two images [44].

Gabor-filtered images are highly simplified: non-vessel pixels are smoothed to a uniform value and vessels are highly concentrated near an intensity extremum. This lack of texture reduces the effectiveness of dense pixel methods and general-purpose feature detectors, such as SIFT [20]. However, Gabor-filtered images encode the maximum filter response at each pixel. The pixels with the strongest responses consistently belong to the most prominent vessels in the image. Because of this, we proceed as follows to find good locations in the source image:

The center pixel ${\mathbf{c}}_1^s$ of the first window $W_1^s$ is the pixel with the strongest Gabor response:

$${\mathbf{c}}_1^s=\underset{\mathbf{p}\in P}{\text{argmax}}{G}_s\left(\mathbf{p}\right).$$ (22)

For subsequent window centers, and to ensure that windows are not clustered together, we mask out from further consideration pixels that lie too close to previously selected centers:

$$f\left(\mathbf{p}\right)<t_{\text{d}}\Rightarrow G_s\left(\mathbf{p}\right)\leftarrow \varphi .$$ (23)

Here,

$$f\left(\mathbf{p}\right)=\underset{\mathbf{c}\in C_s}{\text{min}}{\Vert \mathbf{p}-\mathbf{c}\Vert }_2$$ (24)

is the shortest Euclidean distance from a previously chosen window center, $C_s=\left\{{\mathbf{c}}_1^s,\dots ,{\mathbf{c}}_{k-1}^s\right\}$ is the current set of window center pixels, t_d is a distance threshold, and ϕ is a value that indicates that a pixel is invalid. We then determine subsequent center pixels from the part of image that has not been masked away:

$${\mathbf{c}}_k^s=\underset{\mathbf{p}\notin P^{\varphi }}{\text{argmax}}{G}_s\left(\mathbf{p}\right),$$ (25)

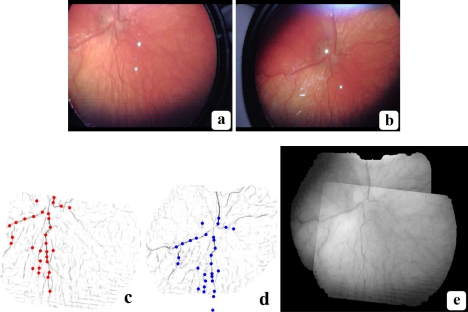
where P^ϕ is the set of masked pixels. As Fig. 9 (c) shows, this procedure distributes the points throughout the image, and places them mainly along the most prominent vessels.

Fig. 9.

Registration between two frames: (a) Source frame. (b) Target frame. (c) Source correspondence points on Gabor image. (d) Matched points on target image. Poorly matched source points are discarded. (e) Registered green channel overlay. The source frame is correctly aligned with the target frame.

For each source window $W_k^s$ thus found, we compute the best corresponding window $W_k^t$ in the target image by the FFT SSD method outlined in Subsection 5.1.1, thereby determining the most likely rotation and translation for each window pair:

$${\mathbf{d}}_k,{\theta }_k=\underset{\mathbf{d},\theta }{\text{argmin}}\sum _{\mathbf{p}\in W_k^s}{\left(W_k^s\left(\mathbf{p}\right)-W_k^t\left(R\mathbf{p}+\mathbf{d}\right)\right)}^2.$$ (26)

The matching center pixel in the target image is then

$${\mathbf{c}}_k^t=R_k{\mathbf{c}}_k^s+{\mathbf{d}}_k.$$ (27)

5.1.3. Global affine match

The third stage estimates the global affine transformation between the two images by packaging the K point matches into two 3×K matrices C′_s and C′_t containing the homogeneous coordinates c′ = [c,1]^T of the points to be aligned, and solving the following optimization problem:

$$A_{L_1}=\underset{A}{\text{argmin}}{\Vert A{\mathbf{C}}_s^{\prime }-C_t^{\prime }\Vert }_1.$$ (28)

Image noise, poor contrast and the occasional absence of corresponding retinal structures in the target image can cause poor feature matching. These outliers preclude the use of ordinary least squares minimization for Eq. (28) [45, 46]. Instead, we employ a robust L₁-norm minimization to obtain A_L1. We iteratively converge on A_L1 by using the biconjugate gradient stabilized method [47, 48] on the absolute difference ||AC′_s – C′_t||₁ to solve for the unknown affine parameters in the 3 × 3 matrix A_L1 [49].

5.2. Color mapping

VIO frames exhibit global variations in illumination that need to be compensated for prior to the final mosaicing. As illustrated in Fig. 5 (a), without color adjustment, inter-frame boundaries can form artificial border artifacts. To address this problem, we align the color space of each frame I to that of the current mosaic J by solving an absolute orientation problem in color space. Absolute orientation seeks the translation d_a and rotation matrix R_a that minimize the SSD between two matched point sets in ℝ³ space under rigid body transformations [50]:

$${\mathbf{d}}_a,R_a=\underset{\mathbf{d},R}{\text{argmin}}\sum _{\mathbf{p}\in P}{\Vert J\left(\mathbf{p}\right)-\left(RI\left(\mathbf{p}\right)+\mathbf{d}\right)\Vert }_2^2.$$ (29)

Equation (29) has a similar form to Eq. (18), but with two key differences: First, R_a and d_a are applied to the image values (three-dimensional vectors), not the positions. Second, the operation is on the RGB color images I and J, not the grayscale Gabor filtered image G. We use Horn’s closed form solution [51] to align the color spaces between two frames.

5.3. Pixel selection

Spatial registration and color mapping minimize geometric and photometric inter-frame differences, placing all pixel positions and values in a common frame of reference. We select the actual mosaic pixel values by a two step process consisting of feathering the pixels close to each frame’s retinal boundary followed by Gabor-weighted color maximization, as described next.

5.3.1. Retinal boundary feathering

A successful mosaic minimizes inter-image seams. To reduce the visual impact of image borders, we attenuate pixel values near the edge of the valid retinal data by weights related to their Euclidean distance to the closest non-retinal pixel:

$$w_{\text{E}}\left(\mathbf{p}\right)=\underset{{\mathbf{p}}_i\notin P_R}{\text{min}}{\Vert \mathbf{p}-{\mathbf{p}}_i\Vert }_2,$$ (30)

where P_R is the set of retinal pixels in I. This weighting is also known as feathering [32]. However, using the Euclidean distances as weights directly produces excessive gradation. We apply a logistic sigmoid function to w_E to enforce feathering only near the retinal boundary:

$$w\left(\mathbf{p}\right)=\frac{1}{1+e^{-\lambda w_{\text{E}}}\left(\mathbf{p}\right)},\lambda >0$$ (31)

where λ controls the speed of weight decay. Since w_E(p) is non-negative, w(p) ∈ [0.5,1].

5.3.2. Gabor-weighted color maximization

For the final pixel value selection, we weigh the color data from each frame by the corresponding Gabor responses. We determine the final mosaic in two steps. First, we compute the brightest value of each color vector’s components independently at each pixel position, and across all N′ images to be merged:

$$M_C^h\left(\mathbf{p}\right)=\underset{n}{\text{max}}{I}_n^h\left(\mathbf{p}\right),\hspace{0.17em}n\in \left[1,N^{\prime }\right],$$ (32)

Here, I has been spatially and photometrically registered, and the h superscript indicates an RGB color channel. We then construct a complement Gabor mosaic separately:

$${\widehat{M}}_G\left(\mathbf{p}\right)=\underset{n}{\text{min}}{\widehat{G}}_n\left(\mathbf{p}\right),\hspace{0.17em}n\in \left[1,N^{\prime }\right].$$ (33)

As noted in Section 4, in a complement image, the image values are inversely proportional to the filter responses. We use the complement Gabor images in order to keep vessels darker than the surrounding tissue. The final mosaic is a convex combination of the two mosaics:

$$M=\alpha M_c+\left(1-\alpha \right){\widehat{M}}_G.$$ (34)

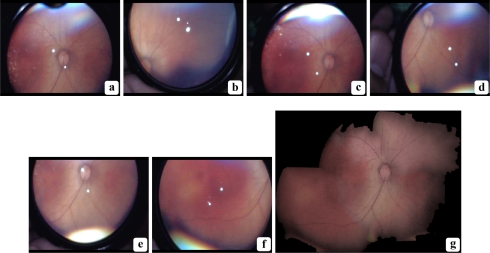
In Section 6, we empirically determined the best value of α for the quantitative experiments. Figures 10 and 11 show two mosaics constructed using this method. They illustrate that our proposed pipeline can convert raw videos of the quality represented by Fig. 4 into seamless mosaics of a neonate’s retina. These mosaics not only extend the FOV of the original frames, but significantly reduce the artifacts and spurious data found in the constituent images.

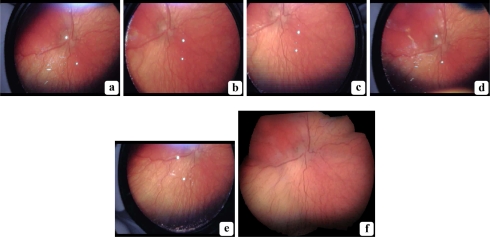
Fig. 10.

VIO mosaic: A mosaic generated from five frames selected from a single VIO video. (a)–(e): each original frame; (f): the five-frame mosaic. Note the larger FOV of the mosaic relative to each individual frame, and the lack of artifacts in the final image. All images are at the same scale, and are best viewed on screen.

Fig. 11.

VIO mosaic: A mosaic generated from six frames selected from a single VIO video. (a)–(f): each original frame; (g): the six-frame mosaic. Note the larger FOV of the mosaic relative to each individual frame, and the lack of artifacts in the final image. All images are at the same scale, and are best viewed on screen.

6. Clinical experiments

The mosaics of Fig. 10 and 11 verify that our pipeline produces wide FOV mosaics with minimal artifacts that are suitable for human visual inspection. Nevertheless, while manual IO is the standard of care for ROP, quantitative approaches to ROP and plus disease diagnosis are becoming increasingly important. It is therefore crucial for our methodology to be suitable for automated and semi-automated processing as well. As a motivating example, we first examined both of these mosaics and the best, hand-picked frame for each source video with ROPTool. As Fig. 12 shows, the mosaics allowed us extract longer, more numerous vessels in less time compared to the single frames.

Fig. 12.

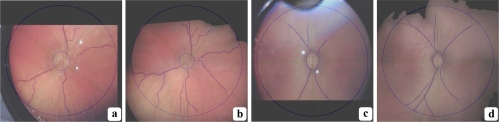
ROPTool analysis comparison: ROPTool analysis of the mosaics of Fig. 10 and 11 as well as the best hand-picked frames from the corresponding videos: (a), (c) Hand-picked frames; (b), (d) Mosaics. Images are best viewed on screen. The blue lines inside the large blue circle indicate the vessel paths obtained with ROPTool. At least one, but preferably two major vessels from each quadrant are needed to provide a full ROP diagnosis. ROPTool is able to extract longer and more numerous vessels when analyzing the mosaics than the hand-picked frames. Furthermore, ROPTool analysis of the mosaics is faster due to fewer ROPTool mistakes. The examination times (in minutes) were: (a) 2:45, (b) 2:00, (c) 2:35, (d) 1:30

To more broadly verify the clinical usefulness of our proposed approach, we carried out a pilot study using ROPTool [6] in which we compared our automatic mosaicing pipeline to the current state-of-the-art procedure for semi-automatic ROP analysis. This procedure relies on manually selected frames captured from a live feed during the actual IO examination. First, while the physician carries out the IO examination, the recorded video feed is displayed on a bedside computer. Meanwhile, an assistant observes the live feed and manually selects a few dozen potentially good frames by clicking on a frame capture button. The physician later sifts through the captured frames and selects the two best frames, one for each eye. Finally, the physician performs the ROPTool analysis on the two selected frames.

There are a number of drawback to this procedure. The first is that it requires careful manual examination of the recorded video feed. Any loss of concentration by the assistant can result in valuable frames been overlooked. Second, the frame capture operation is approximate due to two sources of lag: (1) the time between when the assistant sees a good frame and when he or she clicks the screen capture button, and (2) the time between which the computer registers the mouse click and when it performs the frame grabbing operation. Furthermore, even if the assistant manages to select the single best frame in a video, it can still be affected by limited FOV and numerous imaging artifacts. Finally, even in this best-case scenario, most of the video’s information is discarded. In the following three subsections, we first detail the methods used to obtain and analyze the VIO data, then describe the exact mosaicing steps and parameters used, and finally present and discuss the ROPTool results.

6.1. Methods

We obtained 31 VIO videos from six ROP examination sessions performed by two expert pediatric ophthalmologists on 15 different patients at the Neonatal Intensive Care Unit at the Duke University Medical Center in Durham, NC. All the videos were recorded using a Keeler Wireless Digital Indirect Ophthalmoscope (Keeler, Instruments Inc, Broomall, PA). The videos in all the sessions were captured at a resolution of 720 × 576 pixels in 24-bit color and saved as Audio Video Interleaved (AVI) files. During each IO examination, an assistant observed a live version of the video feed at 30 fps and manually selected several dozen frames per video. After the IO examination, we then separately constructed a full mosaic from each video with our proposed method. For consistency, all manually selected images and mosaics are of each patient’s right eye.

Dr. Cabrera, an expert pediatric ophthalmologist, independently carried out a ROPTool analysis of both types of images. She first selected the best manual frame for each right eye from the several dozen captured by the assistant and then performed the ROPTool analysis on this frame and the corresponding mosaic. She first located the optic nerve. Based on its location, ROPTool divided the image into four quadrants. She then clicked on a point within each visible vessel in the image and ROPTool traced the rest of the selected vessel. She then determined if the image was traceable, based on the criteria detailed in [6]. In summary, a vessel is deemed traceable if it can be traced for a distance of at least one optic disc diameter outward from its junction with the edge of the optic nerve and a quadrant is traceable if there is at least one traceable vessel in it. An image as a whole is traceable if at least three out of four quadrants are traceable. ROPTool then provided a diagnosis based on the tortuosity and dilation of the traced vessels. She then recorded the examination time and compared ROPTool’s diagnosis based on the image with the diagnosis given by either Dr. Wallace or Dr. Freedman during the IO examination.

6.2. Implementation details

To obtain a mosaic from a VIO video, we first empirically determined suitable parameter values for the dataset based on the mosaics in Fig. 10 and 11. We used the same set of parameters for all videos. For every video, we then applied HSV classification to every frame using an interactively chosen retinal pixel value v. We converted this RGB pixel value into HSV: v_HSV and set it as the center of the closed surface S. We only needed one pixel for every video. We constructed S by forming three intervals: $\left[{\mathbf{v}}_{\text{HSV}}^h-t_h,{\mathbf{v}}_{\text{HSV}}^h+t_h\right]$, $\left[{\mathbf{v}}_{\text{HSV}}^s-t_s,{\mathbf{v}}_{\text{HSV}}^s+t_s\right]$, $\left[{\mathbf{v}}_{\text{HSV}}^v-t_v,{\mathbf{v}}_{\text{HSV}}^v+t_v\right]$. The value for t_h, t_s and t_v was 0.1.

The frames with the highest 10% of HSV scores (generally 100 to 300 frames per video) were then analyzed using the spatial frequency measure. We used smoothing parameters σ_m = 0.25 and σ_l = 0.1. We obtained a convex combination score of the two measures using υ = 0.3, in Eq. (7). The top 20% to 50% of those frames–2% to 5% of total frames, about 20 frames per video–were saved as TIFF files. Retaining a higher percentage of frames was not needed since frames with lower percentile scores were rarely of interest. From these 20 images, a small number (usually 4 to 6) were manually selected per video, in order to ensure that they all corresponded to the right eye. For each of the selected frames, we applied directional local contrast filtering with a removal threshold of 1.1 above the frame’s median value. We applied multiscale LoG (σ = [0.11,0.51], with step-size σ_Δ = 0.1) and Gabor wavelet filtering (a = 10,b = 10,u = 0.05,v = 0.05, β = 30,θ = [0,170], with step-size θ_Δ = 10) for vessel mapping. The most central frame was selected as the target frame and the remaining frames were registered in two stages. We determined a global fit by iteratively searching over a range of r rotations with r_Δ stepsize. We used values r = [−π/12,π/12] and r_Δ = 3. For each rotation, we determined the optimal translation using phase correlation. We selected 30 control points on the source image, each with a 20 pixel buffer zone, and locally registered 10 × 10-pixel windows around each one. We estimated the full affine matrix by applying gradient descent on the sum of absolute differences between the matched pixel pairs. We used an update weight γ of 0.01 and a maximum of 5000 iterations. We used absolute orientation to map every source frame’s color to the same target frame. We used a λ of 0.1 for feathering the borders of the valid retinal regions in each frame. Finally, the mosaic was composed using Gabor-weighted color maximization, treating each channel separately. To determine the optimal value for α, Dr. Cabrera analyzed a number of mosaics using ROPTool for three settings of α: [0.25,0.5,0.75]. Her analysis established that α = 0.75 produced the best results.

6.3. Results

Table 1 presents the results from our pilot ROPTool study, in which we analyzed 31 hand-picked frames and 31 corresponding mosaics from the right eyes of 15 neonate patients. As Dr. Cabrera observed, the automatically constructed mosaics allowed ROPTool to extract longer vessels with fewer tracing errors compared to even the best hand-picked frames. Most importantly, ROPTool’s diagnosis was more often in agreement with the ROP experts’ diagnosis for our mosaics than for the hand-picked frames. The difference is particularly striking for the percentage of correctly diagnosed images relative to the total number of images (77.4% vs. 61.3%); the total number of images was 31 in both cases. This value represents how often ROPTool is clinically valuable and suggests that our mosaicing pipeline improves the diagnostic accuracy of semi-automated ROP analysis by almost 20%. Finally, in spite of being able to trace more vessels, our mosaics allow the operator to reduce the tracing time by an average of 37%.

Table 1.

Quantitative ROPTool analysis of 31 mosaics and their corresponding best hand-picked frames

Image type	Traceable	Diagnosis agreement	Tracing time (in minutes)
Mosaics	30 (96.8%)a	24 (80.0%)b (77.4%)a	1:41 (± 0.03)
Handpicked images	26 (83.9%)a	19 (73.1%)b (61.3%)a	2:42 (± 0.04)

^aPercentage of total frames (31).

^bPercentage of traceable frames.

7. Conclusions

We have developed an effective and efficient pipeline for constructing a high quality, large FOV mosaic from a raw VIO video. The mosaic is suitable for human or machine analysis and diagnosis. Our initial results suggest that the use of mosaics allows semi-automated ROP analysis programs such as ROPTool to better match the diagnostic assessments of human experts. By removing artifacts, mapping vessels in different frames and fusing the automatically selected best frames, we were able to overcome the numerous complications that arise from VIO recording.

The next step in our research will involve further validating the diagnostic utility of these mosaics by means of a larger scale clinical study. We will more precisely determine the statistical significance of using our mosaics for accurate human and semi-automated ROP diagnoses.

The algorithms presented in this paper were mainly discussed for the specific task of VIO retinal imaging. However, the mathematical techniques are general and can be modified to enhance the quality of other en-face imaging modalities. Moreover, the 2-D methodology presented here may be generalized for creating 3-D mosaic. Generalizing our methods to confocal scanning laser ophthalmoscopy and spectral domain optical coherence tomography is part of our ongoing work [52].