Fast macro-scale transmission imaging of microvascular networks using KESM

Abstract

Accurate microvascular morphometric information has significant implications in several fields, including the quantification of angiogenesis in cancer research, understanding the immune response for neural prosthetics, and predicting the nature of blood flow as it relates to stroke. We report imaging of the whole mouse brain microvascular system at resolutions sufficient to perform accurate morphometry. Imaging was performed using Knife-Edge Scanning Microscopy (KESM) and is the first example of this technique that can be directly applied to clinical research. We are able to achieve ≈ 0.7μm resolution laterally with 1μm depth resolution using serial sectioning. No alignment was necessary and contrast was sufficient to allow segmentation and measurement of vessels.

1. Introduction

The ability to acquire high-resolution three-dimensional images of microvascular structure has a significant impact in clinical research, particularly in the study of angiogenesis. Angiogenic therapies have shown promise in cancer research, where manipulating microvessel growth can have a direct effect on tumor size and ability to metastasize. The quantification of microvascular structure is important for evaluating angiogenic cancer therapies designed to control blood flow to tumors [1, 2]. Microvascular structure is also a major factor in the immune response to neural prosthetics [3]. A strong understanding of microvasculature may provide insights into limiting damage or supressing immune response to neural implants. Finally, microvascular reconstruction can be used to aid in understanding of blood flow as it relates to stroke and vascular disease [4] and in quantifying vascular remodeling in implanted tissue [5].

We report the use of Knife-Edge Scanning Microscopy (KESM) for imaging of the whole mouse brain microvascular structure in a timespan useful for evaluation in clinical research. The proposed technique produces high-contrast three dimensional images at a resolution of 0.6μm × 0.7μm × 1.0μm. At the imaging rate and resolution that we describe, a 1cm³ tissue block requires ≈50 hours to image. The data produced are high contrast and can be segmented using thresholds to build a high-resolution model. We show visualizations of the large-scale vascular network and demonstrate the effectiveness of vessel segmentation using threshold-based skeletonization algorithms and level-sets.

2. Previous Work

Current methods for both in vivo and in vitro imaging of microvasculature are time consuming and the resulting data are difficult to reconstruct. Studies of vascular morphometry have been performed on human brain slices perfused with India ink and imaged using a confocal microscope at a reported resolution of approximately 1.22μm × 1.22μm × 3μm [6, 7]. These studies rely on individual tissue sections for reconstruction since imaging depth is limited by light penetration into the sample and contrast loss due to scattered photons.

The only methods that we are aware of for potentially constructing a complete microvascular map of macro-scale three-dimensional tissue samples are All-Optical Histology [8] and multi-scale Synchrotron Radiation Micro Computed Tomography (SRμCT) [9].

All-optical histology [8] uses a multi-photon microscope to image to a designated depth using optical sectioning. The imaged tissue is then ablated using a femto-second laser and optical sectioning continues at the new block face. One major advantage of this technique is that transgenic animals with targeted expression of fluorescent proteins can be used to quantitatively determine the relationships between cells and microvessels. However, the low speed of multi-photon microscopy currently makes imaging of cm³ tissue samples impractical.

Heinzer et al. [9] performed a multi-scale morphometry study on the mouse brain using bench-top Micro-CT in conjunction with high-resolution imaging with Synchrotron Radiation (SR). CT imaging was performed on a cast created by perfusing a polymer resin (polyurethane 4ii) [10] through the vascular system and dissolving the surrounding tissue. They were able to achieve an isotropic voxel size of 1.4μm³ by limiting scans to cylindrical regions-of-interest (ROI) 1.4mm in diameter and 1.4mm deep. ROI imaging required 88 minutes using an SRμCT facility. At this rate, a 1cm³ tissue block would require approximately one month to image at constant operation.

KESM imaging has been demonstrated on large-scale tissue samples, such as the whole brain, using cellular stains like thionin [11]. These methods can be used to reconstruct microvessels, since cell bodies are dyed and vascular networks appear transparent. This technique is low contrast and requires complex methods for segmentation [12]. In addition, thionin requires 1–2 months for diffusion staining and approximately 3–4 weeks when the dye is perfused transcardially.

Whole-brain imaging of fibrous neuronal structures has been performed using tissue samples stained with Golgi-Cox [11] at 10X magnification while more recent work by Li et al. [13] has adopted these techniques to perform imaging of Golgi-stained brain tissue using a 40X (0.8NA) objective. However, Li et al. perform imaging in reflection which requires the use of reflective stains that must be applied en bloc. The only example of this that we are aware of is Golgi, which (a) is highly specific and applicable to only brain tissue, (b) stains less than 1% of the cells and cellular structures, and (c) stains a large number of features that are below the diffraction limit and cannot be resolved with standard optical microscopes using visible light. These include neural and glial processes. This limits the applicability of reflection in KESM, particularly in clinical research where a quantitative understanding of the tissue’s complete structure is necessary. In addition, the proposed Golgi staining must be performed en bloc, requiring over 180 days to apply to a whole-brain tissue sample.

The method that we describe uses transmission illumination to perform whole-brain imaging, and therefore does not depend on reflective stains. In addition, use of the diamond knife as an optical instrument provides greater illumination near the knife tip, improving imaging speed and signal-to-noise. This allows us to use stains that label entire anatomical components, such as the mouse brain microvascular system, in time-scales more conducive to large-scale clinical research.

3. Methods

Vascular staining was performed using India ink perfusion, which has been demonstrated on several different sample types including brain [14], bone [15], and muscle [16]. The mouse was deeply anesthetized and then perfused transcardially with 4% buffered paraformaldehyde followed by 3cc of India ink. The brain and spinal cord were then removed and embedded in Araldite plastic following a standard protocol [17].

The tissue embedding requires 1–3 weeks, depending on the size of the tissue sample, for full infiltration. However, staining and embedding is a relatively inexpensive process and several trials can be performed in parallel in order to achieve maximum imaging throughput. In contrast, tissue preparation for SRμCT requires ≈ 2 days to form the hardened polyurethane 4ii cast followed by ≈ 2 days for dissolving the surrounding tissue. Confocal imaging requires only india-ink perfusion and fixation, which can be done in a matter of hours, while all-optical histology can be performed on unembedded and unstained tissue. Compared to previous whole-brain imaging methods, the proposed technique is significantly faster than the Nissl staining methods described in our previous work (≈ 3–4 months) [18] and Golgi staining performed by Li et al. (over 180 days) [13].

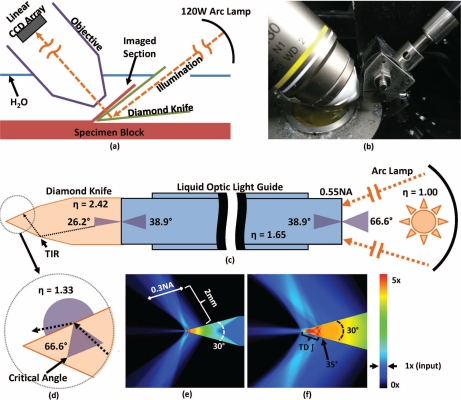
Imaging was performed using Knife-Edge Scanning Microscopy (KESM), a high-throughput optical technique for digitizing three-dimensional tissue samples using concurrent imaging and serial sectioning [18] (Fig. 1(a)–1(b)). The tissue specimen was mounted on a three-axis stage composed of an Aerotech ABL2000 air-bearing stage (x-axis), an ALS130 linear drive stage (y-axis), and an AVL112 vertical lift stage (z-axis). The specimen was submerged in water to improve the optical resolution. This also provides a method for removing ablated sections by pulling them out of the specimen tub using an Iwaki magnet pump (3.1 gal/min). Tissue sections were cut and imaged simultaneously by moving the embedded specimen while keeping the optics and cutting tool stationary. The tissue was removed in 1.44mm-wide ribbons across the specimen surface (Fig. 2(d)).

Fig. 1.

Knife-edge scanning microscopy. Serial sections are concurrently cut and imaged under water (a–b). Imaging is performed in transmission mode by sending illumination through a diamond cutting tool. Image capture is synchronized with stage position and performed using a line-scan camera. Illumination is provided using a mercury vapor short arc lamp to send light to the knife through a liquid-optic light guide (0.55NA, η = 1.65). Geometric angles of the refracted light are shown for each interface (c). Total internal reflection (TIR) within the diamond knife at the diamond/water interface results in light scattering and emission through the knife tip when the incident angle is less than the critical angle (33.3°) for a diamond knife (η = 2.42) immersed in water (η = 1.33) (d). The density of illumination around the knife is estimated using a first-order Monte Carlo simulation (e–f). The amount of scattering is determined by the NA of the light guide. Light intensity is shown as a factor of input intensity using the associated color map. Imaging is performed using time-delayed integation (TDI) as the tissue moves along the 35° bevel at the knife tip. Using TDI increases the SNR and increases the amount of scattered illumination used to construct the final image.

Fig. 2.

(a) Single coronal KESM section of the mouse cerebellum and mid-brain and closeup showing a (b) 500μm and (c) 200μm view of the same section. (d) A single tissue cross-section at any depth z is composed of several adjacent sections with a width that falls within the objective FOV.

Physical sectioning allows z-axis resolution beyond the limits of the point-spread function (PSF) produced by the objective. This is achieved by eliminating underlying tissue that would normally contribute out-of-focus and backscattered light to the image [19]. In addition, higher intensity illumination is used to increase the signal-to-noise ratio (SNR). The tissue section is imaged using a linear charge-coupled device (CCD) array. Image capture was triggered by an LN noncontact linear encoder oparating on the x-axis stage, providing under 0.2μm resolution. TDI was triggered every 0.7μm. This is slightly below the maximum resolution of the objective based on the Nyquist limit (≈ 0.6μm), however sub-sampling is necessary when incorporating TDI to compensate for slight compression (≈ 15%) of the tissue along the cutting direction. The x-axis sampling rate is determined experimentally for the embedding medium by adjusting the trigger rate until a sharp image is achieved. The trigger rate is constant for the entire volume. Performing imaging during the sectioning process also allows continuous imaging for large tissue samples. This principle has been demonstrated for samples ≈1cm³, such as the whole mouse brain [11, 13].

The tissue sample was imaged through a Nikon Plan Apo 10X (0.3 NA) water-immersion objective with a field-of-view of 2.4mm. The light was collimated at the source and directed through the diamond knife using a liquid light guide attached to an X-Cite 120 with a 120W mercury vapor short arc lamp (Fig. 1(c)). Time-delayed integration is used to increase SNR, reduce lighting irregularities at the knife surface, and collect an increased number of scattered photons.

An average speed of 22mm/sec was used for sectioning and imaging with an average deviation of 2mm/sec. Varying the velocity reduces chatter by limiting the reinforcement of sinusioidal variations on the tissue surface [20]. Line-scan imaging is synchronized with stage position so that variations in imaging speed do not affect resolution or image quality. However, higher velocities reduce image intensity by decreasing exposure time. Image intensity is therefore scaled based on velocity so that the intensity across all images is normalized.

Before images are stored, cyclical patterns due to AC power fluctuations in the light source are removed. While these patterns are simple to model, subtle changes in phase and wavelength vary for each slice. These patterns are removed by scaling each row in the image by the median intensity of that row. This is a modification of the mean-rescaling method proposed previously [21] and does not result in the suppression of high-frequency components. A notch filter applied in the Fourier domain of the raw image could also be used [13], however this will result in some blurring along the cutting direction. No image processing techniques beyond normalization and de-striping are applied, and these operations can be performed parallel to imaging.

The resulting data set is ≈ 2TB in size and composed of ≈10k coronal cross-sections. Each cross-section of the brain was cut at 1μm thickness, resulting in a final voxel size of 0.6μm × 0.7μm × 1.0μm. This is sufficient to detect and resolve all microvessels in the mouse brain based on the previously-reported minimum diameter of ≈ 4μm, determined using SRμCT and validated with serial electron microscopy (EM) [9].

4. Evaluation

The difference in the index of refraction of the diamond knife (η = 2.49) and surrounding water (η = 1.33) result in total internal reflection (TIR), focusing illumination near the knife tip. A Monte Carlo ray-tracing simulation of light through the diamond knife was used to estimate the amount of light from the arc lamp that contributes to image formation (Fig. 1(e)–1(f)). Approximately 10.4% of the light from the source was passed through the tissue section and captured by the objective and CCD array. The contribution of the source lamp in a reflection system was estimated by assuming a uniformly illuminated circle of Kohler illumination with a diameter equal to the field-of-view (FOV) of the objective. The fraction of light passing through the imaged tissue region is therefore defined by:

$$F=\frac{2\Delta x}{\pi r}$$ (1)

where r is the radius of the Kohler illumination (half the width of the imaged tissue slice) and Δx is the pixel size in the cutting direction. With a 96-register TDI camera utilizing the full FOV of the proposed objective (Δx = 0.7μm, r = 1.2mm), the estimated contribution of light is ≈ 3.56%. In both reflection and transmission cases, we assume that the collector NA is identical and that the tissue section causes minimal light scattering.

Tissue samples from the data set were then reconstructed and visualized for evaluation. Volumetric images were loaded into memory as ≈ 512³ pixel blocks. A threshold was first applied to segment vessels from the background. A dilation filter was then used to fill holes caused by detector noise and missing slices. We used topology-preserving thinning to create a 1-pixel thick volumetric skeleton [22, 23]. We then computed the distance transform by solving the Eikonal equation

$$\left|\nabla u\left(\mathbf{x}\right)\right|=F\left(\mathbf{x}\right)$$ (2)

for a constant velocity value of F(x) = 1. Boundary conditions are specified such that u(x) = 0,x ∈ Γ, where Γ is the set of all voxels that lie on the extracted skeleton. The radius of each vessel is shown along with the corresponding color-map in Fig. 3(h)–3(i). Segmentation and thinning were implemented using the Insight Toolkit (ITK) [24] while the solution to the Eikonal equation (Eq. 2) was found using the Fast Marching Method [25].

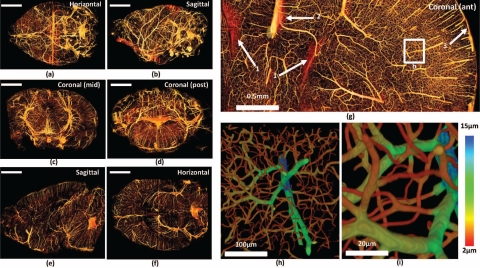
Fig. 3.

Visualization of the whole-brain vascular data set. The whole downsampled brain is shown (a–b) along with cross-sections composed of ≈ 200 slices (c–f). Scale bars = 2mm. (g) Close-up of an anterior coronal section through the cortex. Features labeled are (1) surface of the lateral ventricles, (2) Pericallosal artery, and (3) the cortical surface with descending microvessels. (h–i) Close-up of a volume reconstruction of the labeled region. Color value indicates estimated vessel radius computed by performing a distance transform on the medial axis.

A quantitative method described by Cassot et al. [14] to validate the accuracy of vascular models is the percentage of disconnected or disrupted segments, since the vascular network should be completely connected (with rare exceptions such as pathological endings and angiogenesis). Their models are able to achieve 89% connectivity in the human cortex [14]. In comparison, our methods are able to achieve 97.3% connectivity using similar thinning methods applied to a series of 512³ sample volumes. 99.2% connectivity can be achieved after applying proposed repair methods [12]. In addition, KESM does not have the ability to re-image data in the event of an error. Improperly imaged sections therefore must be eliminated. In this experiment, ≈1.1% of the sections were damaged or unusable.

Raw images of the resulting data set are shown in Fig. 2(a)–2(c). Volume visualizations of cross-sections (≈1000 pixels thick) are shown in Fig. 3(a)–3(f) in standard orthogonal planes through the data set. A close-up view of the cerebral cortex is shown in Fig. 3(g). Figure 3(h)–3(i) demonstrate the use of the distance transform to represent radius on the segmented isosurface using a color-map.

5. Conclusion and Future Work

In this paper, we have shown that microvascular imaging can be performed on a large scale (≈ 1cm³) using KESM with India ink perfusion. The proposed method has direct applications in angiogenic studies and brain microvascular research. In addition to providing smaller voxel sizes than previous data sets used to study microvessel morphometry, the proposed techniques are substantially faster than previous methods, allowing imaging of an embedded 1cm³ specimen in approximately 50 hours. Human intervention is required only for staining, embedding, and initialization of the imaging process. Note that this technique is destructive, and therefore provides a static image of a tissue sample at the time of embedding. However, KESM allows morphometric measurements that are far more detailed than in vivo measurements, such as the blood-oxygen level dependence (BOLD) response measured in functional MRI and the use of ultrasmall paramagnetic iron oxide contrast agents to indirectly measure vasculature in standard MRI [1]. As such, our proposed imaging method offers an alternative to time-consuming histological reconstruction when detailed morphometry is required. In addition, the imaging speed provided by transmission KESM may also provide an alternative to in vivo studies in cases where accurate microvascular quantification outweighs the need for time-resolved results.

For target applications in biomedical and clinical research, tissue preparation can be performed in parallel in order to amortize embedding time across multiple trials and achieve the maximum imaging rate. However, tissue preparation becomes a bottleneck for possible applications in diagnosis, such as 3D imaging of lesions and tumor biopsies. There are several avenues for future work in this area, including (a) the evaluation of faster embedding methods and (b) use of polymer casts which do not require tissue infiltration.

The current bottleneck in KESM imaging is the rate at which data can be transmitted across the PCI bus. Current solutions include recent advances in CameraLink protocols, buffering, and compression. However, when working with multi-terabyte data sets, we find that the most time-consuming component is image processing and modeling. We believe that there are significant steps that can be made in the area of parallel image processing, particularly using GPU-based methods, for high-throughput data processing.

The vascular data set imaged during this study is publicly available through the KESM Brain Atlas (kesm.cs.tamu.edu) [26]. The software used for skeletonization, level set segmentation, and Monte Carlo simulation is available at the Brain Networks Lab (BNL) website (http://research.cs.tamu.edu/bnl/static/software.html).