Distributed Lag Linear and Non-Linear Models in R: The Package dlnm

Abstract

Distributed lag non-linear models (DLNMs) represent a modeling framework to flexibly describe associations showing potentially non-linear and delayed effects in time series data. This methodology rests on the definition of a crossbasis, a bi-dimensional functional space expressed by the combination of two sets of basis functions, which specify the relationships in the dimensions of predictor and lags, respectively. This framework is implemented in the R package dlnm, which provides functions to perform the broad range of models within the DLNM family and then to help interpret the results, with an emphasis on graphical representation. This paper offers an overview of the capabilities of the package, describing the conceptual and practical steps to specify and interpret DLNMs with an example of application to real data.

1. Introduction

The main purpose of a statistical regression model is to define the relationship between a set of predictors and an outcome, and then to estimate the related effect. A further complexity arises when the dependency shows some delayed effects: in this case, a specific occurrence of a predictor (let us call it an exposure event) affects the outcome for a lapse of time well beyond the event period. This step requires the definition of more complex models to characterize the association, specifying the temporal structure of the dependency.

1.1. Conceptual framework

The specification of suitable statistical models for delayed effect, and the interpretation of their results, is aided by the development of a proper conceptual framework. The key feature of this framework is the definition of an additional dimension to characterize the association, which specifies the temporal dependency between exposure and outcome on the scale of lag. This term, borrowed by the literature on time series analysis, represents the time interval between the exposure event and the outcome when evaluating the delay of the effect. In case of protracted exposures, the data can be structured by the partition in equally-spaced time periods, defining a series of exposure events and outcomes realizations. This partitioning also defines lag units. Within this time structure, the exposure-response relationship can be described with either of two opposite perspectives: we can say that a specific exposure events produces effects on multiple future outcomes, or alternatively that a specific outcome is explained in terms of contributions by multiple exposure events in the past. The concept of lag can then be used to describe the relationship either forward (from a fixed exposure to future outcomes) or backward in time (from a fixed outcome to past exposures).

Ultimately, the main feature of statistical models for delayed effects is their bi-dimensional structure: the relationship is simultaneously described both along the usual space of the predictor and in the additional dimension of the lags.

1.2. Distributed lag models

The issue of delayed effects has been recently addressed in studies assessing the short term effects of environmental stressors: several time series studies have reported that the exposure to high levels of pollution or extreme temperatures affects health for a period lasting some days after the its occurrence (Braga et al. 2001; Goodman et al. 2004; Samoli et al. 2009; Zanobetti and Schwartz 2008).

The time series study design offers several advantages in order to deal with delayed effects, given the defined temporal structure of the data and the straightforward definition of the lag dimension, where the time partitioning is directly specified by the equally-spaced and ordered time points. In this setting, delayed effects are elegantly described by distributed lag models (DLMs), a methodology originally developed in econometrics (Almon 1965) and recently been used to quantify health effects in studies on environmental factors (Schwartz 2000; Zanobetti et al. 2000; Muggeo and Hajat 2009). This methodology allows the effect of a single exposure event to be distributed over a specific period of time, using several parameters to explain the contributions at different lags, thus providing a comprehensive picture of the time-course of the exposure-response relationship.

Conventional DLMs rely on the assumption of a linear effect between the exposure and the outcome. Some attempts to relax this assumption and explore delayed effects of factors showing non-linear relationships have been proposed (Roberts and Martin 2007; Braga et al. 2001). In particular, Muggeo (2008) introduced a methodology based on constrained segmented parameterization, assuming distributed lag linear effects of hot and cold temperatures beyond two thresholds. This methodology is implemented in an R package presented in a previous issue of this Journal (Muggeo 2010).

More recently, a general approach has been proposed to further relax the linearity assumption, and flexibly describe simultaneously non-linear and delayed effects. This step has lead to the generation of the new modeling framework of distributed lag non-linear models (DLNMs) (Gasparrini et al. 2010; Armstrong 2006), implemented in the R package dlnm (Gasparrini and Armstrong 2010).

1.3. Aim of the paper

The package dlnm within the statistical environment R (R Development Core Team 2011) offers a set of tools to specify and interpret the results of DLNMs. The aim of this paper is to provide a comprehensive overview of the capabilities of the package, including a detailed summary of the functions, with an example of application to real data. The example refers to the effects on all-cause mortality of two environmental factors, air pollution (ozone) and temperature, in the city of Chicago during the period 1987-2000. A thorough methodological description of DLNMs, together with the complete algebraical development, have been given elsewhere (Gasparrini et al. 2010). In this paper I reconsider the main conceptual and practical steps to define a DLNM, predict the effects and interpret the results with the aid of graphical features. The description of the functions included in the package and the related code for each step will be presented. The code is also available as supplemental material.

The paper is structured as follows: Section 2 considers the general problem of modeling non-linear or delayed effects, with an overview of the statistical approaches proposed so far. In the next three Sections, the development of the methodology is illustrated in details, showing the specification (Section 3), effect prediction (Section 4) and representation (Section 5) of DLNMs. Section 6 shows an example of alternative modeling approaches and the issue of model selection, while Section 7 discusses specific data requirements. Section 8 describes potential future developments. Final comments are provided in Section 9.

The package dlnm (current version 1.4.1) is expected to be loaded in the session, by typing:

R> library(“dlnm”)

Complementary information on the capabilities of the package, together with additional examples of application to real data, can be found in the vignette dlnmOverview. This document is included in the implementation of the package, and can be visualized by typing:

R> vignette(“dlnmOverview”, package = “dlnm”)

2. Non-linear and delayed effects

In this section I present the basic formulation for a time series model, then introducing the methods to describe non-linear and then delayed effects, the latter through the specification of simple DLMs. The developtment will be formulated in such a way to facilitate the introduction of the DLNM framework in Sections 3–5.

2.1. The basic model

A model for time series data may be generally represented by:

$$g\left({\mu }_t\right)=\alpha +\sum _{j=1}^J{s}_j(x_{tj};{\beta }_j)+\sum _{k=1}^K{\gamma }_k{u}_{tk}$$ (1)

where μ_t ≡ E(Y_t), g is a monotonic link function and Y_t is a series of outcomes with t = 1, … , n, assumed to arise from a distribution belonging to the exponential family (Dobson and Barnett 2008). The functions s_j specify the relationships between the variables x_j and the linear predictor, defined by the parameter vectors β_j. The variables u_k include other predictors with linear effects specified by the related coefficients γ_k.

In the illustrative example on Chicago data described in Section 1.3, the outcome Y_t is daily death counts, assumed to originate from a so-called overdispersed Poisson distribution with E(Y) = μ, V(Y) = 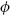μ, and a canonical log-link in (1). The analysis follows a conventional approach used in time series studies on environmental epidemiology (Dominici 2004; Touloumi et al. 2004), where the association between daily ozone and temperature levels on mortality is controlled for other confounding factors like seasonal and long time trend and day of the week. However, the framework is general and applies to every outcome and predictors measures collected as time series data.

The non-linear and delayed effects of ozone and temperature are modeled through as particular functions s_j which define the relationship along the two dimensions of predictor and lags.

2.2. Non-linear exposure-response relationships

The first step in the development of DLNMs is to define the relationship in the space of the predictor. Generally, non-linear exposure-response dependencies are expressed in regression models through appropriate functions s. Within completely parametric approaches, several different functions have been proposed, each of them characterized by different assumptions and degree of flexibility. The main choices typically rely on functions describing smooth curves, like polynomials or spline functions (Braga et al. 2001; Dominici et al. 2004); on the use of a linear threshold parameterization (Muggeo 2010; Daniels et al. 2000); or on the simple stratification through dummy parameterization.

All of these functions apply a transformation of the original predictor to generate a set of transformed variables included in the model as linear terms. A useful generalization is achieved introducing the concept of basis: a space of functions of which we believe s to be an element (Wood 2006). The related basis functions comprise a set of completely known transformations of the original variable x that generate a new set of variables, termed basis variables. An algebraic representation may be given by:

$$s(x_t;\beta )={{\mathbf{z}}_t}_{.}^{⊺}\beta$$ (2)

with z_t· as the t^th row of the n×v_x basis matrix Z. In the parametric approach adopted here, the basis dimension v_x equals the degrees of freedom (df) spent to define the relationship in this space, and is proportional to the degree of flexibility of the function. The unknown parameters β can be estimated including Z in the design matrix of the model in (1) .

This first step in the definition of DLNMs is performed in the package dlnm with the function mkbasis(), used to create the basis matrix Z. The purpose of this function is to provide a general way to include non-linear effects of x, with different choices specified as different arguments of mkbasis(). As an example, I build a basis matrix applying the selected basis functions to the vector x = [1, … , 5]: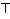

R> mkbasis(1:5, type = “bs”, df = 4, degree = 2, cenvalue = 3)

$basis

         b1      b2     b3     b4

[1,] −0.12500 −0.75000 −0.12500 0.0000

[2,] 0.53125 −0.46875 −0.12500 0.0000

[3,] 0.00000 0.00000 0.00000 0.0000

[4,] −0.12500 −0.46875 0.53125 0.0625

[5,] −0.12500 −0.75000 −0.12500 1.0000

$type

[1] “bs”

$df

[1] 4

$degree

[1] 2

$knots

33.33333% 66.66667%

 2.333333 3.666667

$bound

[1] 1 5

$int

[1] FALSE

$cen

[1] TRUE

$cenvalue

[1] 3

The result is a list object storing the basis matrix and the arguments defining it. In this case, the chosen basis is a quadratic spline with 4 df, defined by the arguments type, df and degree. The basis variables are centered to the value of 3.

Different types of basis may be chosen through the second argument type. The available options are natural cubic or simple B-splines (type = “ns” or “bs”, through a call to the related functions in the package splines); strata through dummy variables (“strata”); polynomials (“poly”); threshold-type functions such as low, high or double threshold or piecewise parameterization (“lthr”, “hthr”, “dthr”); and simply linear (“lin”). The argument df defines the dimension of the basis (the number of its columns, basically the number of transformed variables). This value may depend on the argument knots (which overcomes df), specifying the position of the internal knots for types “ns” and “bs” (with boundary knots specified by bound), the cut-off points for “strata” (defining right-open intervals) and the thresholds/cut-off points for “lthr”, “hthr” and “dthr”. If not defined (as in the example above), the knots are placed at equally-spaced quantiles by default, and the boundary knots at the range of the predictor values. The argument degree select the degree of polynomial for “bs” and “poly”.

The arguments cen and cenvalue are used to center the basis for continuous functions (types “ns”, “bs”, “poly”, and “lin”), with default to the mean of the original variable if cenvalue is not provided. An ”intercept” can be included with the argument int, set by default at FALSE to avoid identifiability problems. The concept of intercept is different between bases: types “ns” and “bs” apply a complex parameterization where the intercept is implicitly built within the basis variables (see the related help pages typing ?ns and ?bs); in type “strata”, the intercept corresponds to the dummy variable for the baseline stratum (the first one by default), which is excluded if int = FALSE; the intercept is the usual vector of 1’s in the other types. See the help page (typing ?mkbasis) for additional information.

2.3. Delayed effects

The second step to define a DLNM is to specify the function to model the relationship in the additional dimension of lags, allowing for delayed effects. In this situation, the outcome Y_t at a given time t may be explained in terms of past exposures x_t−ℓ, with ℓ as the lag. Given a maximum lag L, the additional lag dimension can be expressed by the n × (L + 1) matrix Q, such as:

$$Q_t.={\left[x_t,\dots ,x_t{\_}_{\ell },\dots ,x_t{\_}_L\right]}^{⊺}$$ (3)

with q_t· as the t^th row of Q. The vector of lags ℓ = [0, … , ℓ, … , L]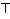 corresponds to the scale of this additional dimension.

Simple DLMs allow for delayed effects of linear relationships using a function to describe the dependency between the outcome and lagged exposures. Several alternatives have been proposed, from an unconstrained DLM (simply a parameter for each x_t−ℓ with ℓ 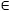ℓ) (Hajat et al. 2005), to the use of strata (Pattenden et al. 2003), polynomials (Schwartz 2000) or splines (Zanobetti et al. 2000; Armstrong 2006). A compact and general algebraic definition of a DLM is given by (see Gasparrini et al. 2010, Section 3.2):

$$s(x_t;\eta )={q_t}_{.}^{⊺}{\mathrm{C}}_{\eta }$$ (4)

where C is an (L+1)×v_ℓ matrix of basis variables derived from the application of the specific basis functions to the lag vector ℓ, and η a vector of unknown parameters. This basis matrix is used to define the relationship along the lag dimension. All the DLMs described above differ only in the choice of the basis to derive the matrix C.

This second step is carried out in dlnm through the function mklagbasis(), which calls mkbasis() in order to build the basis matrix C. For example:

R> mklagbasis(maxlag = 5, type = “strata”, knots = c(2, 4))

$basis

     b1 b2 b3

lag0  1  0  0

lag1  1  0  0

lag2  0  1  0

lag3  0  1  0

lag4  0  0  1

lag5  0  0  1

$type

[1] “strata”

$df

[1] 3

$knots

[1] 2 4

$int

[1] TRUE

$maxlag

[1] 5

In this example, after the maximum lag is fixed at 5 through the first argument maxlag, the lag vector 0:maxlag, corresponding to ℓ = [0, … , 5]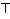, is automatically created and the chosen function applied to it. In this case, a dummy parameterization with strata defined by the cut-off points 2 and 4 (right-open intervals) included in knots. The available functions, and the arguments to specify them, are essentially the same illustrated above for mkbasis(). The only difference is that the basis matrix is never centered and by default includes an intercept (int = TRUE, see ?mklagbasis). In addition, the knots (if not specified) are placed by default at equally-spaced values in the log scale, allowing more flexibility in the first lag period. The specific argument type = “integer” produces strata variables for each integer values, defining C as an identity matrix, and may be used to specify unconstrained DLMs.

3. Specifying a DLNM

The last step in the specification of a DLNM involves the simultaneous definition of the relationship in the two dimensions of predictor and lags, as described in Sections 2.2 and 2.3. In spite of the different terminology of non linearity and delayed effects, the two procedures are conceptually similar: to define a basis which expresses the relationship in the related space. This similarity is highlighted by the analogy of the two functions mkbasis() and mklagbasis().

DLNMs are then specified by the definition of a cross-basis, a bi-dimensional functional space describing at the same time the dependency along the range of the predictor and in its lag dimension. Algebraically, this reduces to concurrently apply the two transformations explained in (2) and (3). First, choosing a basis for x to derive Z, then creating the additional lag dimension for each one of the derived basis variables of x, producing a n × v_x × (L + 1) array 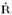. With C defined in (4), a DLNM can be represented by:

$$s(x_t;\eta )=\sum _{j=1}^{v_x}\sum _{k=1}^{v_{\ell }}{\mathbf{r}}_{tj}^{⊺}.{\mathbf{c}}_{.k}{\eta }_{jk}={w_t}_{.}^{⊺}\eta$$ (5)

with w_t· as the t^th row of the cross-basis matrix W. Additional details are given in Gasparrini et al. (2010, Section 4.2).

Choosing a cross-basis amounts to selecting two sets of basis functions as described above, which will be combined to generate cross-basis functions. This is carried out by the function crossbasis(), which calls the functions mkbasis() and mklagbasis() to generate the two basis matrices Z and C, respectively, than combining them through a tensor product to produce W following (5). This function can be applied to specify the two cross-bases for ozone and temperature in the example described in Section 2.1. The related code is:

R> basis.o3 <− crossbasis(chicagoNMMAPS$o3, vartype = “hthr”,
+    varknots = 40.3, lagtype = “strata”, lagknots = c(2, 6), maxlag = 10)
R> basis.temp <− crossbasis(chicagoNMMAPS$temp, vartype = “bs”,
+    vardegree = 3, vardf = 6, cenvalue = 25, lagdf = 5, maxlag = 30)

The result is an object of class ‘crossbasis’, corresponding to the cross-basis matrix W in (5) and the related arguments as attributes. The first argument x of crossbasis() is the predictor series, in this case chicagoNMMAPS$o3 and chicagoNMMAPS$temp available in the dataset included in the package (see ?chicagoNMMAPS). In the current implementation, the values in x are expected to represent an equally-spaced and ordered series, with the interval defining the lag unit. The series must be complete, although missing values are allowed (see Section 7). The argument maxlag defines the maximum lag.

The other arguments are similar to those enumerated in Sections 2.2 - 2.3. The function crossbasis() passes the arguments with prefix var- to mkbasis(), in order to specify Z, and the arguments with prefix lag- to mklagbasis(), producing C. In this example, the cross-basis for ozone comprises a threshold function for the space of the predictor, with a linear relationship beyond 40.3 μgr/m³, and a dummy parameterization assuming constant distributed lag effects along the strata of lags 0-1, 2-5 and 6-10. In contrast, the options for temperature are a cubic spline with 6 df (knots at equally-spaced percentiles by default) centered at 25°C, and a natural cubic spline (lagtype = “ns” by default) with 5 df (knots at equally-spaced values in the log scale of lags by default), up to a maximum of 30 lags.

As explained in Section 2.2, the basis variables for the space of the predictor are centered by default for continuous functions. The default centering point is the predictor mean, if not set with cenvalue (for example at 25°C for the cross-basis of temperature above). This value represents the reference for predicted effects from a DLNM (see Section 4). The choice of the reference value does not affect the fit of the model, and different values may be chosen depending on interpretational issues. The reference in non-continuous functions is automatically set to the first interval in strata and integer, or to the flat region in lthr, hthr, dthr. As suggested in Section 2.2, it is strongly recommended to avoid the inclusion of an intercept in the basis for the predictor space (varint must be FALSE, as default), otherwise a rank-deficient cross-basis matrix will be specified, causing some of the cross-variables to be excluded in the regression model. A complete overview of the available options is given in the help page (typing ?crossbasis).

These choices may be checked by the function summary.crossbasis(). For example:

R> summary(basis.temp)

CROSSBASIS FUNCTIONS

observations: 5114

range: −26.66667 , 33.33333

total df: 30

maxlag: 30

BASIS FOR VAR:

type: bs with degree 3

df: 6 , knots at: 1.666667 10.55556 19.44444

boundary knots at −26.66667 33.33333

centered on 25

BASIS FOR LAG:

type: ns

df: 5 , knots at: 1.105502 3.322105 9.983144

boundary knots at 0 30

with intercept

The cross-basis matrices can be included in the model formula of a common regression function in order to estimate the corresponding parameters η in (5). In the example, the final model includes also a natural cubic spline with 7 df/year to model the seasonal and long time trend components and a factor for day of the week, specified by the function ns() in the package splines, which needs to be loaded in the session. The code is:

R> library(splines)

R> model <− glm(death ~ basis.temp + basis.o3 +    ns(time, 7 * 14) + dow,
+ family = quasipoisson(), chicagoNMMAPS)

4. Predicting from a DLNM

As shown in Section 3, the specification of a DLNM involves a complex parameterization of the exposure series, but the estimation of the parameters η is carried out with common regression commands. However, the meaning of such parameters, which define the relationship along two dimensions, is not straightforward. Interpretation can be aided by the prediction of lag-specific effects on a grid of suitable exposure values and the L + 1 lags. In addition, the overall effects, predicted from exposure sustained over lags L to 0, can be computed by summing the lag-specific contributions. The algebraic details to derive such estimates have been described elsewhere (see Gasparrini et al. 2010, Section 4.3).

Predicted effects are computed in dlnm by the function crosspred(). The following code computes the prediction for ozone and temperature in the example:

R> pred.o3 <− crosspred(basis.o3, model, at = c(0:65, 40.3, 50.3))

R> pred.temp <− crosspred(basis.temp, model, by = 2)

The first two arguments passed to crosspred() are the object of class ‘crossbasis’ and the model object used for estimation. The vector of exposure values for which the effects must be predicted may be directly specified by the argument at, as in the first example above. Here I chose the integers from 0 to 65 μgr/m³ in ozone, plus the value of the chosen threshold and 10 units above (40.3 and 50.3 μgr/m³, respectively). The values are automatically ordered and made unique. Alternatively, the vector may be selected through the arguments by, from, to, as in the second example above. In this case I simply chose rounded values within the temperature range with an increment of 2°C. The function crosspred() extracts from model the parameters (coefficients and (co)variance matrix) corresponding to the cross-basis variables through method functions coef() and vcov(). For model classes for which such methods are not available, the parameters must be manually extracted and included in the arguments coef and vcov. The function then calls crossbasis() to build a prediction cross-basis and to generate the predicted effects and standard errors given the parameters in model. The result is a list object of class ‘crosspred’ which stores the predicted effects. It includes a matrix of lag-specific effects and a vector of overall effects, with corresponding matrix and vector of standard errors. If model includes a log or logit link, exponentiated effects and confidence intervals are returned as well. The confidence level of the intervals is defined by the argument ci.level, with default 0.95. The argument cumul (default to FALSE) adds the matrices of cumulative effects and standard errors along lags.

The results stored in the ‘crosspred’ object can be directly accessed to obtain specific figures or customized graphs other than those produced by dlnm plotting functions, illustrated in Section 5. For example, the overall effect for the 10-unit increase in ozone, expressed as RR and 95% confidence intervals, can be derived by:

R> pred.o3$allRRfit[“50.3”]

   50.3

1.05387

R> cbind(pred.o3$allRRlow, pred.o3$allRRhigh)[“50.3”,]

[1] 1.003354 1.106930

See the help page (typing ?crosspred) for additional information.

5. Representing a DLNM

The bi-dimensional exposure-response relationship estimated by a DLNM may be difficult to summarize. A general description is provided by the graphical representation of the association. The method functions plot(), lines() and points() for class ‘crosspred’ offer flexible plotting tools to aid the interpretation of results. The method plot() calls high-level functions plot.default(), persp() and filled.contour() to produce scatter plots, 3-D and contour plots of overall and lag-specific effects. These methods allow the user to specify the whole range or arguments of the plotting functions above, providing complete flexibility in the choice of colours, axes, labels and other graphical parameters. Methods lines() and points() may be used as low-level plotting functions to add lines or points to an existing plot.

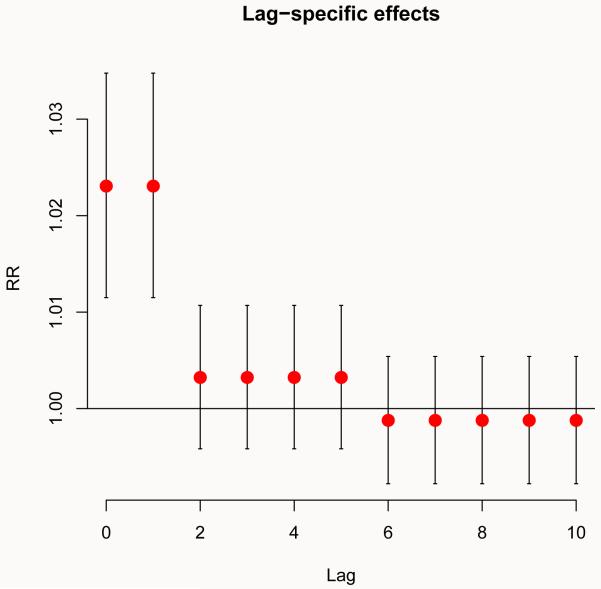
For example, the association between ozone and mortality can be summarized by the RR for an increase of 10 μgr/m³ above the threshold at each lag. This plot, illustrated in Figure 1 (left), is obtained by:

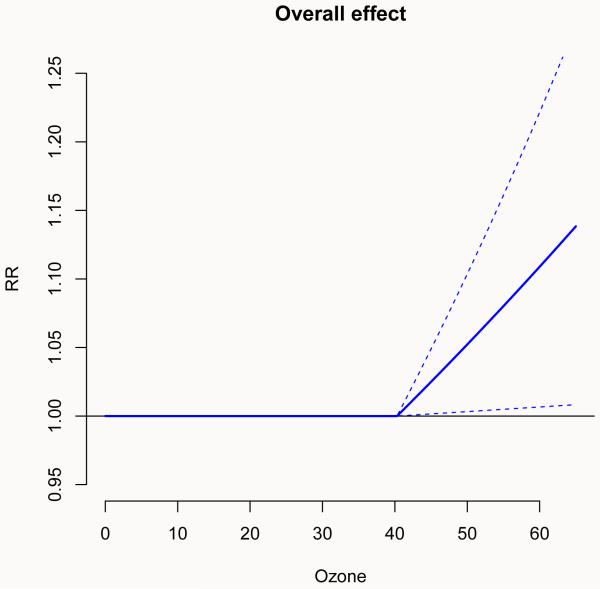
Figure 1.

Lag-specific (left) and overall (right) effects on all-cause mortality for a 10-unit increase in ozone above the threshold (40.3 μgr/m³). Chicago 1987–2000.

R> plot(pred.o3, “slices”, type = “p”, pch = 19, cex = 1.5, var = 50.3,
+    ci = “bars”, ylab = “RR”, main = “Lag-specific effects”)

The first argument x of the method function plot() indicates the object of class ‘crosspred’ where the results are stored. The second argument ptype = “slices” specifies the type of plot, in this case a slice of the matrix of predicted effect along the space of the lag at the predictor value var=50.3, corresponding to the 10-unit increase above the threshold set at 40.3 μgr/m³. The argument ci indicates the plot type for confidence intervals. Exponentiated effects are automatically returned for models with log or logit links, or forced by the argument exp. Cumulative effects may be plotted with cumul=TRUE, if this option has been previously set when generating the prediction with crosspred(). Additional parameters are passed to the high-level plotting function (plot.default() in this example) to define points, title and the axis labels. See the help of the original high-level functions for additional details and a complete list of the arguments.

Following the conceptual definition described in Section 1.1, the left plot in Figure 1 can be read using two different perspectives: it represents the increase in risk in each t + ℓ future day following a single exposure at 50.3 μgr/m³ in ozone at day t (forward interpretation), or otherwise the contributions of each t − ℓ past day with ozone at 50.3 μgr/m³ to the increase in risk at day t (backward interpretation).

Alternatively, it is possible to plot the overall effect, computed by summing the lag-specific contributions via the argument ptype = “overall”:

R> plot(pred.o3, “overall”, ci = “lines”, ylim = c(0.95, 1.25), lwd = 2,
+    col = 4, xlab = “Ozone”, ylab = “RR”, main = “Overall effect”)

The plot is shown in Figure 1 (right). Note the different representation of confidence intervals obtained by the argument ci, and non-default colour and line type.

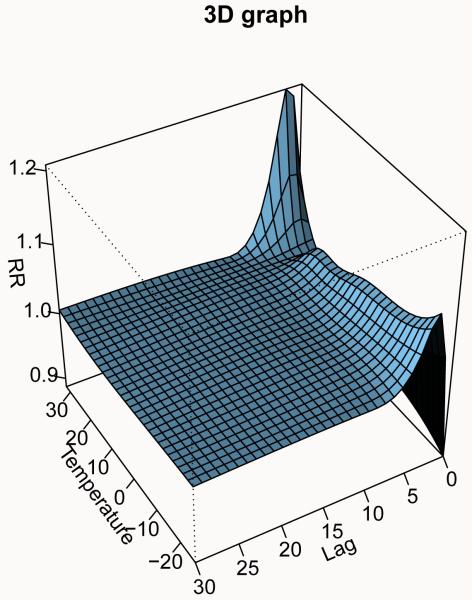
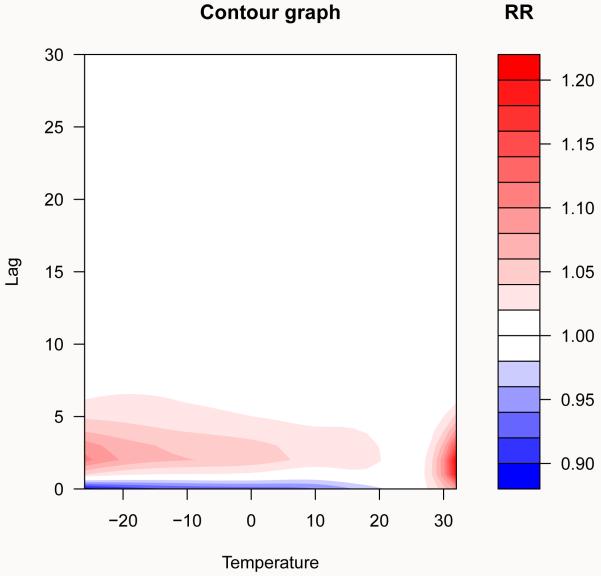
A more detailed approach is instead required to represent the smooth relationship between temperature and mortality, where splines functions have been used to define the dependency in both dimensions. A general description of this complex dependency may be given using 3-D and contour graphs (the default ptype = “3d” or ptype = “contour”), which illustrates the effect surface given by the whole grid of predicted effects. The graphs, shown in Figure 2, are obtained by:

Figure 2.

Three-dimensional graphs of the exposure-response relationship between temperature and all-cause mortality, with reference at 25°C. Chicago 1987–2000.

R> plot(pred.temp, xlab = “Temperature”, theta = 240, phi = 40,
+    ltheta = −185, zlab = “RR”, main = “3D graph”)

R> plot(pred.temp, “contour”, plot.title = title(xlab = “Temperature”,
+    ylab = “Lag”, main = “Contour graph”), key.title = title(“RR”))

The reference point (here 25°C) is the value at which the crossbasis functions have been centered in crossbasis(). Arguments theta, phi, ltheta and plot.title, key.title are used to modify the perspective and lighting in the 3-D plot and the labels in the contour plot, respectively. Other additional parameters may be specified as well (see ?persp and ?filled.contour).

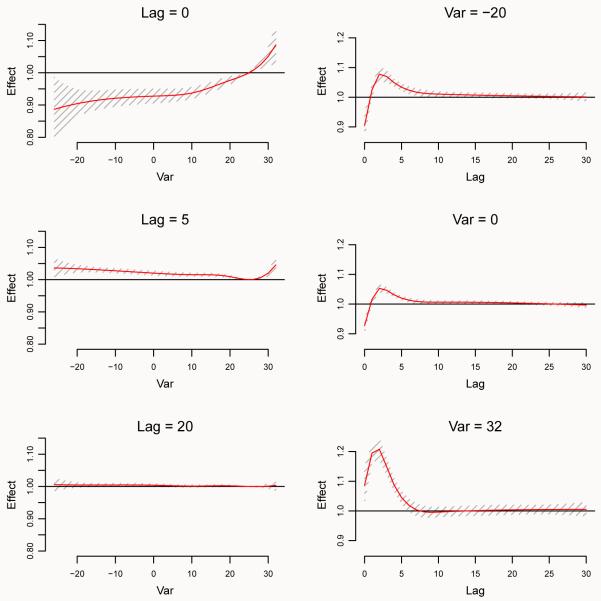
Tri-dimensional or contour plots offer a comprehensive summary of the relationship, but are limited in their ability to inform on effects at specific values of predictor or lags. In addition, they are also limited for inferential purposes, as the uncertainty of the estimated effects is not reported. A more comprehensive picture is given by Figure 3, obtained by:

Figure 3.

Lag-specific effects at different temperatures (left panel, and right column in right panel) and temperature-specific effects at different lags (left column in right panel) on all-cause mortality, with reference at 25°C. The right panel also shows 99% confidence intervals. Chicago 1987–2000.

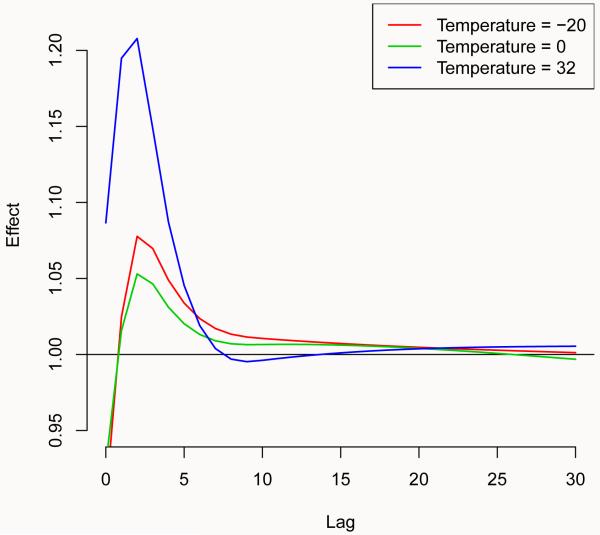
R> plot(pred.temp, “slices”, var = −20, ci = “n”, ylim = c(0.95, 1.22),
+    lwd = 1.5)

R> for(i in 1:2) lines(pred.temp, “slices”, var = c(0, 32)[i], col = i + 2,
+    lwd = 1.5)

R> legend(“topright”, paste(“Temperature =”, c(−20, 0, 32)), col = 2:4,
+    lwd = 1.5)

R> plot(pred.temp, “slices”, var = c(−20, 0, 32), lag = c(0, 5, 20),
+    ci.level = 0.99, xlab = “Temperature”, +    ci.arg = list(density = 20, col = grey(0.7)))

Figure 3 (left) shows predicted lag-specific effects for temperature values selected by the argument var in plot() and lines(). Alternatively, Figure 3 (right) illustrates a multiple plot of predicted effects along temperature for specific lags (left), and the same lag-specific effect plotted in Figure 3 (right), together with 99% confidence intervals. The arguments var and lag define the values in the two dimensions, while ci.level specifies the confidence level of the intervals. The argument ci.arg includes a list of arguments to be passed to low-level plotting functions, which draw confidence intervals. In this case, the default ci = “area” calls the function polygon(), and the arguments in ci.arg are used to select a shading area with increased grey contrast. However, plotting features such as labels and titles may not be included in this automatic multi-plot representation.

These graphs suggest different patterns for the effects of hot and cold temperatures, with a very strong and immediate effect of heat and a more delayed association with cold, negative in the very first lags. This analytical level is not obviously reached with simpler models.

6. Modeling strategies

The DLNM framework offers the opportunity to specify a wide selection of models through the choice of the basis functions for each of the two dimensions of predictor and lags. The example illustrated in the previous sections represents one of the potential modeling alternatives. In order to discuss the flexibility of the methodology, and the related problems with model selection, a comparison with different models to estimate the association with temperature is shown below. Specifically, polynomial and strata functions are selected for the space of the predictor, while keeping the same natural cubic spline to model the distributed lag curve up to 30 days of lag. The code to specify the cross-basis, run the models and predict the effect is:

R> basis.temp2 <− crossbasis(chicagoNMMAPS$temp, vartype = “poly”,
+    vardegree = 6, cenvalue = 25, lagdf = 5, maxlag = 30)

R> model2 <− update(model, .~. − basis.temp + basis.temp2)

R> pred.temp2 <− crosspred(basis.temp2, model2, by = 2)

R> basis.temp3 <− crossbasis(chicagoNMMAPS$temp, vartype = “dthr”,
+    varknots = 25, lagdf = 5, maxlag = 30)

R> model3 <− update(model, .~. − basis.temp + basis.temp3)

R> pred.temp3 <− crosspred(basis.temp3, model3, by = 2)

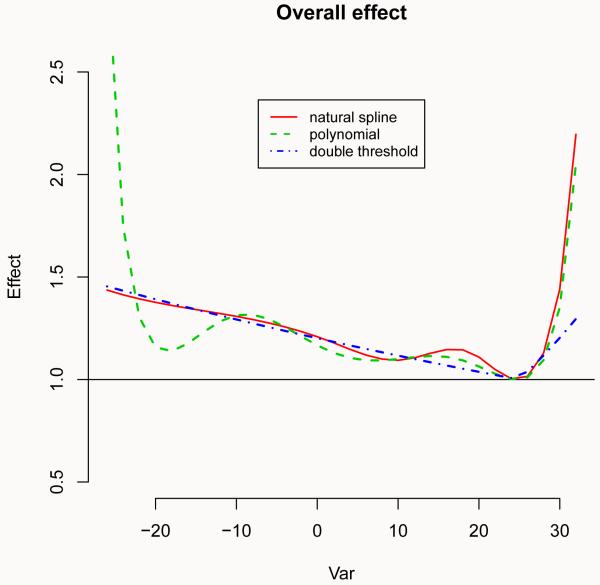
The first alternative proposes, for the predictor dimension, a polynomial function with the same degrees of freedom as the original cubic spline in Section 5. The second model is based on a simpler double threshold function with a single threshold placed at 25°C, previously identified as the point of minimum mortality. This choice also facilitates the comparison of the models, as this is the centering point for the other two continuous functions. The overall effect estimated by the three models is displayed in Figure 4 (left), produced by the code:

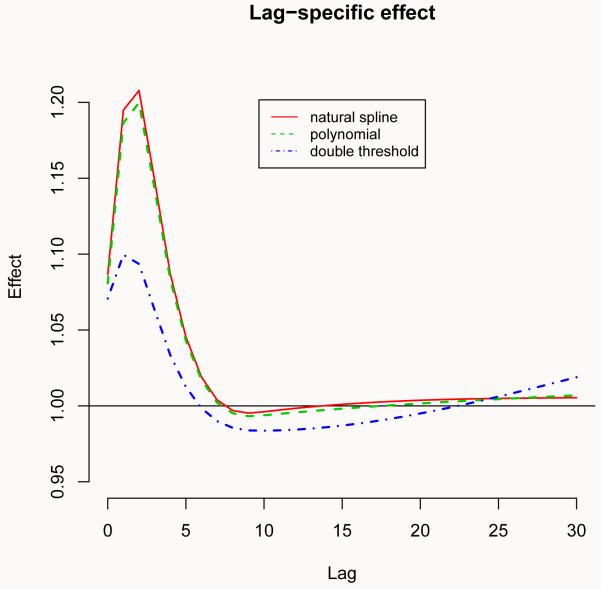
Figure 4.

Overall effect (left) and lag-specific effect at 32°C (right) of temperature on all-cause mortality for 3 alternative models, with reference at 25°C. Chicago 1987-2000.

R> plot(pred.temp, “overall”, ylim = c(0.5, 2.5), ci = “n”, lwd = 1.5,
+    main = “Overall effect”)

R> lines(pred.temp2, “overall”, col = 3, lty = 2, lwd = 2)

R> lines(pred.temp3, “overall”, col = 4, lty = 4, lwd = 2)

R> legend(“top”, c(“natural spline”, “polynomial”, “double threshold”),
+    col = 2:4, lty = c(1:2, 4), lwd = 1.5, inset = 0.1, cex = 0.8)

As expected, the alternative models produce different results. In particular, the polynomial model estimates a “wiggly” relationship for cold temperatures, if compared to the original cubic spline with equally-spaced knots. Instead, the two functions provide very close estimates for the effect of hot temperatures. Conversely, while the linearity assumption of the double threshold model seems adequate to model the dependency for cold, there is some evidence that this approach tends to underestimate the effect of heat. A second comparison of the estimated distributed lag curves is illustrated in Figure 4 (right), following:

R> plot(pred.temp, “slices”, var = 32, ylim = c(0.95, 1.22), ci = “n”,
+    lwd = 1.5, main = “Lag-specific effect”)

R> lines(pred.temp2, “slices”, var = 32, col = 3, lty = 2, lwd = 2)

R> lines(pred.temp3, “slices”, var = 32, col = 4, lty = 4, lwd = 2)

R> legend(“top”, c(“natural spline”, “polynomial”, “double threshold”),
+    col = 2:4, lty = c(1:2, 4), inset = 0.1, cex = 0.8)

Although exactly the same function for the space of lag was selected in all the three models, a different choice for the predictor dimension provides different estimates of the distributed lag curve, representing the effect at 32°C compared to the common reference point of 25°C. In particular, the spline and polynomial models produce very similar effects (as expected, given the almost identical fit in the other dimension for the hot tail), while the curve for the double threshold models shows quite a different shape. Specifically, the suggestion of an harvesting effect (the negative estimate at longer lags) may represent an artifact due to the lack of flexibility of this model.

Such richness in the specification of different alternatives is tempered by the lack of general criteria to select, among the available choices, the best model to summarize the association. In the example above, I showed a clear preference for the spline model. This choice is based both on knowledge of the properties of the function, such as flexibility and stability, and on reasonable arguments given the results plotted in Figure 4. However, this conclusion is questionable, and not grounded on solid and general statistical selection criteria. Moreover, the conclusion is based on several a-priori choices, just like the threshold location or the number of knots or polynomial degree.

Generally, within DLNMs, two different levels of selection may be described. The first one pertains to the specification, in both dimensions, of different functions. As illustrated above, this choice should be based both on the plausibility of the assumed exposure-response shape, and on a compromise between complexity, generalizability and ease of interpretation. The second level focuses on different choices within a specific function, such as the number and location of knots for the definition of a spline basis. The latter is more difficult to address, although not inherent to DLNM development. Several researchers have investigated this issue within time series analysis, proposing methods based on information criteria (Akaike, Bayesian and other variants), partial autocorrelation or (generalized) cross-validation (Peng et al. 2006; Baccini et al. 2007). The user may apply the same methods within DLNMs, but he should bear in mind that the bi-dimensional nature of these models brings along additional complexities, such as the definition of the maximum lag. Moreover, the evidence on the performance of different criteria is not conclusive, and this represents an issue of current debate (Dominici et al. 2008). Further research is needed to provide some guidance on model selection within DLNMs.

Alternative approaches may be suggested. Muggeo (2008) proposed a model with a constrained segmented parameterization for the space of the predictor, and a doubly penalized spline-based distributed lag parameterization. This methods includes an automatic selection for the threshold(s) and for the smoothness of the distributed lag curve, and it is fully implemented in the R package modTempE (Muggeo 2010). The comparison of such an approach with flexible DLNMs which relax the assumptions on the shape in the dimension of the predictor may provide some additional insights on the relationship.

7. Data requirements

The DLNMs framework introduced in this paper is developed for time series data. The general expression of the basic model in (1) allows this methodology to be applied to any family distribution and link function within (generalized) linear models (GLM), with extensions to generalized additive models (GAM) or models based on generalized estimating equations (GEE). However, the current implementation of DLNMs requires single series of equally-spaced, complete and ordered data.

Each value in the series of transformed variables is computed also using previous observations included in the selected lag period. Therefore, the first maxlag observations in the transformed variables are set to NA. Missing values in x are allowed, but, for the same reason, the same and the next maxlag transformed values will be set to NA. Although correct, this could generate computational problems for DLNMs with long lag periods in the presence of scattered missing observations. Some imputation methods may be considered in this case.

One of the main advantages of the dlnm package is that the user can perform DLNMs with standard regression functions, simply including the cross-basis matrix in the model formula. Its use is straightforward with the functions lm(), glm() or gam() (package mgcv, see Wood 2006). However, the user can apply different regression functions, compatibly with the time series structure of the data. These functions should have methods for coef() and vcov(), or alternatively the user must extract the parameters and include them in the arguments coef and vcov of crosspred() (see Section 4).

8. Future developments

The conceptual framework depicted in Section 1.1 is general, and may be applied to other study designs and data structures other than time series. This idea is hidden by the ordered nature of the time series approach, where each observation is naturally included in a temporal sequence specified by the index t. This represents the unique temporal scale of the study design, and the lag dimension, which lies on the same scale, is automatically defined as t − ℓ. The temporal structure of different study designs may be more complex, implying multiple time scales. However, the lag dimension can be still expressed through exposure histories for each observation, defining an additional temporal scale. This step involves a slightly different definition of the matrix Q in (3), where each q_i· represents the exposure history for the observation i from the exposure vector x, which does not express anymore a series of observations ordered in time. Interestingly, the conceptual and algebraical process outlined above, concerning the definition, prediction and representation of DLNMs, still applies. Preliminary tests on the application of the functions included in the package dlnm in case-control, cohort and longitudinal data are promising. Further development may lead to a general framework to describe delayed effects, which spans different study designs.

The current implementation of dlnm only comprises completely parametric methods to specify the model in (1). A potential alternative is offered by generalized additive models (GAM) based on penalized splines (Wood 2006). Specification and estimation methods for tensor product bases for bivariate smoothing, closely related to the DLNM definition, have been already developed in this framework, and well implemented in the R package mgcv. This methodology show clear advantages, primarily the higher flexibility and automatic smoothness selection. Interestingly, the algebraic development of cross-basis described in (5) is still valid, and the actual problem reduces to define suitable penalization methods for the parameters of the cross-basis functions. An extension of DLNMs with penalized splines is currently under development.

9. Final comments

The class of DLNMs represents a unified framework to describe phenomena showing both non-linear and delayed effects. The main advantage of this model family is to unify many of the previous methods to deal with delayed effects in a unique framework, also providing more flexible alternatives regarding the shape of the relationships. The specification of a DLNM involves only the choice of two bases to generate the cross-basis functions in (5), including, for example, linear thresholds, strata, polynomials, and spline transformations.

This flexibility is retained in the implementation of the methodology in the dlnm package, which provides functions to specify the model, predict the effects and plot the results. Several different models with an increasing level of complexity can be performed using a simple and general procedure. The example included in this paper illustrates the application of these functions to describe the association between two environmental stressors and mortality, although the framework is easily generalized to other applications. The package includes a thorough documentation of the functions. An overview of its capabilities, together with an update of the last advancements, is provided in the vignette dlnmOverview accompanying the implementation.

The separation of cross-basis specification and parameters estimation offers several advantages. First, as illustrated in the example, more than one variable showing delayed effects can be transformed through cross-basis functions and included in the model. Second, standard regression commands can be used for estimation, with the default set of diagnostic tools and related functions. More importantly, this implementation provides an open platform where additional models specified with different regression commands can be implemented, aiding the development of the methodology in other contexts or study designs.