On the utility of graphics cards to perform massively parallel simulation of advanced Monte Carlo methods

Abstract

We present a case-study on the utility of graphics cards to perform massively parallel simulation of advanced Monte Carlo methods. Graphics cards, containing multiple Graphics Processing Units (GPUs), are self-contained parallel computational devices that can be housed in conventional desktop and laptop computers and can be thought of as prototypes of the next generation of many-core processors. For certain classes of population-based Monte Carlo algorithms they offer massively parallel simulation, with the added advantage over conventional distributed multi-core processors that they are cheap, easily accessible, easy to maintain, easy to code, dedicated local devices with low power consumption. On a canonical set of stochastic simulation examples including population-based Markov chain Monte Carlo methods and Sequential Monte Carlo methods, we nd speedups from 35 to 500 fold over conventional single-threaded computer code. Our findings suggest that GPUs have the potential to facilitate the growth of statistical modelling into complex data rich domains through the availability of cheap and accessible many-core computation. We believe the speedup we observe should motivate wider use of parallelizable simulation methods and greater methodological attention to their design.

1 Introduction

We describe a case-study in the utility of graphics cards involving Graphics Processing Units (GPUs) to perform local, dedicated, massively parallel stochastic simulation. GPUs were originally developed as dedicated devices to aid in real-time graphics rendering. However recently there has been an emerging literature on their use for scientific computing as they house multi-core processors. Examples include Stone et al. (2007) and Friedrichs et al. (2009), which discuss their use in molecular modelling and dynamics. Suchard and Rambaut (2009) investigate phylogenetic inference using MCMC on GPUs and Suchard et al. (2010) investigate using GPUs for inference in mixture models. Here we show that many advanced population-based Monte Carlo algorithms are ideally suited to GPU simulation and offer significant speed up over single CPU implementation. The focus is therefore on the parallelization of general sampling methods as opposed to the parallelization of the evaluation of likelihoods within a standard sampling method such as Metropolis-Hastings as done in Suchard and Rambaut (2009) and Suchard et al. (2010). Moreover, we show how the choice of population-based Monte Carlo algorithm for a particular problem can depend on wheter one is running the algorithm on a GPU or a CPU (see Section 4.1.3).

To gain an understanding of the potential benefits to statisticians we have investigated speedups on a canonical set of examples taken from the population-based Monte Carlo literature. These include Bayesian inference for a Gaussian mixture model computed using a population-based MCMC method and a sequential Monte Carlo (SMC) sampler and sequential Bayesian inference for a multivariate stochastic volatility model implemented using a standard SMC method, also known as a particle filter in this context. In these examples we report substantial speedups from the use of GPUs over conventional CPUs.

The potential of parallel processing to aid in statistical computing is well documented (see e.g. Kontoghiorghes (2006)). However, previous studies have relied on distributed multi-core clusters of CPUs for implementation. In contrast, graphics cards for certain generic types of computation offer parallel processing speedups with advantages on a number of fronts, including:

• Cost: graphics cards are relatively cheap, being commodity products.

• Accessibility: graphics cards are readily obtainable from consumer-level computer stores or over the internet.

• Maintenance: the devices are self-contained and can be hosted on conventional desktop and laptop computers.

• Speed: in line with multi-core CPU clusters, graphics cards offer significant speedup, albeit for a restricted class of scientific computing algorithms.

• Power: GPUs are low energy consumption devices compared to clusters of traditional computers, with a graphics card requiring around 200 Watts. While improvements in energy efficiency are application-specific, it is reasonable in many situations to expect a GPU to use around 10 per cent of the energy to that of an equivalent CPU cluster.

• Dedicated and local: the graphics cards slot into conventional computers offering the user ownership without the need to transport data externally.

The idea of splitting the computational effort of parallelizable algorithms amongst processors is certainly not new to statisticians. In fact, distributed systems and clusters of computers have been around for decades. Previous work on parallelization of MCMC methods on a group of networked computers include, among others, Rosenthal (2000) and Brockwell (2006). Rosenthal (2000) discusses how to deal with computers running at different speeds and potential computer failure while Brockwell (2006) discusses the parallel implementation of a standard single chain MCMC algorithm by pre-computing acceptance ratios. The latency and bandwidth of communication in these systems make them suitable only in cases where communication between streams of computation, or threads, is infrequent and low in volume. In other words, while many algorithms involve computation that could theoretically be distributed amongst processors, the overhead associated with distributing the work erases any speedup. In contrast, many-core processor communication has very low latency and very high bandwidth due to high-speed memory that is shared amongst the cores. Low latency here means the time for a unit of data to be accessed or written to memory by a processor is low whilst high bandwidth means that the amount of data that can be sent in a unit of time is high. For many algorithms, this makes parallelization viable where it previously was not. In addition, the energy efficiency of a many-core computation compared to a single-core or distributed computation can be improved. This is because the computation can both take less time and require less overhead. Finally, we note that these features enable the use of parallel computing for researchers outside traditional high-cost centres housing high-performance computing clusters.

We choose to investigate the speed up for the simulation of random variates from complex distributions, a common computational task when performing inference using Monte Carlo (see e.g. Robert and Casella (2004)). In particular, we focus on population-based MCMC methods and SMC methods for producing random variates as these are not algorithms that typically see significant speedup on clusters due to the need for frequent, high-volume communication between computing nodes. We emphasize that this work focuses on the suitability of many-core computation for Monte Carlo algorithms whose structure is parallel, since this is of broad theoretical interest, as opposed to a focusing on parallel computation of application-specific likelihoods.

The algorithms are implemented for the Compute Uni ed Device Architecture (CUDA) and make use of GPUs which support this architecture. CUDA offers a fairly mature development environment via an extension to the C programming language. We estimate that a programmer proficient in C should be able to code effectively in CUDA within a few weeks of dedicated study. For our applications we use CUDA version 2.1 with an NVIDIA GTX 280 as well as an NVIDIA 8800 GT. The GTX 280 has 30 multiprocessors while the 8800 GT has 14 multiprocessors. For all current NVIDIA cards, a multiprocessor comprises 8 arithmetic logic units (ALUs), 2 special units for transcendental functions, a multithreaded instruction unit and on-chip shared memory. For example, for single-precision floating point computation, one can think of the GTX 280 as having 240 (30 × 8) single processors. At present, the retail price of the GTX 280 is just over double that of the 8800GT and it requires just over twice the power. The current generation of GPUs is 4-8 times faster at single precision arithmetic than double precision. Fortunately, single precision seems perfectly sufficient for the applications in this paper since the variance of the Monte Carlo estimates exceeds the perturbations due to finite machine precision.

2 GPUs for Parallel Processing

GPUs have evolved into many-core processing units, currently with up to 30 multiprocessors per card, in response to commercial demand for real-time graphics rendering, independently of demand for many-core processors in the scientific computing community. As such, the architecture of GPUs is very different to that of conventional central processing units (CPUs). An important difference is that GPUs devote proportionally more transistors to ALUs and less to caches and flow control in comparison to CPUs. This makes them less general purpose but highly effective for data-parallel computation with high arithmetic intensity, i.e. computations where the same instructions are executed on different data elements and where the ratio of arithmetic operations to memory operations is high. This single instruction, multiple data (SIMD) architecture puts a heavy restriction on the types of computation that optimally utilize the GPU but in cases where the architecture is suitable it reduces overhead.

Figure 1 gives a visualization of the link between a host machine and the graphics card, emphasizing the data bandwidth characteristics of the links and the number of processing cores. A program utilizing a GPU is hosted on a CPU with both the CPU and the GPU having their own memory. Data is passed between the host and the device via a standard memory bus, similar to how data is passed between main memory and the CPU. The memory bus between GPU memory and the GPU cores is both wider and has a higher clock rate than a standard bus, enabling much more data to be sent to the cores than the equivalent link on the host allows. This type of architecture is ideally suited to data-parallel computation since large quantities of data can be loaded into registers for the cores to process in parallel. In contrast, typical computer architectures use a cache to speed up memory accesses using locality principles that are generally good but do not fully apply to data-parallel computations, with the absence of temporal locality most notable.

Figure 1.

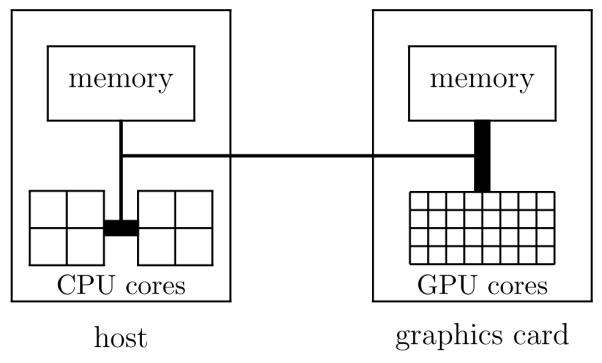
Link between host and graphics card. The thicker lines represent higher data bandwidth while the squares represent processor cores.

2.1 Programming with Graphics Cards

CUDA provides the interface to compliant GPUs by extending the C programming language. Programs compiled with CUDA allow computation to be split between the CPU and the GPU. In this sense, the GPU can be treated as an additional, specialized processor for data-parallel computation. In the following text, host code refers to code that is executed on the CPU whilst device code is code that is executed on the GPU. We present a simple example in Figures 2-4, explained below, that computes a classical importance sampling estimate (see Section 3). In the code snippets, keywords in the C language are in bold face whilst CUDA keywords are both bold and italicized. A line beginning with a“//” is a comment and is ignored by the compiler.

Figure 2.

Kernel that evaluates an importance weight and test function

Figure 3.

Device functions for evaluating the target density, the proposal density and the test function. The target is an equally weighted, two-component mixture of normals with equal variances of 0.25 and means at −1 and 1.5 while the proposal is a standard normal distribution. The test function squares its input so that the integral that is estimated is the expectation of the second moment of a random variable distributed according to the target density.

Figure 4.

Host code

CUDA allows users to de ne special functions, called kernels, that are called by the host code to be executed in parallel on the GPU by a collection of threads. Figure 2 shows an example of a kernel function, which can be invoked in host code using the syntax

importance_sample<<<nb,nt>>>(N, d_array, d_array_out);

where nb is the number of blocks of threads and nt is the number of threads per block. The total number of threads created by this call is the product of nb and nt and one can think of a threads as being a single stream of computation. For most kernels, the numbers of threads and blocks can be changed to tune performance on different cards or with different data. A more detailed description of blocks and threads and their relation to the hardware is given in Section 2.2.

A kernel is defined with the __global__ qualifier. Kernels are special in that they are always invoked in parallel with the numbers of blocks and threads specified and have a void return type. In Figure 2, a kernel is defined that takes as input an array of random values sampled from a proposal distribution and places, for each value, the product of the test function and the importance weight at that value in a separate array. One can see that each thread is responsible for N/tt values, assuming N is a multiple of tt. Within a kernel, special functions can be called that have been defined with the __device__ qualifier. These functions can only be called by __global__ functions or __device__ functions themselves. In Figure 2, target_pdf, proposal_pdf and phi are examples of this, and their definitions are provided in Figure 3. In this particular kernel we see that each thread first computes its absolute thread identifier tid and the total number of threads tt. It then computes an importance weight and evaluates the test function for each value in d_array it is responsible for and stores the result in d_array_out. Since there is no thread interaction in this example kernel, it is reasonably straightforward to verify its correctness.

Figure 4 gives a snippet of code that is run on the host and completes our example. First, memory is allocated on both the host and the graphics card using the malloc and cudaMalloc functions respectively. The host function populate_randn then puts N standard normal random variates in array. These values are copied into the GPU array, d_array, via the cudaMemcpy function. In Figure 1, this is a transfer along the memory bus that connects host and graphics card memory. At this point, the kernel is called with 64 blocks of 128 threads per block. The reduce function is a CPU function that returns the sum of the elements in a GPU array. Of course, this function can itself invoke a GPU kernel. Finally, the importance sampling estimate is obtained by dividing this sum by N and memory is freed. Note that this code has been written so as to expose the most common functions that are used in GPU programming using CUDA. For example, it would be faster to create the random variates on the GPU itself but this would not have allowed any memory transfer operations to be shown here.

This basic example highlights the most important characteristics of CUDA programs: memory management, kernel specification and kernel invocation. Memory management is a key component in algorithm design using graphics cards since there is often need for transfer between CPU and GPU memory as standard host functions can only access CPU memory and kernels can only access GPU memory. With respect to kernel specification and invocation, the level of abstraction provided by CUDA is close to the hardware operations on the device. This ensures that programmers are acutely aware of the benefits of writing kernels that can be mapped cleanly to the hardware.

2.2 Blocks and Threads

CUDA abstracts the hardware of the GPU into blocks and threads to simultaneously provide a relatively simple view of the architecture to developers while still allowing a low-level abstraction of the hardware for performance reasons. One can generally think of each thread as being computed on a virtual processor. The block abstraction is necessary to provide the concept of a virtual microprocessor. Threads within a block are capable of more interaction than threads in separate blocks, mainly due to the fact that all threads in a block will be executed on the same microprocessor. As such, they have access to very fast, dynamically allocated, on-chip memory and can perform simple barrier synchronization. In Section 2.1, this advanced functionality is not required by the example kernel.

2.3 GPU Parallelizable Algorithms

In general, if a computing task is well-suited to SIMD parallelization then it will be well-suited to computation on a GPU. In particular, data-parallel computations with high arithmetic intensity (computations where where the ratio of arithmetic operations to memory operations is high) are able to attain maximum performance from a GPU. This is because the volume of very fast arithmetic instructions can hide the relatively slow memory accesses. It is crucial to determine whether a particular computation is data-parallel on the instruction level when determining suitability. From a statistical simulation perspective, integration via classical Monte Carlo or importance sampling are ideal computational tasks in a SIMD framework. This is because each computing node can produce and weight a sample in parallel, assuming that the sampling procedure and the weighting procedure have no conditional branches. If these methods do branch, speedup can be compromised by many computing nodes running idle while others nish their tasks. This can occur, for example, if the sampling procedure uses rejection sampling.

In contrast, if a computing task is not well-suited to SIMD parallelization then it will not be well-suited to computation on a GPU. In particular, task-parallel computations where one executes different instructions on the same or different data cannot utilize the shared flow control hardware on a GPU and often end up running sequentially. Even when a computation is data-parallel, it might not give large performance improvements on a GPU due to memory constraints. This can be due to the number of registers required by each thread (see Sections 4.2 and 5) or due to the size and structure of the data necessary for the computation requiring large amounts of memory to be transferred between the host and the graphics card.

Many statistical algorithms involve large data sets, and the extent to which many-core architectures can provide speedup depends largely on the types of operations that need to be performed on the data. For example, many matrix operations derive little speedup from parallelization except in special cases, e.g. when the matrices involved are sparse Whiley and Wilson (2004). It is difficult to classify concisely the types of computations amenable to parallelization beyond the need for data-parallel operations with high arithmetic intensity. However, experience with parallel computing should allow such classifications to be made prior to implementation in most cases.

2.4 Parallel Random Number Generation

One important aspect of any Monte Carlo simulation is the generation of pseudorandom numbers. Fortunately, many uniform pseudorandom number generators can be implemented efficiently in parallel. The key idea is that each thread computes a contiguous block of numbers within a single overall stream. The thread can jump to the start of its block of numbers using a“skip-ahead” algorithm which enables it to skip n places in O(log n) operations (e.g. see L’Ecuyer et al. (2002)). The uniform pseudorandom numbers can then be transformed to match various different output distributions as needed. In our applications we use a parallelized version of the multiple recursive generator MRG32k3a presented in L’Ecuyer (1999) as well as a parallelized version of a xorshift random number generator Marsaglia (2003). In the case of the xorshift random number generator, more time must be spent to compute the seeds for each thread before any computation is done but the random number generation itself is faster and the initialization can be done offline. Generating random numbers on the GPU allows us to avoid copying blocks of random numbers from the CPU to the GPU. However, one must be careful using parallel random number generation algorithms not to exceed the period of the overall algorithm but for most applications there are methods with a long enough period such that this is not an issue.

3 Parallelizable Sampling Methods

In this section we consider a number of sampling methods for which parallel implementations can be produced without significant modification. There is an abundance of statistical problems that are essentially computational in nature, especially in Bayesian inference. In many such cases, the problem can be distilled into one of sampling from a probability distribution whose density π we can compute pointwise and up to a normalizing constant, i.e. we can compute π*(·) where π(x) = π*(x)/Z. A common motivation for wanting samples from π is so we can compute expectations of certain functions. If we denote such a function by 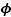, the expectation of interest is

$$I\triangleq {\int }_{x\in \mathcal{X}}\varphi \left(\mathbf{x}\right)\pi \left(\mathbf{x}\right)d\mathbf{x}.$$

The Monte Carlo estimate of this quantity is given by

$${\widehat{I}}_{MC}\triangleq \frac{1}{N}\sum _{i=1}^N\varphi \left({\mathbf{x}}^{\left(i\right)}\right)$$

where ${\left\{{\mathbf{x}}^{\left(i\right)}\right\}}_{i=1}^N$ are samples from π.

Clearly, we need samples from π in order to compute this estimate. In practice, however, we often cannot sample from π directly. There are two general classes of methods for dealing with this. The first are importance sampling methods, where we generate weighted samples from π by generating N samples according to some importance density γ proportional to γ* and then estimating I via

$${\widehat{I}}_{IS}\triangleq \sum _{i=1}^N{W}^{\left(i\right)}\varphi \left({\mathbf{x}}^{\left(i\right)}\right)$$

where W⁽ⁱ⁾ are normalized importance weights

$$W^{\left(i\right)}=\frac{w\left({\mathbf{x}}^{\left(i\right)}\right)}{{\sum }_{j=1}^{N}w\left({\mathbf{x}}^{\left(j\right)}\right)}\text{and}w\left({\mathbf{x}}^{\left(i\right)}\right)=\frac{{\pi }^{\ast }\left({\mathbf{x}}^{\left(i\right)}\right)}{{\gamma }^{\ast }\left({\mathbf{x}}^{\left(i\right)}\right)}.$$

The asymptotic variance of this estimate is given by C(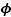, π, γ)/N, i.e. a constant over N. For many problems, however, it is difficult to come up with an importance density γ such that C(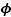, π, γ) is small enough for us to attain reasonable variance with practical values of N.

The second general class of methods are MCMC methods, in which we construct an ergodic π-stationary Markov chain sequentially. Once the chain has converged, we can use all the dependent samples to estimate I. The major issue with MCMC methods is that their convergence rate can be prohibitively slow in some applications.

There are many ways to parallelize sampling methods that are not the focus of this work. For example, naive importance sampling, like classical Monte Carlo, is intrinsically parallel. Therefore, in applications where we have access to a good importance density γ we can get linear speedup with the number of processors available. Similarly, in cases where MCMC converges rapidly we can parallelize the estimation of I by running separate chains on each processor. While these situations are hoped for, they are not particularly interesting from a parallel architecture standpoint because they can run equally well in a distributed system. Finally, this paper is not concerned with problems for which the computation of individual MCMC moves or importance weights are very expensive but themselves parallelizable. While the increased availability of parallel architectures will almost certainly be of help in such cases, the focus here is on potential speedups by parallelizing general sampling methods. Example of recent work in this area can be found in Suchard and Rambaut (2009) and Suchard et al. (2010), in which speedup is obtained by parallelizing evaluation of individual likelihoods.

Much work in recent years has gone into dealing with the large constants in the variance of importance sampling estimates and slow convergence rates in MCMC and it is in these ‘advanced’ Monte Carlo methods that we direct our interest. This is mainly because while they are parallelizable, they are not trivially so and stand to benefit enormously from many-core architectures. In the remainder of this section we briefly review three such methods: population-based MCMC, SMC and SMC samplers.

3.1 Population-Based MCMC

A common technique in facilitating sampling from a complex distribution π with support in $\mathcal{X}$ is to introduce an auxiliary variable $\mathbf{a}\in \mathcal{A}$ and sample from a higher-dimensional distribution $\stackrel{‒}{\pi }$ with support in the joint space $\mathcal{A}\times \mathcal{X}$, such that $\stackrel{‒}{\pi }$ admits π as a marginal distribution. With such samples, one can discard the auxiliary variables and be left with samples from π. Note that in this section, a kernel will generally refer to a Markov chain transition kernel as opposed to a CUDA kernel.

This idea is utilized in population-based MCMC, which attempts to speed up convergence of an MCMC chain for π by instead constructing a Markov chain on a joint space ${\mathcal{X}}^M$ using M − 1 auxiliary variables each in $\mathcal{X}$. In general, we have M parallel ‘subchains’ each with stationary distribution ${\pi }_i,i\in \mathcal{M}\triangleq \{1,\dots ,M\}$ and π_M = π. Associated with each subchain i is an MCMC kernel L_i that leaves π_i invariant, and which we run at every time step. Of course, without any further moves, the stationary distribution of the joint chain is

$$\stackrel{‒}{\pi }\left({\mathbf{x}}_{1:M}\right)\triangleq \underset{i=1}{\overset{M}{\Pi }}{\pi }_i\left({\mathbf{x}}_i\right)$$

and so if ${\mathbf{x}}_{1:M}~\stackrel{‒}{\pi }$, then x_M ~ π. This scheme does not affect the convergence rate of the independent chain M. However, since we can cycle mixtures of $\stackrel{‒}{\pi }$-stationary MCMC kernels without affecting the stationary distribution of the joint chain Tierney (1994), we can allow certain types of interaction between the subchains which can speed up convergence (Geyer 1991; Hukushima and Nemoto 1996). In general, we apply a series of MCMC kernels that act on subsets of the variables. For the sake of clarity, let us denote the number of second-stage MCMC kernels by R and the MCMC kernels themselves as K₁, … ,K_R, where kernel K_j operates on variables with indices in ${\mathcal{I}}_j\subset \mathcal{M}$. The idea is that the R kernels are executed sequentially and it is required that each K_j leave ${\Pi }_{i\in {\mathcal{I}}_j}{\pi }_i$ invariant.

Given π, there are a wide variety of possible choices for M, π_1:M−1, L_1:M, R, ${\mathcal{I}}_{1:R}$ and K_1:R which will affect the convergence rate of the joint chain. For those interested, Jasra et al. (2007) gives a review of some of these. It is clear that the first stage of moves involving L_1:M is trivially parallelizable. However, the second stage is sequential in nature. For a parallel implementation, it is beneficial for the ${\mathcal{I}}_j$’s to be disjoint as this allows the sequence of exchange kernels to be run in parallel. Of course, this implies that ${\mathcal{I}}_{1:R}$ should vary with time since otherwise there will be no interaction between the disjoint subsets of chains. Furthermore, if the parallel architecture used is SIMD (Single Instruction Multiple Data) in nature, it is desirable to have the K_j’s be nearly identical algorithmically. The last consideration for parallelization is that while speedup is generally larger when more computational threads can be run in parallel, it is not always helpful to increase M arbitrarily as this can affect the convergence rate of the chain. However, in situations where a suitable choice of M is dwarfed by the number of computational threads available, one can always increase the number of chains with target π to produce more samples.

3.2 Sequential Monte Carlo

SMC methods are a powerful extension of importance sampling methodology that are particularly popular for sampling from a sequence of probability distributions. In the context of state-space models, these methods are known as particle filtering methods; Doucet and Johansen (2010) and Liu (2008) give recent surveys of the field. In this context, let {x_t}_t≥0 be an unobserved Markov process of initial density x₀ ~ p₀(·) and transition density x_t ~ f(·|x_t−1) for t ≥ 1. We only have access to an observation process {y_t}_t≥1; the observations are conditionally independent conditional upon {x_t}_t≥0 of marginal density y_t ~ g(·|x_t) for t ≥ 1. SMC methods are used to approximate recursively in time the filtering densities p(x_0:t|y_0:t) which are proportional to $p({\mathbf{x}}_{0:t},{\mathbf{y}}_{0:t})\triangleq p_0\left({\mathbf{x}}_0\right){\Pi }_{i=1}^{t}f({\mathbf{x}}_i\mid {\mathbf{x}}_{i-1}){\Pi }_{i=1}^{t}g({\mathbf{y}}_i\mid {\mathbf{x}}_i)\text{for}t=1,\dots ,T$. These distributions are approximated with a set of random samples called particles through use of a sequential version of importance sampling and a special particle-interaction step known as resampling.

Parallelization of SMC methods is reasonably straightforward. The importance sampling step used at each time step is trivially parallelizable as it involves only the local state of a particle. The resampling step, in which some particles are replicated and others destroyed depending on their normalized importance weights, comprises the construction of an empirical cumulative distribution function for the particles based on their importance weights followed by sampling from this N times, where N is the fixed number of particles used throughout the computation. While neither of these tasks is trivially parallelizable, they can benefit moderately from parallelization. The bulk of the speedup will generally come from the parallelization of the evolution and weighting steps. As such, using criteria like effective sample size (Liu and Chen 1995) to avoid resampling at every time step is beneficial.

3.3 Sequential Monte Carlo Samplers

SMC samplers (Del Moral et al. 2006) are a more general class of methods that utilize a sequence of auxiliary distributions π₀, … , π_T, much like population-based MCMC as discussed in Jasra et al. (2007). However, in contrast to population-based MCMC, SMC samplers start from an auxiliary distribution π₀ and recursively approximate each intermediate distribution in turn until finally π_T = π is approximated. The algorithm has the same general structure as classical SMC, with differences only in the types of proposal distributions, target distributions and weighting functions used in the algorithm. As such, parallelization of SMC samplers closely follows that of SMC.

The difference between population-based MCMC and SMC samplers is subtle but practically important. Both can be viewed as population-based methods on a similarly defined joint space since many samples are generated at each time step in parallel. However, in population-based MCMC the samples generated at each time each have different stationary distributions and the samples from a particular chain over time provide an empirical approximation of that chain’s target distribution. In SMC samplers, the weighted samples generated at each time approximate one auxiliary target distribution and the true target distribution is approximated at the last time step (see also Section 4.1.3).

4 Canonical Examples

To demonstrate the types of speed increase one can attain by utilizing GPUs, we apply each method to a representative statistical problem. We use Bayesian inference for a Gaussian mixture model as an application of the population-based MCMC and SMC samplers, while we use a factor stochastic volatility state-space model to gauge the speedup of our parallel SMC method. We ran our parallel code on a computer equipped with an NVIDIA 8800 GT GPU, a computer equipped with an NVIDIA GTX 280 GPU and we ran reference single-threaded code on a Xeon E5420 / 2.5 GHz processor. The resulting processing times and speedups are given in Tables 1 - 3. We justify the comparison with single-threaded CPU code by observing that we are less interested in comparing GPUs with CPUs than we are in investigating the potential of many-core processors for statistical computation. Moreover, as noted in the introduction one advantage of GPU-based simulation is that it provides researchers outside traditional, expensive high-performance computing centres with access to a powerful parallel processing architecture.

Table 1.

Running times for the Population-Based MCMC Sampler for various numbers of chains M.

M	CPU (mins)	8800GT (secs)	Speedup	GTX280 (secs)	Speedup
8	0.0166	0.887	1.1	1.083	0.9
32	0.0656	0.904	4	1.098	4
128	0.262	0.923	17	1.100	14
512	1.04	1.041	60	1.235	51
2048	4.16	1.485	168	1.427	175
8192	16.64	4.325	230	2.323	430
32768	66.7	14.957	268	7.729	527
131072	270.3	58.226	279	28.349	572

Table 2.

Running times for the Sequential Monte Carlo Sampler for various values of N.

N	CPU (mins)	8800GT (secs)	Speedup	GTX280 (secs)	Speedup
8192	4.44	1.192	223.5	0.597	446
16384	8.82	2.127	249	1.114	475
32768	17.7	3.995	266	2.114	502
65536	35.3	7.889	268	4.270	496
131072	70.6	15.671	270	8.075	525
262144	141	31.218	271	16.219	522

Table 3.

Running time (in seconds) for the Sequential Monte Carlo method for various values of N.

N	CPU	8800GT	Speedup	GTX280	Speedup
8192	2.167	0.263	8	0.082	26
16384	4.325	0.493	9	0.144	30
32768	8.543	0.921	9	0.249	34
65536	17.425	1.775	10	0.465	37
131072	34.8	3.486	10	.929	37

The applications we discuss here are representative of the types of problems that these methods are commonly used to solve. In particular, while the distribution of mixture means given observations is only one example of a multimodal distribution, it can be thought of as a canonical distribution with multiple well-separated modes. Therefore, the ability to sample points from this distribution is indicative of the ability to sample points from a wide range of multimodal distributions. Similarly, performance of a latent variable sampler in dealing with observations from a factor stochastic volatility model is indicative of performance on observations from reasonably well-behaved but non-linear and non-Gaussian continuous state-space models.

4.1 Mixture Modelling

Finite mixture models are a very popular class of statistical models as they provide a flexible way to model heterogeneous data (McLachlan and Peel 2000). Let y = y_1:m denote i.i.d. observations where $y_j\in 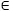\mathbb{R}$ for j {1, … ,m}. A univariate Gaussian mixture model with k components states that each observation is distributed according to the mixture density

$$p(y_j\mid {\mu }_{1:k},{\sigma }_{1:k},w_{1:k-1})=\sum _{i=1}^k{w}_{i}f(y_j\mid {\mu }_i,{\sigma }_i)$$

where f denotes the density of the univariate normal distribution. The density of y is then equal to ${\Pi }_{j=1}^{m}p(y_j\mid {\mu }_{1:k},{\sigma }_{1:k},w_{1:k-1})$.

For simplicity, we assume that k, w_1:k−1 and σ_1:k are known and that the prior distribution on μ is uniform on the k-dimensional hypercube [−10, 10]^k. We set k = 4, σ_i = σ = 0.55, w_i = w = 1/k for i 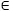{1, … , k}. We simulate m = 100 observations for μ = μ_1:4 = (−3, 0, 3, 6). The resulting posterior distribution for μ is given by

$$p(\mu \mid \mathbf{Y})\propto p(\mathbf{Y}\mid \mu ){\rm I}{\rm I}(\mu \in {[-10,10]}^4).$$

The main computational challenge associated with Bayesian inference in finite mixture models is the nonidentifiability of the components. As we have used exchangeable priors for the parameters μ_1:4, the posterior distribution p(μ|y) is invariant to permutations in the labelling of the parameters. Hence this posterior admits k! = 24 symmetric modes, which basic random-walk MCMC and importance sampling methods typically fail to characterize using practical amounts of computation (Celeux et al. 2000). Generating samples from this type of posterior is therefore a popular method for determining the ability of samplers to explore a high-dimensional space with multiple well-separated modes.

4.1.1 Population-Based MCMC

We select the auxiliary distributions π_1:M−1 following the parallel tempering methodology, i.e. π_i(x) 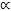π(x)^β_i with 0 < β₁ < … < β_M = 1 and use M = 200. This class of auxiliary distributions is motivated by the fact that MCMC converges more rapidly when the target distribution is flatter. For this problem, we use the cooling schedule β_i = (i/M)² and a standard $\mathcal{N}(0,I_k)$ random walk Metropolis-Hastings kernel for the first stage moves.

For the second stage moves, we use only the basic exchange move (Geyer 1991; Hukushima and Nemoto 1996): chains i and j swap their values with probability min{1, α_ij} where

$${\alpha }_{ij}=\frac{{\pi }_i\left({\mathbf{x}}_j\right){\pi }_j\left({\mathbf{x}}_i\right)}{{\pi }_i\left({\mathbf{x}}_i\right){\pi }_j\left({\mathbf{x}}_j\right)}.$$

Further, we allow exchanges to take place only between adjacent chains so that all moves can be done in parallel. We use R = M/2 and ${\mathcal{I}}_{1:R}$ is either {{1, 2}, {3, 4}, … , {M − 1, M}} or {{2, 3}, {4, 5}, … , {M − 2 M − 1}, {M, 1}}, each with probability half. We emphasize that all first stage MCMC moves are executed in parallel on the GPU, followed by all the exchange moves being executed in parallel.

To test the computational time required by our algorithms we allow the number of chains to vary but fix the number of points we wish to sample from the marginal density π_M = π at 8192. As such, an increase in the number of chains leads to a proportional increase in the total number of points sampled. Processing times for our code are given in Table 1, in which one can see that using 131072 chains is impractical on the CPU but entirely reasonable using the GPU. Figure 5 shows the estimated posterior density p(μ_1:2|y) from an increased set of 2²⁰ MCMC samples from π_M with M = 32768, which is nearly identical to the estimated marginal posterior densities of any other pair of components of μ. This marginal density has 12 well-separated modes in ${\mathbb{R}}^2$ but it is worth noting that the joint density p(μ_1:4|y) has 24 well-separated modes in ${\mathbb{R}}^4$. Figure 6 shows the number of points from each mode for various values of M. We also computed the average number of iterations taken for the samplers to traverse all modes for the different values of M. For M = 1 and M = 2, the sampler did not traverse all the modes at all, while for values of M between 4 and 32 the traversal time decreased from 80000 to 10000, after which it was unchanged with increases in M. These numbers should be compared to 24 × H₂₄ ≈ 91 - the expected number of samples required to cover every mode if one could sample independently from π - where H_i is the ith harmonic number.

Figure 5.

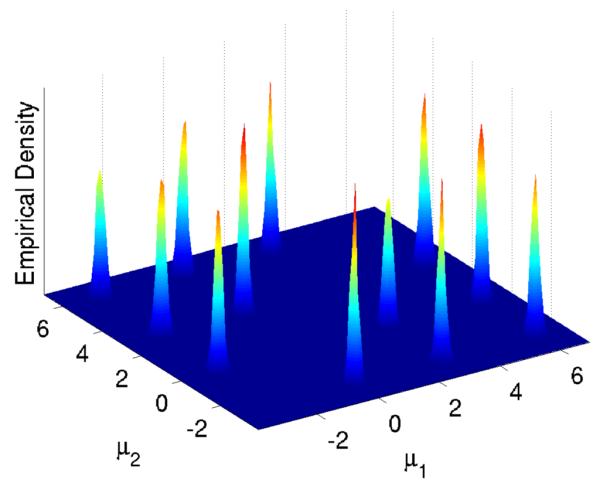
Estimated marginal posterior density p(μ_1:2|y) from MCMC samples.

Figure 6.

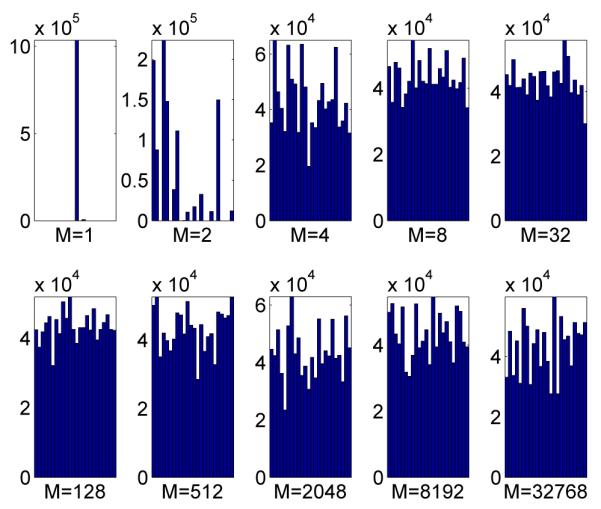
Number of MCMC samples from each mode. M is the number of auxiliary variables or chains.

4.1.2 SMC Sampler

As with population-based MCMC, we use a tempering approach and the same cooling schedule, i.e. π_t(x) 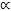π(x)^β_t with β_t = (t/M)² and M = 200. We use the uniform prior on the hypercube to generate the samples $\left\{{\mathbf{x}}_0^{(1:N)}\right\}$ and perform 10 MCMC steps with the standard $\mathcal{N}(0,I_k)$ random walk Metropolis-Hastings kernel at every time step. We use the generic backwards kernel suggested in Neal (2001) and Del Moral et al. (2006) for the case where each kernel is π_t-stationary so that the unnormalized incremental importance weights are of the form π_t(x_t−1)/π_t−1(x_t−1). Processing times for our code are given in Table 2. The estimated posterior density p(μ_1:2|y) using the SMC sampler is almost indistinguishable from that shown in Figure 5. Figure 7 shows the number of points from each mode for various values of N.

Figure 7.

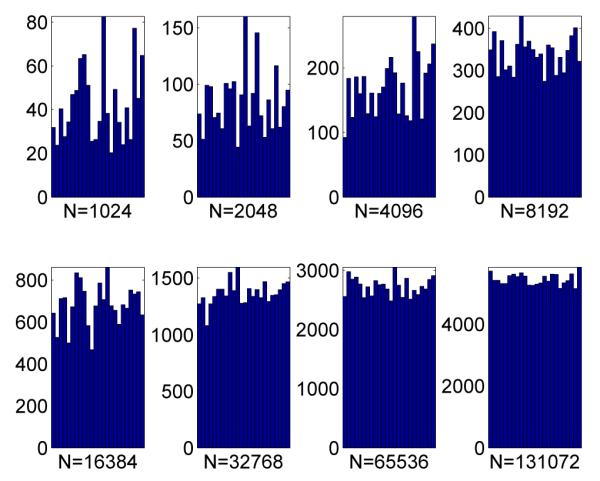
Effective number of SMC samples from each mode. N is the number of particles.

In this case, the GPU parallelization of the method is slightly more complex, as noted in Section 3.2. The MCMC steps are performed trivially in parallel whilst the resampling step, while implemented in a parallel fashion, benefits very little from parallelization due to the cumulative sum and multinomial sampling steps. These same issues are present in the implementation of the factor stochastic volatility example in Section 4.2 since the particle filtering and sequential Monte Carlo sampling algorithms are nearly the same.

4.1.3 Comparison

While both methods are capable of exploring the posterior distribution for μ, there are important differences in how the methods make use of parallelization. In particular, the SMC sampler parallelizes across particles approximating the same auxiliary distribution whilst the MCMC sampler parallelizes across auxiliary distributions at the same iteration. As such, to make full use of the graphics card the SMC sampler requires many particles while the MCMC sampler requires many auxiliary distributions. In most cases, however, one will be happy to use in excess of 8192 particles for SMC but one may not want to use in excess of 32768 auxiliary distributions. Indeed, for the application described above there seems to be no benefit in increasing the number of chains beyond 128, although this might also be due to the choice of cooling schedule and random walk variances. However, there are situations in which a large number of intermediate temperatures are required for exchange acceptance probabilities to be greater than some preset value, for example when the dimension of the distribution of interest increases Predescu et al. (2004).

The SMC sampler appears to be more efficient than the MCMC sampler for this problem. Indeed, with only 8192 particles the SMC sampler gives a reasonable representation of the posterior, taking only 597ms. The MCMC sampler requires around 2²⁰ samples to give a reasonably uniform number of samples per mode, and this takes just over 2 minutes.

For Bayesian inference in mixture models, there are many ways of dealing with the identiability of the mixture parameters; Jasra et al. (2005) includes a review of these. It is worth mentioning that for this type of model, we can permute samples as a post-processing step or within an MCMC kernel so traversal of the modes can be achieved trivially. The speedup of both methods is unaffected by the use of such mechanisms. We note that the speedup is unaffected by increases in the number of observations since this affects computation time by a constant and the modes are already well-separated. In this formulation, the speedup decreases only linearly in the number of mixture components since these components are stored in registers and the memory required per thread dictates the number of threads that can be run in parallel.

4.2 Factor Stochastic Volatility

Many financial time series exhibit changing variance. A simple multivariate volatility model that allows us to capture the changing cross-covariance patterns of time series consists of using a dynamic latent factor model. In such models, all the variances and covariances are modelled through a low dimensional stochastic volatility structure driven by common factors (Liu and West 2000; Pitt and Shephard 1999). We consider here a factor stochastic volatility model most similar to that proposed in Liu and West (2000) with ${\mathbf{y}}_t~\mathcal{N}({\mathbf{Bf}}_t,\Psi )$, ${\mathbf{f}}_t~\mathcal{N}(0,{\mathbf{H}}_t)$ and ${\mathbf{x}}_t~\mathcal{N}(\Phi {\mathbf{x}}_{t-1},\mathbf{U})$, where $\Psi \triangleq \text{diag}({\psi }_1,\dots ,{\psi }_M)$, ${\mathbf{H}}_t\triangleq \text{diag}\left(\text{exp}\left({\mathbf{x}}_t\right)\right)$ and $\Phi \triangleq \text{diag}({\varphi }_1,\dots ,{\varphi }_K)$.

Here, f_t is K-dimensional, y_t is M-dimensional and B is an M × K factor loading matrix with zero entries above the diagonal for reasons of identifiability. The latent variable at each time step t is the K-dimensional vector x_t. The likelihood of the data, y_t, given x_t is Gaussian with

$${\mathbf{y}}_t\mid {\mathbf{x}}_t~\mathcal{N}(0,{\mathbf{BH}}_t{\mathbf{B}}^T+\Psi ).$$

We generate data for times t = 1, … ,T = 200, M = 5, K = 3, x₀ = 0, ψ_i = 0.5, i 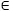{1, … ,M}, 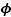_i = 0.9, i 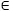{1, … ,K},

$$B=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0.5\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 1\hfill \\ \hfill 0.2\hfill & \hfill 0.6\hfill & \hfill 0.3\hfill \\ \hfill 0.8\hfill & \hfill 0.7\hfill & \hfill 0.5\hfill \end{array}\right)\text{and}U=\left(\begin{array}{ccc}\hfill 0.5\hfill & \hfill 0.2\hfill & \hfill 0.1\hfill \\ \hfill 0.2\hfill & \hfill 0.5\hfill & \hfill 0.2\hfill \\ \hfill 0.1\hfill & \hfill 0.2\hfill & \hfill 0.5\hfill \end{array}\right).$$

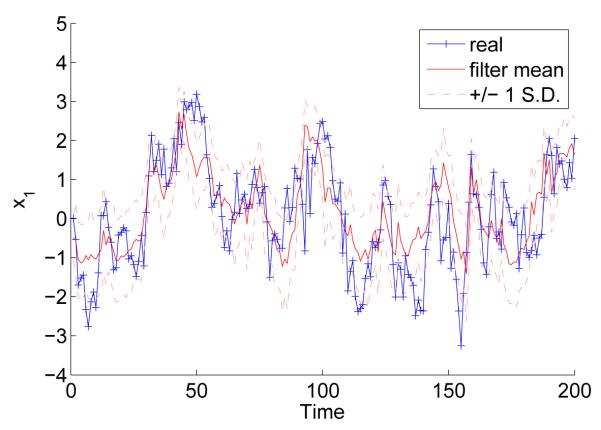
This is a simple example of a multivariate, non-linear and non-Gaussian continuous state-space model for which particle filters are commonly employed to sample from the posterior p(x_0:T|y_1:T). Processing times for our code are given in Table 3. In Figure 8 we plot the filter means for each component of x with ±1 sample standard deviations alongside the true values of x used to generate the observations.

Figure 8.

Estimated and real values of the first component of x

The speedups obtained in this application are considerably less than for mixture model inference problem. This can be explained by lower arithmetic intensity, higher space complexity in each thread and increased resampling rate as compared to the SMC sampler example above. The mixture model likelihood calculation contains a compute-intensive product-sum operation involving 104 values whilst the factor stochastic volatility likelihood consists mainly of matrix operations. In the latter case, the speedup is independent of T but not the dimension of the observations since the amount of memory required per thread increases quadratically in the dimension of each observation. For example, we attained a speedup of 80 on the GTX 280 when running a particle filter for a multivariate stochastic volatility model with M = K = 2. The frequency of resampling is an issue with respect to speedup because it can typically only attain around 10 to 20 fold speedup for practical values of N, mainly due to the parallel scan operation. This potentially gives rise to tradeoffs in speedup between the transition and weighting steps and the time between resampling steps for some models, since more sophisticated proposal distributions that parallelize less cleanly might reduce the resampling rate. This type of performance, however, still provides considerable speedup and may be more representative of what practitioners can expect in general.

4.3 Floating Point Precision

For all three algorithms discussed above, we ran identical algorithms with the same random numbers on the CPU using double precision floating point numbers and the resulting estimates of expectations of interest were affected by an order of magnitude less than the Monte Carlo variance of the estimates.

5 Discussion

The speedup for the population-based MCMC algorithm and the SMC sampler is tremendous. In particular, the evaluation of p(y|μ) for the mixture-modelling application has high arithmetic intensity since it consists of a product-sum operation with 400 Gaussian log-likelihood evaluations involving only 104 values. In fact, because of the low register and memory requirements, so many threads can be run concurrently that SIMD calculation of this likelihood can be sped up by 500 times on the 8800 GT and 800 times on the GTX 280. However, the speedup attained for the standard SMC algorithm may be more representative of the kinds of gains one can expect in most applications with only reasonable arithmetic intensity. Even so, speedups of 10 to 35 make many problems tractable that previously were not by reducing a week’s worth of computation to a few hours. For example, estimation of static parameters in continuous state-space models or the use of SMC proposals within MCMC can require thousands of runs, so a speedup of this scale can substantially reduce the computation time of such approaches (see e.g. Andrieu et al. (2010)). It is worth noting also that we can expect speedups in the vicinity of 500 with SMC if few resampling steps are required and each weighting step has small space complexity and moderate time complexity.

The GTX 280 outperforms the 8800 GT by a factor of about 2 in all situations in which the GPUs are used to capacity. This is the case in all but the population-based MCMC algorithm, in which the number of threads is determined by the number of auxiliary distributions. The reason for this is simple: the algorithms presented are register-bound on the inputs given, in that the number of registers required by each thread is the critical quantity that bounds the number of threads that can be run concurrently. The GTX 280 has twice the number of registers per multiprocessor and more than twice the multiprocessors compared to the 8800 GT. Hence, one could expect more speedup on many-core chips with even more registers. In fact, further improvements could be made using multiple cards with large amounts of memory, configurations of which are now available in NVIDIA’s Tesla line. These Tesla ‘personal supercomputers’ comprise 3 or more high-performance GPUs, each with 4GB of memory and a CPU with at least as much memory as the GPUs’ combined.

It should be noted that while we have used CUDA to implement the parallel components of algorithms, the results are not necessarily specific to this framework or to GPUs. It is expected that the many-core processor market will grow and there will be a variety of different devices and architectures to take advantage of. However, the SIMD architecture and the sacrifice of caching and flow control for arithmetic processing is likely to remain since when it is well-suited to a problem it will nearly always deliver considerable speedup. For users who would like to see moderate speedup with very little effort, there is work being done to develop libraries that will take existing code and automatically generate code that will run on a GPU. An example of this is Accelereyes’ Jacket engine for MATLAB code.

The speedups attainable with many-core architectures have broad implications in the design, analysis and application of SMC and population-based MCMC methods. With respect to SMC, it allows more particles to be used for the same or even less computation time, which can make these samplers viable where they previously were not. When faced with designing a population-based MCMC sampler, the results expectedly show that there is little cost associated with increasing the number of auxiliary distributions until the GPU reaches the critical limit of threads it can run concurrently. In our application, this does not occur until we have around 4096 auxiliary distributions. One might notice that this number is far larger than the number of processors on the GPU. This is due to the fact that even with many processors, significant speedup can be attained by having a full pipeline of instructions on each processor to hide the relatively slow memory reads and writes. In both SMC and MCMC, it is also clear from this case-study that it is beneficial for each thread to use as few registers as possible since this determines the number of threads that can be run simultaneously. This may be of interest to the methodology community since it creates a space-time tradeo that might be exploited in some applications.

A consequence of the space-time tradeo mentioned above is that methods which require large numbers of registers per thread are not necessarily suitable for parallelization using GPUs. For example, operations on large, dense matrices that are unique to each thread can restrict the number of threads that can run in parallel and hence dramatically affect potential speedup. In cases where data is shared across threads, however, this is not an issue. In principle, it is not the size of the data that matters but the space complexity of the algorithm in each thread that dictates how scalable the parallelization is.

The parallelization of the advanced Monte Carlo methods described here opens up challenges for both practitioners and for algorithm designers. There are already an abundance of statistical problems that are being solved computationally and technological advances, if taken advantage of by the community, can serve to make previously impractical solutions eminently reasonable and motivate the development of new methods.