On a psychophysical transformed-rule up and down method converging on a 75% level of correct responses

Abstract

Tranformed-rule up and down psychophysical methods have gained great popularity, mainly because they combine criterion-free responses with an adaptive procedure allowing rapid determination of an average stimulus threshold at various criterion levels of correct responses. The statistical theory underlying the methods now in routine use is based on sets of consecutive responses with assumed constant probabilities of occurrence. The response rules requiring consecutive responses prevent the possibility of using the most desirable response criterion, that of 75% correct responses. The earliest transformed-rule up and down method, whose rules included nonconsecutive responses, did not contain this limitation but failed to become generally accepted, lacking a published theoretical foundation. Such a foundation is provided in this article and is validated empirically with the help of experiments on human subjects and a computer simulation. In addition to allowing the criterion of 75% correct responses, the method is more efficient than the methods excluding nonconsecutive responses in their rules.

Transformed-rule up and down (UDTR) methods seem to constitute the most popular group of psychophysical methods for stimulus detection experiments. The fundamentals of the methods were reviewed in a classical article of Levitt's appearing in 1970 (1). He refers to the original publications of Wetherill (2) and of Wetherill and Levitt (3) introducing these methods. The methods are usually applied in connection with a two-interval forced choice procedure and an automated step wise variation of the stimulus investigated. The latter is presented at random in one of two sequential time intervals marked by light flashes or some other markers. Usually, the probability of the stimulus appearing in one or the other time interval is 0.5. It is assumed that the probability of detecting the stimulus depends on its magnitude, which is controlled by a response rule. A typical rule goes as follows. The subject decides on the interval of time in which he/she thinks the stimulus was presented. Whenever the response is incorrect, the stimulus is increased by a predetermined constant step. After three consecutive correct responses, the stimulus is decreased by a step of the same size. If the probability of a correct response is P_c, the probability of an incorrect response must be P_i = 1 − P_c, because no other response possibilities are allowed, and the probability of either a correct or incorrect response must sum to unity: P_c + P_i = 1. If the probability of a correct response is P_c, then the probability of three consecutive correct responses must be P_c³. According to the accepted rule, this is the same probability as the probability of a step down in the stimulus magnitude: P_d = P_c³. The probability of a step up is, under the rule, P_u = P_i. The stimulus magnitude equilibrates when P_d = P_u. Because the sum of the probabilities P_d and P_u must equal unity, this means that P_u and P_d must become 0.5, so that P_c³ = 0.5 and P_c = (0.5) (1/3), or P_c = 0.794.

Instead of three consecutive correct responses, the rule may call for only two. Then, a target level of 0.707 correct responses is obtained. Many other rules are possible. As described by Levitt (1), they all have in common that they rely on sets of consecutive responses. Under these conditions, the probabilities of correct responses, and of incorrect responses, if such are involved in a set, remain constant within the set and allow the mathematical formulation exemplified above; the probability of a set occurring is the product of the component probabilities involved.

The UDTR methods sketched above have many advantages, as described by Levitt (1). Undoubtedly, they are the reason for their popularity. However, they have an uncomfortable deficiency. They fail to achieve the target of 75% correct responses obtained in constant-stimuli two-interval forced-choice procedures, which corresponds to 50% of positive responses in yes/no procedures. This target is important in processing of statistically distributed data.

A UDTR method of a different kind, which achieves this target, was proposed ahead of them by Zwislocki et al. (4), already in 1958, and was used sporadically in various experiments (4–6) but failed to find general acceptance. Several reasons may account for this result. First, it was introduced as only one of several methods used to investigate a problem of a nonmethodological nature, and its fundamental significance was easy to miss. Second, its theoretical foundation was never published. Third, it required statistical evaluation deviating from classical procedures. This is reflected in Levitt's (1) review where its citation is completely misleading. In the present article, we explain its statistical foundation and validate it with the help of experiments performed on human subjects and by computer simulation.

Statistical Basis

The statistical basis of the method can be explained perhaps the most clearly with the help of a specific numerical example before it is generalized. Let us assume a two-interval forced-choice detection experiment in which the stimulus intensity is varied adaptively. The rule for the intensity variation is as follows: After every incorrect response, the stimulus intensity is increased by a constant step; after three correct responses, not necessarily consecutive, the intensity is decreased by a step of the same size. Allowing nonconsecutive responses constitutes a fundamental departure from the methods reviewed by Levitt (1). It is important to note that, because the intensity is increased between two correct responses separated by one or more incorrect responses, the detection probability of the correct responses in a sequence of three may not be constant, given that the probability depends on stimulus intensity. As a consequence, the statistics used in connection with the methods in which the correct responses must be consecutive for an intensity decrement to occur cannot be applied. This seems to have been the main objection to the method. However, the targeted average probability of correct responses can be calculated with the help of a different approach not involving the probability of each individual response.

Let us assume a sufficiently long period over which the stimulus intensity hovers around a value producing the targeted proportions of correct and incorrect responses. Let us assume further that n_c, correct response, and n_i, incorrect responses, occur over this time period, summing to n_t total responses. Then, the proportion of correct responses can be expressed as P_c = n_c/n_t, and the proportion of incorrect responses, as P_i = n_i/n_t. Because no other responses are allowed, we must have P_c + P_i = 1, or P_i = 1 − P_c.

Let us assume next that, in connection with the rule specified above, there are N_u trials followed by an intensity increment and N_d trials followed by an intensity decrement and that, in addition, there are N_o trials not followed by an intensity change, in total, N_t trials, where N_t = N_u + N_d + N_o. In terms of proportions, we obtain for the steps up in intensity P_u = N_u/N_t, and for the steps down, P_d = N_d/N_t; in addition, for no steps, P_o = N_o/N_t. As a result, P_u + P_d + P_o = 1. Intensity equilibrium is achieved when P_u = P_d.

In total, there must be as many intensity control events as subject responses: N_t = n_t. According to the rule, we have N_u = n_i and N_d = n_c/3, so that P_u = P_i, and P_d = P_c/3. As a consequence, we must have at the intensity equilibrium, P_i = P_c/3 or 1 − P_c = P_c/3. Accordingly P_c = 0.75, or 75%. Because the proportion, P_c, is equivalent to the average probability, the rule achieves the target level of 75% correct responses.

The method can be generalized by rewriting the rule in terms of variables: P_d = P_c/α and P_u = P_i/β, where α and β can be equal to any positive whole number. Note that more than one, not necessarily consecutive, incorrect responses may be required for an incremental step. By analogy to the calculations of the preceding paragraph, we obtain P_c = α/(α + β). This formulation allows the target proportion of correct responses to be varied over a wide range.

Verification

The theory introduced above was verified informally in the past on several occasions with the help of human observers. Here, two illustrative examples selected from past experiments in addition to a computer simulation are used. One example has been derived from the auditory experiment used in 1958 (4) to introduce the method and the other, from a tactile detection experiment (7). The computer simulation has been performed especially for this article.

Example I.

The experiment belonged to a series of experiments performed by means of several psychophysical methods with the purpose of finding out if practice and motivation affected the measured threshold of audibility. Not surprisingly, the greatest effects were obtained with Békésy's (8) tracking method that may be regarded as an adaptive method of limits and in which the responses depend on a subject's detection criterion. Nevertheless, somewhat unexpectedly, the effects showed up, although to a lesser extent, even when the methods of constant stimuli and two interval forced choice were combined to minimize the criterion effect. Because the resulting method was awkward and, not being adaptive, did not allow direct tracking of the threshold, a new adaptive procedure was introduced, which combined Békésy's tracking with two interval forced choice. The new method, which could be called “forced-choice tracking” minimized the effect of a subject's criterion, so prominent in Békésy's method.

The new method was executed as follows. The stimuli consisted of 500-msec bursts of a 100-Hz tone. They were presented at random in one of two time intervals marked by flashes of white light. The observers had to decide in which time interval the stimulus was presented and vote accordingly by pressing an appropriate control key. Whenever their decision was incorrect, the sound intensity was increased by a 2-dB step before the next stimulus presentation. After three correct responses, not necessarily consecutive, the intensity was decreased by a 2-dB step. The stepped intensity level was recorded on a graph paper that was advanced by a constant step along the time axis every time the intensity was incremented or decremented. Feedback was provided for the observers by means of light flashes—green for correct responses and red for the incorrect ones. There were four listening sessions, each divided into three 7-min test periods with 5-min rest periods in between. The experiment was performed on 10 unpracticed observers.

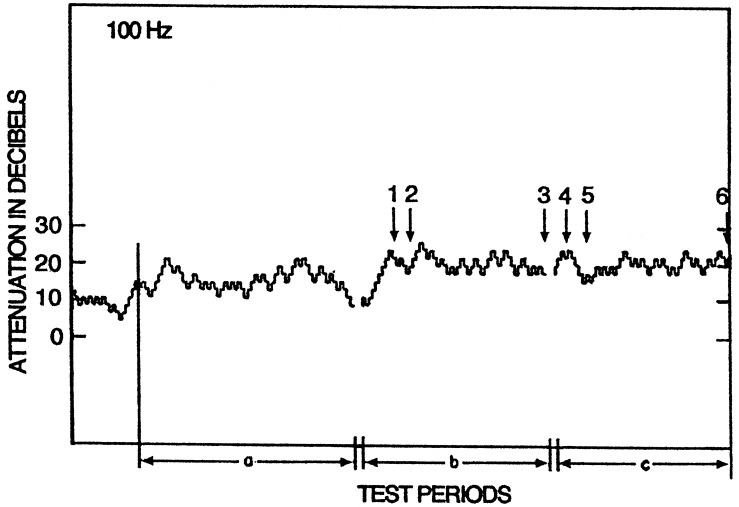
A graphical example of the results, obtained on one observer, is shown in Fig. 1. The abscissa axis is proportional to time; the ordinate axis shows attenuator settings relative to an arbitrary reference. Note that attenuation increments are the inverse of intensity increments. Every vertical step is equal to 2 dB; the downward steps following incorrect responses, the upward steps, sequences of three correct responses, not necessarily consecutive. The test periods, marked a, b, and c, are shown separated by short empty intervals corresponding to the rest periods.

Figure 1.

Attenuator tracing of the detection threshold of one observer for a 100-Hz tone in one experimental session consisting of three test periods of ≈7-min each separated by 5-min rest periods. The vertical steps are 2 dB in size. The arrows indicate four periods over which the numbers of steps were counted. Note that attenuation steps are the inverse of intensity steps. (Modified from ref. 4).

It should be evident on sight that the average attenuation in the first test period is lower than in the following two test periods. The difference was attributed to the effect of practice. It was consistent with similar findings obtained in preceding experiments performed with different psychophysical methods. The difference in attenuation between the remaining two sessions is negligible and the attenuation remains reasonably constant within the test periods, except at the very beginning. The results of these two test periods are suitable for verification of the expected average proportion of 75% correct responses at the equilibrium attenuation level.

To determine the average proportion of correct responses at the tracked attenuation level, it is sufficient to count the downward and upward steps over a sufficiently long time interval and multiply the number of the latter by three, the required number of correct responses per step. The counts were performed over four time intervals selected from the second and third test periods and marked by arrows. The number of up steps between arrows 1 and 3 was 21, giving 63 correct responses when multiplied by 3. The number of down steps, equal to incorrect responses, was 24, so that there were 87 responses in total. The quotient of the number of correct responses and of all of the responses came out to be 0.724, or 72.4%. Similar calculations for the time intervals between the arrows 2 and 3, 4 and 6, and 5 and 6 gave the proportions of correct responses of 75, 74, and 77.5%, respectively. The average for all four time intervals amounts to 74.7% correct responses, very close to the targeted 75%.

Example II.

The experiments concerned tactile sensitivity to mechanical vibration oriented perpendicularly to the skin surface (7). The vibration was delivered to the thenar eminence of the right hand by a flat contactor with a circular circumference and a diameter of 2.9 cm. It was driven by an electrodynamic vibrator whose vibration amplitude was measured with a calibrated accelerometer. The coupling of the probe to the skin surface was carefully controlled by taping the hand to a rigid surface surrounding the contactor and determining the first contact between the contactor, made of metal, and the skin surface with the help of an electrical continuity measurement. Subsequently, the probe was pushed into the skin until an indentation of 0.5 mm was produced. In this way, interruption of the contact during vibration was prevented.

The experiments were performed at three vibration frequencies, 70, 200, and 400 Hz presented in 330-msec bursts with 25-msec on and off ramps. The size of the contactor and the stimulus parameters assured predominant stimulation of Pacinian corpuscles rather than of other tactile receptors. The purpose of the experiments was to study phenomena of masking produced by sinusoids and random noise. However, here, only the initial trials performed without masking on three observers are considered.

The psychophysical procedure was the two-interval forced-choice tracking procedure proposed by Zwislocki et al. (4) and executed as follows. The stimulus was presented at random in one of two observation intervals of 720-msec duration, marked by lights of equal duration: the first by a red light and the second by a green one. The probability of the signal appearing in one or the other interval was 50%. The observation intervals were separated by response intervals of 3,400 msec marked by a blue light. The observers had to respond during these intervals by choosing the observation interval that they believed contained the stimulus and by pressing a corresponding button. Incorrect responses were signaled to the observers by a flash of white light.

The responses were registered on the chart of a Békésy (7) attenuator advanced along the time axis by a constant step every time a change in signal attenuation occurred. The latter was controlled by an electronic logic according to the Zwislocki et al. (4) rule. Every time an incorrect response occurred, the attenuation decreased by a 1-dB step. An equally large upward step in attenuation occurred after every three correct responses, not necessarily consecutive. In this way, the attenuator was expected to track the attenuation level producing on the average a proportion of 75% correct responses, as explained above.

A measurement was accepted as successful when 4–4.5 min (≈50 steps) of stable tracking was achieved. Stable trucking meant that the deviations of attenuation from the mean level did not exceed more than −2.5 db. The empirical average proportion of correct responses was ascertained during the stable tracking in 10 separate measurements by simply counting the number of up and down attenuation steps, as in the preceding example. The proportion varied between 72 and 78%, averaging to 75%. Thus, the theoretical prediction was verified.

Computer Simulation.

A computer program was written to simulate the performance of a modeled observer responding to a two-interval forced-choice task. The probability of a correct response was modeled by a Weibull function, as described by Relkin and Pelli, for example (9). The parameters were chosen so that the function matched closely the psychometric function shown in Fig. 15 of Zwislocki et al. (4).

The intensity at 75% correct responses was set arbitrarily to 0 dB. The only other free parameter (β, in Relkin and Pelli's paper) was determined by the slope of the psychometric function. For the Weibull function, the slope equals 4.24β %/dB at the point where the function equals 82% correct responses. At that point, for the data in Zwislocki et al. (4), the slope was approximated to be 6%/dB. Thus, a value of 1.42 was used for β. For each simulated trial, the probability of a correct response was calculated with the help of the Weibull function. A pseudorandom number, uniformly distributed between 0 and 1, was computed to determine the response of the simulated observer. If the random number was less than or equal to the probability of a correct response at the respective intensity, the observer responded correctly. Otherwise, the observer responded incorrectly. Intensity was adjusted exactly as described for the actual psychophysical experiments.

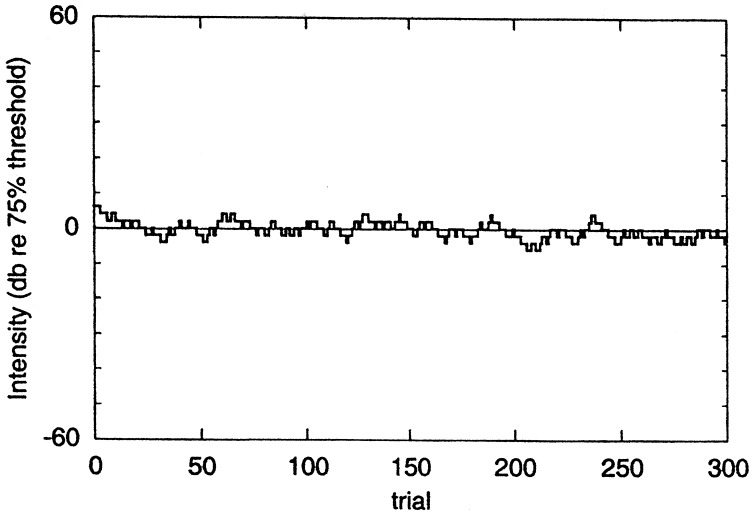
The results for one simulation are shown in Fig. 2 where the starting intensity has been arbitrarily chosen to be 5 dB and the attenuation step size has been fixed at 2 dB as in the previous examples. The axes of the graph in Fig. 2 have been chosen to be similar to those of Fig. 1. One difference between Fig. 2 and Fig. 1 is that intensity is plotted for each trial rather than only when the attenuation is changed. The results are shown for 300 trials, a number similar to the total number of trials for the data shown in Fig. 1. The average intensity for the final 200 trials was 0.7 dB less than the value corresponding to 75% correct responses on the Weibull function. For the same group of trials, the percentage correct was computed for each intensity on the basis of the Weibull function and the average was found to be 72.8%. Agreeing very closely with theoretical predictions, the simulated observer responded correctly for 75.5% of these 200 trials. Many simulations were run with varying starting points, all showing a similar equilibrium pattern. The total number of correct responses, after equilibrium was achieved, was recorded for the final 200 trials of 10 runs of the computer simulation. The percentage of correct responses varied between 74% and 76%, with an average of 75%.

Figure 2.

Graphic representation of an example of the computer simulation of the procedure with a starting level 5 dB above the target eqilibration level and a 2-dB step size. The axes of the figure are similar to those of Fig. 1, but the tracing differs somewhat in that the level is plotted for every trial rather than only when the level is changed.

Discussion

This article provides the statistical foundation and empirical validation for a UDTR method, called “forced-choice tracking” suggested in 1958 (4), which targets the stimulus level at 75% correct responses. This is the only constant-step method known to us that achieves this desirable target. The methods based on probability products of consecutive responses, reviewed by Levitt (1970), do not do so. The 1958 method preceded the currently popular UDTR methods but failed to find general acceptance. There are three probable reasons for the failure. The method was presented as one item in a substantive rather than methodological article concerning the “effects of practice and motivation on the threshold of audibility” (4), its statistical foundation was not provided, it called for a statistical theory deviating from a classical approach based on nonconsecutive responses. A typical response rule went as follows: Every time an observer commits an error in a two-interval forced-choice procedure, the stimulus level is increased by a constant step; it is decreased be a step of the same magnitude after three correct responses, not necessarily consecutive. The admission of nonconsecutive responses appeared to introduce a statistical problem because incorrect responses made between the correct ones changed the probabilities of the latter. As a consequence, the probabilities of correct responses in a set of three nonconsecutive ones were not constant. This precluded application of the statistics used in connection with sets of consecutive responses. In this article, it is shown that the average level, in particular, the 75% level of correct responses can be derived theoretically without referring to individual probabilities of correct responses. The derivation is based on proportions of correct and incorrect responses made during a sufficiently long test period at which an approximately constant stimulus level is maintained. Of course, the proportions are equivalent to average probabilities. It may be mentioned here that, even in the UDTR methods based on products of consecutive responses, the assumption of constant probabilities of these responses is an idealization. The probabilities are not really constant because of natural fluctuations in an observer's sensitivity.

In addition to achieving the 75% target of correct responses, the response rule allowing sets of nonconsecutive responses has an added advantage of increasing the efficiency of the method. When consecutive correct responses are required, they may be erased by incorrect responses occurring before a required number of the correct responses is completed. Then, the correct responses have to be accumulated anew. The time taken up by an incomplete and erased set of correct responses is wasted. When nonconsecutive responses are accepted, no responses have to be erased.

The derived target of 75% correct responses was verified in the past empirically in several experiments on human observers. Two examples, one from audition and one from the sense of touch, are given. The verification is very simple. It is sufficient to count the number of stimulus steps corresponding to incorrect and correct responses during a stable response period and to multiply the resulting numbers by the numbers of responses prescribed by the response rule. The number of correct responses so obtained is divided by the total number of responses. For test periods containing ≈50 steps, the mean proportions of correct responses were found to range from ≈72 to 78%, averaging at ≈75% over several test periods.

In addition, the targeted response level of 75% correct responses has been verified for this paper by computer simulation.

Abbreviation

UDTR

transformed-rule up and down