Topological basis of epileptogenesis in a model of severe cortical trauma

Abstract

Epileptic activity often arises after a latent period following traumatic brain injury. Several factors contribute to the emergence of post-traumatic epilepsy, including disturbances to ionic homeostasis, pathological action of intrinsic and synaptic homeostatic plasticity, and remodeling of anatomical network synaptic connectivity. We simulated a large-scale, biophysically realistic computational model of cortical tissue to study the mechanisms underlying the genesis of post-traumatic paroxysmal epileptic-like activity in the deafferentation model of a severely traumatized cortical network. Post-traumatic generation of paroxysmal events did not require changes of the structural connectivity. Rather, network bursts were induced following the action of homeostatic synaptic plasticity, which selectively influenced functionally dominant groups of intact neurons with preserved inputs. This effect critically depended on the spatial density of intact neurons. Thus in the deafferentation model of post-traumatic epilepsy, a trauma-induced change in functional (rather than anatomical) connectivity might be sufficient for epileptogenesis.

interictal epileptiform discharges (IEDs), characterized by brief, repetitive (∼200–500 ms) bursts of highly correlated population activity, are often considered as an important diagnostic feature of epileptic seizures (Dzhala and Staley 2003; Wendling et al. 2005). Despite the fundamental significance of IEDs, the mechanisms responsible for their generation in epileptic brains are still elusive (de Curtis and Avanzini 2001; Keller et al. 2010). IEDs could reflect complex network interactions in heterogeneous neuronal populations (Keller et al. 2010), which depend on many different network organization parameters, such as connectivity and topological correlations (Bogaard et al. 2009; Srinivas et al. 2007).

To address this question, we designed a large-scale model of a cortical network to study the characteristics of post-traumatic IED activity, which often arises in vivo after a latent period that follows traumatic brain injury (Pitkänen et al. 2006). Understanding how brain trauma affects the propensity to observe IEDs can help reveal the ways in which a traumatized brain can become epileptic. Earlier studies indicated that in the traumatized network, adjustable remodeling of a network's anatomical connectivity can result in transition from normal (asynchronous) to burst-like, collective activity (Dyhrfjeld-Johnsen et al. 2007; Morgan and Soltesz 2008). Other studies suggested that intrinsic and synaptic homeostatic plasticity (Turrigiano et al. 1998) after brain trauma may contribute to epileptogenesis (Avramescu and Timofeev 2008; Frohlich et al. 2008; Houweling et al. 2005; Timofeev et al. 2010).

In this study, we show that the transition to IED does not necessarily rely on changes in the network topology. Rather, the emergence of paroxysmal bursts critically depends on the functional connectivity that is determined primarily by the spatial distribution of trauma-surviving (intact) neurons and the dominant synaptic connections between them. We further show that topological determinants of this intact subnetwork only weakly affect the rate of post-traumatic interictal activity; rather, the spatial density of intact neurons is the pivotal parameter. This suggests a new, previously overlooked role for the spatial pattern of brain trauma in determining the chances of developing pathological activity.

MATERIALS AND METHODS

The cortical network model.

A cortical network was modeled as a two-dimensional (2D) network (80 × 80 neurons), in which each neuron could establish synapses with its peers with probability, p_c = 0.6, within its local footprint (10 × 10 neurons). Pyramidal (PY) neurons constituted 80% of the network population (5,120 out of 6,400 neurons), and inhibitory (IN) neurons constituted the remaining 20% (1,280 out of 6,400 neurons). We have not implemented layer-specific features in the model, because our goal was to define general properties of a cortical network responding to traumatic intervention. This is a common approach that has both its advantages (many layer-specific properties are not well known, and the generic model captures common dynamics of the cortical network) and disadvantages (layer-specific features; e.g., predisposition of the specific layers or areas to the epileptogenesis cannot be tested).

Parameters were tuned such that in the baseline conditions, model PY and IN neurons fired with average rates of 5 and 10 Hz, respectively (see Fig. 2A). For each model neuron, the current equation was

$$C_m\frac{d{V}_m}{dt}=-I_{ion}\left(t\right)+I_{syn}\left(t\right)+I_{EX}\left(t\right)$$ (1)

The ionic current evolved according to Prescott et al. (2006)

$$I_{ion}\left(t\right)=G_{Na}w\left(V_m\right)\left(V_m-50\right)+G_K{m}_{\infty }\left(V_m\right)\left(V_m+100\right)+G_L\left(V_m+70\right)+G_A\left(t\right)\left(V_m+100\right)$$ (2)

The fraction of open sodium (Na) channels was

$$\frac{dw}{dt}=0.15\left(w_{\infty }\left(V_m\right)-w\left(V_m\right)\right)\cosh \left(\left(V_m+2\right)/42\right)$$ (3)

The steady-state fractions of Na and potassium (K) channels were, correspondingly

$$w_{\infty }\left(V_m\right)=0.5\left(1+\tanh \left(\left(V_m+2\right)/21\right)\right);m_{\infty }\left(V_m\right)=0.5\left(1+\tanh \left(\left(V_m+1.2\right)/23\right)\right)$$ (4)

Adaptation conductance, G_A(t), was nonzero only for PY neurons

$$G_A\left(t\right)=\left(3mS/c{m}^2\right)z\left(t\right)$$ (5)

$$\frac{dz}{dt}=0.005·\left(-z+\frac{1}{1+\exp \left(-V_m/5\right)}\right)$$ (6)

Values of other parameters

$$G_{Na}=10mS/c{m}^2,G_K=10mS/c{m}^2,G_L=1.3mS/c{m}^2,C_m=1\mu F/c{m}^2$$

Fig. 2.

Trauma-induced transformation of network electrical activity. A: “healthy” cortical network exhibited asynchronous activity, with pyramidal (PY) neurons firing at ∼5 Hz and inhibitory neurons firing at ∼10 Hz. B–D: examples of post-traumatic steady-state collective activity (left) for different spatial patterns of trauma parameterized with different spatial densities of intact neurons (ρ_I; right). In the left plots, the y-axis indexes the 250 sampled neurons. In center panels, we show temporal profiles of representative paroxysmal bursts for each scenario. In the right plots, black dots denote the intact neurons that survived the trauma. The white space within the boxes represents the deafferented neurons that lost their afferent excitation following the trauma. Because we considered cases of severe deafferentation (only up to 5% of network neurons survive the trauma), the density (definition given in materials and methods, Spatial density of intact model neurons) of intact neurons is close to 1 for all cases considered. E: following deafferentation, the network-averaged PY firing rate dropped dramatically but then slowly recovered due to the action of homeostatic synaptic plasticity (HSP). Temporal dynamics (fluctuations) of the firing rate depended on the spatial pattern of deafferentation. Each dot represents network-averaged firing rate of model PY neurons in the window of 4 s. Different colors correspond to the different spatial densities ρ_I of intact neurons: green line, ρ_I = 0.02; red line, ρ_I = 0.06; black line, ρ_I = 1. B–E: the number of intact neurons was the same (N_I = 100).

Synaptic dynamics.

Synaptic transmission was modeled as a deterministic process, in which both α-amino-3-hydroxy-5-methylisoxazolepropionic acid (AMPA) and GABAa conductances were described as

$$\frac{d{g}_X}{dt}=-\frac{g_X}{{\tau }_D}+G_{X}D\delta \left(t-t_{SPIKE}\right)$$ (7)

where τ_D = 5 ms was the time of synaptic conductance decay. Per-spike synaptic conductances were

$$G_{PP}=74.4\mu S/c{m}^2,G_{IP}=89.28\mu S/c{m}^2,G_{PI}=372\mu S/c{m}^2,G_{II}=74.4\mu S/c{m}^2$$

N-methyl-d-aspartate (NMDA) conductance dynamics was modeled as

$$g_{NMDA}\left(t\right)=\frac{g_S\left(t\right)-g_F\left(t\right)}{1+0.264\exp \left(-0.06V_m\right)}$$ (8)

with

$$\frac{d{g}_{F,S}}{dt}=-\frac{g_{F,S}}{{\tau }_{F,S}}+G_{NMDA}D\delta \left(t-t_{SPIKE}\right)$$ (9)

NMDA receptor activation parameters were

$$G_{NMDA}=8.928\mu S/c{m}^2,{\tau }_F=2ms,{\tau }_S=80ms$$

The parameter D accounted for short-term synaptic depression at AMPA/NMDA synapses

$$\frac{dD}{dt}=\frac{1-D}{{\tau }_R}-U\delta \left(t-t_{SPIKE}\right)$$ (10)

Depression parameters were: τ_R = 0.8 s, U = 0.07. All synaptic currents were related to their conductances by I_X(t) = −g_X(t)/(V_m − E_X), with E_AMPA = E_NMDA = 0 mV, E_GABA = −70 mV. In addition to network current, each model neuron received an excitatory current I_EX(t) = −g_EX(t)(V_m − E_EX) from “the rest” of the cortex. Synaptic conductance of this current evolved according to dg_Ex / dt = g_Ex / τ_Ex + G_Exδ(t − t_Ex) and was stimulated at ×t_EX at the baseline Poisson rate of V_EX = 100 Hz. Other parameters of external stimulation were G_EX = 300 μS/cm²; τ_EX = 5 ms; E_EX = 0 mV. This external stimulation will be henceforth referred to as “afferent excitation”, which was responsible for the generation of background electrical activity in network models. Afferent excitation was present throughout the simulations in all model neurons, albeit its intensity for a given neuron depended on the specific trauma scenario that we studied, as described below.

Trauma.

In its simplest form, trauma can be described as deafferentation, following which, the amount of external input to the network is reduced (Grafstein and Sastry 1957; Prince and Tseng 1993). In the present model, we assumed that deafferentation is parameterized by both the number of deafferented neurons and the reduction in the rate of their afferent excitation. Thus the trauma in our model was described by two parameters: f_D, fraction of deafferented neurons, and r_D, the remaining (relative to baseline scenario of ν_EX = 100 Hz) rate of afferent excitation. As an example, (f_D = 0.3, r_D = 0.4) describes a scenario, in which the external stimulation rate to 30% of randomly picked neurons is reduced to 40% (40 Hz) of its value in a “healthy” network (100 Hz). We mainly considered scenarios with almost complete deafferentation. A small number of model neurons (1–5% of the total network population, labeled as N₁) preserved their external afferent inputs after the trauma (i.e., at all times after the trauma, the rate of afferent excitation to these neurons was the same as in the baseline model, ν_EX = 100 Hz). These neurons were referred to as “intact” neurons and were distributed in space as described below.

Spatial density of intact model neurons.

One of our main results is the observation that the rate of paroxysmal discharges in a severely traumatized network critically depends on the distribution of intact neurons—the neurons that preserve intact afferent input after deafferentation. To vary the spatial distribution of these intact neurons, we defined their spatial density as follows. We first defined the area in which intact neurons could be distributed as a square (symmetric with respect to the center of our 2D lattice on which the network was built) of side L₁ (in lattice units). A predefined number N₁ of neurons were then randomly selected from all L₁ × L₁ neurons in the region of interest (each lattice site in our 2D lattice could accommodate only one model neuron). These selected neurons preserved their input after deafferentation. All other neurons in the network were deafferented. The ratio, ρ_I = N₁/(L₁ × L₁), then defined the spatial density of intact neurons within the L₁ × L₁ area after deafferentation. According to this definition, ρ_I = 1 implies that all of the neurons within the selected L₁ × L₁ area were intact and that all of the deafferented neurons were distributed outside of this area. ρ_I = 0 implies that all the neurons of the network were deafferented. Note that this definition of “intact neuron density” applies only to the case of a traumatized network when the population of model neurons can be subdivided into “deafferented” and intact on the basis of the afferent excitation they receive.

Homeostatic synaptic plasticity.

Following earlier studies (Frohlich et al. 2008; Houweling et al. 2005), we used an approximation, whereby homeostatic adjustments of collateral synaptic conductances (of intra-network connections) were calculated at the end of every 4 s of simulation on the basis of activity during the preceding 4 s. The following equations were applied to adjust collateral synaptic conductances

$$G_{PP}=G_{PP}+{10}^{-3}\left(v_0-\overline{v}\right)G_{PP};G_{PI}=G_{PI}-5·{10}^{-4}\left(v_0-\overline{v}\right)G_{PI}$$ (11)

in which v̄ is the averaged (over all PY neurons in the network) firing rate during the preceding 4 s, and ν₀ is the target firing rate (5 Hz). Longer monitoring intervals (8 and 12 s) affected the rate with which the network approached its post-traumatic steady state but had no qualitative effect on results or conclusions of the present study. Note also that in our present model, homeostatic synaptic plasticity scaled all PY-PY synaptic conductances by the same amount, and all PY-IN conductances were scaled by the same amount as well (although different from that of the PY-PY case). Because of this similarity across all synapses of the same type, we could quantify the extent of homeostatic synaptic plasticity (HSP) simply by computing the percentage of change in synaptic conductance relative to its value in the baseline model. Thus taking PY-PY synapse as an example, HSP = 100·G_pp(t = T) − G_pp(t = 0) / G_pp(t = 0), where the time T is taken to be sufficiently long after the trauma event (in the new post-traumatic steady state).

Analysis of network structure.

We applied several widely used measures to characterize organization of the intact subnetwork. The interconnectedness of the intact subnetwork was quantified by computing the network-averaged in-degree 〈k_i〉, the mean number of incoming connections received by a typical intact neuron from other intact neurons. To quantify the topological correlations in the subnetwork of intact neurons, we computed its clustering coefficient. The clustering coefficient of the ith intact neuron was defined as

$$c_i=\frac{{\displaystyle \sum _{j=1,m=1}^{N_K}{e}_{ij}{e}_{im}{e}_{jm}}}{N_K\left(N_K-1\right)}$$ (12)

where N_K is the number of intact neurons that send synaptic connections to the ith intact neuron, e_ij = 1, if the jth intact neuron projects a synapse to the ith intact neuron (and e_ij = 0 if there is no such synaptic connection), and the double sum runs over all pairs of intact neurons that send synaptic connections to the ith intact neuron. The clustering coefficient measures the abundance of “connectivity triangles” and thus can be used to estimate the number of elementary recurrent circuits in the subnetwork of presynaptic intact neurons that send synapses to a given intact neuron. A network-averaged clustering coefficient of the intact subnetwork was obtained by averaging c_i over all intact neurons.

In a set of simulations, we replaced the intact subnetworks with their equivalent random graphs. These graphs were composed of the same set of intact neurons N_i, had the same mean in-degree 〈k_i〉 (same averaged number of synapses from other intact neurons to a given neuron) but uniform probability p_ij = (N_i − 1)/〈k_i〉 to establish a pair-wise connection between intact neurons, and were characterized by a much lower clustering coefficient compared with the intact subnetworks of the baseline model from which they were derived (see Fig. 1 for schematic diagram; see also Fig. 4A for quantification of clustering coefficient reduction).

Fig. 1.

Schematic diagram of manipulations to network connectivity schemes. Left: the baseline subnetwork of intact neurons. Because the synaptic footprint is local, distant, intact neurons are not connected. Center: the subnetwork with randomized connectivity. Number of intact connections per intact neuron is the same as in the baseline model, locations of intact neurons are the same, but the correlation structure of connectivity is destroyed by allowing distant intact neurons to be connected. Right: the subnetwork with fixed connectivity. Number of intact connections per intact neuron is the same as in the baseline model, and the correlation structure of connectivity is the same as well. Spatial proximity between intact neurons is destroyed by randomly redistributing them through the network.

Fig. 4.

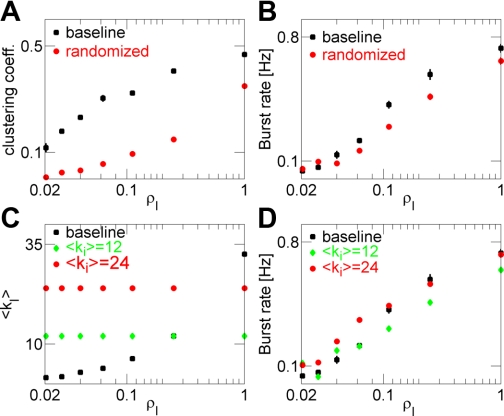
Network topology weakly affects paroxysmal activity. A: network-averaged clustering coefficient for the baseline intact network (squares) and equivalent randomized network (circles) vs. the density of intact neurons. B: burst rate plotted vs. the density of intact neurons for scenarios considered in A. C: mean number of intact synapses per intact neuron in the baseline intact network (squares) and intact network with fixed connectivity (green diamonds, 〈k_i〉 = 12; red circles, 〈k_i〉 = 24) vs. the spatial density of intact neurons. D: burst rate plotted vs. the spatial density of intact neurons for scenarios considered in C. For all cases, N_I = 100, and rate-drop parameter (r_D) = 0.1. Data points are mean ± SEM (n = 4).

As we show in results, Spatial density but not topology, of the intact subnetwork is causal in increasing the rate of IEDs in the traumatized newtwrok, the mean number of incoming connections in intact subnetworks increased as the density of intact neurons increased. Thus either one of these parameters (incoming connectivity or spatial density of intact neurons) could, in principle, affect the rate of paroxysmal discharges. To clearly determine the relative role of connectivity vs. spatial density, in another set of simulations, we replaced the intact subnetworks with a network that had preset connectivity (the same mean number of incoming connections per intact neuron was used for subnetworks with a different spatial distribution of their neurons). Specifically, for each density scenario, we determined the intact neurons (same number of intact neurons was used regardless of their spatial density) and then imposed synaptic connections between them (same mean number of synapses to a given intact neuron from other intact neurons was used, regardless of their spatial density), in addition to synaptic connections, which those intact neurons formed with deafferented neurons (Fig. 1). This allowed us to avoid mixing the effects of spatial distribution of intact neurons with the changes in their interconnectedness in the intact subnetwork.

RESULTS

Rate of post-traumatic IEDs depends on the spatial distribution of intact neurons.

To study effects of synaptic deafferentation on the network dynamics, we designed large-scale network model of the cortical excitatory neurons and IN interneurons (see materials and methods, The cortical network model), which displayed random, asynchronous activity in the physiological frequency range (Fig. 2A). Immediately following the deafferentation, the averaged firing rate of PY neurons dropped to very low levels (<1 Hz; Fig. 2B). Synaptic interactions significantly contributed to neuronal dynamics in our model: thus after deafferentation, the firing rate of intact neurons was also reduced. The extent of the drop in the firing rate of intact neurons depended on the parameters for deafferentation and on the spatial density of intact neurons (e.g., for the scenario considered in Fig. 2C, the initial drop in averaged firing rate of intact neurons was from 5 Hz to ∼0.4 Hz, but for the scenario considered in Fig. 2D, the initial drop was from 5 Hz to ∼3 Hz). Evidence from experimental studies and clinical data suggests that post-traumatic networks undergo significant remodeling of anatomical and functional connectivity that aims to compensate for the trauma-induced reduction of excitability and activity (Avramescu and Timofeev 2008; Butz et al. 2009; Dyhrfjeld-Johnsen et al. 2007; Jin et al. 2006). In particular, trauma-induced, acute reduction of activity may modify synaptic strengths by activating HSP (Avramescu and Timofeev 2008), which upregulates depolarizing influences (e.g., excitatory intrinsic and synaptic conductances) and downregulates hyperpolarizing ones (e.g., IN conductances) (Turrigiano et al. 1998). This regulatory process depends on the ongoing network activity and operates on a faster timescale than do the mechanisms of structural network reorganization [e.g., post-traumatic sprouting; see Dyhrfjeld-Johnsen et al. (2007) and Morgan and Soltesz (2008)]. We implemented HSP in our model of post-traumatic network reorganization.

In our model, homeostatic regulation adjusted the strengths of synaptic conductances to bring the network-averaged firing rate to a preset target level of 5 Hz, corresponding to a typical rate of asynchronous firing in the intact neocortex (Fig. 2E). We previously demonstrated that HSP-mediated upregulation was able to recover normal, asynchronous spiking activity for low-to-moderate levels of deafferentation only (Frohlich et al. 2008; Houweling et al. 2005). A result of homeostatic regulation following severe deafferentation was the transformation of collective activity from asynchronous (for a healthy cortex; Fig. 2A) to burst-like activity (Fig. 2, B–D), which resembled the IEDs; each burst lasted ∼200 ms and gradually recruited all model neurons. Importantly, however, here, we found that the effect of HSP on the mean firing rate depended on the spatial distribution of intact neurons (see definition of intact neuron density in materials and methods, Spatial density of intact model neurons), with low-density scenarios (intact neurons widely scattered in space; low ρ_I) resulting in failure to achieve the preset rate for physiological levels of synaptic scaling [maximal upregulation limited at 100%, corresponding to the double value of the initial synaptic strength, as in Turrigiano et al. (1998)]. The rate at which bursts were generated depended on the density, ρ_I, of the intact subpopulation (Fig. 2, B–D). The bursts emerged only after homeostatic plasticity changed synaptic conductances to become sufficiently strong, suggesting that this mode of collective activity depends on synaptic interactions. In lower-density scenarios, model neurons fired more spikes per burst compared with the higher-density scenario (compare Fig. 2, B–D), thus compensating for the lower burst rate and helping to bring the network-average firing rate of PY neurons toward its target value. Taken together with the apparent dependence of post-traumatic burst rate on spatial distribution of intact neurons, this suggests that the network organization of a small set of coupled intact neurons may significantly affect post-traumatic activity in a whole network; this important issue was the focus of the current study.

Topological determinants of the intact subnetwork correlate with the rate of post-traumatic IEDs.

We now quantify the effects of the spatial distribution of intact neurons on reorganization of collective activity in the post-traumatic network. The spatial density of intact neurons was varied by uniformly distributing them in square blocks of preset dimensions. We found that the rate at which IEDs were generated significantly changed with the density of intact neurons ρ_I (Fig. 3A). The asymptotic (after a sufficiently long time) level of homeostatic synaptic scaling increased for the network with a low density of intact neurons until it saturated at 100% (Fig. 3B). For a given spatial density, the rate of IEDs depended nonlinearly on deafferentation—the amount of reduction in the rate of extra-layer afferent stimulation (see below, Fig. 6A). Earlier studies by other groups (Bogaard et al. 2009; Dyhrfjeld-Johnsen et al. 2007; Netoff et al. 2004) suggested that changes of the network topology (e.g., averaged number of incoming connections per neuron, clustering coefficient of a network, or minimal path length) can lead to epileptic-like activity. To understand how the network organization of a small number of intact neurons, which survived the trauma, determines the chances of generating collective interictal dynamics in our model networks, we computed the clustering coefficient of the directional graph that described subnetwork ω of intact neurons (ω⊂Ω, where Ω denotes the entire network) for different spatial densities of intact neurons. A clustering coefficient of the ith neuron, c_i, measures the abundance of connectivity triangles (elementary, recurrent circuits) in the subnetwork, defined by that neuron's projections from other intact neurons (see materials and methods, Analysis of network structure); thus higher c_i is expected to lead to a more-correlated and possibly stronger excitation of the ith neuron. As is seen from Fig. 3C, in our networks, the distribution of c_i was much broader with the high peak near zero when intact neurons were scattered in low density, compared with the high-density scenario in which the intact neurons were clustered in space. The network-averaged clustering coefficient of the intact subnetwork was positively correlated with the rate of IEDs that engulfed the entire traumatized network (Fig. 3E) and was also positively correlated with the spatial density of intact neurons (Fig. 3D). Thus we conclude that topological determinants of network structure positively correlate with the rate of paroxysmal burst generation.

Fig. 3.

Post-traumatic interictal activity depends on spatial organization of trauma-surviving neurons. A: burst rate vs. spatial density of intact neurons. Number of intact neurons: N_I = 100 (squares); N_I = 400 (triangles). B: amount of HSP at model synapses. Symbols are the same as in A. C: distributions of local clustering coefficient (C_i) in the intact subnetwork. D: averaged clustering coefficient of intact subnetwork plotted vs. the spatial density of intact neurons. E: burst rate plotted vs. the network-averaged clustering coefficient. F: mean number of collateral intact synapses (<k_i>) vs. density of intact neurons. Data points are mean ± SEM (n = 4).

Fig. 6.

Reduction in the rate of afferent excitation determines the propensity for burst generation. A: burst rate plotted vs. the r_D for different densities of trauma-surviving neurons: ρ_I = 1 (black squares); ρ_I = 0.06 (red circles); ρ_I = 0.02 (green diamonds). B: SD (across all PY neurons) of firing rates of PY model neurons plotted [σ(ν_PY)] vs. the r_D. Symbols are the same as in A. C: firing rate of isolated neuron plotted vs. r_D. Data points are averages over 100 neurons. D: amount of HSP at model synapses. Symbols are the same as in A. A, B, and D: data points are mean ± SEM (n = 4). E: schematic presentation showing how the peak burst rate arises due to the competing action of intracellular excitability (black line; strong for mild trauma) and HSP (gray line; strong for strong trauma). Hypothetical burst rate is dashed red line (not to scale).

Spatial density, but not topology, of the intact subnetwork is causal in increasing the rate of IEDs in the traumatized network.

Is the rate of paroxysmal discharges in the post-traumatic network determined solely by the topological organization of the intact subnetwork? Both the clustering coefficient and the mean number of collateral synapses 〈k_i〉, between intact neurons scaled up with the density of intact neurons (Figs. 3, D and F). In general, these two characteristics of the network topology are independent, and the observed burst rate increase after deafferentation could be conflated with either of them or with both. Alternatively, the burst rate increase can be mediated primarily by an increase of the spatial density of intact neurons. To answer this question, in simulations below, we alternated the connectivity structure of the population of intact neurons that “survived” deafferentation.

To determine the role of topological clustering in paroxysmal burst generation, we substituted, immediately after deafferentation, the equivalent random graph for the subnetwork ω of all intact neurons. This graph consisted of the same set of intact neurons, with each neuron receiving the same averaged number of synapses from other intact neurons, but probability to establish a pair-wise connection between intact neurons was uniform (see materials and methods, Analysis of network structure). Such randomization of intact subnetwork topology significantly reduced the average clustering coefficient of the network (Fig. 4A), while resulting in a small but significant decrease in the incidence of post-traumatic paroxysmal bursts (Fig. 4B). Thus a higher clustering coefficient correlated with an increased rate of paroxysmal discharge but explained only a small part of it.

To assess the extent to which an increased number of collateral synapses in the intact subnetwork affect the rate of paroxysmal discharges, we substituted, immediately after deafferentation, the network with fixed connectivity for the subnetwork ω of all intact neurons. Specifically, we replaced connectivity between intact neurons by fixed connectivity with the same mean number of synapses, regardless of the spatial density of intact neurons (see materials and methods, Analysis of network structure). Thus in this fixed connectivity network, the structure and number of synapses between intact neurons were kept constant, regardless of their density (Fig. 4C). Interestingly, in the networks with fixed connectivity, the rate of IEDs still showed a very strong dependence on the spatial density of intact neurons (Fig. 4D). When density was low, synaptic drive to deafferented neurons from intact ones was insufficient to initiate spikes required for global activity propagation, regardless of the connectivity pattern between intact neurons. Thus increased collateral connectivity of the intact subnetwork correlated with the increased rate of paroxysmal discharge but also explained only a small part of it.

Network-averaged minimal path length defines the averaged number of connected neurons that separate any two neurons in the network. Minimal path length is relatively low in networks with random structure of synaptic connectivity. It has been suggested that the low path length could facilitate fast signal propagation in networks (Dorogovtsev and Mendes 2003); thus it could also affect the rate at which paroxysmal events are generated (Netoff et al. 2004). However, our results suggest that in our model, path length is not causally related to the rate of burst generation. Indeed, in a network with fixed connectivity (Fig. 4C), path length was also fixed (path length was two for the case 〈k_i〉 = 12, and was 1.75 for the case 〈k_i〉 = 24), but that did not, in itself, eliminate the increase in burst rate with increasing spatial density of intact neurons (Fig. 4D). Furthermore, the rate of paroxysmal bursts was nearly the same between two networks with different path length.

Collectively, these results suggest that the topological parameters of a network of intact neurons that survived deafferentation only weakly affected the form of post-traumatic activity; nonetheless, the spatial density of trauma-surviving neurons per se had a dominant role.

Patterns of electrical activity are modulated by properties of synaptic transmission at PY-PY synapses.

Since burst initiation and propagation in our networks critically relied on synaptic interactions, we wanted to further elaborate the extent to which properties of synaptic transmission (in particular, at PY-PY synapses) could shape collective activity in post-traumatic networks. We focused on the effects of NMDA conductance and short-term synaptic depression at PY-PY synapses.

In principle, burst initiation could be affected by the NMDA conductance at PY-PY synapses. Initiation of intense bursting requires effective summation of activity from several presynaptic neurons. Given the relatively slow time scale of NMDA current decay, it could affect the excitability of the postsynaptic neuron, affect temporal summation of excitatory input from collateral synapses, and thus affect the propensity for burst generation. We tested the role of slow NMDA currents by removing NMDA conductance from PY-PY synapses. Removal of NMDA conductance from PY-PY synapses had dramatic effects on the properties of collective electrical activity in post-traumatic networks (Fig. 5). For sufficiently high density of intact neurons, bursts were generated at a high rate (Fig. 5A) and propagated through the network as sharp waves, during which, each model neuron fired, at most, one action potential (Fig. 5C). Homeostatic synaptic scaling in these networks without NMDA conductance attained highest-allowed values (maximal upregulation of 100%; Fig. 5B), yet the network-averaged firing rate of PY neurons failed to reach the target value of 5 Hz. Notably, below a critical spatial density, the characteristics of electrical activity (burst rate, HSP scaling factor) were the same for baseline model networks and for networks without NMDA conductance. Thus we conclude that NMDA conductance at PY-PY synapses can modulate the pattern of collective electrical activity (by increasing the number of spikes fired by a PY model neuron per burst, thus increasing the mean neuronal firing rate and decreasing the rate of paroxysmal discharges), but its effects again depended on the spatial density of intact neurons. Without NMDA conductance, the target values of the network firing rate could only be achieved as a result of extreme upregulation of the fast excitatory synapses that led to the very high level of synchrony of firing.

Fig. 5.

Properties of synaptic transmission modulate collective electrical activity in the post-traumatic network. A: burst rate vs. the spatial density of intact neurons for different scenarios of synaptic transmission at PY-PY synapses: the baseline model with synaptic depression and N-methyl-d-aspartate (NMDA) conductance at PY-PY synapses (squares), the model with synaptic depression but without NMDA conductance at PY-PY synapses (triangles), the model without synaptic depression but with NMDA conductance at PY-PY synapses (diamonds). B: amount of HSP at model PY-PY synapses for different scenarios shown in A. Data keys are the same ones as in A. C: representative sample raster plots of collective electrical activity for different scenarios shown in A—the baseline model (top panel), the model without NMDA conductance (middle panel), the model without synaptic depression (bottom panel). For all plots, ρ_I = 1 (all of the neurons within a selected area in the middle of the network are intact). D: network-averaged firing rate of PY model neurons for different scenarios shown in A. Data keys are the same ones as in A.

Synaptic transmission could also be affected by the presence of short-term synaptic depression, which was incorporated at PY-PY synapses in our model network. The strength of synaptic depression in our model was characterized by the “resource usage” parameter U, which quantified how much “synaptic resource” was used by a synapse per each synaptic spike (lower values of U mean milder depression). Reducing U to 50% of its baseline value led to a reduction in burst rate (Fig. 5A). At the same time, bursts became wider, with each model neuron firing intensely during the bursting event (Fig. 5C). The amount of HSP at model synapses and the mean firing rate of PY neurons were also affected (Figs. 5, B and D). When synaptic depression was removed completely from PY-PY synapses, bursts were generated at a very low rate (0.035 Hz; data not shown), but each bursting event lasted about 5 s, with neurons firing intensely during the entire burst, similar to seizure-like activity.

Thus properties of synaptic transmission at PY-PY synapses could modulate the emerging pattern of collective activity in post-traumatized networks. With only weak depression of synaptic coupling between PY neurons, collective activity resembled seizures (periods of intense activity, each lasting several seconds) occurring at a low rate. Stronger depression led to earlier burst termination and promoted generation of paroxysmal-like network bursts of short duration at a higher rate. In all cases, the rate at which these bursts were generated critically depended on the spatial density of intact neurons.

Functional severity of cortical trauma affects initiation and propagation of paroxysmal bursts.

The spatial density of intact neurons affects the rate of IEDs through strong excitation of nearby deafferented neurons, which occurred because of the larger number of intact neurons firing at a relatively high rate, projecting to a given, deafferented neuron, and promoted burst propagation through the network in spite of low excitability of traumatized neurons. A single intact neuron is not likely to excite its postsynaptic, deafferented target to a point of spike generation. However, when several intact neurons are close enough in space, there is a possibility that they are synaptically coupled, as well as share one or more postsynaptic targets. Thus there is an increased chance for activity to be propagated through the intact subnetwork, and intact neurons can provide stronger input to nearby deafferented neurons, increasing the chance for the latter to fire action potentials. Upregulation of synaptic conductances by HSP increases synaptic coupling and so, would further increase the excitation of deafferented neurons by their intact peers. We reasoned that neuronal excitability (partially controlled in our networks by parameter r_D, the remaining rate of afferent stimulation of traumatized neurons after deafferentation) could also affect the rate of post-traumatic paroxysmal bursts. As Fig. 6A shows, the burst rate peaked for a certain density-invariant value of r_D, with low rates of activity both for strong (low r_D) and mild (high r_D) trauma scenarios. The amount of HSP needed to reach these levels of activity was monotonic, increasing function of trauma severity (Fig. 6D).

One interesting observation from Fig. 6A is that the rate of paroxysmal discharges depended on the spatial density of intact neurons (characterized by ρ_I) only in the severe trauma regime (small r_D) and was largely independent of the spatial density for milder trauma (high r_D). To understand why this difference between severe and mild trauma regimes arose, we computed the SD of the firing rate of all PY neurons in the network (Fig. 6B). In mild trauma regime, SD of PY neuron firing rates was largely the same for all density scenarios and attained smaller values for higher r_D (milder trauma). This suggests that in a mild trauma regime, deafferented neurons become more like their intact peers. The milder the trauma, the less is the drop in afferent stimulation, and deafferented neurons are more excitable immediately after deafferentation. In addition, for milder trauma, HSP is able to compensate for a reduction in firing rate incurred by a relatively small decrease in afferent excitation. Thus in this scenario, the excitability level of deafferented neurons is close to that of their intact peers. Consequently, the exact spatial configuration of intact neurons (a critical factor that determines the ability of an intact subnetwork to engage the deafferented neurons' paroxysmal burst) becomes less important, thus blurring the role of spatial density. By the same token, the differences between intact and deafferented neurons become more pronounced in severe trauma regimes (low r_D), thus underscoring the role that the spatial configuration of the intact subnetwork has in burst generation (Fig. 6A, severe trauma regime).

Another interesting feature seen in Fig. 6A is that for medium and low spatial density of intact neurons (low ρ_I), the rate of paroxysmal discharges exhibited a peak when plotted vs. the functional severity of trauma, r_D. We explain this finding using the following heuristic argument: first, note that the HSP is strongest for most severe trauma and then monotonically reduces for milder trauma (Fig. 5D); second, note that the excitability of an isolated model neuron, which is driven only by afferent external input, increased for milder trauma (Fig. 6C) vs. more severe trauma. This offers the following explanation for the nonmonotonic dependence of the burst rate on the severity of trauma: quite generally, the rate of IEDs depends on two factors—neuronal excitability and the strength of collateral synaptic connections. Excitability of traumatized neurons is low in severe trauma cases (low r_D), making it unlikely that a network can initiate and propagate global IEDs, despite the very strong synaptic conductance that is scaled up by HSP to its maximum value at 100%. Those events require correlated activity of remaining intact neurons and are therefore rarely generated in the network of randomly spiking cells. On the other hand, in a mild trauma scenario (high r_D), neurons are relatively excitable and noisy, but collateral connections, even after HSP upregulation, are not strong enough to ensure reliable propagation of correlated burst. Thus in this limit, the network favors the asynchronous mode over the IEDs. For traumatic events of a moderate severity, IEDs can be generated at the highest rate that is limited by the balance of intrinsic (remaining rate of afferent stimulation) and synaptic (HSP) excitability (Fig. 6E).

DISCUSSION

Alterations in network connectivity can significantly promote epileptogenesis through establishment of long-range connections, which lead to the formation of “small-world” networks (Dyhrfjeld-Johnsen et al. 2007; Netoff et al. 2004). Here, we studied the emergence of IEDs in the deafferentation model of post-traumatic epileptogenesis. Our results suggest that structural change in connectivity might be a sufficient but not a necessary condition for the generation of IEDs. In our model, bursting depended on the change in the functional connectivity (the extent to which one neuron can affect another) of the intact subnetwork, as well as on the ability of the traumatized network to convey the burst that was generated by the intact neurons. Thus we showed that the geometrical organization of a small number of trauma-surviving neurons can be a decisive factor in determining the properties of post-traumatic IEDs.

The mechanism by which a small number of intact neurons affected burst generation in our model was based on their geometrical organization. Because of the local synaptic footprint, intact neurons had to be proximal enough in space to be able to form recurrent connections between them and also to create a situation in which nearby deafferented neurons would have a sufficiently large number of synaptic contacts from their intact peers. Proximity of intact neurons elevated their firing rates by means of their synaptic interaction, which consequently, elevated the excitation of deafferented neurons. HSP further upregulated synaptic coupling strength and thus also contributed to the increased firing rate of intact neurons and to the increased excitation of nearby deafferented neurons. When sufficiently excited by their intact peers, deafferented neurons generated action potentials that further propagated through the network of deafferented neurons in the form of a paroxysmal burst. Synaptic depression and time course of synaptic conductance (slow NMDA) affected the time-dependent strength of synaptic coupling and thus modulated the rate of paroxysmal burst generation.

In the model presented in this study, we assumed a population of intact neurons embedded in a “sea” of traumatized neurons. Thus we implicitly assumed that even in what might appear to be a completely deafferented piece of cortical tissue, there might be some small number of neurons that preserve their intact afferent input after deafferentation. In reality, trauma is more likely to create a traumatized region surrounded by the intact network; however, in this situation, it is difficult to correctly define the spatial density of intact neurons. Experimental data (Topolnik et al. 2003) and our preliminary modeling results suggest that paroxysmal bursts were generated by intact neurons at the boundary between traumatized and intact regions. Nevertheless, we chose, in this study, to focus on the effects of spatial density and investigate the scenario in which a small set of intact neurons is embedded in a large, traumatized network.

Netoff et al. (2004) showed, in a computational model of hippocampal network, that bursting (but not seizing) is facilitated in networks with low clustering coefficient and short path length. Analysis of in vitro glutamate injury models of hippocampal neuronal networks led to the same conclusion—an increase in burst rate was accompanied by a strong reduction in network clustering coefficient (Srinivas et al. 2007). Our own results suggest that while a clustering coefficient of the intact subnetwork positively correlates with the rate of interictal events, in itself, it is not a causal factor leading to the IED generation. Significant change of the clustering coefficient in the model led to only a slight change of the burst rate. However, those earlier studies focused on epileptogenesis in networks of cells with homogeneous excitability properties. By contrast, in our model, the trauma created two populations of neurons (deafferented and intact) with different excitability properties. Subsequent action of HSP only increased this difference. Burst generation depended on the ability of the intact population to “ignite” the deafferented population of neurons. This differs from the conclusions of earlier studies (Netoff et al. 2004; Srinivas et al. 2007), in which, bursting depended on the ability to quickly propagate spikes in a network of neurons with the same excitability. Indeed, neither one of the topological parameters of our model (clustering coefficient and minimal path length between model neurons) had a causal influence on the rate of paroxysmal discharges; however, the rate of bursts was critically affected by the spatial density of intact neurons. Thus in the deafferentation model of post-traumatic epilepsy, structural changes in connectivity may not be a primary factor in burst generation.

Earlier computational models stressed the importance of network interconnectedness (mean number of synapses received by a neuron) in setting the rate of interictal bursting activity, suggesting that more interconnected networks can generate bursts of collective activity at a higher rate [Fig. 4, C and F, in Netoff et al. (2004)]. Our own results suggest that in the post-traumatic epilepsy scenario, the mean number of connections between intact neurons may not play a central role—the rate of IEDs in model networks with fixed connectivity of the intact subnetwork was virtually indistinguishable from that of the baseline model (Fig. 4, C and D). At first, this may appear to contradict the conclusions of an earlier study (Netoff et al. 2004). However, in contrast to the IEDs induced by stronger recurrent connectivity (Netoff et al. 2004), the trauma in our model of IEDs significantly reduced the network excitability by decreasing the afferent excitation (captured by the parameter r_D in our model), thus making the post-traumatic network harder to excite. We found that increasing the mean number of connections between intact neurons only increased the burst rate if it was accompanied by an increasing mean number of projections from intact neurons to deafferented cells. The last occurred when spatial density of intact neurons was increased.

HSP in post-traumatic cortical networks might be mediated by diffusible TNF-α (Stellwagen and Malenka 2006). This molecule is believed to be released from astrocytes in response to neural trauma (Lau and Yu 2001), and it was shown that TNF-α plays a critical role in synaptic scaling (Steinmetz and Turrrigiano 2010; Stellwagen and Malenka 2006). Initially, after a traumatic event, an astrocytic response might create “patches” of high TNF-α concentration colocalized with those parts of the network that are more severely affected by the trauma. In such an early post-traumatic scenario of spatially heterogeneous trauma, the model of HSP will need to be critically revised to reflect the dependence of HSP on local levels of synaptic inactivity. In contrast, our present model assumes that HSP is evaluated based on the global, network-wide level of inactivity, an assumption that reflects the situation when the levels of TNF-α have equilibrated by diffusion (Edelstein-Keshet and Spiros 2002). This is likely to occur during the late stage of post-traumatic reorganization, after the network has reached its new steady state. Thus our present model might implicitly reflect the situation in the post-traumatic steady state. Our preliminary results (to be published elsewhere) indicate that during the early post-traumatic phase, the spatially localized action of the HSP might render the cortical network strong sensitivity toward local perturbations of electrical activity, thus potentially resulting in a high rate of paroxysmal bursts. However, experimentally, no (or very little) epileptic-like activity has been observed immediately following the trauma. This suggests that the network might use additional, neuroprotective mechanisms that would reduce the rate of paroxysmal discharge, in spite of high sensitivity to perturbations. These mechanisms and their actions are being investigated in ongoing work.

The HSP that followed the deafferentation in our model increased connectivity strength, which in turn, increased the firing rate of intact neurons. However, this increased firing rate was not always communicated to the rest of the network—only in special space configurations (a relatively high density of intact neurons) could intact neurons collectively nucleate sufficiently strong activity that initiated spiking in deafferented neurons and took the form of IEDs propagating through the cortical network. Thus the excitability and the spatial distribution of a small number of neurons that preserved their inputs after trauma overshadow the role of network topology and connectivity in the generation of post-traumatic IEDs. Several studies have indicated that topological correlation in connectivity can enhance burst generation (Bogaard et al. 2009; Dyhrfjeld-Johnsen et al. 2007); however, this can be heavily affected by the dynamics of neuronal excitability. Thus more detailed studies, aiming to investigate the interplay of trauma pattern, synaptic connectivity, and intrinsic neuronal excitability, are required to understand the emergence of pathological rhythms in the traumatized brain.

GRANTS

This research was supported by the National Institute of Neurological Disorders and Stroke Grants R01-NS-059740 and R01-NS-060870 and the Howard Hughes Medical Institute.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).