Abstract
Abnormal oscillatory synchrony is increasingly acknowledged as a pathophysiological hallmark of Parkinson's disease, but what promotes such activity remains unclear. We used novel, nonlinear time series analyses and information theory to capture the effects of dopamine depletion on directed information flow within and between the subthalamic nucleus (STN) and external globus pallidus (GPe). We compared neuronal activity recorded simultaneously from these nuclei in 6-hydroxydopamine-lesioned Parkinsonian rats with that in dopamine-intact control rats. After lesioning, both nuclei displayed pronounced augmentations of beta-frequency (∼20 Hz) oscillations and, critically, information transfer between STN and GPe neurons was increased. Furthermore, temporal profiles of the directed information transfer agreed with the neurochemistry of these nuclei, being “excitatory” from STN to GPe and “inhibitory” from GPe to STN. Separation of the GPe population in lesioned animals into “type-inactive” (GP-TI) and “type-active” (GP-TA) neurons, according to definitive firing preferences, revealed distinct temporal profiles of interaction with STN and each other. The profile of GP-TI neurons suggested their output is of greater causal significance than that of GP-TA neurons for the reduced activity that periodically punctuates the spiking of STN neurons during beta oscillations. Moreover, STN was identified as a key candidate driver for recruiting ensembles of GP-TI neurons but not GP-TA neurons. Short-latency interactions between GP-TI and GP-TA neurons suggested mutual inhibition, which could rhythmically dampen activity and promote anti-phase firing across the two subpopulations. Results thus indicate that information flow around the STN-GPe circuit is exaggerated in Parkinsonism and further define the temporal interactions underpinning this.
Keywords: maximum entropy, Parkinson's disease, coding capacity
it is unclear how loss of midbrain dopamine neurons in Parkinson's disease (PD) disturbs the activities of their targets in corticobasal ganglia circuits, which must ultimately support the observed behavioral deficits. Studies in unmedicated patients with PD have shown that beta oscillations (13–30 Hz) often prevail in the cortex and basal ganglia (Alonso-Frech et al. 2006; Amirnovin et al. 2004; Brown 2003; Brown et al. 2001; Levy et al. 2002; Moran et al. 2008; Williams et al. 2002). These beta oscillations decrease when patients are on dopamine replacement medication or when they initiate movements, hinting at their functional significance (Amirnovin et al. 2004; Brown et al. 2001; Brown and Williams 2005; Kuhn et al. 2004; Levy et al. 2002; Williams et al. 2002, 2003, 2005). Excessively synchronized beta oscillations also arise in these circuits after chronic dopamine depletion in the 6-hydroxydopamine-lesioned rat model of PD (Degos et al. 2009; Mallet et al. 2008a, 2008b; Sharott et al. 2005b). Whether these oscillations have a direct negative effect on neural representations and the information coding capacity of these circuits (Cruz et al. 2009) or only indirectly reflect changes in the underlying computations therein is not clear, and neither are the precise changes in microcircuit properties that support them. It is known, however, that excessive beta oscillations in this animal model develop over a period of days/weeks following lesions of dopamine neurons (Degos et al. 2009; Mallet et al. 2008b) and that they arise in key circuit nodes, such as the subthalamic nucleus (STN) and external globus pallidus (GPe).
The reciprocally connected network formed by the glutamatergic neurons of the STN and the GABAergic neurons of GPe might be particularly important for generating synchronized oscillations in the basal ganglia in PD (Bevan et al. 2002). Indeed, the incidence of oscillatory synchronization between the STN and GPe, as measured by standard (linear) cross-correlations between neuron pairs, greatly increases after dopamine depletion in animals (Mallet et al. 2008b). However, changes in cross-correlations do not necessarily reflect changes in the interactions between these two nuclei. For example, if the autocorrelations (including those arising from oscillatory activity) in the GPe changed, the measured cross-correlation would also change, even when the influence of the GPe on the STN had not. This is because the cross-correlation is the convolution of the autocorrelation function and the transfer function of the system (Papoulis 1991). Stated another way, linear cross-correlations reflect both the changes within each nucleus and the interaction between the nuclei. Therefore, cross-correlations do not necessarily best represent the effect of a spike in one nucleus on the probability of a spike in the other nucleus, which is the quantity of interest. Analytical models that are based on logistic regression (Truccolo et al. 2005) and mutual information (Cruz et al. 2009) offer some advantages in that they can account for the effects of the changes within each nucleus when they assess the interactions between nuclei, although they do not unambiguously distinguish between direct (monosynaptic) effects and indirect network effects. We have applied these modeling approaches to examine how the interactions or “directed information flow” within the STN-GPe network are changed following chronic dopamine depletion.
METHODS
Data collection.
Experimental procedures were carried out on adult, male Sprague-Dawley rats (Charles River, Margate, UK) and were conducted in accordance with licenses granted by the UK Home Office under the Animals (Scientific Procedures) Act 1986 (UK). The electrophysiological data set on which this study was based has been published previously (Mallet et al. 2008a). Therefore, we will only briefly describe the recording methods in this report.
Electrophysiological recordings were made in 10 dopamine-intact control rats and 18 parkinsonian rats [6-hydroxydopamine (6-OHDA) lesioned]. Anesthesia was induced with 4% (vol/vol) isoflurane (Isoflo; Schering-Plough, Welwyn Garden City, UK) in O2 and maintained with urethane (1.3 g/kg ip, ethyl carbamate; Sigma, Poole, UK) and supplemental doses of ketamine (30 mg/kg ip, Ketaset; Willows Francis, Crawley, UK) and xylazine (3 mg/kg ip, Rompun; Bayer, Leverkusen, Germany). Simultaneous extracellular recordings of the spikes fired by ensembles of single neurons in the STN and GPe were most often made using multicontact “silicon probes” (NeuroNexus Technologies, Ann Arbor, MI), where the distance between contacts was 100 μm. Some recordings of STN units were made using glass electrodes instead of silicon probes, according to standard methods (Mallet et al. 2008b). Unit activity in the nuclei was recorded during episodes of spontaneous “cortical activation,” which contain patterns of activity that are similar to those observed during the awake, behaving state (Steriade 2000). Cortical activation was defined according to electrocorticograms recorded simultaneously with unit activity (Mallet et al. 2008a). In 6-OHDA-lesioned animals, exaggerated beta oscillations emerge in corticobasal ganglia circuits during activated brain states (Mallet et al. 2008a, 2008b), thus accurately mimicking the oscillatory activity recorded in awake, unmedicated PD patients (Brown et al. 2001).
6-OHDA lesions of dopamine neurons.
Unilateral 6-OHDA lesions were carried out as described previously (Mallet et al. 2008a, 2008b). Twenty-five minutes before the injection of 6-OHDA, all animals received a bolus of desipramine (25 mg/kg ip; Sigma) to minimize the uptake of 6-OHDA by noradrenergic neurons (Schwarting and Huston 1996a). Anesthesia was induced and maintained with isoflurane (as described above). The neurotoxin 6-OHDA (hydrochloride salt; Sigma) was dissolved immediately before use in ice-cold 0.9% (wt/vol) NaCl solution containing 0.02% (wt/vol) ascorbate to a final concentration of 4 mg/ml. Next, 3 μl of 6-OHDA solution were injected adjacent to the medial substantia nigra (4.5 mm posterior and 1.2 mm lateral of bregma, and 7.9 mm ventral to the dura; Paxinos and Watson 1986). The extent of the dopamine lesion was assessed 14 or 15 days after 6-OHDA injection by challenge with apomorphine (0.05 mg/kg sc; Sigma; Schwarting and Huston 1996b). The lesion was considered successful in those animals that made >80 net contraversive rotations in 20 min. Note that the emergence of exaggerated beta oscillations after 6-OHDA lesions is not dependent on apomorphine (Sharott et al. 2005b). Electrophysiological recordings were carried out ipsilateral to 6-OHDA lesions in anesthetized rats 21–45 days after surgery, when pathophysiological changes in the basal ganglia are likely to have leveled out near their maxima (Vila et al. 2000).
Model.
We previously developed an analytical approach based on log-linear models (Cruz et al. 2009; Truccolo et al. 2005) that allows us to characterize the impact of various features of neural activity on network entropy, a measure of the upper bound of information coding capacity of a given neural population. This modeling approach can be readily extended to describe the mutual information between pairs of neurons in two distinct populations, e.g., STN and GPe. Mutual information in this case affords an estimate of how well the “response” (i.e., spiking activity) of a neuron in one nucleus can be predicted from the response of a neuron in another nucleus. In effect then, it can give insights into what information can potentially be transferred between the two nuclei. Our modeling approach is an example of nonlinear time series analysis (Kantz and Schreiber 2004), and we do it within the framework of Granger causality (Bollimunta et al. 2009). More specifically, when we estimated the interactions between STN and GPe neurons (or between different types of GPe neuron), we used only (Granger) causal activity, which is to say that we considered only those effects with non-negative time delays between nuclei. Moreover, when we examined the mutual information between nuclei, we measured the amount of additional information about the activity of neuron i at the current time point that can be obtained from neuron j recorded in the other nucleus, but only after first accounting for all of the information that can be extracted from the past activity of neuron i itself. For example, if neuron i were an intrinsic oscillator, its activity could be accurately predicted from its own firing history, and thus the activity of other neurons (j, etc.) would not be additionally useful. Thus, if we first modeled the effects of neuron i on itself, and then checked how much better we could do by including neuron j in the model, we would not find an improvement. However, it should be noted that the model affords a conservative estimate of the effects of neuron j on neuron i. It is conservative because the prior history of neuron i may have been affected by the history of neuron j, and yet this will also be taken out. But why should there be any interaction remaining between neuron j and neuron i after the past activities of both neurons are taken into account? In a perfectly regular system of coupled oscillators, removing the effects of the autocorrelation of each oscillator would entirely suppress their cross-correlation. However, if the oscillations present in two spike trains are not perfectly regular, the presence of “phase slips” over time will mean that some cross-correlation features survive after the autocorrelations have been accounted for. Previous studies have confirmed the presence of numerous phase slips in the oscillations within spike trains of basal ganglia neurons (Hurtado et al. 2004, 2005; Park et al. 2010). Hence, the firing history of either neuron may not fully predict their interactions, and this is likely the case for the networks of STN and GPe neurons considered in the study (see below). In short then, with our conservative approach, any effects of neuron j on i do not include past influences. Nevertheless, the fact that many of the constituent neurons of the STN-GPe network are intrinsic pacemakers (Surmeier et al. 2005) makes this conservative approach important because it discounts the past history of a neuron. Our analytical approach thus has advantages over computing standard linear cross-correlations (also see Introduction). However, this approach does make assumptions, despite the fact that it has often been called “direct” or “model free” (Strong et al. 1998). More specifically, the temporal resolution of the spiking activity (or the bin width for analyses) must be preselected, and the level of interaction between spikes at different times must also be selected. The validity of both selections can be tested, to some extent (see below).
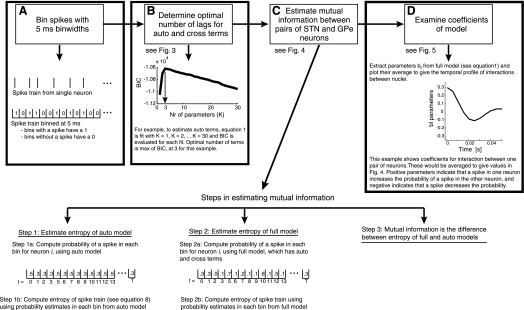
All analyses were carried out in MATLAB (The MathWorks, Natick, MA). An analysis flow chart is presented in Fig. 1. Model fitting began with binning the spike time data (point process) at 5 ms, where a bin received a value of 1 if there were one or more spikes in it or 0 if there were no spikes in it. At this bin size, <0.01% of the bins from STN and GPe neurons had two spikes in them. Thus pairs of spikes in a single bin were very rare. Furthermore, this bin size preserves temporal structure up to the 100-Hz Nyquist frequency, and therefore it preserves much of the relevant temporal structure of the spike trains recorded in the STN and GPe. To assess the validity of this temporal resolution, we carried out pilot analyses using smaller bin sizes and found that results were consistent with those reported in this study using the 5-ms bin size. We also assessed whether including higher order interactions between spikes at different times improved the model, as we did in our previous study (Cruz et al. 2009). We found that these higher order interactions did not enhance the model fits. To some extent, however, finding effects of higher order interactions is limited by the amount of data available for fitting the model, so one can never be sure that effects would not be found if more data were available.
Fig. 1.
Analysis flow chart. A: data binning and conversion to a binary signal. B: selection of optimal number of lags using the Bayesian information criterion (BIC). C: mutual information estimation. D: analysis of the temporal profile of interactions between nuclei. STN, subthalamic nucleus; GPe, external globus pallidus.
After binning of the spike trains, we fit the following model to pairs of spike trains (e.g., 1 from STN, 1 from GPe):
| (1) |
The left hand side, P(si,t|...) is the probability of a spike (s) fired by neuron i in time bin t conditioned on the other variables under consideration, which depend on the model used (see below). The variable i represents the neuron whose response is being predicted, j represents another neuron (e.g., from the other nucleus), t indicates the current time bin, K indicates the number of lagged time bins from neuron i that are being used (as an “auto predictor”), and L indicates the number of lagged time bins from neuron j that are being used to predict the activity of neuron i (a “cross predictor”). The terms ak are referred to as auto terms, because they model nonlinear autocorrelations, and the terms bl are referred to as cross terms, because they model nonlinear cross-correlations. The latter are the parameters plotted in Figs. 5 and 7. The values of K and L were optimized individually for each neuron pair using the model selection procedure described below. The sum over l terms starts at 0, which is to say that we used synchronous spikes for prediction. We have carried out all analyses with and without this term, and the results are equivalent. However, we chose to include this term because the propagation time of activity between the STN and GPe can be <5 ms (i.e., bin size used in this study) in the adult rat in vivo (Kita et al. 1983; Kita and Kitai 1991). The function g captures the nonlinearity that constrains the prediction of a spike in each bin to be between 0 and 1, i.e., it constrains it to be a probability. It is given by the following logistic function:
| (2) |
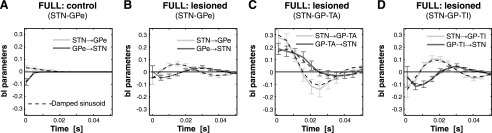
Fig. 5.
Transfer functions between STN and GPe neurons derived from the full model (which includes both auto and cross terms) in control rats and lesioned parkinsonian rats. A: model parameters for STN neurons and all GPe neurons in control rats, where there is little temporal structure to the transfer functions and thus minimal interactions between nuclei. B: model parameters for STN neurons and all GPe neurons in lesioned rats. Note that short-latency interactions are out of phase. C: model parameters for STN neurons and only GP-TA neurons in lesioned animals. Note that STN→GP-TA and GP-TA→STN transfer functions are in phase at short latencies. D: model parameters for STN neurons and only GP-TI neurons in lesioned rats. Note that the transfer functions are not in phase at short latencies. Dotted lines in each plot are the fits of damped sinusoids to the transfer functions. Positive and negative bl parameters indicate excitatory and inhibitory transfer, respectively.
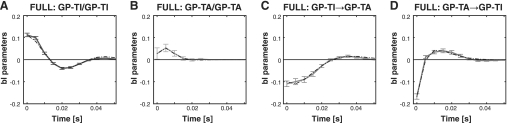
Fig. 7.
Transfer functions between different types of GPe neuron derived from the full model (which includes both auto and cross terms) in lesioned parkinsonian rats. A: model parameters for pairs of GP-TI neurons. B: model parameters for pairs of GP-TA neurons. C: model parameters for GP-TI→GP-TA transfer. D: model parameters for GP-TA→GP-TI transfer. Dotted lines in each plot are the fits of damped sinusoids to the transfer functions.
The logistic transform makes Eq. 1 nonlinear. However, it is a static nonlinearity, as opposed to a dynamic nonlinearity that would be a function of time or time lags. Because Eq. 1 is nonlinear, it differs from the linear interactions that are captured by cross-correlations, coherence, and other standard time- and frequency-domain analyses.
Parameter estimation.
The parameters of the model were fit by maximizing the likelihood of correctly predicting whether a spike did or did not occur in each bin. Thus the model attempts to have P(si,t|...) be as close to 1 as possible every time a spike occurs and as close to 0 as possible when there is no spike. This is done by maximizing the log-likelihood (ll) function, given by
| (3) |
where θ is the parameter vector for the current model.
The nonlinear model from Eq. 1 was fit with subsets of parameters set to 0, to partial out different effects. Specifically, the “auto” model included only the lagged time bins from one neuron in a given cell pair (i.e., the ak terms) and estimated the effect of autocorrelations, that is, oscillations at the single-cell level, on the mutual information. The “full” model, on the other hand, included all terms, i.e., both the ak and bl terms. Thus, for the auto models, θ = {a0, a1,..., ak}, and for the full models and pairs of neurons, θ = {a0, a1, ..., ak, b0,..., bL}. We use sm as shorthand to indicate the set of lagged parameters appropriate to the corresponding model such that, for example, for the auto model, sm = {si,t−1,..., si,t−K}.
We maximized this function using an online version of the iteratively reweighted least-squares algorithm. The parameter updates at iteration n for this algorithm are given by
| (4) |
In this case, sm is the vector of spikes being used for prediction at the corresponding time step for the model, containing either auto or cross terms. We fit this model using the early stopping rule. To do this, the data set was split in half and Eq. 4 was iterated on half of the data and the log-likelihood (Eq. 3) was estimated on the other half of the data. Iteration was stopped when the change in the log-likelihood was below a criterion value given by
| (5) |
Usually, the early stopping rule is used to control for overfitting, and in this case one looks for minima of the log-likelihood. However, because we had far more data than parameters in our model, the log-likelihood reached a plateau, and we used a small change in this plateau as our estimate of convergence.
Model selection.
The number of lagged time bins, variables K and L, for the nonlinear auto and cross components of the models, respectively, had to be estimated. To do this, we estimated models with 1–30 lagged time bins (i.e., K = 1, K = 2,..., K = 30) and used model selection techniques to determine the optimal number of lags (see Fig. 3). We found that our entropy estimates (see below) were not strongly dependent on the number of lags used, as long as we used enough lags. The number of relevant lags is an interesting quantity by itself, because it provides information about the time scale of the correlations in the data. Thus, if correlations extend over a longer period of time, more lags will be necessary to capture them. On the other hand, if the significant number of lags is zero, then there are no significant interactions. To estimate the optimal number of lags, we used the Bayesian information criterion (BIC). This is given by
| (6) |
where v is the number of parameters in the model, ll is the log-likelihood, and T is the amount of data available for estimating the model. The optimal number of lags was determined by maximizing the BIC function. We also examined entropy estimates using Akaike's information criterion (AIC) (Tong 1990). Although the number of lagged terms was always larger, because AIC penalizes with −2v instead of −vln(T) and T was large in our data, the actual entropy estimates were statistically indistinguishable.
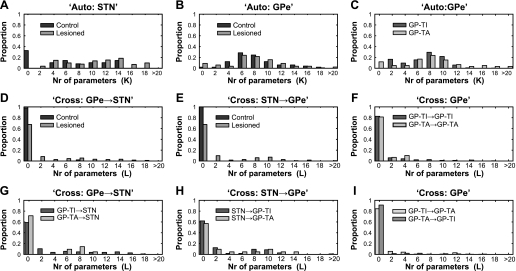
Fig. 3.
Optimal numbers of lags for autocorrelations and cross-correlations. A and B: autocorrelations for all STN neurons and all GPe neurons, respectively, in control and lesioned rats. C: autocorrelations for distinct cell types, GP-TI and GP-TA neurons, in lesioned animals. D and E: cross-correlations for transfer in direction from GPe to STN (D) and from STN to GPe (E) in control and lesioned rats. F: cross-correlations between GP-TI/GP-TI pairs and GP-TA/GP-TA pairs in lesioned rats. G and H: cross-correlations for transfer in direction from GP-TA or GP-TI to STN (G) and from STN to GP-TI or GP-TA (H) in lesioned rats. I: cross-correlations for transfer from GP-TI to GP-TA and for GP-TA to GP-TI in lesioned animals. In all cases, optimal numbers (Nr) of 5-ms time bins (K or L) were selected with BIC. Note that lags of 0 indicate no significant interactions.
Mutual information.
After the models were optimized for each pair of STN/GPe neurons (or GPe/GPe neurons), we used them to estimate the causal mutual information (the directed information flow) between the same pairs. This mutual information, Icausal, is given by
| (7) |
where H(x) is the entropy of the spike train under the corresponding model calculated with the standard equation (Cover and Thomas 1991)
| (8) |
Damped sinusoids.
The temporal structures of interactions (lagged parameters for bl) between STN and GPe, and within GPe itself, were found to resemble damped beta-frequency profiles (see Fig. 5). To characterize this more specifically, we fit damped sinusoids to the average interaction terms. They were fit by minimizing the squared error between the measured parameters and the damped sinusoid, which was given by
| (9) |
The parameter α is the maximum amplitude, β is the damping rate (in seconds), and θ is the phase of the cosine function (in radians). We report these parameters and the frequency characteristics (f) in the results. Minimization was done using fminsearch in MATLAB.
RESULTS
Comparison of STN-GPe network dynamics in control rats and parkinsonian rats.
Extracellular unit activity was recorded simultaneously from neurons in the STN and GPe in dopamine-intact control rats and 6-OHDA-lesioned parkinsonian rats. The data set was composed of 49 pairs of STN/GPe neurons in control animals (10 single neurons in the STN and 49 in the GPe) and 184 pairs of STN/GPe neurons in lesioned animals (26 single neurons in the STN and 133 in the GPe). The GPe neurons analyzed in this study comprise a subset of the GPe neurons considered in our previous study (Cruz et al. 2009), since in this study we only included those GPe neurons that were simultaneously recorded with at least one STN neuron. In a first set of analyses, we considered all GPe neurons in control animals as a single population and all GPe neurons in lesioned animals as another single population. In a second set of analyses, we split the single GPe population recorded in lesioned animals and grouped the neurons according to previously identified cell types (Mallet et al. 2008a). Specifically, two main types of GPe neuron can be identified in lesioned animals using their distinct firing patterns (Mallet et al. 2008a). Type-A GPe neurons (GP-TA neurons, n = 26 STN/GP-TA cell pairs) preferentially discharge during the “active components” of cortical slow (∼1 Hz) oscillations, whereas type-I GPe neurons (GP-TI neurons, n = 105 STN/GP-TI cell pairs) preferentially discharge during “inactive components.” This functional dichotomy is preserved, that is, GP-TA and GP-TI neurons tend to still fire in “anti-phase,” during the excessive beta oscillations that arise in lesioned animals during activated cortical states (Mallet et al. 2008a), as were studied presently. Given this functional dichotomy in GPe during excessive beta oscillations, it was important to examine whether GP-TA and GP-TI neurons interact differently with STN neurons, among themselves, or with each other. As reported previously (Mallet et al. 2008a), most GPe cells could be considered as GP-TA or GP-TI neurons, but for these secondary analyses, 58 pairs of STN/GPe neurons were not included because the GPe cell could not be unambiguously identified as either type. Also, we did not similarly split the population of GPe neurons recorded in control rats, because when dopamine is intact, most of these cells fire independently of the cortical slow oscillation (Mallet et al. 2008a).
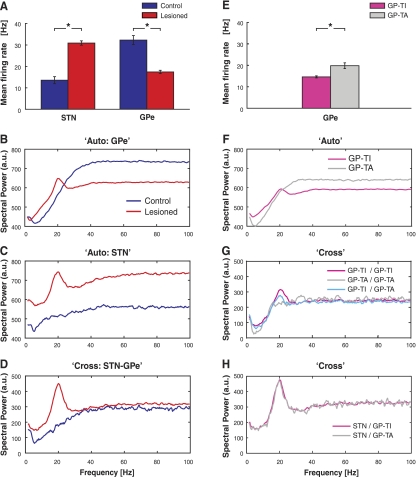
Mean firing rates of STN neurons recorded during activated brain states in control and lesioned animals were 13.5 and 30.9 Hz, respectively, whereas the mean firing rates of the whole populations of GPe neurons were 32.0 and 17.4 Hz, respectively (Fig. 2A). Thus chronic loss of dopamine is associated with a significant increase of STN activity (t-test, P < 0.001) and a decrease in GPe firing (t-test, P < 0.001). When GPe neurons recorded in lesioned animals were grouped according to cell type, the mean firing rates of GP-TI neurons and GP-TA neurons were 14.5 and 19.7 Hz, respectively (Fig. 2E, t-test, P < 0.001). Dopamine depletion also led to increased prevalence of ∼20 Hz (beta frequency) oscillations in the spike trains of single neurons in the GPe (Fig. 2B) and STN (Fig. 2C), as well as the emergence of a well-defined peak at beta frequencies in the average cross-spectra between STN and GPe (Fig. 2D). The mean autospectra of GP-TI neurons but not that of GP-TA neurons showed clear beta oscillations (Fig. 2F). Furthermore, beta peaks were seen in the cross-spectra between different cell types in GPe (Fig. 2G), as well as between STN and GP-TI neurons and between STN and GP-TA neurons (Fig. 2H).
Fig. 2.
Comparison of GPe, type-inactive (GP-TI) and type-active GPe (GP-TA), and STN network dynamics and interactions in dopamine-intact control rats and 6-hydroxydopamine (6-OHDA)-lesioned parkinsonian rats. A: mean firing rates of all STN and GPe neurons in control and lesioned animals. B: mean autospectra for all GPe neurons in control and lesioned animals. C: mean autospectra for STN neurons in control and lesioned animals. D: mean cross-spectra between pairs of GPe and STN neurons. E: mean firing rates of GP-TI neurons and GP-TA neurons in lesioned rats. F: mean autospectra for GP-TI and GP-TA neurons in lesioned rats. G: mean cross-spectra between GP-TI pairs, between GP-TA pairs, and between GP-TI/GP-TA pairs of neurons in lesioned rats. H: mean cross-spectra between STN/GP-TI pairs and between STN/GP-TA pairs of neurons in lesioned rats. Asterisks in A and E indicate significant differences. a.u., arbitrary units.
Parameter estimation for nonlinear models of spiking activity in STN-GPe network.
The primary goal of this study was to compare directed information flow or transfer between the STN and GPe in control and parkinsonian animals. To this end, we fitted two models to the response of each STN or GPe neuron that had been recorded simultaneously with a neuron in the other nucleus. First, we fitted a model (auto) that had only autocorrelation terms. This allowed us to examine how well the response of an individual neuron could be estimated from its own spiking history. This model was fit by optimizing (adding) lagged time bins until no additional information could be extracted from the response history to predict activity in the current time bin. Lags of zero indicate no significant interactions. If correlations extend over a longer period of time, more lagged time bins are necessary to capture them. Therefore, the optimal number of lagged time bins that provide information about the current activity of a neuron is an estimate of the dependence of current activity on past activity, or the correlation length of the spike train. We found that for most STN neurons, in either control or lesioned animals, the number of significant lagged bins was between 5 and 20 (Fig. 3A). Since each bin was 5 ms, this meant that the previous 25- to 100-ms history of a STN neuron's activity contained information about whether the same neuron would fire a spike in the current bin. However, the distributions of lagged bins differed significantly for STN neurons in control and lesioned animals [Kolmogorov-Smirnov (KS) test, P < 0.001]. Indeed, STN neurons in controls had fewer significant interactions than those in lesioned animals, as indicated by a larger proportion of lagged bins at zero, and thus fewer lags above zero (Fig. 3A). The spiking of GPe neurons could be accounted for by 5–12 lagged bins in both control and lesioned animals (Fig. 3B). These distributions of lagged bins did not differ between control and lesioned rats (KS-test, P = 0.759). When the single GPe population data from lesioned animals were split into GP-TI and GP-TA neurons (Fig. 3C), it could be seen that the number of lagged time bins was similar between these two groups (KS-test, P = 0.184).
After the estimation of the auto model, we estimated the cross model, which included the cross terms, to account for interactions between STN and GPe or interactions between pairs of neurons within GPe. The first step, similar to the procedure with the auto model, was to estimate the number of significant lagged time bins. In all cases, fewer terms were necessary to account for interactions between neurons than were necessary to model the autocorrelations for single neurons. When interactions between nuclei in control animals were considered, there were only two significant interactions (out of a total of 49 pairs) from the GPe to the STN (see large proportion of 0 lags in Fig. 3D), and there were no significant interactions from the STN to the GPe (Fig. 3E). In the lesioned animals, however, we found that in about 35% of the STN/GPe pairs, there was a significant interaction of at least one bin from both the GPe to the STN (Fig. 3D) and from the STN to the GPe (Fig. 3E), and the interactions extended to 50–75 ms. Thus, when GPe neurons were not grouped according to cell type, interactions between the nuclei were substantially increased (almost 10-fold) after dopamine depletion (GPe to STN, KS-test, P < 0.001; STN to GPe, KS-test, P < 0.001). Within and between GP-TI and GP-TA neurons, there were no significant interactions in about 80% of the pairs considered (Fig. 3, F and I). In the pairs that had significant interactions, between 2 and 10 lagged bins were significant, showing interactions over 10–50 ms. Finally, when STN interactions with either GPe cell type were considered, there were no differences in the interactions from GP-TI or GP-TA to the STN (Fig. 3G, KS-test, P = 0.999) or from the STN to either GP-TI or GP-TA (Fig. 3H, KS-test, P = 0.936).
Mutual information in the STN-GPe network in control rats and parkinsonian rats.
Having examined the time scales of the interactions, we went on to calculate the mutual information between pairs of simultaneously recorded STN/GPe neurons. We did this by computing the difference in entropy, a measure of information coding capacity, between the auto and full models, where the nonlinear full model contains both the auto- and cross-correlation terms. Thus this analysis quantifies the additional information (reflected as a reduction in entropy) that can be obtained about the responses of a given STN neuron (or GPe neuron) using the activity of a paired GPe (STN) neuron, after first taking into account the information about the responses of the first STN (GPe) neuron contained in its own spiking history. Critically, this analysis is directional, so the information flow can be assessed from the STN to the GPe, as well as from the GPe to the STN. Qualitatively, this analysis is similar to examining the amount of extra variance (or increase in R2) that one would obtain in linear regression, when the cross terms were included in the model. Thus it is an estimate of how much better spikes in one nucleus can be predicted by spikes in another nucleus.
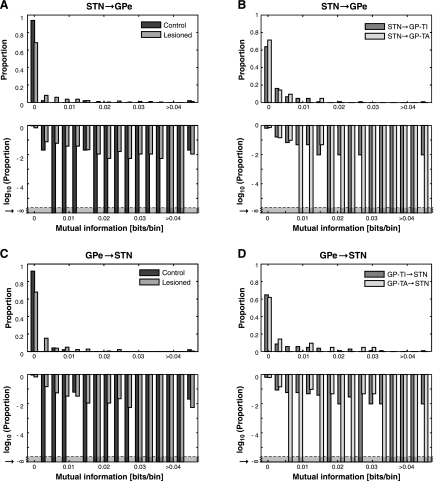
We found that, consistent with the analysis examining the number of significant lagged bins in cross-correlations between STN and GPe neurons (see Fig. 3, D and E), there was significantly more mutual information between nuclei in the lesioned animals (Fig. 4, A and C) than in the control animals (STN to GPe, KS-test, P < 0.001; GPe to STN, KS-test, P = 0.002). Thus, after chronic dopamine depletion, the spike trains of STN neurons could be better predicted using the spike trains of GPe neurons, and vice versa. When we split the GPe cell population in lesioned animals, we found that 30–40% of STN/GP-TI and STN/GP-TA pairs had significant interactions, but the amount of information flow between the STN and GP-TI neurons was similar to that between STN and GP-TA neurons, considered in either direction (Fig. 4B, KS-test, P = 0.504; Fig. 4D, KS-test, P = 0.411).
Fig. 4.
Information transfer across the STN-GPe network. Top plots show untransformed probabilities; bottom plots are same data replotted with log-transform to emphasize the smaller proportions. A: information transfer from STN to GPe in control and lesioned rats. B: information transfer from STN to GP-TI or GP-TA in lesioned rats. C: information transfer from GPe to STN in control and lesioned rats. D: information transfer from GP-TI or GP-TA to STN in lesioned rats. GPe neurons were not divided and grouped according to cell type in A and C.
Temporal profiles of directed information flow in the STN-GPe network.
We next examined the temporal profiles of the interactions between nuclei. The temporal structure can be characterized by examining the average value of the lagged parameters for the cross terms (bl) in the model (see Eq. 1 in methods). These terms characterize the sign (i.e., positive or negative) and amplitude of the effect of a spike in one nucleus on the probability of a spike in the other nucleus at the indicated time lag. We found that the parameters in the lesioned animals, but not in the control animals, resembled damped beta-frequency profiles, with ∼50-ms cycle periods, and thus were centered at ∼20 Hz (Fig. 5). Taking into account conduction delays of at least a few milliseconds between nuclei and the rise times of postsynaptic potentials (Kita et al. 1983; Kita and Kitai 1991), interactions at short latencies (5–10 ms) are most informative when studying the monosynaptic influences of neurons in the STN-GPe network. Importantly, then, at similar short latencies, the interactions from the STN to the GPe and from the GPe to the STN in lesioned animals were clearly out of phase (Fig. 5B), being “excitatory” (positive bl parameters in Fig. 5) from the STN to the GPe and “inhibitory” (negative bl parameters) from the GPe to the STN. Thus, considering delays arising from propagation and integration, and all recorded neuronal pairs, the parameters that account for interactions between nuclei are consistent with the neurochemistry of this reciprocally connected network. However, when GPe neurons were divided according to cell type, we found that the temporal profiles of the GP-TA neurons did not reflect the known microcircuitry and neurochemistry in a direct manner, i.e., the interactions from STN to GP-TA and from GP-TA to STN were in phase, both being excitatory at short latencies (Fig. 5C). In contrast, the temporal profile of the more numerous GP-TI neurons was similar to the average profile for all GPe neurons, i.e., the interactions from STN to GP-TI and from GP-TI to STN were markedly out of phase, being excitatory and inhibitory, respectively, at short latencies (Fig. 5D). Interactions had a similar time scale for both the GP-TI and GP-TA cell groups, and in both directions. Thus bidirectional information transfer between STN and GPe was significantly increased by dopamine depletion, and it was primarily the phase that differentiated STN interactions with these two types of GPe neuron.
The temporal profiles of the interaction parameters in the STN-GPe network of lesioned animals resembled damped beta-frequency oscillations. To investigate this issue further, we fitted a damped oscillator function (sinusoid) to each set of interaction parameters. A damped sinusoid fit the coefficient data in this study well (Table 1), at least for data recorded in the lesioned parkinsonian rats (Fig. 5, B–D, dashed lines).
Table 1.
Parameters of damped sinusoids that best fit the transfer functions between STN and GPe neurons
| Interacting Pairs | R2 | α | β, s | f, Hz | θ, rad |
|---|---|---|---|---|---|
| STN to GPe (controls) | 0.99 | 0.07 | 0.006 | 14.2 | 5.20 |
| GPe to STN (controls) | 0.99 | 0.11 | 0.002 | 187.3 | 2.37 |
| STN to GPe (lesioned) | 0.98 | 0.10 | 0.032 | 20.2 | 4.20 |
| GPe to STN (lesioned) | 0.94 | 0.05 | 0.048 | 19.4 | 2.46 |
| STN to GP-TA | 0.98 | 0.32 | 0.023 | 21.4 | −0.41 |
| STN to GP-TI | 0.95 | 0.18 | 0.031 | 20.7 | 0.63 |
| GP-TA to STN | 0.96 | 0.26 | 0.019 | 16.1 | 2.28 |
| GP-TI to STN | 0.94 | 0.16 | 0.023 | 21.9 | 1.88 |
Parameter values are given for maximum amplitude (α), damping rate (β), phase of the cosine function (θ), and frequency characteristics (f) in subthalamic nucleus (STN) and external globus pallidus (GPe) neurons. Note that type-active (GP-TA) and type-inactive GPe (GP-TI) neurons were only defined as such in lesioned animals.
Mutual information and temporal interactions between different types of GPe neuron.
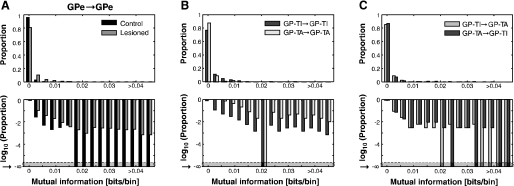
In the final analyses we considered the mutual information between GP-TI and GP-TA neurons. This analysis is complementary to previous analyses we have carried out, in which we estimated the entropy of the entire GPe population irrespective of cell type (Cruz et al. 2009). When all recorded neuronal pairs were considered, we found significantly more mutual information between GPe neurons in the lesioned rats than in the control rats (Fig. 6A, KS-test, P < 0.001). Interestingly, when GPe neurons in lesioned animals were divided according to cell type, there was more information between GP-TI neurons than there was between GP-TA neurons (Fig. 6B, KS-test, P < 0.001). However, there were no differences in mutual information between pairs of GP-TI/GP-TA neurons when they were considered from both directions (Fig. 6C, KS-test, P = 0.881). The temporal profile of the GP-TI/GP-TI interactions was initially excitatory and oscillated at beta frequencies (Fig. 7A). Interactions between only GP-TA neurons were also initially excitatory, but they did not oscillate as strongly at beta frequencies (Fig. 7B), consistent with the corresponding cross-correlations. Interactions between GP-TI and GP-TA neurons were both inhibitory at short latencies, but the GP-TI–to–GP-TA interaction remained inhibitory over the first 20 ms, whereas the GP-TA–to–GP-TI interaction went immediately to excitatory at a lag of 5 ms (Fig. 7, C and D). Thus there were differences in their temporal profiles, which were reflected in the phase of their interactions. Again, damped oscillator functions could be fitted to the temporal profiles of interaction parameters (Table 2). Thus, although bidirectional information transfer between GPe neurons was significantly increased by dopamine depletion, the amount and temporal profile of information transfer depended on the type(s) of GPe neuron.
Fig. 6.
Information transfer within the GPe. Top plots show untransformed probabilities; bottom plots are same data replotted with log-transform to emphasize the smaller proportions. A: information transfer between all GPe neurons in control and lesioned rats, irrespective of cell type. B: information transfer between only GP-TI neurons and between only GP-TA neurons in lesioned rats. C: information transfer from GP-TI to GP-TA and from GP-TA to GP-TI neurons in lesioned rats.
Table 2.
Parameters of damped sinusoids that best fit the transfer functions within GPe
| Interacting Pairs | R2 | α | β, s | f, Hz | θ, rad |
|---|---|---|---|---|---|
| GP-TI to GP-TI | 0.94 | 0.16 | 0.010 | 25.0 | 4.89 |
| GP-TA to GP-TA | 0.98 | 0.12 | 0.020 | 22.4 | 6.04 |
| GP-TI to GP-TA | 0.99 | 0.16 | 0.017 | 15.0 | 2.24 |
| GP-TA to GP-TI | 0.99 | 0.44 | 0.007 | 12.2 | 4.33 |
DISCUSSION
Chronic loss of dopamine from corticobasal ganglia circuits profoundly alters neuronal activity therein and often leads to the emergence of excessively synchronized oscillations, as documented in patients with PD (Amirnovin et al. 2004; Brown 2003; Brown et al. 2001; Levy et al. 2002; Moran et al. 2008; Williams et al. 2002) and parkinsonian animals (Bergman et al. 1998; Degos et al. 2009; Goldberg et al. 2004; Mallet et al. 2008a, 2008b; Nini et al. 1995; Raz et al. 1996, 2000, 2001; Sharott et al. 2005b). The changes in microcircuit properties that give rise to these changes remain to be elucidated, but it is possible that altered interactions in the reciprocally connected network of glutamatergic STN neurons and GABAergic GPe neurons contribute to these oscillations. In the present study we used nonlinear time series analysis and information theory techniques to quantitatively assess the interactions between STN and GPe neurons in 6-OHDA-lesioned parkinsonian rats and dopamine-intact control rats. This approach allowed us to directly estimate changes in the transfer of information from one nucleus (or neuron type) to the other while controlling for potentially confounding changes in activity within an individual nucleus (or neuron), therefore overcoming some of the limitations of linear cross-correlations. Our key finding is that bidirectional information transfer between STN and GPe neurons, and between different types of GPe neuron, was significantly increased by chronic dopamine depletion. Importantly, these augmented causal interactions in the parkinsonian state reflected an underlying network oscillation in the beta-frequency band.
Limitations.
Our analytical approach is innovative, and as such, it was important to explore its utility in a well-characterized data set (Cruz et al. 2009; Mallet et al. 2008a), seeking corroboration of previous findings (so-called “face validity”). Thus, in our first set of analyses, we did not distinguish between types of GPe neuron, but we could still define internuclear interactions that were independent of activity within nuclei. When GPe neurons were considered as a single population, we were able to confirm that model parameters correctly reflected the known neurochemistry and microcircuitry of the STN-GPe network. Accordingly, excitatory interactions, presumably mediated by glutamate, dominated information transfer from STN to GPe, and inhibitory interactions, presumably mediated by GABA, dominated information transfer from GPe to STN.
One key issue with our approach is the meaning of “information transfer” between nuclei. We define this in the information theoretic (statistical) sense and consider information transfer to occur when a spike in the GPe alters the probability of a spike in the STN, and vice versa. The course of this statistical interaction affords what we term “directionality” and can be underpinned by both direct and indirect synaptic connections, including common inputs (Sharott et al. 2005a). Information transfer, defined as above, will then encompass whatever aspects of internuclear interaction represent the physiological means of communication. However, the two are not synonymous, and there are features of the dependent activity in one nucleus that may be irrelevant for the “real” neural code (whatever this may be).
Novel insights.
The major novel findings were made when we split the population of recorded GPe neurons into two different, physiologically defined subpopulations, namely, GP-TI and GP-TA neurons (Mallet et al. 2008a). Importantly, we found that only the more numerous GP-TI neurons showed interactions consistent with monosynaptic reciprocal connections with STN. Indeed, causal information transfer from GP-TA neurons to STN neurons was initially excitatory. This finding is surprising, because although the neurochemistry and connections of GP-TA (and GP-TI) neurons have yet to be elucidated, the vast majority of GPe neurons are thought to be GABAergic and project to STN (Bevan et al. 1998; Smith et al. 1998). Our results suggest that the activity of GP-TI neurons is of greater causal significance than that of GP-TA neurons for the periods of reduced activity or quiescence that punctuate the spiking of STN neurons during parkinsonian beta oscillations (Kuhn et al. 2005; Levy et al. 2002; Mallet et al. 2008a, 2008b). However, precisely timed inputs from GP-TA neurons could still serve to sculpt the intermittent periods of increased activity and bursting exhibited by STN neurons. The STN–to–GP-TA connection was excitatory at very short lags (0–5 ms), which is remarkable because the spiking response of GPe neurons to STN neuron discharge should take, on average, ≥10 ms to develop (Kita and Kitai 1991). However, in light of the predicted time course, our analyses also imply that STN input to GP-TI neurons is of causal importance for their recruitment into the excessively synchronized GPe ensembles that emerge during beta oscillations. It is unclear why STN and GP-TA neurons should fire so close in time, but a common extrinsic input, perhaps arising from frontal cortex and/or intralaminar thalamus (Kita 2007), and/or inhibitory inputs from GP-TI neurons might underlie this tight temporal coupling. Common input, either excitatory or inhibitory, might also explain why causal information transfer between pairs of GP-TI neurons or pairs of GP-TA neurons was initially excitatory. For GP-TI neurons, a common driving input is likely STN. On the other hand, the short-latency inhibitory interactions between GP-TI/GP-TA pairs suggests these cell types inhibit each other, periodically dampening activity and promoting antiphase firing across the two subpopulations.
Wider implications.
Considerable theoretical work on networks of neurons generating oscillations suggests that, generally speaking, oscillations require some sort of excitatory/inhibitory neuronal interaction (see for example, Brunel 2000; Cohen et al. 1992; Ermentrout and Chow 2002; Terman et al. 2002). This can occur within a single neuron, between neurons in a network (de Solages et al. 2008), or some combination of these. All of these conditions are satisfied in the STN-GPe network. Specifically, most STN and GPe neurons function as autonomous pacemakers (Surmeier et al. 2005). Moreover, the dominant STN-to-GPe/GPe-to-STN interaction is excitatory/inhibitory, providing a possible substrate for oscillatory interactions at the network level. Under normal circumstances, some features of the STN-GPe network make synchronized oscillations unlikely. Indeed, network-level oscillations can occur in the so-called “balanced regime” (Renart et al. 2004), and the STN-GPe network in the dopamine-intact animal is probably not in this regime. A feature of the balanced regime is that neurons receive a large amount of balanced excitatory and inhibitory input. Thus, if inhibitory input is strongly decreased, the activity in excitatory neurons will become epileptic (Renart et al. 2004). This is not the case in the normal STN-GPe circuit, however, because destruction of GPe leads to only a small increase in STN activity (Ryan and Clark 1992). However, in the present study we show that Parkinsonism is associated with a 10-fold increase in causal information transfer in the STN-GPe circuit, arguably bringing it into a balanced state in which oscillations may be generated (Holgado et al. 2010). Both increases in the strength of functional coupling between nuclei and decreases in the difference in the intrinsic oscillation frequency between nuclei can lead to phase-locked oscillations in neural responses (Ermentrout and Chow 2002; Strogatz 1994). Both effects are suggested by our results, in so far that internuclear coupling increased and oscillations of single neurons in STN and GPe became matched, with a frequency of ∼20 Hz. The resulting tendency to phase-locked oscillations in STN-GPe could contribute to resonance phenomena seen in parkinsonism. Indeed, our model parameters were well fit by damped oscillators with resonance frequencies of ∼20 Hz. Similar patterns of resonance have been reported between the STN and cerebral cortex in PD patients (Eusebio et al. 2009). Thus excessive beta oscillations in PD might arise from changes in STN-GPe interactions, without ruling out the possibility that they instead may arise elsewhere (outside the STN-GPe circuit), and are then perhaps amplified by the resonance properties of the STN-GPe circuit. Overall, these observations suggest that, at the systems level in rodents and humans, elements of the corticobasal ganglia circuit are well described as damped oscillators with beta-band resonance in the parkinsonian state and that this is true despite the differences between activity conduction times in rodents and humans. Our current analysis adds to this by also indicating that such resonance is not merely a consequence of the autocorrelation function of individual neurons in parkinsonism. Beta-band resonance is thus a highly conserved feature of (dys)function in these networks after dopamine loss.
Conclusions.
We have used nonlinear time series analysis to quantify the interactions between the STN and GPe in control and parkinsonian rats. Chronic dopamine depletion changed firing rates and led to strong beta-frequency oscillations in the STN-GPe network. This was accompanied by a pronounced increase in bidirectional interactions between these nuclei, measured with causal mutual information. This increased strength of reciprocal effective coupling may not only contribute to excessive beta synchrony in Parkinsonism but also impede information flow and representation within the STN-GPe network and the rest of the basal ganglia.
GRANTS
A. V. Cruz was supported by Fundação para a Ciência e Tecnologia Grant SFRH/BD/33201/2007 and Fundação Gulbenkian. N. Mallet and P. J. Magill were supported by the Medical Research Council UK, The Dana Foundation USA, and Parkinson's UK Grant G-0806. P. Brown was supported by the Medical Research Council UK and the Oxford National Institute for Health Research Biomedical Centre. B. B. Averbeck was supported by the Wellcome Trust and the National Institute of Mental Health Intramural Research Program.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
REFERENCES
- Alonso-Frech F, Zamarbide I, Alegre M, Rodriguez-Oroz MC, Guridi J, Manrique M, Valencia M, Artieda J, Obeso JA. Slow oscillatory activity and levodopa-induced dyskinesias in Parkinson's disease. Brain 129: 1748–1757, 2006 [DOI] [PubMed] [Google Scholar]
- Amirnovin R, Williams ZM, Cosgrove GR, Eskandar EN. Visually guided movements suppress subthalamic oscillations in Parkinson's disease patients. J Neurosci 24: 11302–11306, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergman H, Feingold A, Nini A, Raz A, Slovin H, Abeles M, Vaadia E. Physiological aspects of information processing in the basal ganglia of normal and parkinsonian primates. Trends Neurosci 21: 32–38, 1998 [DOI] [PubMed] [Google Scholar]
- Bevan MD, Booth PA, Eaton SA, Bolam JP. Selective innervation of neostriatal interneurons by a subclass of neuron in the globus pallidus of the rat. J Neurosci 18: 9438–9452, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bevan MD, Magill PJ, Terman D, Bolam JP, Wilson CJ. Move to the rhythm: oscillations in the subthalamic nucleus-external globus pallidus network. Trends Neurosci 25: 525–531, 2002 [DOI] [PubMed] [Google Scholar]
- Bollimunta A, Chen Y, Schroeder CE, Ding M. Characterizing oscillatory cortical networks with granger causality. In: Coherent Behavior in Neural Networks, edited by Josic K, Rubin J, Matias MA, Romo R. New York: Springer, 2009, p. 304 [Google Scholar]
- Brown P. Oscillatory nature of human basal ganglia activity: relationship to the pathophysiology of Parkinson's disease. Mov Disord 18: 357–363, 2003 [DOI] [PubMed] [Google Scholar]
- Brown P, Oliviero A, Mazzone P, Insola A, Tonali P, Di Lazzaro V. Dopamine dependency of oscillations between subthalamic nucleus and pallidum in Parkinson's disease. J Neurosci 21: 1033–1038, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown P, Williams D. Basal ganglia local field potential activity: character and functional significance in the human. Clin Neurophysiol 116: 2510–2519, 2005 [DOI] [PubMed] [Google Scholar]
- Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J Comput Neurosci 8: 183–208, 2000 [DOI] [PubMed] [Google Scholar]
- Cohen AH, Ermentrout GB, Kiemel T, Kopell N, Sigvardt KA, Williams TL. Modelling of intersegmental coordination in the lamprey central pattern generator for locomotion. Trends Neurosci 15: 434–438, 1992 [DOI] [PubMed] [Google Scholar]
- Cover TM, Thomas JA. Elements of Information Theory. New York: Wiley, 1991 [Google Scholar]
- Cruz AV, Mallet N, Magill PJ, Brown P, Averbeck BB. Effects of dopamine depletion on network entropy in the external globus pallidus. J Neurophysiol 102: 1092–1102, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Solages C, Szapiro G, Brunel N, Hakim V, Isope P, Buisseret P, Rousseau C, Barbour B, Lena C. High-frequency organization and synchrony of activity in the Purkinje cell layer of the cerebellum. Neuron 58: 775–788, 2008 [DOI] [PubMed] [Google Scholar]
- Degos B, Deniau JM, Chavez M, Maurice N. Chronic but not acute dopaminergic transmission interruption promotes a progressive increase in cortical beta frequency synchronization: relationships to vigilance state and akinesia. Cereb Cortex 19: 1616–1630, 2009 [DOI] [PubMed] [Google Scholar]
- Ermentrout GB, Chow CC. Modeling neural oscillations. Physiol Behav 77: 629–633, 2002 [DOI] [PubMed] [Google Scholar]
- Eusebio A, Pogosyan A, Wang S, Averbeck B, Gaynor LD, Cantiniaux S, Witjas T, Limousin P, Azulay JP, Brown P. Resonance in subthalamo-cortical circuits in Parkinson's disease. Brain 132: 2139–2150, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg JA, Rokni U, Boraud T, Vaadia E, Bergman H. Spike synchronization in the cortex/basal-ganglia networks of Parkinsonian primates reflects global dynamics of the local field potentials. J Neurosci 24: 6003–6010, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holgado AJ, Terry JR, Bogacz R. Conditions for the generation of beta oscillations in the subthalamic nucleus-globus pallidus network. J Neurosci 30: 12340–12352, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurtado JM, Rubchinsky LL, Sigvardt KA. Statistical method for detection of phase-locking episodes in neural oscillations. J Neurophysiol 91: 1883–1898, 2004 [DOI] [PubMed] [Google Scholar]
- Hurtado JM, Rubchinsky LL, Sigvardt KA, Wheelock VL, Pappas CTE. Temporal evolution of oscillations and synchrony in GPi/muscle pairs in Parkinson's disease. J Neurophysiol 93: 1569–1584, 2005 [DOI] [PubMed] [Google Scholar]
- Kantz H, Schreiber T. Nonlinear Time Series Analysis. Cambridge: Cambridge University Press, 2004, p. 369 [Google Scholar]
- Kita H. Globus pallidus external segment. In: GABA and the Basal Ganglia: From Molecules to Systems, edited by Tepper JM, Abercrombie ED, Bolam JP. New York: Elsevier, 2007, p. 111–133 [Google Scholar]
- Kita H, Chang HT, Kitai ST. Pallidal inputs to subthalamus: intracellular analysis. Brain Res 264: 255–265, 1983 [DOI] [PubMed] [Google Scholar]
- Kita H, Kitai ST. Intracellular study of rat globus pallidus neurons: membrane properties and responses to neostriatal, subthalamic and nigral stimulation. Brain Res 564: 296–305, 1991 [DOI] [PubMed] [Google Scholar]
- Kuhn AA, Trottenberg T, Kivi A, Kupsch A, Schneider GH, Brown P. The relationship between local field potential and neuronal discharge in the subthalamic nucleus of patients with Parkinson's disease. Exp Neurol 194: 212–220, 2005 [DOI] [PubMed] [Google Scholar]
- Kuhn AA, Williams D, Kupsch A, Limousin P, Hariz M, Schneider GH, Yarrow K, Brown P. Event-related beta desynchronization in human subthalamic nucleus correlates with motor performance. Brain 127: 735–746, 2004 [DOI] [PubMed] [Google Scholar]
- Levy R, Ashby P, Hutchison WD, Lang AE, Lozano AM, Dostrovsky JO. Dependence of subthalamic nucleus oscillations on movement and dopamine in Parkinson's disease. Brain 125: 1196–1209, 2002 [DOI] [PubMed] [Google Scholar]
- Mallet N, Pogosyan A, Marton LF, Bolam JP, Brown P, Magill PJ. Parkinsonian beta oscillations in the external globus pallidus and their relationship with subthalamic nucleus activity. J Neurosci 28: 14245–14258, 2008a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallet N, Pogosyan A, Sharott A, Csicsvari J, Bolam JP, Brown P, Magill PJ. Disrupted dopamine transmission and the emergence of exaggerated beta oscillations in subthalamic nucleus and cerebral cortex. J Neurosci 28: 4795–4806, 2008b [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran A, Bergman H, Israel Z, Bar-Gad I. Subthalamic nucleus functional organization revealed by parkinsonian neuronal oscillations and synchrony. Brain 131: 3395–3409, 2008 [DOI] [PubMed] [Google Scholar]
- Nini A, Feingold A, Slovin H, Bergman H. Neurons in the globus pallidus do not show correlated activity in the normal monkey, but phase-locked oscillations appear in the MPTP model of parkinsonism. J Neurophysiol 74: 1800–1805, 1995 [DOI] [PubMed] [Google Scholar]
- Papoulis A. Probability, Random Variables and Stochastic Processes. New York: McGraw-Hill Higher Education, 1991 [Google Scholar]
- Park C, Worth RM, Rubchinsky LL. Fine temporal structure of beta oscillations synchronization in subthalamic nucleus in Parkinson's disease. J Neurophysiol 103: 2707–2716, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paxinos G, Watson C. The Rat Brain in Stereotaxic Coordinates. Sydney: Academic, 1986 [DOI] [PubMed] [Google Scholar]
- Raz A, Feingold A, Zelanskaya V, Vaadia E, Bergman H. Neuronal synchronization of tonically active neurons in the striatum of normal and parkinsonian primates. J Neurophysiol 76: 2083–2088, 1996 [DOI] [PubMed] [Google Scholar]
- Raz A, Frechter-Mazar V, Feingold A, Abeles M, Vaadia E, Bergman H. Activity of pallidal and striatal tonically active neurons is correlated in mptp-treated monkeys but not in normal monkeys. J Neurosci 21: RC128, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raz A, Vaadia E, Bergman H. Firing patterns and correlations of spontaneous discharge of pallidal neurons in the normal and the tremulous 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine vervet model of parkinsonism. J Neurosci 20: 8559–8571, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renart A, Brunel N, Wang XJ. Mean-field theory of irregularly spiking neuronal populations and working memory in recurrent cortical networks. In: Computational Neuroscience A Comprehensive Approach, edited by Feng J. London: Chapman and Hall, 2004, p. 431–490 [Google Scholar]
- Ryan LJ, Clark KB. Alteration of neuronal responses in the subthalamic nucleus following globus pallidus and neostriatal lesions in rats. Brain Res Bull 29: 319–327, 1992 [DOI] [PubMed] [Google Scholar]
- Schwarting RK, Huston JP. The unilateral 6-hydroxydopamine lesion model in behavioral brain research. Analysis of functional deficits, recovery and treatments. Prog Neurobiol 50: 275–331, 1996a [DOI] [PubMed] [Google Scholar]
- Schwarting RK, Huston JP. Unilateral 6-hydroxydopamine lesions of meso-striatal dopamine neurons and their physiological sequelae. Prog Neurobiol 49: 215–266, 1996b [DOI] [PubMed] [Google Scholar]
- Sharott A, Magill PJ, Bolam JP, Brown P. Directional analysis of coherent oscillatory field potentials in the cerebral cortex and basal ganglia of the rat. J Physiol 562: 951–963, 2005a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharott A, Magill PJ, Harnack D, Kupsch A, Meissner W, Brown P. Dopamine depletion increases the power and coherence of beta-oscillations in the cerebral cortex and subthalamic nucleus of the awake rat. Eur J Neurosci 21: 1413–1422, 2005b [DOI] [PubMed] [Google Scholar]
- Smith Y, Bevan MD, Shink E, Bolam JP. Microcircuitry of the direct and indirect pathways of the basal ganglia. Neuroscience 86: 353–387, 1998 [DOI] [PubMed] [Google Scholar]
- Steriade M. Corticothalamic resonance, states of vigilance and mentation. Neuroscience 101: 243–276, 2000 [DOI] [PubMed] [Google Scholar]
- Strogatz S. Nonlinear Dynamics and Chaos. Cambridge, MA: Westview, 1994, p. 497 [Google Scholar]
- Strong SP, Koberle R, de Ruyter van Steveninck RR, Bialek W. Entropy and information in neural spike trains. Phys Rev Lett 80: 197–200, 1998 [Google Scholar]
- Surmeier DJ, Mercer JN, Chan CS. Autonomous pacemakers in the basal ganglia: who needs excitatory synapses anyway? Curr Opin Neurobiol 15: 312–318, 2005 [DOI] [PubMed] [Google Scholar]
- Terman D, Rubin JE, Yew AC, Wilson CJ. Activity patterns in a model for the subthalamopallidal network of the basal ganglia. J Neurosci 22: 2963–2976, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong H. Non-Linear Time Series. A Dynamical System Approach. Oxford: Oxford University Press, 1990, p. 564 [Google Scholar]
- Truccolo W, Eden UT, Fellows MR, Donoghue JP, Brown EN. A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects. J Neurophysiol 93: 1074–1089, 2005 [DOI] [PubMed] [Google Scholar]
- Vila M, Perier C, Feger J, Yelnik J, Faucheux B, Ruberg M, Raisman-Vozari R, Agid Y, Hirsch EC. Evolution of changes in neuronal activity in the subthalamic nucleus of rats with unilateral lesion of the substantia nigra assessed by metabolic and electrophysiological measurements. Eur J Neurosci 12: 337–344, 2000 [DOI] [PubMed] [Google Scholar]
- Williams D, Kuhn A, Kupsch A, Tijssen M, van Bruggen G, Speelman H, Hotton G, Loukas C, Brown P. The relationship between oscillatory activity and motor reaction time in the parkinsonian subthalamic nucleus. Eur J Neurosci 21: 249–258, 2005 [DOI] [PubMed] [Google Scholar]
- Williams D, Kuhn A, Kupsch A, Tijssen M, van Bruggen G, Speelman H, Hotton G, Yarrow K, Brown P. Behavioural cues are associated with modulations of synchronous oscillations in the human subthalamic nucleus. Brain 126: 1975–1985, 2003 [DOI] [PubMed] [Google Scholar]
- Williams D, Tijssen M, Van Bruggen G, Bosch A, Insola A, Di Lazzaro V, Mazzone P, Oliviero A, Quartarone A, Speelman H, Brown P. Dopamine-dependent changes in the functional connectivity between basal ganglia and cerebral cortex in humans. Brain 125: 1558–1569, 2002 [DOI] [PubMed] [Google Scholar]