Generalized methods and solvers for noise removal from piecewise constant signals. I. Background theory

Abstract

Removing noise from piecewise constant (PWC) signals is a challenging signal processing problem arising in many practical contexts. For example, in exploration geosciences, noisy drill hole records need to be separated into stratigraphic zones, and in biophysics, jumps between molecular dwell states have to be extracted from noisy fluorescence microscopy signals. Many PWC denoising methods exist, including total variation regularization, mean shift clustering, stepwise jump placement, running medians, convex clustering shrinkage and bilateral filtering; conventional linear signal processing methods are fundamentally unsuited. This paper (part I, the first of two) shows that most of these methods are associated with a special case of a generalized functional, minimized to achieve PWC denoising. The minimizer can be obtained by diverse solver algorithms, including stepwise jump placement, convex programming, finite differences, iterated running medians, least angle regression, regularization path following and coordinate descent. In the second paper, part II, we introduce novel PWC denoising methods, and comparisons between these methods performed on synthetic and real signals, showing that the new understanding of the problem gained in part I leads to new methods that have a useful role to play.

1. Introduction

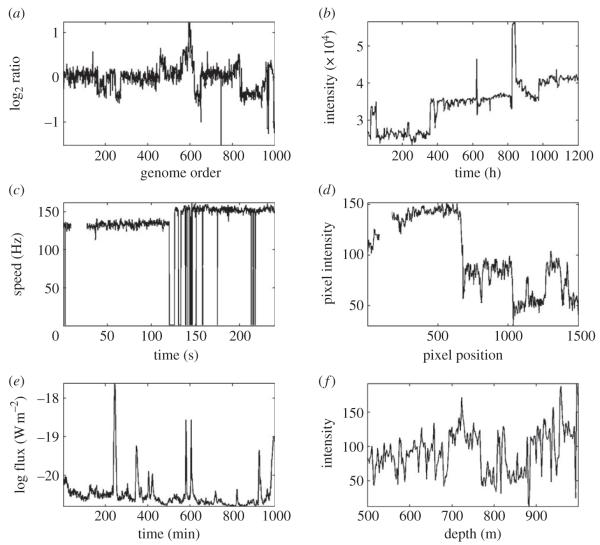
Piecewise constant (PWC) signals exhibit flat regions with a finite number of abrupt jumps that are instantaneous or effectively instantaneous because the transitions occur in between sampling intervals. These signals occur in many contexts, including bioinformatics (Snijders et al. 2001), astrophysics (O’Loughlin 1997), geophysics (Mehta et al. 1990), molecular biosciences (Sowa et al. 2005) and digital imagery (Chan & Shen 2005). Figure 1 shows examples of signals that could fit this description that are apparently contaminated by significant noise. Often, we are interested in recovering the PWC signal from this noise, using some kind of digital filtering technique.

Figure 1.

Examples of signals that could be modelled as piecewise constant (PWC) signals obscured by noise. (a) Log normalized DNA copy-number ratios against genome order from a microarray-based comparative genomic hybridization study (Snijders et al. 2001); (b) Cosmic ray intensity against time recorded by neutron monitor (O’Loughlin 1997); (c) rotation speed against time of R. Sphaeroides flagellum (Pilizota et al. 2009), (d) pixel red intensity value against horizontal pixel position for a single scan line from a digital image, (e) short-wavelength solar X-ray flux against time recorded by GOES-15 space weather satellite (Bloom 2009) and (f ) gamma ray intensity against depth from USGS wireline geological survey well log (Ryder et al. 2009).

Because such signals arise in a great many scientific and engineering disciplines, this noise filtering problem is of enduring interest. However, it goes under a confusing array of names. An abrupt jump can be called a shift, edge, step, change, change point or less commonly, singularity or transition (sometimes combined, e.g. step change), and to emphasize that this jump is instantaneous, it can occasionally also be sharp, fast or abrupt. The constant regions are often also called levels. Bearing in mind that finding the location of the jumps usually allows estimation of the level of the flat regions, the filtering process itself (usually smoothing) can also be called detection or approximation, and less commonly classification, segmentation, finding or localization.

Statisticians have long been interested in this and related problems. Some of the earliest attempts to solve the related change point detection problem arose in the 1950s for statistical process control in manufacturing (Page 1955), which began a series of statistical contributions that continues to this day, see, for example, (Pawlak et al. 2004). The running median filter was introduced in the 1970s (Tukey 1977) as a proposed improvement to running mean filtering, bringing robust statistical estimation theory to bear on this problem. Following this, robust statistics features heavily in a diverse range of approaches reported in the statistics (Fried 2007), signal processing (Elad 2002; Dong et al. 2007) and applied mathematics literature (Gather et al. 2006).

The PWC with noise model is also important for digital images, because edges, corresponding to abrupt image intensity jumps in a scan line, are highly salient features (Marr & Hildreth 1980). Therefore, noise removal from PWC signals is of critical importance to digital image processing, and a very rich source of contributions to the PWC filtering problem has been devised in the image signal processing community, such as mathematical morphology (Serra 1982), nonlinear diffusion filtering (Perona & Malik 1990), total variation denoising (Rudin et al. 1992) and related approaches, developed through the 1970s to this day. These efforts established strong connections with, and assimilated some of the earlier work on, robust filtering (Elad 2002; Mrazek et al. 2006). The fact that piecewise Lipschitz functions are good models for PWC signals implies that they have a parsimonious representation in a wavelet basis (Mallat 2009), and wavelets for PWC denoising were introduced in the 1990s (Mallat & Hwang 1992). The signal processing community have addressed the problem of PWC coding with wavelets and piecewise polynomials from a rate-distortion point of view, using segmentation based on dynamic programming algorithms (Prandoni 1999).

In apparent isolation from the image processing and statistics communities, other disciplines have described alternative algorithms. Beginning in the 1970s, exploration geophysicists devised a number of novel PWC denoising algorithms, including stepwise jump placement (Gill 1970)—apparently reinvented almost 40 years later by biophysicists (Kerssemakers et al. 2006). In the 1980s, hidden Markov models (Godfrey et al. 1980) were introduced by geophysicists, with biophysics following this trend in the 1990s (Chung et al. 1990). Neuroscientists described novel nonlinear filters that attempt to circumvent the edge smoothing limitations of running mean filtering around the same time (Chung & Kennedy 1991).

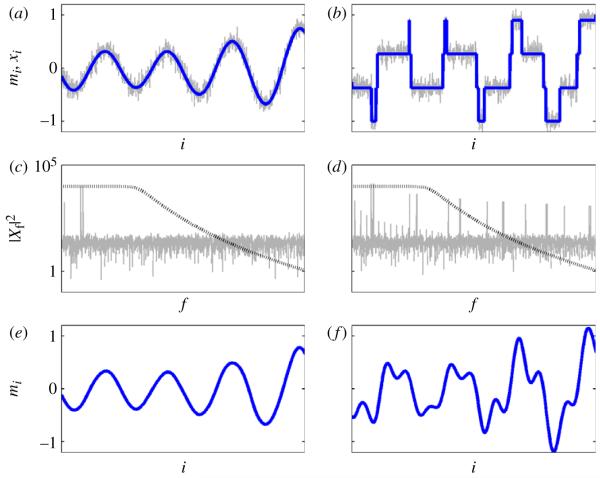
Superficially, this problem does not appear to be particularly difficult, and so it is reasonable to ask why it still deserves attention. To answer this from a signal processing perspective, abrupt jumps pose a fundamental challenge for conventional linear methods, e.g. finite impulse response, infinite impulse response or fast Fourier transform-based filtering. In the Fourier basis, PWC signals converge slowly: that is, the magnitudes of Fourier coefficients decrease much slower with increasing frequency than the coefficients for continuous functions (Mallat 2009). Signal recovery requires removing the noise, and conventional linear methods typically achieve this by low-pass filtering, that is, by removal of the high-frequency detail in the signal. This is effective if the signal to be recovered is sufficiently smooth. But PWC signals are not smooth, and low-pass filtering of PWC signals typically introduces large, spurious oscillations near the jumps known as Gibb’s phenomena (Mallat 2009). The noise and the PWC signal overlap substantially in the Fourier basis and so cannot be separated by any basic approach that reduces the magnitude of some Fourier coefficients, which is how conventional low-pass noise removal works. This typical inadequacy of conventional linear filtering is illustrated in figure 2. Therefore, we usually need to invoke nonlinear techniques in order to achieve effective performance in this digital filtering task. The nonlinearity of these techniques makes them harder to understand than linear techniques, and, as such, there is still much to discover about the PWC denoising problem, and it remains a topic of theoretical interest.

Figure 2.

Noise removal from PWC signals is a task for which no linear filter is efficient, because, for independent noise, the noise and the PWC signal both have infinite bandwidth, e.g. there is no maximum frequency above which the Fourier components of either have zero magnitude. (a) A smooth signal (blue) with added noise (grey), constructed from a few sinusoidal components of random frequency and amplitude; (b) a PWC signal (blue) with added noise (grey), constructed from ‘square-wave’ components of the same frequency and amplitude as the smooth signal. (c) (Discrete) Fourier analysis of the noisy smooth signal shows a few large magnitude, low-frequency components and the background noise level that occupies the whole frequency range. (d) Fourier analysis of the noisy PWC signal in (b), showing the same low-frequency, large magnitude components, but also many other large magnitude components across the entire frequency range (which are harmonics of the square-wave components). The black, dotted line in (c) and (d) shows the frequency response (magnitude not to scale) of a low-pass filter used to perform noise removal; this is applied to the noisy, smooth signal in (e) and the noisy PWC signal in (f). It can be seen that while the smooth signal is recovered effectively and there is little noticeable distortion, although noise is removed from the PWC signal, the jumps are also smoothed away or cause spurious oscillations (Gibb’s phenomena). (Online version in colour.)

The literature on this topic is fragmented across statistics, applied mathematics, signal and image processing, information theory and specialist scientific and engineering domains. While relationships between many of the algorithms discussed here have been established in the image processing and statistics communities—such as the connections between nonlinear diffusion, robust filtering, total variation denoising, mean shift clustering and wavelets (Candes & Guo 2002; Elad 2002; Steidl et al. 2004; Chan & Shen 2005; Mrazek et al. 2006; Arias-Castro & Donoho 2009)—here, we identify some broader principles at work:

• —The problem of PWC denoising is fruitfully understood as either piecewise constant smoothing, or as level-set recovery owing to the fact that typically, there will be either only a few isolated jumps in the signal, or just a few, isolated levels. The PWC view naturally suggests methods that fit 0-degree (constant) splines to the noisy signal and which typical find the jump locations that determine the levels. By contrast, the level-set view suggests clustering methods that attempt to find the levels and thus determine the location of the jumps.
• —Building on work from the image processing literature, all the methods we study here are associated with special cases of a generalized, functional equation, with the choice of terms in this functional determining the specifics of each PWC method. A few, general ‘component’ functions are assembled into the terms that go to make up this functional. We show here that this functional is broadly applicable to a wide set of methods proposed across the disciplines.
• —All these methods function, either explicitly by the action of the solver, or implicitly by nature of the generalized functional, by application of a sample distance reduction principle: to minimize the sum in the functional, the absolute differences between some samples in the input signal have to reduce sufficiently to produce solutions that have what we call the PWC property. A solution with this property has a parsimonious representation as a constant spline or level-set.
• —All the PWC methods we study here attempt to minimize the generalized functional obtained using some kind of solver. Although, as presented in the literature, these solvers are all seemingly very different, we show that these are in fact special cases of a handful of very general concepts, and we identify the conditions under which each type of solver can be applied more generically.

These findings provide us with some structural insights about existing methods and their relationships that we explore in this paper, and allow us to develop a number of novel PWC denoising techniques, and some new solvers, that blend the relative merits of existing methods in useful ways. The detailed nature of the extensive ground work in this paper (part I) is necessary to make it clear how the novel methods we propose in part II are relevant, useful and solvable in practice.

A summary of this first paper, part I, is as follows. Section 2 motivates and formalizes the spline and level-set models for discrete-time PWC signals. Section 3 introduces the generalized functional that connects all the methods in this paper, and describes how this functional can be built from component functions. It introduces the sample distance reduction principle. It shows how existing PWC denoising algorithms are associated with special cases of this functional. Section 4 discusses general classes of solvers that minimize the generalized functional, and some new observations about existing PWC denoising methods that arise when considering the properties of these solvers. In part II, we present a set of new methods, look at how the approaches perform with outliers and drift, summarize their behaviour on steps, compare their computational efficiency and consider a case study for experimental data.

2. Piecewise constant signals as splines and level-sets

In this paper, we wish to recover an N sample PWC signal $m_i\in \mathbb{R}$, for i = 1, 2 … N. We assume that the discrete-time signal is obtained by sampling of the continuous-time signal m(t), t [t₁, t_N] (note that the use of ‘time’ here simply stands in for the fact that the signal is just a set of values ordered by the index i or t, and we will often suppress the index for notational clarity). The observed signal is corrupted by an additive noise random process $e_i\in \mathbb{R}$, i.e. x = m + e.

PWC signals consist of two fundamental pieces of information: the levels (the values of the samples in constant regions), and the boundaries of those regions (the locations of the jumps). A common theme in this paper is the distinction between (i) PWC signals described by the locations of the jumps, which in turn determine the levels according to the specifics of the noise-removal method, and (ii) signals described by the values of the levels, which then determine the location of the jumps through the properties of the method.

By way of motivating the jump interpretation, we consider Steidl et al. (2006) showing that the widely used total variation regularization PWC denoising method has, as solutions, a set of discrete-time, constant 0-degree splines, where the location of the spline knots is determined by the regularization parameter γ and the input data x. This result provides the first intuitive model for PWC signals as constructed from constant splines, and PWC denoising as a spline interpolation problem. The spline model is usually a compact one because it is generally the case that the PWC signal to be recovered has only a small number of discontinuities relative to the length of the signal, that is, there are only a few jumps (i.e. a jump occurs where at indices i and i + 1, m_i ≠ m_i+1). The M jumps in the signal occur at the spline knots with locations {r₁, r₂, … r_M+1} (together with the ‘boundary knots’ r₀ = 1 and r_M+1 = N + 1 for completeness). The PWC signal is reconstructed from the values of the constant levels {l₁, l₂, … l_M+1} and the knot locations, e.g. m_i = l_j for r_j−1 ≤ i < r_j, where j = 1, 2 … M + 1.

Alternatively, one can view the problem of PWC denoising as a clustering problem, classically solved using techniques such as mean shift or K-means clustering (Cheng 1995). In this context, it is natural to apply the level-set model, and indeed, this may sometimes be more useful (and more compact) than the spline description (Chan & Shen 2005). The level-set for the value l Ω (Ω refers to the set of all unique values in the PWC signal) is the set of indices corresponding to l, Γ(l) = {i : m_i = l}. The complete level-set over all values of the PWC signal Γ is formed from the union of these level-sets, which also makes up the complete index set, Γ = ∪_lΩΓ(l) = {1, 2 … N}. The level-sets form a partition of the index set, so that Γ(l_A) ∩ Γ(l_B) = for all l_A ≠ l_B where l_A, l_B Ω. The spline and level-set descriptions are, of course, readily interchangeable using appropriate transformations.

Since this paper is concerned with discrete-time signals only, the definition of a PWC signal used in this paper is that they have a simple representation as either 0-degree splines or as level-sets. By simple, we mean that the number of jumps is small compared with the number of samples, M/N << 1, or, that the number of unique levels is small compared with the number of samples |Ω|/N ≈ 1. If a signal satisfies either condition we say that it has the PWC property.

3. A generalized functional for piecewise constant denoising

As discussed in §1, all the PWC denoising methods investigated in this paper are associated with special cases of the following general functional equation:

$$H\left[m\right]=\sum _{i=1}^N\sum _{j=1}^N\mathit{\Lambda }(x_i-m_j,m_i-m_j,x_i-x_j,i-j).$$ (3.1)

Here, x is the input signal of length N, and m is the output of the noise removal algorithm of length N. This functional combines difference functions into kernels and losses. See tables 1 and 2 and the next section for details. In practice, useful kernel and loss functions for PWC denoising are typically of the form described in the tables. A large number of existing methods can be expressed as special cases of the resulting functional assembled from these functional components (table 1). Various solvers can be used to minimize this functional to obtain the output m; these are listed in table 3.

Table 1.

‘Components’ for PWC denoising methods. All the methods in this paper can be constructed using all pairwise differences between input samples, output samples and sequence indices. These differences are then used to define kernel and loss functions. Loss functions and kernels are combined to make the generalized functional to be minimized with respect to the output signal m. Function I(S) is the indicator function such that I(S) = 1 if the condition S is true, and I(S) = 0 otherwise.

(a) difference d	description
xi − mj	input–output value difference; used in likelihood terms
mi − mj	output–output value difference; used in regularization terms
xi − xj	input–input value difference; used in both likelihood and  regularization terms
i − j	sequence difference; used in both likelihood and regularization  terms

(b) kernel function	description
1	global
I(|d|≤W)	hard (local in either value or sequence)
I(|d|2/2≤W)
exp(−β|d|)	soft (semi-local in either value or sequence)
exp(−β|d|2/2)
I(d = 1)	isolates only sequentially adjacent terms when used as sequence  kernel
I(d = 0)	isolates only terms that have the same index when used as  sequence kernel
	influence function (derivative of loss function)

(c) loss function	kernel × direction	composition
L0(d) = |d|0		simple
L1(d) = |d|1	$L_1^{\prime }\left(d\right)=1\times \mathrm{sgn}\left(d\right)$
L2(d) = |d|2/2	$L_2^{\prime }\left(d\right)=1\times d$
LW,1(d) = min(|d|, W)	$L_{W,1}^{\prime }\left(d\right)=I(\mid d\mid \le W)\times \mathrm{sgn}\left(d\right)$	composite
LW,2(d) = min(|d|2/2, W)	$L_{W,2}^{\prime }\left(d\right)=I({\mid d\mid }^2∕2\le W)\times d$
Lβ,1(d) = 1 − exp(−β|d|)/β	$L_{\beta ,1}^{\prime }\left(d\right)=\exp (-\beta \mid d\mid )\times \mathrm{sgn}\left(d\right)$	composite
Lβ,2(d) = 1 − exp(−β|d|2/2)/β	$L_{\beta ,2}^{\prime }\left(d\right)=\exp (-\beta {\mid d\mid }^2∕2)\times d$

Table 2.

A generalized functional for noise removal from piecewise constant (PWC) signals. The functional combines differences, losses and kernel functions described in table 1 into a function to be minimized over all samples, pairwise. Various solver algorithms are used to minimize this functional with respect to the solution; these are described in table 3.

generalized functional for piec ewise constant noise removal
$H\left[m\right]=\underset{i=1}{\overset{N}{\Sigma }}\underset{j=1}{\overset{N}{\Sigma }}\mathit{\Lambda }(x_i-m_j,m_i-m_j,x_i-x_j,i-j)$
existing methods	function Λ	notes
linear diffusion	(1/2)|mi − mj|2I(i − j = 1)	solved by weighted mean  filtering; cannot produce PWC  solutions; not PWC
step-fitting (Gill 1970;  Kerssemakers et al. 2006)	(1/2)|xi − mj |2I(i − j = 0)	termination criteria based on  number of jumps; PWC
objective step-fitting  (Kalafut & Visscher 2008)	(1/2)|xi − mj|2I(i − j = 0)  +λ|mi − mj|0I(i − j = 1)	likelihood term the same upto  log transformation;  regularization parameter λ  fixed by data; PWC
total variation regularization  (Rudin et al. 1992)	(1/2)|xi − mj|2I(i − j = 0)  + γ|mi − mj|I(i − j = 1)	convex; fused Lasso signal  approximator is the same;  PWC
total variation diffusion	|mi − mj|I(i − j = 1)	convex; partially minimized by  iterated 3-point median filter;  PWC
mean shift clustering	min((1/2)|mi − mj|2, W)	non-convex; PWC
likelihood mean shift  clustering	min((1/2)|xi − mj|2, W)	non-convex; K-means is similar  but not a direct special case  (see text); PWC
soft mean shift clustering	1 − exp(−β|mi − mj|2/2)/β	non-convex; PWC
soft likelihood mean shift  clustering	1 − exp(−β|xi − mj|2/2)/β	non-convex; soft-K-means is  similar but not a direct special  case (see text); PWC
convex clustering shrinkage  (Pelckmans et al. 2005)	(1/2)|xi − mj|2I(i − j = 0)  + γ|mi − mj|	convex; PWC
bilateral filter (Mrazek et al. 2006)	[1 − exp(−β|mi − mj|2/2)/β]  ×I(|i − j| ≤ W)	non-convex

Table 3.

Solvers for finding a minimizer of the generalized PWC noise-removal functional in table 2. The first column is the solver algorithm, the second is the different PWC methods to which the technique can be applied in theory.

solver	can apply to	notes
analytical convolution	linear diffusion	problems with only square  loss functions are  analytical in a similar way
linear programming  (Boyd & Vandenberghe 2004)	robust total variation  regularization	direct minimizer of  functional; also all  piecewise linear convex  problems
quadratic programming  (Boyd & Vandenberghe 2004)	total variation regularization  convex clustering shrinkage	direct minimizer of  functional; also all  problems that combine  square likelihood with  absolute regularization  loss
stepwise jump  placement (Gill 1970;  Kerssemakers et al. 2006; Kalafut & Visscher 2008)	step-fitting objective  step-fitting jump penalization  robust jump penalization	greedy spline fit minimizer  of functional
finite differencing  (Mrazek et al. 2006)	total variation regularization  total variation diffusion  convex clustering shrinkage  mean shift clustering  likelihood mean shift  clustering soft mean shift  clustering soft K-means clustering	finite differences are not  guaranteed to converge for  non-differentiable loss  functions
coordinate descent  (Friedman et al. 2007)	total variation regularization  robust total variation  regularization
iterated mean  replacement  (Cheng 1995)	mean shift clustering likelihood  mean shift clustering	obtainable as adaptive  step-size forward Euler  differencing
weighted iterated mean  replacement  (Cheng 1995)	soft mean shift clustering soft  likelihood mean shift  clustering	obtainable as adaptive  step-size forward Euler  differencing
piecewise linear  regularization path  follower (Rosset & Zhu 2007; Hofling 2009)	total variation regularization  convex clustering shrinkage
least-angle regression  path follower  (Tibshirani & Taylor 2010)	total variation regularization	reverse of piecewise linear  regularization path  follower

(a) Differences, kernels and losses

As described in table 1, the basis of the unification of these methods into a single functional equation is the quantification of the differences between all pairs of input x and output samples m, and their indices i, j (table 1a). In the statistical literature, the generalized functional (3.1) would typically be derived from specification of likelihood and prior distributions, where the likelihood would involve terms in x_i − m_j and the prior involve functions of m_i − m_j. A minimizer for the functional would be a regularized maximum likelihood or maximum a posteriori estimator. In this paper, we will therefore describe terms in x_i − m_j as likelihood terms, and terms in m_i − m_j as regularization terms.

Using these differences, loss functions (table 1c) and kernels (table 1b) are constructed. By kernels, here we simply mean non-negative functions of absolute difference (we call this distance), which are usually symmetric. The loss functions are non-negative functions of distances. We define two different kinds of losses: simple losses that increase with distance, and composite losses that are only increasing with distance over a certain range of the distance. The derivative of the loss function: the influence function (a term borrowed from the robust statistics literature) plays an important role in some iterative algorithms for minimizing the functional (for example, see §4f below). With composite loss functions, the influence function is seen to be a product of an associated kernel term that represents the magnitude of the gradient of the loss, and a term that represents the direction of the gradient of the loss. In this paper, we will focus on simple symmetric distance functions. The three cases we will focus on are the non-zero count count p = 0 defining |d|⁰, which is 0 if d is 0, and one otherwise; the case p = 1 corresponding to the absolute distance, and the case p = 2 corresponding to the square distance |d|²/2.

We distinguish between differences in the values of input and output samples, x_i − m_j, m_i − m_j and x_i − x_j, and the difference between the sequence of samples i − j. Thus, a kernel based on differences between pairs of variables x, m we call a value kernel, to distinguish it from a kernel based on i − j which we call a sequence kernel. We make further distinctions between hard and soft kernels. Hard kernels are non-zero for some range of distances, and outside this range, they are zero. Soft kernels take non-zero values for all values of the distance. We also describe the trivial kernel that is 1 for all values of distance as the global kernel. When used as a sequence kernel the global kernel means that all pairwise terms enter into the sum, and when used as a value kernel it implies that all differences in value are weighted equally. All other kernels are therefore local kernels. The special local sequence kernels I(d = 1) and I(d = 0) isolate only adjacent terms in the generalized functional sum, and terms that are aligned to the same index value, respectively (where I(S) is an indicator function that takes a value of 1 if S is true and zero otherwise).

The loss functions are assembled into the function Λ in equation (3.1) that quantifies the loss incurred by every difference. Summation of Λ over all pairs of indices in the input and output signals leads to the functional H[m] to be minimized with respect to the output m.

(b) The sample distance reduction principle

The generalized presentation of the PWC denoising methods in this paper allows us to see that the basic operation of these methods is to reduce the distance between samples in the input signal. In this section, we give a non-rigorous explanation for this behaviour. As the simplest example, consider Λ = |m_i − m_j|^p/p; for p ≥ 1, this leads to a convex functional that has the optimum, constant solution m_i = c (this can be shown by differentiating H with respect to each m_i and setting each equation to zero). Throughout the paper, we use the notation m^k to denote the output signal obtained at iteration k of a solver (we thus have a mixed notation in which the context defines the interpretation of m: it can either be the unknown PWC signal we are trying to estimate or represents our current best estimate). Our solvers would typically be initialized with m⁰ = x and then successive attempts at solutions, m^k, are conditional on past attempts. We expect good iterative solvers initialized with m⁰ = x to reduce the distance between input samples in successive iterations, the natural termination of this process being the constant solution m_i = c. This occurs with the simple loss |m_i − m_j|^p/p that increases with increasing difference, and minimizing the total sum of losses requires that the differences must be reduced in absolute value.

Of course, this trivial constant solution is of no use in practice. One way in which this trivial solution is avoided is by regularization: for the purpose of illustration, consider the functional arising from Λ = (1/p)|x_i − m_j|^pI(i − j = 0) + γ/p|m_i − m_j|^p for p ≥ 1 (table 2). The resulting functional has when the property that the regularization parameter γ = 0, the optimal solution is m = x; but as γ → ∞, the second term dominates, forcing the samples in the output signal to collapse onto a single constant. A useful PWC output consisting of several different levels might lie between these two extremes.

The trivial constant solution is also avoided by the introduction of kernels. Consider, for example, the soft-mean shift functional Λ = 1 − exp(−β|m_i − m_j|^p/p)/β for p ≥ 1 (table 2), and an iterative solver initialized with m⁰ = x. With this modification to the simple loss function (table 1c), the loss attached to distances between samples does not increase strongly with increasing differences: beyond a certain distance, the loss remains effectively unchanged. Thus, in minimizing the total sum of losses in the functional, some pairs of samples are forced closer together, whereas others are free to become further apart. Those that are constrained eventually collapse onto a few levels. Therefore, a minimum of the functional is often a useful PWC solution. Note that the trivial constant solution is a minimizer, but because the functional is not convex, a non-trivial PWC solution is usually reached first by a gradient descent solver.

Sequence kernels allow the distance reduction to become localized in index. For the diffusion filter Λ = |m_i − m_j|^pI(i − j = 1) with m⁰ = x and p ≤ 1, only samples that are adjacent to each other must become closer to each other under minimization of the functional (see §4c). The difference between samples that are not adjacent is irrelevant. Locally constant runs of similar values can, therefore, emerge to produce a PWC output. Note that here, for the case p = 2, the only possible PWC output is the trivial constant output because the diffusion is then linear.

Kernels applied to differences of the input samples alone can also prevent the output from collapsing down onto a single constant. For example, by modifying the simple loss (table 1c) with the hard kernel (table 1b) applied to the input differences, as in Λ = (1/p)|m_i − m_j|^pI(x_i − x_j|^p/p ≤ W), p ≥ 1, with solver initialization m⁰ = x, only those samples in the output signal that have the same index as samples in the input signal that are close in value, end up making a contribution to the sum in the functional. Because of this, minimizing the functional requires only that the distance between those samples in the output signal must be reduced, the rest are unconstrained. Therefore, the outputs that minimize this (convex) functional can include ones that consist of more than one level.

(c) Existing methods in the generalized functional form

(i) Diffusion filtering-type methods

These methods, with Λ = (1/p)|x_i − m_j|^qI(i − j = 0) + γ|m_i − m_j|^p(i − j = 1) can be understood as combining sequentially aligned likelihood terms with adjacent regularization terms (see §3a), using simple losses, with the regularization parameter γ. We mention the case q = p = 2 for completeness: this can be solved using a (cyclic) running-weighted mean filter or using Fourier filtering (see §4c). It is, however, of no practical use in PWC denoising because it is purely quadratic, and hence has a linear filtering operation as solver, a situation discussed in §1. Of more value is the case where q = 2 and p = 1: this is total variation regularization (Rudin et al. 1992). Where q = 2 and p = 0, we obtain many jump placement methods that have been proposed in the scientific and engineering literature (Gill 1970; Kerssemakers et al. 2006; Kalafut & Visscher 2008). The corresponding diffusion filtering methods, that are not constrained by the input signal (but that typically have the signal as the initial condition of an iterative solver: m⁰ = x), are obtained when the likelihood term is removed, e.g. with Λ = (1/p)|m_i − m_j|^pI(i − j = 1).

(ii) Convex clustering shrinkage

This clustering method has Λ = (1/2)|x_i − m_j|²I(i − j = 0) + γ|m_i − m_j|, and combines aligned differences in the likelihood term with a global regularization term with regularization parameter γ. It uses only simple losses. The likelihood term uses the square loss, whereas the regularization term has absolute value loss (Pelckmans et al. 2005).

(iii) Mean shift clustering-type methods

This class of methods uses global likelihoods or regularizers, where the losses (table 1c) are associated with hard, local value kernels (table 1b). For Λ = min(|m_i − m_j|, W) coupled with an adaptive step-size finite difference solver, we have mean shift clustering, and with Λ = min(|x_i − m_j|, W) we obtain a clustering method that has important similarities to K-means clustering, we will call this likelihood mean shift clustering (Fukunaga & Hostetler 1975; Cheng 1995), also see §4f. Since these methods use composite losses as defined in table 1c, differences between samples have to be small in order to make a difference to the value of the functional. Hence, samples that start off close under some iterative solver initialized with m⁰ = x will become closer under iteration of the solver, this induces the ‘clustering’ effect of these methods (see §4f for further details).

(iv) Bilateral filtering-type methods

These methods exploit soft value kernels, and hard sequence kernels in the regularization term, and have Λ = [1 − exp(−β|m_i − m_j|)/β]I(i − j| ≤ W). One way of describing these methods is that they are similar to mean shift clustering with soft value kernels, but combined with sequentially local, hard kernels (Mrazek et al. 2006). They, therefore, inherit some of the clustering effect of mean shift clustering, but also the effect of clustering owing to sequence locality.

4. Solvers for the generalized functional and some new observations for existing methods

We distinguish two broad classes of solvers for the generalized functional: (a) those that directly minimize the functional, and (b) those that solve the descent ordinary differential equations (ODEs) obtained by differentiating the functional with respect to m. In category (a), we find greedy methods that attempt to fit a 0-degree spline to the noisy signal, convex optimization methods including linear and quadratic programming, coordinate descent, subgradient and many others. In category (b), we find a very large number of techniques that can be identified as numerical methods for the (simultaneous) initial value problem, we obtain by differentiating the functional with respect to the output signal m_i. The goal of this section is to discuss these solvers in the context of important PWC denoising methods that have found frequent use in practice.

Here, we expand upon the descent ODEs in a special case that is important for those solvers in category (b). A minimum of the generalized functional is obtained at ∂H/∂m_i = 0 for each i = 1, 2 … N (which parallels the first-order optimality condition in variational calculus). It will not be possible in general to solve this resulting set of equations analytically, so one approach is to start with a ‘guess’ solution m = a and to evolve this trial solution in the direction that lowers the value of H the most, until the solution stops changing at a minimum of the functional. This is the idea behind the (steepest) descent ODEs defined as dm_i/dη = −∂H/∂m_i, with the initial conditions m_i(0) = a_i. The solution depends on the solver parameter η. Many of the algorithms we describe in this paper can be written in the form Λ = F(x_i − m_j)k₁(i − j) + γG(m_i − m_j)k₂(i − j), where F, G are loss functions, κ_1,2 are any sequence kernels and γ is the regularization parameter, and the steepest descent ODEs are then

$$\frac{\mathrm{d}{m}_i}{\mathrm{d}\eta }\left(\eta \right)=\frac{\partial H}{\partial m_i}=-\sum _{j=1}^{N}F\prime (x_j-m_i\left(\eta \right))k_1(i-j)-\gamma \sum _{j=1}^{N}G\prime \left(m_i\left(\eta \right)\right)-m_j\left(\eta \right)k_2(i-j).$$ (4.1)

Here, the dependence of the outputs on the solver parameter η has been made explicit, but we will usually suppress this for clarity. Typically, it is arranged such that, when η = 0, m = x and x is often used as the initial condition for these ODEs. As the ODEs are evolved forward in η, the output m becomes closer to having the PWC property on each iteration.

(a) Stepwise jump placement

A conceptually simple and commonly proposed algorithm for directly minimizing H[m] is stepwise jump placement that starts with a spline with no knots as a trial solution and then introduces them to the spline one at a time (Gill 1970; Kerssemakers et al. 2006; Kalafut & Visscher 2008). The location of each new knot is determined by greedy search, that is, by a systematic scan through all locations i = 1, 2 … N, finding the location that reduces the functional the most at each iteration. If the iteration stops after a few knots, this ensures that the solutions satisfy the PWC property. At iteration k, we denote the spline knot locations as {r₁, r₂, … , r_k}. Then the values of the constant levels {l₁, l₂, … , l_k+1} are determined that minimize the generalized functional given these fixed knot indices. Here, we make the new observation that stepwise jump placement methods typically define a functional of the form:

$$H\left[m\right]=f\left(\sum _{i=1}^N\sum _{j=1}^N\left(\frac{1}{2}\right)\mid x_i-m_j{\mid }^{2}I(i-j=0)\right)+g\left(\sum _{i=1}^N\sum _{j=1}^N\mid m_i-m_j{\mid }^{0}I(i-j=1)\right),$$ (4.2)

where f, g are strictly increasing functions—and we observe that since they are increasing, this functional has the same minimizer as the functional obtained from Λ = (1/2)|x_i − m_j|²I(i − j = 0) + λ|m_i − m_j|⁰I(i − j = 1), with a regularization parameter λ > 0 that is determined by either the properties of the input signal or the choice of the number of jumps. In particular, the ‘objective step-fitting’ method of Kalafut & Visscher (2008) has f(s) = N log(s) and g(s) = log(N)s. Since the number of jumps is fixed at each iteration, the optimum levels in the spline fit are just the mean of the samples x for each level:

$$l_j=\frac{1}{r_j-r_{j-1}}\sum _{i=r_{j-1}}^{(r_j-1)}{x}_i,$$ (4.3)

for j = 1, 2 … k + 1. Only the likelihood term must be evaluated to perform the greedy scan for the index of each new knot at iteration k + 1. Given the functional above, it can be that no new knot index can be found that reduces H[m] below the previous iteration; this is used as a criteria to terminate the placement of new knots (Gill 1970; Kalafut & Visscher 2008). Stopping after a predetermined number of jumps have been placed (Gill 1970), or determining a peak in the ratio of the likelihood term to the likelihood evaluated using a ‘counter-fit’ (Kerssemakers et al. 2006), similar in spirit to the F-ratio statistic in analysis of variance, are two other suggested termination criteria.

(b) Linear and quadratic programming

For purely convex problems (that is, problems where the loss functions are all convex in m), the unique minimizer for H[m can be found using standard techniques from convex optimization (Boyd & Vandenberghe ] 2004). In particular, both total variation regularization (Rudin et al. 1992) and convex clustering shrinkage (Pelckmans et al. 2005) can be transformed into a quadratic program (quadratic problem with linear inequality constraints), which can be solved by interior-point techniques. Fast, specialized primal-dual interior-point methods for total variation regularization have been developed recently (Kim et al. 2009). We make the observation here that the scope for linear programs is very wide, and it applies to loss functions such as the loss based on the absolute distance, but also for asymmetric quantile loss functions such as L(d) = [q − I (d < 0)]d, where q is the appropriate quantile q [0, 1]. Quantiles are minimizers for these asymmetric losses, the median being the special, symmetric case (Koenker 2005), and these losses would be useful if it is expected that the noise distribution has asymmetric outliers.

(c) Analytical solutions to the descent ordinary differential equations

In general, all useful PWC methods have functionals that cannot be minimized analytically; it is informative for the flow of this paper, however, to study a functional that can be minimized analytically, even though it is not useful in practice. For the special case of simple square loss functions, minimization of the functional can be carried out directly using matrix arithmetic. We start by considering linear diffusion filtering:

$$\mathit{\Lambda }=\left(\frac{1}{2}\right){\mid m_i-m_j\mid }^{2}I(i-j=1).$$ (4.4)

The associated initial value descent ODEs are

$$\frac{d{m}_i}{d\eta }=-\frac{\partial H}{\partial m_i}=m_{i+1}-2m_i+m_{i-1},$$ (4.5)

with m(0) = x, the boundary cases defined by m_i ≡ 0 for i < 1 and i > N. We can write this in matrix form as dm/dη = Am where A is the system matrix with −2 on the main diagonal, and +1 on the diagonals above and below the main diagonal. This can be understood as a semi-discrete heat equation, with the right-hand side being a discrete approximation to the Laplacian. This set of homogeneous, linear, constant coefficient ODEs can be solved exactly by finding the eigenvalues λ and eigenvectors of the system matrix A which are

$${\lambda }_i=-2+2\cos \left(\frac{i\pi }{N+1}\right),V_{ij}=\sin \left(\frac{ij\pi }{N+1}\right),i,j=1,2\dots N.$$ (4.6)

The matrix of eigenvectors V is orthogonal, and can be made orthonormal without loss of generality. This matrix is then unitary so V = V^T = V⁻¹, and the solution is written explicitly in terms of the eigenvectors:

$$m\left(\eta \right)=V\left[\begin{array}{c}\hfill c_1\text{exp}\left({\lambda }_1\eta \right)\hfill \\ \hfill ⋮\hfill \\ \hfill c_N\text{exp}\left({\lambda }_N\eta \right)\hfill \end{array}\right].$$ (4.7)

The N constants of integration c are determined by the initial condition m(0) = x by calculating c = Vx. This matrix operation can, in fact, be seen to be the discrete sine Fourier transform of the input signal, so the constants are Fourier coefficients of the expansion of the solution in the sine basis, and the solution is merely the inverse discrete sine transform of the discrete sine Fourier domain representation of the input signal, where each frequency component is scaled by exp(λ_iγ). Since the eigenvalues are always negative, the contribution of these frequency components in the solution decays with increasing η, tending to zero as η → ∞. This confirms, by a different route, that the solution can only be entirely constant when all samples are zero. Additionally, λ_i+1 < λ_i for all i = 1, 2 … N so that high-frequency components decay more quickly with increasing η than low-frequency components. Therefore, high-frequency fluctuations owing to noise are quickly smoothed away, and slowly varying frequency components remain.

We will now make a connection to the weighted running mean filter, a ubiquitous linear smoothing technique. The linearity and translation invariance with respect to η of this system allows the solution to be written in terms of a (circular) convolution with the Green’s function (impulse response in the signal processing literature). Using the special initial condition m_i(0) = 1 for i = [N/2] and m_i(0) = 0 otherwise, the Green’s function is

$$h=V\left[\left(V_m\left(0\right)\right)\mathrm{o}\left[\begin{array}{c}\hfill \exp \left({\lambda }_1\Delta \eta \right)\hfill \\ \hfill ⋮\hfill \\ \hfill \exp \left({\lambda }_N\Delta \eta \right)\hfill \end{array}\right]\right],$$ (4.8)

for a particular Δη > 0 (here _o denotes the entrywise product). Because multiplication of the frequency components is equivalent to convolution in the domain i, we can now write the solution as

$$m_i\left(\Delta \eta \right)=h\star x_i=\underset{j=-N∕2}{\overset{N∕2-1}{\Sigma }}{h}_{(j-1)}\mathrm{mod}N+1_{x_{i+j-1}}\mathrm{mod}N+1,$$ (4.9)

where indicates circular convolution. The Green’s function h is of the form of a Gaussian ‘pulse’ centred in the middle of the signal. Iterating the convolution k-times, _k, gives the solution at multiples of Δη, i.e. m(kΔη) = h _kx. For small Δη, the Gaussian pulse has small effective width and so the Green’s function, centred around the Gaussian pulse, can be truncated to produce an (iterated) weighted running mean filter with short window length (2W + 1) < N:

$$m_i^{k+1}=\underset{j=-W}{\overset{W}{\Sigma }}{h}_j{m}_{i-j}^k,$$ (4.10)

with m⁰ = x and the 2W + 1 weights, obtained by centring and truncating the Green’s function, are normalized ${\sum }_{j=-W}^W{h}_j=1$. At the boundaries, we define m_i ≡ 0 for i < 1 and i > N. The smoothing behaviour of this linear filter is useful for noise removal, but, as discussed in §1, since jumps in PWC signals also have significant frequency contributions at the scale of noise fluctuations, these are smoothed away simultaneously. Thus, the smoothing functional obtained by the square regularization loss is of little practical value in PWC denoising applications, despite the tantalizing availability of an exact analytical minimizer and its practical implementation as a simple running weighted mean filter.

(d) Iterated running median filter

While it was seen above that the iterated running (weighted) mean filter is of no essential value in noise removal from PWC signals owing to its linearity, the nonlinear iterated running median filter has been proposed instead. This finds the median (rather than the mean) of the samples in a window of length 2W + 1 that slides over the signal

$$m_i^{k+1}=\text{median}(m_{i-W}^k,\dots ,m_{i+W}^k)=\underset{\mu \in \mathbb{R}}{argmin}\underset{j=-W}{\overset{W}{\Sigma }}\mid m_{i+j}^k-\mu \mid ,$$ (4.11)

with m⁰ = x, and the boundaries are defined through m_i ≡ 0 for i < 1 and i > N. The above minimization expresses the idea that the median is the constant μ that minimizes the total absolute deviations from μ of the samples in each window. This contrasts with the (equal weighted) running mean filter that minimizes the total squared deviations instead. It is well-known that the running median filter does not smooth away edges as dramatically as the running mean filter under conditions of low noise spread (Justusson 1981; Arias-Castro & Donoho 2009), and therefore this filter has value as a method for PWC denoising in a limited range of applications.

Iterated median filtering has some value as a method for PWC denoising, so it is interesting to ask how it is related to other methods in this paper. We observe here a new connection between total variation diffusion filtering and the iterated median filter. We prove in the appendix that applying the median filter with window size 2W + 1 = 3 to a signal cannot increase the total variation of the signal, e.g. TV[m^k+1] ≤ TV[m^k], where $TV\left[m\right]={\sum }_{i-1}^{N-1}\mid m_{i+1}-m_i\mid$. If we consider a numerical solver for the total variation diffusion ODEs obtained from the generalized functional with Λ = |m_i − m_j|I(i − j = 1)

$$\frac{d{m}_i}{d\eta }=\mathrm{sgn}(m_i-m_{i+1})-\mathrm{sgn}(m_i-m_{i-1}),$$ (4.12)

with the initial condition m(0) = x, this solver must also reduce the total variation on each iteration (because it is an integrator that lowers the total variation functional at each iteration). The window length 3 iterated median filter differs from such an integrator because every iterated median filter converges on a root signal that depends on x, that is, a signal that is fixed under the iteration of the filter (Arce 2005). Therefore, unlike the solution to the total variation diffusion ODEs (that eventually leads to a constant signal with zero total variation), this iterated median filter cannot remove all jumps for all signals x, and so it does not necessarily reduce the total variation to zero. Determining the knots in the spline representation is not a simple matter for the iterated median filter. After convergence, whether the solutions have the PWC property depends on the initial conditions, and the number of iterations to reach convergence.

(e) Finite differences

Few other solvers have such widespread applicability as numerical methods for the descent ODEs (4.1). For example, in §4f, we will see that many important PWC clustering algorithms can be derived as special cases of such numerical methods. Initial value problems such as equation (4.1) can be approximately integrated using any of a wide range of numerical methods, including Euler (forward) finite differences (Mrazek et al. 2006)

$$m_i^{k+1}=m_i^k-\Delta \eta \underset{j=1}{\overset{N}{\Sigma }}F\prime (m_i^k-x_j)K_1(i-j)-\gamma \Delta \eta \underset{j=1}{\overset{N}{\Sigma }}G\prime (m_i^k-m_j^k)K_2(i-j),$$ (4.13)

where Δη is the discretization size, together with initial condition $m_i^0=a_i$, a set of constants.

This is accurate to first order in the discretization size. Higher order accurate integrators could be used instead if required. In the special case, where all the loss functions are convex and differentiable, this method converges on the unique minimizer for H[m]. If any one of the loss functions is not differentiable everywhere, then convergence is not guaranteed, but achieving a good approximation to the minimizer may still be possible, particularly if the loss function is non-differentiable at only a small set of isolated points. If the loss functions are not convex but are differentiable, then convergence to a minimizer for the functional is guaranteed; but this may not be the minimizer that leads to the smallest possible value for the functional. Without differentiability, then convergence cannot be guaranteed either. For non-convex losses, one useful heuristic to gain confidence that a proposed solution found using finite differences is the minimizer associated with the smallest possible value for the functional is to restart the iteration several times from randomized starting conditions and iterate until convergence (or approximate convergence). One can then take the solution with the smallest value of the functional from these (approximately) converged solutions.

(f) Finite differences with adaptive discretization

In this section, we will provide an analysis showing that many standard clustering algorithms as special cases of the finite differences introduced above. For the Euler forward finite difference solver, the fixed discretization size Δη can be replaced with an adaptive discretization size. This trick can be used to derive mean shift, and the soft version of this method, as well as the bilateral filter (Mrazek et al. 2006), but it can be used more generally. We note here that the popular K-means method is conceptually extremely similar although not a direct special case of the functional (3.1). In this section, we show how to derive a new method, we call likelihood mean shift (table 2) that is a relevant special case of the functional (3.1).

As discussed earlier, if the loss function is composite (table 1c), then the influence function is the product of a kernel and a direction term (Cheng 1995). In particular, for the local, hard loss functions min(|d|, W) and min(|d|²/2, W), the influence functions are I(|d| ≤ W) × sgn(d) and I(|d|²/2 ≤ W) × d, so in the latter case, the kernel is the hard window of size W, and the direction term is just the difference d.

With composite square loss functions, such as min(|d|²/2, W), and by equation (4.13), the Euler finite difference formula can be

$$m_i^{k+1}=m_i^k-\Delta \eta \underset{j=1}{\overset{N}{\Sigma }}I({\mid m_i^k-x_j\mid }^2∕2\le W)(m_i^k-x_j)k_s(i-j)-\gamma \Delta \eta \underset{j=1}{\overset{N}{\Sigma }}I({\mid m_i^k-m_j^k\mid }^2∕2\le W)(m_i^k-m_j^k)k_s(i-j),$$ (4.14)

where k_s is any sequence kernel (here, for simplicity, we have shown the case where the form of the kernels used in the likelihood and regularization terms are the same, but they need not be in general). Now, we set an appropriate adaptive discretization size

$$\Delta {\eta }_i={\left[\underset{j=1}{\overset{N}{\Sigma }}I({\mid m_i^k-x_j\mid }^2∕2\le W)k_s(i-j)+\underset{j=1}{\overset{K}{\Sigma }}I({\mid m_i^k-m_j^k\mid }^2∕2\le W)k_s(i-j)\right]}^{-1},$$ (4.15)

ensuring steps become larger in flatter regions. Classical mean shift (§3c and table 2) uses the hard local, square loss function; the sequence kernel is global, so the finite difference formula becomes

$$m_i^{k+1}=m_i^k-\Delta \eta \underset{j=1}{\overset{N}{\Sigma }}I({\mid m_i^k-m_j^k\mid }^2∕2\le W)(m_i^k-m_j^k).$$ (4.16)

Replacing the discretization size with the adaptive quantity $\Delta {\eta }_i={\left({\sum }_{j=1}^{N}I({\mid m_i^k-m_j^k\mid }^2∕2\le W)\right)}^{-1}$, after some algebra we get

$$m_i^{k+1}=\frac{\underset{j=1}{\overset{N}{\Sigma }}I({\mid m_i^k-m_j^k\mid }^2∕2\le W)m_j^k}{\underset{j=1}{\overset{N}{\Sigma }}I({\mid m_i^k-m_j^k\mid }^2∕2\le W)}$$ (4.17)

which is the classical mean shift algorithm that replaces each output sample value with the mean of all those within a distance W. What we are calling likelihood mean shift (§3c and table 2), has, similar to mean shift the adaptive step size, $\Delta {\eta }_i={\left({\Sigma }_{j=1}^{N}I({\mid m_i^k-m_j^k\mid }^2∕2\le W)\right)}^{-1}$ leading to the iteration

$$m_i^{k+1}=\frac{\underset{j=1}{\overset{N}{\Sigma }}I({\mid m_i^k-m_j^k\mid }^2∕2\le W)x_j}{\underset{j=1}{\overset{N}{\Sigma }}I({\mid m_i^k-m_j^k\mid }^2∕2\le W)},$$ (4.18)

that replaces each cluster centroid m_i, i = 1 … N with the mean of all the input samples within a distance W. Soft versions of both algorithms are obtained by using the soft kernel instead of the hard kernel.

Up until now, it has been assumed that for each sample value at i, x_i, there is a corresponding estimate for the PWC signal m_i; in this case 1 ≤ i ≤ N is acting as an index for ‘time’ for both input and output signals. For our particular discussion of K-means below, it is necessary to allow that the index of m_i need not be a proxy for time but instead indexes each distinct level in the PWC output signal: there might be K distinct levels in the PWC output signal and it is possible that K < N. Deriving the classical K-means algorithm—requires the construction of the value kernel

$$k_C(m_i,x_j)=I(m_i=\underset{1<\alpha <K}{\mathrm{argmin}}\mid m_{\alpha }-x_j\mid ),$$ (4.19)

which is the indicator function of whether the cluster centroid m is the closest to the input sample x. Then the iteration

$$m_i^{k+1}=\frac{\underset{j=1}{\overset{N}{\Sigma }}{k}_C(m_i^k,x_j)x_j}{\underset{j=1}{\overset{N}{\Sigma }}{k}_C(m_i^k,x_j)},$$ (4.20)

can be seen to replace the cluster centroids with the mean of all samples that are closer to it than to any other centroid. Cheng (1995) shows that k_C(m_i, x_j) can be obtained as the limiting case of the smooth function

$$\frac{\exp (-\beta {(m_i-x_j)}^2∕2)}{\underset{p=1}{\overset{K}{\Sigma }}\exp (-\beta {(m_p-x_j)}^2∕2)}\to k_C(m_i,x_j),$$ (4.21)

when β → ∞. Indeed, for finite β, this yields the soft K-means algorithm. However, as we discussed above (§3a), there are two reasons why the classical K-means algorithm departs from the generalized functional (3.1) in this paper. The first is because the number of distinct output samples in the K-means algorithm is K ≤ N, m_i for i = 1, 2 … K. However, if there are many less than N levels in a PWC signal, the K-means solver typically merges the input samples down onto this small number of unique output values. The second departure is that the kernel k_C cannot be obtained directly from the particular form of the generalized functional (3.1), because each term Λ must then be a function of differences of all samples in m and x, not just differences of samples indexed by the pair i, j. However, K-means is an important PWC method and it is conceptually very similar to mean shift. In fact, we make the new observation here that the really critical difference is that the K-means algorithm iterates on the likelihood difference x_i − m_j, whereas mean shift iterates on the regularization difference m_i − m_j (compare equations (4.18) with (4.20)) This is our reason for calling the clustering method based on the likelihood x_i − m_j the likelihood mean shift method.

The bilateral filter (§3c and table 2) combines the hard local sequence kernel I(|i − j| ≤ W) and the soft loss term 1 − exp(−β|m_i − m_j|²/2)/β and this leads to the following finite difference updata:

$$m_i^{k+1}=m_i^k-\Delta \eta \underset{j=1}{\overset{N}{\Sigma }}\exp (-\left(\beta {\mid m_i^k-m_j^k\mid }^2\right)∕2)(m_i^k-m_j^k)I(\mid i-j\mid \le W).$$ (4.22)

Inserting the adaptive discretization size $\Delta {\eta }_i={\left({\sum }_{j=1}^N\text{exp}(-\left(\beta {\mid m_i^k-m_j^k\mid }^2\right)∕2)I(\mid i-j\mid \le W)\right)}^{-1}$ obtains the bilateral filter formula (Mrazek et al. 2006):

$$m_i^{k+1}=\frac{\underset{j=1}{\overset{N}{\Sigma }}\exp (-\left(\beta {\mid m_i^k-m_j^k\mid }^2\right)∕2)I(\mid i-j\mid \le W)m_j^k}{\underset{j=1}{\overset{N}{\Sigma }}\exp (-\left(\beta {\mid m_i^k-m_j^k\mid }^2\right)∕2)I(\mid i-j\mid \le W)}.$$ (4.23)

See also Elad (2002) for a very instructive alternative derivation involving Jacobi solvers for the equivalent matrix algebra formulation.

This section has shown how adapting the discretization size of the Euler integrator leads to a number of well-known clustering algorithms for appropriate combinations of loss functions. We now observe how the dynamics of the evolving solution can be understood in terms of the level-set model. For mean shift clustering, initially, $m_i^0=x$, and (assuming noise), each $m_i^0$ will typically have a unique value, so every level-set contains one entry (which is just the index for each sample), Γ(m_i) = i. As the iterations proceed, Cheng (1995) shows that if W is sufficiently large that the support of the hard value kernel covers more than one sample of the initial signal, these samples within the support will be drawn together until they merge onto a single value after a finite number of iterations. After merging, they always take on the same value under further iterations. Therefore, after merging, there will be a decreased number of unique values in m, and fewer unique level-sets, that consist of an increased number of indices. Groups of merged samples will themselves merge into larger groups under subsequent iterations, until a fixed point is reached at which no more changes to m^k occur under subsequent iterations. Therefore, after convergence, depending on the initial signal and the width of the kernel, there will typically only be a few level-sets that will consist of a large number of indices each, and the level-set description will be very compact.

In the case of K-means clustering, there are K values in the PWC signal output m^k and at each step, every level-set at iteration k is obtained by evaluating the indicator kernel k_C for every i = 1, 2 … N: $\Gamma \left(m_i^k\right)=\{j\in 1,2\dots N:k_C(m_i^k,x_j)=1\}$. Note that it is possible for two of the levels to merge with each other, in which case the associated level-sets are also merged. After a few iterations, K-means converge on a fixed point where there are no more changes to m^k (Cheng 1995). Soft kernel versions of K-means and mean shift have similar merging behaviour under iteration, except the order of the merging (that is which sets of indices are merged together at each iteration) will depend in a more complex way upon the initial signal and the kernel parameter β.

Bilateral filtering can be seen as soft mean shift, but with the addition of a hard sequential window. Therefore, it inherits similar merging and convergence behaviour under iteration. However, for samples to merge, they must both be close in value and temporally separated by at most W samples (whereas for mean shift, they need only be close in value). The additional constraint of temporal locality implies that each merge does not necessarily assimilate large groups of indices, and the level-set description is not typically as compact as with mean shift.

(g) Piecewise linear path following

For nearly all useful functionals of the form (3.1), analytical solutions are unobtainable. However, it turns out that there are some important special cases for which a minimizer can be obtained with algorithms that might be described as semi-analytical, and we describe them in this section. For useful PWC denoising, it is common that the right-hand side of the descent ODE system is discontinuous, which poses a challenge for conventional numerical techniques such as finite differences. However, it has been shown that if the likelihood term is convex and piecewise quadratic (that is, constructed of piecewise polynomials of order at most two), and the regularization term has convex loss functions that are piecewise linear, then the solution to the descent ODEs is continuous and constructed of piecewise linear segments (Rosset & Zhu 2007). Formally, there is a set of L regularization points 0 = γ₀ < γ₁ < ⋯ γ_L = ∞ and a corresponding set of N-element gradient vectors ε⁰, ε¹ … ε^L, in terms of which the full regularization path, that is, the set of all solutions obtained by varying a regularization parameter γ ≥ 0, can be expressed. We can write this as

$$m\left(\gamma \right)=m\left({\gamma }_j\right)+(\gamma -{\gamma }_j){\epsilon }^j,{\gamma }_j\le \gamma \le {\gamma }_{j+1}$$ (4.24)

for all j = 0, 1 … L − 1. PWC denoising algorithms that have this piecewise linear regularization path property include total variation regularization and convex clustering shrinkage (Pelckmans et al. 2005). The values of the regularization points and the gradient vectors can be found using a general solver proposed by Rosset & Zhu (2007), but specialized algorithms exist for total variation regularization; one finding the path in ‘forward’ sequence of increasing y (Hofling 2009), and the other, by expressing the convex functional in terms of the convex dual variables (Boyd & Vandenberghe 2004), obtains the same path in reverse for decreasing γ (Tibshirani & Taylor 2010).

Total variation regularization has been the subject of intensive study since its introduction (Rudin et al. 1992). Strong & Chan (2003) show that a step of height h and width w in an otherwise zero signal is decreased in height by 2γ/w, and is ‘flattened’ when 2γ/w ≥ h. Here, we make the further observation that these findings can be explained by the sample reduction principle we have introduced: the form of the regularization term acts to linearly decrease the absolute difference in value between adjacent samples m_i(γ) and m_i−1(γ) as γ increases (a process known as shrinkage in the statistics literature), and once adjacent samples eventually coincide for one of the regularization points γ_j, they share the same value for all γ ≥ γ_j. Thus, pairs of samples can be viewed as merging together (a process known as fusing) to form a new partition of the index set, consisting of subsets of indices in consecutive sequences with no gaps.

Initially, at γ = γ₀, this partition is the trivial one where each subset of the index set contains a single index. Subsets of indices in the current partition assimilate their neighbouring subsets as y increases, until the partition consists of just one subset containing all the indices at γ = γ_L−1, and this is also where m_i = E[x]. Thus, total variation regularization recruits samples into constant ‘runs’ of increasing length as γ increases.

This offers another new and intuitive explanation for why constant splines afford a compact understanding of the output of total variation regularization. For the backward path following solver (Tibshirani & Taylor 2010) that begins at the regularization point γ_L−1, the spline consists of no jumps, and only the boundary knots r₀ = 1, r₁ = N + 1 and one level l₁ = E[x]. As the path is followed backward to the next regularization point γ_L−2, the spline is split with a new knot at location i and one new level l₂ is added, so that the spline is described by the set of knots knots {r₀ = 1, r₁ = i, r₂ = N + 1} and levels {l₁, l₂}. The solver continues adding at each regularization point until there are N levels and N + 1 knots. The forward path following algorithm starts at this condition and merges levels by deleting knots at each regularization point.

Piecewise linear path following requires the computation of the regularization points γ_j, and it is possible to directly compute the maximum useful value of the regularization parameter where all the output samples are fused together (Kim et al. 2009)

$${\gamma }_{L-1}={\parallel {\left(D{D}^T\right)}^{-1}Dx\parallel }_{\infty },$$ (4.25)

where ||·||_∞ is the elementwise vector maximum, and D is the N × N first difference matrix:

$$D=\left[\begin{array}{ccccc}\hfill 1\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill \end{array}\right].$$ (4.26)

Using this result, and knowing that a step of height h and unit width is flattened when γ ≥ h/2, allows us to make a novel suggestion for an estimate for the minimum useful value that is just larger than the noise spread. If the noise is Gaussian with standard deviation σ, then setting γ ≥ 2σ will remove 99 per cent of the noise. Therefore, the useful range of the regularization parameter for PWC denoising can be estimated as 2σ ≤ γ ≤ γ_L−1.

(h) Other solvers

The descent ODEs define an initial value problem that is a standard topic in the numerical analysis of nonlinear differential equations, and there exists a substantial literature on numerical integration of these equations (Iserles 2009). These include the finite difference methods discussed above, but also predictor–corrector and higher order methods such as Runge–Kutta, multi-step integrators and collocation. The cost of higher accuracy with high-order integrators is that an increased number of evaluations of the right-hand side of the descent ODEs are required per step. However, the main departure of this problem from classical initial value problems is the existence of discontinuities in the right-hand side of the descent ODE system that arise when the loss functions are not differentiable everywhere, and most of the useful loss functions for PWC denoising methods are non-differentiable. As a solution, flux and slope-limiters have been applied to total variation regularization in the past (Rudin et al. 1992). We also mention here the very interesting matrix algebra interpretation of PWC denoising methods that opens up the possibility of using solvers designed for numerical matrix algebra including the Jacobi and Gauss–Seidel algorithms, and variants such as successive over-relaxation (Elad 2002).

5. Summary

In this first of two papers, we have presented an extensively generalized mathematical framework for understanding existing methods for performing PWC noise removal, which will allow us, in the sequel, to develop several new PWC denoising methods and associated solver algorithms that attempt to combine the advantages of existing methods in new and useful ways.

In order to devise these new PWC denoising methods, this theoretical background study has presented a generalized approach to understanding and performing noise removal from PWC signals. It is based on generalizing a substantial number of existing methods, found through a wide array of disciplines, under a generalized functional, where each method is associated with a special case of this functional. The generalized functional is constructed from all possible differences of samples in the input and output signals and their indices, over which simple and composite loss functions are placed. PWC outputs are obtained by seeking an output signal that minimizes the functional, which is a summation of these kernel loss functions. The task of PWC denoising is then formalized as the problem of recovering either a compact constant spline or level-set description of the PWC signal obscured by noise. Minimizing the functional is seen as constraining the difference between appropriate samples in the input signal. A range of solver algorithms for minimizing the functional are investigated, through which we were able to provide some novel observations on existing methods.

Appendix A

To prove that the 3-point iterated median filter cannot raise the total variation of the signal, we examine two adjacent windows and apply a simple combinatorial argument over the input signal x₁, x₂, x₃, x₄, so that the two input windows have the values x₂, x₃, and the two output windows have the values y₂ = median(x₁, x₂, x₃) and y₃ = median(x₂, x₃, x₄). Now, label x₂, x₃ as ‘inner’ values, and the other two as ‘outer’ values. The non-increasing total variation condition is that |y₂ − y₃| ≤ |x₂ − x₃|. Since the median operation selects one of the values in the input set, there are four different cases to consider. First, consider when both windows select the same input, i.e. y₂ = y₃, their difference is zero and the condition is satisfied trivially. Similarly, trivial is the case when the two inner values are swapped, i.e. y₂ = x₃ and y₃ = x₂, the condition is satisfied at equality. Thirdly, if one of the windows selects one of the inner values, and the other one of the outer values, then it must be that the selected outer value lies in between the two inner values, and so is closer to either of the inner values than the inner values are to themselves, satisfying the condition. The final case is when both outer values x₁, x₄ are selected, but in that case, they both lie in between the inner values and so the condition is again satisfied. This proves that |y₂ − y₃| ≤ |x₂ − x₃| implying that the median operation applied to these two windows cannot increase the total variation. The final step in the proof is to extend this to the entire signal: the total variation over every pair of adjacent values cannot increase, so the total variation over the entire signal cannot increase either. Thus, 3-point median filtering can only either leave the total variation of a signal unchanged or reduce it after each iteration.