Abstract
A novel Empirical Mode Decomposition (EMD) algorithm, called 2T-EMD, for both mono- and multivariate signals is proposed in this paper. It differs from the other approaches by its computational lightness and its algorithmic simplicity. The method is essentially based on a redefinition of the signal mean envelope, computed thanks to new characteristic points, which offers the possibility to decompose multivariate signals without any projection. The scope of application of the novel algorithm is specified, and a comparison of the 2T-EMD technique with classical methods is performed on various simulated mono- and multivariate signals. The monovariate behaviour of the proposed method on noisy signals is then validated by decomposing a fractional Gaussian noise and an application to real life EEG data is finally presented.
Keywords: Analysis of non-linear and non-stationary signals, Computational complexity, EEG denoising, Extrema and barycenters of oscillation, Filter bank structure, Frequency modulation, Hurst exponent estimation, Interpolation, Intrinsic Mode functions, Mono- and Multivariate Empirical Mode Decomposition, Oscillators, Robustness, Spline, Time varying representation
I. Introduction
Empirical Mode Decomposition (EMD) was originally introduced in the late 1990’s to study water surface wave evolution [1]. The EMD can be considered as an emerging technique in signal processing with a very important topic of research and development in various fields such as biomedical signal analysis [2], Hurst exponent estimation [3], speech processing [4], texture analysis [5], etc. It decomposes adaptively a given signal, s, into a sum of N AM-FM components, dn (referred to as the Intrinsic Mode Functions, IMFs), plus a residue aN. An IMF is defined [1] as a locally centered function where the number of extrema and the number of zero-crossings must differ at most by one. More precisely, for a given signal s = a0, the EMD sequentially computes the N IMFs dn, and N corresponding trends an, such that an−1=an+dn. The EMD key issue is then the extraction of the N IMFs dn. In practice, such a signal is obtained by stopping a so-called sifting process, using a Cauchy-like criterion [6]. If k denotes the number of iteration in the sifting process, the so-called sifting process can be summarized as follows:
Initialization with dn,0 = an−1.
Computation of the mean envelope
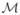 (dn,k).
(dn,k).Extraction of the detail dn,k+1 = dn,k −
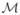 (dn,k).
(dn,k).Incrementation of k and return to step 2 if dn,k+1 is not designated as an IMF else stop of the procedure.
As proposed by Huang [1], the mean envelope
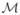 (dn,k) is generally given by the half sum of the upper and the lower envelopes, which are obtained by interpolation between the local maxima points and the local minima points of dn,k, respectively.
(dn,k) is generally given by the half sum of the upper and the lower envelopes, which are obtained by interpolation between the local maxima points and the local minima points of dn,k, respectively.
Simplicity and efficiency of the original EMD, named Huang hereafter, [1] is seducing but, even if we ignore the theoretical lacks of the classical EMD algorithm, one important limitation lies in its strictly monovariate definition. Indeed, even if the major part of the algorithm seems to be quite general, extension to multivariate signals defined from
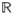 to
to
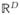 with D > 1 is difficult due to the definition of the mean operator
with D > 1 is difficult due to the definition of the mean operator
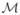 . Some recent work tried to overcome this limitation. The bivariate approaches developed in [7], [8] are extensions of Huang’s solution to specifically handle complex-valued signals whereas the algorithm proposed in [9] makes use of quaternion to perform trivariate decompositions. Regarding the geometrical algorithms proposed in [10], they allow us to process bivariate signals. Indeed in [10], Rilling’s algorithm corresponding to the second scheme (called Rilling2 method in the sequel) especially computes a bivariate mean envelope by projecting the signal on different angular planes and by performing a monovariate EMD of each signal projection. Very recently, Rehman et al. [11] proposed a generalization of Rilling’s approach, called Rehman in the sequel, to any multivariate signal: the mean envelope is obtained by averaging multiple signal projections on a regularly sampled hypersphere.
. Some recent work tried to overcome this limitation. The bivariate approaches developed in [7], [8] are extensions of Huang’s solution to specifically handle complex-valued signals whereas the algorithm proposed in [9] makes use of quaternion to perform trivariate decompositions. Regarding the geometrical algorithms proposed in [10], they allow us to process bivariate signals. Indeed in [10], Rilling’s algorithm corresponding to the second scheme (called Rilling2 method in the sequel) especially computes a bivariate mean envelope by projecting the signal on different angular planes and by performing a monovariate EMD of each signal projection. Very recently, Rehman et al. [11] proposed a generalization of Rilling’s approach, called Rehman in the sequel, to any multivariate signal: the mean envelope is obtained by averaging multiple signal projections on a regularly sampled hypersphere.
This paper aims at proposing an alternative to Rehman’s algorithm [11] and at unifying mono- and multivariate EMD to process signals with values in
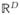 (D ≥ 1) whatever the dimension D is. The proposed method, called 2T-EMD (Turning Tangent EMD), differs by its computational lightness and its algorithmic simplicity. This method is essentially based on a redefinition of the signal mean envelope computed thanks to new characteristic points, which are also defined for D > 1. The scope of application of the novel algorithm is discussed, and a comparison of the 2T-EMD technique with classical methods is performed on various simulated mono- and multivariate signals. The monovariate behavior of the proposed method on noisy signals is then validated by decomposing fractional Gaussian noises [3] and an application to surface EEG signal denoising is finally presented.
(D ≥ 1) whatever the dimension D is. The proposed method, called 2T-EMD (Turning Tangent EMD), differs by its computational lightness and its algorithmic simplicity. This method is essentially based on a redefinition of the signal mean envelope computed thanks to new characteristic points, which are also defined for D > 1. The scope of application of the novel algorithm is discussed, and a comparison of the 2T-EMD technique with classical methods is performed on various simulated mono- and multivariate signals. The monovariate behavior of the proposed method on noisy signals is then validated by decomposing fractional Gaussian noises [3] and an application to surface EEG signal denoising is finally presented.
II. The 2T-EMD approach for both mono- and multivariate signals
In order to get a unified framework for mono- and multivariate EMD [12], the signal mean trend and consequently the mean operator
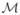 have to be redefined. In some words, the signal mean trend is redefined as the signal which interpolates the barycenters of particular oscillations, called elementary oscillations hereafter.
have to be redefined. In some words, the signal mean trend is redefined as the signal which interpolates the barycenters of particular oscillations, called elementary oscillations hereafter.
A. Elementary oscillations and barycenters
An elementary oscillation of a given function s with values in
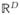 (D≥1) can be viewed as a piece of s defined between two consecutive local extrema of s. But, for functions with values in a D-dimensional (D > 1) space, the notion of extremum has to be defined.
(D≥1) can be viewed as a piece of s defined between two consecutive local extrema of s. But, for functions with values in a D-dimensional (D > 1) space, the notion of extremum has to be defined.
Let s be a class
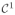 function, say differentiable with a continuous first derivative. The function tangent vector to s, denoted by Ts, is defined from
function, say differentiable with a continuous first derivative. The function tangent vector to s, denoted by Ts, is defined from
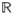 to
to
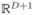 by:
by:
| (1) |
Now, let αs be the function given by:
| (2) |
For every t in
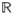 , the value αs(t) can be interpreted as the Euclidean inner product of
, the value αs(t) can be interpreted as the Euclidean inner product of
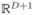 , denoted by 〈·, ·〉, between the tangents to s just before and after point t. In fact, αs is maximum at point t when both vectors Ts(t−h) and Ts(t+h) are collinear and it vanishes at point t when both vectors are orthogonal. In other words, function αs is an indicator of the local oscillation of s at every point of
, denoted by 〈·, ·〉, between the tangents to s just before and after point t. In fact, αs is maximum at point t when both vectors Ts(t−h) and Ts(t+h) are collinear and it vanishes at point t when both vectors are orthogonal. In other words, function αs is an indicator of the local oscillation of s at every point of
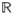 . Moreover, due to the continuity of the inner product, we have:
. Moreover, due to the continuity of the inner product, we have:
| (3) |
Next, since s is in
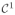 , we get:
, we get:
| (4) |
where || . || abusively represents the Euclidean norm of both
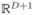 and
and
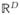 . Thus, we define an oscillation extremum of function s as a local minimum of function αs. From (4), it also corresponds to a local minimum of the following function:
. Thus, we define an oscillation extremum of function s as a local minimum of function αs. From (4), it also corresponds to a local minimum of the following function:
| (5) |
Clearly, the definition of oscillation extremum does not depend on the output space dimension D, which makes it suitable in multivariate EMD contexts. For D=1, the reader can check that the oscillation extrema computed from function βs (5) include the classical scalar extrema used in Huang’s solution [1], but also the saddle points (stationary points which are not local extrema) of s and the inflexion points corresponding to positive and negative maxima of the derivative of s. It is noteworthy that oscillation extrema are different of inflexion [13] and curvature [14] extrema. In addition, curvature extrema may require the computation of the second and third derivatives of s, respectively, which may be more sensitive to sampling frequency. Moreover, neither inflexion points nor curvature extrema are defined for multivariate signals, say signals from
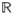 to
to
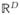 with D>1, hence our preference goes to oscillation extrema.
with D>1, hence our preference goes to oscillation extrema.
So an elementary oscillation of a given function s with values in
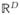 (D≥1) is considered in this paper as a piece of s defined between two consecutive oscillation extrema of s. Let P1 =[t1, s(t1)]⊤ and P2 =[t2, s(t2)]⊤ be two consecutive oscillation extrema. The barycenter, MP1→P2, of the associated elementary oscillation is given by:
(D≥1) is considered in this paper as a piece of s defined between two consecutive oscillation extrema of s. Let P1 =[t1, s(t1)]⊤ and P2 =[t2, s(t2)]⊤ be two consecutive oscillation extrema. The barycenter, MP1→P2, of the associated elementary oscillation is given by:
| (6) |
The mean trend
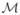 (s) could then be redefined as the function which interpolates between oscillation barycenters of s. Nevertheless, a straightforward interpolation of all oscillation barycenters of s appears in practice to significantly emphasize the phenomena of over-decomposition of AM-FM signals. A robust computation of the mean trend is preferably obtained for 2T-EMD by averaging two envelopes: a first envelope interpolates the even indexed barycenters which include signal borders, and a second envelope interpolates the odd indexed barycenters which also include signal borders. This operation lightly increases the algorithm computational complexity (see subsection II-D for more details) but makes its behavior considerably more robust.
(s) could then be redefined as the function which interpolates between oscillation barycenters of s. Nevertheless, a straightforward interpolation of all oscillation barycenters of s appears in practice to significantly emphasize the phenomena of over-decomposition of AM-FM signals. A robust computation of the mean trend is preferably obtained for 2T-EMD by averaging two envelopes: a first envelope interpolates the even indexed barycenters which include signal borders, and a second envelope interpolates the odd indexed barycenters which also include signal borders. This operation lightly increases the algorithm computational complexity (see subsection II-D for more details) but makes its behavior considerably more robust.
Indeed, this robustness may be roughly justified in a monodimensional context. The spline interpolation typically behaves as a linear filter (up to some border effects) whose frequency response I(f), for unit spaced knots, slowly decreases in the interval f ∈ [0, 1] and approximately vanishes when f > 1 [15]. Let’s consider now a narrowband AM-FM signal whose carrier frequency is fc. If the modulation is not too strong, the typical spacing between oscillation barycenters for such a signal is 1/(2fc). In the case of a direct interpolation between oscillation barycenters, the spline interpolation could then have a non-negligible content for f ∈ [0, 2fc], which includes fc and therefore allows the interpolation to oscillate at the same frequency as the AM-FM signal. On the other hand, the use of two interleaved spline interpolations leads to a frequency content typically limited to f < fc, which approximately guarantees that the resulting mean trend oscillates more slowly than the initial AM-FM signal. Therefore, the use of two envelopes prevents from over-decomposition phenomena and also has the advantage to bring the frequency resolution of the proposed method on a par with the traditional EMD approaches (for signals with simple waveforms). It finally approximately guarantees that the local frequency of successive IMFs decreases. Those remarks seem to be also empirically verified (see section 2) in a multivariate context.
Consequently, the resulting mean operator
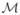 enjoys a frequency property similar to that of the classical one but can be applied to both mono- and multivariate signals without any dimension restriction.
enjoys a frequency property similar to that of the classical one but can be applied to both mono- and multivariate signals without any dimension restriction.
B. Implementation of the 2T-EMD technique
Several important points have to be considered to achieve a robust and efficient implementation of the 2T-EMD algorithm. First, the derivative necessary to the computation of
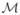 (s) is calculated by means of a centered finite difference scheme. However, in practice the resulting numerical derivative may have more local minima than the theoretical one. Minima are thus detected using an ε precision equal to 10−15 in our code. More precisely, the i-th time index ti will be a minimum of βs if βs(ti) + ε≤ βs(ti−1) and βs(ti) + ε≤ βs(ti+1). Therefore, this ε precision limits the influence of numerical artifacts for the extrema detection but one should be careful and adjust the ε value in the case of very high sampling frequency to avoid the miss of legitimate extrema. The integral involved in the computation of barycenters is then calculated using a simple rectangle method. Second, the interpolation is performed using cubic splines with classical boundary conditions as for the classical EMD, where the signal borders are directly added to the list of estimated oscillation barycenters. In other words, there is no complex management of boundary conditions. Third, the sifting process is stopped using a modified Cauchy-like criterion. More especially, the following normalized Euclidean norm ||dn,k+1(t) − dn,k(t)||/||dn,k(t)|| is computed at each point t. If a given percentage of the latter norms, for instance 90%, is below a certain threshold fixed to 10−2 in our code, then the sifting process is stopped. The normalized Euclidean norm could be obviously not defined for dn,k(t) = 0 but the set of points where this zero value is reached is likely to have a zero Lebesgue measure which justifies in practice the use of such a criterion.
(s) is calculated by means of a centered finite difference scheme. However, in practice the resulting numerical derivative may have more local minima than the theoretical one. Minima are thus detected using an ε precision equal to 10−15 in our code. More precisely, the i-th time index ti will be a minimum of βs if βs(ti) + ε≤ βs(ti−1) and βs(ti) + ε≤ βs(ti+1). Therefore, this ε precision limits the influence of numerical artifacts for the extrema detection but one should be careful and adjust the ε value in the case of very high sampling frequency to avoid the miss of legitimate extrema. The integral involved in the computation of barycenters is then calculated using a simple rectangle method. Second, the interpolation is performed using cubic splines with classical boundary conditions as for the classical EMD, where the signal borders are directly added to the list of estimated oscillation barycenters. In other words, there is no complex management of boundary conditions. Third, the sifting process is stopped using a modified Cauchy-like criterion. More especially, the following normalized Euclidean norm ||dn,k+1(t) − dn,k(t)||/||dn,k(t)|| is computed at each point t. If a given percentage of the latter norms, for instance 90%, is below a certain threshold fixed to 10−2 in our code, then the sifting process is stopped. The normalized Euclidean norm could be obviously not defined for dn,k(t) = 0 but the set of points where this zero value is reached is likely to have a zero Lebesgue measure which justifies in practice the use of such a criterion.
C. Scope of application
Let’s now specify in more details the set of signals that 2T-EMD can decompose successfully. As previously mentioned, the considered signals have to be in class
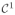 or at least, in the case of irregular signals (especially real and/or noisy signals), an appropriate numerical estimation of the derivative has then to be proposed (see section II-B). Note that some existing methods based on inflexion [13] or curvature [14] extrema require more regularity. In addition, if {dn}1≤n≤N represents the theoretical set of IMFs composing the signal to analyze, it is obvious that any dn with a piecewise constant function βdn (5) is not visible by 2T-EMD (assuming that the definition of derivative is extended to irregular signal as mentioned before). Indeed a piecewise constant function has no ε-local minimum. Thus, any signal in class
or at least, in the case of irregular signals (especially real and/or noisy signals), an appropriate numerical estimation of the derivative has then to be proposed (see section II-B). Note that some existing methods based on inflexion [13] or curvature [14] extrema require more regularity. In addition, if {dn}1≤n≤N represents the theoretical set of IMFs composing the signal to analyze, it is obvious that any dn with a piecewise constant function βdn (5) is not visible by 2T-EMD (assuming that the definition of derivative is extended to irregular signal as mentioned before). Indeed a piecewise constant function has no ε-local minimum. Thus, any signal in class
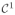 having one IMF with a piecewise constant derivative norm cannot be properly decomposed by 2T-EMD. It mainly concerns monovariate signals with piecewise linear IMFs, and bivariate signals with purely circular rotating IMFs. Nevertheless, any bivariate rotating signal with a sufficient eccentricity can be decomposed by 2T-EMD.
having one IMF with a piecewise constant derivative norm cannot be properly decomposed by 2T-EMD. It mainly concerns monovariate signals with piecewise linear IMFs, and bivariate signals with purely circular rotating IMFs. Nevertheless, any bivariate rotating signal with a sufficient eccentricity can be decomposed by 2T-EMD.
D. Note on computational complexity
The computational complexity of the 2T-EMD algorithm can be precisely evaluated and compared with the one of classical methods. For a given EMD algorithm, let N, Kn, dn,k be the number of extracted IMFs, the number of sifting iterations performed to extract the n-th IMF and the n-th IMF computed at the k-th iteration of the sifting process, respectively. In addition, MH(n, k), MR(n, k, p), MRM(n, k, p), and M2T(dn,k) will denote the number of extrema detected in dn,k by Huang [1], the number of extrema detected in the p-th projection of dn,k by Rilling2 [10] when P projection planes are used, the number of extrema detected in the p-th projection of dn,k by Rehman [11] when P projection directions are used, and the number of barycenters detected in dn,k by 2T-EMD. Then the number F(dn,k+1) of multiplications and divisions (usually called number of flops) of one sifting iteration necessary to obtain dn,k+1 from dn,k is given in table I for the four methods. These results were obtained by considering a standard tridiagonal implementation of the spline interpolation and a signal from
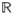 to
to
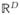 of L samples. The total computational cost, C(s), of the four methods can be obtained straightforwardly by summing the elementary complexities, F(dn,k), given in table I over both the number of iterations and the number of IMFs.
of L samples. The total computational cost, C(s), of the four methods can be obtained straightforwardly by summing the elementary complexities, F(dn,k), given in table I over both the number of iterations and the number of IMFs.
TABLE I.
Computational complexity for one sifting iteration of 2T-EMD and three classical methods.
III. Simulation results
The aim of this section is to analyze the performance of 2T-EMD on several classes of simulated mono- and multivariate signals satisfying the conditions given in subsection II-C. First the stability and the convergence speed of 2T-EMD sifting process are studied and compared with three classical methods: i) Huang [1] for monovariate signals (D = 1), ii) Rilling2 [10] using P = 8 projection planes for bivariate signals (D = 2) and iii) Rehman [11] for trivariate and quadrivariate signals using P = 2D projection directions on the associated hypersphere. From an implementation point of view, the sifting process termination criterion and the border management of those classical techniques are identical to the ones used in 2T-EMD (see subsection II-B for more details). Secondly, a benchmark involving those classical EMD algorithms is presented to evaluate and compare the 2T-EMD performance in the context of a full decomposition. Finally, an example of quadrivariate decomposition illustrates the ability of 2T-EMD to work for a signal dimension greater than 3. First, let’s introduce the signal selection and the performance criteria used in this section.
A. Signals selection
The test signals are mono-, bi-, tri- and quadrivariate signals with various AM-FM behaviors, defined on the time interval T = [−1, 2] and sampled at fs = 10 kHz.
Monovariate signals
Four monovariate signals of the form are used in this study where is the n-th IMF of s1i. The first signal is defined by:
The second signal is given by:
The third signal (a(13) represents a residue) is defined by:
Eventually, the fourth signal with a residue a(14) is given by:
More particularly, signal s11 is the sum of two sinusoidal components. Next s12 is the sum of two sinusoidal components modulated in amplitude (from 1 to 2 on interval T) with extrema of oscillation that do not match with classical extrema. As far as s13 is concerned, it is the sum of one FM component (from 200 to 400 Hz on interval [0, 1]), one linear AM component and a quadratic residue. Eventually s14 is the sum of one sinusoidal component, one FM component (from 10 to 20 Hz on interval T), one AM (from 1 to 2 on interval T) - FM (from 50 to 70 Hz on interval T) component and a linear residue.
Bivariate signals
Four bivariate signals of the form are used in this analysis where is the n-th IMF of s2i. The first signal is given by:
The second signal is defined by:
The third signal is given by:
The fourth signal is given by:
In fact, signals s21, s23 and s24 are globally rotating signals with various AM and FM modulations. Regarding the conditions addressed in subsection II-C the latter signals have a large enough eccentricity to be processed by 2T-EMD. As far as signal s22 is concerned, it is the result of planar components after a rotation around the temporal axis.
Trivariate signal
One trivariate signal is used for comparison and is defined by:
where and denote the three AM-FM IMFs of signal s31.
Quadrivariate signal
The quadrivariate signal used to show the efficiency of the approach in higher dimensions is given by:
where and denote the three AM-FM IMFs of signal s41.
B. Performance criteria
The different EMD algorithms analyzed in this section have been evaluated and compared in terms of performance and numerical complexity. Given I a subinterval of T = [−1, 2], let’s define the following quadratic errors:
| (7) |
where d̂n denotes the estimate of the n-th IMF dn of signal s. The latter errors allow us to evaluate the ability of the EMD algorithms to accurately extract one or all expected IMFs. By considering I = [0, 1] where border effects should be low, both errors allow us to compute a performance independent of any border effects. On the contrary, with I = [−1, 0] ∪ [1, 2], both errors permit to evaluate the ability of a given algorithm to minimize border effects (all algorithms have the same border management in our study). Indeed, such effects are often critical especially in real life data and their minimization should facilitate the practical exploitation of the IMFs. Eventually, the numerical complexity of an EMD method is evaluated using the criterion C(s) presented in section II-D.
C. Sifting process analysis
In this first experiment, 2T-EMD’s sifting process is studied and compared to that of Huang, Rilling2 and Rehman in terms of convergence. To do so, the sifting process is launched for 100 iterations to extract the first IMF of all monovariate and multivariate signals presented in section III-A. Figure 1 displays criterion e[0,1](d1) at the output of 2T-EMD, Huang, Rilling2 and Rehman as a function of the number of iterations of the sifting process. On each curve, a circular-shaped marker indicates the iteration for which the Cauchy-like sifting stop criterion would have in practice interrupted the sifting process. First, one can observe that the sifting process of 2T-EMD converges for almost all monovariate and bivariate test signals with precision and speed very similar to those obtained by the considered classical algorithms. The proposed algorithm even succeeds in extracting the first component of signal s12 whereas the standard Huang algorithm failed in such a decomposition. Except for the multivariate signals s24 and s41, this simulation tends to show the stability of the proposed algorithm during a sifting process. The signal s24 with four IMFs including especially two FM components seems to suffer from over-decomposition. It is noteworthy that this sensitivity is also observed in Rilling2 and may especially suggest that the first component is not considered as an IMF by both algorithms. Regarding the signal s41, Rehman seems to be less sensitive to over-decomposition phenomenon than 2T-EMD. However, for all proposed signals, including signals s24 and s41, the sifting stop criterion prevents from any over-decomposition phenomenon by stopping the sifting process at an appropriate optimal iteration. In addition, note that the quadratic error e[0,1](d1) at marker points is satisfactory for all studied signals (the maximum error encountered in this simulation is equal to 0.02) and is, globally, comparable to the one obtained by the classical algorithms.
Fig. 1.
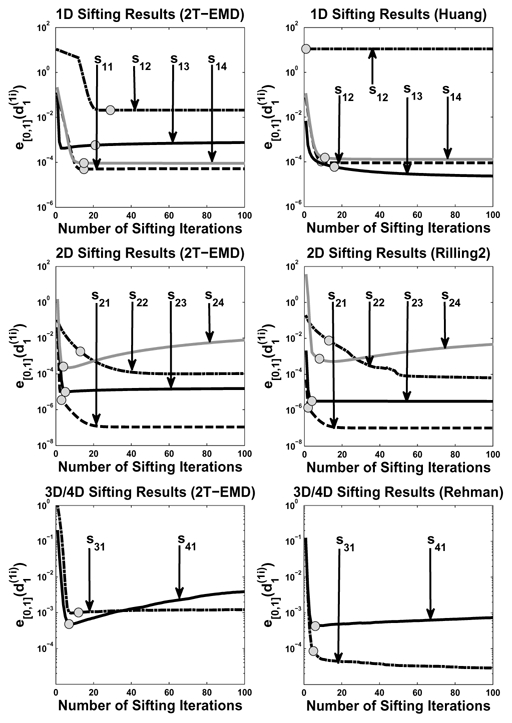
2T-EMD quadratic error on first IMF as a function of the number of iterations during the sifting process.
D. Performance study of the full process
This subsection aims at comparing the full process of 2T-EMD for D ∈ {1, 2, 3, 4} with Huang, Rilling2 and Rehman using criteria e[0,1](s) and e[−1,0]∪[1,2](s) and C(s). Results are depicted in figure 2: the left, middle and right columns deal with the monovariate, bivariate and multivariate (D ∈ {3, 4}) cases, respectively. It appears that for no border effects both performance and computational complexity of 2T-EMD are globally equivalent to those of the reference methods. More finely and as specified previously, in the monovariate case, signal s12 with extrema of oscillation which differ from the standard extrema, is better decomposed by our approach. On the contrary, the signal s13 with a first fast FM IMF seems to be better processed by Huang. In the bivariate case, Rilling2 seems to offer a better performance on the nearly pure rotating signal s21 but 2T-EMD is more efficient on signal s22 made of rotated planar components. For signals s31 and s41, the behaviors of 2T-EMD and Rehman are quasi-similar. Regarding border effects on performance, 2T-EMD generally offers slightly more efficient results and seems to provide a more accurate management of border effects than reference approaches. When focusing on the computational complexity, figure 2 clearly shows that for D = 1 the computational complexities of 2T-EMD and Huang are quasi-equivalent. On the contrary, for D = 2, 2T-EMD generally requires less sifting iterations and less computational operations than Rilling2. For D > 2, the results clearly show the computational efficiency of 2T-EMD, which is about three times cheaper than Rehman. From a more illustrative point of view, figure 3(a) represents the quadrivariate signal s41 (dark line) and the associated local mean (gray line) on the restricted [0.50; 0.52] time interval projected on the three frames (W,X, Y), (X, Y,Z) and (Y,Z,W). The local mean seems to nicely go through the original signal on the three frames. Figure 3(b) presents the expected and computed decompositions of signal s41 projected on the four main axis (from left to right), namely W, X, Y and Z. The three IMFs and the corresponding residue are displayed from the top to the bottom of the figure. Note that only a central zoom of the IMFs on the temporal axis has been represented for the sake of clarity. A good behavior of the algorithm can be observed and the low residue highlights the efficiency of the proposed method. This result shows clearly that, for signal s41, the sifting stop criterion prevents from any over-decomposition phenomenon.
Fig. 2.
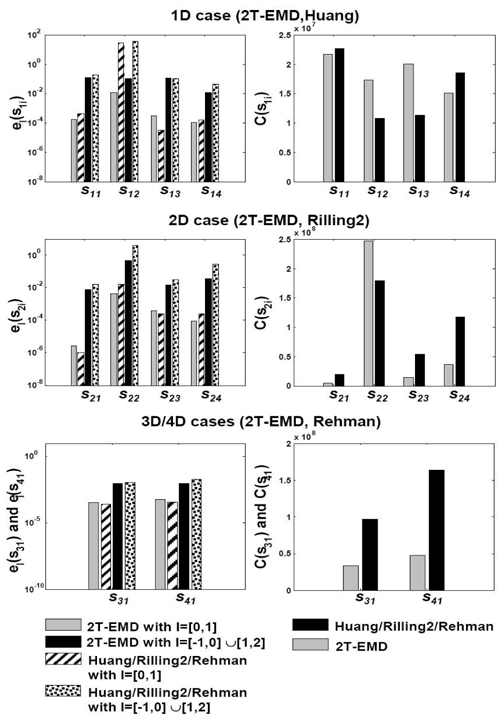
Comparative study of 2T-EMD versus Huang (1D), Rilling2 (2D) and Rehman (3D, 4D) reference methods.
Fig. 3.
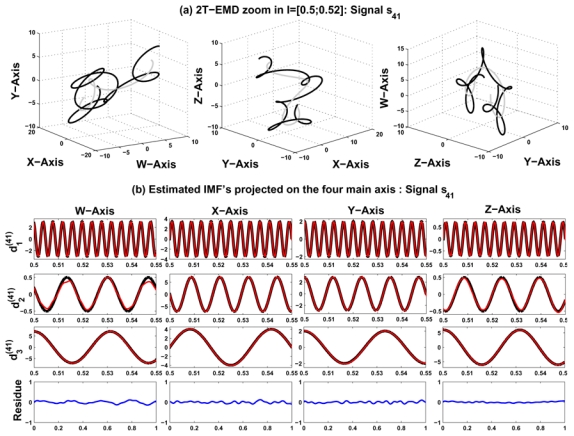
2T-EMD quadrivariate decomposition of the signal s41: (a) original signal (dark) and its 2T-EMD local mean (gray), and (b) exact (dashed line) and estimated (plain line) IMFs projected on the four main axis W, X, Y and Z.
In conclusion, all these results exhibit the ability of 2T-EMD to process signals with values in
 for any dimension D ≥ 1. They also show the advantage of the use of oscillation barycenters in a general multivariate context.
for any dimension D ≥ 1. They also show the advantage of the use of oscillation barycenters in a general multivariate context.
IV. Decomposition of fractional Gaussian noise
One important property, enjoyed by the classical Huang algorithm, is the filter bank property observed when decomposing a fractional Gaussian noise (fGn). This section aims at demonstrating how the 2T-EMD algorithm also enjoys this filter bank property by reproducing simulations and results already obtained in previous works with the standard Huang’s algorithm [16], [3]. Note that computing 2T-EMD on such a noisy signal may be feasible using an adapted definition of the derivative (see II-B). As in [3], extensive simulations are carried out on fGn’s, with Hurst coefficient H varying from 0.1 to 0.9. The data length is typically set to 512 and for each value of H, 1000 independent sample paths of fGn are generated via the algorithm described in [17] and decomposed using 2T-EMD on a limited number of 7 IMFs (it should be mentioned that the sifting process is stopped when 90% of values ||dn,k+1(t) − dn,k(t)||/||dn,k(t)|| are lower than 10−2, see section II-B). For each value of H, the number of zero-crossings zH[n] in the n-th mode (1 ≤ n ≤ 7) is firstly evaluated. A linear regression of the mean log number of zero-crossings log(zH[n]) on the mode number n is then computed. The good fitness of such a regression, represented in the left column of figure 4 for each value of H, strongly suggests that the number of zero-crossings zH[n], which is a rough indication of the mean frequency of each mode n, is a decreasing exponential function of the mode number, i.e., with ρH close to 2. These results are very similar to those obtained in [3, figure 2] and suggest the hierarchical structure of an equivalent filter bank as shown in [3] and [16] for the classical EMD. For all IMFs dn (with n > 1), a self-similarity in this filter-bank could also be further checked showing that 2T-EMD approximately acts on fGn as a dyadic filter bank of constant-Q bandpass filters for high values of H (H ≥ 0.5). Assuming this filter bank structure, and as shown in [3] for the classical EMD, it becomes possible to get access to the Hurst exponent via the variance progression across IMFs by with the specific choice α = 2H − 1. When plotted as a function of the Hurst exponent H, the IMF log-variance slope is almost linear when H ≥ 0.5, in accordance with the simplified model p(H) = 2log(ρH)(H − 1) as depicted in the right column of figure 4. Those results consequently highlight the very similar properties shared by 2T-EMD and Huang ([3, figure 4]), and may validate the use of the proposed algorithm on irregular signals.
Fig. 4.
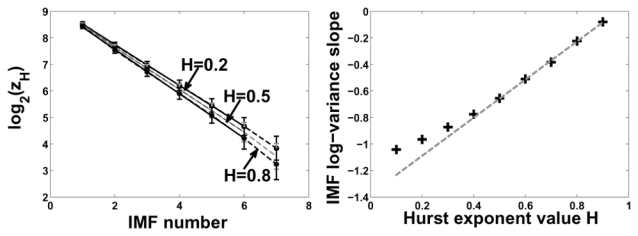
2T-EMD applied to fGn decompositions. At the left, IMF zero-crossings: the (base 2) logarithm of the average number of zero-crossings is plotted as a function of the IMF number, for 3 different values of the Hurst exponent (H: 0.2 (circles), 0.5 (crosses), and 0.8 (stars)). At the right, IMF variance and estimation of the Hurst exponent H: the IMF log-variance slope plotted as a function of the Hurst exponent H and the associated linear regression over 0.5 ≤ H ≤ 0.9.
V. Application to surface EEG denoising
Surface ElectroEncephaloGraphy (EEG) is a popular neuroimaging technique used for exploring human brain activity. While this technique is simple and low cost, the obtained signals suffer from noise and artifacts, such as broken wire contacts, ocular movements (ElectroOculoGram, EOG), muscular activity, etc. Thus, one of the challenging tasks in signal processing is to detect and extract very weak non-stationary brain source signals corrupted by noise and artifacts from EEG data. Such issues are of great interest when EEG features are used for diagnosis and assistance [18]. Some recent studies show that the use of classical EMD [1] in order to denoise EEG data [19], [20] and/or to detect some EEG patterns [21], give interesting results. In this section, we propose to remove EOG artifacts from contaminated EEG data by using the proposed 2T-EMD algorithm. Note that, the goal here is not to propose a new method in order to denoise the surface EEG data, but to show the behavior of 2T-EMD, in comparison to that of the existing EMD method, in the case of real world signals. The used EEG signals are issued from our polysomnographic database [22]. More precisely, EEG signals (figure 5, line 1) are acquired from two temporal electrodes, in front of the higher part of the ears, denoted by F7m and F8m (where “m” stands for modified, see [22] for more details). Additionally, EOG reference recordings (figure 5, line 6) are taken from two temporal sensors located near each eye (EOGL and EOGR), slightly moved toward the median plan in order to simultaneously observe horizontal and vertical eye movements.
Fig. 5.
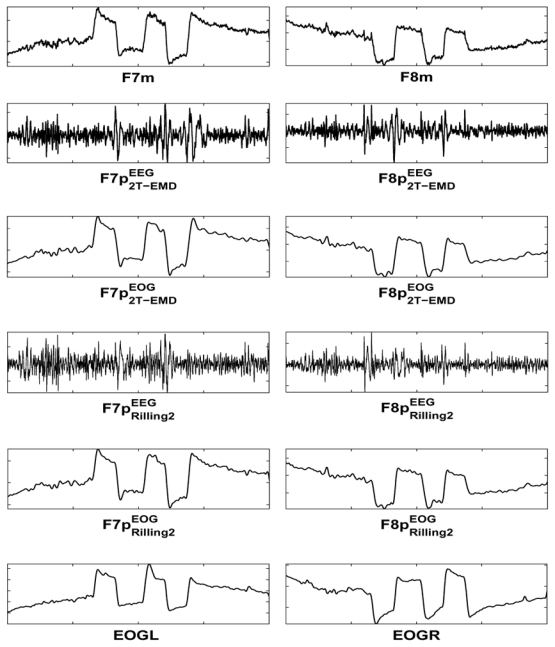
Comparison between the bivariate 2T-EMD approach and Rilling2 in the context of EOG artifacts removing from EEG.
Rilling2 and the bivariate 2T-EMD method are then applied with a limited number of 10 IMFs, for each bivariate observation [F7m,F8m] and [EOGL,EOGR], respectively. The obtained bivariate results are then projected on two main axis (left head side and right head side), namely F7p and F8p for EEG data and EOGLp and EOGRp in the case of EOG data (“p” stands for projected). In order to identify the projected IMFs related to the EOG artifacts in the bivariate EEG observation [F7m,F8m], we firstly compute the Fourier transform of all projected IMFs extracted from the two bivariate observations ([F7m,F8m] and [EOGR,EOGL]) [19]. Then, for each bivariate method and each brain hemisphere (F7p/EOGLp on the left side and F8p/EOGRp on the right side), i) one-minus-correlation distance is computed for between projected IMFs in order to evaluate any spectral similarity between the IMFs issued from EEG signals [F7m,F8m] and EOG reference signals [EOGR,EOGL], and ii) the distances are hierarchically clustered using the single linkage algorithm [21]. It is noteworthy that, the clustering procedure first treats the power spectrum vector of each projected IMF as a singleton cluster and then successively aggregates both most similar clusters, until all clusters merge into a single cluster that contains the power spectrum vectors of all projected IMFs. For each method and for each projected plan, the set of IMFs for which the distances (one-minus-correlation) below 0.2 are considered as similar and originate from EOG artifacts. The sum of those IMFs [ ] are then compared in figure 5 to the EOG reference recordings [EOGL,EOGR]. The channels of the EOG signal estimated by 2T-EMD (line3) and Rilling2 (line 5) are quasi-identical and they are strongly correlated to EOGL and EOGR (correlation coefficients greater than 0.92). This high correlation is also observed between the residual high-frequency channels (associated to EEG activity in our case) obtained by 2T-EMD method, [ ], and those recovered by Rilling2 namely, [ ]. All these results tend to show that 2T-EMD has similar behavior in comparison to classical EMD algorithms [3] in the case of real world data. In addition, they demonstrate that the 2T-EMD technique which takes advantage of the mutual-information contained in the two signals, preserves the frequency information of each channel.
VI. Conclusion and perspectives
A novel approach for EMD computation is proposed in this paper. The algorithm called 2T-EMD is mainly based on a new geometric definition of the mean envelope operator. Under certain assumptions on signals, this novel definition enables both mono- and multivariate decompositions without any modification in the 2T-EMD algorithm, without any signal projection and with light computational cost. These two last points are the key benefits regarding the existing approaches of the literature. Details to obtain a robust implementation of 2T-EMD have been listed and justified. In addition, simulations and comparisons performed in this work suggest that 2T-EMD seems to offer a satisfactory convergence during the sifting step and a good robustness to over-decomposition. Competitive performance and computational complexities plus a good border management also characterize 2T-EMD. Simulations on noisy signals and an application to real data show that the proposed algorithm has quasi-identical behavior in comparison with classical EMD algorithms and demonstrate the interest of 2T-EMD in practical situations. Conditions that signals should verify to be successfully decomposed by 2T-EMD have been precisely enumerated in order to help the user. It would be now more particularly interesting to evaluate the performance of 2T-EMD in other real life contexts for which classical EMD approaches have already demonstrated interesting properties and to compare it with that of other techniques [18].
Acknowledgments
We would like to thank all anonymous reviewers for their valuable and constructive comments for improving the quality of the paper. This work was supported by the French Government under an ANR contract, namely mv-EMD (BLAN07-0314-02).
This work was supported by the National Research Agengy (ANR) of France under Grant mv-EMD BLAN07-0314-02.
References
- 1.HUANG N, SHEN Z, LONG S, WU M, SHIH H, ZHENG Q, YEN N-C, TUNG C, LIU H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London, Series A. 1998 [Google Scholar]
- 2.HUALOU L, QIU-HUA L, CHEN J. Application of the empirical mode decomposition to the analysis of esophageal manometric data in gastroesophageal reflux disease. IEEE Transactions on Biomedical Engineering. 2005;52(10):620–623. doi: 10.1109/TBME.2005.855719. [DOI] [PubMed] [Google Scholar]
- 3.RILLING G, FLANDRIN P, GONCALVES P. Empirical mode decomposition, fractional Gaussian noise and Hurst exponent estimation. IEEE International Conference on Acoustics, Speech, and Signal Processing. 2005;4:489–492. [Google Scholar]
- 4.CHATLANI N, SORAGHAN J. EMD-based noise estimation and tracking (ENET) with application to speech enhancement. 17th European Signal Processing Conference (EUSIPCO); Glasgow, Scotland. August 24–28 2009.pp. 180–184. [Google Scholar]
- 5.NUNES JC, GUYOT S, DELECHELLE E. Texture analysis based on local analysis of the bidimensional empirical mode decomposition. Journal of Machine Vision and Applications. 2005;16(3):177–188. [Google Scholar]
- 6.RILLING G, FLANDRIN P, GONCALVES P. On empirical mode decomposition and its algorithms. IEEE EURASIP Workshop Nonlinear Signal Image Processing; Grado, Italy. 2003. [Google Scholar]
- 7.TANAKA T, MANDIC D. Complex empirical mode decomposition. IEEE Signal Processing Letters. 2007;14(2):101–104. [Google Scholar]
- 8.BIN ALTAF M, GAUTAMA M, TANAKA T, MANDIC DP. Rotation invariant complex empirical mode decomposition. IEEE International Conference on Acoustics, Speech and Signal Processing. 2007;3:III-1009–III-1012. [Google Scholar]
- 9.REHMAN N, MANDIC DP. Empirical Mode decomposition for trivariate signals. IEEE Transactions on Signal Processing. 2010;58(3):1059–1068. [Google Scholar]
- 10.RILLING G, FLANDRIN P, GONCALVES P, LILLY J. Bivariate empirical mode decomposition. IEEE Signal Processing Letters. 2007;14(12):1–10. [Google Scholar]
- 11.REHMAN N, MANDIC DP. Multivariate empirical mode decomposition. Proceedings of the Royal Society of London, Series A. 2010;466(2117):1291–1302. [Google Scholar]
- 12.FLEUREAU J, KACHENOURA A, NUNES JC, ALBERA L, SENHADJI L. 3A-EMD: a generalized approach for monovariate and multivariate EMD. Proceedings of the 10th International Conference on Information Sciences, Signal Processing and their Applications; Kuala Lumpur, Malaysia. May 10–13 2010.pp. 300–303. [Google Scholar]
- 13.DELECHELLE E, LEMOINE J, NIANG O. Empirical mode decomposition: an analytical approach for sifting process. IEEE Signal Processing Letters. 2005;12(11):764–767. [Google Scholar]
- 14.NIANG O. PhD of University of Paris XII. France: Sep, 2007. Décomposition modale empirique: contribution à la modélisation mathématique et application en traitement du signal et de l’image. [Google Scholar]
- 15.UNSER M. Splines: A perfect fit for signal processing. IEEE Signal Processing Magazine. 1999;16(6):22–38. [Google Scholar]
- 16.WU Z, HUANG NE. A study of the characteristics of white noise using the empirical mode decomposition method. Proceedings of the Royal Society of London, Series A. 2004;460(2046):1597–1611. [Google Scholar]
- 17.PERRIN E, HARBA R, JENNANE R, IRIBARREN I. Synthèse exacte et efficace du mouvement brownien fractionnaire 1D. 18ème Colloque sur le traitement du signal et des images (GRETSI); 2001. pp. 797–800. [Google Scholar]
- 18.KACHENOURA A, ALBERA L, SENHADJI L, COMON P. ICA: a potential tool for BCI systems. IEEE Signal Processing Magazine. 2008;25(1):57–68. [Google Scholar]
- 19.RUTKOWSKI TM, CICHOCKI A, TANAKA T, RALESCU AL, MANDIC DP. Clustering of spectral patterns based on EMD components of EEG channels with applications to neurophysiological signals separation. Proceedings of the 15th international conference on Advances in neuro-information processing; 2009. pp. 453–460. [Google Scholar]
- 20.MOLLA MKI, TANAKA T, RUTKOWSKI TM, CICHOCKI A. Separation of EOG artifacts from EEG signals using bivariate EMD. IEEE International Conference on Acoustics, Speech and Signal Processing; 2010. pp. 562–565. [Google Scholar]
- 21.RUTKOWSKI TM, MANDIC DP, CICHOCKI A, PRZYBYSZEWSKI AW. EMD approach to multichannel EEG data - the amplitude and phase components clustering analysis. Journal of Circuits, Systems, and Computers. 2010;19(1):215–229. [Google Scholar]
- 22.POREE F, KACHENOURA A, GAUVRIT H, MORVAN C, CARRAULT G, SENHADJI L. Blind source separation for ambulatory sleep recording. IEEE Transactions on Information Technology in Biomedicine. 2006;10(2):293–301. doi: 10.1109/TITB.2005.859878. [DOI] [PMC free article] [PubMed] [Google Scholar]


