Abstract
Dynamic contrast enhanced MRI (DCE-MRI) involves the acquisition of images before, during, and after the injection of a contrast agent (CA). In order to perform quantitative modeling on the resulting signal intensity time course, data must be acquired rapidly, which compromises spatial resolution, signal-to-noise, and/or field of view. One approach that may allow for gains in temporal or spatial resolution or signal-to-noise of an individual image is to use compressed sensing (CS) MRI. In this study, we demonstrate the accuracy of extracted pharmacokinetic parameters from DCE-MRI data obtained as part of pre-clinical and clinical studies in which fully sampled acquisitions have been retrospectively undersampled by factors of 2, 3, and 4 in Fourier space and then reconstructed with CS. The mean voxel-level concordance correlation coefficient for Ktrans (i.e., the volume transfer constant) obtained from the 2× accelerated and the fully sampled data is 0.92 and 0.90 for mouse and human data, respectively; for 3× the results are 0.79 and 0.79, respectively; for 4×, the results are 0.64 and 0.70, respectively. The mean error in the tumor mean Ktrans for the mouse and human data at 2× acceleration is 1.8% and −4.2%, respectively; at 3×, 3.6% and −10%, respectively; at 4×, 7.8% and −12%, respectively. These results suggest that CS combined with appropriate reduced acquisitions may be an effective approach to improving image quality in DCE-MRI.
Keywords: compressed sensing, DCE-MRI, kinetic modeling, breast cancer, lung cancer
1. Introduction
Dynamic contrast enhanced magnetic resonance imaging (DCE-MRI) involves the serial acquisition of images before, during, and after the injection of a paramagnetic contrast agent (CA). The CA increases the contrast between different tissues by changing their inherent relaxation times, T1 and/or T2. By collecting serial images each pixel in each image yields a signal intensity time course that can be fit to an appropriate model to estimate physiological parameters such as the volume transfer constant (Ktrans), extravascular extracellular volume fraction (ve), and the plasma volume fraction (vp) (Choyke et al. 2003, Yankeelov et al. 2009). Ktrans and vp, in particular, noninvasively and quantitatively report on tumor vascular status. Consequently, DCE-MRI has successfully been applied to assess vascular characteristics in both pre-clinical and clinical settings (see, e.g., Zwick et al. 2009, Jensen et al. 2010, Lockhart et al. 2010, Mannelli et al. 2010).
However, in order to accurately derive DCE parameters, data must be acquired at both high temporal and spatial resolution as well as with a high signal-to-noise ratio (SNR). High temporal resolution data are required because the rate of change of CA in the tissue and in the feeding vessel must be accurately characterized. Unfortunately, the need to acquire high temporal resolution data limits the ability to probe tumor heterogeneity and scan large sections of tissue at high resolution—primary requirements for clinical adoption of the technique because high spatial resolution data covering large sections of tissue are required for clinical reading and applying, for example, the RECIST (Response Evaluation Criteria in Solid Tumors, Eisenhauer et al. 2009) criteria within clinical trials. Furthermore, the acquisition of high temporal and spatial resolution data compromises the image signal-to-noise ratio and adversely affects the analysis of the voxel signal time courses. In short, the demanding acquisition requirements of DCE-MRI limit its broad use and applicability.
To address these issues, some investigators have explored the use of “keyhole imaging” and “half-scan” techniques (Jones et al. 1993, van Vaals et al. 1993, Chenevert et al. 1995, Dougherty et al. 2007). These terms refer to the spatial frequency domain, or “k-space,” wherein low spatial frequencies are located at the center of the data matrix. Keyhole imaging means that a subset of the full data matrix, located around the low-frequency center (the “keyhole”) is collected with each acquisition. High spatial frequencies are collected less frequently, thus reducing the data collection time on average. The high cadence, low-frequency data are then combined with the high-frequency data from the most recent full-resolution collection to create a composite full resolution image that captures dynamic changes occurring at low frequencies. “Half scan” refers to a technique in which most of one side of k-space, either positive or negative, is omitted and the missing information is estimated from the data of the opposite sign. This technique is widely employed in clinical MRI.
Compressed sensing (CS) MRI is a recent development that may provide image quality gains with fewer drawbacks than other, more established, accelerated acquisition methods. CS is a form of constrained optimization that fills in missing signal data subject to a specified penalty. In CS MRI, omitted Fourier coefficients can be estimated by choosing data that minimize the sparsity of the gradient of the reconstructed image (Lustig et al. 2007). It has already been shown that CS can allow for dramatically accelerated MRI data acquisitions with only a small loss in reconstructed image quality (Lustig et al. 2007). CS MRI has mostly been shown to be beneficial in applications that rely on anatomical image quality (Trzasko et al. 2009, Otazo et al. 2010), but only recently has attention turned to employing CS reconstructions to measure quantitative parameters. This question is particularly relevant in quantitative dynamic MRI studies, where image quality is only a proxy for the accuracy of the derived parameter maps.
Chen et al. (2010) and Wang et al. (2010) have both recently described accelerating breast DCE-MRI studies with constrained reconstruction techniques. Chen et al. used regular Fourier undersampling and halfscan techniques coupled with a gradient-regularized reconstruction to achieve a factor of six reduction in scan time with negligible loss in accuracy of the pharmacokinetic parameters, but no parallel imaging was employed. Wang et al. achieved a factor of ten reduction in scan time by using a combination of random Fourier undersampling and a fully sampled reference image with a constrained reconstruction. Neither of these two techniques employs parallel imaging acceleration, such as sensitivity encoding (SENSE) or generalized autocalibrating partially parallel acquisitions (GRAPPA), that is available with multiple coils are used to acquire data, so the true gains over conventional clinical breast protocols that use parallel imaging on up to 16-channel coils (for breast imaging) and half Fourier techniques are somewhat smaller.
Here, we explore the effects of a Cartesian CS MRI acquisition with no temporal constraints on the accuracy of pharmacokinetic parameters estimated from dynamic mouse and human breast scans. The omission of a temporal data constraint eliminates one possible bias in the quantitative parameters by altering the time-intensity curves for individual voxels. Any remaining bias will be due to purely spatial effects. This approach is straightforward to implement, extremely fast, and is fully compatible with parallel and half-Fourier techniques.
2. Materials and Methods
Our approach has been evaluated on both animal and patient DCE-MRI data, so subsequent sections are divided accordingly.
2.1. Animal Studies
Calu-6 human lung carcinoma cells were grown according to the protocol developed in Wedge et al (2005). A single cell suspension containing 1 × 106 cells suspended in 100 μL of medium were injected subcutaneously on the flank of 10 female fox nu/nu mice (8–10 weeks of age). Tumors were grown for 15 to 20 days to reach a size of approximately 200–250 mm3 before imaging. A 26-gauge jugular catheter was surgically implanted to allow for delivery of a contrast agent. During imaging, the mice were anesthetized using a 2%/98% isoflurane/oxygen mixture and body temperature was maintained via a flow of warm air through the magnet bore. All experimental procedures were reviewed and approved by the Vanderbilt University Institutional Animal Care and Use Committee.
Animal MR imaging was performed using a Varian 9.4T, 21-cm bore scanner (Varian, Inc. Palo Alto, CA) equipped with a 38-mm quadrature volume coil. Pre-contrast T1 maps were obtained using an inversion recovery snapshot FLASH (Fast Low Angle SHot) gradient echo sequence with an adiabatic inversion pulse over nine inversion times (TI) ranging from 20–10,000 ms. Imaging parameters were as follows: TR/TE/α = 12100 ms/3.44 ms/15° and 4 excitations, FOV = 35 mm2, and matrix = 1282 over 15 slices. The DCE-MRI protocol employed a T1-weighted, gradient echo sequence to obtain 40 serial images for each of 15 axial planes in 18 minutes of imaging. The parameters were as follows: TR/TE/α = 100 ms/2.83 ms/25°, NEX = 2, with the same acquisition matrix and FOV as for the T1 map. A 120 μL bolus of 0.1 mmol/kg of gadopentetate dimeglumine, Gd-DTPA, (Magnevist, Wayne, NJ) was delivered over 2.5 seconds with an automated Harvard pump (2.4 mL/min) via the jugular catheter beginning after the acquisition of the fifth temporal dynamic image. A population based arterial input function (AIF), was obtained from the left ventricle in a separate group of animals as previously reported (Loveless et al. 2010).
Data collected for the T1 map were fit using a nonlinear least squares method in Matlab 2008a (The Mathworks, Natick, MA, USA) to
| (1) |
where S0 and S are the signal intensities at baseline and at the inversion time, respectively.
2.2. Patient Studies
Ten patients with locally advanced breast cancer were enrolled in an ongoing clinical trial. The patients provided informed consent, and the study was approved by the ethics committee of the Vanderbilt-Ingram Cancer Center. DCE-MRI data were acquired using a Philips 3T Achieva MR scanner (Philips Healthcare, Best, The Netherlands). A four-channel receive double-breast coil (Invivo, Inc., Gainesville, FL) covering both breasts was used for all imaging. Data for constructing a T1 map were acquired with a 3D gradient echo multi-flip angle approach with TR = 7.9 ms, TE = 1.3 ms, and ten flip angles from 2 to 20 degrees in two degree increments. The acquisition matrix was 192 × 192 × 20 (full-breast) over a sagittal square field of view (22 cm2) with slice thickness of 5 mm, one signal acquisition, and a sensitivity encoding (SENSE) factor of 2 for an acquisition time of just under three minutes. The dynamic scans used identical parameters and a flip angle of 20°. Each 20-slice set was collected in 16.5 seconds at 25 time points for approximately seven minutes of scanning. A catheter placed within an antecubital vein delivered 0.1 mmol/kg of the contrast agent Magnevist over 20 seconds (followed by a saline flush) via a power injector after the acquisition of three baseline dynamic scans for the DCE study.
An individual AIF was obtained from the axillary artery of each patient as previously reported. While details are provided elsewhere (Li et al. 2010), the AIF estimation algorithm is initialized by defining a 5×5 kernel centered on a single, manually selected seed point located within the axillary artery in one slice. In a slice adjacent to the one containing the seed, a 10×10 ROI is defined centered on the voxel corresponding to the seed point location. For each voxel in the ROI, a 5×5 “local window” centered on that voxel is defined and the correlation coefficient (CC) of the signal intensity between the kernel and each local window is calculated. The local window with the maximum CC is considered as a new kernel and the center point of this kernel is assigned as the new seed point to be used for the next slice. The procedure is repeated for all slices. All voxels yielding a local window that return a CC >0.7 are then used to generate an AIF if they satisfy the following criteria: 1) the Cp maximum must occur within the first three time points post contrast injection; 2) the Cp maximum is 20 times greater than the standard deviation of Cp of the first three frames; and 3) the mean Cp of the last 10 frames is < 40% of the maximum Cp. Similar filters have been used previously (Chen et al., Med Image Comput Comput Assist Interv Int Conf Med Image Comput Comput Assist Interv. 2008;11:594–601. Mouridsen et al., Magn Reson Med. 2006;55:524–31.).
Data collected for the T1 map were again fit using a nonlinear least squares method to (2):
| (2) |
where α is the flip angle, S0 is a constant describing the scanner gain and proton density, and we have assumed that TE ≪ T2*.
2.3. Compressed Sensing Reconstruction
Compressed sensing (Candes 2006, Donoho 2006) can accelerate MRI data acquisitions by sampling fewer spatial frequencies than satisfying the Nyquist criterion would require. The missing data are then iteratively reconstructed with a regularized least squares algorithm in which, typically, the gradient of the reconstructed image serves as a regularizer. Specifically, the reconstructed image u in compressed sensing MRI is usually a solution to the unconstrained minimization problem
| (3) |
where S is a sparsity transform, such as a wavelet decomposition or the gradient, F is the partial Fourier measurement operator, d are the scanner data collected, and λ controls the relative weighting of the two norm terms, defined as and .
In a Cartesian CS MRI acquisition scheme, the ability to undersample the Fourier domain is restricted to randomly omitting 1-D phase encodes, corresponding to entire rows from the Fourier matrix in 2-D or 3-D acqusitions. In the reconstructions presented here, the lowest spatial frequencies are fully sampled, while at higher frequencies the sampling density of phase encodes follows k−1, where k is spatial frequency. This nonuniform distribution of spatial frequency samples is designed to more thoroughly sample low spatial frequencies, which increases signal and contrast, with a small loss in accuracy of high frequency features. During the reconstruction, missing phase encode data are chosen to minimize the isotropic gradient of the image, defined as
| (4) |
with boundaries treated periodically and each slice treated independently. It is important to note that this transform does not have a simple relationship to the desired pharmacokinetic parameters, so it is not clear that a time independent CS MRI reconstruction will retain the necessary dynamic information to retrieve accurate DCE parameters. Additionally, our DCE-MRI data sets are relatively low resolution (1282 for mouse, 1922 for human), and the image is consequently “less sparse” in the gradient domain than high-resolution data. Each phase encode thus contains a larger fraction of the total image information, and pushing the acquisition to large undersample factors can be difficult.
The CS reconstruction here was performed using a non-convex, total variation (TV) regularized Cartesian split Bregman algorithm (Goldstein & Osher, 2009). The non-convexity comes from the use of the L1/2 quasi-norm instead of the typical L1 norm of the gradient according to the prescription of Chartrand (2007). The optimization problem as implemented here then becomes
| (5) |
where .
As shown in Chartrand et al., this modification to the basic CS MRI reconstruction algorithm improves image quality and reduces artifacts. With a non-convex optimization problem, however, the reconstructed image is no longer assured to be a global optimum, but for DCE-MRI a solution that maintains fidelity of the derived pharmacokinetic parameters is sufficient. Additionally, we choose λ = 20 to reduce the smoothing that occurs when minimizing the gradient representation, which tends to correlate voxel intensities in space and decorrelate them in time. For simplicity, the effects of a temporal gradient constraint were not explored here.
Fully sampled DCE and T1 multiflip data sets were retrospectively undersampled by discarding random phase encode data consistent with a randomly generated CS MRI acquisition scheme. Undersampling factors of 2×, 3×, and 4× were chosen, corresponding to retention of 50%, 33%, and 25% of the original data. Missing phase encode rows were zero-filled. All slices and time points were sampled with the same subset of phase encodes; this is equivalent to using the same in-plane sampling scheme throughout the scan for all slices and all dynamics. Undersampling of the mouse T1-weighted inversion recovery data was not explored due to limited potential gains. This particular inversion recovery sequence was single-shot, so only a small fraction of the time is spent reading data; most of the sequence duration is spent idle while waiting for longitudinal magnetization to recover. Reducing the number of phase encodes acquired can reduce only the readout time.
2.4. DCE-MRI Analysis
In order to perform quantitative DCE-MRI data analysis the longitudinal relaxation time, T1, must be related to the concentration of CA in the tissue, Ct (t). Usually, a linear relationship between the two quantities is assumed:
| (6) |
where R10 is the R1 value of the tissue before CA administration, and r1 is the relaxivity of the contrast agent. In actual DCE-MRI experiments the Ct time course cannot be directly measured and thus (6) needs to be expressed in terms of the quantities that are actually measurable in an MRI experiment: the relaxation rate constants. Towards this end, the measured T1-weighted signal intensity time courses are used, in conjunction with the pre-contrast T1 map, to estimate at T1 time course. More specifically, Eq. (6) is substituted into Eq. (2) so that the measured signal intensity can be related to Ct which is, in turn, describe by Eq. (7):
| (7) |
where Ktrans is the CA extravasation rate constant, ve is the extravascular extracellular volume fraction, vp is the plasma fraction, and Cp (t) is the concentration of CA in blood plasma, the arterial input function (AIF). Eq. (7) represents a commonly used extension of the well-known Kety relationship (Kety 1951). To derive tissue parameters, the AIF is first discretized, and then Eq. (7) is fit to the tissue curves using nonlinear least squares. For simplicity, the same AIF was used for both the fully sampled and the CS reconstructions. Since characterizing the individual AIF in both patients and pre-clinical studies is extraordinarily difficult, population-based AIFs are frequently employed in DCE-MRI studies and that is the approach we take here. The overall goal of this work is to see how undersampling in Fourier space combined with a CS reconstruction affects the values of Ktrans, ve, and vp when compared to those derived from a fully sampled data set.
2.5. Statistical Analysis
Concordance correlation coefficients (CCCs; Lin 1989) were used as the primary measure of agreement between sets of DCE parameters derived from the fully sampled and undersampled data. CCCs measure the extent to which the voxel intensities in the CS reconstruction are identical to the voxel intensities in the fully sampled image.
The means of Ktrans, ve, and vp across the tumor were also compared as relative differences, as this is what is most commonly reported in clinical studies. We define the “error in tumor mean” (EITM) for the parameters as
| (8) |
| (9) |
and
| (10) |
where the angle brackets denote the average over tumor voxels. This notation will be used henceforth when referred to the relative means of parameters across the tumor.
3. Results
3.1. Animal Studies
Figure 1 shows a representative reconstructed slice for the fully sampled data (upper left) set, 2× (upper right), 3× (lower left), and 4× (lower right) CS reconstructions for one representative animal data set. An example time-intensity curve for a tumor voxel is shown for the human data (figure 4). The color overlay is the Ktrans value at each voxel in the tumor; observe how this particular tumor displays a well-perfused rim surrounding a more centrally located necrotic region. The images show qualitative similarity, though the 3× data set (lower left) does begin to overestimate the Ktrans values in the central, necrotic region. To better characterize the voxel-level and tumor-wide differences between the fully sampled data and the CS accelerated data, we next examine concordance correlation coefficients and compare tumor mean parameters.
Figure 1.
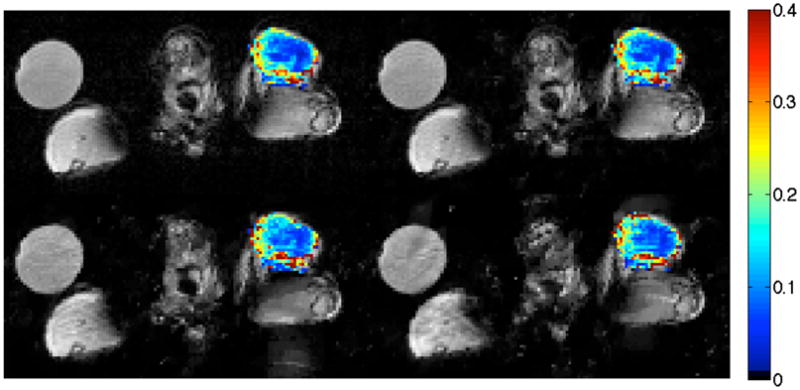
Example of reconstructed tumor Ktrans maps for one mouse data set. Images are an axial view of the fully sampled data (upper left), 2× CS (upper right), 3× CS (lower left), and 4× CS (lower right). The color overlay is the Ktrans value at each voxel in the tumor. This hind-leg tumor displays a well-perfused rim surrounding a more centrally located necrotic region, a feature well reproduced in both CS reconstructions. The circular object at upper left is a water vial.
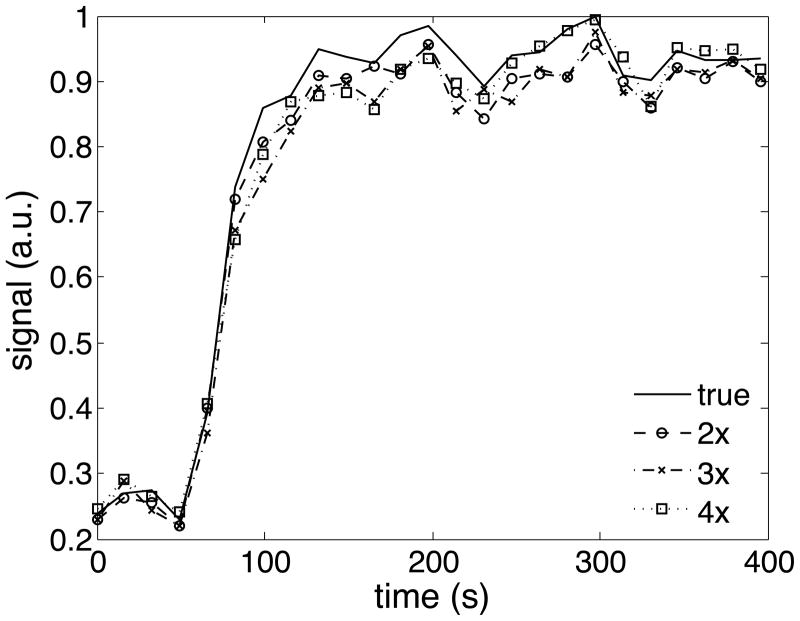
Figure 4.
Example of a time-intensity curve for a tumor voxel for one human breast data set. The CS accelerated curves show a slight underestimation of the contrast peak.
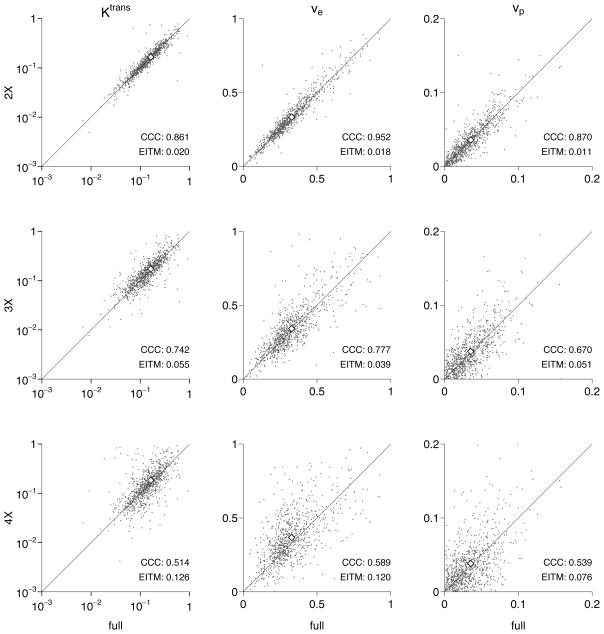
Figure 2 shows the comparison between the kinetic parameters estimated by the fully sampled data and those for the CS-accelerated reconstructions for a typical mouse. “Typical” is defined here as a mouse having CCC values for Ktrans and ve for the 2×-accelerated data set nearest the median values for the population. It is clear that, even for the 4× accelerated reconstruction, the mean parameter values (shown by open diamonds) are still quite close to those calculated for the fully sampled data despite the large scatter in the individual voxel values. In the lower right of each panel of the figure, the CCC and EITM value for that particular mouse and CS reconstruction are shown.
Figure 2.
Comparison of derived pharmacokinetic parameters for a typical mouse data set, as defined by the mean CCC(Ktrans) and CCC(ve) at 2× acceleration. Parameter means are shown as open diamonds, and the diagonal line shows equality.
Table 1 lists the CCCs for all mice for all three CS reconstructions. We find that an undersampling of 2× reproduces both Ktrans, ve, and vp with high fidelity, even on a voxel scale; the CCC for Ktrans, hereafter given as CCC(Ktrans), is greater than 0.83, CCC(ve) ≥ 0.89, and CCC(vp) ≥ 0.83 for all mice. At 3× acceleration, the CCC(Ktrans) ≥ 0.61, CCC(ve) ≥ 0.68, and CCC(vp) ≥ 0.54 for all mice. And at 4× acceleration, the CCC(Ktrans) ≥ 0.51, CCC(ve) ≥ 0.45, and CCC(vp) ≥ 0.33 for all mice.
Table 1.
Concordance correlation coefficients for the mouse data. Minimum and maximum values for each parameter are in bold.
| Mouse | 2× | 3× | 4× | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ktrans | ve | vp | Ktrans | ve | vp | Ktrans | ve | vp | |
| 1 | 0.88 | 0.95 | 0.93 | 0.85 | 0.86 | 0.83 | 0.63 | 0.66 | 0.69 |
| 2 | 0.94 | 0.94 | 0.88 | 0.82 | 0.83 | 0.70 | 0.66 | 0.75 | 0.48 |
| 3 | 0.91 | 0.93 | 0.89 | 0.61 | 0.68 | 0.54 | 0.51 | 0.45 | 0.33 |
| 4 | 0.86 | 0.95 | 0.87 | 0.74 | 0.78 | 0.67 | 0.51 | 0.59 | 0.54 |
| 5 | 0.89 | 0.94 | 0.89 | 0.79 | 0.87 | 0.80 | 0.65 | 0.70 | 0.66 |
| 6 | 0.97 | 0.96 | 0.90 | 0.88 | 0.87 | 0.78 | 0.79 | 0.79 | 0.58 |
| 7 | 0.83 | 0.89 | 0.83 | 0.75 | 0.81 | 0.68 | 0.57 | 0.71 | 0.54 |
| 8 | 0.93 | 0.96 | 0.92 | 0.78 | 0.85 | 0.77 | 0.58 | 0.73 | 0.62 |
| 9 | 0.96 | 0.96 | 0.91 | 0.79 | 0.85 | 0.70 | 0.69 | 0.77 | 0.55 |
| 10 | 0.97 | 0.97 | 0.85 | 0.88 | 0.89 | 0.66 | 0.77 | 0.78 | 0.39 |
Table 2 lists the EITMs for all ten mice and all three CS reconstructions. For 2× acceleration, the EITM(Ktrans) ≤ 4.1%, EITM(ve) ≤ 4.0%, and EITM(vp) ≤ 5.2%. For 3× acceleration, EITM(Ktrans) ≤ 10%, EITM(ve) ≤ 10%, and EITM(vp) ≤ 18%. For 4× acceleration, EITM(Ktrans) ≤ 13%, EITM(ve) ≤ 26%, and EITM(vp) ≤ 48%.
Table 2.
Error in the tumor mean (EITM) in % for the mouse data. Absolute maximums for each parameter are in bold.
| Mouse | 2× | 3× | 4× | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ktrans | ve | vp | Ktrans | ve | vp | Ktrans | ve | vp | |
| 1 | 3.0 | 2.3 | 0.55 | −1.3 | 3.4 | −0.052 | 9.9 | 13 | 17 |
| 2 | 0.14 | 2.4 | 5.2 | 4.4 | 5.1 | 4.3 | 2.0 | 6.7 | 12 |
| 3 | 2.6 | 3.1 | 3.3 | 10 | 10 | 18 | 8.9 | 26 | 48 |
| 4 | 2.0 | 1.8 | 1.1 | 5.5 | 3.9 | 5.1 | 13 | 12 | 7.6 |
| 5 | 4.1 | 1.6 | 2.1 | 2.2 | 5.1 | 7.1 | 4.8 | 2.7 | 16 |
| 6 | 3.0 | 0.59 | 3.4 | 8.4 | 1.9 | 2.0 | 9.8 | 1.7 | 14 |
| 7 | 1.1 | 2.1 | 0.72 | 0.79 | 3.9 | 3.5 | 0.19 | 6.3 | 5.3 |
| 8 | −0.92 | 1.5 | 2.3 | 0.20 | 3.8 | 8.6 | 9.2 | 3.5 | 4.0 |
| 9 | 3.2 | 4.0 | 3.3 | 2.3 | 8.3 | 9.0 | 12 | 14 | 16 |
| 10 | −0.36 | 0.47 | 3.9 | 2.6 | 2.4 | 0.62 | 8.1 | 8.0 | 19 |
A global trend in the EITM is clear in table 2: almost every EITM is positive. This means that the parameters derived from the accelerated scan are being systematically overestimated by, roughly, a few percent. For 2× acceleration, the mean EITMs of Ktrans, ve, and vp across all mice are 1.8%, 2.0%, and 2.6%, respectively, while the standard deviations in the EITMs are 1.7, 1.1, and 1.5, respectively. The mean EITMs are thus comparable to the standard deviations, so one could still argue that the primary effect of CS acceleration at the 2× level is to add a noise-like component to the derived parameters.
3.2. Human Studies
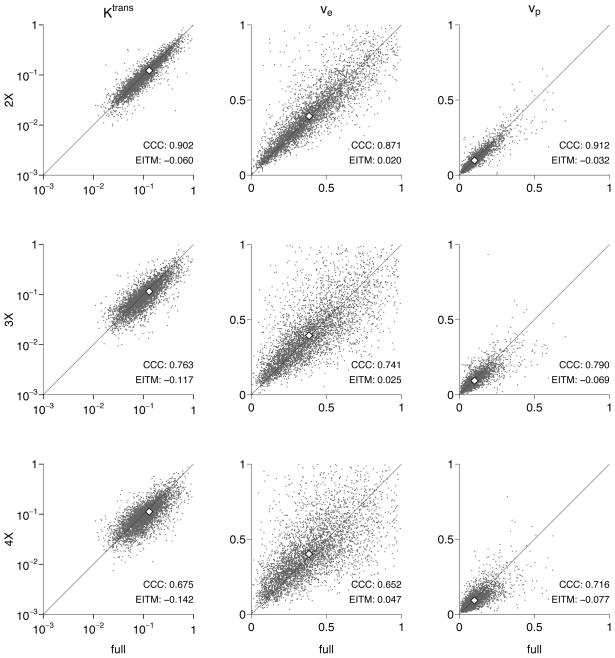
A slice of the human breast data with the Ktrans map superimposed is shown in figure 3, an example time-intensity curve for a tumor voxel is shown in figure 4, and a typical human breast parameter set is shown in figure 5. Once again, typical is defined as a set having CCC(Ktrans) and CCC(ve) nearest to the population mean for the 2× accelerated reconstruction. Again, the calculated pharmacokinetic parameters for the human data are faithfully reproduced at 2× acceleration. Tables 3 and 4 show the CCCs and EITMs for all ten patients and all three CS reconstructions.
Figure 3.
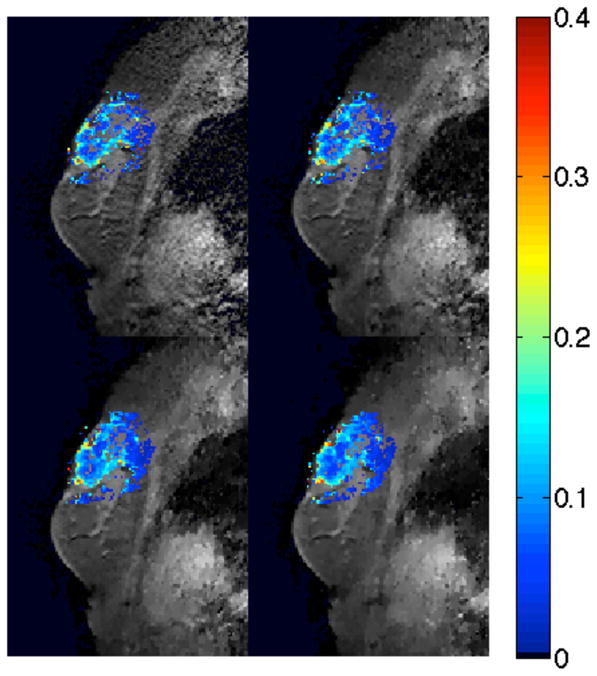
Example of reconstructed tumor Ktrans maps for one human breast data set. Images are a sagittal view of the fully sampled data (upper left), 2× CS (upper right), 3× CS (lower left), and 4× CS (lower right). The color overlay is the Ktrans value at each voxel in the tumor.
Figure 5.
Comparison of derived pharmacokinetic parameters for a typical human data set, as defined by the mean CCC(Ktrans) and CCC(ve) at 2× acceleration. Parameter means are shown as open diamonds, and the diagonal line shows equality.
Table 3.
Concordance correlation coefficients for the human data. Maximum and minimum values for each parameter are in bold.
| Patient | 2× | 3× | 4× | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ktrans | ve | vp | Ktrans | ve | vp | Ktrans | ve | vp | |
| 1 | 0.89 | 0.92 | 0.86 | 0.67 | 0.71 | 0.68 | 0.54 | 0.57 | 0.53 |
| 2 | 0.95 | 0.95 | 0.96 | 0.88 | 0.88 | 0.89 | 0.83 | 0.87 | 0.85 |
| 3 | 0.90 | 0.92 | 0.93 | 0.78 | 0.81 | 0.81 | 0.70 | 0.71 | 0.72 |
| 4 | 0.97 | 0.94 | 0.98 | 0.91 | 0.83 | 0.92 | 0.84 | 0.77 | 0.84 |
| 5 | 0.86 | 0.91 | 0.95 | 0.80 | 0.79 | 0.82 | 0.67 | 0.67 | 0.68 |
| 6 | 0.82 | 0.86 | 0.68 | 0.75 | 0.73 | 0.58 | 0.55 | 0.71 | 0.50 |
| 7 | 0.94 | 0.92 | 0.96 | 0.85 | 0.82 | 0.84 | 0.80 | 0.77 | 0.85 |
| 8 | 0.90 | 0.87 | 0.91 | 0.76 | 0.74 | 0.79 | 0.68 | 0.65 | 0.72 |
| 9 | 0.84 | 0.86 | 0.92 | 0.72 | 0.71 | 0.80 | 0.66 | 0.58 | 0.74 |
| 10 | 0.92 | 0.84 | 0.93 | 0.80 | 0.66 | 0.82 | 0.74 | 0.58 | 0.77 |
Table 4.
Errors in the tumor mean (EITM) in % for the human data. Absolute maximums for each parameter are in bold.
| Patient | 2× | 3× | 4× | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ktrans | ve | vp | Ktrans | ve | vp | Ktrans | ve | vp | |
| 1 | −6.6 | −1.6 | −6.2 | −18 | −4.3 | −14 | −21 | −4.7 | −15 |
| 2 | −0.2 | 1.1 | −0.6 | −6.7 | −1.2 | −5.7 | −9.2 | −2.6 | −6.9 |
| 3 | −3.8 | 1.6 | −1.9 | −8.8 | 3.3 | −5.8 | −9.4 | 5.4 | −4.7 |
| 4 | −0.9 | 0.4 | −0.4 | −3.1 | 0.1 | −1.7 | −3.1 | −0.8 | −3.3 |
| 5 | −4.0 | 2.3 | −4.2 | −12 | 7.3 | −11 | −14 | 8.7 | −16 |
| 6 | −6.2 | −3.3 | −2.9 | −9.7 | −9.2 | −8.8 | −12 | −12 | −12 |
| 7 | −4.1 | −0.8 | −1.8 | −9.8 | −4.3 | −7.3 | −8.9 | −1.8 | −7.8 |
| 8 | −6.0 | 2.0 | −3.2 | −12 | 2.5 | −6.9 | −14 | 4.7 | −7.7 |
| 9 | −6.0 | 3.9 | −3.3 | −12 | 7.5 | −8.5 | −15 | 9.9 | −10 |
| 10 | −4.0 | 7.4 | −1.1 | −9.6 | 11 | −6.8 | −9.1 | 12 | −8.2 |
Across all patients, at 2× acceleration, CCC(Ktrans) ≥ 0.82, CCC(ve) ≥ 0.84, and CCC(vp) ≥ 0.68; and EITM(Ktrans) ≤ 6.6%, EITM(ve) ≤ 7.4%, and EITM(vp) ≤ 6.2%. At 3×, the agreement declines but is still quite good, with CCC(Ktrans) ≥ 0.67, CCC(ve) ≥ 0.66, and CCC(vp) ≥ 0.58; and EITM(Ktrans) ≤ 18%, EITM(ve) ≤ 11%, and EITM(vp) ≤ 14%. Finally, at 4×, CCC(Ktrans) ≥ 0.54, CCC(ve) ≥ 0.57, and CCC(vp) ≥ 0.50, and EITM(Ktrans) ≤ 21%, EITM(ve) ≤ 12%, and EITM(vp) ≤ 16%.
The EITMs in table 4 tend to be negative, suggesting a systematic underestimation. The fact that the systematic effect for the human data is opposite to that for the mouse data suggests that the systematic effect itself may be random and may be of either sign. We suspect this is due to some property of the random Fourier sampling pattern, but the search space of possible sampling patterns is so large that exploring the effect of the pattern on the data is beyond the scope of this effort. We instead have focused here on the variability across patients and animals for a range of CS accelerations.
4. Discussion
For both the human and animal studies, we find that very little uncertainty in Ktrans, ve, and vp is introduced by undersampling in the phase encode direction by a factor of two. Larger accelerations cause a greater uncertainty in the true pharmacokinetic parameters, but the accuracy nevertheless may be sufficient for some applications. For example, if the expected change in parameters due to an administered drug is expected to be much larger than the EITM for 3×, then the ability to increase SNR by averaging three acquisitions could potentially produce less statistical uncertainty. Finally, we note that for data acquired at higher spatial resolution in the phase encode direction, parameter agreement should theoretically improve for a given acceleration factor, since one can easily show that the sparsity of the gradient of an anatomical image typically increases with increasing spatial resolution. This means that 3× or even 4× could be viable with in-plane acquisitions of 2562 and higher and no change in the CS reconstruction algorithm.
It is heartening to realize that, even though in the 4× reconstructions a majority of the Fourier data has been discarded, the mean pharmacokinetic parameters for only one mouse and one human fell outside 20% of the true values. While this example may be a bit extreme for practical use, it clearly demonstrates the potential of a simple spatial gradient constraint to retrieve accurate dynamic information. Furthermore, these results have been obtained using a very simple simulated CS MRI acquisition, with a fixed phase encode scheme and TV regularization being performed in-plane only, with no regard to voxel properties across slices or in time.
We have achieved significant acceleration of the DCE-MRI protocol with negligible loss in fidelity of derived pharmacokinetic parameters using a simple Cartesian CS MRI scheme with undersampling in the phase encode direction and a reconstruction regularized by the 2-D in-plane gradient only, so improving on these results should be straightforward. The basic CS MRI reconstruction problem can be easily adapted to this particular application to improve the fidelity of the parameters derived from the accelerated scan. For example, the gradient transformation (4) can be extended to the three dimensions with
| (11) |
where the index k could refer either to the time or slice dimensions. Extending the gradient to four or more dimensions is done similarly. The addition of an extra dimension, for example, for smoothing voxel intensities over time and encouraging slow variations over fast ones should help retain the slow contrast enhancement curve and remove noise. Model-based methods could also enforce consistency of the collected Fourier data while penalizing some property of the derived pharmacokinetic parameters. This approach could eschew gradient-based constraints entirely.
A final note about this analysis is that it does not fairly compare CS MRI techniques with a conventional scan. Even the smallest CS acceleration presented here would allow for twice as many acquisitions to be performed in the amount of time that the fully sampled scan would require. This extra data, already shown here to contain accurate information about the pharmacokinetic parameters, could be used to derive more accurate parameters than the full scan, either by signal averaging to increase SNR or by producing better fits to equation (7) by having more time points at similar SNR. This comparison is not possible with our retrospective analysis, but the retrospective analysis used here allowed us to examine the effects of CS on larger data sets that require long periods of time to collect.
In summary, we have demonstrated that a moderate level of scan acceleration through the use of basic compressed sensing MRI techniques can allow for accurate estimation of pharmacokinetic parameters in DCE-MRI. This introduces an opportunity to increase spatial or temporal resolution or SNR of both animal and human DCE-MRI studies with little penalty to the accuracy of derived pharmacokinetic parameters.
Acknowledgments
We thank the National Institutes of Health for funding through NCI R01CA138599, R01CA129961, NIBIB T32 EB001628, NCI 1U01CA142565, and NCI P30 CA68485.
References
- Candes E. Compressive Sampling. Proc. Intl. Congress Math; Madrid, Spain. 2006. [Google Scholar]
- Chartrand R. Exact reconstruction of sparse signals via nonconvex minimization. IEEE Sig Proc Lett. 2007;14:707–10. [Google Scholar]
- Chen L, Schabel MC, DiBella EVR. Reconstruction of dynamic contrast enhanced magnetic resonance imaging of the breast with temporal constraints. Mag Reson Imag. 2010;28:637–45. doi: 10.1016/j.mri.2010.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chenevert TL, Helvie MA, Aisen AM, Francis IR, Adler DD, Roubidoux MA, Londy FJ. Dynamic three-dimensional imaging with partial k-space sampling: initial application for gadolinium-enhanced rate characterization of breast lesions. Radiology. 1995;196:135–42. doi: 10.1148/radiology.196.1.7784556. [DOI] [PubMed] [Google Scholar]
- Choyke PL, Dwyer AJ, Knopp MV. Functional tumor imaging with dynamic contrast-enhanced magnetic resonance imaging. J Magn Reson Imaging. 2003;17:509–20. doi: 10.1002/jmri.10304. [DOI] [PubMed] [Google Scholar]
- Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006;52:1289–1306. [Google Scholar]
- Dougherty L, Isaac G, Rosen MA, Nunes LW, Moate PJ, Boston RC, Schnall MD, Song HK. High frame-rate simultaneous bilateral breast DCE-MRI. Magn Reson Med. 2007;57:220–5. doi: 10.1002/mrm.21114. [DOI] [PubMed] [Google Scholar]
- Eisenhauer EA, et al. New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1) Eur J Cancer. 2009;45:228–47. doi: 10.1016/j.ejca.2008.10.026. [DOI] [PubMed] [Google Scholar]
- Goldstein T, Osher S. The split Bregman method for L1 regularized problems. SIAM J Imag Sci. 2009;2:323–43. [Google Scholar]
- Jensen LR, Huuse EM, Bathen TF, Goa PE, Bofin AM, Pedersen TB, Lundgren S, Gribbestad IS. Assessment of early docetaxel response in an experimental model of human breast cancer using DCE-MRI, ex vivo HR MAS, and in vivo 1H MRS. NMR Biomed. 2010;23:56–65. doi: 10.1002/nbm.1426. [DOI] [PubMed] [Google Scholar]
- Jones RA, Haraldseth O, Muller TB, Rinck PA, Øksendal AN. K-space substitution: a novel dynamic imaging technique. Magn Reson Med. 1993;29:830–4. doi: 10.1002/mrm.1910290618. [DOI] [PubMed] [Google Scholar]
- Jung H, Ye JC. Performance evalution of accelerated functional MRI acquisition using compressed sensing. Proc IEEE Int Symp Biomed Imag. 2009:702–5. [Google Scholar]
- Kety SS. Peripheral blood flow measurement. Pharmacol Rev. 1951;3:1–41. [PubMed] [Google Scholar]
- Li X, Welch EB, Chakravarthy AB, Mayer I, Kelley M, Meszoely I, Means-Powell J, Gore JC, Yankeelov TE. A semi-automated method for obtaining the arterial input function in dynamic breast data. Proc Intl Soc Mag Reson Med (ISMRM) 2010:2729. [Google Scholar]
- Lin LI-K. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989;45:255–68. [PubMed] [Google Scholar]
- Lockhart AC, et al. Phase I study of intravenous vascular endothelial growth factor trap, aflibercept, in patients with advanced solid tumors. J Clin Oncol. 2010;28:207–14. doi: 10.1200/JCO.2009.22.9237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loveless ME, Halliday J, Liess C, Xu L, Dortch R, Whisenant J, Waterton JC, Gore JC, Yankee-lov TE. A quantitative comparison of the influence of individual versus population-derived vascular input functions on DCE-MRI in small animals. Magnetic Resonance in Medicine. 2010 doi: 10.1002/mrm.22988. 2011. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Mag Reson Med. 2007;58:1182–95. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- Mannelli L, et al. Evaluation of nonenhancing tumor fraction assessed by dynamic contrast-enhanced MRI subtraction as a predictor of decrease in tumor volume in response to chemoradiotherapy in advanced cervical cancer. AJR Am J Roentgenol. 2010;195:524–47. doi: 10.2214/AJR.09.3437. [DOI] [PubMed] [Google Scholar]
- Otazo R, Kim D, Axel L, Sodickson D. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med. 2010;64:767–76. doi: 10.1002/mrm.22463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trzasko J, Haider C, Manduca A. Practical nonconvex compressive sensing reconstruction of highly-accelerated 3D paralllel MR angiograms. Proc IEEE Int Symp Biomed Imag. 2009:1349. [Google Scholar]
- Van Vaals JJ, Brummer ME, Dixon WT, Tuithof HH, Engels H, Nelson RC, Gerety BM, Chezmar JL, den Boer JA. “Keyhole” method for accelerating imaging of contrast agent uptake. J Magn Reson Imag. 1993;3:671–75. doi: 10.1002/jmri.1880030419. [DOI] [PubMed] [Google Scholar]
- Wang H, et al. Feasibility of high temporal resolution breast DCE-MRI using compressed sensing theory. Med Phys. 2010;37:4971–81. doi: 10.1118/1.3483094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedge SR, et al. AZD2171: a highly potent, orally bioavailable, vascular endothelial growth factor receptor-2 tyrosine kinase inhibitor for the treatment of cancer. Cancer Res. 2005;65:4389–400. doi: 10.1158/0008-5472.CAN-04-4409. [DOI] [PubMed] [Google Scholar]
- Yankeelov TE, Gore JC. Dynamic contrast enhanced magnetic resonance imaging in oncology: Theory, data acquisition, analysis, and examples. Curr Med Imag Rev. 2009;3:91–107. doi: 10.2174/157340507780619179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwick S, et al. Assessment of vascular remodeling under antiangiogenic therapy using DCE-MRI and vessel size imaging. J Magn Reson Imag. 2009;29:1125–33. doi: 10.1002/jmri.21710. [DOI] [PubMed] [Google Scholar]